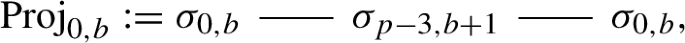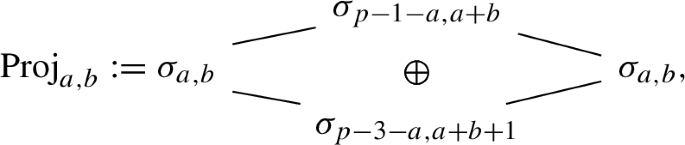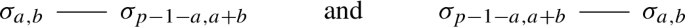Abstract
We formulate a local analogue of the ghost conjecture of Bergdall and Pollack, which essentially relies purely on the representation theory of \({{\,\textrm{GL}\,}}_2({\mathbb {Q}}_p)\). We further study the combinatorial properties of the ghost series as well as its Newton polygon, in particular, giving a characterization of the vertices of the Newton polygon and proving an integrality result of the slopes. In a forthcoming sequel, we will prove this local ghost conjecture under some mild hypothesis and give arithmetic applications.



Similar content being viewed by others
References
Andreatta, F., Iovita, A., Pilloni, V.: Le halo spectral. Ann. Sci. Éc. Norm. Supér. (4) 51(3), 603–655 (2018)
Barthel, L., Livné, R.: Irreducible modular representations of \({\rm GL}_2\) of a local field. Duke Math. J. 75(2), 261–292 (1994)
Bergdall, J.: Upper bounds for constant slope \(p\)-adic families of modular forms. Selecta Math. (N.S.) 25(4), 59 (2019)
Bergdall, J., Levin, B.: Reductions of some two-dimensional crystalline representations via Kisin modules. Int. Math. Res. Not. IMRN 2022(4), 3170–3197 (2022)
Bergdall, J., Pollack, R.: Slopes of modular forms and the ghost conjecture. Int. Math. Res. Not. IMRN 2019(4), 1125–1244 (2019)
Bergdall, J., Pollack, R.: Slopes of modular forms and the ghost conjecture, II. Trans. Am. Math. Soc. 372(1), 357–388 (2019)
Bergdall, J., Pollack, R.: Slopes of modular forms and reducible Galois representations: an oversight in the ghost conjecture. Proc. Am. Math. Soc. Ser. B 9, 432–444 (2022)
Berger, L., Li, H., Zhu, J.: Construction of some families of \(2\)-dimensional crystalline representations. Math. Ann. 329(2), 365–377 (2004)
Bhattacharya, S., Ghate, E.: Reductions of Galois representations for slopes in \((1,2) \). Doc. Math. 20, 943–987 (2015)
Bhattacharya, S., Ghate, E., Rozensztajn, S.: Reduction of Galois representations of slope \(1\). J. Algebra 508, 98–156 (2018)
Breuil, C: Representations of Galois and of GL\(_2\) in characteristic \(p\). Cours à l’université de Columbia, automne 2007, https://www.imo.universite-paris-saclay.fr/~christophe.breuil/PUBLICATIONS/New-York.pdf (2007)
Breuil, C.: Sur quelques représentations modulaires et \(p\)-adiques de \({\rm GL}_2({{\mathbb{Q} }}_p)\). II. J. Inst. Math. Jussieu 2(1), 23–58 (2003)
Breuil, C., Hellmann, E., Schraen, B.: Une interprétation modulaire de la variété trianguline. Math. Ann. 367(3–4), 1587–1645 (2017)
Breuil, C., Paškūnas, V.: Towards a modulo \(p\) Langlands correspondence for \({\rm GL}_2\). Mem. Am. Math. Soc. 216(2016) (2012)
Buzzard, K.: On \(p\)-adic families of automorphic forms. In: Modular Curves and Abelian Varieties. Progr. Math., vol. 224, pp. 23–44. Birkhäuser, Basel (2004)
Buzzard, K.: Questions about slopes of modular forms. Astérisque 298, 1–15 (2005)
Buzzard, K.: Eigenvarieties. In: L-functions and Galois Representations. London Math. Soc. Lecture Note Ser., vol. 320, pp. 59–120. Cambridge University Press, Cambridge (2007)
Buzzard, K., Calegari, F.: A counterexample to the Gouvêa–Mazur conjecture. C. R. Math. Acad. Sci. Paris 338(10), 751–753 (2004)
Buzzard, K., Gee, T.: Explicit reduction modulo \(p\) of certain \(2\)-dimensional crystalline representations, II. Bull. Lond. Math. Soc. 45(4), 779–788 (2013)
Buzzard, K., Gee, T.: Slopes of modular forms. In: Families of Automorphic Forms and the Trace Formula, Simons Symposia, pp. 93–109. Springer, Berlin (2016)
Buzzard, K., Kilford, L.: The 2-adic eigencurve at the boundary of weight space. Compos. Math. 141(3), 605–619 (2005)
Calegari, F., Emerton, M.: Completed cohomology—a survey. In: Non-abelian Fundamental Groups and Iwasawa Theory, London Math. Soc. Lecture Note Ser., vol. 393, pp. 239–257. Cambridge University Press, Cambridge (2012)
Caraiani, A., Emerton, M., Gee, T., Geraghty, D., Paškūnas, V., Shin, S.W.: Patching and the \(p\)-adic local Langlands correspondence. Camb. J. Math. 4(2), 197–287 (2016)
Clay, L.: Some conjectures about the slopes of modular forms, Ph.D. thesis. Northwestern University, Evanston, IL (2005)
Coleman, R., Mazur, B.: The eigencurve. In: Galois Representations in Arithmetic Algebraic Geometry (Durham, 1996). London Math. Soc. Lecture Note Ser., vol. 254, pp. 1–113. Cambridge University Press, Cambridge (1998)
Colmez, P.: Fonctions d’une variable \(p\)-adique. Astérisque 330, 13–59 (2010)
Davis, C., Wan, D., **ao, L.: Newton slopes for Artin–Schreier–Witt towers. Math. Ann. 364(3–4), 1451–1468 (2016)
Emerton, M.: \(2\)-adic modular forms of minimal slope, Ph.D. Thesis. Harvard University, Cambridge, MA (1998)
Emerton, M.: On the interpolation of systems of eigenvalues attached to automorphic Hecke eigenforms. Invent. Math. 164(1), 1–84 (2006)
Emerton, M.: Ordinary parts of admissible representations of \(p\)-adic reductive groups I. Definition and first properties. Astérisque 331, 355–402 (2010)
Emerton, M., Gee, T.: A geometric perspective on the Breuil–Mézard conjecture. J. Inst. Math. Jussieu 13(1), 183–223 (2014)
Fontaine, J.-M., Laffaille, G.: Construction de représentations \(p\)-adiques. Ann. Sci. Éc. Norm. Supér. (4) 15(4), 547–608 (1982)
Ganguli, A., Ghate, E.: Reductions of Galois representations via the mod \(p\) Local Langlands Correspondence. J. Number Theory 147, 250–286 (2015)
Gee, T., Newton, J.: Patching and the completed homology of locally symmetric spaces. J. Inst. Math. Jussieu 21(2), 395–458 (2022)
Gee, T., Kisin, M.: The Breuil–Mézard conjecture for potentially Barsotti–Tate representations. Forum Math. Pi 2, e1 (2014)
Gouvêa, F.: Where the slopes are. J. Ramanujan Math. Soc. 16(1), 75–99 (2001)
Gouvêa, F., Mazur, B.: Families of modular eigenforms. Math. Comput. 58(198), 793–805 (1992)
Jacobs, D.: Slopes of compact Hecke operators, Ph.D. Thesis. Imperial College of Science, Technology and Medicine, London (2004)
Kedlaya, K.: \(p\)-adic Differential Equations, Cambridge Studies in Advanced Mathematics, vol. 125. Cambridge University Press, Cambridge (2010)
Kilford, L.J.P.: On the slopes of the \(U_5\) operator acting on overconvergent modular forms. J. Théor. Nombres Bordeaux 20(1), 165–182 (2008)
Kilford, L.J.P., McMurdy, K.: Slopes of the \(U_7\) operator acting on a space of overconvergent modular forms. LMS J. Comput. Math. 15, 113–139 (2012)
Kisin, M.: The Fontaine–Mazur conjecture for \({\rm GL}_2\). J. Am. Math. Soc. 22(3), 641–690 (2009)
Lazard, M.: Groupes analytiques \(p\)-adiques. Inst. Hautes Études Sci. Publ. Math. 26, 389–603 (1965)
Liu, R., Wan, D., **ao, L.: The eigencurve over the boundary of the weight space. Duke Math. J. 166(9), 1739–1787 (2017)
Loeffler, D.: Spectral expansions of overconvergent modular functions. Int. Math. Res. Not. IMRN 2007(16), Art. ID rnm050 (2007)
Loeffler, D.: Overconvergent algebraic automorphic forms. Proc. Lond. Math. Soc. (3) 102(2), 193–228 (2011)
Newton, J.: Completed cohomology of Shimura curves and a \(p\)-adic Jacquet–Langlands correspondence. Math. Ann. 355(2), 729–763 (2013)
Paškūnas, V.: Coefficient systems and supersingular representations of \(\rm {GL}_2(F)\). Mém. Soc. Math. Fr. (N.S.) (99), vi+84 (2004)
Paškūnas, V.: The image of Colmez’s Montreal functor. Publ. Math. Inst. Hautes Études Sci. 118, 1–191 (2013)
Paškūnas, V.: On the Breuil–Mézard conjecture. Duke Math. J. 164(2), 297–359 (2015)
Pilloni, V.: Overconvergent modular forms. Ann. Inst. Fourier (Grenoble) 63(1), 219–239 (2013)
Reduzzi, D.: Reduction mod \(p\) of cuspidal representations of \({\rm GL}_2({{\mathbb{F} }}_{p^n})\) and symmetric powers. J. Algebra 324(12), 3507–3531 (2010)
Ren, R.: The slope-invariant of local ghost series under direct sum. ar**v:2207.12145 (2022)
Roe, D.: The \(3\)-adic Eigencurve at the boundary of weight space. Int. J. Number Theory 10(7), 1791–1806 (2014)
Schneider, P., Teitelbaum, J.: Banach space representations and Iwasawa theory. Isr. J. Math. 127, 359–380 (2002)
Serre, J.-P.: Galois Cohomology, Springer Monographs in Mathematics. Springer, Berlin (1997)
Wan, D.: Dimension variation of classical and \(p\)-adic modular forms. Invent. Math. 133(2), 449–463 (1998)
Acknowledgements
This paper will not be possible without the great idea from the work of John Bergdall and Robert Pollack [5, 6]. Many proofs are inspired by their numerical evidences. We especially thank them for sharing ideas and insights at an early stage and for many interesting conversations. We thank Matthew Emerton and Yongquan Hu for multiple helpful discussions. We also thank Jiawei An, Christophe Breuil, Keith Conrad, Toby Gee, Bao Le Hung, Álvaro Lozano-Robledo, Vincent Pilloni, and Rufei Ren for their interest in the project and inspiring comments. We thank all the people contributing to the SAGE software, as lots of our argument rely on first testing by a computer simulation. R. Liu is partially supported by the National Natural Science Foundation of China under Agreement No. NSFC-11725101 and the Tencent Foundation. N. Truong is partially supported by L. **ao’s NSF under Grant DMS-1752703. L. **ao is partially supported by Simons Collaboration under Grant #278433, and NSF under Grant DMS-1502147 and DMS-1752703, the Chinese NSF grant NSFC-12071004, Recruitment Program of Global Experts of China, and a grant from the Chinese Ministry of Education. B. Zhao is partially supported by AMS-Simons Travel Grant.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
Ruochuan Liu is an editor for Peking Mathematical Journal and was not involved in the editorial review or the decision to publish this article. All authors declare that there are no competing interests.
Appendices
Appendix A: Recollection of Representation Theory of \({\mathbb {F}}[{{\,\textrm{GL}\,}}_2({\mathbb {F}}_p)]\)
In this appendix, we recall some basic facts on (right) \({\mathbb {F}}\)-representations of \({{\,\textrm{GL}\,}}_2({\mathbb {F}}_p)\). Our main references are [11] and [48] which work with left representations. Our convention will be the corresponding right representation given by transpose.
A.1 Setup
Throughout this appendix, we fix an odd prime number p. We set
The coefficient field will be a finite extension \({\mathbb {F}}\) of \({\mathbb {F}}_p\). Write \(\omega : {\mathbb {F}}_p^\times \rightarrow {\mathbb {F}}^\times \) for the character induced by inclusion. For a character \(\chi _{a,b}:=\omega ^a \times \omega ^b\) and an \({\mathbb {F}}\)-representation V of \({\bar{\textrm{G}}}\), we write \(V(\chi )\) for the subspace of V on which \({\bar{\textrm{T}}}\) acts by \(\chi \).
Let \({\bar{s}}={\big ({\begin{matrix}0&{}1\\ 1&{} 0\end{matrix}} \big )}\) represent the nontrivial element in the Weyl group of \({\bar{\textrm{G}}}\). If \(\chi \) is a character of \({\bar{\textrm{T}}}\), we use \(\chi ^s\) to denote the character defined by
For a pair of non-negative integers (a, b), we use \(\sigma _{a,b}\) to denote the right \({\mathbb {F}}\)-representation \({{\,\textrm{Sym}\,}}^a{\mathbb {F}}^{\oplus 2} \otimes \textrm{det}^b\) of \({\bar{\textrm{G}}}\) (in particular, b is taken modulo \(p-1\)). The right action is the transpose of the left action in [11, 48]; explicitly, it is, realized on the space of homogeneous polynomials of degree a
When \(a \in \{0, \dots , p-1\}\) and \(b \in \{0, \dots , p-2\}\), \(\sigma _{a,b}\) is irreducible. These representations exhaust all irreducible (right) \({\mathbb {F}}\)-representations of \({{\,\textrm{GL}\,}}_2({\mathbb {F}}_p)\), and are called Serre weights. We use \(\textrm{Proj}_{a,b}\) to denote the projective envelope of \(\sigma _{a,b}\) as a (right) \({\mathbb {F}}[{{\,\textrm{GL}\,}}_2({\mathbb {F}}_p)]\)-module.
Lemma A.2
The projective envelope \(\textrm{Proj}_{a,b}\) can be described explicitly as follows.
-
(1)
For any b, \(\textrm{Proj}_{0,b}\) is of dimension p over \({\mathbb {F}}\), and admits a socle filtration
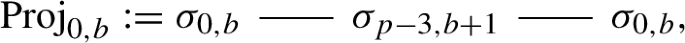
where the \(\sigma _{0,b}\) on the left represents the socle, the \(\sigma _{0,b}\) on the right represents the cosocle, and each line represents a (unique up to isomorphism) nontrivial extension between the two Jordan–Hölder factors.
-
(2)
When \(1 \le a \le p-2\), \(\textrm{Proj}_{a,b}\) is of dimensional 2p over \({\mathbb {F}}\), and admits a socle filtration
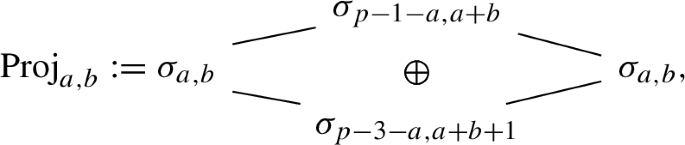
where the \(\sigma _{a,b}\) on the left represents the socle, the \(\sigma _{a,b}\) on the right represents the cosocle, and each line represents a (unique up to isomorphism) nontrivial extension between the two factors. (Here, when \(a=p-2\), the term \(\sigma _{p-3-a, a+b+1}\) is interpreted as 0.)
-
(3)
For any b, the Serre weight \(\sigma _{p-1,b}\) is projective, i.e., \(\textrm{Proj}_{p-1,b} = \sigma _{p-1,b}\). In particular, \(\dim _{\mathbb {F}}\textrm{Proj}_{p-1,b} = p\).
Moreover, in either case \(\textrm{Proj}_{a,b}\) is also the injective envelope of \(\sigma _{a,b}\) as an \({\mathbb {F}}\)-representation of \({{\,\textrm{GL}\,}}_2({\mathbb {F}}_p)\).
Proof
The dimensions of the projective envelopes follow from [48, Lemma 4.1.7]. The socle filtrations of the projective envelopes in (1) and (2) follow from [14, Lemma 3.4, Lemma 3.5]. Part (3) follows from [48, Corollary 4.2.22]. \(\square \)
A.3 Induced Representations
Consider the following character \(\eta \) of \({\bar{\textrm{B}}}\):
For \(k \in {\mathbb {Z}}\), we have an induced representation
which we equip with the right action given by
This is the transpose of the usual left action.
Lemma A.4
-
(1)
For any integer \(1\le k\le p-1\), we have an exact sequence of \({\bar{\textrm{G}}}\)-representations
$$\begin{aligned} 0\rightarrow \sigma _{k,0}\rightarrow {{\,\textrm{Ind}\,}}_{{\bar{\textrm{B}}}}^{{\bar{\textrm{G}}}}\eta ^{k}\rightarrow \sigma _{p-1-k, k}\rightarrow 0.\end{aligned}$$(A.4.1)The above exact sequence splits if and only if \(k=p-1\).
-
(2)
Taking \({\bar{U}}\)-invariants of (A.4.1) gives an exact sequence of \({\bar{\textrm{U}}}\)-invariants
$$\begin{aligned} 0\rightarrow \sigma _{k,0}^{{\bar{\textrm{U}}}}\rightarrow \big ({{\,\textrm{Ind}\,}}_{{\bar{\textrm{B}}}}^{{\bar{\textrm{G}}}}\eta ^{k}\big )^{{\bar{\textrm{U}}}}\rightarrow \sigma _{p-1-k, k}^{{\bar{\textrm{U}}}}\rightarrow 0. \end{aligned}$$ -
(3)
In the description of \(\textrm{Proj}_{a,b}\) of Lemma A.2 (2), the extensions
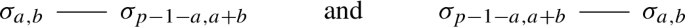
are twists of induced representations \({{\,\textrm{Ind}\,}}_{{\bar{\textrm{B}}}}^{{\bar{\textrm{G}}}}\eta ^{a} \otimes \textrm{det}^b\) and \({{\,\textrm{Ind}\,}}_{{\bar{\textrm{B}}}}^{{\bar{\textrm{G}}}}\eta ^{p-1-a} \otimes \textrm{det}^{a+b}\), respectively.
Proof
(1) follows from [48, Proposition 3.2.2, Lemma 4.1.3]. (2) follows from [48, Lemma 3.1.11]. (3) follows from [48, Lemma 4.1.1]. \(\square \)
Lemma A.5
When \(1 \le a\le p-2\), in terms of the socle filtration in Lemma A.2 (2), the \({\bar{\textrm{U}}}\)-invariant subspace of \(\textrm{Proj}_{a,b}\) is a 2-dimensional subspace given by
where the first term is the \(\sigma _{a,b}\) in the socle. In particular, the actions of \({\bar{\textrm{T}}}\) on these two 1-dimensional subspaces are given by the characters
Proof
Since \(\textrm{Proj}_{a,b}\) is a free module over \({\mathbb {F}}[{\bar{\textrm{U}}}]\), we know that \(\dim (\textrm{Proj}_{a,b})^{{\bar{\textrm{U}}}} = 2\). However, \({{\,\textrm{Ind}\,}}_{{\bar{\textrm{B}}}}^{{\bar{\textrm{G}}}}\eta ^a \otimes \textrm{det}^b\) is a subrepresentation of \(\textrm{Proj}_{a,b}\) by Lemma A.4 (3) and has already 2-dimensional \({\bar{\textrm{U}}}\)-invariants by Lemma A.4 (2). Therefore, we have
\(\square \)
Lemma A.6
For any integer \(k\ge p+1\), we have an exact sequence of \({\bar{\textrm{G}}}\)-represent-ations
Proof
This is [52, Proposition 2.4]. For the convenience of the readers, we recall the definition of the two maps. The map i is given by multiplication by the homogeneous polynomial \( f_p(X,Y)=X^pY-XY^p\) of degree \(p+1\). It is straightforward to check that i is \({\bar{\textrm{G}}}\)-equivariant and injective. The map \(\pi \) comes from adjunction
(Note that both \(\sigma _{k,0}\) and the induced representations are right representations, coming from the transpose of the natural left action.) The vector \(X^k \in \sigma _{k,0}\) is \({\bar{\textrm{U}}}^-\)-invariants and is an eigenvector of \({\bar{\textrm{T}}}\) with eigencharacter \(\eta ^k\). \(\square \)
We conclude the appendix with the following result that is claimed in Remark 2.23(2).
Proposition A.7
Let \({\bar{\rho }} = {\big ({\begin{matrix}\omega _1^{a+b+1}&{}*\ne 0\\ 0&{} \omega _1^b\end{matrix}} \big )}\) with \(1\le a \le p-4\) and \(0 \le b \le p-2\) be as in Definition 2.22 and let \({\widetilde{\textrm{H}}}\) is a primitive \({\mathcal {O}}\llbracket \textrm{K}_p\rrbracket \)-projective augmented module of type \({\bar{\rho }}\). In particular, \({\overline{\textrm{H}}} = {\widetilde{\textrm{H}}} / (\varpi , \textrm{I}_{1+p\textrm{M}_2({\mathbb {Z}}_p)})\) is isomorphic to \(\textrm{Proj}_{a,b}\) as a right \({\mathbb {F}}[{{\,\textrm{GL}\,}}_2({\mathbb {F}}_p)]\)-module. Then, \(\textrm{S}_2^\textrm{Iw}(\omega ^b\times \omega ^{a+b})\) is of rank 1 over \({\mathcal {O}}\), and the \(U_p\)-action on this space is invertible (over \({\mathcal {O}}\)); in particular, the \(U_p\)-slope on this space is zero.
Proof
By Proposition 4.1, \(\textrm{S}_2^\textrm{Iw}(\omega ^b\times \omega ^{a+b})\) is free of rank 1 over \({\mathcal {O}}\).
Consider three characters \(\varepsilon =1\times \omega ^a\), \(\varepsilon '=\omega ^a\times 1\) and \(\psi =\omega ^a\times \omega ^a\). By Corollary 4.4 and Proposition 4.7, we have \(d_{p+1-a}^\textrm{Iw}(\psi )=2\) and \(d_{p+1-a}^\textrm{ur}(\psi )=0\). We choose a set \(\{\tilde{u}_j={\big ({{\begin{matrix}1&{}{}0\\ j&{}{} 1\end{matrix}}} \big )},j=0,\dots , p-1,\tilde{u}_\infty ={\big ({{\begin{matrix}0&{}{}1\\ 1&{}{} 0\end{matrix}}} \big )} \}\) of coset representatives of \(\textrm{Iw}_p\setminus \textrm{K}_p\). The formula
defines a map \(\textrm{pr}:\textrm{S}_{p+1-a}^\textrm{Iw}(\psi )\rightarrow \textrm{S}_{p+1-a}^\textrm{ur}(\psi )\). Here \((\cdot )|_{\tilde{u}_j}\) in the above formula is the right action of \(\textrm{K}_p\) defined in (2.20.1). On the other hand, a straightforward computation gives an equality of operators \(\textrm{AL}_{p+1-a,\psi }\circ \textrm{pr}-\textrm{AL}_{p+1-a,\psi }=U_p\) on \(\textrm{S}_{p+1-a}^\textrm{Iw}(\psi )\). Since \(\textrm{S}_{p+1-a}^\textrm{ur}(\psi )=0\), we actually have \(\textrm{U}_p=-\textrm{AL}_{p+1-a,\psi }\) on \(\textrm{S}_{p+1-a}^\textrm{Iw}(\psi )\). Therefore, by Proposition 3.12, the \(U_p\)-slopes on \(\textrm{S}_{p+1-a}^\textrm{Iw}(\psi )\) are \(\frac{p-1-a}{2}\) with multiplicity 2. By Proposition 3.10, we have \(v_p(c_1^{(\varepsilon ')}(w_{p+1-a}))\ge \frac{p-1-a}{2}>1\). Since \(c_1^{(\varepsilon ')}(w)\in {\mathcal {O}}\llbracket w\rrbracket \) and \(v_p(w_{p+1-a})\ge 1\), \(v_p(w_2)\ge 1\), we have \(v_p(c_1^{(\varepsilon ')}(w_2))\ge 1\). Since \(d_2^\textrm{Iw}(\varepsilon ')=1\), by Proposition 3.10 and Proposition 3.12, we see that the \(U_p\)-slope on \(\textrm{S}_2^\textrm{Iw}(\varepsilon ')\) is exactly 1. Now, by Proposition 3.12, the \(U_p\)-slope on \(\textrm{S}_2^\textrm{Iw}(\varepsilon )\) is 0.
\(\square \)
Appendix B: Errata for [44]
We include some errata for [44] here.
B.1 [44, Proposition 3.4]
This is just a bad convention, the action \(||_{\delta _p}^{[\cdot ]}\) is a right action; however, [44, Proposition 3.4] uses the column vector convention. Ideally, one should swap the indices of \(P_{m,n}(\delta _p)\). This does not create an mathematical error.
B.2 [44, §5.4]
In [44, (5.4.1)], we defined a closed subspace
of the space of continuous functions \({\mathcal {C}}^0({\mathbb {Z}}_p; \Lambda ^{>1/p})\). Unfortunately, as stated, this subspace is not stable under the \({\textbf{M}}_1\)-action. If one insists on having an \({\textbf{M}}_1\)-action, one has to replace the completed direct sum above with direct product, then the rest of the estimate stays valid, except that the space \(S_{\textrm{int}}^{D, \dagger , 1}\) is not a Banach module over \(\Lambda ^{>1/p}\) in the usual sense; it is the \(\Lambda ^{>1/p}\)-linear dual of a Banach module over \(\Lambda ^{>1/p}\). The compactness of \(U_p\) needs be interpreted otherwise.
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Liu, R., Truong, N.X., **ao, L. et al. A Local Analogue of the Ghost Conjecture of Bergdall–Pollack. Peking Math J 7, 247–344 (2024). https://doi.org/10.1007/s42543-023-00063-7
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s42543-023-00063-7
Keywords
- Eigencurves
- Slope of \(U_p\) operators
- Overconvergent modular forms
- Completed cohomology
- Weight space
- Gouvêa’s conjecture
- Gouvêa–Mazur conjecture