1 Introduction

Ultrasound Image Velocimetry (UIV) was previously identified as the most appropriate technique to monitor flow dynamics in natural high-density cohesive sediments, commonly referred to as fluid mud [7]. This makes it a valuable asset for various experimental research topics involving mud, which in turn are relevant to various hydraulic, chemical and mechanical engineering challenges [38]. The most known examples are experiments to assess the rheological properties [11, 22, 37] or sedimentation and consolidation behaviour [4, 12]. More directly applied research involving mud is also being conducted. Examples include the studies by [18, 30, 31] on the interactions between an object and a mud layer through or above which the object moves. These studies contribute to nautical safety by providing insight into the forces acting on a ship when it passes through a channel of which the bottom is formed by fluid mud. Given the global problem of silting ports, such research is of great importance for marine engineering.

Subsequently, the accuracy and limitations of the application of UIV to fluid mud were investigated and evaluated in [9]. Using medical ultrasound imaging equipment, a depth range of several tens of millimetres was achieved. While this is considered sufficient for the application in the setup for settling and rheometer experiments, it is not for the experiments facilitating the aforementioned nautical research. The latter is what prompted this study, aimed at enlarging the depth range of UIV in fluid mud.

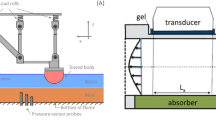
An experimental setup like that of [31] was considered the goal for implementation of UIV (see Fig. 1). His experiments consisted of towing a cylindrical body through a flume filled with mud and with a layer of water on top of a layer of mud. During these experiments, forces and pressures acting on the body were measured, as well as pressure changes in the mud layer at fixed positions in the flume. Before and after each test, a mud sample was taken, of which the rheological properties were determined using a laboratory rheometer [11]. In this way, the measured pressures and forces can be linked to the rheological properties of the mud, generating a database on which Computational Fluid Dynamics (CFD) models can be based. Because pressure measurements require probes, the number of measurement locations is limited. For validation of high-resolution CFD models, a higher count is preferred. Furthermore, due to the high labour intensity of the experiments and the additional uncertainty caused by the imperfect repeatability of mud behaviour [8], repetition experiments whilst relocating the pressure measurement probes, are not considered. Preferably, this deficiency is remedied by applying a whole-flow-field velocimetry technique. Hence the aforementioned research resulting in the recommendation to apply UIV.

Fig. 1
figure 1

A sketch of the experimental setup for studying the interactions between mud, water and a passing body. Apart from the ultrasound transducer (bottom left), this sketch illustrates the experimental setup used by [31]. The addition of the ultrasound transducer illustrates how UIV could be implemented in this setup

Full size image

The concept of UIV first entails generating ultrasound images of the flowing mud, from a stationary reference. These images are then processed with a cross-correlation Particle Image Velocimetry (PIV) algorithm. In this process the images are divided into (interrogation) windows. Windows with corresponding content are searched for in consecutive images and their relative displacement determined. With the known time span between the acquisitions of the images, the velocity of displacement can be determined. The output consists of a field of velocity vectors, where each vector corresponds to an interrogation window. The size of the vector field corresponds to the size of the images, while the vectors indicate the velocity and direction of the flow at different points in that field. For the application of UIV, an ultrasound array transducer is placed in the mud or on the outside of a wall of the recipient containing the mud, like depicted in Fig. 1. Such an array consists of multiple (typically 64 or 128) piezoelectric elements that convert electrical pulses into sound waves. For UIV, the array is preferably operated in plane wave mode. Hereby, all elements of the array emit simultaneously, creating a plane of sound waves [34]. For each of these emissions, one ultrasound image can be generated. This allows for high frame rates, which is required for recording high flow velocities. The thickness of the mud layer in the setup used by [31] varies between 250 and 500 mm. A depth range of the UIV technique of minimum 250 mm is thus envisaged in high density natural fluid mud. The maximum depth range attained so far in such mud is limited to only 50 mm, with no conclusive understanding of the limiting factors.

The mud considered in this research is a water-saturated mixture of organic matter, various clay minerals and small amounts of sand and silt [4], and is not to be confused with a common mixture of sand and water, also often referred to as ”mud”. It possesses a yield strength which, when left at rest, develops with time and needs to be overcome before it starts flowing. It is therefore classified as a non-Newtonian thixotropic fluid [36]. Similar to [30, 31], the mud used in this study was obtained from the Zeebrugge docks of the Port of Antwerp-Bruges, Belgium. It typically consists mainly of clay minerals and organic material, resulting in fine particle sizes ranging from 0.3 to \(120\,\upmu \hbox {m}\) and a median particle size (\(\hbox {d}_{\text {50}}\)) of \(7\,\upmu \hbox {m}\).

An ultrasound image is generated based on the received backscattered or reflected signals. The time to generate an image thus depends on the depth range of the image and the speed of sound through the mud. The latter has been determined to be 1465 \(\hbox {m}\cdot \hbox {s}^{-1}\) [7]. Thus, for a depth range of 50 mm, the sound waves need about 0.068 ms to propagate back and forth to generate an image. The applied frame rate was about 350 frames per second, meaning the time window available to generate each image was 2.86 ms. So in this case, the frame rate was not the limiting factor for the depth range. Because of the interaction between numerous backscattered signals, ultrasound imaging in Brightness mode (B-mode) in mud results in speckle images [7]. The intensity of the backscattered signals is reflected in the brightness of the pixels on the generated image. High intensity results in bright pixel brightness and vice versa. Due to attenuation of the ultrasound by the mud, the intensities of the backscattered signals decrease with depth and hence also the brightness of the pixels of the images (see Fig. 2). It therefore seems reasonable to presume that pixel brightness may determine the depth range. Consequently, there must be a minimum pixel brightness level for the PIV algorithm to work effectively. Earlier experiments presented in [6] showed that the acoustic attenuation of mud is governed by the ultrasound frequency and the density of the mud. Moreover, ultrasound imaging uses a single and constant ultrasound frequency. This implies that in the case of mud with homogeneous density, the attenuation and hence the rate of degradation of pixel brightness is constant, as illustrated by the linear trendline in Fig. 2. The slope of the trendline reflects the attenuation. A decrease in attenuation (i.e. less steep slope of the trendline) is therefore expected to increase the depth range. Secondly, by increasing the intensity of the emitted ultrasound, the intensity of the reflected signals and in turn the overall pixel brightness on the image will increase proportionally. This way the trendline of Fig. 2 shifts to higher Sound Pressure Level (SPL) values, hence enhancing the depth range.

Fig. 2
figure 2

On the left, an image generated by ultrasound B-mode imaging in mud, typically showing only speckle pattern. A decreasing trend of pixel brightness with increasing depth can be observed. On the right, plots of a vertical profile of Sound Pressure Levels (SPLs) of the backscattered signals, corresponding to the brightness values of the pixels of the vertical profile indicated by the blue line on the image on the left. The red dashed trendline illustrates the decreasing trend. The slope of the trendline is proportional to the attenuation

Full size image

The primary objective of this research is to determine the limiting factor(s) of the depth range of UIV in fluid mud. First a series of experiments are presented in which UIV was applied in flowing mud with variable ultrasound frequency, mud density and power. Based on the results of the experiments, it is examined whether the depth range is governed by attenuation and thus dependent on ultrasound frequency and mud density, as presumed. Subsequently, the influence of these variables on the depth range is evaluated to determine how they can be tweaked to enhance the depth range.

2 Experiments

2.1 Experimental setup

All experiments were conducted with three batches of Zeebrugge mud, each with their own density of about 1.120 \(\hbox {g}\cdot \hbox {cm}^{-3}\) (low density), 1.150 \(\hbox {g}\cdot \hbox {cm}^{-3}\) (medium density) and 1.175 \(\hbox {g}\cdot \hbox {cm}^{-3}\) (high density), respectively. The mud originally provided was therefore diluted by mixing it with seawater sourced from the same location. This was done just before conducting the experiments to ensure a homogeneous density of the mud throughout the experiments. The duration of the experiments themselves was limited to a few minutes, such that the influence of sedimentation can be ignored. The different mud batches were prepared and retained in separate buckets to allow convenient and swift change of mud density during the experiments. Multiple ultrasound arrays were used to cover a wide spectrum of ultrasound frequencies. A lower range from 1.75 to 2.5 MHz was covered using a flexible linear array, type XACT-10134 from Olympus. This array consists of 128 elements with a pitch of 0.41 mm and generates an ultrasound spectrum with a centre frequency of 2.5 MHz over a fractional bandwidth of 55 %. A mid-range from 2.5 to 4.5 MHz was covered using a phased array transducer, type P2-5AC from Samsung. This array consists of 64 elements with a pitch of 0.22 mm and generates an ultrasound spectrum with a centre frequency of 3.5 MHz over a fractional bandwidth of 60 %. A final range from 4.62 MHz to 6.67 MHz was covered using a linear array transducer, type L7-Xtech from Vermon. This array consists of 128 elements with a pitch of 0.3 mm and generates an ultrasound spectrum with a centre frequency of 7.5 MHz over a fractional bandwidth of 60 %. The flexible linear and phased arrays were operated by the HD-Pulse system [21], while the linear array was controlled by the DiPhAS beamformer system [25]. A correlation of 10 pixels per mm was set for all experiments. As conventionally done in medical ultrasound imaging the recordings are converted in digital images by envelope detection (absolute value of Hilbert transform), log compression (\(20\cdot\)log10(Data)) and normalisation to maintain a dynamic range of −60 to 0 dB.

Both the difference in operating system and array transducer design can affect the resulting images. Of the aforementioned available ultrasound equipment, the flexible linear array transducer and the DiPhAS control system are the biggest outliers in this regard. To maintain the flexibility of the array transducer, the dam** material behind the piezoelectric elements is minimised. Dam** is generally used to reduce the pulse length of the ultrasound signals, thereby improving the axial resolution of the images [1]. More conventional array transducers like the phased and the linear arrays therefore have more dam** material and hence greater dam** capacity. Apart from axial resolution, dam** capacity also affects other properties of transducers. Less dam**, for instance, increases the intensity of the emitted ultrasound, enhances the sensitivity of the transducer and reduces its bandwidth [28]. To allow for an unbiased evaluation of the physical interactions between the ultrasound and the mud, the choice was made to disable any gain (amplification) of the received signals. This was not successful when using the DiPhAS operating system for the linear array, where Time Gain Compensation (TGC) was applied during the acquisitions. TGC is a function in ultrasound imaging to compensate for the accumulating attenuation with depth by applying increasing gain with depth, resulting in better image quality. In ultrasound imaging, depth is derived from the time between transmission of the ultrasound and receipt of the reflection signals, based on the speed of sound through the medium. Depth and time are thus related when using ultrasound. How the TGC was applied during the acquisitions could not be retrieved from the system. Because of these major differences in equipment, the results of experiments using different equipment cannot be compared. Yet even when limiting comparison of the results to experiments conducted with the same equipment, the SPL scale can still vary because of the decreasing intensity of the emitted sound waves as the ultrasound frequency deviates from the centre frequency of the transducer. Therefore, in this study, only the results of experiments with the same equipment are compared and the comparison is based solely on a difference in trends.

A sketch of the experimental setup is shown in Fig. 3. The ultrasound array transducers are clamped to an appendage extending over a bucket containing a mud sample. To enable effective transmission of the ultrasound in the mud, the arrays were positioned face down, with the part from where the ultrasound is emitted and received penetrating the mud. All arrays were inserted in a water-filled, sheathing rubber to protect them from the corrosive seawater in the mud. A magnetic stirrer was used to induce a circular flow in the mud. The power of the stirrer was set to the level where a laminar flow was noticeable at the surface of the mud. Due to increasing viscosity with increasing density, this was only just achieved for the highest mud density. With this setup, the velocity of the induced flow is unknown. The obtained velocity measurements can therefore not be validated. Based on the results of previous research [9], the measured velocities are considered to be correct.

Fig. 3
figure 3

Sketch of the experimental setup used during this study. (1) bucket containing the mud; (2) magnetic stirrer to induce circular flow in the mud; (3) ultrasound transducer clamped on an appendage fixed to a laboratory stand

Full size image

2.2 PIV algorithm settings

The open access OpenPIV python script [17] was used as the PIV algorithm to process the acquired ultrasound images. The script validates the obtained vectors using four configurable filters based on maximum displacement, global standard deviation, the median test and Signal-to-Noise Ratio (SNR). For these experiments, all filters were configured to be virtually disabled. This way, the evaluation of the influence of pixel brightness on depth range could not be biased.

Two iterations were performed during PIV processing. For each array, the optimal window size that maximises the depth range was sought, considering only square windows. For the flexible linear array, these were window sizes of 80/40 pixels (first iteration/second iteration), while for both the phased and linear arrays, these were sizes of 48/24 pixels. The overlap of the interrogation windows was set to a recommended value of 50 % [26].

2.3 Experimental programme

For each combination of array and mud density, ultrasound scans were performed at multiple ultrasound frequencies. The image recording time was limited to approximately 1 s to contain the amount of data. An overview of all applied combinations of ultrasound frequency and mud density is provided in Table 1. All experiments from Table 1 were performed with the transducer operating at a voltage of 60 V, generating sinusoidal waves of 2 to 3 cycles with an absolute amplitude of 60 V. One additional experiment was performed by repeating the experiment with the ultrasound frequency set at 3.5 MHz and a mud density of 1.151 \(\hbox {g}\cdot \hbox {cm}^{-3}\) but with the transducer operating at a higher voltage of 150 V.

Table 1 Overview of all experiments performed with the ultrasound transducers operated at a constant voltage of 60 V. Three different ultrasound array transducers, a flexible linear array, a phased array and a linear array, were used to cover a wide spectrum of ultrasound frequencies. Although they are different in design, they were all operated similarly. The densities mentioned were measured after preparation of the mud samples. Given their similarity, the densities are grouped into generically named groups: low, medium and high density. Unless a specific experiment is referred to, densities are referred to by these group names throughout the remainder of this manuscript
Full size table

3 Limiting factor of depth range

The OpenPIV script applies a cross-correlation between two images to determine the displacement of speckle patterns between the two images. In case of consecutive images of which the time between the two acquisitions is known, the velocity and direction of movement of the speckle patterns during this time interval can be derived. These velocities and directions are considered to correspond to the flows in the fluid. The output of the OpenPIV script is provided as vector fields of which the size matches that of the processed images. The resolution of the vector grid depends on the size of the interrogation windows and their overlap. The vector fields are generated in both data format (txt file) and image format (PNG file). The data files can be used for further analysis. An appropriate method to determine the depth range of each vector field is established first. This way, the influence of various parameters on the depth range can be further evaluated objectively.

3.1 Results

By the design of the experimental setup, the resulting vectors are expected to be coherent. The results show that this holds true up to a certain depth, from where non-validated and unrealistic vectors alternate (see Fig. 4).

Fig. 4
figure 4

A vector field resulting from the experiment with an ultrasound frequency of 2.5 MHz (flexible linear array) and a mud density of 1.146 \(\hbox {g}\cdot \hbox {cm}^{-3}\). The red dotted line indicates the depth from which the tendency of coherent vectors stops. The increase in vector size (i.e. flow velocity) with depth, correlates with the experimental setup. Velocities up to 350 \(\hbox {mm}\cdot \hbox {s}^{-1}\) were measured at the transition level from coherent to incoherent vectors

Full size image

The depth of this transition is considered the depth range of the UIV and is determined based on the appearance of the non-validated vectors. Such vectors are indicated by ”NaN” (Not a Number) in the data file for the corresponding vector. For each vector column (i.e. vertical profile) of each vector field, the depth from where successive NaN values are found is considered the depth of this transition. Hence, for each experiment, the average of all these transition depths is regarded as the depth range for the corresponding combination of ultrasound frequency and mud density. These averages are presented in Fig. 5.

Fig. 5
figure 5

Plots of the average depth range found for each experiment representing a combination of ultrasound frequency and mud density. A trendline based on the depth ranges obtained is plotted as dashed lines for each combination of mud density and array transducer used. Variation in depth ranges is indicated by the shades. The frequency ranges of the array transducers are mentioned in section 2.1 and indicated on the horizontal axis

Full size image

Knowing the depth ranges for each experiment, the corresponding pixel brightness values can be determined. To assess the presumed relation with attenuation, the pixel brightness values of the images are converted to Sound Pressure Levels (SPL), expressed on a logarithmic scale in decibels. The correlation between pixel brightness and SPL depends on the bit depth and dynamic range of the images (see Eq. 1). For all experiments in this study, these were fixed at 16 bits and 60 dB, respectively.

$$\begin{aligned} L_{p} = \frac{C_{\text {pixel}}}{2^n}\cdot r_{\text {dyn}} \end{aligned}$$
(1)

Where \(L_{p}\) is the Sound Pressure Level (SPL) of the returning sound wave upon receipt by the transducer [dB], \(C_{\text {pixel}}\) is the linear greyscale intensity value of a pixel, corresponding to its brightness [-], n is the bit depth of the images [bits] and \(r_{\text {dyn}}\) the dynamic range applied to produce the images [dB].

Subsequently, for each experiment, the average SPL of each pixel row across all images is calculated. The result is an average vertical SPL profile for each combination of mud density and ultrasound frequency. Together with its Coefficient of Variation (CV) such an average SPL profile is shown in Fig. 6. Based on the average SPL profiles, the average SPL corresponding to the assessed depth range can be determined, as illustrated in Fig. 6. This SPL is further considered the minimum SPL required for the application UIV in that experiment. This was done for all experiments. The resulting minimum SPLs are summarised in Fig. 7.

In conventional PIV, cross-correlation is based on patterns formed by various visualised scatterers contrasting with the image background [24]. This is different when speckle pattern images are used. Speckle occurs when the density of scatterers is so high that the backscattered signals interfere (constructively and destructively), creating an illusory image based on the position of the scatterers without visualising them themselves [35, 39]. As a result, images are completely filled with speckle patterns, leaving no ”blank” background to contrast with (see Fig. 2). Cross-correlation between speckle pattern images is thus based on patterns of contrast which are part of the speckle image. Along with the fading pixel brightness with depth, the contrasts in the speckle patterns degrade with depth. To assess the detectability of such patterns with depth, a Contrast Ratio (CR) profile is determined. The CR of a section of the image is defined as the ratio of the difference between the maximum and minimum SPLs within that section to the dynamic range of the image. In this study, the sections for which the CRs are determined are 10 by 10 pixels in size. For each column of 10 pixels wide, a vertical CR profile is thus determined with a vertical resolution of 10 pixels. By doing so for each 10-pixel-wide column of an image and for all images of an experiment, an average vertical CR profile can be determined for each experiment. For the corresponding experiment, such a CR profile together with its CV are shown along in Fig. 6.

Fig. 6
figure 6

Plots of the average vertical SPL profile and the corresponding coefficient of variation (CV) for the experiment with an ultrasound frequency of 2.0 MHz and a mud density of 1.146 \(\hbox {g}\cdot \hbox {cm}^{-3}\). The red dashed line indicates the average depth range determined for the experiment (Fig. 5). The intersection between the two provides an indication of the minimum SPL and hence pixel brightness (Eq. 1) required for UIV. Profiles of the average Contrast Ratio (CR) and the corresponding coefficients of variation (CV) are plotted along. Similar plots for other experiments are annexed in Appendix A

Full size image
Fig. 7
figure 7

Plots of the minimum SPLs attained for each experiment (see Table 1). The diagrams enclose the results for each array transducer. The dashed lines are trendlines for each combination of density and the array transducer used

Full size image

3.2 Discussion

For each array transducer, the results plotted in Fig. 5 reveal an increasing depth range with a decrease in both mud density and ultrasound frequency. These observations confirm the depth range of UIV is primarily dictated by the attenuation of the ultrasound by mud.

With the significantly lower depth ranges for the linear array experiments, the influence of the TGC (Sect. 2.1) is clearly visible. This is however somewhat counterintuitive. After all, for diagnostic imaging, gain is used to improve image quality. Greater depth ranges could therefore be expected. Since the TGC is applied to the recordings prior to normalisation (including a cutoff of values below -60 dB), a larger range of data is compressed in the dynamic range of 60 dB (see Sect. 2.1). Consequently, it narrows the distinction between signals, ultimately leading to a loss of contrast between surrounding pixels. This in turn complicates the preservation of speckle patterns and thus the cross-correlation between successive images. In a way, gain thus creates an additional filter that eliminates low-contrast speckle patterns, thereby reducing the depth range of UIV. The influence of TGC can also be observed in the significantly lower SD of the average depth ranges (Fig. 5). This means that due to gain the depths at which cross-correlation is no longer successful becomes less variable. An explanation must therefore be sought in the vertical \(\hbox {CR}_{\text {CV}}\) profiles as presented in Fig. 6 and Appendix A. These profiles show that for the experiments using the flexible linear array and the phased array the variation in CR is more or less constant with depth until just above the specified maximum depth, from where variation in CR increases. This is different for the experiments using the linear array. These results show consistent or even slightly decreasing variation in CR with depth. This means that the depth from where the minimum CR values are encountered is more delineated, and hence also the identified depth ranges.

To facilitate the analysis of the minimum SPLs shown in Fig. 7, diagrams have been drawn enclosing the results for each array transducer. Generally a trend of decreasing minimum SPL with increasing frequency can be observed. Assuming that there is a fixed minimum CR defining the depth range, this observation implies that the differences in SPLs of surrounding pixels increase as the ultrasound frequency increases. After all, the CR is determined by the range of SPLs of nearby pixels. This is confirmed by the differences in \(\hbox {SPL}_{\text {CV}}\) profiles of the experiments, as shown in Fig. 11, Fig. 12 and Fig. 13, enclosed in Appendix A. Within each series of plots of a combination of mud density and array transducer used, it can be seen that the rate at which \(\hbox {SPL}_{\text {CV}}\) increases with depth becomes faster with higher ultrasonic frequencies. Because of the random interference of backscattered sound waves, greater variance in recorded SPLs can be explained by higher intensities of the backscattered signals. This, however, contradicts with the greater attenuation of higher-frequency ultrasound. Therefore, this observation can only be explained by the number of particles that scatter the ultrasound, which increases when the frequency of the ultrasound is higher. Indeed, the number of scatterers depends on the ratio between the size of the scatterers and the wavelength of the sound waves [33]. This is further elaborated in Sect. 4.1.

4 Optimisation of depth range

In previous section it is shown that the depth range of UIV applied to natural cohesive mud is determined by the pixel brightness of the speckle pattern images. As discussed in section 1, when ultrasound imaging is applied to a volume of mud of homogeneous density, the pixel brightness of the images degrade with depth at a constant rate proportional to the attenuation of the applied ultrasound by the mud. Hence, the depth range can be optimised by reducing the attenuation or increasing the intensity of the initially emitted ultrasound.

4.1 Lowering attenuation

The attenuation of ultrasound by mud is determined by the density of the mud and the applied ultrasound frequency (see Eq. 2 from [6]).

$$\begin{aligned} \alpha _{\text {mud}}=(7.035 f + 8.831).(\rho _{\text {mud}} - 1) \end{aligned}$$
(2)

where \(\alpha _{\text {mud}}\) is the ultrasound attenuation [\(\hbox {dB}\cdot \hbox {cm}^{-1}\)], 7.035 an empirically determined constant multiplier [\(\hbox {cm}^2\cdot \hbox {dB}\cdot \hbox {g}^{-1}\cdot \hbox {MHz}^{-1}\)], f the ultrasound frequency [MHz], 8.831 an empirically determined constant coefficient [\(\hbox {cm}^2\cdot \hbox {dB}\cdot \hbox {g}^{-1}\)] and \(\rho _{\text {mud}}\) the mud density [\(\hbox {g}\cdot \hbox {cm}^{-3}\)].

For experimental fluid dynamics involving natural cohesive fluid mud, variation in these two parameters is limited. In fact, the density of mud can vary from 1.050 to 1.500 \(\hbox {g}\cdot \hbox {cm}^{-3}\) or even more. However, in most research topics involving mud density, this is an imperative parameter. Therefore, it is considered unwanted to change the density solely to optimise the UIV depth range. For diagnostic imaging, high ultrasound frequencies are preferred to achieve optimal axial resolution to clearly distinguish boundaries or transitions. Because of their uniformity, this is less crucial for images containing only speckle. In order to reduce acoustic attenuation, it therefore seems obvious to use low ultrasound frequencies. This is however limited. In ultrasound imaging, speckle patterns arise from the interference of scattered sound waves. In turn, scattering occurs when tiny particles (scatterers), with an acoustic impedance different from that of its surrounding media, are insonified with ultrasound of which the wavelength is larger than the size of these particles [13]. Different scattering regimes are distinguished based on the \(k\cdot a\) ratio (Eq. 3).

$$\begin{aligned} k\cdot a = \frac{2\cdot \pi }{\lambda }\cdot a \end{aligned}$$
(3)

Where k is the spatial frequency of a wave also referred to as the wavenumber [\(\hbox {m}^{-1}\)], \(\lambda\) is the wavelength of the ultrasound wave [m] (equal to the speed of sound divided by the wave frequency) and a is the radius of the irradiated particle causing the scattering (i.e. scatterer).

The ultrasound frequencies applied during the experiments of this study ranged between 1.75 and 6.67 MHz (see Table 1). With a speed of sound of 1465 \(\hbox {m}\cdot \hbox {s}^{-1}\) [7], this corresponds to a range of wavelengths between 220 and \(837\,\upmu \hbox {m}\). Since the maximum particle radius is \(60\,\upmu \hbox {m}\) (see Sect. 1), the wavelength of the ultrasound is always much larger than the particles. According to [33], this results in diffusive scattering, where the intensity of the scattered signals (\(I_s\)) is proportional to the frequency to the fourth power (see Eq. 4). Since the returning sound waves are attenuated as they propagate through the mud, a minimum backscattering intensity (\(I_s\)) is required for them to reach back to the transducer. Consequently, a lower limit for the ultrasound frequency can be expected beyond which the quality of the speckle images become insufficient. Due to attenuation, this is expected to occur first at greater depths, with the ultrasound frequency thus becoming the limiting factor for the depth range.

$$\begin{aligned} \frac{I_s}{I_i}=\frac{k^4.a^6}{9.r^2}.\left[ 1-\frac{3.cos\phi }{2}\right] ^{2} \end{aligned}$$
(4)

Where \(I_s\) is the scattering intensity [\(\hbox {W}\cdot \hbox {m}^{-2}\)], \(I_i\) is the incoming intensity [\(\hbox {W}\cdot \hbox {m}^{-2}\)], k is the wavenumber [\(\hbox {m}^{-1}\)], a is the radius of the scattering particle [m], r is the distance to the scattering particle [m] and \(\phi\) the angle of the scattered signals relative to the incoming sound wave [rad].

Equation 4 was derived from the expression defined by Lord Rayleigh [32] and [20] for the scattering of pressure waves by spheres much smaller than the wavelength of the pressure waves. It therefore shows great resemblance to other derived expressions such as for scattering of electromagnetic waves in the Rayleigh scattering regime (e.g. by [27]). In fact, the parts expressing the influence of wavelength and particle size (factors k and a) are equal. While a bottom limit for significant scattering of electromagnetic waves is identified around \(k\cdot a = 0.002\), no such limit for ultrasound scattering was found in literature. Although the size of the actual scatterers cannot be assessed, an estimate of such a lower limit can be made based on the experiments conducted and a particle size distribution of the mud. After all, the lowest ultrasound frequency of 1.75 MHz still provided adequate images for the application of UIV and can thus be used as a reference. A particle size distribution of the mud was acquired using a Malvern Mastersizer 2000 [19], see Fig. 8. Since difference in density of mud samples of the same origin is solely attributable to the water content, the particle size distribution is independent of the density.

Fig. 8
figure 8

Particle size distribution of a sample of Zeebrugge mud as used during the experiments of this study. The distribution is plotted both cumulatively (blue) and differentially (orange). This particle size distribution applies to all densities of Zeebrugge mud

Full size image

The cumulative distribution shows a \(\hbox {d}_{\text {10}}\) particle size (the size compared to which 10 percent of the particles are smaller) of \(0.766\,\upmu \hbox {m}\). This means that when insonified with an ultrasound frequency of 1.75 MHz, a \(k\cdot a\) ratio of at least 0.003 applies for ninety percent of the particles. This lower limit of the \(k\cdot a\) ratio is just above the aforementioned limit of negligible scattering intensity for electromagnetic waves. Because of the resemblances to electromagnetic scattering, it is provisionally presumed that this limit can be adopted for the scattering of ultrasound waves. Because the intensity of the sound waves eventually returning to the transducer is the result of the superposition of various backscattered signals, the number of scatterers present will also have an impact on this. In [7], the chemical compounds silicon dioxide (\(\hbox {SiO}_2\)) and aluminium oxide (\(\hbox {Al}_2\hbox {O}_3\)) were identified as probable ultrasound reflectors present in Zeebrugge mud. Silicon dioxide, or silica, is mostly found in nature as quartz in silt and sand [2, 15], which in turn are classified as particles with sizes ranging from 2 to \(63\,\upmu \hbox {m}\) and \(63\,\upmu \hbox {m}\) to \(2000\,\upmu \hbox {m}\), respectively [5]. Aluminium oxide, in turn, is a so-called associated mineral commonly found in clays. Depending on the literature consulted, in geoengineering, clay minerals are considered smaller than \(2\,\upmu \hbox {m}\) or \(4\,\upmu \hbox {m}\) [3, 10]. Based on the particle size distribution of Zeebrugge mud (see Fig. 8),it can thus be concluded that scatterers may be found across the entire spectrum of particle sizes present in Zeebrugge mud. To set a limit somewhere, the smallest particle size further considered to cause adequate scattering when insonified with 1.75 MHz ultrasound is the \(\hbox {d}_{\text {20}}\) with a size of \(2.4\,\upmu \hbox {m}\). The corresponding \(k\cdot a\) ratio is 0.009. This is illustrated by the green area in Fig. 9 which represents correlations of ultrasound frequency and particle size that result in \(k\cdot a\) ratios larger than 0.009. Hence, its lower boundary is specified by a curve of constant \(k\cdot a\) ratio equal to 0.009. Similar curves of constant \(k\cdot a\) ratio corresponding to particle sizes \(\hbox {d}_{\text {50}}\) and \(\hbox {d}_{\text {80}}\) are shown as well. Furthermore, particle sizes \(\hbox {d}_{\text {20}}\), \(\hbox {d}_{\text {50}}\) and \(\hbox {d}_{\text {80}}\) of Zeebrugge mud are marked by vertical red dashed lines. The intersection of the \(\hbox {d}_{\text {50}}\) line with the \(k\cdot a_{(d_{20})}\) curve indicates that with an ultrasound frequency of 0.6 MHz, half of the particles still qualify for adequate scattering intensity for UIV. In such case, with a \(k\cdot a\) ratio of 0.003, even the intensity of the signals scattered by particles of size equal to the \(\hbox {d}_{\text {20}}\) is still above the aforementioned lower limit of 0.002. In fact, as long as sufficient scatterers are present in the larger particle size ranges, even lower ultrasound frequencies down to 0.2 MHz may still suffice.

Fig. 9
figure 9

Illustration of the applicable \(k\cdot a\) ratios for insonation of scatterers as a function of scatterer size and ultrasound frequency. Where k is the wavenumber of the ultrasound and a is the radius of the scatterer. Three curves of constant \(k \cdot a\) ratio are plotted in dashed grey lines. The \(k \cdot a\) ratios of these curves apply to the insonation with 1.75 MHz ultrasound of scatterers with sizes equal to the \(\hbox {d}_{\text {20}}\), \(\hbox {d}_{\text {50}}\) and \(\hbox {d}_{\text {80}}\) particle sizes of Zeebrugge mud. The green fill indicates the correlations of ultrasound frequency and scatterer size for which the \(k\cdot a\) ratio exceeds the presumed minimum of 0.009. The vertical red dashed lines indicate the \(\hbox {d}_{\text {20}}\), \(\hbox {d}_{\text {50}}\) and \(\hbox {d}_{\text {80}}\) particle sizes of Zeebrugge mud (see Fig. 8)

Full size image

Based on Eq. 2, the attenuation of 0.6 MHz ultrasound by Zeebrugge mud with a density around 1.15 \(\hbox {g}\cdot \hbox {cm}^{-3}\) is approximately 2 \(\hbox {dB}\cdot \hbox {cm}^{-1}\). While the depth range of 50 mm was achieved in Zeebrugge mud of similar density with an ultrasound frequency of 3.5 MHz and thus an attenuation of 5 \(\hbox {dB}\cdot \hbox {cm}^{-1}\) [9]. Hence, lowering the ultrasound frequency to 0.6 MHz would increase the depth range by a factor of 2.5 to 125 mm.

It should be emphasised that only Zeebrugge mud is considered in this research. Muds of other origins have different particle size distributions. Hence, the optimal ultrasound frequency for applying UIV will be different for each mud. Equation 4 shows that the intensity of the scattered ultrasound (\(I_{s}\)) is proportional to the size of the scatterers (a) to the power six. In this way, the size of the particles affects the depth range of UIV twofold. On the one hand, larger particles in the mud will generate scattered ultrasound of higher intensity. The scattered ultrasound can thus propagate further, which eventually results in an increased depth range of the UIV. On the other hand, since the attenuation of ultrasound is largely determined by the extent of scattering, the rate at which ultrasound is attenuated by the mud will also increase with increasing particle sizes. This in turn again limits the depth range of UIV. Whether one of these effects predominates the other or whether they compensate for each other is best assessed experimentally.

4.2 Increasing ultrasound intensity

In case of a mud sample of homogeneous density, the attenuation and hence the deterioration rate of pixel brightness is constant with depth (see Fig. 2. This enables to shift the minimum pixel brightness to greater depths by increasing the intensity of the emitted ultrasound, proportionally increasing the SPLs of the returning sound waves. This was tested by repeating an experiment with a higher voltage applied to the transducer (see section 2.3). All original experiments listed in Table  1 were conducted with a voltage of 60 V. The repetition experiment was conducted with a voltage of 150 V. The increase in emitted SPL can be estimated using Eq. 5 [14]. For the aforementioned increase in voltage this results in a theoretical increase of 8.0 dB.

$$\begin{aligned} \Delta L_{p} = 20\cdot \log {\frac{U_{\text {2}}}{U_{\text {1}}}} \end{aligned}$$
(5)

Where \(\Delta L_{p}\) is the difference in emitted SPL between emissions where the transducer was operated with different voltages (\(U_{\text {1}}\) and \(U_{\text {2}}\)). A random but corresponding SPL profile resulting from both experiments is shown in Fig. 10. These plots show a shift of the SPL profile towards higher values when a higher voltage is applied to the transducer. Averaged across all profiles of all images, an increase of 7.3 dB was determined, matching well with the estimated increase. With an attenuation of 2 \(\hbox {dB}\cdot \hbox {cm}^{-1}\), like when insonifying Zeebrugge mud of density around 1.15 \(\hbox {g}\cdot \hbox {cm}^{-3}\) with 1.75 MHz ultrasound, this increase in SPL yields an additional depth range of 36.7 mm.

Fig. 10
figure 10

Random but corresponding SPL profiles of the recorded returning sound waves after transmission with the transducer operating at 60 V (blue markers) and 150 V (orange markers)

Full size image

5 Conclusion

UIV is an effective technique to measure flow velocities in natural high density cohesive muds. The depth range is however limited. A depth range of 50 mm was attained in a previous study in Zeebrugge mud. This limitation is presumed to be caused by the attenuation of ultrasound by the mud, which in turn is linearly proportional to both the applied ultrasound frequency and the density of the mud. Multiple experiments applying UIV with varying ultrasound frequency in various mud samples of different density were therefore performed during this study. The results of these experiments confirm an increasing depth range with both decreasing ultrasound frequency and decreasing mud density and thus decreasing attenuation in general. A maximum depth range of 70 mm was obtained in mud with a density of 1.12 \(\hbox {g}\cdot \hbox {cm}^{-3}\) with 2 MHz ultrasound.

The results of the linear array experiments stand out for their shallow depth ranges and low variation in the assessed depth ranges. This can be attributed to the TGC applied by the operating system for the linear array. The greater consistency in depth range does not outweigh the decrease in depth range. Therefore, gain can generally be considered unfavourable for the depth range of UIV. Together with the conclusion of [29] that gain does not enhance the accuracy of cross-correlation between ultrasound images, it can be concluded that the application of gain should not be considered for future application of UIV.

The results of the experiments also allowed an assessment of possible measures to increase the depth range without changing the ultrasound equipment. Because the density of mud is usually fixed in experimental research involving mud, a reduction in this was not considered. The aforementioned depth range of 50 mm was achieved in mud with a density of 1.15 \(\hbox {g}\cdot \hbox {cm}^{-3}\) using 3.5 MHz ultrasound. In conjunction with the results of an additional particle size analysis of the mud, doubling this depth range is considered feasible by lowering the ultrasound frequency to 0.6 MHz. If sufficient scatterers are present among the larger particles in the mud (i.e. above the \(\hbox {d}_{\text {50}}\)), even greater depth ranges are possible by further lowering the ultrasound frequency. Without knowing the size, occurrence and chemical composition of the particles in mud, a more precise assessment cannot be made. Unfortunately, this assessment could also not be verified because such low ultrasound frequencies are far below the frequency range of the equipment available for this study and by extension ultrasound equipment for medical diagnostics.

Secondly, increasing the power of the emitted ultrasound proved to be an effective way to increase the depth range. By increasing the voltage applied to the ultrasound transducer from 60 to 150 V, an average increase of 7.334 dB was observed. The increase in depth range resulting from this depends on the attenuation rate. In case of the aforementioned example of Zeebrugge mud with a density of 1.15 \(\hbox {g}\cdot \hbox {cm}^{-3}\) and an ultrasound frequency of 0.6 MHz, an additional depth range of 36.7 mm can be achieved this way. Together with the lowering of the ultrasound frequency, a total depth range of 136.7 mm is thus considered feasible. This does not yet meet the targeted goal of 250 mm for application in experimental research as carried out by [30, 31]. It does offer options for an alternative intrusive setup, where the transducer is placed at an offset to the bottom of the flume or even inside the the towed object, flush with its outer shell.

The ultrasound power emitted by medical ultrasound scanners is limited due to safety limits for patient protection [23]. More powerful ultrasound imaging equipment, such as ultrasound flaw detectors or high resolution sonars used for offshore site surveying and archaeology, are thus preferred for the application of UIV in mud. The latter for instance emit ultrasound with an intensity of about 200 dB, potentially resulting in a depth range in mud of up to 90 cm. The maximum recordable flow velocity with this may well be limited because the frame rate of such equipment is significantly lower compared to medical equipment. In turn, this can however be compensated for by the greater widths of the transducers [9]. Alternatively, the output of medical devices can be further optimised using novel processing techniques such as the pulse compression technique. This increases the depth range while respecting power limitations for patient safety [16]. A conventional compression of 100 cycles results in an increase in transmitted SPL of 20 dB. For the aforementioned example, this results in an additional depth range of 10 cm. Such a technique was not used in this study, as it requires more specialised equipment and experience.

This manuscript first provides a good insight in the physics determining the depth range of UIV in natural high density cohesive mud. Based on these insights, optimisations were found without changes in ultrasound imaging equipment. This has broadened the potential applications of medical ultrasound for UIV in experimental fluid dynamics with mud. Moreover, based on these insights, other options for further optimisation can be evaluated.