1 Introduction

In recent years, electric vehicles (EVs) have gained tremendous because of the advantages of eco-friendliness, low maintenance cost, and autonomous-driving development. In addition, EVs can be in charge of an energy storage bank in smart microgrid systems for energy management. In EVs, various low-voltage loads are essentially equipped and powered by the high-voltage DC bus. Consequently, step-down converters with a high conversion voltage ratio to drop the bus voltage to power in-vehicle equipment have to be adopted [1]. In addition to installation in EVs, high step-down converters also have other various kinds of applications, for instance, supplying data centers [2, 3], LED arrays [4, 5], and DC loads of microgrids [6]. Step-down converters have been enlarging their applications in many fields and becoming a converter design trend.

High step-down converters can be mainly divided into two categories: isolated structures and non-isolated ones. One advantage of isolation configuration is that it can provide the feature of galvanic isolation and obtain a high conversion ratio [7,8,9,10]. However, most isolated converters utilize a high turn ratio to carry out a high conversion ratio. Efficiency and leakage inductance consequently become other problems that must be dealt with in converter design. Besides, the feedback control with isolation will also increase the complexity of the circuitry. Non-isolated structures can be a considerable choice for the advantages over isolated ones. In a non-isolated structure, common ground between the input and output can benefit a more straightforward circuit design and feedback accuracy because of noise reduction. Easy to accomplish higher power density is another merit of a non-isolated structure [11,12,13].

Some buck-derived non-isolation configurations for step-down features are mainly derived from conventional converters [14, 15]. However, the buck-derived converters still cannot drop the input voltage to a much lower level except by utilizing an extreme duty cycle. Merging switched capacitors and coupled inductors into a converter design can be feasible. Nevertheless, some problems probably exist. Adopting switched capacitors will result in relatively lower regulation capability and more switches required [16,17,18,19], while coupled inductors lead to a larger size and nonlinearity in high-power applications [20,21,22]. Besides, more components should be used in the main stage, resulting in more sophisticated circuit structures and lower efficiency.

In high-current applications, interleaved converters are considered owing to the ability to provide more paths for current sharing and ripple suppressing. Based on the interleaving operation, this type of converter intrinsically has the advantages of easy filter design, lower current stress and ripple, and higher power-density achievement. Even with the mentioned benefits, interleaved converters need more passive and active power components, significantly increasing the converter cost and the complexity of the control mechanism, especially in multiphase configurations [23].

In [24], the interleaved converter can step down its input voltage and obtain continuous current at the output. However, it requires a total number of active switches of up to five, and a pulsating current exists at the input. In [25], the converter utilizes switched capacitors and buck-based structures to fulfill the step-down feature and obtain continuous currents at both the input and output sides. Nevertheless, this converter must employ three active switches, and the input and output ports cannot be in common ground. Besides, it lacks expandability for applications that require a much higher voltage conversion ratio.

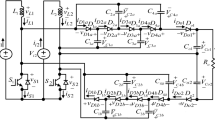
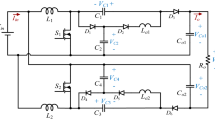
This paper proposes an interleaved step-down converter (ISDC), as shown in Fig. 1, to overcome the abovementioned problems. The ISDC embeds a capacitor-diode voltage splitter (CDVS) and a buck-derived interleaved circuit (BDIC) to accomplish the features: extra-high voltage conversion ratio, low current ripples at both sides of input and output, minimum active switches required, cost-effectiveness, common ground, equal current sharing, and expandable ability. Capacitors and diodes structure the CDVS without any active switch, which can significantly split a high input voltage. The BDIC is a buck-derived circuit that further lowers the high voltage and ensures that the output current of the converter is continuous with low current ripples. The S1 in Fig. 1 also serves as a bridge to connect the front-end stage, CDVS, and the downstream circuit, BDIC, based on which the proposed converter can reduce the employ of active switches to accomplish the minimum switch characteristic.

Fig. 1
figure 1

The proposed interleaved extra-high step-down converter

Full size image

This paper consists of 8 sections. Section 2 describes the converter operation principle after the introduction in Sect. 1. In Sect. 3, the steady-state analysis of the ISDC is discussed, mainly including voltage gain, voltage stress, and current stress of semiconductors, followed by Sect. 4, which discusses the design consideration of the converter. Section 5 explains the converter expandability, while comparisons with some state-of-the-art topologies are shown in Sect. 6. Section 7 presents and discusses the experimental results measured by a prototype. Finally, Sect. 8 concludes the paper.

2 Converter operation principle

The definition of voltage polarity and current direction of ISDC is depicted in Fig. 2. The ISDC is able to operate over the total duty ratio. That is, duty ratio D ranges from 0 to 1. While D is less than 0.5, the voltage-gain expression of the ISDC is different from that when D is greater than 0.5. While D is less than 0.5, ISDC achieves a superior voltage step-down feature over that in D > 0.5. Therefore, D < 0.5 is the primary operation range.

Fig. 2
figure 2

Definitions of voltage polarity and current direction of the ISDC

Full size image

In order to simplify the operation description, the following assumptions are considered.

  1. 1)

    All the components are assumed to be ideal, so the ON-resistance RDS(on) of the switches and equivalent series resistance of all passive components can be neglected.

  2. 2)

    The values of all capacitors are assumed to be large enough to keep capacitor voltages constant.

  3. 3)

    The inductances of L2 and L3 in the BDIC are identical.

  4. 4)

    The control signals of S1 and S2 have the same duty cycle D, and both are less than 0.5 with 180° out of phase.

  5. 5)

    The converter has been operating in a steady-state condition and continuous conduction mode (CCM).

In Fig. 2, the input is the bus voltage Vbus, and Vo indicates the output voltage. S1 and S2 are power switches, D1–D5 denote diodes, C1–C3 and Co are capacitors, and L1, L2, and L3 stand for inductors. While duty ratio D is less than 0.5, the converter operation can be mainly divided into four modes over one switching period, Ts. Figure 3 depicts the conceptual waveforms; meanwhile, Fig. 4 presents the corresponding equivalents of the modes. The converter operation is discussed mode by mode as follows:

Fig. 3
figure 3

Conceptual waveforms of the proposed converter in CCM

Full size image
Fig. 4
figure 4

Equivalent circuit of the proposed converter as D < 0.5. a Mode 1. b Mode 2. c Mode 3. d Mode 4

Full size image

Mode 1 [t0 < t < t1]: This mode begins when S1 is turned on. During Mode 1, switch S2 is in the OFF state. Figure 4a shows the related equivalent circuit, in which the diodes D1, D2, and D5 are forward-biased. In addition, the Vbus charges C3, L1, and L2, and it also powers the load. At the same time, the capacitors C1 and C2 discharge, and the inductor L3 releases its stored energy to the load Ro. The voltages of C1 and C2 are equal, that is, VC1 = VC2. In addition, the voltages across inductors L1, L2, and L3, vL1, vL2, and vL3, are expressed as Vbus –VC1, VC1 –VC3 –Vo, and –Vo, respectively, which are all constant. The currents iL1 and iL2 increase linearly, but iL3 decreases linearly. Mode 1 will last until switch S1 is turned off at t = t1.

Mode 2 [t1 < t < t2]: Mode 2 lasts for t1 to t2, in which both switches S1 and S2 are OFF. As shown in Fig. 4b, the diodes D3, D4, and D5 are forward-biased, but D1 and D2 are OFF. The Vbus and the inductor L1 are in series to charge C1 and C2. The voltage across inductor L1, vL1, is equal to Vbus –VC1 –VC2. Simultaneously, the energy stored in inductors L2 and L3 supply the load Ro, and voltages across both inductors are identical, that is, vL2 = vL3 = –Vo. All inductor currents decrease linearly. This mode will end when the switch S2 is turned on.

Mode 3 [t2 < t < t3]: The equivalent of Mode 3 is shown in Fig. 4c, in which the switch S2 is turned on at t = t2, but S1 remains OFF. Diodes D3 and D4 conduct, kee** the same state as in Mode 2, but D5 is OFF. The Vbus and inductor L1 still charge the capacitors C1 and C2; meanwhile, the inductor L2 forwards its energy to the load. The capacitor C3 provides stored energy to the inductor L3. Hence, the voltage of inductor L3, vL3, equals VC3 –Vo. When switch S2 is turned off, Mode 3 ends.

Mode 4 [t3 < t < t4]: Both switches S1 and S2 are OFF again in this mode. The Vbus and inductor L1 charge capacitors C1 and C2, while inductors L2 and L3 release energy to the load Ro. As illustrated in Fig. 4d, the current paths resemble that in Mode 2. This mode closes when switch S1 is turned on again, and converter operation over one switching cycle is completed.

3 Steady-state analysis

In this section, the steady-state analysis of the converter is carried out in the condition that D < 0.5. The study includes voltage gain, voltage and current stresses of semiconductors, inductance and capacitance calculation, and converter expandability.

3.1 Voltage gain analysis

As discussed in Sect. 2, the inductors L1 and L2 absorb energy in Mode 1 and release their stored energy in the other modes. In addition, the inductor L3 absorbs energy in Mode 3 and releases its stored energy in the others. Applying the volt-second balance criterion to inductors L1, L2, and L3, respectively, the relationships of (1)–(3) can be accordingly obtained.

$$ (V_{bus} - V_{C1} )DT_{s} = (V_{bus} - V_{C2} )DT_{s} = - (V_{bus} - V_{C1} - V_{C2} )(1 - D)T_{s} $$
(1)
$$ (V_{{C1}} - V_{{C3}} - V_{o} )DT_{s} = (V_{{C2}} - V_{{C3}} - V_{o} )DT_{s} = V_{o} (1 - D)T_{s} $$
(2)
$$ (V_{{C{3}}} - V_{o} )DT_{s} = V_{o} ({1} - D)T_{s} . $$
(3)

The D is the duty ratio of the switches, and Ts denotes the switching period. Solving for VC1, VC2, and VC3 from (2) and (3) yields

$$ V_{C1} = V_{C2} = \frac{{2V_{o} }}{D} $$
(4)
$$ V_{C3} = \frac{{V_{o} }}{D}. $$
(5)

Substituting (4) and (5) into (1) can yield the ratio of Vo to Vbus, MCCM:

$$ M_{{{\text{CCM}}}} = \frac{{V_{o} }}{{V_{bus} }} = \frac{D}{4 - 2D}{.} $$
(6)

In (6), the expression of the converter voltage gain is for the condition that D is less than 0.5. The ISDC is able to operate over the full-range duty ratio. As the duty ratio is greater than 0.5, based on a similar procedure of derivation for voltage gain, the expression of the converter voltage gain becomes

$$ M^{\prime}_{{{\text{CCM}}}} = \frac{{V_{o} }}{{V_{bus} }} = \frac{{D^{2} }}{2 - D} \, {.} $$
(7)

For better understanding, the relationship between voltage gain and duty ratio over 0 < D < 1 of the proposed converter is depicted in Fig. 5, in which it can be observed that D < 0.5 has an excellent step-down feature.

Fig. 5
figure 5

The relationship between voltage gain and duty ratio over the entire range

Full size image

3.2 Voltage stresses of semiconductors

Suppose the voltages across capacitors C1, C2, and C3 are considered constant. Referring to Fig. 4a, the voltage stress of S2, Vds2,stress, can be determined, while the voltage stress of S1, Vds1,stress is found based on Fig. 4c. Then,

$$ V_{ds1, stress} = V_{C1} + V_{C2} - V_{C3} = \frac{{3V_{bus} }}{4 - 2D} $$
(8)
$$ V_{ds2, stress} = V_{C1} = V_{C2} = \frac{{V_{bus} }}{2 - D}. $$
(9)

To determine the diode voltage stresses for D1, D2, and D5, Fig. 4c is referred to, while Fig. 4a is for the diodes of D3 and D4. As a result, the expression of voltage stresses of D1–D5 is illustrated as follows:

$$ V_{D1, stress} = V_{C2} = \frac{{V_{bus} }}{2 - D} $$
(10)
$$ V_{D2, stress} = V_{C1} = \frac{{V_{bus} }}{2 - D} $$
(11)
$$ V_{D3, stress} = V_{C1} = V_{C2} = \frac{{V_{bus} }}{2 - D} $$
(12)
$$ V_{D4, stress} = V_{C1} - V_{C3} = \frac{{V_{bus} }}{4 - 2D} $$
(13)
$$ V_{D5, stress} = V_{C3} = \frac{{V_{bus} }}{4 - 2D}. $$
(14)

3.3 Current stresses of semiconductors

According to (6), the ratio of the DC input current and output currents can be expressed as

$$ \frac{{I_{bus} }}{{I_{o} }} = \frac{D}{4 - 2D}. $$
(15)

In ISDC, the average of the inductor current, IL1(avg), is equal to the input current. That is,

$$ I_{L1(avg)} = \frac{D}{4 - 2D}I_{o} . $$
(16)

In addition, while the duty ratios of both switches are equal, the average currents of L2 and L3, IL2(avg) and IL3(avg), will be identical and half the output current Io.

$$ I_{L2(avg)} = I_{L3(avg)} = \frac{1}{2}I_{o} . $$
(17)

Therefore, the current stresses of S1 and S2 can be determined from Fig. 4a, c, respectively.

$$ I_{ds1,stress} = I_{L2(avg)} = \frac{1}{2}I_{o} $$
(18)
$$ I_{ds2,stress} = I_{L3(avg)} = \frac{1}{2}I_{o} . $$
(19)

For diodes, the current stresses of D1 and D2 can be determined based on Fig. 4a, both of which are half the inductor current of L1 and can be expressed as

$$ I_{D1,stress} = \frac{1 - D}{{4 - 2D}}I_{o} $$
(20)
$$ I_{D2,stress} = \frac{1 - D}{{4 - 2D}}I_{o} . $$
(21)

While referring to Fig. 4b, the current stresses of D3 and D5 will equal the inductor current of L1 and L3, respectively. In addition, from Fig. 4b, c, the current stress of D4 can be determined by the inductor currents of L2 and L3. Therefore,

$$ I_{D3,stress} = \frac{D}{4 - 2D}I_{o} $$
(22)
$$ I_{D4,stress} = \frac{1}{2 - 4D}I_{o} $$
(23)
$$ I_{D5,stress} = \frac{1}{2}I_{o} . $$
(24)

4 Design consideration

4.1 Boundary condition of inductance

The determination for the inductances of L1, L2, and L3 have to be contacted to ensure that the ISDC can be in CCM operation. The procedure for finding the boundary condition of an inductor is first to derive the expression of its minimum current and then set this value to zero.

The minimum current of L1, IL1(min), is equal to IL1(avg)–0.5ΔiL. The IL1(avg) is illustrated in (16), and the current change, ΔiL1, can be estimated as

$$ \Delta i_{L1} = L_{1} \frac{{dv_{L1} }}{dt} = \frac{{2(1 - D)V_{o} }}{{L_{1} f_{s} }}. $$
(25)

In (25), the fs stands for switching frequency. Assume IL1(min) is zero. Accordingly, the minimum value of L1 for CCM operation, L1(min), is thus obtained as

$$ L_{1(min)} = \frac{{{2}(2 - D)(1 - D)}}{{Df_{s} }}R_{o} . $$
(26)

For L2 and L3, which have the same values and share output current equally with interleaving, their current ripple is estimated as

$$ \, \Delta i_{L2} = \Delta i_{L3} = \frac{{(1 - D)V_{o} }}{{L_{2} f_{s} }}. $$
(27)

Therefore, the minimum inductance to ensure CCM operation will be

$$ L_{2(min)} = L_{3(min)} = \frac{(1 - D)}{{f_{s} }}R_{o} . $$
(28)

If Ro = 4.6 Ω and fs = 100 kHz, based on (26), Fig. 6a depicts the relationship between inductance L1 and duty ratio D. Similarly, according to (28), Fig. 6b illustrates the relationship between L2 (L3) and duty ratio D.

Fig. 6
figure 6

The relationship between inductance and duty cycle: a L1 and b L2 and L3

Full size image

4.2 Capacitance

The value of a capacitor directly influences the variation of voltage ripple. As discussed in Sect. 2, capacitors C1 and C2 discharge parallelly during Mode 1 and charge in series during the other modes. Therefore, the following relationship holds:

$$ \begin{gathered} C_{1} \Delta V_{C1} = C_{2} \Delta V_{C2} \\ = \frac{{I_{L2(avg)} - I_{L1(avg)} }}{2}DT_{s} = I_{bus} \left( {1 - D} \right)T_{s} . \\ \end{gathered} $$
(29)

The capacitor C3 charges and discharges its stored energy in Mode 1 and Mode 3, respectively.

$$ C_{3} \Delta V_{C3} = I_{L2(avg)} DT_{s} = I_{L3(avg)} DT_{s} . $$
(30)

As for output capacitor Co, it absorbs energy in Modes 1 and 3 and releases stored energy in Modes 2 and 4. Then,

$$ \begin{gathered} C_{o} \Delta V_{Co} = \left( {I_{L2(avg)} + I_{L3(avg)} - I_{o} } \right)DT_{s} \\ = \left( {I_{L2(avg)} + I_{L3(avg)} - I_{o} } \right)\left( {0.5 - D} \right)T_{s} . \\ \end{gathered} $$
(31)

In addition, the DC voltages across the capacitors C1–C3 and Co can be determined by (4)–(6), and the ratio of input current to output current is given in (15). Besides, the average currents, IL1(avg), IL2(avg), and IL1(avg), are calculated as (16) and (17). Then, substituting (15)–(17) into (29)–(31) can yield the estimation of all capacitances, which are summarized as follows:

$$ C_{1} = \frac{{D(1 - D)V_{o} }}{{\Delta V_{C1} (4 - 2D)R_{o} f_{s} }} $$
(32)
$$ C_{2} = \frac{{D(1 - D)V_{o} }}{{\Delta V_{C2} (4 - 2D)R_{o} f_{s} }} $$
(33)
$$ C_{3} = \frac{{V_{o} D}}{{\Delta V_{C3} {2}R_{o} f_{s} }} $$
(34)
$$ C_{o} = \frac{{(1 - 2D)V_{o} }}{{{16}L_{2} \Delta V_{Co} f_{s}^{2} }} = \frac{{(1 - 2D)V_{o} }}{{{16}L_{3} \Delta V_{Co} f_{s}^{2} }}. $$
(35)

5 Expandability

The proposed ISDC can achieve a much lower conversion ratio by increasing the number of CDVS cells, as illustrated in Fig. 7. While with m cells of CDVS, the voltage gain of the ISDC in CCM, MCCM_m, is expressed as

$$ M_{CCM\_m} = \frac{{V_{o} }}{{V_{bus} }} = \frac{D}{2 + 2m - 2mD}. $$
(36)
Fig. 7
figure 7

The ISDC with expandability for achieving a much higher conversion ratio

Full size image

For example, as shown in Fig. 7, the ISDC contains three cells of CDVS, according to (36), which can obtain a voltage gain of 0.033 under a duty ratio of 0.22. Figure 8 depicts the relationship of the voltage gain and duty ratio under different m.

Fig. 8
figure 8

The curves of the conversion ratio versus duty cycle at different m

Full size image

6 Performance comparison

A performance comparison is carried out in this section to illustrate the effectiveness of the proposed converter. Table 1 summarizes the comprehensive comparison with other similar converters in the literature. Assume that turns ratio n = 1 for all converters and the proposed ISDC only with a single CDVS. In Fig. 9, the proposed converter can achieve a better step-down feature over a wide duty-ratio range as compared with other similar state-of-the-art converters. In addition, Table 1 describes that the proposed converter has the advantages of the common ground feature, continuous current operation on both sides of input and output, a wide range of duty-cycle processes, and expandability. Compared with the converter in [27], the ISDC can achieve a better step-down feature even with fewer components. In addition, the ISDC can be in CCM on the input side. In [28], the converter can have a more excellent conversion ratio when D > 0.38. However, its duty cycle is confined within 0.5, unsuitable for a wide input voltage range. Besides, this converter lacks expendable flexibility and is without continuous input current. Concerning [30], even though the converter can accomplish CCM operation at the input and output by utilizing fewer power components, its voltage conversion ratio is unsuitable for high step-down applications and without expandable ability.

Table 1 Comparison of the proposed topology and other converters
Full size table
Fig. 9
figure 9

Voltage gain comparison between ISDC and other similar converters

Full size image

7 Experimental results

A prototype with a 500-W power rating to process 400-V bus voltage and 24-V output is developed to validate the feasibility of the proposed converter. The photo of the prototype is presented in Fig. 10. The switching frequency is 100 kHz. Detailed specifications of the prototype, along with component parameters, are provided in Table 2.

Fig. 10
figure 10

The photo of the experimental prototype

Full size image
Table 2 Experiment parameters and components
Full size table

Figure 11 shows the practical waveforms, in which the duty cycles of switches S1 and S2 are 22%, operating at interleaving with 180° out of phase. Figure 11a presents control signals vgs1 and vgs2 and the corresponding inductor current iL1. Evidently, the inductor L1 operates in CCM. Figure 11b shows the measurement of the interleaved currents of output inductors, which illustrates that the ISDC can effectively suppress output current ripple. Figure 11c is the practical waveforms of switch S1, which reveals that the voltage and current stresses are about 336 V and 10.41 A, respectively, in consistency with (8) and (18). For switch S2, its voltage and current waveforms are shown in Fig. 11d, in which the voltage stress of S2 is around 224 V, and the current stress is 10.41 A, in accordance with (9) and (19), respectively.

Fig. 11
figure 11

Measured waveforms of the proposed converter. a Control signals of S1 and S2 and the corresponding inductor current iL1. b The currents of L2, L3, and the output current. c Voltage and current of S1. d Voltage and current of S2

Full size image

Figure 12 displays the measured waveform of the step-load-change response, in which the load changes from full load to half load and then returns to full load. The measured waveform reveals that the ISDC can keep its output voltage constant even under step load change. In addition, from the zoomed-in waveforms, it can be observed that the output voltage fluctuation is within 1.5 V (that is, below 6%), and the transient time is less than 0.6 ms during the loading and unloading phases of 10 A.

Fig. 12
figure 12

Experimental result: step change of load between 10 and 20 A

Full size image

The diodes D4 and D5 can be replaced with switches S3 and S4 as synchronous rectifiers, as illustrated in Fig. 13, to enhance efficiency further. Figure 14 depicts the efficiency curves from light load to full load, with and without synchronous rectifiers. The maximum measured efficiency is 92.74% without synchronous rectifiers at 350 W and 94.73% with synchronous rectifiers also at 350 W load. While the ISDC is in a situation without the use of synchronous rectifiers, the power budget is estimated in Fig. 15 at full load. Diodes cause a significant part of power loss. That is, utilizing the synchronous rectifiers can accomplish a much better efficiency.

Fig. 13
figure 13

The proposed converter utilizing synchronous rectifiers

Full size image
Fig. 14
figure 14

Efficiency of the proposed converter with and without synchronous rectifiers

Full size image
Fig. 15
figure 15

The power budget of the converter at full load without the utilization of synchronous rectifiers

Full size image

8 Conclusion

An interleaved high step-down converter, ISDC, is proposed in this paper, which is developed by embedding a capacitor-diode voltage splitter and a buck-derived interleaved circuit. The ISDC can intrinsically possess the advantages: high step-down conversion ratio, continuous current on both sides of input and output, EMI interference reduction, expandability for a much higher conversion ratio, interleaving operation at low voltage side, current ripple reduction, low voltage stress and low current stress on active switches, and high efficiency. A 500-W prototype to step down a 400-V voltage to 24 V is carried out to validate the proposed converter. The measurements have verified the correctness of the theoretical analysis and the feasibility of the converter. The maximum efficiency is 92.74% at 350 W. While utilizing synchronous rectifiers, the maximum efficiency can increase to 94.73%. The ISDC can be easily expanded to obtain a much higher conversion ratio, only raising the number of diodes and capacitors without any additional active switch.