1 Introduction

In geotechnical and marine engineering, cohesive coastal and estuarine sediments are commonly referred to as mud. It is a saturated mixture of water, various clay minerals, organic matter and small amounts of sand and silt [3]. This is not to be confused with the customary mixture of water and sand, also called mud. They differ not only in composition but also in behaviour. The flow behaviour of a water–sand mixture changes from Newtonian to granular with increasing sand concentration. Cohesive mud is classified as a non-Newtonian fluid as it possesses a yield strength attributable to the presence of clay minerals. Subjected to stresses smaller than the yield strength, the mud exhibits visco-elastic behaviour. When the yield strength is exceeded, visco-plastic behaviour is observed. This yield strength is the result of inter-particle bondings formed by the clay minerals when the mud is in a low energy environment. This means that the parameters determining this yield strength change with time, which is called thixotropy [34, 37]. The cohesive mud considered in this study originates from the Zeebrugge docks of the Port of Antwerp-Bruges, Belgium. It typically consists mainly of clay minerals and organic material, resulting in fine grain sizes ranging from 0.3 \(\upmu\)m to 120 \(\upmu\)m and a median grain size (d50) of 6.5 \(\upmu\)m. Because of the various hydraulic, chemical and mechanical challenges associated with mud, its behaviour has been and remains the subject of many research projects [37].

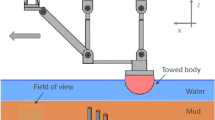
Various physical experiments are used during such projects. Settling experiments in transparent columns are used to study sedimentation and consolidation behaviour of mud [2,3,4, 11, 14, 15, 20, 22, 27, 39]. The objective of these studies is to develop mathematical models to estimate mud sedimentation rates. The sedimentation rate however changes with changing density during the settling process [36], adding to the complexity of such models. The rheological properties of mud are studied using a vane-type rotational rheometer capable of performing both shear stress and shear rate controlled experiments [9, 35]. The rheological properties found, however remain an estimate because they are deduced from the experimental results using an intermediate step where the mud flow velocity during the experiments is estimated based on theoretical calculations. A more specific study is the nautical research on the interaction between a passing vessel, the intermediate water layer and the fluid mud forming the bottom of the navigation channel. Previous studies concluded that further research should preferably be carried out through Computational Fluid Dynamics (CFD) models [13, 38]. Nonetheless, physical towing tank experiments are used to validate such CFD models [21, 29]. The experiments of Sotelo [29] comprised of towing a body through a flume filled with either mud alone or a layer of water on top of a mud layer. During towing, pressure changes in the mud layer and pressures and forces exerted on the body are measured as shown in Fig. 1A. In addition, the emerging flows in the mud are of interest. Also here the correlation between the measured data and the mud flows are however theoretical. Despite monitoring movement of or in the mud would be of great interest for the aforementioned experiments and studies, there is no known technique by which this can be done adequately.

The incentive for this study is the FWO (Fonds Wetenschappelijk Onderzoek) funded project ”Development of a CFD tool and associated experimental validation techniques for fluid mud bottoms disturbed by moving objects” of which the experiments of Sotelo [29] were part. While the settling and rheometer experiments would already benefit from point measurements, a whole-flow field velocimetry technique, like Particle Image Velocimetry (PIV), is preferred for towing experiments. Especially because the preparations for such experiments are labour-intensive, while due to its non-Newtonian and thixotropic properties, the level of repeatability of the behaviour of mud introduces additional uncertainty [7]. For efficiency and quality of the experiments, a single experiment is therefore preferred to a combination of measurements at different locations during multiple experiments. Currently, PIV is widely used in experimental fluid dynamics [26]. In most cases, a transparent fluid is studied, such as air and water. This enables visualisation of the particles through optical illumination. Optical light, however, is greatly attenuated by mud, resulting in hardly any penetration (< mm). This was experimentally observed by Dankers [11], who wanted to track the settlement of particles in mud during sedimentation tests in transparent columns, but was unsuccessful because illumination could not penetrate the mud. Alternative means to visualise particles in mud are therefore required to enable the application of a whole-flow field velocimetry technique in mud.

Fig. 1
figure 1

A Sketch of a towing test setup as currently operated at Flanders Hydraulics (FH), but with the addition of an ultrasound transducer for the application of Ultrasound Image Velocimetry (UIV) as anticipated for in the future. The width of the flume facilitating this setup is 560 mm and the combined thickness of the water and mud layers can reach 500 mm. Towing velocities up to 1.5 m·s−1 are feasible. Apart from the ultrasound transducer, the sketch corresponds to the setup of Sotelo [29]. The ultrasound transducer has been added to illustrate how it can be implemented in such a setup to enable the application of UIV. B Sketch of an experimental setup, previously used by Gurung [16] to study the capability of UIV on sediment-laden flows. The sketch shows a close-up of the interface between the ultrasound transducer and the pipe. This image is copied from Gurung [16]. The main difference with the envisaged setup for towing tests A is the encapsulation of the fluid by the pipe material, causing unwanted loss of ultrasound radiation energy

Full size image

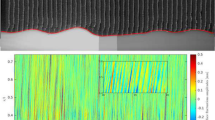
Like for medical purposes, ultrasound imaging, using ultrasound radiation in the megahertz frequency range, allows visualisation in opaque media. It therefore gained interest in the fluid dynamics community, leading to the development of Ultrasound Image Velocimetry (UIV), also known as echo-PIV [24]. The application of UIV in fluid dynamics is relatively new and has developed over the past two decades for various applications. As an example, Crapper [10] was one of the first reported application for sediment transport. Yet only a low density kaolin (clay) suspension was used at very low flow rates. Further development of UIV on sediment laden flows was performed by Chinaud [8] by identifying the limiting factors. The limited recordable flow rates in particular posed a problem for further use of UIV. This is mainly caused by the conventional operating principle of an ultrasonic array for diagnostic imaging. An ultrasonic array is a transducer that contains a number of individually connected piezoelectric elements [31]. It is these elements that convert electrical energy into mechanical energy, in this case sound waves, and vice versa. To optimise image resolution, the elements are excited one after the other. In this process each excitation generates a narrow segment of the overall final image. Merging all the segments forms the overall final image. This is referred to as ”electronic swee**” [30]. The time required to obtain the total image is thus equal to the number of elements times the return time of the sound wave after reflection at the desired depth range (Fig. 2). Because in diagnostic imaging the importance of image quality prevails, this incremental process, which results in a ”slow” acquisition rate, is not an issue. Since the application of UIV requires the ability to capture the displacement at the flow rate between two consecutive images, the acquisition rate in sweep mode may quickly prove insufficient, even for a limited depth range. This was addressed by Poelma [25] by introducing a novel steering sequence of the elements, referred to as ”interleaved imaging”, enabling to double the frame rate. This technique however requires access to the transducer imaging read-out protocol allowing it only to be used with research oriented equipment. Another operational mode that allows higher acquisition rates is used in plane wave imaging. Hardware limitations aside, plane wave imaging allows frame rates in the kilohertz range [33]. In plane wave mode, all piezoelectric elements are excited simultaneously. In this way, an image with a width equal to the width of the array is generated in the time frame of a single acquisition. For example, in the case of an array transducer consisting of 64 piezoelectric elements, the frame rate in plane wave mode is 64 times faster than in swee** mode (Fig. 2). Recently, plane wave imaging has been further developed for medical purposes, making it more available in medical devices [18]. Plane wave imaging was therefore used by Dash [12] to further develop UIV in particle-laden flows at higher flow rates up to almost 1.5 m·s−1.

Fig. 2
figure 2

Sketches outlining the difference between the operating principles of swee** and plane wave of a linear ultrasonic array. When swee**, the piezoelectric elements are excited consecutively. The time between two excitations allows sufficient time for the sound wave to propagate to the desired depth and back to the transducer after reflection. Each excitation results in an image with a width equal to the width of the element. Merging all the images derived from the excitation of each element creates an overall image with a width equal to the width of the array. In plane wave mode, all elements are excited simultaneously, resulting in an image with a width equal to the width of the array in a single acquisition. Hence, the difference is the time required to acquire the image, which is the number of elements times faster in plane wave than in swee** mode. This increase in acquisition rate does come at the expense of image quality. The ultrasound images shown are speckle pattern images as in the case of ultrasound imaging of mud

Full size image

Meanwhile, the application of UIV to sediment-laden flows has found various applications. Gurung [17] used UIV to determine rheological properties of the fluid. Others used UIV to characterise the topography of a sediment bed [41] or infer sediment concentration from local scattering intensity [40]. However, clay suspensions and drilling fluids were used in these studies and not natural muds. In addition, most experiments were performed with a fluid flowing through a pipe (see Fig. 1B), which restricts the depth and makes it impossible to determine the full depth range of UIV. Moreover, the intermediate pipe material between the ultrasound transducer and the mud causes unwanted loss of ultrasound energy. Both by reflection at the two interfaces, transducer-pipe and pipe-fluid interfaces, and by attenuation while propagating through the pipe material. To fully utilise the potential of the ultrasound energy, it is therefore preferred to install the ultrasound transducer flush with the walls containing the mud, as illustrated in Fig. 1A. The capability of UIV to record flow dynamics in natural mud was assessed in [6]. This study showed that ultrasound imaging in mud results in speckle pattern images. Speckle pattern images have a grainy structure resulting from the interference of backscattered ultrasound signals. The image shown as the result of ultrasound imaging in Fig. 2 is a speckle pattern image. The variation in pixel brightness make such images ideal for cross-correlation techniques like PIV. Because the speckle patterns are determined by the position of scatterers in the fluid, such techniques can be used to record flow dynamics in that fluid. Using the speckle tracking function of a standard medical ultrasound scanner, the proof of concept was provided in Zeebrugge mud with a density of 1.13 g·cm−3 to a depth of about 25 mm. Speckle tracking is a cross-correlation algorithm similar to PIV, but specifically developed for application to images containing speckle patterns.

Due to attenuation of ultrasound radiation, the quality of ultrasound images degrades with increasing depth. To further customise UIV for application in towing experiments such as those conducted by Sotelo [29] and Lovato [21], the acoustic attenuation rate of Zeebrugge mud was assessed earlier in [5]. This degradation of image quality with depth is likely to affect both the depth range as well as the accuracy of the measurements. The latter is examined in this study by means of experiments in which UIV was applied in Zeebrugge mud. To create a reference against which the output of the UIV can be compared, the choice was made to move the ultrasonic transducer at a known velocity while the mud remains at rest. After all, the velocity of this relative motion between the transducer and the mud can be accurately controlled by simple mechanics. The towing velocities applied by Sotelo [29] range from 100 mm·s−1 to 500 mm·s−1. Based on the potential theory of flow around the cylinder [1], flow velocities double the towing velocity are to be expected. Multiple velocities ranging between 500 mm·s−1 and 1750 mm·s−1 were therefore applied during the experiments of this study.

2 Experiments

2.1 Experimental setup

To validate a cross-correlation flow velocity measurement technique, the technique is usually applied to a flow with known or measured properties. In this way, the output of the technique can be verified. As discussed in section 1, current existing CFD models developed to simulate the behaviour of mud are based on simplifications and do not take into account the full complexity of mud. Therefore, an induced mud flow, however controlled, cannot yet be used for validation. Moreover, because of the preferred open-channel arrangement (Fig. 1), flow measurement using an alternative measurement technique, such as an electromagnetic flowmeter [12], is no option either. Therefore, it was chosen to work the other way round, by moving the recording device, in this case the ultrasonic transducer, through stationary mud at known velocities. Using simple mechanics the motion of the transducer, and hence the relative velocity between the transducer and the mud, can be well controlled. To enable transmission of ultrasound radiation in the mud, the emitting part of the ultrasonic transducer must be immersed in the mud. Moving the transducer while immersed will induce flows in the mud, biasing the flow measurements. Because of the viscosity of the mud [29], the depth to which flows are induced is however expected to be limited.

To facilitate this, a small-scale setup as shown in Fig. 3 was prepared. The setup consists of a basin of about 100 mm wide, 100 mm high and 500 mm long, to contain the mud. The mud used originates from the Zeebrugge docks of the Port of Antwerp-Bruges (Belgium). Prior to starting the experiments, it was prepared to a homogeneous density of 1.15 g·cm–3 by mixing it with seawater sampled at the same location. The experiments took about 30 min. Although sedimentation starts immediately when the mud is left at rest, no significant settling occurs in such a time frame [7]. A uniform density can thus be considered throughout the experiments. Consequently, the ultrasound attenuation and ultimately the depth range of the UIV technique can be considered equal for all experiments. Similarly, the speed of sound through mud, which is hardly affected by the density of the mud anyway [6], can also be considered the same for all experiments and was set at 1470 mm·s−1 to determine the vertical scale (Z-axis in Figs. 3 and 4). A rail was mounted above the basin to provide horizontal motion of a carriage. A stepper motor was installed next to the rail to drive the carriage, which was transmitted by a belt. The resolution of the stepper motor (i.e. movement per step) was fixed to allow accurate control of the velocity. A downward stand was attached to the carriage on which the ultrasonic transducer was clamped. The horizontality of the rail and verticality of the stand were set with the accuracy of a conventional spirit level. The tip of the transducer, from where the ultrasound radiation is transmitted and received, is inserted several millimetres into the mud. This is to avoid the presence of a layer of air between the transducer and the mud. Such a layer of air would cause high reflection and thus prevent the ultrasound energy from entering the mud. Because of the corrosive nature of the seawater present in the mud, the tip of the transducer was protected by a sheath-shaped rubber. The rubber was filled with water, again to avoid the presence of air and maximise the transfer of radiation from the transducer to the rubber material.

Fig. 3
figure 3

Sketch of the experimental setup used during this study: (1) basin to contain the mud; (2) stepper motor providing the drive of the carriage; (3) belt transmitting the drive from the stepper motor to the carriage; (4) carriage with vertically fixed stand; (5) ultrasound array transducer clamped to the stand

Full size image

Prior to the experiments, the accuracy of the carriage velocity was verified, by measuring the attained velocities and comparing them with the set target velocities. A velocity of 500 mm·s−1 was produced with an accuracy of 99.72 %, while for higher velocities a decrease in accuracy of 0.15 % per 250 mm·s−1 velocity increment was observed.

2.2 Instrumentation and data processing

2.2.1 Ultrasound imaging equipment

Ultrasound images were acquired using the ultrasound imaging system HD-PULSE, which was developed for medical research [23]. The scanner was equipped with a linear phased array transducer (P2-5AC Samsung) consisting of 64 elements with a pitch of 0.22 mm. It generates sound waves with a centre frequency of 3.5 MHz over a fractional bandwidth of 60 %. The array was operated in plane wave mode (see section 1), resulting in an average image acquisition rate of 354.2 ± 8.2 frames per second.

2.2.2 Data processing

Conversion of the raw data into conventional digital images was done by envelope detection (absolute value of Hilbert transform), log compression (20\(\cdot\)log10(Data)) and normalisation to maintain a dynamic range of -60 dB to 0 dB. No additional image processing of the images was performed prior to analysis by the PIV algorithm. This way, a set of 500 images was acquired for each experiment, representing a time frame of about 1.4 s. In preparation for processing with the PIV algorithm, each image other than the first and last is copied. This allows 499 pairs of consecutive images to be formed to facilitate cross-correlation processing. Each pair results in a vector field as output from the PIV algorithm.

2.2.3 PIV algorithm settings

The open access OpenPIV python script [19] was used as the PIV algorithm. Because all elements emit ultrasound pulses simultaneously, there is no steering [32], so the width of the images is constant and equal to the size of the array. With the array used, this is limited to 13.9 mm or 139 pixels (correlation of 10 pixels/mm). Even for UIV, such limited width of images is unusual. A linear array is commonly used [12, 16], which typically has a width of about 40 mm. The use of a phased array in this study was dictated by the required frame rate, which was more limited for the scanner compatible with the available linear array. For the application of PIV, this limited width poses constraints on the choice of interrogation window sizes and overlap. Two main restrictions of the OpenPIV script must be taken into account when choosing the size of the interrogation windows and their overlap. Firstly, because the correlation is Fast Fourier Transform (FFT) based, the maximum recordable displacement is limited to half the size of the interrogation windows. And secondly, the dimensions selected should accommodate for at least four windows, i.e. three window overlaps, in both vertical and horizontal directions:

$$\begin{aligned} \frac{image\;width - window\;size}{window\;size - overlap}\ge 3 \end{aligned}$$
(1)

To avoid oversampling of the data (i.e. excessive resolution of the vector field output of the OpenPIV script), an overlap of 50 % of the window size is additionally recommended and commonly used [28]. In case of images limited in width, this recommendation, in combination with the aforementioned limitations, strongly limits the maximum recordable displacement and hence velocity. In this case, with a maximum window size of 54 x 54 pixels and thus an overlap of 27 pixels, this is limited to 956 mm·s−1. The recording of higher velocities is however envisaged. This requires larger interrogation windows and therefore greater window overlap to meet the requirement of at least three window overlaps (Eq. 1). This in turn will increase the resolution of the vector field, since the spacing between the vectors is equal to the difference between the size of the windows and their overlap. The latter leads to longer processing times, which is not always wanted. Given the nature of this study, which is merely to validate the UIV technique, larger overlaps were permitted, although at the cost of longer processing times. To maintain a practical processing time, the combination of a window size of 100 x 100 pixels and an overlap of 88 pixels is considered the limit, resulting in a theoretical maximum recordable velocity of 1771 mm·s−1. Two iterations were allowed for each run of the OpenPIV script. The window size and overlap of the second iteration are half of those of the first iteration. The window size of the first iteration determines the maximum recordable displacement, while the window size and overlap of the second iteration will determine the resolution of the vector field. Further settings are the threshold values for the vector validation filters. Four filters are applied based on the displacement, the signal-to-noise ratio (SNR - ratio of the maximum possible measure (power) of the signal to the power of distorting noise (i.e. peak-to-peak)), the global standard deviation and the median test. The filter based on the displacement was disabled by setting a threshold far too high. The other threshold values were determined after multiple processing with varying values to assess their impact. Thereby the UIV depth range showed to be optimal with the SNR threshold set at 1.25. Therefore, this value was retained for all further experiments. The influence of the set thresholds for global standard deviation and median test was found to be marginal. The thresholds for these two statistical filters were therefore set to arbitrary values, 5 and 3, respectively. Vectors that do not meet the set thresholds are masked and not considered further.

2.3 Experimental programme

All scans were performed with the ultrasound frequency set at 3.5 MHz. The carriage accelerated until the target velocity was reached. This velocity was maintained for a maximised period followed by deacceleration to a final stop. Target velocities range from 500 mm·s−1 to 1750 mm·s−1 in increments of 250 mm·s−1. The useful length over which the carriage could move was limited to 480 mm. The acceleration was limited by the stability of the clamped ultrasound array. For most experiments, an acceleration of 6000 mm·s−2 was sufficient for an adequate period of uniform velocity. For the last experiment with target velocity of 1750 mm·s−1, the acceleration had to be increased to 7000 mm·s−2. For each experiment, the combinations of minimum interrogation window size and overlap that allow at least the acquisition of the target velocity were determined. The results are summarised in Table 1.

Table 1 Overview of the settings of each experiment, along with the minimum required window size and overlap to allow recording of the enforced uniform velocity
Full size table

3 Experimental results

As mentioned in section 2.2.2, the OpenPIV algorithm produces vector fields as output. This vector field is generated in both data format (txt file) and visual format (image file). An example of such a visualised vector field is shown in Fig. 4. Each vector represents the velocity and direction of flow at the corresponding point in the cross section. Considering the configuration of the experimental setup, the direction of the vectors should be consistent, which can be verified visually. For each row of vectors, representing a depth according to the vertical spacing between the vectors (see section 2.2.3), the average velocity is calculated, resulting in a average vertical velocity profile. As an example, the vector row corresponding to a depth of 24 mm is marked in yellow on Fig. 4. Doing so for all vector fields generates 499 average vertical velocity profiles for each experiment. These profiles are used for further processing of the experimental results.

Fig. 4
figure 4

Example of a visualised vector field generated by the OpenPIV algorithm. This concerns vector field number 204 of experiment 1, corresponding to the period of uniform velocity. Consequently, the vectors visualise the target velocity of 500 mm\(\cdot\)s\(^{-1}\). To ratify this, the horizontal and vertical velocity components (u and v) of the marked vector on the left are specified. Apart from some artefacts, the direction of the vectors is uniform and virtually horizontal from right to left. The row of vectors corresponding to a depth of 24 mm is marked in yellow

Full size image

3.1 Average velocity profile over time

Based on the average vertical velocity profiles, the measured change in velocity can be plotted as a function of time for each depth corresponding to a vector row and for each experiment. To validate the measured velocities, a profile of the enforced velocity is plotted along, as shown for multiple experiments in Fig. 5.

Fig. 5
figure 5

Plots of the average velocities measured at a depth of 24 mm (blue markers) along with the imposed velocity during the experiment (orange curve). Both plotted as a function of time. The velocities were measured using UIV. Multiple plots are depicted for different experiments with target velocities of 500 mm\(\cdot\)s\(^{-1}\) (A), 750 mm\(\cdot\)s\(^{-1}\) (B), 1000 mm\(\cdot\)s\(^{-1}\) (C) and 1500 mm\(\cdot\)s\(^{-1}\) (D), respectively

Full size image

3.2 Measurement accuracy as a function of depth

To allow further examination of the influence of depth on the accuracy of the velocity measurements, a selection of vector fields corresponding to the periods of uniform velocity during the experiments was made for each experiment. Using the average vertical velocities profiles of these selected vector fields (see section 3.1), the average and standard deviation of the velocities over the period of uniform velocity are calculated for each vector row. Each row of vectors represents a depth, which is determined by the vertical distance between the vectors (see section 2.2.3). By plotting these average measured velocities against the depth at which they were measured, as shown in Fig. 6, the influence of depth on the accuracy of the measured velocities can be assessed.

Fig. 6
figure 6

Graphs showing the average and standard deviation of the velocities measured during the period of uniform velocity, as a function of depth. The upper graph is the result of the measurements of experiment 1, with target velocity 500 mm·s−1. The lower graph is the result of the measurements of experiment 3, with target velocity 1000 mm·s−1. Arbitrary boundaries of ± 5 % and ± 10 % deviation from the target velocity are indicated by the green and red dashed lines

Full size image

3.3 Depth range as a function of window size

To assess the influence of interrogation window size on the depth range, additional processing of the images was performed using multiple window sizes. Using all combinations of window size and overlap listed in columns 5 and 6 of Table 1, multiple graphs as shown in Fig. 6 were generated for each experiment. The depths from where the average velocities tend to deviate more than ± 5 % and ± 10 % under the influence of window size and for different velocities are presented in Fig. 7. Overlap** curves indicate such a rapid decline in average velocity, making it impossible to distinguish between the depths from which the deviation starts to exceed ± 5 % and ± 10 %. When no markers are shown in the curves at an applied window size, it means that there was no validated output in that case.

Fig. 7
figure 7

Curves showing the depths at which the average velocities starts to deviate by more than ± 5 % and ± 10 % of the enforced velocities, as a function of the window size used during cross correlation processing and per velocity. The reference values for deviation of ± 5 % and ± 10 % are chosen arbitrarily and visualised by a solid curve with circular markers and a dashed curve with diamond-shaped markers, respectively

Full size image

4 Discussion

4.1 Validation of velocity measurements

Plots A, B and C in Fig. 5 show a good match between the measured and the enforced velocities. Plot D shows that the measurable velocity is limited, in this case to approximately 1100 mm·s−1. Nonetheless, as elaborated in section 2.2.3, the combination of window size (100 pixels) and overlap (88 pixels) used for this experiment (see Table 1) should allow the measurement of velocities up to 1771 mm·s−1. This indicates that factors other than window size also can limit the maximum recordable displacement, hence velocity.

While searching for the minimum window size and overlap to allow recording of the target velocity (see section 2.3), such limits in the recordable displacement (d\(_{max,rec}\)), and thus velocity, smaller than those imposed by the window size (d\(_{max,set}\)) were also encountered. An overview is provided in Table 2. Apart from the value associated with the window size of 72 pixels, the different values for the ratio \(\frac{d_{max,rec}}{d_{max,set}}\) show an inverse proportional relation with the window sizes. The inconsistent value for the window size of 72 pixels is caused by outlier maximum velocities in the dataset. Such outliers are not present in the datasets of the other window sizes. When excluding these outliers, the maximum velocity in the dataset of window size of 72 pixels is 1075 mm·s−1. The corresponding \(\frac{d_{max,rec}}{d_{max,set}}\) ratio does fit well with the overall linearly decreasing trend.

So as the windows enlarge to enable measurement of larger displacements and hence velocities, the largest measured displacement deviates further from the theoretically maximum measurable displacement. In other words, with increasing velocities, the largest measurable velocity is determined more by constraints other than the theoretical maximum displacement of half the window size. The decreasing number of markers with increasing velocity in the plots of Fig. 5 already indicate this. Each vector field (499 per experiment, see section 2.2.2) should yield a marker in these plots. However, if there are no validated vectors at the selected depth in that vector field, no marker is plotted.

Table 2 Overview of the largest recorded displacements, arranged by window size, and how they relate to the maximum recordable displacement equal to half the window size. WS stands for window size, d\(_{max,set}\) is the maximum recordable displacement following the settings during processing with the OpenPIV script [mm], V\(_{max}\) is the largest measured velocity across all experiments processed using the corresponding window size and d\(_{max,rec}\) is an approximation of the largest recorded displacement determined by dividing the largest measured velocity by the average frame rate of 354.2 Hz (see section 2.2.1)
Full size table

Based on the set thresholds of the vector validation filters and the observed impact of these filters (see section 2.2.3), the SNR-based filter seems to be a plausible cause for the increasing number of unvalidated vectors. A curve showing the number of validated vectors as a function of the measured horizontal velocity is therefore shown in Fig. 8. A clear decrease in the number of validated vectors with increasing velocity can be observed, confirming this hypothesis. Furthermore, peaks in the number of validated vectors can be observed around the target velocities of the experiments. These peaks become less pronounced at higher velocities. Plots of markers corresponding to the SNR values of the validated vectors relative to the horizontal velocity (also shown in Fig. 8) show that this is merely caused by the longer periods of uniform velocity corresponding to these target velocities. Indeed, considering the values of each experiment separately, it can be observed that high SNR values are also recorded during the periods of acceleration and deceleration (i.e. at lower velocities).

The identified relation between SNR and velocity is however indirect. In fact, the decrease in SNR is caused by the enlarged windows enabling the recording of larger displacements and hence velocities. This is illustrated by Fig. 9, which shows two series of SNR values resulting from processing the same recordings from an experiment, but using different window sizes. Both window sizes are sufficient to capture the displacements corresponding to the target velocity. Yet a clear distinction is observed in SNR’s, with higher values after processing with smaller windows.

Fig. 8
figure 8

Plot of the SNR of validated vectors relative to the horizontal velocity component of those same vectors. The SNR values are plotted as markers corresponding the the vertical axis on the left. Secondly, a red curve is plotted showing the total number of validated vectors as a function of velocity. This curve corresponds to the vertical axis on the right. All validated vectors at a depth of 24 mm of experiments 1, 2 and 3 are considered (Table 1)

Full size image
Fig. 9
figure 9

Plots of the SNR of all velocity vectors at a depth of 24 mm, resulting from experiment 1 (see Table 1), relative to the corresponding horizontal velocity component of those vectors. The results of PIV processing with different window sizes (WS) over two iterations are shown. The window sizes of both iterations are mentioned (i.e. first/second iteration) and expressed in pixels

Full size image

4.2 Accuracy of velocity measurements

The plots shown in Fig. 6 should be discussed in conjunction with the plots of average velocities at different depths in Appendix A. The plot at the top in Fig. 6 of experiment 1, with a target velocity of 500 mmm·s−1, shows that the deviation of the average measured velocities from the target velocity remain under ± 5 % and ± 10 % to depths of about 33 mm and 38 mm, respectively. When measuring at greater depths, the measured velocities are increasingly below the enforced velocity and the standard deviations increase. Both indicate a decrease in accuracy with increasing depth. These conclusions are confirmed by observations in the plots of experiment 1 in Appendix A. Firstly, an increase in the relative number of average measured velocities underestimating the imposed velocity can be observed with increasing depth. Secondly, the degree of underestimation increases with increasing depth. Finally, the number of markers, and thus validated vectors, decreases with depth. At greater depths, such as 54 mm, the number of validated vectors is still sufficient for a correct statistical analysis. Their inaccuracy, however, is too great for them to be relevant.

At higher velocities, as in experiment 3 with a target velocity of 1000 mm·s−1 (plot at the bottom in Fig. 6), the graph first shows a decrease in deviation with increasing depth, until an optimal match with the target velocity is achieved from a depth of, in this case, 20 mm. This is maintained until a depth of about 36 mm. From then on, there is a trend of increasing deviation with increasing depth, similar to experiment 1. At the end of the depth range where there is good agreement with the imposed velocity of 1000 mm·s−1 (i.e. between 28 mm and 36 mm), the smaller standard deviations of experiment 3 stand out compared to those of experiment 1. This is unlikely to indicate a lower variation in measurements, and can be explained by the plots of experiment 3 in Appendix A. These plots show the same trends as for experiment 1, but due to the higher velocity, the SNRs of the vectors are lower and the time span of uniform velocity is shorter. Hence, compared to experiment 1, the number of validated vectors (indicated by the number of markers) is already lower at the shallower depths. With a further decrease, the number of validated vectors from a depth of 36 mm, becomes so low that the standard deviation can no longer be considered representative. The aforementioned initial decrease in deviation during the first 20 mm is also unexpected. After all, the intensity of the pixels on the images is high at the beginning and decreases linearly with depth. Therefore it is unlikely that the inaccurate measurements at low depths are related to the pixel intensity. This observation is discussed further in section  4.3, demonstrating that it is solely related to the setup of the experiments.

Figure 7 shows that there is an optimal window size for each velocity, which optimises the depth to which velocities can be measured within the allowed limits of deviation. This optimal window size increases with increasing velocity. The perception of a decreasing depth range due to oversized windows is however somewhat contradictory. After all, an increase in window size typically increases the SNR and hence the validation of the resulting vector. This at least holds true in the case of a uniform particle density in the windows [26]. For ultrasound speckle pattern images, the particle density corresponds to the contrast ratio in the patterns, and thus to the pixel brightness which in turn degrades with depth [5]. In other words, from a certain depth the contrast ratio becomes insufficient for cross-correlation processing. When approaching this depth limit, the overall detectable displacements per window therefore decrease with increasing window size. Consequently, the SNR value of the vector resulting from those windows decreases, filtering out the vectors earlier and thus reducing the depth range. Furthermore, it can be observed that for velocities of 1000 mm·s−1, the optimum window size will be larger than the maximum window size of 100 pixels for this image width (see section 2.2.3). This indicates that with wider images, not only can higher velocities be measured (see section 2.2.3), but also at greater depths.

4.3 Zone of influence of moving transducer

As discussed in section 2.1, the motion of the immersed transducer will induce flows in the mud that will distort the velocity measurements. Due to the viscosity of mud, the depth to which such flows are induced is expected to be limited. Hence, the validity of the velocity measurements is subject to the depth at which the measurements are conducted. The depth threshold, from which undistorted measurements can be made can be determined from the variation in vertical velocity profiles. Whereas each row of vectors shows a horizontal velocity profile at a given depth (as depicted in Fig. 4), each column of vectors shows a vertical velocity profile at a given horizontal position in the image. For each experiment, a vertical profile of the standard deviation was calculated taking into account all vector columns of all vector fields. A plot of these profiles is shown in Fig. 10. The trend of all profiles is similar. For all profiles, relevant data can only be found from a depth around 10 mm. This is preceded by a blind zone with no recordings and a zone of noise. The blind zone is visualised by the black strip at the top of the ultrasound image (see Fig. 2). Its thickness corresponds to the duration of transmission of ultrasound by the transducer. After all, no recordings can be made while transmitting. The noise is caused by the ultrasound scanner’s electronics. This is more difficult to distinguish from the speckle because it is also visible as a grainy greyscale pattern on the image. Although it is similar for all images, there is some variation, which the cross-correlation algorithm may register as movement. Hence, some SD (Standard Deviation) values can be seen in this zone. Because of their origin, these can be neglected. The relevant data start with high SD values indicating a large variation in measured velocities. The depth range covered by this part increases with increasing velocity. For target velocities of 500 mm·s−1 (experiment 1), 750 mm·s−1 (experiment 2) and 1000 mm·s−1 (experiment 3), it covers up to depths of about 12 mm, 14 mm and 16 mm, respectively. From these depths, the variation in measured velocities is small until the depths with higher inaccuracy are reached (Sect. 4.2), where variation increases again.

Fig. 10
figure 10

Vertical profiles of standard deviation of the measured velocities during the periods of uniform velocities of experiments 1, 2 and 3 (Table 1)

Full size image

Because the depth to which the flow is induced by the moving transducer is likely to increase with increasing velocity, the parts with large standard deviation values (up to depths of 12 mm, 14 mm and 16 mm for experiments 1, 2 and 3, respectively) are considered to correspond to the zone of influence of the moving transducer. The transition to a lower variation in measured velocities as from these depths confirms this. After all, considering the configuration of the test setup, uniform velocity vectors are to be expected.

5 Conclusion

Small scale laboratory experiments conducted during this study show that UIV can be applied in high density natural muds (containing a high fraction of clay minerals and organic matter) to accurately record mud flow velocities. The flow rates and accuracy obtained with the use of ultrasound scanners for medical use demonstrate the suitability of the technique for application in experimental set-ups involving mud, such as settling columns, rheometer tests and towing experiments. Although only laminar flows were simulated during the experiments, the vector resolution obtained (horizontal and vertical vector spacing ranging from 0.6 mm to 1.2 mm) indicates that more complex flows can also be monitored. Restrictions in flow velocity and depth range were observed.

The maximum recordable flow velocity is determined by both the width of the images and the frame rate of the acoustic scanner. To maximise the latter, the transducer is operated in plane wave mode (see Fig. 2). In turn, this limits the width of the images to the width of the acoustic transducer. For this study, a 13.9 mm wide array operated at a frame rate of approximately 350 Hz was used, limiting the maximum flow velocity to 1100 mm·s−1. A wider transducer would allow for larger interrogation windows during PIV processing, resulting in higher recordable flow velocities. This way, recording velocities up to 2800 mm·s−1 is already feasible with a conventional 40 mm wide linear transducer. Enlarged interrogation windows, however, come at the cost of a lower SNR and thus of lower measurement quality. This quality can be restored by increasing the frame rate. Frame rates up to 4000 Hz are achievable, depending on the equipment used [12], allowing even higher flow velocities to be recorded without compromising quality. A more severe restriction is that on the depth range. Accurate measurements maintained only a few centimetres deep. This is presumably caused by the decreasing pixel intensity with increasing depth hindering the PIV algorithm in the detection of patterns. The decrease in pixel intensity is proportional to the attenuation of ultrasound radiation by the mud, which in turn is determined by the applied ultrasound frequency and the density of the mud. These two variables were however fixed during the experiments of this study. To a lower extent, the depth range can be optimised by the size of the interrogation windows. Indeed, an optimum window size can be found for each velocity that maximises the depth range while preserving accuracy.

With the setup used in this study, a maximum deviation of 10 % of the average measured velocities to the enforced velocity was attained to a depth of 50 mm. For use in towing tank setups as shown in Fig. 1A, this is insufficient. Additional experiments in search of adequate means to optimise the depth range are therefore required. A first option is to lower the ultrasound frequency and/or the density of the mud, leading to less attenuation of the ultrasound. Mud density is however more or less fixed as it should remain relevant to the study. Reducing the ultrasound frequency, on the other hand, is usually unwanted for the more common applications of ultrasound imaging to preserve the axial resolution of the images. In the case of speckle images, axial resolution is however less crucial. Hence, lowering the ultrasound frequency is a valid option. During the experiments of this study, ultrasound with a frequency of 3.5 MHz was used. According to Brouwers [5], the attenuation during the experiments of this study was thus about 5 dB\(\cdot\)cm\(^{-1}\), and lowering the ultrasound frequency to 1 MHz would lead to a halving of the attenuation and thus a probable doubling of the depth range. A second option is to increase the initial pixel intensities by boosting the intensity of the emitted ultrasound radiation. Without affecting attenuation, it is anticipated that this will achieve higher pixel intensities at similar depths and thus increase the depth range.