1 Introduction

Semi-Solid Metal (SSM) processing, an evolving technology in metal forming for near-net-shape components, combines traditional forging and casting practices. Initially applied to nonferrous metals like aluminum, copper, lead, and magnesium, SSM processing involves a liquid matrix with nondendritic grains, resulting in a distinctive globular microstructure. This thixotropic behavior in the semisolid slurry reduces microsegregation and porosity in castings. Processed near-net-shape components exhibit excellent surface quality and uniform microstructures, allowing for further heat treatment to enhance mechanical properties. Due the the enhanced mechanical characteristics the SSM processed components were widely used in the automotive industry. Recent research has focused on develo** techniques for generating nondendritic feedstocks during SSM processing, with two main methodologies: agitation and non-agitation routes. Agitation routes include Mechanical Stirring, Magnetohydrodynamic Stirring (MHD), Swirled Enthalpy Equilibrium Device (SEED), Semisolid Rheocasting (SSR), Direct Partial Remelting (DPRM), Strain-Induced Melt Activated (SIMA), and Recrystallization and Partial Melting (RAP). The non-agitation routes comprise UBE's New Rheocasting (NRC) and the Cooling Slope (CS) methods. Among these methods, the cooling slope (CS) technique is considered to be the simplest method of creating fine globular primary particle having a higher degree of sphericity. In addition to this better formation, energy efficiency, portability, productivity, and cost are better compared to other methods. Nourouzi et al. [1] investigated semi-solid (SSM) Al-silicon alloy cast through mechanical stirring process. This study predicted the temperature and speed of stirring as 608 °C and 300 RPM respectively led to uniform grain distribution resulted in better hardness in the casted billets. Elsharkawi et al. [2] investigated the pouring temperature, swirling-time and swirling speed of semi-solid Al359/20%SiC metal matrix composite produced through rheocasting. Through this procedure, appreciable enhancement of tensile properties were observed while comparing with conventional gravity castings that were achieved through another semi-solid process. Bartex et al. [3] investigated a rheocasting process to analyse the microstructures formation along with tensile properties in Mg–Al alloy having La and Ca (Mg–6Al–3La–1Ca) and achieved non-dendritic and globular microstructures. Crosti and Polvara [4] developed a new technique to produce semiliquid cast of aluminium alloys. Birol [5] carried out thixoforming of hypereutectic A390 alloy, which shows good wear resistance, improved strength, high hardness, reduced thermal deformation, better casting ability with reduced density for which it is considered as the material of choice for heavy wear applications. Taghavi and Ghassemi [6] investigated up on the thixotropic microstructure of A356 Al-alloy and its variation with the length and angle of inclination. Analysis shows the 40° inclination and 40 cm of length is the optimum condition with output response of 28 µm minimum grain size and maximum shape factor of 0.70 with highest uniformity is achieved. Haga et al. [7] investigated the effect of cooling slope parameters like, size of nozzle for pouring the melt, the nozzle-height, slope-tilt and slope-length on the process of making semisolid metal. Better cooling and adhesive strength with increasing in slope length is observed, while cooling slope with smaller angle, cooling rate increases with higher adhesive strength.

With the cooling slope method, many researchers reported in semi-solid alloy preparation [8], better microstructure evolution of A356 [1, 9,10,11], and tensile fracture of fluidized rheocasted A356 [10]. Recent studies also revealed through modeling and simulation, the parameters related to the cooling slope process [12], the effect of pouring temperature and plate obliquity [13, 14] A380 semisolid processing [15], optimization of the degree of sphericity in case of A356 [16] prepared through CS method were investigated. In most of the rheocasted and cooling slope methods microstructure improvement [5, 11, 17,18,19,20,21,22,23,24,25,26,27,28] and mechanical properties [18, 21] and wear behaviours [23, 29] are discussed elaborately for A356 and A380 alloys. Works related to thixoforming by cooling slope method, manufacturing of in-situ composite involving Al356 and A356-5TiB [30, 31]. Kolahdooz and Aminian [32] investigated the semifluid-forming process involving A356. Reheating [33], remelting [34] and Mold vibration effect on microstructure [27] after cooling slope casting were found to be favourable for improved microstructure and better mechanical properties. Das and Dutta [35] studied the globularization on the initial phase of Al–7Si–0.3 Mg Alloy isothermal holding past the cooling slope process. The microstructure was found to be more refined after such heat treatment.

Though there are many parameters (both input and output) involved in cooling slope rheocasting process, limited works are reported on the optimization and regression analysis of this metallurgical process. Kumar et al. [30] developed a Taguchi technique to analyze process parameters related to cooling slope casting and predicted the pouring temperature of 640 °C for a cooling slope length of 300 mm and slope-angle of 60° is favourable for better texture. Goutam et al. [36] carried out parametric optimization related to the cooling slope method used in the semi-solid casting of ADC 12 Al-alloy with a 95% confidence level. Using ANOVA as an analysis tool, the degree of sphericity was optimized (0.865) and particle size (49.30) was monitored for a set of process parameters, such as 585 °C pouring temperature, 500 mm slope-length, and 45° slope-angle. Shehata et al. [37] carried out optimization of pouring temperature in the semisolid casting process of Al-Si alloy for achieving small particle size, uniform distribution, and regular shape were 690 °C and 710 °C in the case of metallic and sand molds, respectively. Decision-making tools like ANN [45] and TSA [46] were found to have applications for engineering applications. While a substantial body of literature exists regarding the fabrication of aluminum alloys incorporating the Cooling Slope (CS), with a consideration of various process variables such as cooling slope length, slope angle, pouring temperature, and nozzle diameter [38], [39], there is a notable gap in research related to the fabrication and analysis of A356 casting using a cooling slope after varying the combination of nozzle height, slope angle, and slope length. While many researchers have explored the impact of process parameters on the microstructure and mechanical characteristics of samples, none have specifically focused on develo** mathematical models that accurately represent the variations in responses of rheocasting. This research aims to fill this gap by addressing this objective.

2 Materials and methods

In the present research, aluminium alloy A356, with given chemical composition is presented in Table 1, is considered input material for fabrication of cylindrical ingot specimen. The A356 in bar stock are procured from VENUKA engineering Private Limited, Telangana.

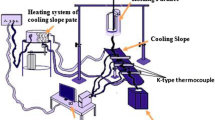
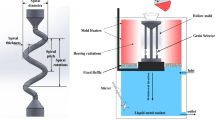
Table 1 Details of A356 and chemical composition
Full size table

During the fabrication process, the predefined weight percentage of A356 is isolated from the bar stock and subjected to heating to its melting state (720 °C) in the furnace shown in Fig. 1a, the heating will be continued and kept at (720 °C) temperature for 45 min to for attain uniform temperature and total dissolution of alloying elements, and then cooled down to pouring temperature and kept for another 45 min. At the desired superheated temperature (630 °C) molten metal was poured into the preheated die cavity through the cooling slope. The cooling slope with a slope length of 1000 mm is fabricated using mild steel (ref. Fig. 2), and the surface is coated with boron nitride to make a smooth passage of molten metal. Here, the cooling slope is designed to act like a counterflow heat exchanger, where water as coolant was allowed to flow underneath at room temperature (30 °C). The flow rate of water was maintained 8 lit per sec. The slope angle is adjustable to perform the experiments at the desired angles as per the requirements. During casting, a constant amount of molten metal is allowed onto the cooling slope through the nozzle, which was kept at the desired height from the surface of cooling slope. The height of the nozzle from the slope was adjustable as per requirement. Once the A356 alloy sample is fabricated, two 10 mm thick circular discs are separated by cutting them from the sample. One circular disc, out of two discs, is given isothermal treatment at 580 °C for 5 min, as reported in [14, 18], and [38]. The test sample using the CS route was fabricated according to the steps mentioned in the flowchart (ref. Fig. 3).

Fig. 1
figure 1

Schematic diagram showing a casting furnace, b split die

Full size image
Fig. 2
figure 2

Schematic diagram of Cooling slope arrangement

Full size image
Fig. 3
figure 3

Flowchart of the methodology

Full size image

3 Measurement of responses

Once the cylindrical specimen of diameter 30 mm and a height of 120 mm is cast, it is cut into a circular disc of a thickness of 10 mm to measure various responses. In the present study, three responses, namely microhardness, grain size, and sphericity, are monitored across the cross-section of the specimen. Before conducting the mechanical and microstructural investigations, the fabricated samples are thoroughly polished with different emery paper grades. Subsequently polished using SiC powder and diamond paste. Further, the polished surface of the sample is chemically treated with Keller’s reagent (1 mL HF, 1.5 mL HCl, 2.5 mL HNO3 and 100 mL H2O) at room temperature to take out unwanted particles on the surface. Once the sample is ready with the glossy surface, it is used to conduct the said investigations. The micrographs shown in Figs. 6 and 7 represent experiment 12 from the design of experiments. From the Figures, it can be noticed that the absence of casting defects such as gas holes, etc. It may be due to the range of process parameters considered at the time of the flow of molten metal over the cooling slope leads to approximately 35–40 percent of the solid fraction of the slurry, estimated using the lever rule. This defined amount of solid fraction will not allow the molten metal to adhere to the cooling slope, resulting in the continuous flow of metal into the die cavity and producing castings without gas holes.

3.1 Microhardness

The microhardness of the sample is measured at three different locations, namely, at the centre, mean, and outer radii of the sample. The Zwick Roell microhardness testing machine and the samples of A356 casting with indentations are given in Fig. 4a and b, respectively. Such analysis is carried out on specimens in two conditions, namely ‘with’ and ‘without’ isothermal treatment.

Fig. 4
figure 4

Schematic diagram showing a Vickers microhardness tester and b specimens with an indentation on the surface

Full size image

While conducting the test, a load of 1 kg is applied for 10 s on the sample using a diamond indenter having an included angle of 136°. The measurements were carried out at five positions along the tracks representing the center, mean, and outer radius (ref. Fig. 2b). The average of five measurements is considered the value of the microhardness of the sample at the respective track.

3.2 Grain size

The size of the grain in the sample is also measured at five locations along the tracks representing the centre, mean and outer radius using the Leica Optical microscope as presented in Fig. 5a. Figures 6 and 7 give such microstructures of the samples prepared with and without isothermal treatment, respectively. The micrographs are considered to evaluate the mean grain size of the test sample taking an area of 400 µm2 as the masking zone, at 4 different locations, with the help of ImageJ software. Each grain's circular diameter in the masking zone is calculated using the Eq. (1) given below.

$$GS=2\sqrt{{A}_{\alpha }/\pi }$$
(1)

here \({A}_{\alpha }\) is the grain area.

Fig. 5
figure 5

Schematic diagram showing a Optical microscope and b sample marked with the tracks along the measurements are taken

Full size image
Fig. 6
figure 6

Micrographs of the sample (SL300mm, SA 60, NH 150 mm) without isothermal treatment at the a center, b mean radius, and c outer radius

Full size image
Fig. 7
figure 7

Micrographs of the sample (SL300mm, SA 60, NH 150 mm) with isothermal treatment at the a center, b mean radius, and c outer radius

Full size image

3.3 Sphericity

The sphericity of the grain is determined by estimating the values of the average grain area and perimeter (ref. Fig. 8) of the grain from the image of the microstructure. It is calculated by using the Eq. (2) given below

$$S=\left(4\pi {A}_{\alpha }/{P}_{\alpha }^{2}\right)$$
(2)

where \({A}_{\alpha }\) and \({P}_{\alpha }\) are the average grain area and perimeter of the grain, respectively. Figure 8 shows the zoomed micrograph with masking area for measurement of grain size and sphericity.

Fig. 8
figure 8

Zoomed view showing the masking area for the measurement of grain size and sphericity

Full size image

3.4 Modelling of CS process using RSM

In the current research, attempts are made to study the influence of various input parameters related to the process of semi-solid A356 alloy pouring along a cooling slope after utilizing RSM. During the CS process, the input variables, namely slope length (SL), slope angle (SA), and nozzle height (NH), are considered as input variables, and micro-hardness (H), grain size (GS), and grain sphericity (S) are taken as process responses. Figure 9 shows the block diagram related to the input–output of the model of the SSM process.

Fig. 9
figure 9

Block diagram of model input–output configuration in the CS method

Full size image

Determining the levels of process parameters was a crucial step taken prior to initiating the experimental work. These parameters were established through a comprehensive literature survey [38], expert recommendations, and preliminary pilot experiments, as outlined in Table 2. Further, the range of parameters namely slope length [13] and [16] nozzle height [7], and slope angle [16] from the experimental studies carried out by various researchers.

Table 2 Input parameters and their levels used in the experimentation
Full size table

Once the casting (ref Fig. 10) is produced as per the levels of the parameters set at the values suggested by the central composite DoEs, the responses like microhardness, grain size, and grain sphericity are recorded. While measuring the responses, two different conditions, namely without and with isothermal heat treatment for 5 min at 580 °C. It is observed that the researchers [13, 14] worked on microstructural investigations of SSM processed samples with isothermal heating at 580 °C for 5 min which is the temperature between liquidus and solidus temperature of the A356 alloy. In the current paper, isothermal heating is done at the above-mentioned temperature to study its effect on the microstructure and mechanical characteristics of the specimen. The responses are recorded at three different points, at the centre, at the mean radius, and at the outer radius of the circular disc (ref. Fig. 5b). The data from the experiment are used to establish the non-linear regression models for the responses, such as H, GS, and S, at three different conditions: isothermal heating with 5 min holding time and without isothermal heating.

Fig. 10
figure 10

Schematic diagram showing a Fabrication of the A356 Alloy sample and b Cast specimen

Full size image

4 Non-linear regression analysis based on CCD

Statistical non-linear regression simulations are developed considering the experimental data obtained during the SSM processing of A356 casting using the CS technique and explained in the subsequent sub-sections. It is important to note that there is a huge variation in the micro-hardness, grain size, and grain sphericity of the casting from the centre to the outer surface. Hence, attempts are made to discuss the influence of process parameters of the CS process on various responses (microhardness, grain size, and sphericity) at the centre, the mean radius, and the outer radius of the circular disc obtained from the casting.

4.1 A356 alloy without isothermal heating

The as-cast A356 alloy sample is cut into a circular disc (ref. Figure 5 (b)), and the readings related to microhardness, grain size, and grain sphericity are measured at three locations across the disc's cross-section. Once the experimental data is obtained, the non-linear regression analysis is performed.

4.1.1 Microhardness

The non-linear regression expression represents the variation of microhardness at three locations, namely, at the center (Hc), the mean radius (Hm), and the outer radius (Ho) of the A356 disc, which are given by Eqs. (3), (4), and represents (5), respectively. It is important to note that a positive coefficient depicts that the value of the independent variable increases leading to an increase in the dependent variables. Further, the magnitude of the coefficient of the independent variable indicates the effect of change in the magnitude of a dependent variable. In the current experimental study, it is observed that the value of the coefficient of slope angle is higher than the value of coefficients of all other factors. Hence, it is considered as the most influencing parameter.

$${H}_{c}=94.31-0.0901SL-0.270SA-0.0018NH+0.000124{SL}^{2}+0.00071{SA}^{2}+0.000054{NH}^{2}\quad +0.00642SL\times SA+0.000054SL\times NH-0.000326SA\times NH$$
(3)
$${H}_{m}=104.01-0.0773SL-0.412SA-0.0237NH+0.000099{SL}^{2}+0.0024{SA}^{2}+0.000069{NH}^{2}+0.000200SL\times SA+0.000165SL\times NH-0.000783SA\times NH$$
(4)
$${H}_{o}=156.65-0.2408SL-1.612SA+0.0224NH+0.000296{SL}^{2}+0.01434{SA}^{2}-0.000149{NH}^{2}+0.000808SL\times SA+0.000229SL\times NH-0.001092SA\times NH$$
(5)

Once the non-linear regression formulations representing the relationship of the microhardness with the process parameters related to the CS process are obtained, the statistical validity of the model is subjected to testing using analysis of variance (ANOVA). The ANOVA tables for Hc, Hm and Ho are given in Table 3a, b and c. From Table 3a, it is understood that all the individual, square, and interaction terms of slope length (SL), slope angle (SA), and nozzle height (NH) are seen to be significant except for the interaction term of SA and NH as the p-values of this term are found to be more than 0.05. Moreover, for the microhardness value at the mean radius, except the square term of slope angle, all other terms are significant (ref. Table 3b). Similarly, for the case of microhardness at the outer radius, except for the square term of nozzle height and the interaction term of slope length and angle, all the terms are significant (ref. Table 3c).

Table 3 Results of ANOVA for microhardness of A356 alloy without isothermal heating
Full size table

Figure 11 shows the surface plots of microhardness with the variation in the level of various input process parameters. From the surface plots (ref. Fig. 11a, b, and c) related to the microhardness at the centre of the specimen, the increase in the values of slope-angle and nozzle height enhances the microhardness. The improvement in the value of the slope angle enhances the metal flow velocity, which washes away the existing nucleation sites and provides space for further fresh nucleation on the cooling slope. Hence, the rate of nucleation increases with slope angle. Moreover, the increase in slope angle provides less duration of contact of molten metal with the slope surface, may not be sufficient for the growth in nuclei, and causes lower solid fractions towards the exit of the cooling slope and entering the die. These nucleation sites contact the neighbouring slurry during solidification and become larger and more spherical, reducing microhardness. The increase in the levels of slope length provides a relatively more contact surface area to the molten metal with the cooling slope. It causes higher nucleation sites with sufficient grain growth time, leading to higher solid fractions.

Fig. 11
figure 11

Impact of input process factors on microhardness of the specimen without isothermal heating at the center (a, b & c), mean radius (d, e, & f), and outer radius (g, h, & i)

Full size image

When this semi-solid slurry enters the die, grains with smaller sizes and less sphericity are formed due to the shortage of neighbouring slurry with lower solid fractions. It is the reason for an increase in the hardness of the casting at the centre. Moreover, the increase in the nozzle height resulted in increasing the microhardness of the casting at the centre. This results in the quick dissipation of heat out of the molten metal before falling onto the slope, leading to rapid cooling and resulting in more amount of solid fraction in the melt. This is the reason for the formation of smaller grain size and sphericity during solidification and resulted in an increase in the value of microhardness of the casting at the centre.

Such surface plots related to the microhardness at the mean radius (ref. Fig. 11d–f) and the outer surface (ref. Fig. 11 g–i) show a similar trend as explained above with respect to the input process variables like slope angle, slope length, and nozzle height. The results show that the microhardness value at the outer radius is higher than the microhardness values at the centre and the mean radius. The said effect may be due to a higher temperature gradient leading to quick cooling and generation of residual stresses resulting increase in microhardness. Further, the R2 values representing the correlation coefficient between the inputs and the responses are equal to 0.982, 0.976, and 0.981 for the microhardness values at the center, mean radius, and outer radius.

4.1.2 Grain size

The regression equations that represent the variation in grain size of the casting at three different locations, namely, at the center (GSc), the mean radius (GSm), and the outer radius (GSo) of the A356 disc are shown in Eqs. (6), (7), and (8), respectively. Since, the negative coefficient indicates due to increase in value of independent variables, the dependent variable also decrease. Further, the level of the coefficient of the independent variable indicates the effect of change in magnitude of a dependent variable. Here, in the regression Eqs. (6–8), it is observed that the value of the coefficient of slope angle is higher than the value of coefficients of all other factors. Hence, it is considered as the most influencing parameter.

$${GS}_{c}=36.27+0.0437SL+0.1308SA+0.00087NH-0.000060{SL}^{2}+0.000346{SA}^{2}-0.000026{NH}^{2}-0.000312SL\times SA-0.000026SL\times NH+0.000326SA\times NH$$
(6)
$${GS}_{m}=26.57+0.0345SL+0.184SA-0.01058NH-0.000044{SL}^{2}-0.00107{SA}^{2}-0.000031{NH}^{2}-0.000089SL\times SA-0.000074SL\times NH+0.000350SA\times NH$$
(7)
$${GS}_{o}=10.25+0.078SL+0.5222SA-0.00725NH-0.000096{SL}^{2}-0.004645{SA}^{2}+0.000048{NH}^{2}-0.000262SL\times SA-0.000074SL\times NH+0.000354SA\times NH$$
(8)

The statistical adequacy of the non-linear regression models developed here for the grain size through the cooling slope casting was conducted by performing ANOVA. Table 4a, b, and c show the ANOVA test results for the grain size variation at the centre, the mean radius, and the outer radius of the casting. From Table 4a, it can be found that the square terms of slope angle and nozzle height and the interaction term of slope angle and nozzle height are seen to have an insignificant contribution to the grain size of the casting at the centre. Further, the square terms of slope length and slope angle and the interaction terms of slope angle and slope length are insignificant to the grain size at the mean radius of the casting (ref. Table 4b). In the case of the grain size variation at the outer surface of the casting (ref. Table 4c), except nozzle height, all the factors are found to have significant contributions to the response.

Table 4 ANOVA output for the grain size of A356 alloy without isothermal heating
Full size table

Figure 12 shows the surface plots indicating variation in grain size at the center, the mean radius, and the outer radius of the casting. From the said plots, it is monitored that the grain size is increased with the increase in the slope angle due to the formation of extra nucleation sites on the cooling slope. Moreover, the grain size is seen to be reduced with the increase in the slope length and nozzle height. It is due to the quick loss of heat that leads to the rapid rise in the solid fractions of the molten metal on the cooling slope. This is the reason for the formation of smaller grain sizes during solidification. Further, the R2 values representing the correlation coefficient between the inputs and the responses are equal to 0.982, 0.976, and 0.981 for the variation of grain size values at the center, mean radius, and outer radius.

Fig. 12
figure 12

Impact of input process factors on grain size of the specimen without isothermal heating at the center (a, b & c), mean radius (d, e, & f), and outer radius (g, h, & i)

Full size image

4.1.3 Sphericity

The mathematical models that represent the variation in sphericity of the fabricated casting specimen at three different locations, namely, at the center (Sc), the mean radius (Sm), and the outer radius (So) of the A356 disc are shown in Eqs. (9), (10), and (11), respectively.

$${S}_{c}=0.4972+0.001352SL+0.00170SA+0.000073NH-0.000002{SL}^{2}+0.00003{SA}^{2}-0.000001{NH}^{2}-0.000011SL\times SA-0.000001SL\times NH+0.000005SA\times NH$$
(9)
$${S}_{m}=0.3735+0.001092SL+0.0033SA+0.000435NH-0.000001{SL}^{2}-0.000007{SA}^{2}-0.000001{NH}^{2}-0.000005SL\times SA-0.000002SL\times NH+0.000009SA\times NH$$
(10)
$${S}_{o}=-0.3044+0.002506SL+0.01859SA-0.000209NH-0.0000036{SL}^{2}-0.00017245{SA}^{2}+0.000001{NH}^{2}-0.000008SL\times SA-0.000002SL\times NH+0.000002SA\times NH$$
(11)

Table 5a, b and c represent the outcome of the ANOVA test conducted for the response sphericity at the center, mean radius, and the outer radius of the A356 cast specimen. It is observed that the square terms of slope angle and nozzle height and the interaction term of slope length with nozzle height are seen to be insignificant in estimating the response sphericity at the center of the casting (ref. Table 5a). In the case of sphericity at the mean radius (ref. Table 5b), except for the square term of nozzle height, and the interaction term of slope angle with slope length has significant contributions. Further, the square term of nozzle height alone is insignificant on the sphericity at the outer radius of the cast specimen (ref. Table 5c).

Table 5 Results of ANOVA for the sphericity of A356 alloy without isothermal heating
Full size table

Further, the response plots showing the variation of sphericity of the grain at the center, mean, and outer radius of the A356 cast specimen are presented in Fig. 13a–i, respectively. It is monitored that an increase in slope angle led to a decrease in slope length and nozzle height has resulted in a rise in the sphericity of the grain. The slope angle increase may lead to lower solid fractions and higher nucleation sites near an exit of the cooling slope. This output in larger grain size with greater sphericity. Moreover, the increase in slope length and nozzle height may result in higher solid fractions and ultimately higher nucleation sites, which causes reduced grain sphericity of the casting. The R2 values of sphericity of the casting at center, the mean, and the outer radius are 0.975, 0.960, and 0.977, respectively.

Fig. 13
figure 13

Impact of input process factors on sphericity of the specimen without isothermal heating at the center (a, b, & c), mean radius (d, e, & f), and outer radius (g, h, & i)

Full size image

4.2 A356 alloy with isothermal heating for 5 min

The isothermal heating is conducted for 5 min at a temperature of 580 °C for the A356 sample produced implementing the cooling slope technique. During isothermal holding, in the early-stage coalescence is the dominant mechanism and later Ostwald ripening appears to be the principal mechanism in the grain growth [5]. This is done to refine the microstructural characteristics and mechanical behavior of the fabricated casting.

4.2.1 Microhardness

The non-linear statistical regression equations represent the variation in microhardness of the casting at three different locations, namely, at the center (Hic), the mean radius (Him), and the outer radius (Hio) of the A356 disc are shown in Eqs. (12), (13), and (14), respectively. Here, in the regression Eqs. (12–14), it is observed that the value of the coefficient of slope angle is higher than the value of coefficients of all other factors. Hence, it is considered as the most influencing parameter. Results of ANOVA for the microhardness of A356 alloy with isothermal heating is presented in Table 6.

Table 6 Results of ANOVA for the microhardness of A356 alloy with isothermal heating
Full size table
$${H}_{ic}=-34.38+0.2227SL+2.441SA+0.0053NH-0.000227{SL}^{2}-0.02318{SA}^{2}+0.000278{NH}^{2}-0.001274SL\times SA+0.000054SL\times NH-0.001711SA\times NH$$
(12)
$${H}_{im}=2.83+0.0898SL+1.994SA-0.0852NH-0.000084{SL}^{2}-0.01948{SA}^{2}+0.000445{NH}^{2}-0.000827SL\times SA+0.000236SL\times NH-0.002063SA\times NH$$
(13)
$${H}_{io}=-17.9+0.2220SL+2.347SA-0.0753NH-0.000305{SL}^{2}-0.02432{SA}^{2}+0.0003885{NH}^{2}-0.000977SL\times SA+0.000236SL\times NH-0.001789SA\times NH$$
(14)

Further, the response plots showing the impact of input process factors on microhardness of the specimen with isothermal heating at the center Fig. 14a–c, mean radius Fig. 14d–f, and outer radius Fig. 14g–i respectively.

Fig. 14
figure 14

Impact of input process factors on microhardness of the specimen with isothermal heating at the center (a, b, & c), mean radius (d, e, & f), and outer radius (g, h, & i)

Full size image

4.2.2 Grain size

The set of mathematical expressions that represent the variation in grain size of the casting at three different locations, namely, at the center (GSic), the mean radius (GSim), and the outer radius (GSio) of the A356 specimen, are shown in Eqs. (15), (16), and (17), respectively.

$${GS}_{ic}=89.00-0.10003SL-1.0932SA+0.00343NH+0.000101{SL}^{2}+0.010330{SA}^{2}-0.000124{NH}^{2}+0.000644SL\times SA-0.000035SL\times NH+0.000688SA\times NH$$
(15)
$${GS}_{im}=72.50-0.0545SL-1.132SA+0.0570NH+0.000061{SL}^{2}-0.01165{SA}^{2}-0.000241{NH}^{2}+0.000435SL\times SA-0.000126SL\times NH+0.000854SA\times NH$$
(16)
$${GS}_{io}=69.17-0.0887SL-0.938SA+0.0301NH+0.000122{SL}^{2}+0.00972{SA}^{2}-0.000154{NH}^{2}+0.000390SL\times SA-0.000094SL\times NH+0.000715SA\times NH$$
(17)

The analysis of the variance of the response grain size at the center, the mean radius, and the outer radius is given in Table 7a, b, and c, respectively. From Table 7a, it was observed that except for the interaction term of slope length with nozzle height, all other terms significantly influence the grain size at the center of the specimen. Further, it is interesting to note that only the square term of slope length is insignificant on the grain size at both the mean and outer radius of the specimen. Moreover, Fig. 15a–i represent the surface plots for the grain size at the center, mean and outer radius of the A356 sample.

Table 7 Results of ANOVA for the grain size of A356 alloy with isothermal heating
Full size table
Fig. 15
figure 15

Impact of input process factors on the grain size of the specimen with isothermal heating at the center (a, b, & c), mean radius (d, e, & f), and outer radius (g, h, & i)

Full size image

The change in grain size with respect to the process parameters has shown a similar trend as that of the variation of grain size under as-cast conditions. The only difference is in the value of grain size variation at all the locations. During isothermal heating for 5 min, the refinement in the microstructure leads to the formation of grains of a larger size. The reason for this is the same as the one discussed above in the case of variation of microhardness of isothermally heated specimens. Finally, the R2 values of grain size at the three specified locations are equal to 0.983, 0.980, and 0.978, respectively.

4.2.3 Sphericity

The statistical models that represent the variation in sphericity of the casting at three different locations, namely, at the center (Sic), the mean radius (Sim), and the outer radius (Sio) of the A356 specimen, are shown in Eqs. (18), (19), and (20), respectively.

$${S}_{ic}=0.2981+0.002062SL+0.00867SA+0.000168NH-0.000002{SL}^{2}-0.000012{SA}^{2}+0.000001{NH}^{2}-0.000018SL\times SA-0.000002SL\times NH+0.000035SA\times NH$$
(18)
$${S}_{im}=0.5722-0.000335SL+0.00867SA-0.000384NH+0.000001{SL}^{2}-0.000092{SA}^{2}+0.000001{NH}^{2}-0.000002SL\times SA-0.000002SL\times NH+0.000002SA\times NH$$
(19)
$${S}_{io}=-0.3459+0.003595SL+0.01515SA+0.000402NH-0.000005{SL}^{2}-0.0001145{SA}^{2}-0.000001{NH}^{2}-0.000013SL\times SA-0.000003SL\times NH-0.000017SA\times NH$$
(20)

Table 8a, b, and c indicate the results of ANOVA for the response sphericity of the A356 specimen at the center, the mean, and the outer radius, respectively. For sphericity at the center of the specimen, except the square terms of slope angle and nozzle height, all other terms have a significant contribution (ref. Table 8a). Further, all the terms are found to be significant (ref. Table 8b) in the case of grain sphericity at the specimen's mean radius. Further, the square term of slope length and the interaction term of slope angle with nozzle height do not significantly contribute to the response sphericity of the grain at the outer radius of the isothermally treated specimen (ref. Fig. 9c).

Table 8 Results of ANOVA for the sphericity of A356 alloy with isothermal heating
Full size table

Moreover, Fig. 16a–i represent the surface plots for the sphericity of the grain at the center, mean and outer radius of the A356 sample. The variation in sphericity of grain with respect to the process parameters has shown a similar trend as that of the variation of sphericity under as-cast conditions. The only difference is in the value of sphericity variation at all the locations. During isothermal heating for 5 min, the refinement in the microstructure leads to the formation of grains of a larger size; hence the sphericity of the grain is high. The reason for this is the same as the one discussed above in the case of variation of grain size of the isothermally heated specimen. Finally, the R2 values of grain size at the three specified locations are equal to 0.971, 0.970, and 0.988, respectively.

Fig. 16
figure 16

Impact of input process factors on the sphericity of the specimen with isothermal heating at the center (a, b, & c), mean radius (d, e, & f), and outer radius (g, h, & i)

Full size image

4.3 Validation of the statistical models

Once the non-linear regression models represent the micro-hardness, grain size, and sphericity of grains of the specimen with and without isothermal treatment, the models are validated for their accuracy in predicting the responses. The variation of microhardness, grain size, and sphericity of grain in specimens with and without isothermal treatment is given in Figs. 17 and 18, respectively, for all the test cases, which are different from the ones used to establish the mathematical models.

Fig. 17
figure 17

Variation of microhardness (a), grain size (b), and sphericity (c) of the cast sample without isothermal treatment

Full size image
Fig. 18
figure 18

Variation of microhardness (a), grain size (b), and sphericity (c) of the cast sample with isothermal treatment

Full size image

From the bar charts of Fig. 17a–c, it is evident that the values of the responses at the outer surface of the specimen provide higher hardness with smaller grain size and sphericity for all the test cases during the as-cast condition. This is because, at the outer surface, the solidification rate is high, yielding the formation of smaller grains with lower sphericity. Further, at the center, the solidification rate is low, leading to the formation of larger grains with high sphericity, which causes a reduction in microhardness.

The said phenomenon is also true with the isothermal treatment, as presented in Fig. 18a–c for microhardness, grain size, and sphericity, respectively. It is also observed that the isothermal treatment of the specimen has produced a low value of hardness with larger grain size and sphericity as compared with the as-cast specimen. This has happened due to the refinement of the microstructure due to the isothermal treatment.

Further, the plots showing the percentage deviation in responses regarding the experimental test cases are given in Figs. 19 and 20, respectively. The percentage deviation in the prediction of the responses microhardness (ref. Fig. 19a), grain size (ref. Fig. 19b), and sphericity (ref. Fig. 19c) of the specimen at the center, the mean and outer radius of the specimen at as-cast condition is seen to be equal to {(4.294842 to − 4.65426), (4.7943 to − 4.6254), (6.0234 to  − 5.969)}, {(4.2948 to − 4.654), (4.052 to − 3.316), (4.976 to − 4.441)} and {(4.867 to − 4.691), (4.11 to − 3.88), (5.074 to − 5.999)}, respectively. Similarly, the percentage deviation in the prediction of the responses at isothermal treatment is found to be equal to {(3.685 to − 2.911), (4.226 to − 5.876), (6.168 to − 6.972)}, {(3.496 to − 3.862), (3.392 to − 5.181), (6.201 to − 2.124)} and {(2.036 to − 3.638.), (3.274 to − 3.153), (5.439 to − 5.0606)}for the responses microhardness (ref. Fig. 20a), grain size (ref. Fig. 20b) and sphericity (ref. Fig. 20c) of the specimen at the center, the mean and outer radius of the specimen. The range of percentage deviation in the prediction of the responses indicates that the regression techniques forcast the responses with reasonably good accuracy.

Fig. 19
figure 19

Graphs showing the percentage deviation in the prediction of the responses of A356 casting at three locations produced without isothermal treatment a microhardness, b grain size, and c sphericity

Full size image
Fig. 20
figure 20

Graphs showing the percentage deviation in the prediction of the responses of A356 casting at three locations produced with isothermal treatment a microhardness, b grain size, and c sphericity

Full size image

5 Comparative analysis with previous work

In the current work, the authors have considered the responses of grain size, microhardness, and sphericity, and the process parameters of slope length, nozzle height, and slope angle. From the literature, it is observed that Gautam et al. [36] conducted experiments to forecast how grain size is affected by slope length and angle. According to the findings, increasing the slope angle decreases sphericity while increasing the slope length increases sphericity, which is consistent with the current findings. Additionally, Hamed et al. [12, 16] observed similar results in terms of sphericity after conducting experimental investigations on A356 alloy during the CS process to assess the effect of slope angle and slope length. Prosenjit et al. carried out experiments by altering the slope length and slope angle in addition to the previously mentioned works. They discovered that the sphericity increases as the slope length increases and decreases as the slope angle increases.

6 Conclusion

In this research work, the experiments were conducted by implementing the Design of Experiments (DOE). The analysis was carried out on the fabricated A356 sample with and without isothermal treatment. Three responses namely, microhardness, grain size, and sphericity, are measured, and the non-linear regression models were established. Such outcomes of ANOVA revealed that all three input parameters are identified to have significant contributions to the responses. The prediction accuracy of the currently developed technique is tested with the experimental test cases and found a reasonably accurate prediction. The estimated precision of prediction shows that the models are worth characterizing the real system. From the regression equation obtained for dependent variables like hardness, grain size and sphericity, it is revealed that the independent variable slope angle is the most dominating influencing factor. It is found that with an increase in angle, the microhardness increases with a decrease in grain size and sphericity. Whereas, when the slope length increases, grain size and sphericity decrease with an increase in microhardness. Moreover, the increase in the nozzle height resulted in increasing the microhardness of the casting with the formation of smaller grain sizes and sphericity. When the casting obtained is passed through the isothermal heat treatment for 5 min at 580 °C, is found that the grain size at the outer zone increases and becomes more spherical. Effect of change in grain size sphericity is found to more at outer zone than core centre zone of casting specimen, followed by a reduction in the microhardness of specimen.

7 Future scope

In the current paper, the authors conducted experiments to find the microstructural and microhardness of the samples produced through CS methodology. Further, castings can also be produced using a vibratory cooling slope to estimate effect variations in the sphericity and grain size. During the said process the base metal can be mixed with reinforcements to enhance the mechanical properties of the castings.

8 Industrial uses

It is observed that the effect of process parameters such as slope angle, slope length, and nozzle height are the most influencing parameters of SSM process. From the experiments, it is observed that with an increase in slope angle, the microhardness increases with a decrease in grain size and sphericity. Whereas, when the slope length increases, grain size and sphericity decrease with an increase in microhardness. Moreover, the increase in the nozzle height resulted in increasing the microhardness of the casting with the formation of smaller grain sizes and sphericity.