1 Introduction

Campylobacteriosis is a bacterial infection caused by campylobacter species, primarily campylobacter jejuni and, to a lesser extent, campylobacter coli. These bacteria are commonly found in the intestines of animals, especially poultry (chickens, turkeys), cattle, and other livestock [1]. Campylobacteriosis is a prevalent global food-borne illness that is commonly contracted through the consumption of contaminated food or water. The main sources of contamination are raw or undercooked poultry, unpasteurized milk, and untreated water. Additionally, the infection can spread through direct contact with infected animals or their feces [2]. Symptoms of campylobacteriosis usually manifest between 2 to 5 days following exposure to the bacteria. The symptoms may include abdominal cramps, Diarrhea and pain, nausea and vomiting, fever, muscle pain and headache [3]. In the majority of instances, the illness is self-limiting and typically resolves within a week, but some individuals, particularly young children, elderly, and immuno-compromised individuals, may experience more severe symptoms and complications. Most cases of campylobacteriosis do not require specific treatment, as the infection will clear up on its own. However, it is essential to stay well-hydrated and manage symptoms like diarrhea. In severe cases or for individuals at higher risk of complications, antibiotics may be prescribed by a health-care professional. Most cases of campylobacteriosis do not require specific treatment, as the infection will clear up on its own. However, it is essential to stay well-hydrated and manage symptoms like diarrhea. In severe cases or for individuals at higher risk of complications, antibiotics may be prescribed by a health-care professional [4].

To prevent campylobacteriosis, it is crucial to follow good food safety practices, such as thoroughly cooking poultry and other meats, avoiding cross-contamination between raw and cooked foods, and consuming pasteurized milk and dairy products. Hand-washing after handling raw meat and before eating is also essential [5]. Campylobacteriosis is classified as a zoonotic disease as it can be transmitted from animals to humans. Avian species, including chickens, geese, and ducks, serve as a key reservoir for campylobacter jejuni infections [6]. Additionally, other reservoirs of campylobacter jejuni include humans and animals such as goats, dogs, cats, pets, and swine [6]. It is important to note that campylobacteriosis cannot be directly transmitted from one human to another. Instead, humans typically acquire Campylobacter infections through the fecal-oral route, involving the consumption of contaminated animal-derived food items such as meat, milk, undercooked chicken, water, and feces from infected humans [7,8,9]. Numerous experimental and mathematical models have been employed to recognize the transmission of zoonotic food-borne diseases, including campylobacteriosis, cholera, salmonellosis, yersiniosis, shigellosis, and listeriosis [10, 11]. In addition to this, mathematical models contribute significantly to visualize the transmission dynamics of diseases and provide new strategies for the control and prevention of diseases [12, 13].

The authors in [14] proposed an epidemic model that incorporated both humans and animals to investigate the dynamics and control of campylobacteriosis using a non-standard finite approach. Their findings demonstrated that reducing contact between susceptible humans, infected humans, and infected animals could effectively control campylobacteriosis. Furthermore, the authors in [8] explored the dynamics of the infection to study campylobacteriosis transmission in humans. Their research emphasized the significance of public health education campaigns, treatment, and sanitation in reducing the transmission of campylobacteriosis among humans. Mathematical modeling has emerged as a powerful tool in understanding the spread and control of infectious diseases [15,16,17]. These models play a crucial role in epidemiology, public health planning, and decision-making processes [18, 19]. Building upon this knowledge, our study proposes a mathematical model that incorporates treatment and cumulative public health education campaigns to enhance hygiene practices and minimize the health-care risks associated with campylobacteriosis among humans. This study, therefore, propose a mathematical model to incorporate treatment and cumulative public health education campaigns for improving hygiene practices aiming at minimize the embedded health-care risks of the campylobacteriosis disease among human.

Mathematical modeling serves as a powerful tool for comprehending real-world problems and capturing the entirety of phenomena across various domains [20,21,22,23]. Fractional calculus plays a vital role in investigating the influence of memory on epidemiological models and generating more accurate results. In essence, fractional calculus offers greater flexibility compared to classical calculus by incorporating the inherent characteristics of memory into the models. Several fractional operators have been introduced in the literature [24, 25], and these operators have been effectively applied in modeling various real-world scenarios. Specifically, fractional calculus has been extensively studied and its diverse applications have been demonstrated in numerous research studies [26,27,28]. It is commonly understood that ordinary differential systems are suitable for describing local dynamical systems without any external influences. The complexity and crossover dynamics exhibited by communicable diseases surpass the abilities of conventional differential operators. In contrast, fractional order (FO) derivatives offer a better fit to real-world data when modeling diverse infection dynamics, and they also yield more efficient experimental results across different fields. Several research studies have effectively employed fractional order derivatives, yielding improved outcomes when examining real-world data across a for diseases [29,30,31,32].

Based on the aforementioned research, we have developed a mathematical model to describe the dynamics of campylobacteriosis infection using a fractional order approach, specifically employing the Caputo–Fabrizio derivative with an order \(\imath \in (0,1]\). The subsequent sections of our research are organized as follows: Sect. 2 provides the fundamental definitions and propositions of the fractional theory. In Sect. 3 of our study, we develop a campylobacteriosis infection model that incorporates the effects of vaccination and treatment using the fractional Caputo–Fabrizio (CF) derivatives. We analyze the equilibria of the model and calculate the reproduction number for the proposed system. In Sect. 4, we examine the existence and uniqueness of solutions for our system using fixed point theory. Moving on to Sect. 5, we introduce a numerical scheme to explore the influence of various input factors on the system’s dynamics. Finally, in Sect. 6, we provide concluding remarks to summarize our study.

2 Fractional concepts

Now we will present the basic concepts and outcomes of the Caputo–Fabrizio (CF) fractional derivatives, which will be utilized for analyzing the dynamics of campylobacteriosis infection. The essential definitions of these concepts are provided below:

Definition 2.1

The CF fractional derivative [25] for function \(h \in \mathfrak {H}^1(r_{1}, r_{2})\) is stated as

$$\begin{aligned} D^{\imath }_{t}(f(t))=\frac{\mathfrak {J}(\imath )}{1-\imath }\int ^{t}_{r_{1}}f'(x)\exp \Big [-\imath \frac{t-x}{1-\imath }\Big ]dx, \end{aligned}$$
(1)

where \(r_{2}>r_{1}\) and \(\mathfrak {J}(\tau )\) represent the normality [25] such that \(\imath \in [0, 1]\). In the case, if \(h \notin \mathfrak {H}^1(r_{1}, r_{2})\), then we obtain

$$\begin{aligned} D^{\imath }_{t}(f(t))=\frac{\imath \textrm{Z}(\imath )}{1-\imath }\int ^{t}_{r_{1}}(f(t)-f(x))\exp \Big [-\imath \frac{t-x}{1-\imath }\Big ]dx. \end{aligned}$$
(2)

Remark 2.1

In the case if \(\zeta =\frac{1-\imath }{\imath }\in [0, \infty )\) and \(\imath =\frac{1}{1+\zeta }\in [0, 1]\), then Eq. (2) gives the following

$$\begin{aligned} D^{\imath }_{t}(f(t))=\frac{ \mathfrak {M}(\zeta )}{\zeta }\int ^{t}_{r_{1}}f'(x) e^{[-\frac{t-x}{\zeta }]} dx,~\mathfrak {M}(0)=\mathfrak {M}(\infty )=1. \end{aligned}$$
(3)

Additionally, we have

$$\begin{aligned} \lim _{\zeta \longrightarrow 0}\frac{1}{\zeta }\exp \Big [-\frac{t-x}{\zeta }\Big ]=\delta (x-t). \end{aligned}$$
(4)

Definition 2.2

[33], The fractional integral of a given function f can be represented below in the context of fractional calculus as

$$\begin{aligned} I^{\imath }_t(f(t))=\frac{2(1-\imath )}{(2-\imath )\textrm{Z}(\imath )}f(t)+\frac{2\imath }{(2-\imath )\textrm{Z}(\imath )}\int ^t_0 f(u)du, \ \ \ t\ge 0. \end{aligned}$$
(5)

where fractional order of the integral is represented by \(\imath\) such that \(0<\imath <1\).

Remark 2.2

Definition 2.2 implies the below stated equation

$$\begin{aligned} \frac{2(1-\imath )}{(2-\imath )\mathfrak {J}(\imath )}+\frac{2\imath }{(2-\imath )\mathfrak {J}(\imath )}=1, \end{aligned}$$
(6)

which shows that \(\mathfrak {J}(\imath )=\frac{2}{2-\imath }\),  \(0<\imath <1\). In the paper [33], the authors utilized Eq. (6) to introduce the following

$$\begin{aligned} D^{\imath }_t(f(t))=\frac{1}{1-\imath }\int ^t_0 f'(x)\exp \Big [\imath \frac{t-x}{1-\imath }\Big ]dx, \end{aligned}$$
(7)

where fractional order is indicated by \(\imath\) with \(0< \imath < 1\).

3 Evaluation of the fractional dynamics

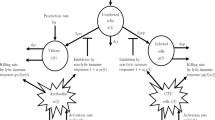
In the formulation of the model, we divided the total humans population into four classes including susceptible \(\texttt {Q}\), vaccinated \(\texttt {K}\), infected \(\texttt {J}\) and recovered class \(\texttt {P}\) while the compybacter population is indicated by \(\texttt {B}\) that refers to all sources of the disease transmissions. The recruitment rate is represented by \(\**\) while \(\mu\) represents the natural death rate. The fraction p represents the vaccinated fraction of the susceptible humans population and \(\beta\) denotes the transmission rate of humans population. In Fig. 1, we illustrated the flow chart of the model to visualize the overall picture of the transmission. Thus from the above stated assumptions we get the following model

$$\begin{aligned} \left\{ \begin{array}{rcl} \frac{d\texttt {Q}}{dt}&{}=&{} \** -\beta \texttt {Q} \texttt {B}- p \texttt {Q}+\nu \texttt {P}-\mu \texttt {Q},\\ \frac{d\texttt {K}}{dt}&{}=&{} p \texttt {Q}-\beta (1-\alpha ) \texttt {K} \texttt {B}-\mu \texttt {K},\\ \frac{d\texttt {J}}{dt}&{}=&{} \beta \texttt {Q} \texttt {B}+ \beta (1-\alpha ) \texttt {K} \texttt {B} -(\mu +\gamma +\delta +\tau )\texttt {J},\\ \frac{d\texttt {P}}{dt}&{}=&{}\gamma \texttt {J}+ \tau \texttt {J} -(\mu +\nu )\texttt {P}, \\ \frac{d\texttt {B}}{dt}&{}=&{} \psi \texttt {J}-\eta \texttt {B},\\ \end{array}\right. \end{aligned}$$
(8)

with the given values of state variables

$$\begin{aligned} \texttt {Q}(0) = \texttt {Q}_{0}, \texttt {K}(0) = \texttt {K}_{0}, \texttt {J}(0) = \texttt {J}_{0}, \texttt {P}(0) = \texttt {P}_{0} \ \ and \ \ \texttt {B}(0) = \texttt {B}_{0}. \end{aligned}$$

The size of population is given by the following

$$\begin{aligned} \mathcal{N}(t) = \texttt {Q}(t) + \texttt {K}(t) + \texttt {J}(t) + \texttt {P}(t)++ \texttt {B}(t), \end{aligned}$$

\(\tau\) represent the treatment rate, \(\delta\) represent the disease induced death rate while the recovery rate is represented by \(\gamma\). In addition, the infected humans shed bacteria into the environment at the rate \(\psi \texttt {J}\). Due to the epidemiological aspects of campylobacteriosis disease, individuals who get infected recover temporarily and hence those who loose immunity relapse to the susceptible population at the waning rate \(\nu \texttt {P}\). Indeed, the rate at which bacteria are wiped out from the environment is \(\eta \texttt {B}\) where \(\eta\) defines the natural clearance rate of bacteria from the environment.

Fig. 1
figure 1

Flow chart of the model to illustrate the transmission dynamics of the diseases

Full size image

Fractional calculus finds extensive utility across various research domains, particularly in the realm of mathematical biology. Empirical evidence indicates that the dynamics of infections can be more accurately represented using fractional calculus compared to classical integer order derivatives. Thus, the aforementioned campylobacteriosis infection model can be expressed within the fractional framework as follows:

$$\begin{aligned} \left\{ \begin{array}{rcl} ^{CF}_0 D^{\imath }_t \texttt {Q}&{}=&{} \** -\beta \texttt {Q} \texttt {B}- p \texttt {Q}+\nu \texttt {P}-\mu \texttt {Q},\\ ^{CF}_0 D^{\imath }_t \texttt {K}&{}=&{} p \texttt {Q}-\beta (1-\alpha ) \texttt {K} \texttt {B}-\mu \texttt {K},\\ ^{CF}_0 D^{\imath }_t \texttt {J}&{}=&{} \beta \texttt {Q} \texttt {B}+ \beta (1-\alpha ) \texttt {K} \texttt {B} -(\mu +\gamma +\delta +\tau )\texttt {J},\\ ^{CF}_0 D^{\imath }_t \texttt {P}&{}=&{} \gamma \texttt {J}+ \tau \texttt {J} -(\mu +\nu )\texttt {P}, \\ ^{CF}_0 D^{\imath }_t \texttt {B}&{}=&{} \psi \texttt {J}-\eta \texttt {B},\\ \end{array}\right. \end{aligned}$$
(9)

where the CF fractional operator order is represented by \(\imath\). The positive invariant region for the proposed fractional system of campylobacteriosis infection is provided below:

Theorem 3.1

Assuming \(\Omega =\{ (\texttt {Q},\texttt {K},\texttt {J},\texttt {P},\texttt {B}) \in R^5_+: 0 \le \texttt {Q}+\texttt {K}+\texttt {J}+\texttt {P}+\texttt {B} \le \textrm{M} \}\), then the set \(\Omega\) remains positively invariant for the proposed system (9) of campylobacteriosis infection.

3.1 Analysis of fractional dynamics

In this section, we will examine the suggested model (9) for campylobacteriosis infection in terms of steady-state and stability. Initially, we investigate the disease-free equilibrium, represented as \(\mathcal{E}_0\), of the suggested system. Considering the aforementioned fractional model of campylobacteriosis infection in steady-states without infection, we get that

$$\begin{aligned} \mathcal{E}_0=\left( \frac{\** }{p + \mu },\frac{p \** }{\mu (p+\mu )},0,0,0 \right) . \end{aligned}$$

To find the reproduction number for the system (9), we will use the following method

$$\begin{aligned} \textrm{F}=\left[ \begin{array}{c} \beta \texttt {B} \texttt {Q}\\ 0 \\ 0 \\ \end{array} \right] , \ \ \ \textrm{V}=\left[ \begin{array}{c} -\beta \texttt {K} \texttt {B}+\alpha \beta \texttt {K} \texttt {B}+(\mu +\gamma +\delta +\tau )\texttt {J}\\ -\gamma \texttt {J}-\tau \texttt {J}+(\mu +\nu )\texttt {P} \\ -\psi \texttt {J}+\eta \texttt {B} \\ \end{array} \right] , \end{aligned}$$

The result obtained by evaluating the Jacobian of matrices \(\textrm{F}\) and \(\textrm{V}\) at the disease-free equilibrium point \(\mathcal{E}_{0}\) is as follows

$$\begin{aligned} \texttt {F}=\left[ \begin{array}{ccc} 0 &{} 0 &{} \frac{\beta \** }{p +\mu }\\ 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 \\ \end{array} \right] , \ \ \ \texttt {V}=\left[ \begin{array}{ccc} \mu +\gamma +\delta +\tau &{}0&{}\frac{-\beta p \** +\alpha \beta p \** }{\mu (p+\mu )}\\ -\gamma -\tau &{}\mu +\nu &{}0\\ -\psi &{}0&{}\eta \\ \end{array} \right] . \end{aligned}$$

Now calculating \(\texttt {V}^{-1}\), we have

$$\begin{aligned}{} & {} \texttt {V}^{-1}\\{} & {} \quad =\left[ \begin{array}{ccc} \frac{\eta \mu +\eta \nu }{(\mu +\nu )\Big (\eta (\gamma +\delta +\mu +\tau )+\frac{(\alpha \beta p \** -\beta p \** )\psi }{\mu (p+\mu )}\Big )}&{}0&{}-\frac{\alpha \beta p \** -\beta p \** }{\mu (p+\mu )\Big (\eta (\gamma +\delta +\mu +\tau )+\frac{(\alpha \beta p \** -\beta p \** )\psi }{\mu (p+\mu )}\Big )}\\ \frac{\gamma \eta +\eta \tau }{(\mu +\nu )\Big (\eta (\gamma +\delta +\mu +\tau )+\frac{(\alpha \beta p \** -\beta p \** )\psi }{\mu (p+\mu )}\Big )}&{}\frac{1}{\mu +\nu }&{}\frac{(\alpha \beta p \** -\beta p \** )(-\gamma -\tau )}{\mu (p+\mu )(\mu +\nu )\Big (\eta (\gamma +\delta +\mu +\tau )+\frac{(\alpha \beta p \** -\beta p \** )\psi }{\mu (p+\mu )}\Big )}\\ \frac{\mu \psi +\nu \psi }{(\mu +\nu )\Big (\eta (\gamma +\delta +\mu +\tau )+\frac{(\alpha \beta p \** -\beta p \** )\psi }{\mu (p+\mu )}\Big )}&{}0&{}\frac{\gamma +\delta +\mu +\tau }{\eta (\gamma +\delta +\mu +\tau )+\frac{(\alpha \beta p \** -\beta p \** )\psi }{\mu (p+\mu )}}\\ \end{array} \right] , \end{aligned}$$

which implies that

$$\begin{aligned}{} & {} \texttt {F}{} \texttt {V}^{-1}\\{} & {} \quad =\left[ \begin{array}{ccc} \frac{\beta \** (\mu \psi +\nu \psi )}{(p+\mu )(\mu +\nu )\Big (\eta (\gamma +\delta +\mu +\tau )+\frac{(\alpha \beta p \** -\beta p \** )\psi }{\mu (p+\mu )}\Big )}&{}0&{}\frac{\beta \** (\gamma +\delta +\mu +\tau )}{(p+\mu )\Big (\eta (\gamma +\delta +\mu +\tau )+\frac{(\alpha \beta p \** -\beta p \** )\psi }{\mu (p+\mu )}\Big )}\\ 0&{}0&{}0\\ 0&{}0&{}0\\ \end{array} \right] . \end{aligned}$$

The basic reproduction number can be determined by finding the spectral radius of the matrix \(\texttt {F}{} \texttt {V}^{-1}\), which is obtained by calculating the eigenvalues of the \(\texttt {F}{} \texttt {V}^{-1}\) matrix. The reproduction number \(\mathcal{R}_{0}\) is stated as follows

$$\begin{aligned} \mathcal{R}_{0}=\frac{\beta \** \mu \psi }{p\gamma \eta \mu +p\delta \eta \mu +p\eta \mu ^2+\gamma \eta \mu ^2+\delta \eta \mu ^2+\eta \mu ^3+p\eta \mu \tau +\eta \mu ^2\tau +\alpha \beta p \** \psi -\beta p \** \psi }. \end{aligned}$$

Theorem 3.2

The disease-free equilibrium of the campylobacteriosis infection model (9) exhibits local asymptotic stability when \(\mathcal{R}_{0}<1\), while it is unstable in other cases.

Proof

In order to prove the theorem, we will compute the Jacobian matrix at \(\mathcal{E}_0\) as follows

$$\begin{aligned} \mathcal{J}_{\mathcal{E}_{0}}=\left[ \begin{array}{ccccc} -(p+\mu )&{}0&{}0&{}\nu &{}\frac{-\beta \** }{p+\mu }\\ p&{}-\mu &{}0&{}0&{}\frac{-\beta (1-\alpha )p \** }{\mu (p+\mu )}\\ 0&{}0&{}-(\mu +\gamma +\delta +\tau )&{}0&{}\frac{\beta (1-\alpha )p \** }{\mu (p+\mu )}\\ 0&{}0&{}\gamma +\tau &{}-(\mu +\nu )&{}0\\ 0&{}0&{}\psi &{}0&{}-\eta \\ \end{array} \right] \end{aligned}$$

By evaluating the above stated matrix \(\mathcal{J}_{\mathcal{E}_{0}}\), we achieve that \(\lambda _{1}=-\mu\), \(\lambda _{2}=-(p+\mu )\) and \(\lambda _{3}=-(\mu +\nu )\), which reduces the matrix \(\mathcal{J}_{\mathcal{E}_{0}}\) to a 2 by 2 matrix, that is

$$\begin{aligned} \mathcal{J}_{\mathcal{E}_{1}}=\left[ \begin{array}{cc} -(\mu +\gamma +\delta +\tau )&{}\frac{\beta (1-\alpha )p \** }{\mu (p+\mu )}\\ \psi &{}-\eta \\ \end{array} \right] \end{aligned}$$

In order to show that the system (9) is locally asymptotically stable we will prove that \(Trace(\mathcal{J}_{\mathcal{E}_{1}})<0\) and \(Det(\mathcal{J}_{\mathcal{E}_{1}})>0\). Thus we have

$$\begin{aligned} Trace(\mathcal{J}_{\mathcal{E}_{1}})=-\mu -\gamma -\delta -\tau -\eta <0, \end{aligned}$$

and

$$\begin{aligned}{} & {} Det(\mathcal{J}_{\mathcal{E}_{1}})=\frac{\gamma \eta \mu ^2+\delta \eta \mu ^2+\eta \mu ^3+\eta \mu ^2\tau +p\eta \mu (\gamma +\delta +\mu +\tau )-p \** \beta \psi +p \** \alpha \beta \psi }{\mu (p+\mu )},\\{} & {} Det(\mathcal{J}_{\mathcal{E}_{1}})=\frac{\beta \** \mu \psi }{\mu (p+\mu )\mathcal{R}_{0}},\\{} & {} Det(\mathcal{J}_{\mathcal{E}_{1}})=\frac{\beta \** \psi }{(p+\mu )\mathcal{R}_{0}}. \end{aligned}$$

Since \(Trace(\mathcal{J}_{\mathcal{E}_{1}})<0\) and \(Det(\mathcal{J}_{\mathcal{E}_{1}})>0\) if \(\mathcal{R}_{0}<1\), which shows that the disease free equilibrium of campylobacteriosis infection model (9) will be locally asymptotically stable if \(\mathcal{R}_{0}<1\) and unstable in other cases.

4 Analysis of the solutions

In this context, our main focus lies in examining the solutions of the proposed fractional system of campylobacteriosis infection. To investigate the existence of solution (9), we employ fixed point theory and proceed as outlined below

$$\begin{aligned} \left\{ \begin{array}{rcl} \texttt {Q}(t)-\texttt {Q}(0)&{}=&{} ^{CF}_0 I^{\imath }_t \bigg \{\** -\beta \texttt {Q} \texttt {B}-p\texttt {Q}+\nu \texttt {P}-\mu \texttt {Q} \bigg \},\\ \texttt {K}(t)-\texttt {K}(0)&{}=&{} ^{CF}_0 I^{\imath }_t \bigg \{ p \texttt {Q}-\beta (1-\alpha ) \texttt {K} \texttt {B}-\mu \texttt {K} \bigg \},\\ \mathcal{ I}(t)-\texttt {J}(0)&{}=&{} ^{CF}_0 I^{\imath }_t \bigg \{ \beta \texttt {Q} \texttt {B}+ \beta (1-\alpha ) \texttt {K} \texttt {B} -(\mu +\gamma +\delta +\tau )\texttt {J} \bigg \},\\ \texttt {P}(t)-\texttt {P}(0)&{}=&{} ^{CF}_0 I^{\imath }_t \bigg \{ \gamma \texttt {J}+ \tau \texttt {J} -(\mu +\nu )\texttt {P} \bigg \}, \\ \texttt {B}(t)-\texttt {B}(0)&{}=&{} ^{CF}_0 I^{\imath }_t \bigg \{ \psi \texttt {J}-\eta \texttt {B} \bigg \}. \end{array}\right. \end{aligned}$$
(10)

By incorporating the concepts introduced in the research [33], we derived the subsequent findings

$$\begin{aligned}{} & {} \mathcal{ S}(t)-\texttt {Q}(0)= \frac{2(1-\imath )}{(2-\imath )\textrm{Z}(\imath )} \bigg \{ \** -\beta \texttt {Q} \texttt {B}\nonumber \\{} & {} \quad -p\texttt {Q}+\nu \texttt {P}-\mu \texttt {Q} \bigg \}\nonumber \\{} & {} \quad +\frac{2\imath }{(2-\imath )\textrm{Z}(\imath )}\int ^t_0 \bigg \{ \** -\beta \texttt {Q} \texttt {B}\nonumber \\{} & {} \quad -p\texttt {Q}+\nu \texttt {P}-\mu \texttt {Q} \bigg \}dy,\nonumber \\{} & {} \quad \texttt {K}(t)-\texttt {K}(0)= \frac{2(1-\imath )}{(2-\imath )\textrm{Z}(\imath )} \bigg \{ p \texttt {Q}\nonumber \\{} & {} \quad -\beta (1-\alpha ) \texttt {K} \texttt {B}-\mu \texttt {K} \bigg \}\nonumber \\{} & {} \quad +\frac{2\imath }{(2-\imath )\textrm{Z}(\imath )}\int ^t_0 \bigg \{ p \texttt {Q}-\beta (1-\alpha ) \texttt {K} \texttt {B}-\mu \texttt {K} \bigg \}dy,\nonumber \\{} & {} \quad \texttt {J}(t)-\texttt {J}(0)= \frac{2(1-\imath )}{(2-\imath )\textrm{Z}(\imath )} \bigg \{ \beta \texttt {Q} \texttt {B}\nonumber \\{} & {} \quad + \beta (1-\alpha ) \texttt {K} \texttt {B} -(\mu +\gamma +\delta +\tau )\texttt {J} \bigg \}\nonumber \\{} & {} \quad +\frac{2\imath }{(2-\imath )\textrm{Z}(\imath )}\int ^t_0 \bigg \{ \beta \texttt {Q} \texttt {B}+ \beta (1-\alpha ) \texttt {K} \texttt {B} \nonumber \\{} & {} \quad -(\mu +\gamma +\delta +\tau )\texttt {J} \bigg \}dy,\nonumber \\{} & {} \quad \texttt {P}(t)-\texttt {P}(0)= \frac{2(1-\imath )}{(2-\imath )\textrm{Z}(\imath )} \nonumber \\{} & {} \quad \bigg \{ \gamma \texttt {J}+ \tau \texttt {J} -(\mu +\nu )\texttt {P} \bigg \}\nonumber \\{} & {} \quad +\frac{2\imath }{(2-\imath )\textrm{Z}(\imath )}\int ^t_0 \bigg \{ \gamma \texttt {J}+ \tau \texttt {J} -(\mu +\nu )\texttt {P} \bigg \}dy,\nonumber \\{} & {} \quad \texttt {B}(t)-\texttt {B}(0)= \frac{2(1-\imath )}{(2-\imath )\textrm{Z}(\imath )} \bigg \{\psi \texttt {J}-\eta \texttt {B} \bigg \}\nonumber \\{} & {} \quad +\frac{2\imath }{(2-\imath )\textrm{Z}(\imath )}\int ^t_0 \bigg \{\psi \texttt {J}-\eta \texttt {B} \bigg \}. \end{aligned}$$
(11)

Moreover, we have

$$\begin{aligned} \left\{ \begin{array}{rcl} \Re _1(t, \texttt {Q})&{}=&{} \** -\beta \texttt {Q} \texttt {B}-p\texttt {Q}+\nu \texttt {P}-\mu \texttt {Q},\\ \Re _2(t, \texttt {K})&{}=&{} p \texttt {Q}-\beta (1-\alpha ) \texttt {K} \texttt {B}-\mu \texttt {K},\\ \Re _3(t, \texttt {J})&{}=&{} \beta \texttt {Q} \texttt {B}+ \beta (1-\alpha ) \texttt {K} \texttt {B} -(\mu +\gamma +\delta +\tau )\texttt {J},\\ \Re _4(t, \texttt {P})&{}=&{} \gamma \texttt {J}+ \tau \texttt {J} -(\mu +\nu )\texttt {P}, \\ \Re _5(t, \texttt {B})&{}=&{} \psi \texttt {J}-\eta \texttt {B}. \end{array}\right. \end{aligned}$$
(12)

Theorem 4.1

If the below stated condition holds true, then the kernels \(\Re _1, \Re _2, \Re _3, \Re _4\), and \(\Re _5\) satisfy the conditions of Lipschitz and contraction,

$$\begin{aligned} 0 \le (M+p+\mu ) <1. \end{aligned}$$

Proof 4.1

To achieve the desired outcomes mentioned above, we begin with \(\texttt {Q}\) and \(\texttt {Q}_1\), and proceed with \(\Re _1\) according to the following approach

$$\begin{aligned} \Re _1(t, \texttt {Q})-\Re _1(t,\texttt {Q}_{1})= & {} -\beta \texttt {B} \{\texttt {Q} (t)-\texttt {Q} (t_1)\}- p \{\texttt {Q} (t)-\texttt {Q}(t_1)\} \nonumber \\{} & {} -\mu \{\texttt {Q}_(t)-\texttt {Q}(t_1)\}. \end{aligned}$$
(13)

Further simplifying (13), we achieve that

$$\begin{aligned}{} & {} \Vert \Re _1(t, \texttt {Q})-\Re _1(t, \texttt {Q}_{1})\Vert \le \Vert \beta \texttt {B} \{\texttt {Q}(t)\nonumber \\{} & {} \quad -\texttt {Q}(t_1)\}||+ \Vert p \{\texttt {Q}(t)-\texttt {Q}(t_1)\}\Vert \nonumber \\{} & {} \quad + \Vert \mu \{\texttt {Q}(t)-\texttt {Q}(t_1)\} \Vert \nonumber \\{} & {} \quad \le \Vert \beta \texttt {B} \Vert \Vert \{\texttt {Q}(t)-\texttt {Q}(t_1)\} ||+ \Vert p \Vert \Vert \{\texttt {Q}(t)-\texttt {Q}(t_1)\} \Vert \nonumber \\{} & {} \quad + \Vert \mu \Vert \Vert \{\texttt {Q}(t)-\texttt {Q}(t_1)\} \Vert \nonumber \\{} & {} \quad \le M \Vert \{\texttt {Q}(t)-\texttt {Q}(t_1)\} ||+ p \Vert \{\texttt {Q}(t)-\texttt {Q}(t_1)\} \Vert \nonumber \\{} & {} \quad +\mu \Vert \{\texttt {Q}(t)-\texttt {Q}(t_1)\} \Vert \nonumber \\{} & {} \quad \le ( M + p +\mu ) \Vert \{\texttt {Q}(t)-\texttt {Q}(t_1)\} \Vert . \end{aligned}$$
(14)

Here, we have \(\Vert \beta \texttt {B} \Vert \le M\) due to boundedness and assume \(\kappa _{1}= (M+p+\mu )\), then we get

$$\begin{aligned} ||\Re _1(t, \texttt {Q})-\Re _1(t, \texttt {Q}_{1})||\le & {} \kappa _{1}|| \texttt {Q}(t)-\texttt {Q}(t_1)||. \end{aligned}$$
(15)

Hence, we have established the Lipschitz condition for \(\Re _1\). Moreover, by satisfying the condition \(0 \le (M+p+\mu ) <1\), we have also obtained the contraction property. Similarly, we can ascertain the Lipschitz conditions as follows

$$\begin{aligned}{} & {} ||\Re _2(t, \texttt {K})-\Re _2(t, \texttt {K}_{1})||\le \kappa _{2}||\texttt {K}(t)-\texttt {K}(t_1)||,\nonumber \\{} & {} \quad ||\Re _3(t, \texttt {J})-\Re _3(t, \texttt {J}_{1})||\le \kappa _{3}||\texttt {J}(t)-\texttt {J}(t_1)||,\nonumber \\{} & {} \quad ||\Re _4(t, \texttt {P})-\Re _4(t, \texttt {P}_{1})||\le \kappa _{4}||\texttt {P}(t)-\texttt {P}(t_1)||,\nonumber \\{} & {} \quad ||\Re _5(t, \texttt {B})-\Re _5(t, \texttt {B}_{1})||\le \kappa _{5}||\texttt {B}(t)-\texttt {B}(t_1)||. \end{aligned}$$
(16)

Further simplification of Eq. (11) yields that

$$\begin{aligned} \left\{ \begin{array}{rcl} \mathcal{ S}(t)&{}=&{}\texttt {Q}(0)+\frac{2(1-\imath )}{(2-\imath ) \textrm{Z}(\imath )}\Re _1(t,\texttt {Q})+\frac{2\imath }{(2-\imath )\textrm{Z}(\imath )}\int ^t_0(\Re _1(y,\texttt {Q}))dy,\\ \texttt {K}(t)&{}=&{}\texttt {K}(0)+\frac{2(1-\imath )}{(2-\imath ) \textrm{Z}(\imath )}\Re _2(t,\texttt {K})+\frac{2\imath }{(2-\imath )\textrm{Z}(\imath )}\int ^t_0(\Re _2(y,\texttt {K}))dy,\\ \texttt {J}(t)&{}=&{}\texttt {J}(0)+\frac{2(1-\imath )}{(2-\imath ) \textrm{Z}(\imath )}\Re _3(t,\texttt {J})+\frac{2\imath }{(2-\imath )\textrm{Z}(\imath )}\int ^t_0(\Re _3(y,\texttt {J}))dy,\\ \texttt {P}(t)&{}=&{}\texttt {P}(0)+\frac{2(1-\imath )}{(2-\imath ) \textrm{Z}(\imath )}\Re _4(t,\texttt {P})+\frac{2\imath }{(2-\imath )\textrm{Z}(\imath )}\int ^t_0(\Re _4(y,\texttt {P}))dy,\\ \texttt {B}(t)&{}=&{}\texttt {B}(0)+\frac{2(1-\imath )}{(2-\imath ) \textrm{Z}(\imath )}\Re _5(t,\texttt {B})+\frac{2\imath }{(2-\imath )\textrm{Z}(\imath )}\int ^t_0(\Re _5(y,\texttt {B}))dy. \end{array}\right. \end{aligned}$$
(17)

moreover, we have

$$\begin{aligned} \left\{ \begin{array}{rcl} \mathcal{ S}_{\aleph }(t)&{}=&{} 2 \frac{(1-\imath )}{(2-\imath ) \textrm{Z}(\imath )}\Re _1(t, \texttt {Q}_{(\aleph -1)})+2\frac{\imath }{(2-\imath )\textrm{Z}(\imath )}\int ^t_0(\Re _1(y, \texttt {Q}_{(\aleph -1)}))dy,\\ \texttt {K}_{\aleph }(t)&{}=&{} 2 \frac{(1-\imath )}{(2-\imath ) \textrm{Z}(\imath )}\Re _2(t, \texttt {K}_{(\aleph -1)})+2\frac{\imath }{(2-\imath )\textrm{Z}(\imath )}\int ^t_0(\Re _2(y, \texttt {K}_{(\aleph -1)}))dy,\\ \texttt {J}_{\aleph }(t)&{}=&{} 2 \frac{(1-\imath )}{(2-\imath ) \textrm{Z}(\imath )}\Re _3(t, \texttt {J}_{(\aleph -1)})+2\frac{\imath }{(2-\imath )\textrm{Z}(\imath )}\int ^t_0(\Re _3(y, \texttt {J}_{(\aleph -1)}))dy,\\ \texttt {P}_{\aleph }(t)&{}=&{} 2 \frac{(1-\imath )}{(2-\imath ) \textrm{Z}(\imath )}\Re _4(t, \texttt {P}_{(\aleph -1)})+2\frac{\imath }{(2-\imath )\textrm{Z}(\imath )}\int ^t_0(\Re _4(y, \texttt {P}_{(\aleph -1)}))dy,\\ \texttt {B}_{\aleph }(t)&{}=&{} 2\frac{(1-\imath )}{(2-\imath ) \textrm{Z}(\imath )}\Re _5(t, \texttt {B}_{(\aleph -1)})+2\frac{\imath }{(2-\imath )\textrm{Z}(\imath )}\int ^t_0(\Re _5(y, \texttt {B}_{(\aleph -1)}))dy, \end{array}\right. \end{aligned}$$
(18)

with initial values

$$\begin{aligned} \texttt {Q}^0(t)= & {} \texttt {Q}(0), \texttt {K}^0(t)= \texttt {K}(0), \texttt {J}^0(t)=\texttt {J}(0),\\ \texttt {P}^0(t)= & {} \texttt {P}(0), \texttt {B}^0(t)=\texttt {B}(0). \end{aligned}$$

We can achieve the difference terms in the following manner

$$\begin{aligned}{} & {} \kappa _{1\aleph }(t)={\texttt {Q}}_\aleph (t)-{\texttt {Q}}_{(\aleph -1)}(t)= \frac{2(1-\imath )}{(2-\imath ) \textrm{Z}(\imath )}(\Re _1(t, \texttt {Q}_{(\aleph -1)})\nonumber \\{} & {} \quad -\Re _1(t, \texttt {Q}_{(\aleph -2)}))\nonumber \\{} & {} \quad +2 \frac{\imath }{(2-\imath )\textrm{Z}(\imath )}\int ^t_0(\Re _1(y, {\texttt {Q}}_{(\aleph -1)})\nonumber \\{} & {} \quad -\Re _1(y, {\texttt {Q}}_{(\aleph -2)}))dy,\nonumber \\{} & {} \quad \kappa _{2\aleph }(t)={\texttt {K}}_\aleph (t)-{\texttt {K}}_{(\aleph -1)}(t)= \frac{2(1-\imath )}{(2-\imath ) \textrm{Z}(\imath )}(\Re _1(t, \texttt {K}_{(\aleph -1)})\nonumber \\{} & {} \quad -\Re _1(t, \texttt {K}_{(\aleph -2)}))\nonumber \\{} & {} \quad +2 \frac{\imath }{(2-\imath )\textrm{Z}(\imath )}\int ^t_0(\Re _1(y, {\texttt {K}}_{(\aleph -1)})-\Re _1(y, {\texttt {K}}_{(\aleph -2)}))dy,\nonumber \\{} & {} \quad \kappa _{3\aleph }(t)={\texttt {J}}_\aleph (t)-{\texttt {J}}_{(\aleph -1)}(t)\nonumber \\{} & {} \quad = \frac{2(1-\imath )}{(2-\imath ) \textrm{Z}(\imath )}(\Re _1(t, \texttt {J}_{(\aleph -1)})-\Re _1(t, \texttt {J}_{(\aleph -2)}))\nonumber \\{} & {} \quad +2 \frac{\imath }{(2-\imath )\textrm{Z}(\imath )}\int ^t_0(\Re _1(y, {\texttt {J}}_{(\aleph -1)})\nonumber \\{} & {} \quad -\Re _1(y, {\texttt {J}}_{(\aleph -2)}))dy,\nonumber \\{} & {} \quad \kappa _{4\aleph }(t)={\texttt {P}}_\aleph (t)-{\texttt {P}}_{(\aleph -1)}(t)\nonumber \\{} & {} \quad = \frac{2(1-\imath )}{(2-\imath ) \textrm{Z}(\imath )}(\Re _1(t, \texttt {P}_{(\aleph -1)})-\Re _1(t, \texttt {P}_{(\aleph -2)}))\nonumber \\{} & {} \quad +2 \frac{\imath }{(2-\imath )\textrm{Z}(\imath )}\int ^t_0(\Re _1(y, {\texttt {P}}_{(\aleph -1)})-\Re _1(y, {\texttt {P}}_{(\aleph -2)}))dy,\nonumber \\{} & {} \quad \kappa _{5\aleph }(t)={\texttt {B}}_\aleph (t)-{\texttt {B}}_{(\aleph -1)}(t)\nonumber \\{} & {} \quad = \frac{2(1-\imath )}{(2-\imath ) \textrm{Z}(\imath )}(\Re _1(t, \texttt {B}_{(\aleph -1)})-\Re _1(t, \texttt {B}_{(\aleph -2)}))\nonumber \\{} & {} \quad +2 \frac{\imath }{(2-\imath )\textrm{Z}(\imath )}\int ^t_0(\Re _1(y, {\texttt {B}}_{(\aleph -1)})-\Re _1(y, {\texttt {B}}_{(\aleph -2)}))dy. \end{aligned}$$
(19)

Observing that

$$\begin{aligned} \left\{ \begin{array}{ll} \texttt {Q}_{\aleph }(t)=\sum ^{\aleph }_{i=1}\kappa _{1i}(t), \ \texttt {K}_{\aleph }(t)=\sum ^{\aleph }_{i=1}\kappa _{2i}(t), \\ \\ \texttt {J}_{\aleph }(t)=\sum ^{\aleph }_{i=1}\kappa _{3i}(t), \ \texttt {P}_{\aleph }(t)=\sum ^{\aleph }_{i=1}\kappa _{4i}(t), \\ \\ \texttt {B}_{\aleph }(t)=\sum ^{\aleph }_{i=1}\kappa _{5i}(t). \end{array} \right. \end{aligned}$$
(20)

Simplifying in the same manner, we achieve that

$$\begin{aligned}{} & {} ||\kappa _{1\aleph }(t)||=||\texttt {Q}_{\aleph }(t)-\texttt {Q}_{(\aleph -1)}(t)||\nonumber \\{} & {} \quad =\bigg \Vert 2 \frac{(1-\imath )}{(2-\imath ) \textrm{Z}(\imath )}(\Re _1(t, \texttt {Q}_{(\aleph -1)})-\Re _1(t,\texttt {Q}_{(\aleph -2)}))\nonumber \\{} & {} \quad +2\frac{\imath }{(2-\imath )\textrm{Z}(\imath )}\int ^t_0(\Re _1(y,\texttt {Q}_{(\aleph -1)})-\Re _1(y, \texttt {Q}_{(\aleph -2)}))dy\bigg \Vert . \end{aligned}$$
(21)

Equation (21) yields that

Theorem 4.2

If it is possible to find a suitable \(t_0\) such that the below stated condition holds

$$\begin{aligned} 2\frac{(1-\imath )}{(2-\imath ) \textrm{Z}(\imath )}\kappa _{1}+2\frac{\imath }{(2-\imath )\textrm{Z}(\imath )}\kappa _{1}t_0<1, \end{aligned}$$

then, we obtain exact coupled solutions for the proposed fractional system (9).

Proof 4.2

With the Lipschitz condition being met and the boundedness of \(\texttt {Q}(t)\), \(\texttt {K}(t)\), \(\texttt {J}(t), \texttt {P}(t)\) and \(\texttt {B}(t)\), we can infer the following from Eqs. (24) and (25):

$$\begin{aligned}{} & {} \Vert \kappa _{1\aleph }(t)\Vert \le ||\texttt {Q}_{\aleph }(0)||\Big [\Big (2\frac{(1-\imath )}{(2-\imath ) \textrm{Z}(\imath )}\kappa _{1}\Big )\nonumber \\{} & {} \quad +\Big (2\frac{\imath }{(2-\imath )\textrm{Z}(\imath )}\kappa _{1} t\Big )\Big ]^\aleph ,\nonumber \\{} & {} \Vert \kappa _{2\aleph }(t)\Vert \le ||\texttt {K}_{\aleph }(0)||\Big [\Big (2\frac{(1-\imath )}{(2-\imath ) \textrm{Z}(\imath )}\kappa _{2}\Big )\nonumber \\{} & {} \quad +\Big (2 \frac{\imath }{(2-\imath )\textrm{Z}(\imath )}\kappa _{2} t\Big )\Big ]^\aleph ,\nonumber \\{} & {} \Vert \kappa _{3\aleph }(t)\Vert \le ||\texttt {J}_{\aleph }(0)||\Big [\Big (2\frac{(1-\imath )}{(2-\imath ) \textrm{Z}(\imath )}\kappa _{3}\Big )\nonumber \\{} & {} \quad +\Big (2\frac{\imath }{(2-\imath )\textrm{Z}(\imath )}\kappa _{3} t\Big )\Big ]^\aleph ,\nonumber \\{} & {} \quad \Vert \kappa _{4\aleph }(t)\Vert \le ||\texttt {P}_{\aleph }(0)||\Big [\Big (2\frac{(1-\imath )}{(2-\imath ) \textrm{Z}(\imath )}\kappa _{4}\Big )\nonumber \\{} & {} \quad +\Big (2\frac{\imath }{(2-\imath )\textrm{Z}(\imath )}\kappa _{4} t\Big )\Big ]^\aleph ,\nonumber \\{} & {} \quad \Vert \kappa _{5\aleph }(t)\Vert \le ||\texttt {B}_{\aleph }(0)||\Big [\Big (2\frac{(1-\imath )}{(2-\imath ) \textrm{Z}(\imath )}\kappa _{5}\Big )\nonumber \\{} & {} \quad +\Big (2\frac{\imath }{(2-\imath )\textrm{Z}(\imath )}\kappa _{5} t\Big )\Big ]^\aleph . \end{aligned}$$
(26)

As a consequence, we attain existence and continuity of the solutions. Additionally, we need to establish that the aforementioned solution is valid for our system (9). To accomplish this, we proceed as outlined below

$$\begin{aligned} \texttt {Q}(t)-\texttt {Q}(0) \ {}= & {} \ \texttt {Q}_{\aleph }(t)-\mathfrak {A}1_{\aleph }(t),\nonumber \\ \texttt {K}(t)-\texttt {K}(0) \ {}= & {} \ \mathcal{C}_{\aleph }(t)-\mathfrak {A}2_{\aleph }(t),\nonumber \\ \texttt {J}(t)-\texttt {J}(0) \ {}= & {} \ \texttt {J}_{\aleph }(t)-\mathfrak {A}3_{\aleph }(t),\nonumber \\ \texttt {P}(t)-\texttt {P}(0) \ {}= & {} \ \texttt {P}_{\aleph }(t)-\mathfrak {A}4_{\aleph }(t),\nonumber \\ \texttt {B}(t)-\texttt {B}(0) \ {}= & {} \ \texttt {K}_{\aleph }(t)-\mathfrak {A}5_{\aleph }(t). \end{aligned}$$
(27)

Next, we take

$$\begin{aligned}{} & {} \Vert B_\aleph (t)\Vert =\Big |\Big |\frac{2(1-\imath )}{(2-\imath ) \textrm{Z}(\imath )}(\Re _1(t,\texttt {Q}_{\aleph })\nonumber \\{} & {} \quad -\Re _1(t, \texttt {Q}_{(\aleph -1)})) +\frac{2\imath }{(2-\imath ) \textrm{Z}(\imath )}\times \nonumber \\{} & {} \quad \int ^t_0(\Re _1(y,\texttt {Q}_{\aleph })-\Re _1(y, \texttt {Q}_{(\aleph -1)}))dy\Big |\Big |,\nonumber \\{} & {} \quad \le \frac{2(1-\imath )}{(2-\imath )\textrm{Z}(\imath )}\Vert (\Re _1(t, \texttt {Q}_{\aleph })-(\Re _1(t, \texttt {Q}_{(\aleph -1)}))\Vert \nonumber \\{} & {} \quad +\frac{2\imath }{(2-\imath )\textrm{Z}(\imath )}\times \nonumber \\{} & {} \quad \int ^t_0||(\Re _1(y, \texttt {Q})-\Re _1(y, \texttt {Q}_{(\aleph -1)}))||dy,\nonumber \\{} & {} \quad \le \frac{2(1-\imath )}{(2-\imath )\textrm{Z}(\imath )}\kappa _{1}\Vert \texttt {Q}\nonumber \\{} & {} \quad -\texttt {Q}_{(\aleph -1)}\Vert +\frac{2\imath }{(2-\imath )\textrm{Z}(\imath )}\kappa _{1}\Vert \texttt {Q}-\texttt {Q}_{(\aleph -1)}\Vert t. \end{aligned}$$
(28)

Additionally, we have

$$\begin{aligned} \Vert \mathfrak {A}1_\aleph (t)\Vert\le & {} \Big (\frac{2(1-\imath )}{(2-\imath ) \textrm{Z}(\imath )}+\frac{2\imath }{(2-\imath ) \textrm{Z}(\imath )}t\Big )^{\aleph +1}\mu ^{\aleph +1}_1a. \end{aligned}$$
(29)

At time \(t_0\), we get

$$\begin{aligned} \Vert \mathfrak {A}1_\aleph (t)\Vert\le & {} \Big (\frac{2(1-\imath )}{(2-\imath )\textrm{Z}(\imath )}+\frac{2\imath }{(2-\imath ) \textrm{Z}(\imath )}t_0\Big )^{\aleph +1}\mu ^{\aleph +1}_1a. \end{aligned}$$
(30)

By following the same procedure and utilizing Eq. (30), we obtain the following

$$\begin{aligned} \Vert \mathfrak {A}1_\aleph (t)\Vert \longrightarrow 0, \ \ \ \aleph \rightarrow \infty . \end{aligned}$$

Similarly, we observe that \(\mathfrak {A}2_\aleph (t), \mathfrak {A}3_\aleph (t), \mathfrak {A}4_\aleph (t),\mathfrak {A}5_\aleph (t)\) tends to 0 as \(\aleph\) tends to \(\infty\). \(\square\)

Fig. 2
figure 2

Illustration of the transmission dynamics of the recommended model of campylobacteriosis infection with different values of the fractional parameter of the system, i.e., \(\imath =0.70, 0.80,0.90,1.00\)

Full size image
Fig. 3
figure 3

Illustration of the transmission dynamics of the recommended model of campylobacteriosis infection with different values of the fractional parameter of the system, i.e., \(\imath =0.50, 0.55,0.60,0.65\)

Full size image
Fig. 4
figure 4

Graphical view analysis of the solution pathways of the recommended model of campylobacteriosis infection with different values of the vaccination rate p, i.e., \(p=0.20, 0.25,0.30,0.35\)

Full size image
Fig. 5
figure 5

Graphical view analysis of the solution pathways of the recommended model of campylobacteriosis infection with different values of the transmission rate \(\beta\), i.e., \(\beta =0.401, 0.431, 0.461,0.491\)

Full size image
Fig. 6
figure 6

Time series analysis of the proposed dynamics of campylobacteriosis infection with various values of the treatment rate \(\tau\), i.e., \(\tau =0.22, 0.26,0.30,0.34\)

Full size image
Fig. 7
figure 7

Time series analysis of the proposed dynamics of campylobacteriosis infection with different values of the input parameter \(\nu\), i.e., \(\nu =0.04, 0.045,0.05,0.055\)

Full size image

To establish the uniqueness of solutions for the system (9), let \((\texttt {Q}_{1}(t)\), \(\texttt {K}_{1}(t)\), \(\texttt {J}_{1}(t)\), \(\texttt {P}_{1}(t)\), \(\texttt {B}_{1}(t))\) is an alternative solution. In such a case, we proceed in the following manner

$$\begin{aligned}{} & {} \texttt {Q}(t)-\texttt {Q}_{1}(t)=\frac{2(1-\imath )}{(2-\imath ) \textrm{Z}(\imath )}(\Re _1(t, \texttt {Q})\nonumber \\{} & {} \quad -\Re _1(t, \texttt {Q}_{1})) +\frac{2\imath }{(2-\imath ) \textrm{Z}(\imath )}\times \nonumber \\{} & {} \quad \int ^t_0(\Re _1(y, \texttt {Q})-\Re _1(y, \texttt {Q}_{1})) \ dy. \end{aligned}$$
(31)

By utilizing norm on (31), we get

$$\begin{aligned}{} & {} \Vert \texttt {Q}(t)-\texttt {Q}_{1}(t)\Vert \le \frac{2(1-\imath )}{(2-\imath ) \textrm{Z}(\imath )}\Vert \Re _1(t, \texttt {Q})-\Re _1(t, \texttt {Q}_{1})\Vert \nonumber \\{} & {} \quad +\frac{2\ell }{(2-\ell ) \textrm{Z}(\ell )}\times \nonumber \\{} & {} \quad \int ^t_0 \Vert \Re _1(y, \texttt {Q})-\Re _1(y, \texttt {Q}_{1})\Vert dy. \end{aligned}$$
(32)

Based on the fulfillment of the Lipschitz condition, we can derive the following

$$\begin{aligned} \Vert \texttt {Q}(t)-\texttt {Q}_{1}(t)\Vert\le & {} \frac{2(1-\imath )}{(2-\imath )\textrm{Z}(\imath )}\kappa _{1}\Vert \texttt {Q}_{h}(t)-\texttt {Q}_{1}(t)\Vert +\frac{2\imath }{(2-\imath )\textrm{Z}(\imath )}\times \\\\{} & {} \int ^t_0\kappa _{1} t \Vert \texttt {Q}(t)-\texttt {Q}_{1}(t)\Vert dy, \end{aligned}$$
(33)

which implies that

$$\begin{aligned} \Vert \texttt {Q}(t)-\texttt {Q}_{1}(t)\Vert \Big (1-\frac{2(1-\imath )}{(2-\imath )\textrm{Z}(\imath )}\kappa _{1}-\frac{2\imath }{(2-\ell ) \textrm{Z}(\imath )}\kappa _{1} t\Big )\le 0. \end{aligned}$$
(34)

Theorem 4.3

If the below stated condition holds

$$\begin{aligned} \Big (1-\frac{2(1-\imath )}{(2-\imath ) \textrm{Z}(\imath )}\kappa _{1}-\frac{2\imath }{(2-\imath )\mathcal{ U}(\imath )}\kappa _{1} t \Big )>0. \end{aligned}$$
(35)

then the system (9) has unique solution.

Proof 4.3

Suppose that the condition mentioned in Eq. (35) is met, then Eq. (34) yields the following

$$\begin{aligned} \Vert \texttt {Q}(t)-\texttt {Q}_{1}(t)\Vert =0, \end{aligned}$$
(36)

from the above, we have

$$\begin{aligned} \texttt {Q}(t)=\texttt {Q}_{1}(t). \end{aligned}$$
(37)

Similarly, we achieve that

$$\begin{aligned} \texttt {K}(t)= & {} \texttt {K}_{1}(t), \texttt {J}(t)=\texttt {J}_{1}(t),\\ \texttt {P}(t)= & {} \texttt {P}_{1}(t), \texttt {B}(t)=\texttt {B}_{1}(t). \end{aligned}$$

\(\square\)

In the upcoming section, we will discuss the solution pathways of the recommended model of the infection to illustrate the impact of different input factors on the system. These analysis will help us to predict the most critical factors of the system to health officials or policy makers.

5 Result and discussion

In this section of the paper, we will present the dynamical behaviour of the recommended model of bacterial infection with the variation of different input factors of the system. The behavior of an epidemic model can vary depending on several factors, including the characteristics of the disease, the population, and the implemented control measures. We performed different simulation to show the key factors of the system for the control and prevention of the infection. The values of input parameters and state variables are assumed for simulation purposes. In Table 1, we represent the values of input parameters of the system.

Table 1 Interpretation of the input values of the model for numerical analysis
Full size table

In the first simulation showcased in Figs. 2 and 3, we have depicted the influence of a fractional parameter on the dynamics of campylobacteriosis infection. Our aim was to demonstrate the behavior of the infection level as affected by the fractional parameter. Figure 2 presents a comparative analysis between classical and fractional operators. Through these figures, we observed a substantial reduction in the level of infection when employing the fractional parameter, indicating its potential as an effective control parameter.

Figure 4 demonstrates the second simulation, which focuses on the conceptualization of the role of vaccination. Through this simulation, we observed that vaccination can serve as an effective measure to control campylobacteriosis infection within a society. By assuming various values for the vaccination rate, we were able to assess the system’s behavior and its response to different vaccination scenarios. Figure 5 displays the third simulation, which focuses on visualizing the role of transmission probability. By presenting solution pathways of the system under different values of the transmission probability parameter \(\beta\), we have demonstrated that \(\beta\) plays a critical role in determining the risk of infection within a society. Our findings highlight that higher values of \(\beta\) can significantly increase the risk of infection. Figure 6 depicts the exploration of treatment’s role in the transmission dynamics of campylobacteriosis infection. The visualization reveals a marginal impact of this parameter on the infection dynamics. Furthermore, in the last simulation showcased in Fig. 7, we examined the variation of the input parameter \(\nu\) and its effect on the solution pathways. Our results demonstrated that this parameter poses a significant risk, as it increases the likelihood of infection.

Our findings indicate that the fractional parameter and vaccination play crucial roles in reducing the infection level within a society. These factors have been shown to be effective in mitigating the spread of the infection. Conversely, we observed that the transmission probability \(\beta\) and the rate of immunity loss \(\nu\) pose significant risks, as they can contribute to the propagation of the infection.

6 Concluding remarks

In this work, we structured a model that captures the transmission dynamics of campylobacteriosis infection by incorporating vaccination and treatment factors using the Caputo–Fabrizio fractional operator. We utilized key principles from fractional calculus to analyze the dynamics of the proposed model of the infection. We studied the equilibria of the model and calculated the reproduction parameter represented by \(\mathcal{R}_{0}\) through next-generation matrix method. We have shown that the infection-free steady-state of the proposed system is local asymptotic stability when \(\mathcal{R}_{0}<1\), while it becomes unstable in other conditions. Applying the theory of fractional derivatives, we proved the existence and uniqueness of the solution of the proposed model of campylobacteriosis infection. In addition to this, We presented a numerical scheme to analyze the time series of the system, which allows us to explore the dynamical behavior. Through numerical simulations, we investigated the impact of various input parameters on the dynamics of campylobacteriosis infection. This enabled us to conceptualize the influence of different input parameters on the infection dynamics. Our findings recommended the most pivotal scenario to the public health authorities and policy makers for the prevention of the infection. This will assist them in implementing appropriate infection control measures to address the situation effectively. In our future work, we will use machine learning techniques to analyze large-scale epidemiological data and optimize model parameters, aiding in real-time disease monitoring and control strategies. Moreover, climate change and environmental factors will be included in the model to gain a deeper understanding of disease dynamics and inform public health policies.