1 Introduction

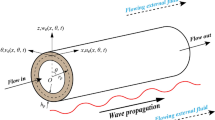
An in-depth review on the wave energy technologies developed until 2010 is given by Falcão [1]. Other wave power technology concepts, not listed in [1], are also under development. One of these consists of utilizing distensible membranes as the primary interface with the incident waves. In this context, the use of a distensible tube for ocean wave-energy absorption started with the Anaconda, a device that was patented by Farley and Rainey in 2006 [2]. Its working principle relies on the propagation of wave-excited pressure bulges in a water-filled distensible tube, when it is aligned head to waves. The longitudinal waves are amplified as they travel downstream inside the tube, their propagation velocity being governed by the tube’s diameter and material properties. In practice the bow of the tube is closed, and its stern is to be connected to a power take-off system (PTO). The experimental research on the Anaconda began in 2007 with the testing of a small Latex tube in a wave flume, submerged just below the still water level [3]. It was demonstrated that resonance could be achieved if the celerity of the incident waves equalled the speed of the bulges. The proof of concept was later carried out in 2012 by Chapin et al. [4], who reported on results obtained with a 1:25 scale model fixed at both ends, equipped with a linear pneumatic PTO of adjustable impedance. Aiming to assess the performance of a freely floating distensible tube, this time connected to a non-linear pneumatic PTO, a \(0.814 \mathrm{m}\) long tube with \(7.83 \mathrm{cm}\) diameter and \(0.16 \mathrm{mm}\) wall thickness was tested in a wave flume by Mendes et al. [5]. The results of this study have shed light on various aspects of the system’s response to the incident waves. Further insights have been given by Smith [6], who modelled analytically the wave-structure interactions for the distensible-tube wave energy converter, based on linear theory.

In 2012 Choplain and Chaplin [7] extended the bulge-wave concept of the Anaconda to a possible seabed version. A model of a long rectangular box was covered with a rubber membrane and placed on the tank bed, parallel to the wave propagation. The performance of this device in harnessing wave power was evaluated by connecting a linear dashpot at its stern. Capture-widths of up to \(2.2\) were obtained, and the bandwidth of maximum power capture was not limited to a single frequency. Except when the rubber membrane was too thin, the experimental results were in good agreement with predictions based on a one-dimensional theoretical model, suggesting that this model could not be used when the bulge wavelengths are much shorter than that of the incoming waves. Another application of distensible interfaces in wave energy was investigated experimentally by Kurniawan et al. [8]. In this case a floating air bag, ballasted with water, expands and contracts as it heaves under wave action. The power extraction is accomplished by connecting this air bag to a secondary volume, by means of an air turbine. Based on linear theory, these authors have shown that the floating bag, pulsating at resonance, can capture about twice as much energy as a rigid device of the same volume. To control the resonance of the device, this concept was later extended in [9] to incorporate elastic tendons in the balloon walls. The effect of having elastic tendons was found to be similar to that of having a larger air volume connected to the bag. Moreover, varying the PTO dam** shifted the peak response of the flexible bag device across a range of periods, with a resulting double-peaked envelope of the mean absorbed power. A recent development on the original bulge-wave concept is also being investigated by the company SBM Offshore. Jean et al. [10] report on a floating distensible tube device, in which the power extraction is accomplished by a group of electro active polymer generators mounted in the tube walls. The proof of concept was achieved in 2010 at ACRI-IN, in Sophia-Antipolis (France), and in 2017 Babarit et al. [11] established a linear numerical model for the dynamic response of this flexible electro active wave-energy converter. Power absorption of a few hundred kilowatts was ultimately predicted for a \(100 \mathrm{m}\) long tube.

In view of further improving the efficiency of the OWC-connected distensible tube system, a clear understanding of the energy losses in the device and of how the tube’s working modes contribute to the wave energy absorption is needed. To this end, a physical model of a floating distensible tube is tested in a wave flume. The bow of the tube is closed by a floating wood nose and its stern is connected to a fixed forward-bent circular vertical shaft. The system is filled with water and tested under a series of deep and intermediate waves having small and finite amplitudes. The wave-excited pressure bulges in the tube induce periodic oscillations of the water column inside the shaft, which in turn pressurise a pneumatic chamber. The impedance of the system is imposed by an orifice plate that connects the pneumatic chamber to the atmosphere, instead of the porous membrane proposed and tested in [12]. Video captions obtained during the experiments show that the tube performs harmonic oscillations, in surge and bending modes, under the action of the incident waves. When adequately coupled with the pressure bulges inside the tube, these oscillations eventually contribute to improve the system’s performance. Assuming incompressible flow conditions, the air flowrate across the orifice is obtained from the measured water-surface velocity in the shaft, by continuity. Bernoulli’s law then delivers the pneumatic chamber pressure and the extracted power at the PTO. The system’s capture-width is obtained dividing this extracted power by the incident wave power. An energy balance is also conducted by analysing the incident, reflected and transmitted wave far-fields, so as to quantify the wave-attenuation efficiency of the system. Subtracting both the energy extracted at the PTO and the energy stored in the oscillating water column, from the portion of incident wave energy that was neither reflected nor transmitted, the energy losses are obtained. The internal friction and flow-separation losses are then assessed, based on the Reynolds and Keulegan–Carpenter numbers. Estimates of capture-width are additionally compared to prior benchmark experiments. The hydrodynamic and overall efficiencies of the system are ultimately provided. The influence of wave steepness upon the system’s efficiency is also evaluated.

The physical model and its dimensions are firstly presented in Sect. 2, and Sect. 3 deals with the generated wave-field and data acquisition. The system dynamics and the power take-off mechanism are addressed next in Sect. 4. Section 5 presents the efficiency results of the experiments. A comprehensive comparison with selected benchmark results is accomplished in Sect. 6. The energy-loss assessment and overall efficiency of the system are then treated in detail in Sects. 7 and 8. Finally, a discussion on the results obtained and their relevance and added value, together with the main conclusions of the work, are respectively provided in Sects. 9 and 10.

2 The physical model

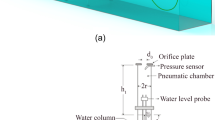
A physical model of the OWC-connected distensible tube system was built and installed in the wave flume, head to waves. The schematic of Fig. 1 details its dimensions. The flume is 8 m long and \(b=0.3 \mathrm{m}\) wide. It is equipped with a variable speed wave-maker on one end and a slo** beach \(1.28 \mathrm{m}\) in length at the opposite end. The system comprises a \(0.904 \mathrm{m}\) long horizontal latex tube, with \(0.16 \mathrm{mm}\) wall thickness, whose bow is closed by a floating wood nose. At its stern the tube is connected to an acrylic vertical circular duct of radius \(r=3.61 \mathrm{cm}\), through a PVC elbow that is partially submerged at a depth \(a=1.9 \mathrm{cm}\). The model was tested while assembled on a bottom standing pillar, in a water depth \(h=0.33 \mathrm{m}\). By pum** water through a tap at the tube’s nose, prior to the wave runs, the head inside the vertical duct may be conveniently adjusted. In the present case it is set to \({h}_{0}=10 \mathrm{cm}\), which results in a pressurized tube diameter \(d=9.78 \mathrm{cm}\). This static head determines not only the natural period of the oscillating water column (OWC), but also the tube tuning period. At rest, the pneumatic chamber height above the still water column in the shaft is \({h}_{1}=57.5 \mathrm{cm}\); it connects to the atmosphere through a \(5 \mathrm{mm}\) thick sharp-edged orifice plate of diameter \({d}_{0}\). A set of calibrated orifice plates of diameters \({d}_{0}\) between \(5.4 \mathrm{mm}\) and \(17.2 \mathrm{mm}\) have been tested. In Table 1 the relevant dimensions of the physical model and PTO system are presented.

Fig. 1
figure 1

Schematic of the physical model in the wave flume 

Full size image
Table 1 Principal dimensions of the system
Full size table

3 Wave generation and data-acquisition

The wave flume and physical model are equipped with four resistive water level probes. Two of them are positioned between the wave generator and the physical model, allowing for a wave reflection analysis [13]. The third probe monitors the water column free-surface displacement \(z(t)\) inside the acrylic vertical duct. The fourth probe, positioned behind the model, accounts for the waves transmitted towards the beach. All wave probes are controlled by a 4-channel HR wave-probe monitoring system, from Wallingford. Their measurement uncertainty is \(\pm 0.5 \mathrm{mm}\) and their output signals were logged at \(200 \mathrm{Hz}\) for \(15 \mathrm{s}\), by a Keithley KUSB-3100 S data acquisition card. A PC running Testpoint V7 is used for instrument control, data acquisition and processing.

The wavemaker is a bottom-hinged vertical paddle, which is driven by a DC electrical motor of adjustable speed. It can generate small and finite amplitude water waves up to \(80 \mathrm{mm}\) wave height. A total of six series of regular waves of wavenumber \(kh=0.69-4.35\) have been generated in the flume. They cover a range of wave periods \(T=0.55-1.78\mathrm{ s}\), in water of constant depth \(h=0.33\mathrm{ m}\). For each of the wave series generated in the wave flume, Table 2 summarizes the ranges of period \(T\), wavenumber \(k\), wave height \(H\), wave steepness \(H/\lambda\), water-depth to wavelength ratio \(h/\lambda\), wave celerity \(c\), Ursell Number \(\mathrm{Ur}\) and incident wave power per unit wave-front \({P}_{i}\).

Table 2 Incident wave-field generated at model scale
Full size table

In Fig. 2 the wave steepness \(H/\lambda\) is shown as a function of the non-dimensional wavenumber \(kh\), for all the deep and intermediate waves tested. Wave series 1 and 2 correspond to small amplitude waves, having \(kH<0.2\). Wave series 3 to 6 have finite amplitudes for periods roughly bellow \(T=1 \mathrm{s}\).

Fig. 2
figure 2

Wave steepness \(H/\lambda\) as a function of the non-dimensional wavenumber \(kh\), for all the wave series tested

Full size image

4 System dynamics and power take-off

The system under analysis is destined for ocean wave power absorption. Its working principle relies on the use of water column oscillations, that are induced by wave-excited pressure bulges in a distensible tube. The intensity of these bulges grows along the length of the tube towards the inlet of the forward-bent duct, thereafter driving periodic water column oscillations with amplitude \(\eta\). The tube also oscillates in bending and surging under the action of the incident waves. Resonant conditions of the water column occur at its natural period of oscillation \({T}_{0}\), and resonant conditions of the tube may be achieved if the celerity of the incident waves \(c\) equals the speed of the pressure bulges [3]. In the absence of hysteresis, the bulge wave speed \(U\) inside the rubber tube is given in Lighthill [14] as \(U=1/\sqrt{{\rho }_{1}D}\), where \({\rho }_{1}\) is the mass-density of water and \(D\) is the distensibility of the tube. For a tube with circular cross-section of diameter \(d\) and wall-thickness \(w\), \(D=d/\left(wE\right)\); \(E\) is the Young’s modulus, which is equal to approximately \(0.91\mathrm{ MPa}\) for latex at 100% strain. Hence, the free bulge-wave speed inside the tube is given by \(U=\sqrt{wE/\left({\rho }_{1}d\right)}\). To achieve \(U=c\), the thickness of the tube must then be \(w={\rho }_{1}{c}^{2}d/E\), where \(c=\left(gT/2\pi \right)\mathrm{ tan\,h}\left(kh\right)\) is the phase velocity of the incident waves in water depth \(h\). The tuning period to be met by the incident waves is:

$$T_{1} = \frac{{2\pi \sqrt {wE/\left( {\rho_{1} d} \right)} }}{{g \tan\!\text{h}\left( {kh} \right)}}$$
(1)

In the present experiment the expected free bulge-wave speed is \(U=1.22\mathrm{ m}/\mathrm{s}\). When the incident waves have a period equal to \({T}_{1}=0.81 \mathrm{s}\), there is a resonant transfer of energy from the incident waves to the tube and the intensity of the pressure bulges is large (see Fig. 3).

Fig. 3
figure 3

Fully-developed pressure bulge near the tuning period \({T}_{1}=0.81 \mathrm{s}\)

Full size image

Let us now consider the oscillating water column inside the forward-bent vertical duct. Neglecting the stiffness and added mass of the tube, the undamped natural period of the OWC harmonic oscillations is \({T}_{0}\cong 2\pi \sqrt{l/g}\). Here \(l\) is the total length of the water column, measured from the inlet of the PVC elbow till the OWC free-surface. This leads to a first approximation of the OWC natural period \({T}_{0}=0.78\mathrm{ s}\), to be experimentally verified. Therefore, the tube’s tuning period is expected to be quite close to the water column natural period.

The coupling between the bulges in the tube and its bending modes is important, especially at the period where the incident wavelength is equal to the tube length (\(T=0.77 \mathrm{s}\)), quite close in this case to \({T}_{0}\) and \({T}_{1}\). As will be demonstrated later on, this is a determining factor of the system’s maximum efficiency. Equally important is the period where \(\lambda =2L\). This is confirmed by the system’s amplification factor \(\zeta\), which is defined as the ratio between the mean water column oscillation height \(2\eta\) and the incident wave height \(H\). This wave height is provided by the reflection analysis performed upstream, sufficiently far from the model so that evanescent modes had decayed. Figure 4 shows this amplification factor as a function of the non-dimensional wavenumber \(kh\), for an orifice with \({d}_{0}=9 \mathrm{mm}\) and wave series 1 to 6. Out of all the orifices tested, this is the one that yielded the highest energy-capture efficiency. While smaller diameter orifices give rise to detrimental viscous scale-effects, larger orifices are not able to generate significant gauge pressure in the pneumatic chamber. At \(T=1.12\mathrm{ s}\) – near where \(\lambda =2L\) –, the water-column oscillation height reaches a maximum of about 5 times the incident wave height, for the small amplitude waves of series 1. When the system is excited by waves of larger amplitudes, its oscillations are less amplified. Moreover, it may be observed that neither the resonance of the tube, nor the water column natural period have a noticeable influence on \(\zeta\).

Fig. 4
figure 4

Amplification factor \(\zeta\) as a function of the non-dimensional wavenumber \(kh\), for all the wave series tested and an orifice diameter \({d}_{0}=9 \mathrm{mm}\)

Full size image

Focusing next on the pneumatic chamber and assuming incompressible flow conditions, the air flowrate across the orifice of diameter \({d}_{0}\) can be directly determined from the water column free-surface displacement measurements, as \(Q=A\frac{dz}{dt}\); here \(A=\pi { r}^{2}\) is the internal cross-sectional area of the vertical shaft. The pressure to volume-flow characteristic can then be derived from Bernoulli’s law for steady incompressible flow, as described in [5]:

$$\Delta p = \frac{8\rho }{{C^{2} \pi^{2} d_{0}^{4} }}{ }Q^{2} = KQ^{2}$$
(2)

Here \(\Delta p=\left|p-{p}_{0}\right|\) – \(p\) being the pressure in the chamber and \({p}_{0}\) the atmospheric pressure outside –, \(K\) is the orifice characteristic and \(\rho\) is the mass density of air. A reasonable empirical value for the discharge coefficient of a small sharp-edged hole in a plate is \(C=0.6\), as explained in [15], resulting in a value of \(K=2.53{d}_{0}^{-4}\) for air at ambient conditions. Only the fundamental component of the measured water column free-surface displacement \(z\left(t\right)\) has been considered in the calculation of \(Q(t)\) and \(\Delta p(t)\).

In Fig. 5, the pressure to air volume-flow characteristic curve is drawn for an orifice with diameter \({d}_{0}=9\mathrm{ mm}\) and all the wave series tested. The mean values \(\overline{\Delta p }\) and \(\overline{Q }\) are obtained from averaging respectively \(\Delta p(t)\) and the absolute values of \(Q(t)\), in a wave period. For a mean flowrate between \(0\) and \(62\,\mathrm{l}/\mathrm{min}\), the pressure in the pneumatic chamber rises to about \(505\mathrm{ Pa}\). The Reynolds number of the airflow through the orifice of diameter \({d}_{0}=9\mathrm{ mm}\) ranges from \(2.07\times {10}^{2}\) to \(9.83\times {10}^{3}\).

Fig. 5
figure 5

Mean absolute-value of the gauge pressure in the pneumatic chamber \(\overline{\Delta p }\), versus the mean absolute value of the air flowrate \(\overline{Q }\) across an orifice of diameter \({d}_{0}=9\mathrm{ mm}\), for all the wave series tested

Full size image

5 Energy capture-width

The instantaneous power extracted at the orifice is given in adiabatic conditions by the air flowrate across the orifice \(Q\left(t\right)\), times the differential pressure \(\Delta p\left(t\right)\). Hence, the mean power \(P\) extracted by the system at each stroke with period \(T\) is:

$$P = \frac{1}{T}\int\limits_{0}^{T} {\Delta p\left( t \right) \cdot \left| {Q(t)} \right|~dt}$$
(3)

Based on the values obtained for the mean extracted power \(P\) and the incident wave power per unit wave front \({P}_{i}\), a suitable measure of the system’s efficiency is the well-known energy capture-width \({C}_{W}\). It may be defined in tube diameters as follows:

$$C_{W} = \frac{P}{{P_{i} d}}$$
(4)

In Fig. 6 the system’s capture-width \({C}_{W}\) is given as a function of the normalized wave period \(T/{T}_{1}\), for an orifice of diameter \({d}_{0}=9\mathrm{ mm}\) and all the wave series tested. Apart from wave series 1 and 2, the peak of efficiency occurs near the system’s resonance, where it attains a maximum of \({C}_{W}=1.9\) tube diameters under wave series 5. In this case the tube’s length is approximately equal to the incident wavelength, and the tube oscillates in a third mode of bending. Apparently, the small amplitude waves of series 1 and 2 are unable to fully excite a tube bending mode that, coupled with the pressure bulges, would result in a high capture-width near where \(\uplambda =L\). This distinct behaviour between small and large amplitude waves can be observed in the video captions of Fig. 7. For the waves of series 1 and 2 the tube bending rather becomes dominant for \(\lambda =2L\), when compared to resonance, reaching \({C}_{W}=1.3\) near \(T=1.13\mathrm{ s}\). In this latter case the tube oscillates in a second mode of bending. Specifically for the small amplitude waves of series 1, there is also a possible detrimental effect caused by standing cross-waves between the tank sidewalls, when \(kb=\pi /2\) (\(T=0.91 \mathrm{s}\)) – see Shemer et al. [16].

Fig. 6
figure 6

Energy capture-width \({C}_{W}\) in tube diameters versus normalized wave period \(T/{T}_{1}\), for an orifice of \({d}_{0}=9 \mathrm{mm}\) and all the wave series tested

Full size image
Fig. 7
figure 7

Distensible tube response to incident waves of period \(T=0.83 \mathrm{s}\) (near \(\lambda =L\)), belonging to wave series 1 (a) and to wave series 6 (b)

Full size image

The influence of the incident wave steepness upon the system’s efficiency is now considered. Figure 8 presents the capture-width \({C}_{W}\) as a function of the wave steepness \(H/\lambda\), for wave series 1 to 6. It may be observed that for each wave series there is a wave-steepness that leads to a maximum \({C}_{W}\). For the range of wave heights tested, the higher the incident wave series the greater is this optimal steepness and maximum \({C}_{W}\). Moreover, for waves of steepness larger than this value, an increase in wave height at constant steepness results in a higher capture-width. For steepness below the optimum value, the opposite is in general true.

Fig. 8
figure 8

Capture-width \({C}_{W}\) in tube diameters as a function of wave steepness \(H/\lambda\), for an orifice with \({d}_{0}=9 \mathrm{mm}\) and all the wave series tested

Full size image

Also of interest is the behaviour of the distensible tube system in extreme wave conditions. Two situations where non-linear and dispersive effects are important have been investigated. They correspond to intermediate and deep-water waves with \(h/\lambda =0.26\) and \(0.72\), respectively. The behaviour of the distensible tube in these two cases is shown in Fig. 9, where the Ursell number \(\mathrm{Ur}=4.9\), and in Fig. 10 where \(\mathrm{Ur}=0.4\). In the first case the wave steepness is \(H/\lambda =0.081\), while in the second case \(H/\lambda =0.146\). The tube performs well in both situations, the first of which is near resonance, still being able to cancel the incident waves in the second case. These extreme conditions didn’t result in the occurrence of aneurisms in the rubber tube.

Fig. 9
figure 9

Distensible-tube system under waves of period \(T=0.84 \mathrm{s}\) (\(\lambda =1.29 \mathrm{m}\)) and wave height \(H=0.105 \mathrm{m}\), propagating in a water depth \(h=0.33 \mathrm{m}\) (\(\mathrm{Ur}=4.9\))

Full size image
Fig. 10
figure 10

Distensible-tube system under waves of period \(T=0.55\mathrm{ s}\) (\(\uplambda =0.46\mathrm{ m}\)) and wave height \(H=0.067\mathrm{ m}\), propagating in a water depth \(h=0.33\mathrm{ m}\) (\(\mathrm{Ur}=0.4\))

Full size image

6 Comparison with benchmark results

The system’s efficiency is herein compared with the benchmark experimental results of [4], obtained with a 1:25 scale floating distensible tube fixed at either end. A useful parameter for comparison of impedance rates between the two models is the normalized impedance \(Z={\overline{Z} }_{PTO} / {Z}_{tube}\). If the air volume-flow through the PTO is assumed sinusoidal, the mean impedance \({\overline{Z} }_{PTO}\) [\(\mathrm{kPa }\,{\mathrm{m}}^{-3}\mathrm{ s}\)] – which is defined as the mean of the pressure difference to flowrate across the orifice – is given by:

$$\overline{Z}_{PTO} = K\left( {\frac{2q}{\pi }} \right)$$
(5)

In this equation \(q\) is the maximum instantaneous flowrate and \(K=2.53{d}_{0}^{-4}\), as given above (Eq. 2). The inherent impedance of the distensible tube \({Z}_{tube}\) is, in turn:

$$Z_{tube} = \frac{{\rho_{1} U}}{{\left( {\frac{{\pi d^{2} }}{4}} \right)}}$$
(6)

here \({\rho }_{1}\) is the mass density of water and \(U\) is the free bulge-wave speed in the tube without hysteresis, previously defined in §4.

The values of the normalized impedance \(Z\) of the present physical model, when equipped with a PTO orifice of diameter \({d}_{0}=9 \mathrm{mm}\) and tested under waves of series 2 and 3, are given in Fig. 11 against the mean air volume flowrate. In this case the orifice PTO has a non-linear characteristic (see Fig. 5), and the wave steepness of series 2 and 3 is between \(0.001\) and \(0.097\). Also represented are two of the normalized impedances imposed by a linear PTO in the model of Chaplin et al. [4]. In this latter case the pneumatic PTO is a set of capillary tubes, within which the Reynolds number is of the order of hundreds, typical of laminar flow; the characteristics of the incident wave field were kept within the range of linearity (\(H/\lambda =0.006-0.013\)). Note that the two linear impedances of [4], that were chosen to adequately compare these two experiments (\(Z=0.64\) and \(Z=1.05\)), are each comprised within the range of non-linear normalized impedances of the present model, which are \(Z=0.01-0.78\) for wave series 2 and \(Z=0.26-1.50\) for wave series 3.

Fig. 11
figure 11

Normalized impedance \(Z\) versus mean air volume flow \(\overline{Q }\): present model with a PTO orifice of \({d}_{0}=9\mathrm{ mm}\), under wave series 2 and 3; benchmark experiments of Chaplin et al. [4], with linear \(Z=0.64\) and \(Z=1.05\)

Full size image

For the compatible normalized impedance rates shown in Fig. 11, the values of capture-width \({C}_{W}\) for these two models are next compared in Fig. 12 as a function of the normalized wave period \(T/{T}_{1}\). Measurements of maximum capture-width are in reasonable agreement. However, for the small amplitude waves of series 2, the maximum \({C}_{W}\) of the present model is shifted to larger wave periods. This is essentially due to the bending mode at \(\lambda =2L\). For the larger wave heights of series 3 the maximum \({C}_{W}\) occurs at resonance, near where \(\lambda =L\), being slightly higher for the present model, possibly due to blockage effects in the flume. The distinct behaviour between the two cases derives from the fact that the benchmark model is held fixed at both ends (thus relying only on a longer stationary bulging tube), while the present distensible tube is shorter and is allowed to additionally oscillate freely, in surge and bending modes. These comparisons show that the coupling of the tube’s bending modes with the pressure bulges is truly beneficial, when \(\lambda =2L\) and \(\lambda =L\), thus contributing to widen the high-efficiency bandwidth.

Fig. 12
figure 12

Capture-width \({C}_{W}\) in tube diameters, versus normalized wave-period \(T/{T}_{1}\): a) present model (\({d}_{0}=9 mm\)) under wave series 2, and benchmark model with linear \(Z=0.64\); b) present model (\({d}_{0}=9 mm\)) under wave series 3, and benchmark model with linear \(Z=1.05\)

Full size image

Comparisons are next made with analytical and numerical solutions available in the literature, for vertical circular OWCs without a distensible tube. In Fig. 13(left), the capture-width of the present model with \(r/h=1/9\) is compared with the analytical solutions of Evans and Porter [17], based on linear theory; these latter results were obtained for a fixed-draft vertical circular OWC, with \(a/h=1/4\) and \(r/h\) varying from \(1/8\) to \(1/2\). The \({C}_{W}\) is here expressed in OWC diameters, as a function of the normalized wave period \(T/{T}_{0}\). By adding a distensible tube to a vertical circular OWC of similar relative draft, comparable maximum capture-widths are attainable with an OWC of smaller radius. Simultaneously, high efficiencies are in this case obtained over a wide bandwidth of wave periods. In Fig. 13(right), comparisons are made with the numerical predictions for an \(a/h=1/5\) bottom-standing circular OWC, given in Deng et al. [18] (where \(a\) is in this case the lip submergence), and with the predictions given by Martins-Rivas and Mei [19] for a fixed-draft vertical circular OWC of \(a/h=1/5\). In this case \({C}_{W}\) is also expressed in OWC diameters, as a function of the normalized wave period \(T/{T}_{0}\). Again, it may be observed that a distensible tube, connected to a much slimmer OWC shaft, delivers higher efficiencies over a wider bandwidth of incident wave periods. This is true relative to both the fixed-draft and bottom standing OWCs.

Fig. 13
figure 13

Comparisons of the capture-width \({C}_{W}\) of the present distensible tube system with: a) the analytical solution obtained in linear theory by Evans and Porter [17], left; b) the numerical solutions of Deng et al. [18] and Martins-Rivas and Mei [19], right

Full size image

7 Energy-loss assessment

The theoretical foundations of wave-power absorption by oscillating bodies were established in [20]. In linear theory, the interactions between the body and the incident waves can be summed up as a wave diffraction-radiation problem, where the maximum hydrodynamic efficiency of the device occurs when its radiated waves fully cancel the waves that are reflected and transmitted. An energy balance which encompasses a far-field analysis of the reflected and transmitted waves, together with the extracted power and energy losses in the system, is thus now accomplished. The energy transmitted by a monochromatic incident wave having a wave height \(H\), wavelength \(\lambda\) and a wave crest equal to the width of the channel \(b\) is given by:

$$E_{i} = \frac{1}{8}\rho_{1} gb\lambda H^{2}$$
(7)

Part of this energy is transferred to the system at its primary interface, the remaining fraction being reflected and transmitted by the tube oscillations or lost due to viscosity. A reflection analysis of the waves upstream yields the total reflection coefficient \(R\), and the transmission coefficient \({T}_{r}\) is monitored by the wave probe located downstream of the model. The wave measurements were performed sufficiently far from the model so that evanescent modes had decayed. The system’s hydrodynamic efficiency being \(1-{R}^{2}-{T}_{r}^{2}\), the amount of energy traded with the system at its primary interface is \(\left(1-{R}^{2}-{T}_{r}^{2}\right){E}_{i}\). A substantial percentage of this energy is extracted at the system’s PTO and later converted into useful power, whose mean value is \(P\). The total energy extracted in a harmonic wave cycle is \(P\times T.\) Another part of the energy exchanged at the system’s primary interface is stored as water column oscillations: \({E}_{S}=\left(\pi {r}^{2}/4\right){\rho }_{1}g{\eta }^{2}\). The remaining is the energy-loss due to viscous friction, turbulence and hysteresis, \({E}_{L}\):

$$E_{L} = \left( {1 - R^{2} - T_{r}^{2} } \right)E_{i} - PT - \frac{{\pi r^{2} }}{4}\rho_{1} g\eta^{2}$$
(8)

The measured values of the total reflection coefficient \(R\) and transmission coefficient \({T}_{r}\) are presented in Fig. 14, where they are shown as a function of the normalized wave period \(T/{T}_{1}\), for the most energetic waves tested (series 3 to 6). At \(T=1.1\mathrm{ s}\), whenever the incident wavelength is close to twice the tube length, the system reflects less than 6.3% of the incident wave height (Fig. 14, left). At this same period the transmitted waves have about one half the incident wave amplitude (Fig. 14, right). Under these conditions (\(T=1.1\mathrm{ s})\), the maximum hydrodynamic efficiency possible is 75%. However, the actual maximum hydrodynamic efficiency is higher and rather occurs at resonance (\({T}_{0}=0.81 \mathrm{s}\)), as shown in Fig. 15 for wave series 3 to 6. It reaches \(92\) to \(95\mathrm{ \%}\), depending on the wave series. One may also observe that the hydrodynamic efficiency decreases sharply for periods above \({T}_{0}\).

Fig. 14
figure 14

Dynamic reflection and transmission coefficients as a function of normalized wave period \(T/{T}_{1}\), for wave series 3 to 6 and an orifice diameter \({d}_{0}=9 \mathrm{mm}\)

Full size image
Fig. 15
figure 15

Hydrodynamic efficiency (\(1-{R}^{2}-{T}_{r}^{2}\)) as a function of the normalized wave period \(T/{T}_{1}\), for wave series 3 to 6 and an orifice of diameter \({d}_{0}=9 \mathrm{mm}\)

Full size image

As explained above, an efficient power absorber is the one that can radiate waves that cancel the waves reflected by diffraction, while kee** the wave transmission at acceptable levels. The wave cancelation mechanism leading to near maximum energy absorption is well depicted in Fig. 16, for incident waves of series 5 with period \(T=0.65 \mathrm{s}\), wave height \(H=5.25 \mathrm{cm}\) and wavelength \(\lambda =0.67 \mathrm{m}\). Upstream of the tube only the pure incident monochromatic waves are visible, while downstream of the model the water free surface is practically at rest. Noteworthy is the fact that, although the cancelation mechanism is efficient in this case, accompanied by a high hydrodynamic efficiency, the capture-width is low due to the energy storage in the OWC and high energy losses of the system.

Fig. 16
figure 16

Cancellation mechanism due to energy absorption, for waves of series 5 with period \(T=0.65 \mathrm{s}\)

Full size image

The fraction of incident wave energy that is stored in the oscillating water column is given by:

$$\frac{{E_{S} }}{{E_{i} }} = \frac{1}{4} kb \left( \frac{r}{b} \right)^{2} \zeta^{2}$$
(9)

This stored energy ratio is thus proportional to the square of the amplification factor, and is related to both the non-dimensional wavenumber \(kb\) and the square of \(r/b\). The ratio \(r/b\) characterizes the blockage influence due to model size to tank spacing. The wavenumbers \(kb=n\pi /2\) (\(n=1, 2, \dots\)) define tank confinement conditions, that correspond to interactions between a row of devices equally spaced a distance \(b\). The stored energy ratio given by Eq. 9 is shown in Fig. 17, now as a function of a normalized wave period \(T/{T}_{0}\). Note that under waves of smaller wave height – like the ones of series 1 – the system can store up to 10% of the energy of the incident waves, when the wavelength is twice the tube’s length. For the most energetic waves of series 3 to 6, the system stores less than 5% of this energy. For larger wavelengths, the stored energy ratio tends asymptotically to zero. At resonance (\(T={T}_{0})\), which is close to where \(\lambda =L\), the ratio of stored energy is low and the efficiency of the system hits its maximum – see Figs. 6 and 15.

Fig. 17
figure 17

Stored energy ratio \({E}_{s}/{E}_{i}\) as a function of the normalized wave period \(T/{T}_{0}\), for all the wave series tested and an orifice of diameter \({d}_{0}=9 \mathrm{mm}\)

Full size image

As the distensible tube oscillates beneath waves it is subjected to hydrodynamic wave forces, whose drag and inertia components are governed by a period parameter, known as the Keulegan–Carpenter number \(\mathrm{Kc}=\pi H/d\) [21]. The energy-loss \({E}_{L}\) (in Joule) has been calculated from Eq. 8, for all the wave series tested, and is next presented in Fig. 18 as a function of \(\mathrm{Kc}\). The mean Reynolds number of the flow around the tube is \(\mathrm{Re}=3.4\times {10}^{2}-4.3\times {10}^{4}\), and the Reynolds number of the OWC is between \(3.88\times {10}^{2}\) and \(1.84\times {10}^{4}\). It may be verified that the energy-loss in the system closely follows a parabolic trend up to about \(\mathrm{Kc}=1.6\), clearly showing an inertia-dominant wave loading up to this value. The contribution of form drag is shown to become important for larger values of \(\mathrm{Kc}\), indicating that in the present case significant separation losses occur in wave series 5 and 6 (\(H/\lambda >0.037\)). This is in agreement with the findings of Chaplin [22], who investigated the wave loading on a horizontal circular cylinder submerged beneath regular waves, and having its axis parallel to the wave crests. This author showed that, for a Reynolds number of about \(\mathrm{Re}={10}^{4}\) the viscous effects may become important, even for waves with moderate steepness where the flow separation is still insignificant. In addition, the oscillatory wave loading is non-linear, a characteristic that is verifiably associated to steady streaming-flow in the cylinder’s oscillatory boundary-layer. When the cylinder approaches the free surface the non-linear contribution to the inertia coefficient becomes more relevant, happening at a \(\mathrm{Kc}<2\). For larger values of the Keulegan–Carpenter number a wake in turn develops, and the wave loading component associated to form drag augments dramatically, accompanied by a significant energy-loss.

Fig. 18
figure 18

Energy-loss \({E}_{L}\) (in Joule), as a function of the Keulegan–Carpenter number \(\mathrm{Kc}\), for all the wave series tested and an orifice of diameter \({d}_{0}=9 \mathrm{mm}\)

Full size image

8 System’s overall efficiency

To complement the performance assessment, an overall efficiency is herein defined as the ratio of the extracted energy \(PT\) to the incident wave energy \({E}_{i}\). Figure 19 gathers the overall efficiency, the hydrodynamic efficiency and energy-loss ratio \({E}_{L}/{E}_{i}\), as a function of the normalized wave period \(T/{T}_{1}\), for wave series 6. Recall that the hydrodynamic efficiency is maximum at resonance (\(T=0.81\mathrm{ s}\)) and falls dramatically as the wave period increases (see Fig. 15). The energy losses are much larger for waves of small periods, decreasing monotonously as the wave period increases. Consequently, the overall efficiency attains a maximum of 0.34 between \(T=0.81\mathrm{ s}\) and \(T=1\mathrm{ s}\). In practice, the system extracts at most 34% of the total wave power available in a wave front equal to the width of the flume. For wave periods bellow the system’s resonance – as is the case of Fig. 16 – the hydrodynamic efficiency is very high and the overall efficiency is poor. This difference reflects a surplus of energy which is not converted to useful power, as discussed in the previous section.

Fig. 19
figure 19

Hydrodynamic efficiency, energy-loss ratio and overall efficiency as a function of normalized wave period \(T/{T}_{1}\), obtained with an orifice of diameter \({d}_{0}=9 \mathrm{mm}\) under wave series 6

Full size image

For small incident wave periods, wave diffraction as well as wave breaking over the nose and on top of the tube may also have contributed to increase the energy losses. Figure 20 illustrates these phenomena, where incident waves of series 5 with period \(T=0.55 \mathrm{s}\) and steepness \(H/\lambda =0.075\) interfere with the tube and tank side-walls, resulting in wave diffraction and eventually wave breaking.

Fig. 20
figure 20

Wave breaking on top of the distensible tube, while operating under waves of series 5 with period \(T=0.55 \mathrm{s}\), steepness \(H/\lambda =0.075\) and wavenumber \(k=13.2\)

Full size image

9 General discussion

A floating distensible tube attenuator is a simple and low-cost device that incorporates well-tried rubber and turbine technologies. Although this device has the potential to deliver significant reductions in the cost of wave energy, its commercial viability still needs to be verified. So far, scientific research on the energy-loss assessment and efficiency improvement of such a device is scarce. To overcome this gap, the goal of the present experimental study is to measure the power extracted by an OWC-connected distensible tube, and to understand how the tube’s working modes contribute to the energy absorption process. Furthermore, a comprehensive assessment of the friction and separation losses is done.

In this experimental study sixty waves per PTO orifice are generated in the wave flume, 23% of which are deep-water waves and 77% are intermediate waves. The interaction of these waves with the distensible tube is assessed through the analysis of the incident, reflected and transmitted wave far-fields, leading to the hydrodynamic efficiency of the system. A methodology that combines this assessment with an energy balance, conducted on the system itself, ultimately leads to the energy losses and overall efficiency. Recall that air compressibility in the pneumatic PTO was neglected, an assumption that is to some extent valid for small-scale laboratory work.

It is found that significant amplifications of the water oscillations in the OWC occur, reaching a maximum of about five times the incident wave height, near where the wavelength is twice the length of the tube. The peak capture-width of the system is about \(2\) tube diameters and rather occurs at resonance, where the wavelength is equal to the tube’s length. Although the system’s capture-width is lower for \(\lambda =2L\), it is found to be independent from the wave height. Nevertheless, between \(\lambda =L\) and \(\lambda =2L\) the system’s capture-width remains high, it's maximum attainable value being strongly dependent on the non-linear effects associated with the incident wave steepness.

The capture-width predictions presented above are validated against a similar experiment, in which a larger and longer tube, fixed at both ends, is tested with a linear PTO impedance and under linear wave conditions. Although both models achieve roughly the same maximum efficiency in similar working conditions, the comparisons put forward the advantages of using a shorter and freely floating tube, having three degrees of freedom. Further comparisons are also made with existing theoretical predictions, obtained for conventional fixed-draft and bottom-standing circular OWCs, based in linear theory. These latter provide evidence of the advantages of coupling a distensible tube to an OWC device, as this sightly augments the maximum capture-width and greatly widens its bandwidth of high efficiency, in this case.

Considering a real tube of about \(7 \mathrm{m}\) in diameter, excited by waves of roughly \(3.8 \mathrm{m}\) wave height and \(7 \mathrm{s}\) wave period, the system can extract all the energy from a \(14 \mathrm{m}\) wave front (\({C}_{W}=2\)), with an overall efficiency of 34%. In these resonant conditions, the maximum hydrodynamic efficiency of the system is \(95\mathrm{ \%}\) and the ratio of energy stored in the OWC is low. This efficiency decreases sharply for larger wave periods. For periods bellow resonance significant internal flow friction and external separation losses occur, contributing to a significant reduction of the overall system efficiency. Apropos, for values of the Keulegan–Carpenter number above \(1.6\) a wake develops from the tube and, consequently, the contribution of form drag becomes important. Additional viscous losses may occur due to wave breaking over the tube.

10 Conclusion

The present experimental study may help to guide the practical design of a floating distensible tube connected to an oscillating-water-column system. It provides evidence on the importance of the tube oscillating modes, and quantifies their contribution to the power extraction from the incident waves, supported by video captions obtained during the experiments. Adding a distensible tube to a forward-bent OWC enables to achieve good performance with smaller devices, thus favouring the reduction of constructions costs. The measured maximum energy capture-width of the system does not exceed \(2\) tube diameters and occurs at resonance, for the most energetic waves, close to where the incident wavelength matches the length of the tube. Under these conditions the hydrodynamic and overall efficiencies achieved are also maximum, reaching respectively 95% and 34%, and the tube oscillates with an extra surging motion, apart from significant bending and bulging. One important limitation of the study relates to the small scale of the physical model tested and consequent important viscous effects. To fully understand how the tube’s working modes contribute to the wave-energy absorption efficiency, the consideration of these scale effects in the wave-energy conversion process is essential. Therefore, to obtain verifiable performance predictions of a full-scale device, future experiments at scales that approach the prototype dimensions are necessary. Other important topics that still need to be addressed are the hysteresis of the rubber, the mooring of the device, phase control of the PTO and the occurrence of aneurisms in the tube, that compromise the system’s survivability in extreme waves.