1 Introduction

Analog Phase Locked Loops (PLL) are a very attractive choice for contemporary radio frequency and wireless communication systems. The performance of analog PLLs largely depends on the voltage-controlled oscillator as it is considered the vital component and necessary building block of the PLL system [1,2,3]. However, analog PLLs contain analog components such as capacitors, resistors and filters that require a large chip area. In addition, it is hard to port analog PLLs from one fabrication process to another due to the sensitivity towards process parameters [4,5,6]. With the advancements in design technologies, the all-digital PLL (ADPLL) has become more popular due to its easy implementation across modern IC technologies and significantly smaller area requirements. ADPLLs employ all digital components, including the digitally-controlled oscillator (DCO). DCO is an essential element of this ADPLL structure, primarily controlling the frequency of oscillation [7, 8]. DCOs are more flexible and robust than their analog counterparts. Designing of ADPLLs requires monolithic DCOs with a wide frequency range and decent phase noise performance. The simplest form of DCO is an inverter-based ring type consisting of an odd count of delay stages/elements.

A digitally controlled delay element (DCDE) is the essential component of a DCO circuit. There are significant approaches for varying the delay of the DCDE. The first approach is the delay path selection in which multiplexors are utilized for the selection of the number of delay stages. This approach is not used standalone and is generally combined with additional techniques owing to its limited resolution [7,8,9,10,11,12]. The second method employs current-starved inverters as delay stages [9, 13, 14]. In this technique, binary-weighted PMOS/NMOS are used in the switching network that is controlled by the input vector [15, 16]. However, increased parasitic capacitance places a constraint on the maximum frequency of the DCO. The third approach is based on CMOS inverters with shunt MOS-based capacitors [14, 17, 18, 20]. In this, binary-weighted MOS-based capacitors are used to change the delay of the inverter by changing the capacitive load. However, shunt-type DCDE eventually becomes saturated as adding a greater number of switched capacitors results in reduced maximum frequency.

In the above-mentioned DCDE designs, there exists a basic trade-off between the tunning range and the maximum achievable frequency. More capacitive loading places a constraint on the maximum oscillation frequency that DCO can achieve and also leads to increased power dissipation. Hence, reducing the power dissipation of the DCO has become a major concern for its application in compact or Internet of Things (IoT) devices [4, 15].

In this manuscript, two new designs of DCDE have been reported. The DCDE designs are based on MOS varactors and an NMOS switching network. The remainder of the manuscript is structured as follows: Sect. 2 provides the design and working of the proposed DCO structures using the reported DCDEs. Further, Sect. 3 provides the results obtained for the proposed DCO circuits. Section 4 provides the conclusion of the reported work.

2 Proposed DCO circuit design

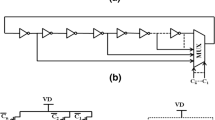
The DCO circuit is designed with two new proposed DCDEs as shown in Figs. 1 and 2. The relationship between the output oscillation frequency and the time delay of each stage can be expressed using the general Eq. (1):

$$f_{o = } {\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 {2Nt_{d} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${2Nt_{d} }$}}$$
(1)

where td is the delay offered by each stage and N is the number of delay stages. This equation highlights that the output frequency is inversely proportional to the delay offered by each stage. As the time delay of each stage decreases, the output frequency increases, and vice versa. This fundamental relationship underscores the dynamic interplay between time delay and output frequency within a DCO.

Fig. 1
figure 1

Proposed Inverter-based DCDE

Full size image
Fig. 2
figure 2

Proposed 3T-NAND gate-based DCDE

Full size image

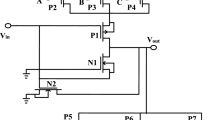
The first DCDE consists of a CMOS inverter and a digitally controlled load element implemented with three NMOS transistors (N2, N3, and N4) to provide the variable frequency. The second design has a 3T-NAND gate-based inverting stage, along with a digitally controlled load element connected at the output. The delay of an inverting stage is given by the Eq. (2):

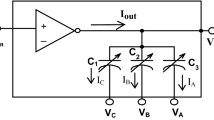
$$t_{d = } {\raise0.7ex\hbox{${C_{Load} V_{PP} }$} \!\mathord{\left/ {\vphantom {{C_{Load} V_{PP} } {I_{D} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${I_{D} }$}}$$
(2)

where \({C}_{Load}\) is the output load capacitance, \({V}_{PP}\) is the peak-to-peak output voltage swing and \({I}_{D}\) is the cell current. Thus, the output oscillation frequency can be tuned by varying the capacitive load and by varying the cell current (\({I}_{D}\)) of the DCDE. Both the DCDEs employ the MOS varactor as the capacitive load at the output. NMOS transistors N2 and N3 work as two MOS varactors connected to the ground through a variable resistance designed with transistor N3. MOS varactor operates in a strong inversion mode when the gate voltage applied is greater than the threshold voltage i.e., VGS > VTH. In this inversion mode, the maximum MOS capacitance is given by the Eq. (3):

$$C_{\max } = C_{ox} = \varepsilon_{0} WL/t_{ox}$$
(3)

Consequently, by changing the width (W) of the MOS varactor, the capacitive load can be varied which in turn leads to a variable time delay offered by each stage and a tunable output frequency can be achieved. Also, the time delay td of the DCO is in turn a function of the input control word ‘D’ [9] and is given by the Eq. (4):

$$t_{d = } f\left( {D_{n - 1} 2^{n - 1} + D_{n - 2} 2^{n - 2} + \ldots + D_{1} 2^{1} + D_{0} 2^{0} } \right)$$
(4)

where D0 to Dn-1 are the control bits applied to the load element. Accordingly, by varying the control bits, current through the cell (\({{\varvec{I}}}_{{\varvec{D}}}\)) can be varied which leads to a large frequency range. Hence, the novel DCDE introduces an extra tuning method involving a variable capacitor, deviating from the conventional delay element that relies on an inverter configuration. This frequency adjustment technique, achieved without modifying the supply voltage, offers the benefit of reduced power dissipation. The equivalent circuit of the proposed DCDE is shown in Fig. 3.

Fig. 3
figure 3

Equivalent circuit of Inverter-based DCDE

Full size image

For an NMOS-based varactor with the drain, source, and body connected together, the capacitance depends on the voltage applied at the gate and source terminal (VGS). Capacitance is higher with a negative VGS, and reduces with a positive VGS. With the application of digital bits D0, D1, and D2, the MOS varactors N6 and N7 provides a variable capacitance. When D0, D1, and D2 are set to [000], the VGS voltage for transistors N2 to N7 of the proposed DCO becomes positive and resulting in a reduction of MOS capacitance and subsequently an increase in the output frequency. The transistors N8 to N10 are binary weighted and contribute to capacitance value depending upon the digital bits D0, D1, and D2. Furthermore, applying a negative VGS to MOS varactors N2 to N7 leads to a reduction in the output frequency.

The power consumption of the DCO circuit is dependent on the supply voltage of the delay stage. Equation (5) gives the relationship between the dynamic component of power and the power supply (VDD) for the proposed DCO circuits.

$$P_{dynamic} = \alpha C_{Load} V_{DD}^{2} f_{clk}$$
(5)

where \(\alpha\) is the switching activity factor, \({C}_{Load}\) is the total load capacitance, \({f}_{clk}\) is the clock frequency, and VDD represents the power supply voltage. With increase in the supply voltage, the power consumption increases. Further, the proposed DCO circuits provide constant power with digital control variation as there is no change in the power supply voltage and demonstrate the advantage of low power over the traditional DCOs.

2.1 DCO circuit design I

Proposed three-bit DCO circuit implemented with the first DCDE is shown in Fig. 4. The MOS transistor size used in the proposed DCO circuit is given in Table 1. The transistor length for all MOS transistors has been chosen as 0.18 µm. CMOS inverter is implemented with two MOS transistors P1 and N1. The MOS varactor has been designed with NMOS transistors N2 to N7. The switching network consists of binary-weighted NMOS transistors N8, N9, and N10 with 1.0, 2.0 and 4.0 µm MOS transistor width (W), respectively. By altering the control bits applied to the NMOS switching network, a tunable frequency is obtained. Further, Fig. 5 demonstrate the five-bit DCO design employing five DCDEs. Additionally, a seven-bit DCO has also been designed utilizing seven DCDEs.

Fig. 4
figure 4

CMOS Inverter-based three-bit DCO design

Full size image
Table1 MOS transistor size used in Inverter-based DCO
Full size table
Fig. 5
figure 5

CMOS Inverter-based five-bit DCO design

Full size image

2.2 DCO circuit design II

DCO circuit II is designed with a second proposed DCDE as shown in Fig. 6. In the alternative DCO design presented, the inverting stage adopts a 3T-NAND gate configuration [19], notable for its minimized transistor count when contrasted with the traditional method. Additionally, a direct connection between the power supply and ground is eliminated which leads to reduced leakage power and hence power consumption is less compared to DCO design I. A digitally controlled load element is connected at the output and consists of one NMOS switching network and two MOS varactors. Wide frequency range is achieved by modifying the control bits applied to the NMOS switching network. An optimized MOS transistor size utilized in the proposed 3T-NAND gate-based DCO is shown in Table 2. Furthermore, Fig. 7 shows the design of a five-bit DCO circuit with five DCDEs. In addition, a seven-bit DCO has been designed, employing seven DCDEs.

Fig. 6
figure 6

Proposed 3T NAND gate-based three-bit DCO

Full size image
Table 2 MOS transistor size used in 3T-NAND gate-based DCO
Full size table
Fig. 7
figure 7

Proposed 3T-NAND gate-based five-bit DCO design

Full size image

3 Results and discussions

The results of the presented DCO designs have been validated using mentor graphics in 180 nm CMOS technology. In the proposed DCDE, frequency tuning is achieved by varying the load element that is connected at the output terminal of each DCDE. Current flow through the load element varies depending upon the digital control bits applied to it. At the different combinations of control bits, the current varies which results in the variation of the delay time of the proposed DCDE. This, in turn, establishes a clear relationship between the output frequency of the ring oscillator and the delay time, resulting in a responsive frequency adjustment mechanism.

Table 3 demonstrates the outcomes of the three-bit DCO circuit. It is observed that by changing the input control bit from [000] to [111], the oscillation frequency decreases from 4.844 GHz to 2.708 GHz for inverter-based DCO design accompanied by a power consumption of 0.958 mW. Further, the output frequency varies from 2.024 GHz to 0.517 GHz for 3T-NAND gate-based DCO design with power dissipation of 0.335 mW. Results indicate lower power consumption in the DCO design with the second DCDE due to MOS transistor width optimization.

Table 3 Output frequency variation and power dissipation for three-bit DCO
Full size table

Tables 4 and 5 illustrate the frequency variations in five-bit and seven-bit DCO circuits, emphasizing the adaptability of the proposed designs. From the Table 4, it is evident that for five-bit DCO circuit, frequency ranges from 2.523 GHz to 0.853 GHz and 0.867 GHz to 0.131 GHz with the variation in control bit from [00000] to [11111]. The corresponding power consumption registers at 1.597 mW and 0.559 mW, respectively. Frequency tuning from 1.364 GHz to 0.253 GHz and from 0.341 GHz to 0.033GHz for a seven-bit DCO circuit designed with inverter-based DCDE and 3T-NAND gate-based DCDE is obtained with control bit variation from [0000000] to [1111111] as given in Table 5. The power consumption is measured at 2.236 mW, and 0.782 mW, respectively. Furthermore, the output oscillation frequency variations along with the control bit variations for three-bit, five-bit, and seven-bit DCOs is shown in Figs. 8, 9, and 10, offering a comprehensive visual understanding of the DCO behavior.

Table 4 Output frequency variation and power dissipation for five-bit DCO
Full size table
Table 5 Output frequency variation and power dissipation for seven-bit DCO
Full size table
Fig. 8
figure 8

Frequency change with control bits in three-bit DCO

Full size image
Fig. 9
figure 9

Frequency change with control bits in five-bit DCO

Full size image
Fig. 10
figure 10

Frequency change with control bits in seven-bit DCO

Full size image

To further comprehend the robustness of our designs, the effects of variation in the power supply voltage on operating frequency and power consumption for inverter-based DCO circuits have been shown in Table 6. For different values of digital control bits, the output oscillation frequency exhibits a variation from 1.452 to 4.844 GHz with a variation in power supply voltage from 1.2 to 1.8 V. Power consumption variations ranging from 0.048 to 0.958 mW is obtained and recorded. The frequency and power variation curves are shown in Figs. 11 and 12. The frequency spectrum of the proposed DCO circuit with fundamental frequency at 4.8 GHz and its output waveform are shown in Fig. 13.

Table 6 Variations in output frequency and power dissipation with power supply (VDD) for Inverter-based three-bit DCO
Full size table
Fig. 11
figure 11

Frequency variation of Inverter-based three-bit DCO with varying VDD

Full size image
Fig. 12
figure 12

Power consumption of Inverter-based three-bit DCO with varying VDD

Full size image
Fig. 13
figure 13

Results of a three-bit Inverter-based DCO circuit at [000] a frequency waveform, b frequency spectrum

Full size image

The performance of 3T-NAND gate-based DCO with variations in the supply voltage (VDD) from 1.2 to 1.8 V is presented in Table 7 for different values of digital control bits [D0–D2]. Figure 14 shows output frequency variations of 3T-NAND gate-based three-bit DCO with varying VDD. A frequency variation from 0.517 to 2.450 GHz is achieved as shown in Table 7 along with a minimal power dissipation of 0.184 to 0.336 mW, further highlights the flexibility inherent in our design. Figure 15 shows the power consumption variation curve at different values of the power supply (VDD). The results indicate that reducing the power supply voltage (VDD) leads to decreased power consumption in the proposed DCO circuit designs. The output frequency curve of the proposed DCO circuit with control bits [010] for a 3T-NAND gate-based three-bit DCO is shown in Fig. 16a. A complete frequency spectrum has been plotted with fundamental frequency at 1.25 GHz in Fig. 16b.

Table 7 Variations in output frequency and power dissipation with power supply (VDD) for 3T-NAND gate-based three-bit DCO
Full size table
Fig. 14
figure 14

Frequency variation of 3T-NAND gate-based three-bit DCO with varying VDD

Full size image
Fig. 15
figure 15

Power Consumption of 3T-NAND gate-based three-bit DCO with varying VDD

Full size image
Fig. 16
figure 16

Results of a three-bit 3T-NAND gate-based DCO circuit at [010] a frequency waveform, b frequency spectrum

Full size image

Further, the phase noise performance of the proposed DCO circuits has been studied and presented in Table 8. The proposed inverter-based DCO achieves phase noise of − 102.61 dBc/Hz, − 99.65 dBc/Hz, and − 117.54 dBc/Hz at 1 MHz for three-bit, five-bit, and seven-bit control words, respectively. In the case of the 3T-NAND gate-based DCO, the measured phase noise values are − 93.51 dBc/Hz, − 113.07 dBc/Hz, and − 106.96 dBc/Hz at 1 MHz for three-bit, five-bit, and seven-bit DCO variants, respectively. Phase noise waveform for the three-bit, five-bit, and seven-bit variants of the two DCO circuits is shown in Figs. 17 and 18.

Table 8 Figure of merit (FoM) and phase noise outcomes of the presented DCO designs
Full size table
Fig. 17
figure 17

Phase noise of Inverter-based DCO for a three-bit, b five-bit, c seven-bit

Full size image
Fig. 18
figure 18

Phase noise of 3T-NAND gate-based DCO for a three-bit, b five-bit, c seven-bit

Full size image

The FoM (figure of merit) is another essential parameter for the evaluation of the performance of the DCO circuits and is calculated using the following equation [21]:

$$\small FoM\left( {dBc/Hz} \right) = 20\log \left( {{\raise0.7ex\hbox{${f_{c} }$} \!\mathord{\left/ {\vphantom {{f_{c} } {\vartriangle f}}}\right.\kern-0pt} \!\lower0.7ex\hbox{${\vartriangle f}$}}} \right) - 10 \log \left( {{\raise0.7ex\hbox{${P_{DC} \left( {mW} \right)}$} \!\mathord{\left/ {\vphantom {{P_{DC} \left( {mW} \right)} {1\left( {mW} \right)}}}\right.\kern-0pt} \!\lower0.7ex\hbox{${1\left( {mW} \right)}$}}} \right) - L\left( {\vartriangle f} \right)$$
(6)

where \({\mathrm{f}}_{\mathrm{c}}\) is the carrier frequency, and \(\Delta \mathrm{f}\) is the offset from the carrier frequency, \({\mathrm{P}}_{\mathrm{DC}}\) denotes the DC power in mW and \(\mathrm{L }(\Delta \mathrm{f})\) represents the phase noise of the proposed DCO in dBc/Hz. FoM is the overall performance measure of a DCO. A higher figure of merit (FoM) is desirable for a DCO design as it indicates a wide frequency tuning range, lower power consumption and low phase noise. FoM varies from 174.94 to 150.30 dBc/Hz for the proposed DCO circuits. Compared with the reported circuits, the proposed DCOs demonstrate a better FoM. Table 8 summarizes the various performance parameters like phase noise, figure of merit (FoM) along with the digital tuning range, output frequency, and power consumption, all of which contribute to the overall assessment of the DCO's efficiency.

A comparison of the proposed DCO designs in terms of the output frequency range, power dissipation, phase noise, and FoM with the earlier published work has been summarized in Table 9. The incorporation of MOS varactors and novel DCDE designs distinguishes reported work from traditional methods, establishing it as a valuable contribution to the current state of research.

Table 9 Performance comparison of the proposed DCO designs with earlier reported DCOs
Full size table

4 Conclusions

In this paper, two different DCO circuits in 180 nm technology, implementing digitally controlled MOS varactor loads to achieve wide frequency variation are presented. The first design utilizes a CMOS inverter as the inverting stage, with digitally controlled MOS varactors serving as capacitive loads in the DCDE. This inverter-based DCO covers a frequency range of 4.844 to 2.708 GHz, 2.523 to 0.853 GHz, and 1.364 to 0.253 GHz for three-bit, five-bit, and seven-bit configurations, respectively. The power consumption records at 0.958 mW, 1.597 mW, and 2.236 mW for these variants. Phase noise levels of − 102.61 dBc/Hz, − 99.65 dBc/Hz, and − 117.54 dBc/Hz at a 1 MHz offset are obtained. In the second DCO design, a 3T-NAND gate serves as the inverting stage, yielding frequency range of 2.024–0.517 GHz, 0.867–0.131 GHz, and 0.341–0.033 GHz for the corresponding three-bit, five-bit, and seven-bit control word. Phase noise measurements stand at − 93.51 dBc/Hz, − 113.07 dBc/Hz, and − 106.96 dBc/Hz at 1 MHz for three-bit, five-bit, and seven-bit control words, respectively. Power consumption of 0.335 mW, 0.559 mW, and 0.782 mW are obtained. Figures of merit (FoM) in the range of 174.94 to 150.30 dBc/Hz have been obtained. The proposed DCO designs show wide operating frequencies and decent phase noise along with improved FoM characteristics making them suitable for high-frequency applications. However, limitations in the specific CMOS technology and trade-offs between frequency and power persist. Future research could explore advanced CMOS technologies, tackle frequency-power trade-offs, and investigate adaptive tuning mechanisms to enhance robustness. These advancements hold the potential to create more efficient and versatile DCOs for diverse applications in communication and sensing systems.