1 Introduction

Gradual changes in the lifestyle of people and the tendency to use convenience facilities have led to a sharp increase in the demand for energy which 82% is provided by fossil fuels [1]. Given the negative environmental impact of fossil fuels and their depletion, there is an urgent need to use renewable energies [2]. Among these, solar energy is the most easily exploitable because it is free and the most promising for the future. Sub-Saharan Africa, and especially Cameroon, receives about 4.5 kWh/m2 /day of solar irradiation [3]. However, for a long time, this country has been facing problems of access to electricity, with 0.2% of solar energy exploited [4]. Several pieces of equipment are used to exploit this solar potential, among them there are photovoltaic panels which produce electricity and thermal collectors which produce thermal energy. However, the low efficiency of photovoltaic (PV) solar panels is linked to the heating of its cells which convert only 20% of solar radiation into electricity while 80% is dissipated in the form of heat, lowering its performance [5]. Indeed, the proper functioning of PV requires a cell temperature below 45 °C, but during solar noon, this temperature is generally reached and the electrical efficiency drops [6]. Studies have shown that the presence of dust could reduce this elevation of the temperature of the cells by preventing the sun’s rays from reaching the surface of the PV module [7]. However, this technique significantly reduces efficiency at the same time. In order to reduce this efficiency to a considerable level while recovering this quantity of heat at the level of the PV cells, a thermal collector has been combined below the PV cell, giving rise to the PV/T hybrid system which is the association of a photovoltaic solar panel above to that of a thermal collector below to be able to produce electricity and thermal energy simultaneously [8]. Several studies have been conducted on photovoltaic/thermal (PV/T) hybridization using heat transfer fluids such as water, air and nanofluids used to cool the system. Sobhnamayan et al. [9] performed an exergy optimization of the water PV/T collector and the genetic algorithm was employed to maximize the exergy efficiency of the hybrid collector. The results obtained showed that a hydraulic diameter of 4.8 mm with an optimal water velocity of 0.09 m/s raised the exergy efficiency to 11.36%. Tamayo et al. [10] used the outgoing tri-dominated genetic algorithm-II (NSGA-II) to determine a set of parameters such as the mass flow rate at 0.008 kg/s, the packing factor at 0.6 and the thickness of the air gap at 8 cm which maximized the electrical and thermal yields of the water PV/T system. Francesco et al. [11], made a 1-D modeling of a PV/T hybrid collector with a flat and unglazed plate. Their study is based on an experimental and numerical analysis whose results showed that the developed model follows the trend of the experimental data with an absolute error of − 1.06 °C, 0.66 °C and 0.63W on the water outlet temperature, the temperature of the aluminum bottom and the electric power respectively. The evaluation of the experiments carried out on the basis of the external conditions of the city of Dobok in the North of Iraq by Omar et al. [12], for three different days in 2019 (April 7, May 16, and November 13) in active mode indicated that electrical exergy varied from 10 to 18% and thermal exergy from 2 to 7%. Subsequently, other researchers made a hybridization of fluids also called bi-fluids to be able to better absorb the heat below the PV cells. Hasila et al. [13] used water and air as bi-fluids in a PV/T collector. This made it possible to maintain an average temperature of the PV cells below 51.42 °C bringing its energy efficiency to 58.10 and 62.31% for air and water respectively and with an optimal flow rate. Kun et al. [14], have proposed a water/air fluid hybridization for a PV/T hybrid system for two seasons. In summer, the PVT/water mode has been adopted and the maximum water outlet temperature is 40.2 °C with an average thermal efficiency of 52.3% and electrical efficiency of 7.8%. In winter, the PVT/air mode has been adopted and the maximum air outlet temperature obtained is 26 °C with an average thermal efficiency of 23.9% and electrical efficiency of 15.3%. Also, Bakar et al. [15] found that a water/air PV/T system gave maximum thermal and electrical efficiency of 51.1 and 11.6% respectively. Further, other authors have developed more efficient coolants. Different operating modes of fluids have been studied in particular nanofluids, air, water, nanofluid/air. Experimental work on nanofluids containing glycerol and sodium acetate trihydrate has shown that this mixture increases the thermal conductivity by 17.2% while reducing the viscosity by 58.03% compared to glycerol at a temperature of 25 °C [16]. The maximum primary energy saving efficiency of the PV/T system using nanofluid/air and water/air is 91.6 and 85.4% respectively. Muzaidi et al. [17] developed a ternary nanofluid composed of CuO/TiO2 /SiO2 nanoparticules and studied its performance for solar thermal applications. The results showed that the nanoparticles play a greater role in the performance of the systems and the use of the three (3) nanoparticles with water as the base fluid significantly increased the temperature at the outlet of the fluid by approximately 73 °C at 700 W/m2. Azhar et al. [18] demonstrated the effect of a glass cover on the efficiency of the PV/T wall with a trunk wall using the nanofluid (water + Al2O3) as heat transfer fluid. They were able to raise the electrical efficiency of the PV/T hybrid system to 14% in the absence of the glass envelope and the maximum efficiency of the PV/T system obtained is 88% at approximately 2 p.m. in the presence of a glass envelope. Monjur et al. [19] demonstrated through their studies that the total exergy efficiency is better for simultaneous operation of the water and air bi-fluids in the PV/T hybrid system. The maximum total exergy efficiency was 4.78% at 0.0026 kg/s of bi-fluid flow. However, the literature does not present a thermo-economic study due to the hybridization of nanoparticles. Table 1 presents a brief description of previous work and its limitations.

Table 1 Brief description of previous work and its limitations
Full size table

The dimensions (length, width, height or thickness) of certain components of the double-cooled PV/T system are generally taken so that the energy produced is optimal. But the combination of design parameters and their effectiveness in converting received solar energy into usable energy must be evaluated. Many studies have been carried out on the cooling of the panels, but these systems have many drawbacks such as energy consumption, maintenance and installation costs [20]. However, several authors have focused on the thermal and electrical energy aspect of the PV/T hybrid collector and few others have made a thermal and electrical exergy analysis of the latter. Moreover, no study shows the influence of ternary nanofluids with double air cooling on the performance of the PV/T hybrid system. So far, the design parameters of the bi-fluid PV/T hybrid collector such as the center-to-center distance between the tubes, the inside and outside diameters of the tubes, the thicknesses of the PV cells, the insulation, the absorber, as well as the angle of inclination of the collector for which there is a maximum exergy efficiency have not been the subject of any study.

Therefore the main objective of this study is to make an exergy optimization of a bi-fluid PV/T hybrid collector and to show the influence of the double cooling with air circulation and ternary nanofluids (TNF) on the system performance. An energy and exergy analysis of the bi-fluid PV/T hybrid collector will be made and a study on the influence of certain design parameters on the total exergy efficiency will be carried out. This study is conducted in the city of Yaounde (Cameroon). A numerical code is written and simulated using Matlab software. The main contributions in this manuscript can be listed as follows:

  • The influence of the optimization parameters on the exergy and electric efficiencies is analyzed and quantified.

  • The outlet temperature distribution of the air/water-CuO/MgO/TiO2 bi-fluid is obtained and also the optimum flow rates.

  • The exergo-economic and environmental analysis of the system is carried out.

The results of this study are valid compared to those of the literature and they indicate a significant improvement. They can therefore be used to better design very efficient and less costly PV/T hybrid systems as well as the development of nanofluides for thermal systems. After this introduction which constitutes the first section of the paper, the second section will focus on the description of the system and its modeling followed by the third section devoted to the results and discussions, then a conclusion as the fourth section.

2 Description and modeling

2.1 Representation

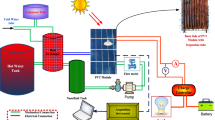
The thermal collector to be modeled is a flat collector with tubes under the absorber which is associated with the monocrystalline type PV panel (Fig. 1) whose characteristics are presented in Table 2. The tube part allows the passage of the water-MgO/CuO/TiO2 mixture and the part below the tubes allows the circulation of air. This geometry is made in such a way that the circulating air recovers the heat at the level of the tubes and simultaneously at the level of the absorber. Figure 1 presents the physical model of the studied system. The physical model is such that the movement of air between the free surfaces of the center-to-center distances between the tubes can cause a vortex effect which improves the heat transfer [21,22,23]. The shade effect on the module is negligible and the temperatures are uniform along each layer as well as the flow of the fluid; It is also considered that the thermo physical properties of each component of the hybrid system are constant.

Fig. 1
figure 1

Diagram of the physical model of the PV/T hybrid collector with its constituents considered in this study

Full size image
Table 2 Constant parameters for the optimization problem [2, 33, 39]
Full size table

2.2 Energy and exergy analysis

The operation of the PV/T system involves several physical phenomena through the exchanges carried out within it and with its external environment. The energy and exergy analysis is based on its elements which then makes it possible to model the studied system.

2.2.1 Energy analysis

Energy analysis is based on the first law of thermodynamics. The energy efficiency is given by Eq. (1) in which \(Q_{u,bi}\) represents the useful heat gain of the bi-fluid given by Eq. (2) and \(Q_{sun}\) the solar flux given by Eq. (3) with G the global solar radiation and \({A}_{c}\) the surface of the collector [24].

$$\upeta _{th} = \frac{{Q_{u,bi} }}{{Q_{sun} }} $$
(1)
$$ Q_{u,bi} = A_{c} F_{r} \left[ {\left( {\tau \alpha } \right)G - U_{L} (T_{in,bi} - T_{{\infty ,{\text{bi}}}} )} \right] $$
(2)
$$ Q_{sun} = A_{c} G $$
(3)

Terms \(Fr\) and \(U_{L}\) in Eq. (2) respectively represent the collector elimination factor and the overall heat loss coefficient respectively given by Eqs. (4) and (5) [25]:

$$ F_{r} = \frac{{(m_{a} C_{a} + m_{TNF} C_{TNF} )}}{{A_{c} U_{L} }}\left[ {1 - \exp \left( {\frac{{F{^{\prime}}.U_{L} .A_{c} }}{{m_{a} .C_{a} + m_{TNF} .C_{TNF} }}} \right)} \right] $$
(4)
$$ U_{L} = \left[ {\frac{N}{{\frac{c}{{T_{p} }}\left[ {\frac{{T_{p} - T_{a} }}{{\left( {N + b_{1} } \right)}}} \right]^{{b_{2} }} }} + \frac{1}{{5.7{ } + { }3.8{\text{V}}}}} \right]^{ - 1} + \left[ {\frac{{\sigma .\left( {T_{p} + T_{a} } \right).\left( {T_{p}^{2} + T_{a}^{2} } \right)}}{{(\varepsilon_{p} + 0.00591.N\left( {5.7{ } + { }3.8{\text{V}}} \right))^{ - 1} + \frac{{2N + b_{1} - 1 + 0.133\varepsilon_{p} }}{{\varepsilon_{c} }} - N}}} \right] + \frac{{k_{i} }}{{\delta_{i} }} $$
(5)

where:

$$ {\text{b}}_{{1}} = (1 + 0,089\left( {5.7{ } + { }3.8{\text{V}}} \right) - 0.1166h_{c} \varepsilon_{p} )\left( {1 + 0.07866N} \right) $$
(6)
$$ c = 520 \left( {1 - 0.000051\beta^{2} } \right) $$
(7)
$$ b_{2} = 0.430\left( {1 - \frac{100}{{T_{p} }}} \right) $$
(8)

The term \(F{\prime}\) represents the collector efficiency factor and can be calculated from relation (9):

$$ F^{\prime} = \frac{{1/U_{L} }}{{W\left[ {\frac{1}{{\pi d_{i} h_{c,t - f} }} + \frac{1}{{C_{b} }} + \frac{1}{{U_{L} \left[ {d_{e} + \left( {W - d_{e} } \right)F} \right]}}} \right]}} $$
(9)

where F is the final efficiency factor and can be calculated from relationship (10):

$$ F = \frac{{tanh\left[ {\frac{{\left( {W - d_{e} } \right)}}{2}\sqrt {\frac{{U_{L} }}{{k_{p} \delta_{p} }}} } \right]}}{{\frac{{\left( {W - d_{e} } \right)}}{2}\sqrt {\frac{{U_{L} }}{{k_{p} \delta_{p} }}} }} $$
(10)

The electrical efficiency of the system can be calculated from relation (11) [26].

$$ \eta_{el} = \frac{{V_{m} I_{m} - \frac{{m_{bi - f} \Delta_{p\_bi - f} }}{{\rho_{bi - f} \eta_{p} }}}}{{{ }A_{c } G}} $$
(11)

In Eq. (11) terms \(m_{bi - f} ,\Delta_{P,bi - f} ,\rho_{bi - f}\) and \(\eta_{P}\) respectively represent the mass flow rate of the bi-fluid, the pressure drop in the collector Eq. (12), the density of the bi-fluid and the efficiency of the pump.

$$ \Delta_{P,bi - f} = \frac{{fL^{2} \rho_{TNF} }}{{2d_{i} W}}\left( {\frac{{4m_{TNF} }}{{\pi \, n \, \rho_{TNF} d_{i}^{2} }}} \right)^{2} + \frac{{2fv_{a}^{2} \rho_{a} }}{{D_{h} }} $$
(12)

And \({m}_{bi-f}\) and \({\rho }_{bi-f}\) representing respectively the sum of the flow rates and densities of TNF and air.

Thus, the overall efficiency of the PV/T collector which is the sum of the thermal efficiency Eq. (1) and electrical Eq. (11), can be determined from Eq. (13) [27].

$$ \eta_{PV/T} = \eta_{PV} + \eta_{T} = \eta_{el} + \eta_{th} $$
(13)

2.2.2 Exergy analysis

Nowadays, thermal studies take into account the irreversibility of heat in order to assess the quality of energy. Thus, exergy is a concept that derives from both the first and the second law of thermodynamics and can be defined as the part of energy that has the potential to be fully converted into mechanical work, which is the most valuable form of thermodynamic energy [28]. Its balance equation is given by Eq. (14) [29]:

$$ \sum E_{xin} - \sum E_{xout} = \sum E_{xd} $$
(14)

where \({E}_{xin}\) represents the exergy of the sun and is calculated as:

$$ E_{xin} = A_{c} G\left[ {1 - \frac{4}{3}\left( {\frac{{T_{a} }}{{T_{s} }}} \right) + \frac{1}{3}\left( {\frac{{T_{a} }}{{T_{s} }}} \right)^{4} } \right] $$
(15)

With \(T_{S}\) and \(T_{a}\) representing respectively the temperature of the sun taken approximately at 5800 K and the ambient temperature.

The outgoing exergy rate is the sum of the thermal and electrical exergy given by Eq. (16) [30]:

$$ E_{xout} = E_{xel} + E_{xth} $$
(16)

With \({E}_{xel}\) and \({E}_{xth}\) given respectively by Eqs. (17) and (18) [31]:

$$ E_{xel} = GA_{c} \eta_{o} \left[ {1 - \beta \left( {T_{c} - T_{a} } \right)} \right] - \frac{{m_{bi - f} \Delta_{p\_bi - f} }}{{\rho_{bi - f} \eta_{p} }} $$
(17)
$$ E_{xth} = Q^{\prime}_{u,bi} \left[ {1 - \left( {\frac{{T_{a} }}{{T_{s} }}} \right)} \right] $$
(18)

with

$$ Q^{\prime}_{u,bi} = \varepsilon \sigma A_{c} \left( {T_{s}^{4} - T_{a}^{4} } \right) $$
(19)

The destroyed exergy rate can be subdivided into seven (7) main terms [12]:

  • The first term represents the exergy losses given by Eq. (20) and which are due to heat leakage from the PV cells:

    $$ E_{xdes,pv} = U_{L} A_{c} \left[ {1 - \left( {\frac{{T_{a} }}{{T_{c} }}} \right)} \right] $$
    (20)

where \({T}_{c}\) is the PV cell temperature calculated from Eq. (21).

$$ T_{c} = T_{a} + \left( {\frac{NOCT - 20}{{800}}} \right) $$
(21)

With NOCT, the nominal operating temperature of the cell (in °C).

  • The second term expresses the exergy losses linked to the pressure drop in the bi-fluid flow pipes which can be calculated by Eq. (22):

    $$ E_{{xdes,\Delta_{p} }} = T_{a} .\frac{{m_{bi - f} . \Delta_{p\_bi - f} }}{{\rho_{bi - f} . \eta_{p} }} $$
    (22)

  • The third term presented in Eq. (23) expresses the optical losses in the surface of the bi-fluid PV/T hybrid system.

    $$ E_{xdes,o} = E_{xin} \left( {1 - \left( {\alpha \tau } \right)_{eff} } \right) $$
    (23)

  • The fourth term given by Eq. (24) expresses the losses due to the temperature difference between the sun and the surface of the bi-fluid collector.

    $$ E_{xdes,s - c} = \left( {\alpha \tau } \right)_{eff} \left( {E_{xin} - \frac{{G.E_{xdes,pv} }}{{U_{L} }}} \right) $$
    (24)

  • The fifth term given to Eq. (25) expresses the losses due to heat transfer from the hybrid system to the bi-fluids:

    $$ E_{xdes,c - bi} = E_{xdes,s - pvt} - \left( {\alpha \tau } \right)_{eff} E_{xin} - E_{xth} - E_{xdes,pv} \left( {T_{cell} - T_{a} } \right) - U_{m} I_{m} $$
    (25)

Thus, the thermal and electrical exergy efficiencies are respectively given by Eqs. (26) and (27) [12, 32].

$$ \eta_{ex,th} = \frac{{E_{xth} }}{{E_{xin} }} $$
(26)

with

$$ E_{xth} = Q^{\prime}_{u,bi} \left[ {1 - \left( {\frac{{T_{a} }}{{T_{s} }}} \right)} \right] $$
(27)

The electrical exergy efficiency is given by Eq. (28) in which \(E_{xelec}\) and \(E_{xin}\) are calculated from the Eqs. (17) and (15) respectively.

$$ \eta_{ex,el} = \frac{{E_{xel} }}{{E_{xin} }} $$
(28)

The electrical exergy rate represents the sum of the electrical exergy rate extracted at the level of the cell minus the electrical exergy consumed by the pump.

The final expression of the total exergy efficiency of the PV/T hybrid collector with bi-fluid is given by Eq. (29) [31]:

$$ \eta_{ex\_total} = \frac{{Q^{\prime}_{u,bi} \left[ {1 - \left( {\frac{{T_{a} }}{{T_{s} }}} \right)} \right] + GA_{c} \eta_{o} \left[ {1 - \beta \left( {T_{c} - T_{a} } \right)} \right] - \frac{{m_{bi - f} \Delta_{p\_bi - f} }}{{\rho_{bi - f} \eta_{p} }}}}{{A_{c} G\left[ {1 - \frac{4}{3}\left( {\frac{{T_{a} }}{{T_{s} }}} \right) + \frac{1}{3}\left( {\frac{{T_{a} }}{{T_{s} }}} \right)^{4} } \right]{ }}} $$
(29)

2.3 Ternary nanofluids (TNF)

A nanofluid is a heat transfer fluid containing nanoparticles that are dispersed in a base fluid [21]. In this work, water is used because of its accessibility in industrial quantities. They are used to improve the thermal performance of solar systems due to their temperature-dependent thermophysical properties. We can cite among these:

  • Copper oxide nanofluids: 2–3 times improvement in thermal conductivity, reduction in viscosity and increase in heat capacity.

  • Nanofluids based on magnesium oxide: increased thermal conductivity and reduced viscosity.

  • Nanofluids based on titanium dioxide: improved heat conduction, improved heat capacity and increased light absorption.

Studies have shown that the combination of these three nanoparticles led to higher thermal performance than one or two nanoparticles [33]. However, given the high cost of these nanoparticles, a thermo-economic analysis would be advantageous. Water, titanium, magnesium and copper are mixed and heated, then grind to have a homogeneous mixture. Thus the stability was then tested to avoid a decomposition of the liquid which can obstruct the tubes. The Zeta potential was between 34.54 and 49 mV demonstrating a tendency to nanoparticles to repel and maintain stability. The mixing process and the equations presenting the thermophysical properties of water/CuO–MgO–TiO2 as well as air are taken from Ref. [33].

2.4 Optimization procedure

The different temperatures of the walls of the PV/T system as well as the temperatures of the output bi-flows are first sought; A discretization is made thanks to the various energy balances evaluated in the Refs. [13, 22, 26] using the iterative method of Gauss–Seidel. These temperatures are therefore evaluated by considering their initial values as equal to room temperature. The values obtained therefore make it possible to have the exergetic efficiency by execution of the genetic algorithm. The methodology employed here is the genetic algorithm. It consists in finding the extrema of an objective function defined on a data space. In this case, the objective function is the exergy efficiency. The principle is therefore to define the parameters of the relation given by Eq. (29) enter y into Table 2 as constants and look for values within specific ranges of design parameters that maximize total exergy efficiency.

The geographical area covered is the city of Yaounde in central Cameroon with an equatorial climate. Geographical coordinate at latitude 3°50″ North and longitude 11°29″ East.

The genetic algorithm is an optimization method that is inspired by the theory of evolution to find an optimal solution to a given problem [34, 35]. The program uses a genetic algorithm with a population size of 300, a mutation rate of 0.01, a selection rate of 0.95 and an outcrossing rate of 0.90. The population size is the number of individuals in the initial population. The mutation rate corresponds to the probability that a gene is modified during reproduction. The selection rate is the proportion of the most suitable individuals that are selected for reproduction. The crossover rate corresponds to the probability that a gene is exchanged between two individuals during reproduction. The type of chromosomes is continuous, which means that genes can take on continuous values rather than discrete values. This allows greater precision in finding the optimal solution.

An optimization algorithm was developed in Matlab using nine (9) design parameters, including collector tilt angle, collector area, thickness of glass, absorber plate, PV cell and insulation, the inner and outer diameters, and the center-to-center distance of the tubes (Fig. 2).

Fig. 2
figure 2

Multi-objective optimization program

Full size image

2.5 Economic and environmental models

The present economic model takes into account the exergy payback time, the avoided CO2 emission rate and the exergy cost of a PV/T bi-fluid hybrid solar collector.

2.5.1 Exergy return time

The exergy return time is used to assess the actual recovery time. It is given by Eq. (30):

$$ E_{x,pb} = \frac{{E_{c} }}{{E_{x} }} $$
(30)

With Ec and Ex representing the exergy consumed by the parameters of the hybrid system (PV cells, glass cover, absorber, insulation, tubes, supports and storage tank, TNF, inverter, cable and battery) and the exergy produced respectively during its duration of life. The exergy produced is given by Eq. (31):

$$ E_{x} = \int_{0}^{365} {(0.93E_{s} \eta_{ex,total} )dt} $$
(31)

Or Es is the solar energy received during the average sunshine duration of 5.5 h and equal to 5.456 kWh/m2. The exergy consumed is estimated at 2004 kWh/m2 during a 25-year lifespan [36].

2.5.2 CO2 emission rate avoided

Designing a better TNF-based two-fluid PV/T hybrid system must be environmentally friendly. The emission rate (TEE) of CO2 avoided by the exergy generated throughout the exergy return time is expressed by Eq. (32).

$$ TEE = e\left( {25 - E_{x,pb} } \right)E_{x} $$
(32)

2.5.3 Cost of exergy

The exergy cost here represents the true cost of the energy that will be produced. It is the ratio of the sum of the investment cost (Ci) Eq. (33) and the system maintenance cost (Co) Eq. (34) on the total exergy produced expressed in Eq. (35) [37]:

$$ C_{i} = 1.5\left[ {a_{1} \left( {A_{p} } \right)^{{b_{1} }} + a_{2} \left( {A_{t} } \right)^{{b_{2} }} + a_{3} \left( {V_{i} } \right)^{{b_{3} }} + a_{4} \left( {A_{g} } \right)^{{b_{4} }} + a_{5} \left( {A_{cell} } \right)^{{b_{5} }} } \right] + a_{6} \left( {\dot{W}_{p} } \right)^{{b_{6} }} + a_{7} L_{t} n_{t} \phi \rho_{TNF} \left( {\frac{{\pi d_{i}^{2} }}{4}} \right) $$
(33)
$$ C_{o} = C_{e} t_{y} W_{p} $$
(34)
$$ COEX = \frac{{aC_{i} + C_{o} }}{{E_{x} }} $$
(35)

where the coefficients ai to bi represent the initial prices of the components of the PV/T hybrid systems [120 60 220 4.5 400 3500 40], [0.9 0.8 1 1 1.01 0.47] respectively. \({C}_{e}\) is the unit price of one kWh of electricity which is $ 0.33. \({t}_{Y}\) is the estimated annual operating time of 2007.5 h. The annual cost factor depends on the inflation rate i which is 6.2% in the city of Yaounde Eq. (36):

$$ a = \frac{i}{{1 - (1 + i)^{( - 25)} }} $$
(36)

The goal of the algorithm is to find the optimal combination of parameters that maximizes exergy efficiency while minimizing costs while considering some parameters as constants. Exergy efficiency is a measure of the efficiency of a system that takes energy losses into account. The digital code stops the execution of the algorithm when the optimal solution is held constant for 1000 generations. This avoids unnecessary searching for solutions that are not significantly better than the current solution. Convergence is reached for a tolerance of 10−5.

With the optimal parameters obtained in Fig. 2, the different steps of the simulation are presented in Fig. 3.

Fig. 3
figure 3

Genetic algorithm process

Full size image

3 Results and discussion

3.1 Numerical validation

In order to validate the results of this simulation, Eq. (37) is used (in %) [38]. It establishes the average of the squares of the differences between the simulated values and those obtained experimentally. This made it possible to check whether these simulations are close to reality and especially whether this model agrees with those from the literature.

$$ RMSD = \sqrt {\frac{{\mathop \sum \nolimits_{j = 1}^{N} \left[ {100 \times \left( {y_{j,exp} - y_{j,sim} } \right)} \right]^{2} }}{N}} $$
(37)

Figure 4 presents the variations of the temperature of the PV module according to the global solar irradiation. It is observed that, as shown in several other studies, this temperature increases with solar irradiation. But the presence of bi-fluids makes it possible to maintain this temperature below 40.5 °C at 1000 W/m2. It is also presented the shape of the temperature of the PV module with that of Lebbi et al. [39] the difference observed is well presented in Table 3.

Fig. 4
figure 4

Comparison of the PV cell temperature of the present simulation results with those obtained experimentally by Lebbi et al. [39]

Full size image
Table 3 Cooled PV cell temperature validation
Full size table

The validation of this model is presented in Table 3. Numerical data from the temperature of the cooled cells for seven (7) cases of solar irradiation are presented.

On average for all cases, the mean relative error obtained is 2.98%. For the RMSD, an average of 3.4% emerges. The deviations observed are hard to the influence of other variable climatic parameters such as wind speed and ambient temperature. Thus, the values of the temperatures of the simulated PV cells present a good compatibility with the values of Lebbi et al. [39].

3.2 Optimization results

Figure 5 shows the instantaneous evolution of the outlet temperatures of the bi-fluids. It is observed that between 6 a.m. and 9 a.m., 3 p.m. and 6 p.m. the bi-fluids tend to have the same temperatures at the outlet. This may be due to the weak influence of climatic parameters during these hours. At 12h25min, the climatic parameters are very influential on the system and the bi-fluids are at their maximum temperature at the outlet. The maximum temperature at the outlet of the TNFs is higher (44.8 °C) than that of the air (43.1 °C). This difference is due to the double TNF/air cooling at the level of the absorber in contact with the tubes. This could be related to the high thermal conductivity of water compared to air. The presence of TNFs in the water may also explain this difference. This maximum value of the air outlet temperature is 0.4 °C lower than that found by Erhan et al. [39] due to the maximum radiation density at 1069 W/m2 during their experiments.

Fig. 5
figure 5

Instantaneous fluid outlet temperatures

Full size image

Figure 6 shows the variation of the exergy efficiency as a function of the angle of inclination of the collector. It can be observed that the total exergy efficiency increases with the angle of inclination until it reaches a maximum of 35% at 26.5° and then decreases by continuing to increase the angle of inclination. This trend can be explained by physical mechanisms related to the proportion of direct solar radiation. Indeed, at low angles of inclination, the proportion of direct solar radiation is low, which leads to a decrease in the efficiency of the system. This may explain the low value of the exergy efficiency at these angles. At higher tilt angles, the amount of direct solar radiation reaching the surface of the PV module increases, resulting in an increase in the efficiency of electricity generation and thermal energy. Even higher tilt angles, however, can reduce efficiency due to losses caused by oblique im**ement on the heat absorber. This angle value for which the optimum is reached differs by 3.5° from the result of the experiment by Koholé and Tchuen [34] carried out in Santa.

Fig. 6
figure 6

Variations in total exergy efficiency as a function of the angle of inclination

Full size image

In Fig. 7 it is shown that the dimension of the collector surface adversely affects the exergy efficiency. For example, when the collector area is one square meter, the total exergy efficiency reaches 26.5%. It could be argued that the underlying reason for this negative effect of collector surface area dimension on exergy efficiency is related to the substantial losses due to increased rates of exergy destroyed, dominated by increased number of PV cells, despite increased interaction with solar radiation. This result is in agreement with that of Rafae et al. [12] who obtained for 0.934 m2, an exergy efficiency of 25%.

Fig. 7
figure 7

Variation of the exergy efficiency according to the surface of the collector

Full size image

Figure 8 shows the variation of the total exergy efficiency as a function of the thickness of the glass layer. The fact is that increasing the glass thickness improves the total exergy efficiency. Indeed, a thickness of the glass cover below 10 mm improves both thermal and electrical performance. The reasons could be due to increased absorption and accumulation of solar radiation and heat respectively. It is possible that the greenhouse effect created reduces optical losses and losses due to the temperature difference between the sun and the surface of the PV/T.

Fig. 8
figure 8

Variations in total exergy efficiency as a function of glass thickness

Full size image

In Fig. 9, by varying the distance between the centers of the tubes from 50 to 200 mm and the inner diameter of the tubes from 1 to 4 mm, it was found that the total exergy efficiency reached its peak for small values of the distance between the tubes and increases for the inner diameter. It should be pointed out that in case of a very high distance between the tubes, that is, 20 mm, the inner diameter does not have much effect on the performance of the system. This can be explained by the fact that a decrease in the thermal energy collection surface at the back of the absorber could reduce the efficiency of the system. A large fluid passage section is therefore recommended.

Fig. 9
figure 9

Variations in total exergy efficiency as a function of the distance between the centers of the tubes and the inner diameter of the tubes

Full size image

According to Fig. 10, it can be observed that the exergy efficiency decreases with the increase in the outer diameter of the tubes. This decrease can be explained by the fact that a larger outer diameter may not favor simultaneous absorption of the heat coming from the absorber and the TNFs circulating in the tube. Another factor could be the rate of exergy destruction between the TNFs and the outer surface of the tubes caused by the temperature gradients between the TNFs, between the tubes and the air flowing underneath.

Fig. 10
figure 10

Variation of the total exergy efficiency according to the outer diameter of the tubes

Full size image

In order to reduce costs, it is envisaged to reduce the thickness of the copper material by adopting a minimum outer diameter and a maximum inner diameter.

Figure 11 highlights the variation of the exergy efficiency as a function of the thickness of the absorber. It should be noted that this curve has a look similar to that which illustrates the surface of the glass collector. It should be noted that the total exergy efficiency reaches its maximum for a minimum thickness of the absorber, that is, 2 mm. This observation stems from the influence of the thickness of the absorber on the overall coefficient of heat loss, an increase in said thickness leads to a decrease in the thermal conductivity of the material. In sum, it clearly appears that the optimization of the thickness of the absorber is a crucial parameter to maximize the exergy efficiency of the system and, consequently, to improve its overall efficiency.

Fig. 11
figure 11

Variations in exergy efficiency as a function of absorber thickness

Full size image

In Fig. 12, by varying the thickness of the insulation and maintaining all the other parameters as constants, the total exergy efficiency increases until it reaches a value of 24.9% at 82 mm; Then decreases slightly after this value. This phenomenon is explained by the thermal variations induced by the insulation, which regulate the amount of thermal and electrical exergy produced. Indeed, for a very low thickness of the insulation, the thermal losses at the rear of the hybrid system are significant, while too great a thickness generates a significant amount of thermal exergy, but a drop in the electrical exergy due to excess heat in front of the insulation. This observation is confirmed by the experimental results mentioned in Ref. [34] relating to a thermal solar collector.

Fig. 12
figure 12

Variations in exergy efficiency as a function of insulation thickness

Full size image

The essential parameter and seat of the photovoltaic effect is the PV cell. The observation made in Fig. 13 is that the exergy efficiency decreases as the thickness of the PV cells increases. The justification could be related to the high electrical exergy destructions due to a larger surface of the PV cells which can lead to excess heat inside the semiconductor material. It is moreover more effective for the cells to facilitate the transfer of heat towards the absorber by having a small thickness.

Fig. 13
figure 13

Variation of total exergy efficiency as a function of PV cell thickness

Full size image

3.3 Influence of bi-fluid flow

Using these design parameters, the airflow was varied first, then the TNFs, and then both at the same time. Figure 14 shows the variation in exergy efficiency as a function of bi-fluid flow rates. Initially, the flow rate of the TNFs is set at 0.008 kg/s while varying that of the air. Also, the same procedure is done for the variation of the flow rate of the TNFs. It can be seen that an increase in flow rates from 0.001 to about 0.006 kg/s improves system performance. This is due to the high viscosity of TNFs due to hybridization which increases the volume concentration [40], and requires a high flow rate to be able to absorb more heat. Between 0.006 and 0.012 kg/s the total exergy efficiency tends to be constant for air but decreases for TNF. Indeed, it is possible that turbulence has occurred in the flow pipes for a TNF flow rate above 0.006 kg/s, thus causing heat loss. Studies have shown that an increase in the flow rate of bi-fluids is favorable to the positive improvement in energy performance due to the cooling of the PV cells that the latter generates. This is totally not the case for exergy performance.

Fig. 14
figure 14

Variation of total exergy efficiency as a function of fluid flow rates

Full size image

Thus, the highest performances were achieved for an identical flow rate of 0.0035 kg/s for the bi-fluids (air/TNF) operating simultaneously. Cooling in synchronous mode could therefore create a movement of heat displacement in a structured way and facilitate heat transfer.

3.4 Comparison with previous works

By comparing the results of this simulation with the design parameters taken from the literature and generally used during experiments, the observation made is that these are closer for the angle of inclination, the surface of the collector, the thickness of the absorber and the PV cells and less close for the glass layer, center to center distance between the tubes, the different diameters and the thickness of the insulation.

Compared with other optimal values in Table 4, the thickness of PV cells is the smallest. For example, for a maximum total exergy yield of 25%, the thickness of the PV cells will be 0.3 mm. Indeed, this layer is the seat of the generation of electricity and heat in the system.

Table 4 Optimal parameters
Full size table

The difference observed with the glass thickness can be attributed to the sunlight trap** by this layer and increasing its performance. Indeed, increasing the thickness of the glass collector would be better economically than double glazing. This is clearly observable in Fig. 15 where the work carried out experimentally by Refs. [12, 39, 41] with respective thicknesses of 4, 4 and 3.2 mm led to yields of 25, 14.7 and 18.71% respectively. For the distance between the centers of the tubes, the inner and outer diameters of the tubes, the good combination shows a larger deviation of the distance between the centers of the tubes with that of Koholé and Tchuen [2] and smaller for the inner diameters and exteriors. Indeed this difference is justified by the double optimization linked to the passage of air directly below the tubes. For insulation thickness, this configuration has a higher gap. Indeed this can be due to the global radiation fixed during their experiments at 500, 650 and 1069 W/m2 respectively and the thermo-physical properties of the insulation which depend on the type of materials (rock wool [2], rigid polyethylene foam [42]).The result synthesis of this paper more or less shows a link with the design parameters of the solar collectors used during the experiments.

Fig. 15
figure 15

Result synthesis of the optimized parameters and comparison with the literature

Full size image

3.5 Technical-exergo-economic and environmental results

The main challenge of implementing a bi-fluid PV/T hybrid solar system lies in the technical–economic and environmental aspect. This is also the criterion that interests the investor in his decision-making. Figure 16 presents the evolution of the total annual cost according to the exergy efficiency. Beyond 25% production efficiency, the low TAC is due to the reduced cost of maintenance. In addition, the price of the air circulating there is not taken into account in the economic analysis. Thus, the more efficient the system, the lower the total annual cost. Thus the bi-fluid PV/T hybrid solar system (TNF/air) is very efficient in converting the solar energy received into useful work.

Fig. 16
figure 16

Variation of the total annual cost according to the exergy yield

Full size image

Taking into account the values of Table 4, Table 5 presents the values obtained from the economic analysis.

Table 5 Values of the technical-exergo-economic and environmental analysis
Full size table

The number of minimized component parameters leads to a reduction in the cost of investment and maintenance of the system. This leads to a reduction in the true cost of exergy ($0.25/ kWh). Efficiency in converting solar energy into energy directly usable reduces the exergy consumed and therefore increases the exergy produced per year. In general, the exergy return time is relatively short for solar PV/T hybrid systems, making them an attractive option from an exergy, economic and environmental perspective.

4 Conclusions

In this study, some design parameters of the PV/T dual-fluid hybrid collector that maximize its exergy performance are evaluated. The results of this study highlight the importance of considering different design parameters to optimize the exergy performance of a solar PV/T hybrid system. The influence of air/water bi-fluids and CuO-MgO-TiO2 ternary nanoparticles on the performance of the system with the climatic data of the city of Yaounde were analyzed. Therefore, the exergy character is used and thanks to a developed multi-objective optimization method, the following conclusions were drawn:

  • The outlet temperature of the TNFs is 44.8 °C thanks to the influence of the hybrid nanoparticles. While that of the air is 43.1 °C with a temperature of the PV cells lower than 40.5 °C.

  • The values of the optimization parameters for which maximum exergy yields were obtained are mostly minimized and the total exergy yield varies from 23.41 to 36.6%.

  • The correct combination of the nine (9) parameters is 26.5° for the angle of inclination, 1 m2 for the surface of the collector, 10 mm for the thickness of the ice, 10 mm for the distance between the centers of the tubes, 4 and 5 mm for inner and outer diameter, 2 mm for plate thickness, 82 and 0.3 mm for insulation and PV cell thickness respectively.

  • For the air/TNF bi-fluids, the remark made is that the air flow at 0.008 kg/s leads to a total exergy yield of 20%, while that of the ternary nanofluids is at 0.00575 kg/s for a yield of 22.15%. However, the system is more efficient with an overall exergy efficiency of 24.2% at 0.0035 kg/s when the two fluids were operating simultaneously.

  • The technical-exergo-economic and environmental assessment revealed an exergy cost of $ 0.25/kWh with an emission rate of 230.5 kg of CO2 eq/m2/year for an exergy return time tending to 3 years.

  • The general comparison of the current numerical study with the experimental results resulting from works of the literature shows a good adequacy. The comparison of the simulation results of the temperature of the PV cells cooled using bi-fluids with those resulting from the experimentation of Ref. [34] shows good agreement with a root mean square error of 3.4%.

This paper establishes that the minimization of the components of the bi-fluid PV/T hybrid collector could reduce the losses inside the latter by favoring the cooling as well as the displacement of the heat at the back of the PV cell. This is advantageous for manufacturing costs and also for the lifetime of the system. The results from this research can be used for the design of more efficient PV/T hybrid solar systems, for the design of cooling systems, and for the development of other more efficient and less expensive TNFs. Similar studies should be done taking into account several other physical operating parameters and different optimal techniques; Taking into account the variation in the thermophysical properties of system components would be a huge consideration for future work.