1 Introduction

Autonomous trucks will bring fundamental changes to the current transport infrastructure. Forthcoming of autonomous truck with full integration into the current traffic mix is a long term process. Currently, various entities are researching with the focus to launch the autonomous trucks with approvals from government agencies [1]. Autonomous truck manufacturers have to conform to safety regulations and challenges with integration into current infrastructure system, since certain errors in terms of perception of surrounding and reaction to unplanned events by autonomous vehicles still exist [2].

Autonomous trucks are kept in the lane with the use of Light Detection and Ranging sensors (LiDARs), ultrasonic sensors, vision cameras and Global Navigation Satellite System (GNSS) sensors [3]. These aforementioned sensors help steer the vehicle in a controlled path. Typically, the original path is primarily a fixed movement of the truck within the lane without any lateral wander. Onboard sensors usually function by observing the lane markings and keep the vehicle with in the lane. Since the autonomous trucks are functionally programmed to follow a controlled path within the lane with the help of onboard sensors, the resulting lateral wander pattern can adversely affect the pavement structure [4].

Since, the use of no lateral wander option for the trucks can create channelized loading on the pavement structure with very little relief time provided for the pavement, rutting and fatigue cracking would occur much sooner. Usage of autonomous trucks with no lateral wander can accelerate the damage to the pavement structure in terms of fatigue cracking and rutting [5,6,7,8]. Another lateral wander mode is derived from human driven trucks. Therefore, autonomous trucks can also be programmed to follow normal distribution [9]. In case of normal distriubtion, the lateral wander is based on human behavior and majority of the travel path exists with the truck being 70% times in the middle of the lane throughout the jouney of 50 km and a bell shaped normal distribution graph is formed [10]. The third option is the use of uniform wander mode. Therefore, the trucks can be programmed to distribute themselves laterally in a uniform fashion with minimized occurrence of channelized loading on the pavement. Fewer repetitions of loading on the same section of pavement would help in prolonging the service life of pavement. Moreover, the use of uniform wander mode allows the truck to uniformly distribute itself laterally in the lane thereby reducing the occurrence of channelized loading. With the help of onboard sensors, lateral trajectory of an autonomous truck can be programmed to perform the lateral wander with uniform distribution of passes on any given point on the pavement.

Platoon size, distribution and configuration for the trucks also affects the pavement's response to repetitive loading. It is observed that rest time given to the pavement can affect the long term performance of the asphalt mixture, since asphalt behaves in a viscoelastic manner under the influence of loading [11]. Therefore, the use of uniform wander option for trucks is beneficial when combined with the use of autonomous truck platoons.

Since the use of uniform wander mode requires the complete use of width of the lane, therefore, a larger width of lane can provide a larger area thereby decreasing the risk of repetitive loading on the pavement. With the conventional lane width in highways available to the trucks, a certain amount of overlap** in wheel paths exists even in case of uniform wander mode [12]. Service life of the pavement be further prolonged by increasing the truck’s lane width. Similarly, the pavement cross section can be adjusted with decreased pavement layer thickness in case of asphalt layer by increasing the pavement width, thereby reducing the initial construction costs.

With reduced construction costs and increased pavement lifetime, pavement rehabilitation strategies can be designed in life cycle costs analysis to maximize the benefits obtained from the use of uniform wander mode. With increased lifetime, using better materials and controlled mode of loading, fewer number of maintenance interventions are required, since the occurrence of fatigue cracking and rutting happens at a much later stage in pavement’s lifetime [13]. Therefore, the decrease in asphalt layer thickness is compensated with increase in the lane width while maintaining the increasing trend of pavement lifetime.

In the next section, literature review is compiled based on the research conducted on life cycle cost analysis. In Sect. 3, detailed methodology related to lane width and asphalt layer thickness variation is explained. Moreover, Sect. 3 also includes pavement layers details, pavement cross section, material model and finite element model details. Section 4 shows the results obtained from finite element analysis for different pavement width and asphalt layer thickness scenarios. Moreover, Sect. 4 also includes comparison graphs between different scenarios. Furthermore, in Sect. 4, detailed calculation of net present value is presented, and life cycle cost analysis is performed for the aforementioned scenarios. In Sect. 5, detailed conclusions in terms of important findings are mentioned.

2 Literature review

Life cycle cost analysis gives information about the economic viability of construction and maintenance procedures by providing different alternatives for types of interventions used [14]. Due to huge amount of expenditures arising from highway infrastructure maintenance costs, LCCA helps in reducing the cost required for maintenance interventions by providing the most economically feasible alternative [15]. LCCA has been performed by various researches using deterministic and probabilistic models in finding the reasonable alternative for pavement maintenance [16,17,18].

Riekstins et al. [17] used the deterministic and probabilistic approach using Monte Carlo method for LCCA by comparing five different maintenance and rehabilitation strategies and evaluated their impacts on CO2 emissions and rehabilitation costs. Two different alternative strategies are Full Depth Removal and Placement and Full Depth Reclamation. The total costs related to maintenance strategies included workforce, materials, periodic maintenance and fuel. Highest amount of costs were exhibited by materials followed by fuel and workforce. Both approach strategies encouraged the use of Full depth reclamation intervention due to lower CO2 emissions of upto 60% and rehabilitation costs upto 50%.

Braham [16] compared the effect of conventional maintenance strategies and full depth reclamation using LCCA procedures provided by Federal Highway Administration (FHWA). LCCA was conducted for the total pavement design life of 50 years. Analysis showed that the costs caused by using conventional rehabilitation strategies by each 4 year maintenance interval surpassed the total cost caused by using the full depth reclamation technique. Results showed that full depth reclamation would also increase the loading capacity of pavement structure during the span of pavement lifetime, being the optimal alternative for pavement rehabilitation procedures.

Akbarian et al. [19] have compared the costs caused using asphalt rubber with the conventional bitumen based asphalt mix. LCCA was performed by using thin structural overlay and milling as rehabilitation alternatives. Maintenance strategies were categorized by traffic volume on specific regions, with pavement having lower traffic volume getting fewer thickness of asphalt overlay during rehabilitation. Deterministic and probability approach was sued using the Net Present Value (NPV) with a discount rate of 4%. Results showed that use of rubber asphalt is a cost-effective alternative with lower cost of rehabilitation strategies required, thus improving the longevity of pavement lifetime.

3 Methodology

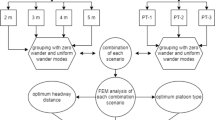
The use of two lateral wander modes with normal distribution and uniform distribution have been analyzed in a conventional layered asphalt pavement. Since, only the change in cross section of asphalt pavement is being analyzed, therefore, the initial construction costs only include the amount of material being used in various scenarios. Reducing the structural width of asphalt layers can have high impacts on reduced construction costs in longer pavement cross sections. Moreover, the width of lane can be increased only be a certain extent, since increasing the width of lane beyond a certain point would increase the construction costs than the base scenario. Therefore, pavement width should be increased until the initial construction costs get equal to or higher than that of base scenario. Moreover, the base scenario in case of zero wander mode is also analyzed for comparison with that of uniform wander mode. Illustration of research methodology is shown in Fig. 1.

Fig. 1
figure 1

Research methodology

Full size image

3.1 Pavement details

The standard pavement width on a highway lane for trucks is 3.75 m as shown in Fig. 2. Increments of 15 cm are given with values of 3.9 m, 4.05 m and 4.2 m and 4.35 m. The design vehicle is an A40 European truck trailer with maximum gross weight of 40 Tonnes and a pavement section length of 50 m. Since the asphalt layer constitute the majority of construction costs in the pavement as compared to other pavement layers with a magnitude of 80% [20,21,22].Since the thickness below 14 cm can be detrimental considering the effects of horizontal tensile strains and vertical compressive strains from a 40 T truck with Average Annual Daily Traffic of greater than 8,000 trucks, therefore, the first trial asphalt thickness starts at 14 cm [23]. The base scenario of asphalt layer thickness is selected to be 20 cm, since it related to the conventional asphalt pavement cross section used in highways where no cement stabilization for base course is used. The decrements of 2 cm for each scenario are selected since variation in thickness of 2 cm can create a reasonable cost difference for a pavement length of 50 m [24].Therefore, the base scenario is selected with the thickness of 20 cm and trial thickness values of 18 cm, 16 cm and 14 cm.

Fig. 2
figure 2

Pavement details

Full size image

A conventional pavement crosssection wihout any cement base stabilization has been considered. Pavement layer properties are shown in Table 1.

Table 1 Pavement layer properties
Full size table

3.2 Material model

Costs of initial pavement construction are taken from Ferreira et al. and Bueno et al. [25, 26] where detailed procedures for cost calculation of asphalt pavement layers based on various thickness values of asphalt layer in the pavement are analyzed. Since, a conventional asphalt pavement is being used in this research, all associated costs related to layer construction are mentioned specifically for a standardized lane width starting with the base width of 3.75 m as shown in Table 2.

Table 2 Simulated scenarios
Full size table

Since only the thickness of asphalt layer has been changed, therefore, the \(cost/{m}^{3}\) of asphalt layer that includes supply, construction and finishing costs has been used from [27] with an amount of 720 \(Euros/{m}^{3}\). Various width and thickness values for asphalt layer are tested with a fixed assumed length of pavement at 100 km. All initial costs for each scenario are shown in Table 3.

Table 3 Initial pavement construction costs for all scenarios
Full size table

3.3 Finite element model details

A typical four layered pavement structure has been modelled consisting of asphalt layer with variable thickness values for 14 cm to 20 cm with 2 cm increments. Lower pavement layers consist of base and subbase course with fixed thickness values resting on the subgrade. Hence, the total model depth varies, depending on the thickness of asphalt layer. Variable lane width also exists for each model constructed, started with the width of 3.75 m going upto 4.35 m. Length of the model is kept constant at 50 m for the A40 truck to perform a complete pass under uniform wander mode. With Annual Average Daily Traffic of 11,000, the simulations are performed for the analysis period of 40 years.

Model consists of CPE8R elements with 8 node linear brick, reduced integration with hour glass control characteristics. Different trials with element sizes were conducted to check the accuracy of the model for all width and thickness scenarios, therefore the final model has 170,852 elements with element size of 10 for increased accuracy and reduced computation time. Model mesh is shown in Fig. 3.

Fig. 3
figure 3

Mesh details

Full size image

Boundary conditions and loading are kept the same for all different scenarios of variable thickness and width values. Layer to layer interaction has been kept normal and continuous, with frictionless characteristics. Nodes are free to move around vertical directions but are restricted in perpendicular horizontal directions. The bottom of the model is assumed elastic and a value of 0.03 is assigned which corresponds to the stiffness of elastic foundation being simulated. Boundary conditions and loading details are shown Fig. 4.

Fig. 4
figure 4

Boundary conditions and loading

Full size image

4 Results and discussion

Simulations have been conducted on ABAQUS by considering the AADT of 11,000 Trucks for a total analysis period of 40 years. An A40 truck has been simulated under a uniform wander mode where different predetermined paths for lateral wander have been selected [6]. Moreover, the term Model Length is used which refers to the evaluation of displacement values under loading along the longitudinal profile of the pavement throughout the length of the pavement model being simulated. Simulations have been run on different models created with varying thickness and width values.

The screenshot taken for the S(Mises) under the base scenario of 3.75 m width for the truck lane and 20 cm thickness assumed for the asphalt layer is shown in Fig. 5. Since this is a base scenario, all other suggested scenarios are compared with this scenario.Microstrains have been taken from the cut section of the model directly under the axle loading area of the wheel footprint. Microstrains show the displacement occurring under loading area. Displacement values would increase as loading time and axle load increase. Accumulated lateral displacement reach a maximum accumulated magnitude of 390 microns under all passes of trucks.

Fig. 5
figure 5

Simulation screenshots for S (mises) at base scenario

Full size image

In the first alternative scenario as shown in Fig. 6, width of the truck lane is increased to 3.9 m and various thickness values of 16 cm and 20 cm are simulated. By decreasing the thickness in this scenario, total accumulated displacement exponentially increase to 560 microns. The reason being the footprint width of the trailer tires of the truck is larger than the width increment provided for adequate uniform wander. Therefore, an extra width of 15 cm from the base scenario would not do any favor in terms of reducing the resulting strains.

Fig. 6
figure 6

Simulation screenshots for S (Mises) at 3.9 m, 16 cm

Full size image

The second alternative scenario as shown in Fig. 7 increases the lane width to 4.05 m and various reduced thickness values of 18 cm, 16 cm and 14 cm are analyzed. This scenario performs better in terms of reduced accumulated strains as compared to the first alternative scenario, however, the accumulated microstrains are still higher than the base scenario especially when less than 16 cm of width is analyzed. Total magnitude of microstrains remain at 440 microns and 415 microns when analyzed at thickness levels of 16 cm and 20 cm respectively. The 20 cm option, however, is not economically preferable.

Fig. 7
figure 7

Simulation screenshots for S (Mises) at 4.05 m, 16 cm

Full size image

The third alternative scenario as shown in Fig. 8 increases the lane width to 4.20 m and thickness values are tested at 18 cm, 16 cm and 14 cm. It can be observed from the figure above that considerable decrease in microstrains occur as compared to the previously mentioned scenarios. This is due to the fact that the rear trailer tires have no more overlaps on the same point of the lane, since enough lateral distance is available for the truck to perform uniform wander adequately. Resulting accumulated microstrains are at 250 microns and 315 microns at thickness values of 16 cm and 14 cm respectively. Thickness values greater than 16 cm would render this scenario uneconomical since a minute level of decrease in accumulated strains occur at higher thickness values, which also compromise the economical value of this scenario.

Fig. 8
figure 8

Simulation screenshots for S (Mises) at 4.20 m, 16 cm

Full size image

The Fourth scenario as shown in Fig. 9 consists of pavement lane width of 4.35 m, which is tested at asphalt layer thickness levels of 16 cm and 18 cm. Increased lane width further decreases the accumulated the strains to 209 microns, however the decrease in this case is not significant as compared to the third alternative. Furthermore, an increased width beyond 4.05 m would render this scenario uneconomical even with the use of 14 cm asphalt layer thickness. In order to utilize this scenario properly, further increment of lane width of upto 30 cm is required. Therefore, the favorable scenario is to use 4.20 m of lane width with 16 cm of asphalt layer thickness.

Fig. 9
figure 9

Simulation screenshots for S(Mises) at 4.35 m, 16 cm

Full size image

The prominent scenarios with varying lane width and asphalt layer thickness values are compared in Fig. 10. It has been found that the use of 14 cm thickness levels for 3.9 m and 4.2 m do not make a significant difference, therefore they are not included in this comparison. Total accumulated strain values are gathered for these scenarios, with the base scenario lying along the middle of this chart at 390 microns. Furthermore, the second alternative peak strains are at 560 microns which is highest among all the scenarios. The third alternative, however, stays at 440 microns, which is better than the second scenario, however still exhibiting higher strains than the base scenario. The third scenario remains at 250 microns for 16 cm thickness value, which is the second last among all other options. Finally, fourth scenario exhibits minimum strain values among all the options, however, the efficiency analysis does not favor the use of 4.35 m scenario as mentioned in the next section.

Fig. 10
figure 10

Accumulative strain comparisons of different scenarios for uniform wander mode

Full size image

Comparison of displacement values for normal distribution are shown in Fig. 11. It can be observed that under normal distribution of trucks within the lane, concentration of loading paths stay closer to the zero wander mode. Therefore, higher concentration of stress occur when compared to uniform wander mode. The second alternative exhibits a peak strain of 644 microns under normal wander mode. The third alternative stays at 283 microns which is subsequently lower than the base scenario and first alternative. An overall increase in displacement of 15% exists when a normal wander mode is used.

Fig. 11
figure 11

Accumulative strain comparisons of different scenarios for normal wander mode

Full size image

Economical worth of the pavement structure at the end of its service life and initial construction costs for the pavement section of 100 km would determine the selection of optimal possible scenario. Therefore, it is important to calculate initial construction costs and conduct performance efficiency analysis for all the considered scenarios with varying thickness and width values. Initial construction costs have been calculated using [16, 18, 27]. Performance analysis compares the economic viability of each scenario with the accumulated microstrains throughout the analysis period. Initial construction costs would increase if the combination of lane width and asphalt thickness magnitudes exceed a certain value. Therefore, it is ideal to test all the scenarios in terms of initial construction costs and perform efficiency testing of each scenario based on accumulated pavement damage. Performance analysis is conducted by performing damage assessment under each scenario with rutting and fatigue cracking evaluation, and further details on damage assessment based on rutting and fatigue cracking can be found in [6].

The Initial Construction costs (IC) for different width and cross secton scenarios are compared in Fig. 12. An increasing trend is observed starting with 3.75 m, 20 cm scenario until the thickness reaches 18 cm for the same scenario. However, for the 3.9 m, 16 cm scenario, costs are reduced due to reduced thickness of the asphalt layer but as the width increase, the IC costs slightly increase proportionally. However, it can be observed that the increase in costs by lane width increment is less than the increase in cost by asphalt layer thickness increment. For the same amount of lane width, an increase in thickness with 2 cm changes the costs by 9 Millions. If the thickness is kept the same and width increases by proportions of 15 cm, the increase in costs are 5 Million. An average difference of 4 Millions exists when between lane width and asphalt layer thickness variation, so 15 cm and 2 cm respectively. The effect increases with longer highway sections.

Fig. 12
figure 12

Initial construction costs for all scenarios

Full size image

Performance efficiency for each scenario is Fig. 13. Since, the uniform wander mode performs better in terms of reduced microstrains occurring in the pavement, only the uniform wander mode has been considered for evaluating performance efficiency of each scenario. A lane width with 3.9 m and 16–18 cm option, provides less performance efficiency in terms of increased lifetime and reduced costs. Since the lane width of 3.9 m is still not enough to increase the savings in lifecycle costs, therefore, this scenario is not favorable. Increase in width to 4.05 m improves the performance efficiency further. However, efficiency increase continues until the increased width of 4.2 m, since the width increase is now up to 45 cm from the base scenario, further increment in the with would render it uneconomical due to higher construction costs however, the pavement lifetime still continues to improve at 4.2 m width and 16 cm thickness, the highest performance efficiency of up to 20% is achieved. The scenario after this point favors in pavement performance but the construction costs also increase due to higher demand of materials, therefore increase in pavement performance is not in par with the rising construction costs making further increase in width uneconomical.

Fig. 13
figure 13

Performance efficiency of different scenarios

Full size image

4.1 Net present value (NPV) and salvage value

Since the traffic mix contains variety of axle groups and axle loading, it is necessary to convert them into an equivalent single axle. Since the use of 4.2 m width for the truck lane exhibits the least amount of initial construction costs with respect to the most prolonged lifetime with cost effectiveness among other scenarios, showing the highest performance efficiency, therefore the intervention period will come later for this scenario than other aforementioned scenarios. Full depth reclamation is used as a pavement rehabilitation strategy. Therefore, two alternative benefits exist, either the pavement thickness for full depth reclamation can be reduced or the salvage value would increase if the full depth reclamation is not performed.

NPV discounts the future costs of the rehabilitation procedures to the present value. Since the prices used for pavement rehabilitation in the future would differ therefore, all the costs must be converted to the present state where the Net Present Value consists of initial pavement construction costs, the rehabilitation costs for full depth reclamation and salvage value after the analysis period. NPV calculation is shown in Eq. (1).

$$NPV=Initial\; cost+\sum_{k=1}^{N}{Rehab\;Cost}_{k}\left[\frac{1}{{(1+i)}^{{n}_{k}}}\right]-Salvage\;Value\lceil\frac{1}{{(1+i)}^{{n}_{a}}}\rceil$$
(1)

where \(NPV\) is net present value, \(i\) is discount rate, \(n\) is time period in years, \({n}_{k}\) is number of years from initial construction and \({n}_{a}\) is length of analysis period. Lower NPV corresponds to higher cost efficiency of rehabilitation strategies.

Salvage values indicates the residual value of the pavement after the analysis period as shown in Eq. (2). Salvage value is linked to the last rehabilitation conducted on the pavement, thus even after the analysis period, the pavement can still continue to perform functionally.

$$Salvage\;value=\frac{Remaining\;service\;life}{service\;life}\times CLR$$
(2)

Where \(CLR\) is the cost of last rehabilitation. Since, the maintenance performance strategy herein is only the full depth asphalt reclamation in the mid span of design life of 40 years therefore, the salvage value for the remaining life and actual service life of full depth reclamation alternative is used. The first option for increase in salvage values is shown below where using the scenario of 4.2 m lane width and using 16 cm with initial asphalt layer thickness, salvage value of the pavement is increased by 13 years.

Data used for LCCA is as follows:

  • Road length. 100 km

  • Lane Width: 3.75 m, 3.9 m, 4.15 m, 4.2 m, 4.35 m at different crosssections

  • Traffic speed: 90 km/h

  • Analysis period: 40 Years

  • Average annual daily truck traffic(AADTT): 11,000 trucks/day

  • Traffic growth rate: 0.75%

  • Discount rate: 4%

4.2 LCCA

It has been assumed that around 75% of pavement structure on its length of 100 km would require the maintenance interventions throughout its lifetime and each intervention being applied to a certain section of the highway since all the AADTT would not cover the entire 100 km of the highway in a single trip. Due to the increased performance period under the 4.2 m lane width scenario, two options are available to design maintenance and rehabilitation strategies. The first option is to remove the major component of maintenance costs for LCCA. The second option is to keep the same interventions options for the 4.2 m lane width scenario as that of the base scenario, which in turn would increase the salvage value of the pavement with increased pavement lifetime.

The first option as shown in Table 4 favours the prolongation of pavement's service life greater than 40 years which is after the analysis period, the salvage value can be further increased as shown in Table above. Base scenario needs the first major rehabilitation intervention after 5 years, while the 4.2 m lane width scenario can stay upto 8 years. Moreover, the cost of general maintenance works is less for the 4.2 m scenario due to lower damage accumulated after first 8 years. Maintenance free period for the 4.2 m can last longer by 5 years than the base scenario. If all the maintenance and rehabilitation interventions are followed for 4.2 m, the same way as for the base scenario, the pavement can function after the analysis period of 40 years and functional life can reach upto 53 years. In this case, the salvage value for the 4.2 m scenario is enhanced to 14.8 M after 53 years, compared to 15.6 M for the base scenario after 40 years. Moreover, for normal wander mode, the salvage value for the base scenario stays at 15.6 M and a decrease in salvage value occurs for normal wander mode for 4.2 m scenario at 12.3 M.

Table 4 Comparison of alternative scenario and base scenario based on increase in performance period
Full size table

Therefore, 4.2 m scenario makes a fundamental difference in life cycle cost reduction of pavement by increasing the salvage value with a prolonged lifetime after analysis period.

In the second option as shown in Table 5, the reduction in rehabilitation interventions is performed by removing the first rehabilitation intervention, that includes the removal and paving of wearing course layer. Hence, all the general maintenance related activities can be removed along the first 16 to 25 years in the pavement lifetime while yielding the same salvage value as the base scenario with reduced maintenance and rehabilitation costs. Since the majority of costs are related to the rehabilitation interventions where milling and replacement is conducted, therefore such costs can be reduced and will have a high impact on the present value of pavement structure.

Table 5 Comparison of base scenario and alternative scenario based on increase in salvage value
Full size table

The rehabilitation maintenance program consists of general maintenance costing 1.2 million Euros followed by the first rehabilitation of removal, of wearing course. In the first maintenance free period, the base scenario maintenance free period last for 5 years, however for the 4.2 m option, maintenance free period lasts for 8 years. Moreover, the cost of general maintenance, which includes crack and chip sealing, varies for each scenario.

In case of a base scenario the cost is 1.2 million Euros while in case of 4.2 m, the cost stands at 0.7 million Euros. Other major rehabilitation phases that include removal of wearing course, removal of asphalt layers and full depth reclamation costs the same for both scenarios however, in case of 4.2 m option the major rehabilitation intervention that includes removal of asphalt layers can be removed. Since the pavement is performing better structurally along the lifetime of 18–28 years. Moreover, in case of uniform wander mode for the base scenario, the salvage value stays at 15.6 M and 13.4 M for normal wander mode. Excessive costs for general maintenance required decrease the salvage value when the normal wander mode is used. Furthermore, a complete salvage value of 58.3 M for the 4.2 m exists after 40 years and subsequently reduced salvage life for normal wander mode exists with 48.4 M. An overall 15% reduction in maintenance related costs exist if uniform wander mode is used. In case of base scenario, the pavement would require an intervention in the 21st year while in case of 4.2 m scenario, the pavement needs the second major intervention only by 29th year. By removing a major portion of rehabilitation intervention, life cycle costs can be saved.

5 Conclusions

Since the use of autonomous trucks require an appropriate form of uniform wander mode, additional lane width available to perform lateral wander can further improve the performance of the pavement. Moreover, due to increase in pavement lane width, the thickness of asphalt layer can be further reduced as bigger lane width would lead to fewer instances of channelized loading under uniform wander mode by autonomous trucks. Therefore, an ideal scenario for increase in pavement lane width and decrease in pavement layer thickness is established to allow for further reduction in initial construction costs and life cycle costs.

It has been assumed in this research that maximum allowable width for the truck lane is limited at 4.35 m. It has been found that the initial 16 cm increment in width from the base sbeario width of 3.75 m does not do significant change in decreased pavement damage, since each trailer tire needs a width grater than 30 cm to avoid overlap** along the same longitudinal path. An optimum combination is created with lane width of 4.2 m and asphalt layer thickness of 16 cm for this aforementioned pavement section. Moreover, two different LCCA scenarios have been proposed where either the pavement leaves a salvage value of 58.3 million Euros at the end of analysis period of 40 years or pavement continues to function for the next 13 years with an optimum performance efficiency.Followng are the finidgs of this research:

  1. 1.

    Selection of the 4.2 m scenario requires higher initial costs than the base scenario of 3.75 m width, but the pavement structure performs better with a longer maintenance free period of 5 years.

  2. 2.

    Initial construction costs are increased by using the 4.2 m scenario by 13 million Euros and increased salvage value after 40 years, with savings staying at 26 million Euros and 20% performance efficiency.

  3. 3.

    Base scenario requires the first maintenance intervention by first 5 years, however the 4.2 m scenario requires the first intervention after 8 years with a salvage value difference of 45 million Euros.

  4. 4.

    Maintenance costs increase by 15% when a normal wander mode is used instead of uniform wander mode.

  5. 5.

    Pavement thickness variation of upto 8 cm does not make any considerable change in the costs of pavement removal and full depth reclamation, since removal and replacement can be accomplished in a single stage.