1 Introduction

Nanofluids have received much attention recently because of their potential use as physical heat transfer in fluids [1] and their importance in medical applications such as drug delivery [2, 3], cancer treatment [4], neurological diseases [5] and breaking down blood clots formed in blood vessels [6]. The main advantage of using nanofluids in biomedical applications is their enhanced heat transfer coefficient compared to other liquids [5]. The heat transfer efficiency in nanofluids depends on the fluid (blood or interstitial fluid) thermal conductivity, the fluid dynamic viscosity, and the nanoparticle (NP) shape thermal properties [6]. The enhancement of the thermal properties of the interstitial fluid or the blood due to the introduction of nanoparticles can be evaluated using mathematical or empirical correlations deduced from various experimental studies in the literature [7, 8].

The idea of enhancing the thermal conductivity of fluids by introducing nanoparticles (NPs) was proposed at the end of the twentieth century. Choi and Eastman [9] introduced the definition of nanofluids and proposed new classes of innovative fluids to improve heat transfer using suspending metallic NPs with conventional fluids. A comprehensive analysis of the factors that enhance the nanofluid thermal properties was presented and analysed by Buongiorno [10].

Introducing NPs into non-Newtonian fluids requires the employment of constitutive models distinct from those employed for Newtonian fluids [11]. For example, the tangent hyperbolic model, first introduced by Pop and Ingham [12], is a non-Newtonian fluid model used to understand and predict various flow properties of some industrial fluids such as paints, nail polish, ketchup, whipped cream, and other fluids [13]. Williamson model is also a non-Newtonian model that describes the flow of pseudoplastic fluids which have various applications in engineering and industry [14]. Second-grade viscoelastic model is another non-Newtonian fluid model used in the literature to study heat and mass transfer in non-Newtonian nanofluids [15]. Furthermore, the Casson model is a non-Newtonian model with less shear stress than the yield stress, but it starts to deform when shear stress becomes more significant than the yield stress. Rafique et al. [16] used the Buongiorno model to investigate Casson nanofluid flow over a nonlinear slanted stretching sheet with chemical reaction and heat generation/absorption. They found that the Casson factor reduced the fluid velocity, while the sheet inclination factor increased heat and mass transfer.

Studying fluid flow in biological tissues can be modelled as flow in a porous medium. Izadi and Sheremet [17] presented the phenomenon of thermal radiation transmission of nanofluid and thermal gravitational through a permeable material exposed to a magnetic field. They noticed a decrease in the Nusselt number value at large values of the Hartmann number. Aboud et al. [18] investigated the nanofluid flow through a hollow cylinder in a magnetic field. Their study showed that the fluid flow increased with the increase in the energy law indicators. In addition, they found a strong influence of the magnetic field on the fluid flow, which improved the heat transfer process by forced convection. Hatami et al. [19] simulated the heat and mass transfer in blood, a non-Newtonian fluid. They incorporated the effect of Brownian motion and thermal separation coefficient into their model. The results revealed that the increase in the thermal conductivity coefficient led to an increase in the temperature of the fluid and an increase in the concentration of the NPs.

On the other hand, they found a noticeable decrease in velocity due to the influence of the magnetic field. Islam et al. [20] analysed the flow of nanofluids in a permeable material surrounded by a cylinder exposed to a magnetic field. They found that the temperature of the nanofluids increased due to an increase in thermal electrophoresis, Brownian motion of the NPs, and the Eckert number, whereas the temperature decreased due to the increase in the Prandtl number. Mirza et al. [21] presented a mathematical model for blood transfusion in hydrodynamic and electromagnetic phases. They studied the influence of magnetic and electrical parameters on the heat transfer in blood and particles and the blood flow. They concluded that the electrical parameters significantly affected blood velocity and NP transport. Azhar et al. [22] studied mathematically the influence of a magnetic field on a Prandtl fluid flow and heat transfer. They found that increasing the Prandtl number improved the heat transfer in the fluid. In addition, they observed that the skin friction increased linearly with the Grashof number.

Mitragotri [23] presented various examples illustrating the importance of physical properties in biology, including size, shape, mechanical properties, and biological applications of biological materials. He concluded that the drug should penetrate the tissue well to obtain effective results for cancer treatment. According to the physiological aspects of cancer, several studies and strategies have been proposed to improve drug delivery efficiency through tumours [24]. For example, the structure of blood vasculature around the cancer is irregular, with a relatively small number of vessels. So, several therapeutical strategies incorporate antibodies or ligands to be compatible with tumour cell receptors to improve drug delivery [25]. Hence, introducing NPs to clinical techniques showed promising results over conventional clinical and preclinical techniques [26].

This paper presents a mathematical model that investigates the NP extravasation from an inclined blood vessel surrounded by tissue and subjected to a magnetic field. Additionally, we mimic the interaction between the magnetic field and the NPs, which generates heat in the tissue. This study also examines the tissue temperature that induces cell death in tumours. We found that the tumour-specific absorption coefficient plays a significant role in NP delivery to the tumour; and the efficacy of the tumour treatment using thermal therapy. The manuscript is structured as follows: Sect. 1 (the introduction) provides information on magnetohydrodynamic nanofluids, intrinsic thermal properties of nanofluids, and applications of nanofluids in biomedicine. The description of the physical model and the corresponding mathematical model are presented in Sect. 2 presents a description of the physical model and its associated mathematical model. Following is an explanation of the numerical solution approach in Sect. 3. Section 4 contains the outcomes of the mathematical model and the discussion, while Sect. 5 provides the conclusion of the paper.

2 Description of the physical model

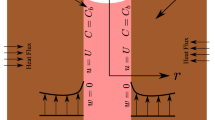
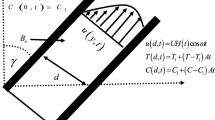
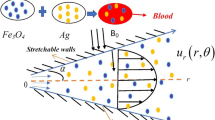
We consider the problem of an extended, circular cylinder inclined at an angle \(\alpha\), placed inside an incompressible viscous liquid and exposed to a magnetic field \({B}_{0}\), as shown in Fig. 1. We assume that both the concentration of NPs (\({C}_{w}\)) in the blood vessel and the blood temperature (\({T}_{f}\)) are constants. Moreover, we simulate the NP transport from the blood vessel to the adjacent tissue exposed to heat flux at the external tissue edge, the problem boundary. The heat source in this model is assumed to be an external heat source, such as an alternating magnetic field, that irradiates tissue at infinity, which is the heat flux source at the boundaries in this model.

Fig. 1
figure 1

The geometry of the problem

Full size image

We defined the incompressible Casson nanofluid by Casson [27] as;

$$\tau_{ij} = \left\{ {\begin{array}{*{20}l} {2 \left( { \mu_{{\varvec{B}}} + \frac{{\tau_{0} }}{{\sqrt {2\pi } }} } \right)e_{ij} ,} \hfill & {\pi > \pi_{c} } \hfill \\ {2\left( { \mu_{{\varvec{B}}} + \frac{{\tau_{0} }}{{\sqrt {2\pi_{c} } }} } \right)e_{ij} ,} \hfill & {\pi < \pi_{c} } \hfill \\ \end{array} } \right.$$
(1)

where, \({\tau }_{ij}\) is the shear stress tensor (Casson yield stress tensor), \({\tau }_{0}\) is an infinite value of the Casson yield stress, \(\pi ={ e}_{ij}{ e}_{ij}\) is the product of the component of the deformation rate with itself, \({\pi }_{c}\) is the critical value of \(\pi\) based on the non-Newtonian model, \({e}_{ij}=\frac{1}{2} \left(\frac{\partial {u}_{i}}{\partial {x}_{j}}+\frac{\partial {u}_{j}}{\partial {x}_{i}}\right)\) is the strain tensor rate where \({u}_{i}\) denoting the components of fluid velocity, and \({\mu }_{{\varvec{B}}}\) is the plastic dynamic viscosity of the non-Newtonian fluid. The kinematic viscosity \(\upsilon\) of the Casson nanofluid is given by

$$\upsilon =\frac{{\mu }_{B}}{\rho } \left(1+\frac{1}{\beta }\right),$$
(2)

where \(\rho\) is the density of fluid and \(\beta =\frac{{{\varvec{\mu}}}_{{\varvec{B}}\boldsymbol{ }\sqrt{2{\pi }_{c}}\boldsymbol{ }}}{{\tau }_{0}}\) is the Casson parameter, which represents the viscosity index of the non-Newtonian Casson nanofluid. Also, in the case \(\pi >{\pi }_{c}\) the shear stress is defined as [28, 29]

$${\tau }_{ij}= {\mu }_{{\varvec{B}}\boldsymbol{ }}\left(1+\frac{1}{\beta }\right),\boldsymbol{ }\boldsymbol{ }{2 e}_{ij}={\mu }_{{\varvec{B}}\boldsymbol{ }}\left(1+\frac{1}{\beta }\right)\left(\frac{\partial {u}_{i}}{\partial {x}_{j}}+\frac{\partial {u}_{j}}{\partial {x}_{i}}\right).$$
(3)

According to the above assumptions, we consider the system of governing equations as follows [30]:

$$\frac{\partial u}{\partial z}+\frac{w}{r}+ \frac{\partial \mathrm{w}}{\partial \mathrm{r}}=0,$$
(4)
$$\left( {u{ }\frac{\partial u}{{\partial z}} + w{ }\frac{\partial u}{{\partial r}}} \right) = \upsilon \left( {1 + \frac{1}{\beta }} \right)\left( {{ }\frac{{\partial^{2} u}}{{\partial r^{2} }} + \frac{1}{r}{ }\frac{\partial u}{{\partial r}}} \right) + g\left[ {\beta_{T} \left( {T - T_{\infty } } \right) + \beta_{c} \left( {C - C_{\infty } { }} \right)} \right]\cos \alpha - \frac{{\sigma B_{0}^{2} { }}}{\rho }u - \frac{{\nu_{eff} }}{K}u,$$
(5)
$$\left(u \frac{\partial T}{\partial z}+w \frac{\partial T}{\partial r}\right)={\alpha }_{f} \left( \frac{{\partial }^{2}T}{\partial {r}^{2}}+\frac{1}{r} \frac{\partial T}{\partial r}\right)+\tau \left[\frac{{D}_{B}}{{\rho }_{p}}\frac{\partial T}{\partial r}\frac{\partial C}{\partial r}+\frac{{D}_{T}}{{T}_{\infty }}{\left(\frac{\partial T}{\partial r}\right)}^{2}\right]+\frac{16{\sigma }^{*}{\mathrm{T}}_{\infty }^{3}}{3\left(\rho {c}_{p}\right){k}^{*}}\left(\frac{{\partial }^{2}T}{\partial {r}^{2}}+\frac{1}{r} \frac{\partial T}{\partial r}\right)+\frac{\upsilon }{{c}_{p}}\left(1+\frac{1}{\beta }\right){\left(\frac{\partial u}{\partial r}\right)}^{2}+\frac{\sigma {B}_{0}^{2} }{\rho {c}_{p}}{u}^{2}+\frac{SAR}{\rho {c}_{p}}\left(C-{C}_{\infty }\right),$$
(6)
$$\left(u \frac{\partial C}{\partial z}+w \frac{\partial C}{\partial r}\right)={D}_{B}\left[\frac{{\partial }^{2}C}{\partial {r}^{2}}+\frac{1}{r} \frac{\partial C}{\partial r}\right]+\frac{{\rho }_{p}{D}_{T}}{{T}_{\infty }}\left[\frac{{\partial }^{2}T}{\partial {r}^{2}}+\frac{1}{r} \frac{\partial T}{\partial r}\right],$$
(7)

where \((w,u\)) are the velocity components of the fluid in the radial direction and along with the vessel axial, respectively, and \(C\) is the concentration of NPs. Furthermore, \(g\) is the gravitational force,\({k}^{*}\) is the mean of the thermal parameter, \(\sigma\) is the electric conductivity, \({\sigma }^{*}\) is the Stefan–Boltzman constant, \({D}_{B}\) is the Brownian diffusion coefficient, \({D}_{T}\) is the thermophoretic diffusion coefficient, \(\alpha\) is the angle of inclination from horizontal, \({\beta }_{c}\) is the concentration expansion coefficient, \({\beta }_{T}\) is the thermal expansion, and \(SAR\) is the specific absorption rate (the rate of energy absorbed by the biological tissue). The heat capacities ratio of the NPs and the base fluid is denoted by \(\tau\), which is defined as \(\tau =\frac{{(\rho {c}_{p})}_{p}}{{(\rho {c}_{p})}_{f}}\), where \({c}_{p}\) denotes the heat capacity at constant pressure.

The boundary conditions corresponding to the model are given as follows:

$$\begin{aligned} & {\text{At }}\;\;\;\user2{ }r = R : u = 0,\;\;w = W,\;\;T = T_{f} , \;\;C = C_{w} . \\ & {\text{As}}\;\;\;r \to \infty \;\;\;\frac{1}{r}\frac{\partial }{\partial r}\left( {rw} \right) \to 0, wT - \left( {\alpha_{eff} + \frac{{16\sigma^{*} T_{\infty }^{3} }}{{3k^{*} \left( {\rho c_{p} } \right)_{eff} }}} \right) \frac{\partial T}{{\partial r}} \to Q_{H} , \\ \end{aligned}$$
(8)
$$wC-{D}_{B}\frac{\partial C}{\partial r}-\frac{{{\varvec{\rho}}}_{{\varvec{p}}}\boldsymbol{ }{D}_{T}}{{T}_{\infty }}\frac{\partial T}{\partial r}\to k,$$
(9)

where \(R\) is the radius of the cylinder.

We reduce the system of PDEs (4)–(9) into a system of ODEs using the subsequent similar transformations [30]:

$$\eta =\sqrt{\frac{{U}_{0}}{\upsilon L}} \left(\frac{{r}^{2}-{R}^{2}}{2R}\right).$$
(10)

The Stokes stream function \(\psi\) is introduced in the form

$$\psi \left(r,z\right)=\sqrt{\frac{{\upsilon U}_{0}}{L}} z R f\left(\eta \right).$$
(11)

The Cauchy Riemann equation \(\psi\) is given by

$$u=\frac{1}{r} \frac{\partial \psi }{\partial r} ,\,\,\, w=\frac{-1}{r} \frac{\partial \psi }{\partial z}.$$
(12)

Substituting Eq. (11) into Eq. (12), we get

$$u = \frac{{z U_{0 } }}{L} f^{\prime}\left( \eta \right) ,\quad w = \frac{ - R}{r} \sqrt {\frac{{\upsilon U_{0} }}{L}} f\left( \eta \right).$$
(13)

Also, we define the dimensionless temperature and NP concentration in the form

$$\theta \left( \eta \right) = \frac{{T - T_{\infty } }}{{T_{f} - T_{\infty } }} ,\;\;\;\varphi \left( \eta \right) = \frac{{C - C_{\infty } }}{{C_{w} - C_{\infty } }}.$$
(14)

Applying the transformations (10–14) to the momentum conservation equation (Eq. 5) we get

$$\left( {1 + \frac{1}{\beta }} \right)\left[ {\left( {1 + 2K\eta } \right)f^{\prime\prime\prime} + 2K f^{\prime\prime}} \right] + ff^{\prime\prime} - f^{{\prime}{2}} - Ha^{2} f^{\prime} + \left[ {G_{r} \theta + G_{m} \varphi } \right]\cos \alpha - K^{*} f^{\prime} = 0,$$
(15)

where \(K=\sqrt{\frac{\upsilon L}{{R}^{2} {U}_{0}}}\) is the curvature of the cylinder, \(H{a}^{2}=\frac{\sigma L {B}_{0}^{2}}{\rho {U}_{0}}\) is the magnetic field parameter, \({G}_{r}=\frac{g {\beta }_{T} \left({T}_{f}-{T}_{\infty }\right) {L}^{2}}{z {U}_{0}^{2}}\) is the thermal Grashof number and \({G}_{m}=\frac{g {\beta }_{c}\left({C}_{w}-{C}_{\infty } \right) {L}^{2}}{z {U}_{0}^{2}}\) is the mass Grashof number, \({K}^{*}=\frac{\upsilon L}{K {U}_{0}}\).

Similarly, applying the transformations (10–14) into the energy equation (Eq. (3)) we get

$$\begin{aligned} & \frac{1}{{P_{r} }}\left( {1 + \frac{4}{3}Rd} \right)\left[ {\left( {1 + 2K\eta } \right)\theta^{\prime\prime} + 2K\theta^{\prime}} \right] + f\theta^{\prime} + \left( {1 + 2K\eta } \right)\left( {Nb \theta^{\prime} \varphi^{\prime} + Nt\theta^{{\prime}{2}} } \right) \\ & \quad + \left( {1 + \frac{1}{\beta }} \right)\left( {1 + 2K\eta } \right)Ec f^{{\prime\prime}{2}} - Ha^{2} Ec f^{{\prime}{2}} + \lambda \frac{Nb}{{Nt Pe}}\varphi \left( \eta \right) = 0, \\ \end{aligned}$$
(16)

where \(Pe=Re Pr\) is the Peclet number, \(Pr=\frac{\upsilon }{{\alpha }_{f}}\) is the Prandtl number, \(Re=\frac{{U}_{w} z}{\upsilon }\) is the local Reynolds number, \({\alpha }_{f}=\frac{{k}_{f}}{{(\rho {c}_{p})}_{f}}\) is the nanofluid thermal diffusivity, \({R}_{d}=\frac{4 {\sigma }^{*}{\mathrm{T}}_{\infty }^{3}}{{K}_{f} {K}^{*}}\) is the thermal radiation parameter, \({N}_{b}=\frac{\tau {D}_{B}({C}_{w}-{C}_{\infty })}{\upsilon {\rho }_{p}}\) is the Brownian motion parameter, \(Nt=\frac{\tau {D}_{T }{(T}_{f}-{T}_{\infty })}{\upsilon { T}_{\infty }}\) is the thermophoresis parameter, \(Ec=\frac{{{U}^{2}}_{w}}{{({c}_{p})}_{f} {(T}_{f}-{T}_{\infty })}\) is the Eckert number, and finally, \(\lambda =\frac{{D}_{T} SAR {U}_{0}{L}^{2}}{{{k}_{f} D}_{B} {T}_{\infty } }\) is the specific absorption rate.

The dimensionless NP volume friction can be derived by applying the transformations (10–14) into the concentration equation (Eq. (7)) in the form

$$\left( {1 + 2K\eta } \right)\varphi^{\prime\prime} + 2K\varphi^{\prime} + \frac{Nt}{{Nb}}\left[ {\left( {1 + 2K\eta } \right)\theta^{\prime\prime} + 2K\theta^{\prime}} \right] + Sc f\varphi^{\prime} = 0,$$
(17)

where \(Sc=\frac{\upsilon }{{D}_{B}}\) is the Schmidt number.

The boundary conditions (Eqs. (8–9)) can also be transformed using the dimensionless transformations (10–14) in the form:

$$\begin{aligned} & at \;\eta = 0: f\left( \eta \right) = \gamma ,\;\;\;f^{\prime}\left( \eta \right) = 0, \theta \left( \eta \right) = 1, \varphi \left( \eta \right) = 1, \\ & as \;\;\eta \to \infty : f^{\prime}\left( \eta \right) = 0, \\ \end{aligned}$$
(18)
$$\begin{aligned} & f \left( {\theta + \xi_{1} } \right)\frac{1}{{\sqrt {Re } }}\left( {1 + 2K\eta } \right)^{ - 0.5} - \frac{{A_{1} }}{{\sqrt {Re } }}\left( {1 + 2K\eta } \right)^{0.5} \left( {1 + \frac{4}{3}Rd} \right)\theta^{\prime} \to Q_{H}^{*} , \hfill \\ & f\left( {\phi + \xi_{2} } \right)\frac{{\left( {1 + 2K\eta } \right)^{ - 0.5} }}{{\sqrt {Re } }} + \frac{{A_{2} }}{{\sqrt {Re } }}\left( {1 + 2K\eta } \right)^{0.5} \left( {\phi^{\prime} + \frac{Nt}{{Nb}}\theta^{\prime}} \right) \to k^{*} . \hfill \\ \end{aligned}$$
(19)

We can explicitly estimate the dimensionless heat flux across the blood vessel wall (see Eq. 19) in the form

$${\left.{Q}_{H}^{*}\right|}_{\eta =0}=\frac{\gamma (1+{\xi }_{1})}{\sqrt{Re }}-\frac{{A}_{1}}{\sqrt{Re }}\left(1+\frac{4}{3}Rd\right){\theta }{\prime},$$
(20)

where\({A}_{1}=\frac{1}{Pr}\), \({A}_{2}=\frac{1}{Sc}\), \({k}^{*}=\frac{-k}{{U}_{0}\left({C}_{w}-{C}_{\infty }\right)}\), \({Q}_{H}^{*}=\frac{-{Q}_{H}}{{U}_{0}\left({T}_{f}-{T}_{\infty }\right)}\) \({\xi }_{1}=\frac{{T}_{\infty }}{{T}_{f}-{T}_{\infty }}\) and \({\xi }_{2}=\frac{{C}_{\infty }}{{C}_{w}-{C}_{\infty }}\).

The skin friction coefficient \({C}_{f}\) and the local Nusselt number \(Nu\), which are defined as:

$${C}_{f}=\frac{{\tau }_{w}}{{\rho }_{f}{U}_{w}^{2}} , \,\,\,Nu=\frac{z {q}_{w}}{k ({T}_{f}-{T}_{\infty })}$$
(21)

where

$${\tau }_{w}=\left({\mu }_{B}+\frac{{\tau }_{0}}{\sqrt{2{\pi }_{c}}}\right){\left[\frac{du}{dr}\right]}_{r=R}^{2} ,\,\,\, {q}_{w}=\left(-k+\frac{16{\sigma }^{*}{\mathrm{T}}_{\infty }^{3}}{3\left(\rho {c}_{p}\right){k}^{*}}\right){\left[\frac{dT}{dr}\right]}_{r=R}$$
(22)

\({\tau }_{w}\) is shear stress and \({q}_{w}\) is the heat flux at the surface of the stretching cylinder. Substituting Eq. (22) into Eq. (21) we get the skin friction and local Nuselt number in the form

$$C_{f} = \left( {1 + \frac{1}{\beta }} \right)Re_{z}^{{{\raise0.7ex\hbox{${ - 1}$} \!\mathord{\left/ {\vphantom {{ - 1} 2}}\right.\kern-0pt} \!\lower0.7ex\hbox{$2$}}}} f^{\prime\prime}\left( 0 \right), \,\,\,Nu = - Re_{z}^{{{\raise0.7ex\hbox{${ - 1}$} \!\mathord{\left/ {\vphantom {{ - 1} 2}}\right.\kern-0pt} \!\lower0.7ex\hbox{$2$}}}} \left( {1 + \frac{4}{3}Rd} \right)\theta^{\prime}\left( 0 \right).$$
(23)

3 Method of solution

We reduce the system of ordinary differential equations (ODEs) into a system of first-order ODEs using the following transformations [31].

So, the Eqs. (15–17) and (18–19) can be written in the form:

$$\begin{aligned} s^{\prime}_{1} & = s_{2} , s^{\prime}_{2} = s_{3} , \\ s^{\prime}_{3} & = f^{\prime\prime\prime} = \frac{ - 2K}{{1 + 2K\eta }} s_{3} - \frac{1}{{\left( {1 + \frac{1}{\beta }} \right)\left( {1 + 2K\eta } \right)}}\left[ {s_{1} s_{3} - s_{2}^{2} - Ha^{2} s_{2} + \left( {Gr s_{4} + Gm s_{6} } \right)\cos \alpha + K^{*} s_{2} } \right], \\ s^{\prime}_{5} & = \frac{ - 2K}{{1 + 2K\eta }}s_{5} - \frac{Pr}{{\left( {1 + \frac{4}{3}Rd} \right)\left( {1 + 2K\eta } \right)}}s_{1} s_{5} + \frac{{Ha^{2} PrEc}}{{\left( {1 + \frac{4}{3}Rd} \right)\left( {1 + 2K\eta } \right)}}s_{2}^{2} - \frac{{PrEc\left( {1 + \frac{1}{\beta }} \right)}}{{1 + \frac{4}{3}Rd}}s_{3}^{2} - \frac{Pr}{{1 + \frac{4}{3}Rd}}\left[ {N_{b} s_{5 } s_{7} + Nt s_{5}^{2} } \right] - \frac{\lambda NbPr}{{Nt Pe\left( {1 + \frac{4}{3}Rd} \right)\left( {1 + 2K\eta } \right)}}s_{6} , \\ s^{\prime}_{7} & = \frac{ - 2K}{{1 + 2K\eta }}s_{7} - \frac{Nt}{{Nb}} \left( {s^{\prime}_{5} - \frac{2K}{{1 + 2K\eta }} s_{5} } \right) - \frac{Sc}{{1 + 2K\eta }}s_{1} s_{7} . \\ \end{aligned}$$
(24)

The boundary conditions (18, 19) can be written in the form

$$\begin{aligned} & {\text{At}}\;\;\;\eta = 0: s_{1} = \gamma ,\,\, s_{2} = 0, \,\,s_{4} = 1,\,\, s_{6} = 1. \\ & {\text{At}}\;\;\;\eta = \infty : s_{3} = 0, \\ & s_{1} \left( {s_{4} + \xi_{1} } \right)\frac{1}{{\sqrt {Re } }}\left( {1 + 2K\eta } \right)^{ - 0.5} + \frac{{A_{1} }}{{\sqrt {Re } }}\left( {1 + 2K\eta } \right)^{0.5} \left( {1 + \frac{4}{3}Rd} \right)s_{5} = Q_{H}^{*} , \\ & s_{1} \left( {s_{6} + \xi_{2} } \right)\frac{1}{{\sqrt {Re } }}\left( {1 + 2K\eta } \right)^{ - 0.5} + \frac{{A_{2} }}{{\sqrt {Re } }}\left( {1 + 2K\eta } \right)^{0.5} \left( {s_{7} + \frac{{N_{t} }}{{N_{b} }}s_{5} } \right) = k^{*} . \\ \end{aligned}$$
(25)

We impose the initial values of the model variables as: \({s}_{1}={s}_{2}={s}_{3}={s}_{4}={s}_{5}={s}_{6}={s}_{7}=0\). We solve the system of Eqs. (24 and 25) using bvp4c, a MATLAB function within a relative error \({10}^{-5}\) which is adequate to achieve convergence [32]. The convergence of the code results was proven using different spatial grids, using the parameter values listed in Table 1. We discuss the outcomes of the mathematical model in the section that follows.

Table 1 The baseline parameter values
Full size table

4 Results and discussion

We have solved the governing Eqs. (15–17) according to the boundary conditions (18 and 19) using a 300-point spatial grid, which corresponds to a relative error of O(\({10}^{-4}\)). The numerical solution has been validated against two published papers in the literature as shown in Table 2. The findings of the model are depicted graphically in Figs. 2, 3, 4 and 5.

Table 2 Comparisons showing computational values of \(-{f}^{{\prime}{\prime}}(0)\) when \(Pr=10, Sc=11, Nb=0.1, Nt=0.1, K=Gr=Gm=\alpha = Rd=\gamma ={K}^{*}=\lambda =0\) and \(\beta \to \infty\) against some value of \(Ha\)
Full size table
Fig. 2
figure 2

The dimensionless numerical results: A NP concentration for different values of \(K\), B nanofluid temperature for different values of \(K\), C Nanofluid velocity in the axial direction for different values of \(K\), D Nanofluid temperature for different values of \(Rd\)

Full size image
Fig. 3
figure 3

The dimensionless numerical results: A NP concentration for different values of \(\gamma\), B Nanofluid temperature for different values of \(\gamma\), C NP concentration for different values of \(Nt\), D Nanofluid temperature for different values of \(Nt\)

Full size image
Fig. 4
figure 4

The dimensionless numerical results: A Nanofluid velocity in the axial direction for different values of \(Nt\) B NP concentration for different values of \(Nb\), C Nanofluid temperature for different values of \(Nb\), D NP concentration for different values of \(\lambda\)

Full size image
Fig. 5
figure 5

The dimensionless numerical results: A Nanofluid temperature for different values of \(\lambda\), B Nanofluid velocity in the axial direction for different values of \(\lambda\), C The Nusselt number against \(Rd\), D Heat flux across the vessel wall against \(Rd.\)

Full size image

Figure 2 depicts the influence of the curvature of the cylinder coefficient (\(K\)) and the thermal radiation parameter \((Rd)\) on the axial velocity of the interstitial fluid (\(f{\prime}\)), the effect of the nanofluid temperature (\(\theta\)), and the NP concentration in the interstitial fluid (\(\phi\)). As expected, both \(\theta\) and \(\phi\) are maximal at the blood vessel wall but monotonically decrease across the tissue, see Fig. 2A, B and D, since the blood vessel is the source of the interstitial fluid and the NPs. However, as \(K\) increases, axial fluid flow in the tissue is resisted due to the increase in the electromagnetic force (Fig. 2C). As illustrated in Fig. 2B, with large values of \(K\), the interstitial fluid temperature elevates since more NPs accumulate in the tissue, increasing the thickness of the mass boundary layer. This spread of NPs across the tumour is due to the reduction in the viscous forces. Therefore, increasing \(K\) assists in delivering more NPs into the tumour, see Fig. 2A.

Interestingly, increasing the radiation parameter \((Rd)\) we observed that \(Rd\) has a negligible effect on the interstitial fluid velocity but a considerable impact on the temperature, as shown in Fig. 2D. Therefore, thermal radiation enhances the nanofluid temperature in the tissue (Fig. 2D).

Figure 3 shows the influence of the velocity of the interstitial fluid at the blood vessel wall (\(\gamma\)) and the influence of the thermophoresis parameter \((Nt)\) on the nanofluid temperature (\(\theta\)) and the NP concentration (\(\phi\)) in the interstitial fluid. The model indicates that the increase in the value of \(\gamma\) causes a considerable decrease in the concentration of NPs in the deep tumour cells (Fig. 3A) and also decreases the nanofluid temperature (Fig. 3B). Therefore, large pores at the blood vessel wall reduces the NP concentration in the tumour, consequently reducing the effectiveness of thermal therapy as a cancer treatment. In Figs. 3C and D the model demonstrates that the increase in the thermophoresis parameter (\(Nt\)) increases the temperature of the nanofluid (Fig. 3D), and the concentration of NPs within the tumour (Fig. 3C), which supports the stability of the NPs within the tumour tissue as a result of an increase in the thickness of the mass boundary layer.

Figure 4 visualise the effect of the of thermophoresis parameter \((Nt)\) on the axial velocity of the interstitial fluid (\({f}{\prime}\)) and the influence of the Brownian motion parameter \((Nb)\) on the nanofluid temperature and the NP concentration in the interstitial fluid. The model results demonstrate that the increase in the thermophoresis parameter raises the axial velocity of the interstitial fluid (Fig. 4A). Similarly, as the Brownian motion of the NPs increases, so does the temperature of the interstitial fluid (Fig. 4C), which raises the tumour temperature, so enhancing the thermal therapy efficacy. However, it significantly reduces the thickness of the mass boundary layer that resists the NP transport in the tissue, as shown in Fig. 4B.

The influence of the specific absorption rate coefficient parameter (\(\lambda\)) on nanofluid temperature, NP concentration and the velocity of interstitial fluid is illustrated in Figs. 4D and 5A and B. The results indicate that increasing \(\lambda\) decreases the NP concentration (Fig. 4D), reducing the thickness of the mass boundary layer. In contrast, increasing \(\lambda\) in the tumour increases both the fluid temperature and the interstitial fluid velocity, as shown in Fig. 5A and B, which improves the NP accumulation in the tumour. Finally, the effect of the Nusselt number (\(Nu\)) and heat flux (\({Q}_{H}^{*}\)) across the vessel wall on the different value of \(Rd\) is depicted in Fig. 5C and D. The results reveal that the increase of parameter \(Rd\) raises the Nusselt number, representing the heat transfer across the vessel wall (Fig. 5C). Similarly, Fig. 5D shows the heat flux at wall of the vessel against the radiation parameter \(Rd\) which confirms the enhancement of heat transfer across the vessel boundaries due to the increase in the radiation parameter.

Finally, in Table 3 we illustrate the impact of the radiation, the radial velocity of the interstitial fluid, and the thermophoresis on the heat transfer (\(Nu\)) and the skin friction at the wall of the vessel. The radiation parameter and the radial velocity of the interstitial fluid at the vessel wall increase the heat transfer from the blood vessel to the surrounding tissue, while the thermophoresis parameter reduces it. On the other hand, the skin friction is increased by the radiation coefficient and the thermophoresis parameter but decreased by the interstitial fluid extravasation velocity.

Table 3 Variation of Nusselt number \(Nu\) and skin friction \({C}_{f}\) for different values of \({R}_{d}\), \({N}_{t}\), \(\gamma\)
Full size table

5 Conclusions

In this work, we studied the numerical analysis of a Casson nanofluid over an inclined cylindrical vessel surrounded by a hot tumour tissue. We looked into the effects of nanofluid velocity, tissue-specific heat absorption, thermal radiation and thermophoresis on NP transport and heat transfer in the tumour tissue. We developed a system of partial differential equations (PDEs) to simulate the fluid flow, NP transport, and heat transfer in the interstitial space. We closed the mathematical model with appropriate boundary conditions to determine the heat and mass flux across the tissue boundaries. Then, using similarity transformations, we converted the system of PDEs to a system of ODEs which were solved numerically by MATLAB.

We observed that NPs could easily permeate tissue at large curvature values of the cylinder, which increases NP concentration in the neighborhood of the vessel. In addition, increasing the velocity of the interstitial fluid reduces the thickness of the mass boundary layer, which resists the mobility of NPs within the tissue. Heat transport by thermophoresis in the tissue, on the other hand, increases the concentration of NPs inside the tissue, stabilising the NPs within the tumour tissue due to the increase in the thickness of the mass boundary layer. In addition, the Brownian motion of NPs raises the temperature in the tumour but reduces the NP concentration in the tissue. Furthermore, enhancing the tumour specific absorption coefficient optimises the efficacy of heat therapy by increasing the interstitial fluid velocity and enhancing the tumour tissue temperature.

However, this study assumed that the fluid flow, NP transport, and heat transfer are homogeneous over the circumference direction. Furthermore, we also assumed a steady state with a continuous supply of NPs from the vessel, which should be generalised in future work to imitate NP elimination by the immune system.