1 Introduction

Nowadays, ultrasonic technology uses in various industrial applications. One of these applications is ultrasonic plastic welding. In this method, a high-power ultrasonic transducer is used as a mechanical vibrations source. Generally, the vibration amplitude at the output surface of transducers is approximately 10–20 microns [1]. To weld plastics, the amplitude of vibrations should be increased to provide the required energy. Boosters and horns do this amplification. To optimize the energy transfer, the natural frequency of the booster and horn must be near to the resonant frequency of the transducer [2]. Some essential requirements such as nodal plan location on the booster, magnification factor, and longitudinal resonant frequency of components, dimensions, and materials properties should be considered in the design of the components [3]. Also, some external parameters have a significant effect on the efficiency and performance of the system. For example, external force and workpieces' stiffness are some of those parameters that their effects have not been investigated analytically so far. Studies show that the design, optimization, and analysis of these components are done thoroughly by finite element software like ANSYS and COMSOL, which requires several iterations of trial and error. Wang et al. [4] designed an optimized horn using FEM for the high amplitude of vibrations. Kumar et al. [5] optimized the location of grooves on the body of block horns by the genetic algorithm to obtain uniform output amplitude. Wei et al. [6] designed a stepped horn using the differential equation of wave in one dimension. The 1D method has low accuracy; therefore, they designed the horn using trial and error in the COMSOL software. Naseri et al. [7] studied a horn for a metal forming process. They experimentally changed the length of the horn in order to tune it for forming metal billets in a mold and reducing forming forces. The system's resonant frequency is directly related to the stiffness of workpieces, but they did not study it. Rosca [2] designed a horn and considered the stiffness of the workpiece using the 1D equation. The external forces and stiffness significantly affect the quality of welding. Bae et al. [8] designed a horn for polymer sheet forming. They experimentally surveyed the effect of external forces on the quality of forming and temperature changes in the workpiece. Shuyu [9] calculated the resonant frequency using the coupled vibrations of a transducer. He presented an approximate analytical method and surveyed the effect of geometrical dimensions on the resonant frequency. The electrical behavior of a transducer depends on boundary conditions like mechanical loads, temperature, etc. By modeling the transducer as an equivalent RLC circuit, its behavior can be investigated under different conditions. Kauczor et al. [10, 11] investigated the frequency response of a high-power ultrasonic transducer utilizing its RLC equivalent circuit. Also, the mechanical quality factor of the transducer can be calculated using this model. Boontaklang and Chompoo-Inwai [12] used an equivalent RLC circuit model to propose a novel tracking and tuning technique for an ultrasonic transducer. They clearly explained a way of calculating the frequency response of an RLC model (e.g., admittance circle, phase, and amplitude diagram). Shuyu et al. [13] studied a tubular high-power composite ultrasonic transducer that generates radial and longitudinal waves. He modeled the transducer as an RLC circuit and calculated its resonant frequency. Moreover, he illustrated the theoretical relationship between the resonant frequency and geometrical dimensions. Digital ultrasonic power supplies generally find the resonant frequency of transducers based on the phase of the admittance. The phase of the admittance is related to different parameters of the transducers, such as their geometry and mechanical properties of the materials. In some cases, the phase of the admittance of the ultrasonic transducer is completely positive. In this condition, the ultrasonic power supply cannot find the resonant frequency. Therefore, the phase diagram of the ultrasonic transducer should be calculated before fabrication to assure if it is suitable to work with a power supply or not. The previous study of the authors [14] was simply an analytical model to design horns and boosters for ultrasonic welding considering coupled three-dimensional wave equations. Modal analysis was done using the previous model. But in this paper, the model included piezoceramics. Therefore, force vibration analysis is done to study the frequency response of the transducer.

In this paper, the effect of the workpiece's stiffness and material properties on the frequency response of an ultrasonic transducer is investigated by an analytical model. A precise mathematical model based on the coupling of longitudinal and lateral vibrations is made to calculate the frequency response, resonant and anti-resonant frequency, mode shape, and magnifying factor of vibrations under different working conditions. First, the analytical model of a transducer, booster, horn, and workpiece is presented. After that, the system is simulated with FEM software to verify the analytical model. Finally, the components are fabricated for experimental tests and verifications.

2 Analytical modeling

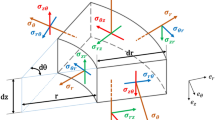
An ultrasonic transducer is usually made up of three types of material: steel, titanium, and piezoelectric. The booster and horn are usually made of aluminum 7075-T6. Every component is modeled as solid or hollow cylinders or exponential parts in this paper. By writing the dynamic equilibrium for stresses on a cylindrical 3D element (Fig. 1).

Fig. 1
figure 1

Cylindrical element of components [14]

Full size image

Ignoring the shear stresses, the equation of motion in the longitudinal direction is as follows:

$$\frac{{\partial^{2} {\varvec{u}}_{{\varvec{z}}} }}{{\partial {\varvec{z}}^{2} }} + {\varvec{k}}_{{\varvec{z}}}^{2} {\varvec{u}}_{{\varvec{z}}} = 0$$
(1)

Which kZ is apparent wave number and is defined as:

$${\varvec{k}}_{{\varvec{z}}} = \frac{{\varvec{\omega}}}{{{\varvec{V}}_{{\varvec{z}}} }}$$
(2)

where ω is the angular frequency, VZ is the apparent speed of the wave, which is defined as:

$${\varvec{V}}_{{\varvec{z}}} = \sqrt {\frac{{{\varvec{E}}_{{\varvec{z}}} }}{{\varvec{\rho}}}}$$
(3)

where ρ is density, EZ is the apparent modulus of elasticity defined as follows:

$${\varvec{E}}_{{\varvec{z}}} = \frac{{\varvec{E}}}{{1 - \frac{{\varvec{\nu}}}{{\varvec{n}}}}}$$
(4)

where E is the real young modulus, ν is the Poisson ratio, and the mechanical coupling coefficient, n, is defined as the ratio of longitudinal stress to lateral stress consisting of radial and circumferential stresses.

$${\varvec{n}} = \frac{{{\varvec{\sigma}}_{{\varvec{z}}} }}{{{\varvec{\sigma}}_{{\varvec{r}}} + {\varvec{\sigma}}_{{\varvec{\theta}}} }}$$
(5)

By solving the differential equation of motion (Eq. 1), longitudinal displacement relation in a cylinder is obtained as follows:

$${\varvec{u}}_{{\varvec{z}}} \left( {\mathbf{z}} \right) = {\varvec{A}}\cos \left( {{\varvec{k}}_{{\varvec{z}}} {\varvec{z}}} \right) + {\varvec{B}}\sin \left( {{\varvec{k}}_{{\varvec{z}}} {\varvec{z}}} \right)$$
(6)

Also, longitudinal displacement relation in exponential parts is:

$$\varvec{u}_{\varvec{z}} \left( {\mathbf{z}} \right) = \varvec{e}^{{ - \varvec{\beta Z}_{{}} }} \left( {\varvec{A}^{'} \cos \left( {\left[ {\sqrt {\varvec{k}_{\varvec{z}}^{2} - {\beta }_{{}}^{2} } } \right]\varvec{z}_{{}} } \right) + {B}^{'} \sin \left( {\left[ {\sqrt {\varvec{k}_{\varvec{z}}^{2} - \varvec{\beta }_{{}}^{2} } } \right]\varvec{z}} \right)} \right)$$
(7)

A, B, A', and B' are unknown coefficients in the above equations. The radial displacement differential equation and its answer are as follows:

$$\frac{{\partial^{2} {\varvec{u}}_{{\varvec{r}}} }}{{\partial {\varvec{r}}^{2} }} + \frac{1}{{\varvec{r}}}\frac{{\partial {\varvec{u}}_{{\varvec{r}}} }}{{\partial {\varvec{r}}}} + \left( {{\varvec{k}}_{{\varvec{r}}}^{2} - \frac{1}{{{\varvec{r}}^{2} }}} \right){\varvec{u}}_{{\varvec{r}}} = 0{ } \to {\varvec{ u}}_{{\varvec{r}}} \left( {\varvec{r}} \right) = {\varvec{CJ}}_{0} \left( {{\varvec{k}}_{{\varvec{r}}} {\varvec{r}}} \right) + {\varvec{DY}}_{0} \left( {{\varvec{k}}_{{\varvec{r}}} {\varvec{r}}} \right)$$
(8)

Radial frequency equations for hollow and solid cylinders are obtained by applying the radial boundary conditions. Radial forces at a hollow cylinder's internal and external radius are zero. The two boundary conditions yield the following frequency equation [15].

$$\frac{{{\varvec{k}}_{{\varvec{r}}} {\varvec{aJ}}_{0} \left( {{\varvec{k}}_{{\varvec{r}}} {\varvec{a}}} \right) - \frac{{\left( {1 - {\varvec{\nu}} - 2{\nu {\varvec n}}} \right)}}{{\left( {1 - {\nu {\varvec n}}} \right)}}{\varvec{J}}_{1} \left( {{\varvec{k}}_{{\varvec{r}}} {\varvec{a}}} \right)}}{{{\varvec{k}}_{{\varvec{r}}} {\varvec{bJ}}_{0} \left( {{\varvec{k}}_{{\varvec{r}}} {\varvec{b}}} \right) - \frac{{\left( {1 - {\varvec{\nu}} - 2{\nu {\varvec n}}} \right)}}{{\left( {1 - {\nu {\varvec n}}} \right)}}{\varvec{J}}_{1} \left( {{\varvec{k}}_{{\varvec{r}}} {\varvec{b}}} \right)}} = \frac{{{\varvec{k}}_{{\varvec{r}}} {\varvec{aY}}_{0} \left( {{\varvec{k}}_{{\varvec{r}}} {\varvec{a}}} \right) - \frac{{\left( {1 - {\varvec{\nu}} - 2{\nu {\varvec n}}} \right)}}{{\left( {1 - {\nu {\varvec n}}} \right)}}{\varvec{Y}}_{1} \left( {{\varvec{k}}_{{\varvec{r}}} {\varvec{a}}} \right)}}{{{\varvec{k}}_{{\varvec{r}}} {\varvec{bY}}_{0} \left( {{\varvec{k}}_{{\varvec{r}}} {\varvec{b}}} \right) - \frac{{\left( {1 - {\varvec{\nu}} - 2{\nu {\varvec n}}} \right)}}{{\left( {1 - {\nu {\varvec n}}} \right)}}{\varvec{Y}}_{1} \left( {{\varvec{k}}_{{\varvec{r}}} {\varvec{b}}} \right)}}$$
(9)

The radial force at the outer radius of a solid cylinder is zero, and the radial displacement in the center of the cylinder is zero. The two boundary conditions yield the following frequency equation.

$${\varvec{ak}}_{{\varvec{r}}} {\varvec{J}}_{0} \left( {{\varvec{k}}_{{\varvec{r}}} {\varvec{a}}} \right) - \left[ {\frac{{\left( {1 - {\varvec{\nu}} - 2\nu {\varvec n}} \right)}}{{\left( {1 - \nu {\varvec n}} \right)}}} \right]{\varvec{J}}_{1} \left( {{\varvec{k}}_{{\varvec{r}}} {\varvec{a}}} \right) = 0$$
(10)

Structural dam** of components is taken into account using an imaginary young's modules as follows:

$$\varvec{\tilde{E}} = \varvec{E} + \varvec{E^{\prime}i} = \varvec{E}\left( {1 + \varvec{\eta i}} \right)$$
(11)

where E is the real young modulus, E' is loss modulus and \(= \frac{{E^{\prime}}}{E}\) is the structural loss factor. Also, the dielectric loss of the piezoelectric is defined as a complex electric permittivity coefficient.

$$\varvec{\tilde{\varepsilon }}_{{33_{{}} }} = \varvec{\varepsilon }_{{33}} \left( {1 + \left( {\tan \varvec{\delta }} \right)\varvec{i}} \right)$$
(12)

where \({\epsilon }_{33}\) is the real electric permittivity along 'Z' direction and \(\mathrm{tan}\delta\) is the loss factor. The following assumptions are taken into account for the analytical model:

(1)The vibration mode does not change in the wave propagation along with the components.

(2)Wave reflection is discarded at contact surfaces.

(3)Shear stresses and strains are ignored.

(4)The waves inside the parts are assumed sinusoidal.

(5)The acoustic impedance of air is ignored, so the horn or booster that works in the air is called "unloaded," and its stress is considered zero.

(6)Differential equations in the radial and longitudinal directions are considered.

(7)Vibrations in longitudinal and radial directions are related to each other using the mechanical coupling coefficient.

(8)To drive the radial frequency equation of exponential segments, the mean radius of these segments is considered.

(9)The piezoelectrics and copper electrodes are considered as integrated components.

(10)Slip and friction between contact surfaces are ignored.

Figure 2 shows the vibrating system. The system is divided into 16 segments, including hollow and solid cylinders and exponential parts. The workpiece is considered a spring that is attached to the radiating surface of the horn. The mass of the workpiece is negligible. The dam** of the workpiece is not considered in the model. The spring stiffness is related to the workpiece's young module, thickness, and contact area. Also, the external force is applied to the booster's flange, and its reaction is on the output surface of the horn.\

Fig.2
figure 2

the vibrating system and boundary conditions

Full size image

The longitudinal displacement relations for each element are as follows.

$${\varvec{u}}_{1} \left( {{\varvec{z}}_{1} } \right) = {\varvec{A}}\cos \left( {{\varvec{k}}_{1} {\varvec{z}}_{1} } \right) + {\varvec{B}}\sin \left( {{\varvec{k}}_{1} {\varvec{z}}_{1} } \right)$$
(13)
$${\varvec{u}}_{2} \left( {{\varvec{z}}_{2} } \right) = {\varvec{e}}^{{ - {\varvec{\beta}}_{1} {\varvec{Z}}_{2} }} \left( {{\varvec{C}}\cos \left( {\left[ {\sqrt {{\varvec{k}}_{2}^{2} - {\varvec{\beta}}_{1}^{2} } } \right]{\varvec{z}}_{2} } \right) + {\varvec{D}}\sin \left( {\left[ {\sqrt {{\varvec{k}}_{2}^{2} - {\varvec{\beta}}_{1}^{2} } } \right]{\varvec{z}}_{2} } \right)} \right)$$
(14)
$${\varvec{u}}_{3} \left( {{\varvec{z}}_{3} } \right) = {\varvec{E}}\cos \left( {{\varvec{k}}_{3} {\varvec{z}}_{3} } \right) + {\varvec{F}}\sin \left( {{\varvec{k}}_{3} {\varvec{z}}_{3} } \right)$$
(15)
$${\varvec{u}}_{4} \left( {{\varvec{z}}_{4} } \right) = {\varvec{G}}\cos \left( {{\varvec{k}}_{4} {\varvec{z}}_{4} } \right) + {\varvec{H}}\sin \left( {{\varvec{k}}_{4} {\varvec{z}}_{4} } \right)$$
(16)
$${\varvec{u}}_{5} \left( {{\varvec{z}}_{5} } \right) = {\varvec{e}}^{{ - {\varvec{\beta}}_{2} {\varvec{Z}}_{5} }} \left( {{\varvec{I}}\cos \left( {\left[ {\sqrt {{\varvec{k}}_{5}^{2} - {\varvec{\beta}}_{2}^{2} } } \right]{\varvec{z}}_{5} } \right) + {\varvec{J}}\sin \left( {\left[ {\sqrt {{\varvec{k}}_{5}^{2} - {\varvec{\beta}}_{2}^{2} } } \right]{\varvec{z}}_{5} } \right)} \right)$$
(17)
$${\varvec{u}}_{6} \left( {{\varvec{z}}_{6} } \right) = {\varvec{K}}\cos \left( {{\varvec{k}}_{6} {\varvec{z}}_{6} } \right) + {\varvec{L}}\sin \left( {{\varvec{k}}_{6} {\varvec{z}}_{6} } \right)$$
(18)
$${\varvec{u}}_{7} \left( {{\varvec{z}}_{7} } \right) = {\varvec{M}}\cos \left( {{\varvec{k}}_{7} {\varvec{z}}_{7} } \right) + {\varvec{N}}\sin \left( {{\varvec{k}}_{7} {\varvec{z}}_{7} } \right)$$
(19)
$${\varvec{u}}_{8} \left( {{\varvec{z}}_{8} } \right) = {\varvec{O}}\cos \left( {{\varvec{k}}_{8} {\varvec{z}}_{8} } \right) + {\varvec{P}}\sin \left( {{\varvec{k}}_{8} {\varvec{z}}_{8} } \right)$$
(20)
$${\varvec{u}}_{9} \left( {{\varvec{z}}_{9} } \right) = {\varvec{e}}^{{{\varvec{\beta}}_{3} {\varvec{Z}}_{9} }} \left( {{\varvec{Q}}\cos \left( {\left[ {\sqrt {{\varvec{k}}_{9}^{2} - {\varvec{\beta}}_{3}^{2} } } \right]{\varvec{z}}_{9} } \right) + {\varvec{R}}\sin \left( {\left[ {\sqrt {{\varvec{k}}_{9}^{2} - {\varvec{\beta}}_{3}^{2} } } \right]{\varvec{z}}_{9} } \right)} \right)$$
(21)
$${\varvec{u}}_{10} \left( {{\varvec{z}}_{10} } \right) = {\varvec{S}}\cos \left( {{\varvec{k}}_{10} {\varvec{z}}_{10} } \right) + {\varvec{T}}\sin \left( {{\varvec{k}}_{10} {\varvec{z}}_{10} } \right)$$
(22)
$${\varvec{u}}_{11} \left( {{\varvec{z}}_{11} } \right) = {\varvec{e}}^{{ - {\varvec{\beta}}_{4} {\varvec{Z}}_{11} }} \left( {{\varvec{U}}\cos \left( {\left[ {\sqrt {{\varvec{k}}_{11}^{2} - {\varvec{\beta}}_{4}^{2} } } \right]{\varvec{z}}_{11} } \right) + {\varvec{V}}\sin \left( {\left[ {\sqrt {{\varvec{k}}_{11}^{2} - {\varvec{\beta}}_{4}^{2} } } \right]{\varvec{z}}_{11} } \right)} \right)$$
(23)
$${\varvec{u}}_{12} \left( {{\varvec{z}}_{12} } \right) = {\varvec{W}}\cos \left( {{\varvec{k}}_{12} {\varvec{z}}_{12} } \right) + {\varvec{X}}\sin \left( {{\varvec{k}}_{12} {\varvec{z}}_{12} } \right)$$
(24)
$${\varvec{u}}_{13} \left( {{\varvec{z}}_{13} } \right) = {\varvec{Y}}\cos \left( {{\varvec{k}}_{13} {\varvec{z}}_{13} } \right) + {\varvec{Z}}\sin \left( {{\varvec{k}}_{13} {\varvec{z}}_{13} } \right)$$
(25)
$${\varvec{u}}_{14} \left( {{\varvec{z}}_{14} } \right) ={{\text A}^{\prime}}\cos \left( {{\varvec{k}}_{14} {\varvec{z}}_{14} } \right) +{{\text B}^{\prime}}\sin \left( {{\varvec{k}}_{14} {\varvec{z}}_{14} } \right)$$
(26)
$${\varvec{u}}_{15} \left( {{\varvec{z}}_{15} } \right) ={{\text C}^{\prime}}\cos \left( {{\varvec{k}}_{15} {\varvec{z}}_{15} } \right) +{{\text D}^{\prime}}\sin \left( {{\varvec{k}}_{15} {\varvec{z}}_{15} } \right)$$
(27)
$${\varvec{u}}_{16} \left( {{\varvec{z}}_{16} } \right) ={{\text E}^{\prime}}\cos \left( {{\varvec{k}}_{16} {\varvec{z}}_{16} } \right) +{{\text F}^{\prime}}\sin \left( {{\varvec{k}}_{16} {\varvec{z}}_{16} } \right)$$
(28)

The stiffness of the workpiece is defined as:

$${\varvec{k}}_{{\varvec{w}}} = \frac{{{\varvec{A}}_{{\varvec{w}}} {\varvec{E}}_{{\varvec{w}}} }}{{{\varvec{L}}_{{\varvec{w}}} }}$$
(29)

In this equation, Aw, Ew and Lw are the contact area, Young's module, and thickness of the workpiece, respectively. In this paper, a polyethylene workpiece with 0.1 GPa Young's modulus and 2 mm thickness is used. Table 1 shows the dimensions of the vibrating system.

Table 1 Dimensions of the vibrating system
Full size table

Using the boundary conditions and without an exciting electrical field, the following matrix equation is obtained to calculate the longitudinal resonant frequency. (The complete matrix equation is given in the appendix).

$$\left[ {\begin{array}{*{20}c} {\varvec{The}\;\varvec{~coefficients}} \\ {\varvec{matrix}} \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} \varvec{A} \\ \varvec{B} \\ {\begin{array}{*{20}c} \vdots \\ {\varvec{E'}} \\ {\varvec{F'}} \\ \end{array} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {\mathbf{F}} \\ 0 \\ {\begin{array}{*{20}c} \vdots \\ {\mathbf{F}} \\ {\begin{array}{*{20}c} 0 \\ \vdots \\ 0 \\ \end{array} } \\ \end{array} } \\ \end{array} } \right]$$
(30)

F is the external force that is placed in the constant matrix. The determinant of the coefficients matrix should be equal to zero to obtain the longitudinal frequency equation. So, external forces are not considered in modal analysis. They do not affect natural frequencies.

Table 2 shows the mechanical properties of the components. The material of the booster and the horn is Al 7075-T6. The backing and the matching of the transducer are made of steel 304 and titanium grade 5, respectively.

Table 2 Mechanical properties of the components
Full size table

Table 3 shows the physical properties of piezoelectric. Due to the different quality of materials in the market, the mechanical characteristics of the prepared PZT-4 were measured.

Table 3 PZT-4 characteristics
Full size table

By solving the system of equations, which includes one longitudinal and 16 radial frequency equations, the resonant frequency of the vibrating set and each element's mechanical coupling coefficient are calculated and shown in Table 4.

Table 4 Solution of the system of equations
Full size table

In the next step, the results obtained from solving the system of equations are used for a forced vibration analysis of the transducer and its frequency response. For this purpose, an electrical field is considered on the piezoelectric.

The electro-mechanical equation of piezoelectric rings can be expressed as follows [18].

$$\left\{ {\varvec{S}} \right\} = \left[ {{\varvec{s}}^{{\varvec{E}}} } \right]\left\{ {\varvec{T}} \right\} + \left[ {\varvec{d}} \right]^{{\varvec{t}}} \left\{ {\varvec{E}} \right\}$$
(31)
$$\left\{ {\varvec{D}} \right\} = \left[ {\varvec{d}} \right]\left\{ {\varvec{T}} \right\} + \left[ {\varepsilon^{{\varvec{T}}} } \right]\left\{ {\varvec{E}} \right\}$$
(32)

where {S} is the mechanical strain vector and {D} is the electric charge density vector. Using piezoelectric equations, the electric field is entered into the matrix equation [17]. Rows 26th and 28th of the constant matrix have electric field terms. By solving the new matrix equation, frequency response, mode shape, and displacement amplitude are calculated, and the effect of workpiece stiffness is investigated.

Electrical admittances related to radial and longitudinal vibrations are obtained from the following equations [17].

$${\varvec{Y}}_{31} = \frac{{{\varvec{I}}_{31} }}{{{\varvec{V}}_{3} }} = - \frac{{2{\uppi \upomega }}}{{\varvec{l}}}\left[ {\left( {\frac{{{\varvec{d}}_{31} + {\varvec{nd}}_{33} }}{{{\varvec{s}}_{11}^{{\varvec{E}}} + {\varvec{s}}_{12}^{{\varvec{E}}} + 2{\varvec{ns}}_{13}^{{\varvec{E}}} }}} \right)\left\{ {\frac{{\left( {{\varvec{s}}_{11}^{{\varvec{E}}} - {\varvec{s}}_{12}^{{\varvec{E}}} } \right)2{\varvec{d}}_{31} }}{{{\varvec{j}}\left( {\varvec{a}} \right){\varvec{y}}\left( {\varvec{b}} \right) - {\varvec{y}}\left( {\varvec{a}} \right){\varvec{j}}\left( {\varvec{b}} \right)}}\left[ {\left( {{\varvec{y}}\left( {\varvec{b}} \right) - {\varvec{y}}\left( {\varvec{a}} \right)} \right)\left( {{\varvec{aJ}}_{1} \left( {{\varvec{k}}_{{\varvec{r}}} {\varvec{a}}} \right) - {\varvec{bJ}}_{1} \left( {{\varvec{k}}_{{\varvec{r}}} {\varvec{b}}} \right)} \right) + \left( {{\varvec{j}}\left( {\varvec{a}} \right) - {\varvec{j}}\left( {\varvec{b}} \right)} \right)\left( {{\varvec{aY}}_{1} \left( {{\varvec{k}}_{{\varvec{r}}} {\varvec{a}}} \right) - {\varvec{bY}}_{1} \left( {{\varvec{k}}_{{\varvec{r}}} {\varvec{b}}} \right)} \right)} \right] - {\varvec{d}}_{31} \left( {{\varvec{a}}^{2} - {\varvec{b}}^{2} } \right)} \right\} + \varepsilon_{33}^{{\varvec{T}}} \left( {\frac{{{\varvec{a}}^{2} }}{2} - \frac{{{\varvec{b}}^{2} }}{2}} \right)} \right]{\varvec{tan}}\left( {\upomega{\text{t}}} \right) \times {\varvec{N}}_{{\varvec{p}}}$$
(33)
$${\varvec{Y}}_{33} = \frac{{{\varvec{I}}_{33} }}{{{\varvec{V}}_{3} }} = \frac{{ -{\uppi \upomega }\left( {{\varvec{a}}^{2} - {\varvec{b}}^{2} } \right)}}{{\varvec{l}}}\left\{ {\left( {\frac{{{\varvec{d}}_{31} }}{{\varvec{n}}} + {\varvec{d}}_{33} } \right){\varvec{E}}_{{\varvec{z}}} \left[ { - \frac{{{\varvec{Yk}}_{{\varvec{z}}} }}{{{\varvec{E}}_{3} }}{\mathbf{sin}}\left( {{\varvec{k}}_{{\varvec{z}}} {\varvec{z}}} \right) + \frac{{{\varvec{Zk}}_{{\varvec{z}}} }}{{{\varvec{E}}_{3} }}{\mathbf{cos}}\left( {{\varvec{k}}_{{\varvec{z}}} {\varvec{z}}} \right) - {\varvec{d}}_{33} } \right] + \varepsilon_{33}^{{\varvec{T}}} } \right\} \times {\varvec{N}}_{{\varvec{p}}} \times {\mathbf{tan}}\left( {\upomega{\text{t}}} \right)$$
(34)

\(l\) is the total length of piezoelectrics, NP is the number of piezoelectric rings, \(I_{31}\) and \(I_{33}\) are currents due to radial and longitudinal vibrations, respectively, and \({V}_{3}\) is the applied voltage to the piezoelectric.

The overall current and admittance of the system are calculated as follows.

$${\varvec{I}}_{3} = {\varvec{I}}_{31} + {\varvec{I}}_{33}$$
(35)
$${\varvec{Y}}_{3} = {\varvec{Y}}_{31} + {\varvec{Y}}_{33}$$
(36)

Figure 3 shows the Nyquist diagram of admittance of the transducer, plotted by the analytical model under loaded and free conditions. The radius of the diagram decreases once the stiffness of the workpiece increases.

Fig. 3
figure 3

The Nyquist diagram of the transducer’s admittance under free and loaded condition

Full size image

Figure 4 indicates that as the stiffness of the workpiece increases, the resonant frequency increases, and both displacement and admittance amplitude decrease. Polyethylene terephthalate (PET), high-density polyethylene (HDPE), and polycarbonates (PC) are taken into account as three workpieces with different stiffness.

Fig. 4
figure 4

a Frequency response of the transducer b Displacement amplitude of the output surface of horn in contact with different workpieces at 300 V

Full size image

Figure 5 shows the effect of voltage on the displacement amplitude of the output surface of the horn at free conditions. As the voltage increases, the displacement increases.

Fig. 5
figure 5

The effect of voltage on the displacement

Full size image

Figure 6 shows the effect of changing density (or mass of the system), Young's modulus, and dam** of aluminum components in the continuum model on the mechanical quality factor.

Fig. 6
figure 6

The effect of a density, b Young's modulus, and c dam** of Aluminum components on the mechanical quality factor using the continuum model

Full size image

The mechanical quality factor for the transducer with the specifications presented in the paper is calculated at 750 using the continuum model. The amount of the Q factor increases by increasing the density of aluminum components.

Figure 7a shows that in the large value of the dam**, the admittance phase is totally positive. Figure 7b shows the Nyquist diagram of admittance and the effect of dam** on the radius of the circle.

Fig. 7
figure 7

a The effect of changing Dam** on the admittance phase in the continuum model b dam** effect on the Nyquist diagram

Full size image

3 Numerical modeling

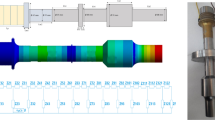
ANSYS software is used for numerical analysis. First, the vibrating system is modeled in CATIA software with the exact dimensions and materials in the analytical model. Next, it is imported into the ANSYS software for modal analysis. The resonant frequency is obtained under free conditions and in contact with a workpiece. Also, the mode shape of the system is computed. Figure 8 shows meshes of components for a 3D simulation. The first-order tetrahedral and hexahedral elements (C3D4 and C3D8) are used for this analysis. The grid type is hybrid with explicit solvers, and the number of nodes is 6841.

Fig. 8
figure 8

Meshed model of the vibrational system

Full size image

The obtained results from the modal analysis show that the resonant frequency of the vibrating system under free conditions is 19280 Hz, which has a 0.3% error with the analytical model (19,208 Hz). Figure 9 shows the modal analysis result while the system encounters a workpiece with a Young modulus of 0.1 GPa.

Fig. 9
figure 9

Third longitudinal mode shape at the frequency of 19,449 Hz

Full size image

Figure 10shows that resonant frequency in both models increases by increasing the young's modulus of the workpiece.

Fig. 10
figure 10

The effect of workpiece young's modulus on the resonant frequency

Full size image

Also, the mode shape of the vibrating system is obtained by the developed analytical model at 300 V and compared with the numerical model's result under free conditions. As Fig. 11 shows, there are three nodal planes on the system. Booster's nodal plane must be on the flange to avoid transfer of vibrations to welding machine structures. Moreover, the magnification factor of each component can be calculated from this figure.

Fig. 11
figure 11

Theoretical mode shape in two different young's modulus of the workpiece

Full size image

4 Fabrication and experimental tests

All the components are fabricated and assembled according to Table 1 dimensions for experimental verifications. Moreover, a fixture is designed to hold the vibrating system in the booster's nodal plane and attach it to the body of the machine (Fig. 12).

Fig. 12
figure 12

a The vibrating system and fixture b Column of a welding machine

Full size image

The system's resonant frequency is measured by an ultrasonic power supply (ULPS 2000, Alfa. Co, Iran). Figure 13 shows experimental tests of the frequency response of the system. As shown in Fig. 13 (c), the resonant frequency of the system is measured at 19,200 Hz at 300 V under free conditions, which has a 0.04% error with the analytical result (19,208 Hz) and a 0.4% error with the numerical result (19,280 Hz). When the vibrating system is encountered with a workpiece Fig. 13 (d), the resonant frequency increases to 19,270 Hz. Also, increasing the voltage, reduces the resonant frequency due to decreasing the piezoelectric Young's modulus Fig. 13 (b). Generally, resonant frequency increases in the experiments by increasing the external force. According to Eq. 29, when the external force increases, the thickness of the workpiece decreases, which causes the stiffness of the spring to increase. So, the resonant frequency increases.

Fig. 13
figure 13

a Ultrasonic power supply b Resonant frequency at 500 V under free condition (19,180 Hz) c Resonant frequency at 300 V under free condition (19,200 Hz) d Resonant frequency at 300 V with the workpiece (19,270 Hz)

Full size image

In order to measure the admittance's frequency response, an LCR meter (LCR-8110G, GW INSTEC, Taiwan) is used. Figure 14 shows the experimental setup to measure the admittance of the vibrating system.

Fig. 14
figure 14

The admittance measurement of the vibrating system with LCR meter

Full size image

The result of this test is compared with the analytical model in Fig. 15. The admittance at resonant and anti-resonant frequencies is compared with the analytical results in Table 5.

Fig. 15
figure 15

Amplitude of the frequency response of the admittance

Full size image
Table 5 Experimental Vs. analytical results
Full size table

The admittance phase is calculated by the analytical model and compared with the experimental results in Fig. 16.

Fig. 16
figure 16

Phase of the frequency response of the admittance

Full size image

To measure the amplitude of displacement of the horn's output surface, a gap sensor (AEC-5509, Applied Electronics, Japan) is used. Figure 17 shows the test and its results.

Fig. 17
figure 17

Displacement measurement of the horn at different voltages

Full size image

According to the graph, the displacement is increased by increasing the voltage in both experimental and analytical results. There is a linear relationship between voltage and displacement. According to the graph, the maximum difference between analytical results and experimental tests is in 500 V which are 130 and 110 microns, respectively.

5 Discussion

The current study proposed an analytical approach for modeling ultrasonic transducers. The frequency response of the transducer was obtained using the analytical model under different boundary conditions. Previous studies used to consider only longitudinal vibrations as a 1D model. Since lateral vibrations have been considered in addition to the longitudinal vibrations in the current model, the amount of error has been decreased. Comparisons with experimental tests and numerical simulations illustrated a good match between the results.

The former study of the authors [14] was simply an analytical model to design horns and boosters of ultrasonic welding considering coupled lateral and longitudinal vibrations. These components do not contain the piezoelectric transducer. Hence, the proposed model in this study is developed for the assembled set of the piezoelectric transducer, booster, and horn. This means that the new model contains an electro-mechanical part that can neither be analyzed using the previous model nor the effect of different boundary conditions on the frequency response of the set can be investigated. Therefore, a novel model was developed based on the previous study of the authors, in which not only electro-mechanical equations of the piezoelectric components were considered but also forced vibrations of the transducer were analyzed. Utilizing the developed model, the frequency response of the set and the effect of different boundary conditions, such as the workpiece’s stiffness on frequency response, were investigated accurately for the first time by the analytical model.

Moreover, the mechanical quality factor, frequency response of the admittance of the set were calculated. These parameters can be optimized using the proposed model. Numerical simulations cannot evaluate some diagrams, such as phase of the admittance.

6 Conclusions

A new analytical model was developed, and its accuracy was examined by comparing its results with numerical model and experimental tests. The proposed analytical model showed excellent results in calculating the resonant frequency and mode shape in contact with workpieces. Also, it had good predictions of resonant and anti-resonant frequencies. On the other hand, the effect of the parameters, like dam**, stiffness, and mass, is investigated by the analytical model. However, there is an inevitable random error in measuring some parameters, such as the amplitude of the vibration. However, the results of the analytical model showed good agreement with the results of the experiments. Simplifications of the analytical model, such as ignoring the reflection of waves on contact surfaces, can be sources of errors in the results of calculating the admittance and the amplitude of vibrations. The effect of changing voltage on the physical properties of piezoceramics is the subject of our future research.