1 Introduction

Conventional weaponry systems being used in the naval warfare are in a very complex interrelation with each other resulting in complex networks of systems [1, 2, 3]. Generally in naval warfare offensive sides initial aim is to detect and eredicate the defensive side. Quite the contrary, the defensive side under attack would try to hide and effort not being detected to survive. For this reason, innovative technology was developed for producing weaponary systems and naval systems. In this regard, materials technologies of the respective era have taken essential part of the research, development and application of such technologies. Innovation and improvement of the materials systems from conventional materials to advanced ceramics and composites have continuously played a key role in so many applications including defense systems as well [4]. Composites, layered structures, metamaterials, porous materials are conventionally used for defence industry [5, 6, 7].

The stealthy materials providing lower acoustical signature present an important opportunities for applications used in naval warfare systems. Stealthy materials, coatings and claddings have been developed for vehicles, vessels, weapons and equipment hiding in underwater i.e., not being easily detected and identified correctly. In the meantime, developed sonar technologies were produced for better detection of underwater objects be it submarines, torpedos and naval mines. The German Navy had used a highly porous elastomeric material for the first time that they called “the Alberich Coating” to reduce acoustical signatures of German submarines. Such an elastomeric cladding material with porosities and cavities on the hull of submarine brought about it hard to be intercepted by sonar systems. Such an engineered rubber layers and coatings have paved the way for lower detection ranges of sonars by absorbing acoustical waves [5, 6, 8, 9]. Combining geometrical form, configuration and variety of shapes of elastomeric layers along with manipulating acoustical impedance result in reduced sonar signals by absorbtion of sound waves [10]. As for the case in the submarines, composite structures are also implemented on the case of naval mines in order to reduce the interception probability of detection by the sonars. Naval mines with composite cases like Rockan and Manta have been in use by many modern naval forces. They are extremely effective and destructive weapons for decreasing acoustical signature along with quite a high damaging effects despite of their small sizes [11].

Naval mines demonstrate considerable strategical effects and advantages over other naval weaponry systems despite their comparatively lower costs [12]. They are also considered as asymmetrical arms (i.e., low cost vs high damage) of extensive uses in naval warfare [13]. Recently, it is estimated that more than 50 navies around the world possess more than 250.000 naval mines of 300 different types and approximately more than 30 countries are manufacturing and selling naval mines [14]. Based on its high efficiency causing extensive damage to the adverseries, such stealthy mines with low acoustical signature are evaluated as critical factors to gain upper hand on strategical superiority. In this respect, a stealth technology of low acoustical signature using coating/cladding techniques on naval weaponry and equipment would play a key role in highly competitive naval warfares.

It is known porous materials can be well adjustable in their properties by means of the porosity [15]. Aside from the surface of submarines, the applications of multi-layered composite/hybrid and porous materials to the case of naval mines are other effective ways to decrease acoustical signature. The materials used for decreasing underwater acoustical signature may not be efficient enough for all the range of frequencies and underwater conditions to provide acoustical stealthiness. Thickness, form, geometry, porosity, tortuousity, density and frequency are other major parameters of adjustment and manipulation of acoustical signatures [16, 17].

Materials with highly porous shape and form and adjustment of acoustical impedance implement considerably lower sonar signals via absorption of sound waves [8, 9, 10, 18]. The effects of porousity to underwater sound absorbtion is widely reviewed in theoretical elsewhere [4, 19]. The majority of the porous materials used for reducing acoustical signature are mostly high porosity polymers, fibrous and perforated metals, foam ceramics with high tortuosities [17, 20]. Highly porous foamy structures are also cost-effective and commercially available acoustical materials which are utilized to transmit, absorb and scatter the sound waves via tortuose and intrigued design of their porous internal structure. A porous and complex structured media is tortuous and meandering through which the paths for acoustical waves are not straight and smooth [21]. Initially, foamy and porous media will vibrate under the influence of incident sound pressure and that leads the acoustic wave to hit the cell walls and eventually scatter. Consequently, acoustical energy is scattered on account of intrigued outlet along with heat transfer and frictional forces. It is underlined that porous structures, such as polyurethane filled open-cell metallic foam, SiC based foam ceramics with high tortuousity and others are also considered as acoustically stealthy coatings for underwater objects. Some experimental studies in low frequencies are investigated despite the lack of the studies at higher frequencies [17].

In this study, 50 cm × 50 cm × 2 cm panels made of open celled SiC foam ceramics are used to evaluate and assess underwater absorbing, transmitting and emitting capabilities in acoustical test pool. The results of such novel complex and convoluted forms of SiC foams are evaluated in the range of 80–100 kHz for the application of lower acoustical signature as an alternative coating and/or a casing material for naval mines.

The paper is structured as fallows: In the next chapter, SiC foam ceramics are choosen to mitigate acoustical signature. An acoustical set-up is created for gathering experimental results in the environment of acoustic test pool. The detection sonars are examined in details and 80 kHz, 85 kHz, 90 kHz, 95 kHz and 100 kHz are used for acoustic test. In Sect. 3, acoustic testing procedure is executed and all the data is structured as tables. In Sect. 4, all values are compared and examined in detail. In this regard, the study shows that SiC foam ceramics are good candidates for sound absorbtion studies for naval mine countermeasure systems and may affect upcoming interest in this field. Finally in chapter 5, the assessments is presented and summarized based on the data gained during acoustial test.

2 Experimental method

2.1 Material selection

The data obtained in experimental studies show that highly porous SiC foam ceramics might be the potential candidates to mitigate acoustical signature in lower frequencies. Sound absorption properties and the theoretical results were in accord with the experimental results gained from liquid filled impedance tubes [16, 17]. Despite a number of studies examining the acoustical behaviors of SiC foam ceramics via impedance tube, there is an obvious lack of experimental studies exploring underwater behavior of highly porous and tortuous SiC foams above the frequencies limited by the impedance tube. However, it should be noted that such measurements have been done for the underwater behaviour of other materials and structures.

In this regard, 10 cm × 10 cm × 2 cm and 10 ppi (pore-per-inch) highly porous (%80–85 porosity) SiC foam ceramics are assembled to form 50 cm × 50 cm x 2 cm plate (Fig. 1). SiC foam ceramics are firmly assembled using fine nylon threads and wrapped with camouflage fabrics to form the plates for the experimental studies.

Fig. 1
figure 1

a A single SiC foam ceramic. b Dimensions of assamble of SiC foam ceramic

Full size image

In general, open celled SiC foam ceramics are produced via impregnation-squeezing technique using polyurethane open cell foams. Thoroughly mixed, a homogeneous SiC based ceramic slurry is impregnated into the polyurethane foams and effectively squeezed to remove excessive slip. Thereafter, it is gradually dried and fired for a full densification during which the polymeric skeleton is burnt and fully removed [22, 23]. SiC foam ceramics are used in various applications such as filters for foundry practices, filtration, heat shielding, heat exchange and others. They have exceptionally interesting properties such as lightweight, high hardness, high temperature durability, high wear and corrosion resistance along with good thermal shock resistance and also high thermal and electrical conductivity [24, 25, 26]. Some of the physical properties of such open pore SiC ceramic foams are given in Table 1[26].

Table 1 Some of the physical properties of such open pore SiC ceramic foams
Full size table

A typical SiC foam ceramic composition consists of > 62.0% SiC, < 10% SiO2, < 28% Al2O3 and others. Other oxide phases are purposely added to the mixture to decrease the sintering temperature for densification. The SiC rich skeleton structure consists of reticulated pores which are completely regular but non-uniform and repeatable. The data with a certain range of values in Table 1 reveals non-uniform internal structure as well as existance of other oxides. High tortuousity with porous and permeable structure of SiC foam is exceptionally rigid and durable. Relatively higher elastic modulus and compressive strength values result into certain stiffness and hardness that fulfil the requirements for underwater cases and/or covers of naval mines. Standart measure of their porosity and tortuousity is their ppi (pore-per-inch) value and it is regulated via initial polyurethane open cell foams. Such a structure of open celled SiC foam ceramics is tought to be a reasonable solution for acoustical impedance mismatch problem at the interface between pores and its surrounding. Highly tortuous, reticulated and non-uniform pore structure may lead to considerable penetration of acoustic waves through the connected i.e., open pores.

Nikon XTH 225 microfocus CT systems is used to characterize and inspect the details of SiC porous inner structure (Fig. 2).

Fig. 2
figure 2

CT System and the SiC high porosity component for high resolution inspection

Full size image

As can be seen in Fig. 3, reconstructed tomography photographs show 3D CT scanned open celled SiC high porosity inner structure. It should be noted that those colored portions represent pores while grey skeleton in between represents SiC frame. Layer by layer inspection of the inner structures is given in Fig. 4. Open celled direct pathways (dotted yellow lines) and those grey skeleton frame demonstrates the highly tortuous structure. In this regard, geometric tortuosity, tg, as the ratio of the average length (dotted red lines), Lg, of the geometric pathway through the pores to the straight-line length, Ls, across the pores (therefore, tg > 1) can be expressed as follows [21]:

$${\text{tg }} = {\text{ Lg}}/{\text{Ls}}$$
(1)
Fig. 3
figure 3

3D CT scanned SiC high porosity structure. Note that, coloured portions represent pores

Full size image
Fig. 4
figure 4

Representative layer by layer cross sectional view of the highly tortuous inner structure. Note that, yellow dotted straight lines are, Ls while red dotted lines are Lg

Full size image

Based upon the inner structure depicted as cross sectional layer by layer representation, geometric tortuosity is estimated to be 1.25–1.41.

As seen in Figs. 1 and 3, SiC foams used in this study have tortuous, reticulated structure with open, non-uniform pores. The structure is fully densified via controlled sintering cycle at high temperature.

2.2 Underwater acoustic testing

Measuring acoustical characteristics of materials may vary according to the environment in which the process are carried out. Acoustic testing pools, small lakes, water filled impedance tubes and natural marine environments are the best tools for evaluation of acoustical characteristics of any materials [27, 28]. Although impedance tubes have some advantages in terms of small sample sizes and short testing span and easy applicability, only limited frequencies can be employed in acoustic tests. The acoustical testing equipment’s capability is the limitation for the acoustical measurements. In other acoustical testing facilities, the scale of test frequencies may vary in a substantially wide range [29, 30]. On the other hand, an impedance tube can also be utilized to measure reflection losses and sound absorption coefficient in an absorptive structure. Furthermore, experimental results showed that measurements in liquid medium presents difficulties and scattering properties are unmeasurable [31]. In this regard, it is also shown that diffraction of acoustic waves through their edges complicates the correct acoustical measurements of transmission and reflection. Roux et.al., presented a three-point panel measurement technique for the determination of scattering coefficients and edge diffraction in an open water tank[32]. In another study related to such factors, Szabo and Bent applied an alternative panel mounting system, in which the panel was surrounded in a reflective baffle[33]. In this study, even tough there is a better agreement with the theoretical data, the results were recorded for small aluminum panel of size of 152 mm. Piquette reported a new method for correcting edge‐diffraction problem and decoupling materials forthis purpose is presented[34]. The new method was demonstrated in the frequency range of 500–11.000 Hz, and utilizes staged transient suppression in its implementation. In this respect, using specially designed hard ceramic material i.e. SiC panel of sizes 500 mm in this study, it is found that the edge diffraction also highly effects measurements. In this regard, transmission values were taken at two different position (The Hydrophone #2 and #3) along with additional measurements with certain angles for scattering and/or diffraction. Transmission and reflection measurements with angles of 30° and 60° are conducted in this study to shed some light on scattering and diffraction problems.

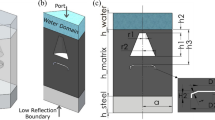
The acoustical test pool for this study is 8,2 m × 4 m × 4,2 m in dimensions. Besides, this acoustical testing pool has a positioning system in order to locate the various sensors and test plates. The contribution of salinity and temperature changes on the acoustical signature is neglected for the estimation of scattering, reflection and transmission values. The acoustical test pool filled with tap water and temperature inside the pool is kept constant (13 °C). The fluctuation and bubbling occured inside the pool hamper the stability of measurements during the exchange of reference steel test plates and SiC ceramic foam plates. All the values are recorded after getting stable values via oscilloscope.

2.3 Frequency ranges used in underwater acoustic tests

Theoretically, mine countermeasure operations are consist of four basic phases respectively[2]: i. Detection, ii. Classification, iii. Identifying and iv. Neutralization. Mine hunters has to conduct the detection phase first to carry out the other upcoming phases. Mine detection sonars are used for finding underwater objects in the detection phase of mine counter measure operations. Thus, 372 MCM ships in commisioned/decommissioned ranks in NATO are examined to deduce the test frequencies. Those 162 ships out of 372 total are mine hunting ships specifically equipped with mine detection sonars such as DUBM-20B, DUBM-21, Type-2193, Type-2093, SQQ-32, DSQS-11. These detection sonars are examined in details and it is found that widely used frequency scales are 80 kHz, 85 kHz, 90 kHz, 95 kHz and 100 kHz. These frequency scales are designated as reference frequencies in this investigation. [3, 13]

2.4 Acoustical testing set up

Contrary to the air acoustics field, there is an obvious lack of military standard available for testing underwater sound absorption materials. The main reason for the gap pertains to the classified military applications that have utmost importance for security purposes. In this regard, all navies prefer to use their own testing standards to ensure the security of their applications [35].

The acoustical set up consists of two sections as, outside of the test pool and inside the test pool. An acoustical signal generator and an oscilloscope (Tektronix mso2014 mixed signal) generates the outside acoustical section. The underwater section consists of a transducer and five hydrophones inside the pool for measuring scattering, reflection and transmission data of test plates as shown in Fig. 5 All the equipments were calibrated in advance so as to avoid miscalculations.

The signal generator transmits short acoustical pulses (400 µs) in assigned frequencies and the values formed on hydrophones are recorded individually as separate RMS values in millivolt through the oscilloscope. All the tools for measurement inside the pool and central point of the plate are positioned in the same direction and fasten to the pool’s bottom [9]. The locations of acoustic testing equipment and test plate is shown in Fig. 5.

Fig. 5
figure 5

Locations of the acoustic testing equipment and test plate

Full size image

3 Results

3.1 Acoustical measurements

In general, stainless steel in different shapes and sizes is the dominant material used for underwater naval systems and conventional weapons. In this regard, a stainless steel test plate with dimensions 50 cm × 50 cm × 2 cm is selected to obtain reference values and the position of this plate is shown in Fig. 5. All the reference values are obtained in assigned frequencies through acoustic testing equipment. The acoustic testing procedure for SiC foam ceramic plates has carried out afterwards. The main function of the located hydrophones is indicated below:

HYPH #1: Measurement of reflection,

HYPH #2 and #3: Measurement of transmission,

HYPH #4 and #5: Measurement of scattering values in 60° and 30°

3.2 Data Obtained on the reference steel plate

Acoustical testing procedure is executed on the reference sample in dedicated reference frequencies and recorded data are shown in Table 2.

Table 2 Measurements on the reference steel plate
Full size table

3.3 Data obtained on porous SiC foam plate

Acoustical measurements are executed on the porous SiC foam ceramic plate in assigned reference frequencies and recorded data are shown in Table 3.

Table 3 Measurements on the porous SiC ceramic foam plate
Full size table

Acoustical measurements initially commenced with the reference stainless steel test plate and continued with the measurement on SiC ceramic foam plates afterwards. The measurements of SiC ceramic foam plate carried out naked and with the nylon threads and camouflage fabrics in order to observe the effect of nylon threads and camouflage fabrics on measurements. No significant change was observed. The fluctuation and bubbling occurred inside acoustical test pool hamper the stability of measurements during the exchange of reference steel plate and SiC ceramic foam plate. All the values are recorded after getting stable values via oscilloscope. Acoustical measurements in the 80 kHz-100 kHz frequency range are compared and evaluated with the reference stainless steel plate since acoustical reflection, transmission and scattering measurements for such materials are lacking in literature. The data comparing measurements against reference steel plate in Table 4 also shows the percent differences on average values.

Table 4 Data comparing measurements against reference steel plate
Full size table

3.4 Data obtained on the hydrophone # 1 (reflection)

Hydrophone # 1 is employed to obtain reflection data on the reference steel plate and SiC foam plate respectively. The measured values is shown in Tables 2 and 3.

As can be revealed in data, reflection measurements on reference steel plate and SiC foam plate vary for all assigned frequencies. It is observed that reflection values of SiC foam plate is lower in 80 kHz and 85 kHz (40% and 30% lower) in comparison with the reference steel plate. In the 90 to 100 kHz band, there is only a small difference between the measured values for steel plate and SiC panel most probably due to hard and stiff internal structure of SiC ceramic reflecting the incident waves. As of the average reflection data shows that SiC plate’s reflection is 19.2% lower compared to the steel test plate.

3.5 Data obtained on the hydrophone # 2 and hydrophone # 3 (transmission)

Hydrophones # 2 and # 3 are employed to obtain transmission data on the reference steel plate and SiC foam plate respectively. The measured values are shown in Tables 2 and 3. As can be seen for the Hydrophone # 2, transmission measurements on reference steel plate (31,6–99 millivolt range) and SiC foam plate (3,9–9,1 millivolt range) vary for all assigned frequencies. It is observed that transmission values of SiC foam plate is much lower (average 90,5% lower) in comparison with the reference steel plate. It is most likely that the transmitted acoustical energies are scattered and absorbed within the complex porous structure of the SiC ceramics.

Transmission measurements for the Hydrophone # 3, on reference steel plate (45,8–103 millivolt range) and SiC foam plate (1,2–3,3 millivolt range) vary for all assigned frequencies. It is observed that transmission values of SiC foam plate is much lower in comparison with the reference steel plate (average 96% lower i.e. even lower than the hydrophone # 2). Transmission data obtained from measurements on hydrophone # 3 and # 2 reveal approximately similar values (90,5% and 96% lower compared to steel plate).

Transmission coefficient values on the Hydrophone #2 and #3 as the ratio of direct mesured incident wave values (i.e. without test plate) given in Table 4 reveal drastic decreases.

3.6 Data on the hydrophone # 4 and hydrophone # 5 (scattering at 60° and 30°)

Hydrophone # 4 is employed to obtain scattering data at 60° on the reference steel plate and SiC foam plate respectively. The measured values is shown in Tables 2 and 3.

Scattering measurements on reference steel plate and SiC foam plate vary for all assigned frequencies. It is observed that scattering values of SiC foam plate is lower (78,4% lower) in comparison with the reference steel plate.

Hydrophone # 5 is employed to obtain scattering data at 30° on the reference steel plate and SiC foam plate respectively.

Scattering measurements on reference steel plate and SiC foam plate vary for all assigned frequencies. It is observed that scattering values of SiC foam plate is lower (68,6% lower) in comparison with the reference steel plate with exception of 13,8% lower data point at 95 kHz.

Scattering coefficient values on the Hydrophone #4 and #5 as the ratio of direct mesured incident wave values (i.e. without test plate) given in Table 4 reveal considerable decreases.

4 Theoretical results

4.1 Sound pressure level (SPL)

Since voltage outputs of microphones and hydrophones generally used in acoustic measurements are proportional to pressure, SPL has wide range of use. It is considered most desirable choice to measure both continuous and pulsed sounds. Three different pressures, which are 20μPa, 1 μbar and 1μPa, are commonly used as reference pressures in the field of acoustics and 1μPa is used as standart reference pressure for water [18, 27, 36].

The Receiving Voltage Response (RVR) of a microphone is defined as the output voltage generated by the transducer per μPa of sound pressure as a function of frequency[36, 37]. It is described by following equation where Vout is the output voltage, P(d) is the acoustic pressure in spesific distance.

$$RVR(f)=20\mathrm{log}(\frac{{V}_{out}}{P(d)})\left[dB re \frac{V}{\mathrm{\mu Pa}}\right]$$
(2)

For the tests omnidirectional calibrated hydrophones (receiving voltage response − 174 dB ± 3 dB re 1 V/μPa) is used. Eq. (2) is used to calculate acoustic pressures for each frequency and calculated acoustic pressures are given in Table 5.

Table 5 Sound pressure sensed by each hydrophone for steel plate/ SiC ceramic foam plate
Full size table

SPL values ares calculated with following formula where where P is sensed the acoustic pressure, and Pref \((1{\mu}\mathrm{Pa})\)) is the reference sound pressure and given in Table 6.

Table 6 SPL values for steel plate/ SiC ceramic foam plate
Full size table
$$SPL\left[dB\right]=20\mathrm{log}\left[\frac{P}{{P}_{ref}}\right]$$
(3)

Another aspect is considered to validate acoustic pressure. The microphone is a transducer that converts the sound pressure into the output voltage. The Voltage Level (VL) is used in terms of voltage units in millivolts per pascal into an open circuit. Due to the conveniences afforded by dB scale, electrical quantities are often specified in term of levels such as Voltage Level (VL) is defined by following as where V is the voltage value corresponding to VL and Vref is 1 Volt.

$$VL (re {V}_{ref}) =20\mathrm{log}\frac{V}{{V}_{ref}}$$
(4)

In complete analogy, an acoustic source is characterized by a source sensitivity and source sensitivity level is given by following where P is the acoustic pressure sensed at specified location and Sref is a reference sensivity which is 1μPa/V.

$$SL(re {S}_{ref}) =20\mathrm{log}\left[\frac{P/V}{{S}_{ref}}\right]$$
(5)

As a result of Eqs. (2 and 5), same results are obtained in terms of SPL.

4.2 Acoustic impedance and transmission coefficient

The ratio of acoustic pressure to the associated particle speed in medium is the specific acoustic impedance and calculated by following equations where ρ is density of the material, c the sound speed on it and Y Young Modulus of the material [36].

$$Z=\rho c$$
(6)
$$c= \sqrt{\frac{Y}{\rho }}$$
(6)

The acoustic impedance of the medium (water), steel plate and SiC ceramic foam is given in Table 7.

Table 7 Acoustic impedance of the medium (water), steel plate and SiC foam
Full size table

Transmission coefficient is calculated by the equation below [38] and given in Table 8:

Table 8 Transmission coefficients of the medium (water), steel plate and SiC foam
Full size table
$$T= \frac{4*({Z}_{1}{Z}_{2})}{{{(Z}_{1}{Z}_{2})}^{2}}$$
(8)

4.3 Insertion Loss (TL)

Insertion Loss (TL) represents the amount of energy loss afrer the insertion of an acoustic barrier like a steel and SiC foam plates and helps to check if an acoustic barrier is effective to attenuate specific sound sources. IL described through the following equation where SPL0 is the SPL before the insertion of the acoustic barrier and SPLa is the SPL after the insertion of it [39].

$$IL \left[dB\right]=SP{L}_{0}-SP{L}_{a}$$
(9)

SPLa is given thanks to the measurements made in Hydrophone 2 and Hydrophone 3 as they described the resulting sound pressure level after the insertion of the acoustic barrier (steel and SiC Foam plates); SPL0 can be estimated from a common propagation of sound through water[36]. In this case free field underwater assumption is considered where the reflections of the walls of the pool are not considered and source is omnidirectional. This propagation model considers the sound intensity equation having the following process:

$$\begin{gathered} \frac{W}{{4\pi r^{2} }} = \frac{{p^{2} }}{{\rho_{0} c_{0} }} \hfill \\ \frac{{W \rho_{0} c_{0} }}{{4\pi r^{2} p_{ref}^{2} }} = \frac{{p^{2} }}{{p_{ref}^{2} }} \hfill \\ 10\log \left( {\frac{{W \rho_{0} c_{0} }}{{4\pi r^{2} p_{ref}^{2} }}} \right) = 10\log \left( {\frac{{p^{2} }}{{p_{ref}^{2} }}} \right) \hfill \\ SPL = 10\log \left( W \right) + 10\log \left( {\frac{{\rho_{0} c_{0} }}{{4\pi p_{ref}^{2} }}} \right) - 20\log \left( r \right) \hfill \\ \end{gathered}$$
(10)

The previous equation describes the SPL at any medium knowing the sound velocity and density of that medium. This equation though, does not consider the attenuation due to the transmission of sound in the medium, just due to the distance from the source; the propagation loss (PL) of sound takes into account the amount of energy attenuated due to its transmission in water, allowing this way that the final estimation of the SPL is calculated from the following equation.

$$SPL= 10\mathrm{log}\left(W\right)+ 10\mathrm{log}\left(\frac{{\rho }_{0}{c}_{0}}{4\pi {p}_{ref}^{2}}\right)-20\mathrm{log}\left(r\right)- \alpha r$$
(11)

where αr is the absorption of sound in water due to transmission at a distance r (in km) from the source, α is the absorption coefficient of water in following equation.

$$\alpha =\left(\frac{\mathrm{0,08}}{\mathrm{0,9}+{f}^{2}}+\frac{30}{3000+{f}^{2}}+4*{10}^{-4}\right)*{f}^{2}$$
(12)

It is possible to calculate expected SPL at a certain position using Eqs. (11 and 12) before the insertion of the acoustic barrier in order to calculate the insertion loss of it. In this case it is considered the position of Hydrophone 3 as it is the closest to the barrier; this hydrophone is located at r = 2,145 m away from the source on axis with it. Following this IL estimated for each barrier is shown in Table 9.

Table 9 Insertion Loss (IL) for each barrier
Full size table

4.4 Transmission loss (TL)

Transmission Loss (TL) could be calculated from the IL estimations considered in as this one takes into account the model of sound propagation after the insertion of the barrier, having the following equation resulting from the Eq. (11) before the barrier where SPLi is the sound pressure level after the insertion of the barrier considering one of the possible sound trajectories through the barrier, \(10\mathrm{log}\left(\large\frac{1}{\tau +ab}\right)\) is the effect of the barrier, where ab is known as the barrier coefficient that has a value of 0,04 for high frequencies, τ is the transmission coefficient that describes the amount of energy transmitted after transferring a partition [39].

$$SP{L}_{i}= 10\mathrm{log}\left(W\right)+ 10\mathrm{log}\left(\frac{{\rho }_{0}{c}_{0}}{4\pi {p}_{ref}^{2}}\right)-20\mathrm{log}\left({d}_{i}\right)- \alpha {d}_{i}-10\mathrm{log}\left(\frac{1}{\tau +ab}\right)$$
(13)

In Eq. (13), r is replaced with di, because every possible sound trajectory that arrives to the study point must be considered. In this case, there are 4 trajectories that diffract after arriving the barrier which are the same as the source and the point of study (position of Hydrophone 3) are located at the center of the whole barrier. Following this idea, the resulting SPL that is sensed by Hydrophone 3 is the result of the superposition of 4 sound trajectories that are the same, each one of them are calculated by Eq. (13), so, it is possible to say that, as all of the trajectories are the same, it is logical to expect that SPLi is going to be the same for the 4 trajectories, having here that the SPL of one trajectory, in relation to the SPL sensed by the Hydrophone 3 is described by following equation.

$$SP{L}_{a}=10\mathrm{log}\left(4*{10}^{\large\frac{SP{L}_{i}}{10}}\right)$$
(14)

Equations (13 and 14) is used to find the relation between the \(SP{L}_{a}\) (i.e. SPL sensed by hydrophone 3) and \(\tau\) to find the TL.

$$\large\tau =\frac{1}{\large{10}^{\frac{10\mathrm{log}\left(W\right)+ 10\mathrm{log}\left(\frac{{\rho }_{0}{c}_{0}}{4\pi {p}_{ref}^{2}}\right)-20\mathrm{log}\left({d}_{i}\right)-\alpha {d}_{i}-SP{L}_{i}}{10}}}-ab$$
(15)

In case that τ is negative, it means that the most amount of energy is absorbed and not transmitted, so for porous materials (like SiC Foam), ab can be despised and τ is recalculated without this value by following equation and tabulated in Table 10.[39].

Table 10 Transmission Loss (TL) for each barrier
Full size table
$$TL=10\mathrm{log}\left(\frac{1}{\tau }\right)$$
(16)

5 Discussion

The measurements of SiC ceramic foam plate carried out naked and with the nylon threads and camouflage fabrics in order to observe the effect of nylon threads and camouflage fabrics on measurements. No significant change was observed during both measurements. It is estimated that of nylon thread and camouflage fabric act transparent due to their thin form (0,1 mm).

The values shown in Tables 2 and 3 is sum up and shown in Table 4. In this, all the measurements values for reference steel plate and SiC foam plate concerning reflection, transmission and scattering are given along with difference in millivolt and as percentage. The SiC foam ceramic plate leads a 19,2% reduction in reflection, 90,5% and 96% lower values are obtained in transmission and 78,4% and 68,6% lower values are obtained at 60° and 30° in scattering compared to the reference steel plate. It is considered that the open pores in the SiC ceramic plate and tortouse structure leads a considerable reduction and it can be assumed that the scattering angle doesn’t have a considerable affect on amplitudes in comparison with the structure of the media.

Transmitted amplitudes for reference steel plate are lower or almost the same (for 80 kHz and 95 kHz) in the Hydrophone # 3 in comparison to the Hydrophone # 2. Incident wave looses its energy while passing through the rigid structure of steel plate and can’t prevent its own acoustic energy from dissipation in order to be able to travel from the Hydrophone # 3 to the Hydrophone # 2. In other words, amplitude attenuation dissipated in direct proportion to distance. On contrary, transmitted amplitudes for SiC foam are always lower in the Hydrophone # 3 in comparison to the Hydrophone # 2. Amplitude attenuation dissipated in inversely proportional to distance. It can be assumed that either the porous structure of the SiC foam or erratic movements of incident wave lead the inversely proportional increase of amplitude attenuation in the Hydrophone # 3 in comparison to the Hydrophone # 2. Reflection from pool’s floor unlikely affect amplitude attenuation, but is not completely excluded.

It can be assesed from the experimental results that SiC ceramic foam is a good acoustic transparent material for water-borne applications with its perfect impedance matching in water.

Sound absorbing performances revealed as lower reflection, transmission and lower scattering at 60° and 30° are due to very complex porous and tortuose structure of SiC foams and scattering through open holes, intrusions and cavities.

Very recently, studies on the various porous sound absorption materials have started to be revealed concerning the sound absorption performances and theories[16, 17, 35]. There have been very limited investigations conducted on such open-celled foam structures. In one of the studies, using air-saturated open-celled SiC foam, impedance match between the foams and water is comparatively good with thickness of 90 mm and pore size of 1 mm [17]. Due to the multiplicity of interfacial surface and junctions within structure, it's to highlight it's exceedingly hard to model sophisticated materials [5]. “Tortuosity” is one of the major parameters however highly complex and meandering in this sense and it would be speculative to set a thorough model to describe its acoustical behaviour [21].

Xu et al. reported that silicon oil filled SiC ceramic foam in the low frequency band (eg.750–4.000 Hz) showed a significant underwater acoustic absorbtion performance. Enhanced sound absorbency at low frequency is also revealed for the foams partially filled with water. It is found that a full saturation with water is deteriorating the underwater absorption performance of the SiC foam ceramics due to impedance mismatch at the interface [17].

The publications on underwater sound absorption concerning open porosity SiC foam structures may not neccassarily carry out a direct evaluative comparison with this current study.

As for the transmission measurements of 90,5% and 96% lower values compared to the steel reference plate demonstrate a desirable coupling between water and foam. As for the scattering measurements at 60° and 30°, 78,4% and 68,6% lower values compared to the steel reference plate are also good indications for improved impedance at the interface.

Calculation of the transmission coefficient through the impedance of the layer and the medium considering this at the single interface (when sound strikes from the water to the layer of the material before trespassing this material) it should be expected that the SiC ceramic foam should have more transmission loss than the steel plate as the SiC ceramic foam has more acoustic impedance than the steel plate. Transmission coefficient for the steel plate is higher due to its lower acoustic impedance, this means that it is expected that sound energy is highly transmitted through the plate (i.e. low values of TL), meanwhile, for the SiC ceramic foam, sound is less transmitted through the partition than the steel one, which means that transmission loss is expected to be higher with SiC ceramic foam. These calculations complements the experimental results which are obtained from hydrophone 2 and hydrophone 3.

In this regard, the novelty and originality of the open-celled SiC foam ceramic structure applied through this study may affect upcoming interest in sound absorption studies for naval mine countermeasure systems.

6 Conclusion

The assessments can be presented and summarized based on the data gained and accumulated during acoustical tests as follows:

  • An open-celled, tortous and porous SiC ceramic foam structure lead a considerable decrease in transmission, scattering and reflection based on underwater acoustic tests. It might be a potential candidate for decreasing acoustical signature and useful for the underwater naval applications required for lower acoustic signature.

  • It is observed that measurements on reference steel plate and SiC foam plate vary for all assigned frequencies. The porous characteristic of the SiC ceramic foam is considered as main factor of the difference. Also, reflecting sound waves from acoustic testing pool’s walls might cause a diversity as well.

  • The fluctuation and bubbling occured inside acoustical test pool hamper the stable execution of measurements during the exchange of reference steel plate and SiC ceramic foam plate.

The current study can be interpreted as a first step in the research on underwater sound properties of SiC foam ceramics in the range of 80 kHz to 100 kHz in acoustic test pool environment. Despite a number of studies examining the acoustical behaviors of SiC foam ceramics via impedance tube, there is an obvious lack of experimental studies exploring underwater behavior of highly porous and tortuous SiC foams above the frequencies limited by the impedance tube. In addition to this, as an limitation, contrary to the air acoustics field, there is an obvious lack of military standard available for testing underwater sound absorption materials. The main reason for the gap pertains to the classified military applications that have utmost importance for security purposes.

In conclusion, an original and novel design of open porosity SiC ceramic foam structure is applicable for underwater reflection, transmission and scattering processes. It is also observed that SiC ceramic foam materials with open-cell porous structure has lower values in terms of transmission and scattering. (as for the transmission measurements of 90,5% and 96% lower and as for the scattering measurements at 60° and 30°, 78,4% and 68,6% lower values compared to reference steel plate). It has a considerable potential to be utilized as a cover/case material for the naval applications to reduce naval mines’ acoustical signature against detection and future research could further focus on the the effects of SiC foam ceramic's thickness and porousity in same frequency ranges.