1 Introduction

The differential amplifier is one of the essential building blocks of electronic systems, commonly designed using operational amplifiers [1]. However, there are various advantages of using transistors to design this differential amplifier, namely higher input and output impedance. An operational amplifier comprises transistors, where transistors are designed to be a differential amplifier at the input terminals [2]. Thus, it is an alternative design method and component that may help to improve products for specific applications. The basic BJT and MOSFET-based differential amplifier consists of two transistors and two resistors and has been further developed by replacing the resistors with transistors. The advantages include its inherent single-ended output, improved Common-Mode Rejection Ratio (CMRR), and greater output impedance [3,4,5]. For cryogenic applications, Zavjalov et al. [6] have designed a differential amplifier for temperatures below 4 K (− 269 °C), while evaluating various parameters such as differential and common-mode gain at different temperatures to verify the design integrity at this level of application. A clear design process and circuital information were provided, showing the addition of a cascade input stage to reduce the Miller effect and voltage follower at the output stage to reduce the output resistance of the amplifier for their application.

A differential amplifier is often utilized with a current mirror to provide adequate current drive, preventing resistors from being the only current-limiting components. Deo et al. [7] have realized the effect of different current-mirror topologies affecting the differential amplifier’s performance. It has been found that the Widlar current mirror exhibits a larger CMRR but the smallest differential gain. In contrast, an active loaded differential amplifier exhibits the most significant differential gain but has an inferior CMRR w.r.t. the Widlar current source. Aziz et al. [8] have proposed a 90 nm single-stage FGMOS amplifier design. The scope of this work has helped highlight the main parameters that new amplifier design should focus on. AC analysis and slew-rate investigations were conducted, which shows a change. A simulation-based model was proposed and tested. Hashem [9] has designed an NMOS differential amplifier with passive loading using a modified Wilson current mirror. The output power which can be produced is 6.66 mW with an output resistance of 2.297 MΩ, observed from the current mirror. A considerable CMRR of 33.35 dB was obtained from this design.

Garcia-Perez et al. [10] have highlighted the need for differential amplifier design as part of an aperture array. Investigating various differential amplifier topologies, the gain of a balanced differential amplifier for a 50 Ω input was much higher than the gain of a fully-differential amplifier, where the minimum gain of the balanced topology was measured at 39 dB, and the maximum gain of the fully-differential topology was approximately 35 dB for a bandwidth of 1.3 GHz. Kabiri and Mokhtari [11] have used a differential amplifier to design Multi-Varied Logic (MVL) circuits, where the differential amplifier built uses a supply voltage of 0–5.5 V, as a dual-supply is used to improve the development of digital devices. Jain et al. [12] have implemented a two-stage differential amplifier using stacked transistors for bio-medical applications. Implemented in cadence and designed with a 45 nm CMOS process for a supply voltage of 0.85 V, the CMRR was measured at 178 dB at 100 Hz and power dissipation of 1.5 μW. It is inevitably noted these measurements prove their design is greatly efficient.

From the literature review, the parameters that must be paid careful attention to, involve the supply voltage (minimization of the maximum supply voltage and minimum supply voltage, to reduce power consumption), differential and common-mode gains, and resulting CMRR (differential gain should be maximized according to application requirements and be stable over a frequency range, whereas the common-mode gain should be minimized, resulting in a higher CMRR) [13].

These discussions show that the differential amplifier can always be improved in various aspects for many applications. In this research work, a differential amplifier has been designed and fabricated using the Double-Gate (DG) MOSFET. Authors have chosen this transistor in sight of the acceptance of the simulation-based model [14]. It also overcomes the Short-Channel Effects (SCEs) that arise as the downscaling is performed on transistor channel lengths [15]. SCEs include threshold voltage roll-off (decay of the threshold voltage due to a decrease in gate length) [16], subthreshold slope degradation, an increase in the OFF-current slope of the MOSFET, which contributes to leakage current [13, 16]. These non-ideal effects are a result of a decrease in the channel length of MOSFET devices, reducing the magnitude of the electric field present in the MOSFET [17]. However, modeling of the drain current and transconductance of the DG MOSFET has proven challenging, as equations and polynomials at the sub-micron level prove difficult to be computationally efficient and accurate [17]. For this reason, ICs have advanced by using multi-gate transistors, such as DG MOSFET, Tri-Gate MOSFET, and Pi-Gate MOSFET [18,19,20].

Pillay and Srivastava [20] have realized that the DG MOSFET provides twice the drain current flow compared to the traditional MOSFET, which improves various circuit parameters, increasing the device performance, and efficiency of the source follower circuit. Two dual-gate MOSFET source follower models, using DC and AC analysis, were realized in this work. In further advancement of that work, in this present research work, an active-loaded differential amplifier has been designed using a prototype set up to assess the differential gain, common-mode gain, frequency response, and CMRR [21]. The differential amplifier was previously designed by Pakaree and Srivastava [22] have examined the resistive-loaded model using the DG MOSFET. However, to extend that work, the authors have investigated the proposed design of a differential amplifier using the active-loaded differential-amplifier topology. Pillay and Srivastava [21] have presented a simulation-based design for this model.

In continuation of the work in [21], this present work highlights the design steps to construct an active-loaded differential amplifier using the DG MOSFET. Using this design process and the desired set of functional requirements, a design process that includes the respective biasing values of voltages, current, and component values has been presented. This paper has been organized as follows. Section 2 has materials and methods. Section highlights the design methodology of the differential amplifier. This includes biasing information and required resources. Section 4 provides a detailed analysis of testing and the results, including slew rate with comparative analysis with existing models. Finally, Sect. 5 concludes the work and recommends the future aspects.

2 Materials and methods

The Operational Amplifier (op-amp) is the most common component used in designing a differential amplifier [23]. Using two inputs and a single output provides a robust and efficient solution in subtracting two signals, fulfilling the purpose of a differential amplifier. However, under the hood, an op-amp utilises transistors to construct the native differential amplifier, along with other circuital building blocks, e.g., cascode stages and class-AB amplifiers [24]. There are two common differential amplifier topologies: the active-loaded and resistive-loaded differential amplifier [25]. For ease of use and design restrictions, a resistive-loaded differential amplifier is usually an attractive option, as it consists of two transistors and two resistors. This can be seen in Fig. 1a, where the RD is the drain resistance and M1,2 are the transistors used. A differential input voltage is applied to both transistors, and the differential output voltage (Vo1 and Vo2) can be given by [17]:

$${\text{V}}_{{{\text{OD}}}} = {\text{A}}_{{{\text{vd}}}} \left( {{\text{V}}_{{{\text{i}}1}} - {\text{V}}_{{{\text{i}}2}} } \right)$$
(1)

where, Avd is the differential gain. A single-ended output can be taken from any output terminal (Vo1 or Vo2) and ground (GND) and will be half the value of the differential output voltage given in Eq. (1).

Fig. 1
figure 1

a Resistive-loaded, b active-loaded differential amplifier

Full size image

The differential gain of this amplifier is determined by the transconductance gm and the value of the RD:

$${\text{A}}_{{{\text{vd}}}} = {\text{g}}_{{\text{m}}} {\text{R}}_{{\text{D}}}$$
(2)

This topology was utilised in designing the differential amplifier [22], and analysed accordingly, exhibiting a differential gain of 8.69 V/V from simulation results. Expounding on this work, the authors have designed an active-loaded differential amplifier using the DG MOSFET. The active-loaded topology can be seen in Fig. 1b, where a single-gate MOSFET was used. Where the differential gain Avd can be given by:

$${\text{A}}_{{{\text{vd}}}} = {\text{g}}_{{\text{m}}} \left( {{\text{r}}_{{{\text{o}}2}} //{\text{r}}_{{{\text{o}}4}} } \right)$$
(3)

which shows ro2 as the output resistance of T2 and ro4 is the output resistance of T4.

In designing and analysing the active-loaded differential amplifier, the following comparisons and advantages/disadvantages (over the differential amplifier designed by [22]) have been noted, which motivate the study of the active-loaded topology:

  • An improved CMRR is aided by the negation of non-ideal effects posed by passive-loads (resistors), such as resistor mismatch [3]. However, active loads (transistors) also introduce transconductance (gm) mismatch.

  • An inherent single-ended output, which aids in circuit design and simplification of IC and Very Large Scale Integration (VLSI) design.

  • It can be realized that common op-amp schematics from popular semiconductor manufacturers [26], such as the LM741 from Texas Instruments, LA6500 from ON-Semiconductors, and the LT1213 from Analog Devices be seen that an active-loaded topology is evidently used in all these op-amps with no use of the resistive-loaded topology.

In assessing the points above, a design process highlighting the use of the DG MOSFET in an active-loaded topology will provide a valuable reference. It can allow engineers to possibly replace the single-gate MOSFET in operational amplifiers and differential amplifier design as a whole. The DG MOSFET is a four-terminal component with a drain, source, and two gates (gate 1 and gate 2). The planar structure can be seen in Fig. 2.

Fig. 2
figure 2

The planar structure of Double-Gate MOSFET (S: Source, D: Drain, G1 and G2: Gate-1 and gate-2, SiO2: Silicon di-oxide) [2]

Full size image

In this application’s biasing of the DG MOSFET, authors are constantly driving the DG MOSFET into saturation to provide stable amplification; hence, the body (or back-gate) of the DG MOSFET is connected to the source internally [2, 27, 28]. The body effect, which is responsible for potentially altering the threshold voltage of a MOSFET, can only be considered when VBS (VBody − VSource) < 0. The differential gain (using circuital components) achieved is 2 V/V at a cut-off frequency of 1 MHz. The input DC-offset range is 1–100 mV with an input peak-to-peak voltage range of 500 mV. These were achieved with drain current ID = 3 mA (under no-load conditions). To design the prototype, four BF998 DG MOSFETs have been used, with a 5 V, 0.5 A supply voltage.

3 Design methodology

  1. (1)

    Common-source amplifier design using DG MOSFET.

To simplify the amplifier’s design, one may realise the differential half-circuit of the schematic shown in Fig. 2 resembles a common-source amplifier. Figure 3 shows the basic layout for a common-source amplifier using a SG MOSFET [3]. A pseudo-schematic has been depicted in Fig. 4, showing the common-source amplifier using the DG MOSFET [29, 30].

Fig. 3
figure 3

The basic layout of the common-source amplifier using the SG MOSFET [3]

Full size image
Fig. 4
figure 4

Pseudo-schematic of common-source amplifier using DG MOSFET

Full size image

From ref. [21], a dual-rail power supply ± 12 V has been used. To reduce power consumption by removing the negative rail and further experimentation, a + 5 V single-rail power supply will be used. However, with the power supply at hand, it is rated at 5.89 V. To calculate the power consumption under no-load conditions:

$${\text{P}} = {\text{V}}_{{{\text{DS}}}} {\text{I}}_{{\text{D}}}$$
(4)

where in the worst-case scenario, VDS = 5.89 V and ID = 3 mA, yields a power consumption of 17.7 mW. Here, gate-1 is utilised as an input for RF signals, and gate-2 is utilised for Local Oscillator (LO) inputs. However, gate-2 will solely be used to bias the DG MOSFET for the desired drain current of 3 mA. Since it has been stated the input-offset voltage VINoffset is 100 mV, VG1 = 0.1 V. While using the typical value noted by the datasheet, gate-2-to-source voltage VG2-S = 4 V, VG2 may be specified as 4.4 V. Thus, VS = 0.4 V. From Fig. 4 R6 can be calculated as:

$${\text{V}}_{{\text{S}}} = {\text{I}}_{{\text{D}}} {\text{R}}_{6}$$
(5)

where the voltage at the source VS = 0.4 V, ID = 3 mA, thus R6 = 133 Ω. E12 values of 100 Ω and 33 Ω can be used in series. Low resistance values will be chosen to reduce the minor effects of resistor noise when biasing gate 2 at a voltage of VG2 = 4.5 V. Given the power supply voltage of 5.89 V, R2 = 100 Ω and R3 = 33 Ω. To calculate the value of R5, which is the current-limiting resistor for the drain terminal, the value VDS may be assessed. The DG MOSFET must be driven into the saturation region to ensure stable amplification, thus providing a constraint in choosing a suitable VDS value. To design the common-source amplifier for the specified frequency response, resistor R4 and capacitor C1 may be used to create a low-pass response with the specified cut-off frequency of 1 MHz. If values fc = 1 MHz, C1 = 2.2 pF:

$${\text{R}}_{4} = \frac{1}{{\left( {2{\uppi }} \right)\left( {f_{c} } \right)\left( {{\text{C}}_{1} } \right)}}$$

which yields a value of R4 \(\cong\) 72 kΩ. Using E12 values, 47 kΩ and 33 kΩ will be used in series. This, in turn, exhibits a frequency response with a cut-off of 904 kHz. Capacitor C2 can be chosen as 0.1 µF as a DC blocking capacitor [31,32,33] and C3 can be chosen as 47 µF. Figure 5 shows a prototype of the common-source amplifier. The differential gain of approximately 2 V/V (input signal of 397 mVpk–pk and the output signal of 1.66 Vpk–pk shown in Fig. 6, and a frequency response showing a cut-off frequency of 904 kHz (a reduction in mid-band gain, from 12.36 to 10.50 dB), the design process has been validated as shown in Fig. 7.

  1. (2)

    Differential amplifier design using common-source amplifier half circuits.

Fig. 5
figure 5

Breadboard prototype of the common-source amplifier

Full size image
Fig. 6
figure 6

Gain at 104 kHz, shown to be 4 V/V, as designed

Full size image
Fig. 7
figure 7

Gain at 980 kHz showing expected frequency response from design

Full size image

Figure 8 shows the schematic of the differential amplifier using the common-source amplifier half-circuits, where a single half-circuit is shown in Fig. 4. This may be labeled as the resistive-loaded differential amplifier using asymmetrical DG MOSFETs. The addition of the current source I1 (shown as “I1” in Fig. 8) of 6 mA is a sum of the equal drain currents for DG MOSFET M1 and M2.

  1. (3)

    Active-loading using DG MOSFETs and Widlar current mirror

Fig. 8
figure 8

Schematic of differential amplifier showing chosen component values

Full size image

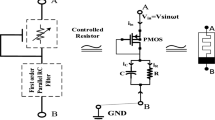
In improving the proposed design in Fig. 8, current-limiting resistors R5 and R7 will be replaced with DG MOSFETs, in unison with a Widlar current mirror replacing the ideal current source I1. This has been shown in ref. [21], which validates the feasibility of the proposed method of current control. The architecture of a Widlar current mirror can be seen in Fig. 9.

Fig. 9
figure 9

Widlar current mirror [3]

Full size image

In the Fig. 9, the drain of Q1 and Q2 is connected to the supply voltage Vsupply (shown in Fig. 8), the current source Iin will be replaced by a resistor Rbias, which would bias the current mirror for the desired current. To calculate Rbias, the drain current of both common-source half-circuits is the sum of 6 mA:

$${\text{R}}_{{{\text{bias}}}} = {\text{V}}_{{{\text{supply}}}} /{\text{I}}_{{{\text{in}}}}$$
$${\text{R}}_{{{\text{bias}}}} = \frac{5.89}{{6 \times 10^{ - 3} }} = 981\Omega$$

To select an E12 value, 1 kΩ will be used. The significance of “active-loading” of a differential amplifier allows the resistors at the drain (or collector for a BJT) to be removed and replaced by current sources which allow the use of a current mirror. Current sources can be modelled using transistors and their output impedance is interpreted as what would be the drain resistances that have been replaced [3]. Configuring the DG MOSFET as a current source can be done using symmetrical DG MOSFETs, where both gate-1 and gate-2 will be connected [34, 35]. Figure 10 provides a bird’s eye view of the breadboard schematic of the proposed differential amplifier. The section enclosed in blue, employs a phase-shift of 180°, to provide a pair of differential signals, injected at the input (blue and yellow arrows, respectively), which are DG MOSFETs M1 and M2, from Fig. 8. The designed differential amplifier can be seen in Fig. 11, encompassed in white. The circuit enclosed in blue denoted the common-source amplifier was designed to provide two signals 180° out-of-phase. The output of the common-source amplifier is a 100 mVpk sinusoid, which forms input-1 of the differential amplifier, shown by the blue arrow. Input-2, shown by the yellow arrow, is the raw input signal from the function generator, which is a 20 mVpk sinusoid.

Fig. 10
figure 10

The circuit arrangement of the active-loaded differential amplifier

Full size image
Fig. 11
figure 11

Experimental setup showing power supply, function generator with a prototype

Full size image

In Fig. 11, the prototype is shown in the bottom-right corner. The orange wire is the power connection (captured in the red box), signal-in is shown by the white wire (captured in a red box), input-1 of the differential amplifier is shown by the blue wire (captured by the blue box), and input-2 of the differential amplifier shown by yellow wire (captured by the yellow box).

4 Testing and analysis with discussions of the prototype design

The testing and other analysis has been performed for the Differential gain and frequency response, Common-mode gain and resulting CMRR, Slew rate measurement.

  1. (1)

    Differential gain and frequency response.

To demonstrate the differential gain of the amplifier, the removal of common-mode (DC) voltages should be shown, where only the difference of the AC components exists at the output [36]. This function demonstrates the functional requirement for a differential amplifier. In the Fig. 11, the input signals of 100 mVpk and 20 mVpk (208 mVpk–pk shown in Fig. 11a, 42 mVpk–pk shown in Fig. 11b are amplified by the gain of 2 V/V, as specified in Sect. 2.A. One may note that calculating VOpk, which would be the peak voltage of the output waveform with the gain applied from Eq. (1)

$${\text{V}}_{{{\text{Opk}}}} = 2\left( {104 - \left( { - 20} \right)} \right) = 248 {\text{mV}}_{{{\text{PK}}}} = 6.02 {\text{dB}}$$

The resulting peak voltage can be seen in the oscilloscope image in Fig. 12 with input-1, input-2, and output of the differential amplifier. Providing a differential gain vs frequency plot to visualise the frequency response, the designed differential amplifier has a cut-off frequency of 1 MHz. In Fig. 13, the frequency response of the constructed differential amplifier has been observed. The bandwidth is noted as 1 MHz (the approximate − 3 dB frequency). Table 1 summarises the testing results of the amplifier.

  1. (2)

    Common-mode gain and resulting CMRR.

Fig. 12
figure 12

Measurement information of a Input-2, b Input-1, c Output of differential amplifier

Full size image
Fig. 13
figure 13

Frequency response of proposed differential amplifier showing distinct − 3 dB response at 1 MHz

Full size image
Table 1 Frequency verses differential output voltage
Full size table

The common-mode gain can be assessed because the differential amplifier has been biased with a DC offset of 100 mV (applied to the input signal). The objective of the differential amplifier is to remove the DC offset applied to the input signals. Common-mode signals may be in electrical noise, which should be suppressed when generating a single-ended differential output signal [3, 36].

To find the common-mode gain, both inputs of the differential amplifier will be injected with the same signal. Figure 14 shows the output signal, which is unchanged for the frequency spectrum as shown in Table 1, where a 4 mVpk output can be seen. Thus, the common-mode gain:

$${\text{A}}_{{\text{V}}} = \left( {\frac{{{\text{V}}_{{{\text{OUTcm}}}} }}{{{\text{V}}_{{{\text{INcm}}}} }}} \right) = \frac{4}{100} = \frac{{0.04{\text{V}}}}{{\text{V}}} = -27.96{\text{ dB}}$$
Fig. 14
figure 14

Common-mode output signal for proposed differential amplifier

Full size image

From this, the CMRR can be calculated and shown in Table 2.

  1. (3)

    Slew rate measurement.

Table 2 Common-mode gain and resulting CMRR for different frequencies
Full size table

The slew rate of an amplifier is an usful parameter that indicates the effect of the parasitic capacitance of the amplifier. It is a large-signal parameter, typically measured in V/µS and is related to the rise time and other transient response parameters [38]. It can be defined as the maximum rate at which an amplifier’s output can change in response to a change in its input [37]. One would expect the slew rate to be directly equivalent to the change in time of the output signal but the slew rate can effectively determine this isn’t the case.

From an analysis into possible slew rate enhancement done by Singh et. al. [39], the fastest slew rate was produced by an Operational Transconductance Amplifier (OTA) using self-cascoded and local feedback techniques which was 158.3 V/µS. Other circuitry tested included a conventional OTA and one lacking the cascade input stage. Using an oscilloscope, a method to estimate the slew rate of an amplifier was described by [40]. This includes measuring the change in voltage over time between 10 and 90% of the signal amplitude. From Fig. 15, where the input signal’s frequency was 100 Hz with a peak-to-peak voltage of 96.8 mV, was injected into the amplifier, the slew rate can be measured as:

$${\text{Slew Rate}} = \frac{\Delta Y}{{\Delta X}} = \frac{{V_{90\% (pk - pk)} - V_{10\% (pk - pk)} }}{{t_{90\% (pk - pk)} - t_{10\% (pk - pk)} }}$$
(6)
Fig. 15
figure 15

Excerpt of oscilloscope measurements showing cursors A and B used for slew rate measurement

Full size image

The slew rate for the above instance would be calculated as:

$${\text{Slew Rate}} = \frac{\Delta Y}{{\Delta X}} = \frac{{0.0872{\text{V}}}}{{4800{\mu s}}} = \, 0.0181\frac{{{\text{mV}}}}{{{\mu s}}}$$

The values used for the computation of the slew rate can be found in Table 3 and it uses Eq. (6) to calculate. For peak-to-peak voltages of 200 mV, 500 mV, and 1 V, the slew rate was computed and presented in Fig. 16. Realizing the slew rate of the differential amplifier, its shortcomings can be observed at a higher frequency (shown by a drastic degradation in its slew rate at 1 MHz) and lower large-signal voltages (demonstrated by the lowest slew rate for 100 mVpeak-to-peak).

  1. (4)

    Comparison of existing topologies and the proposed topology.

Table 3 Slew rate computation for frequencies of 100 Hz–1 MHz for 100 mVpk–pk
Full size table
Fig. 16
figure 16

Slew rates for 100 mV, 200 mV, 500 mV and 1 V

Full size image

To compare this work with the existing work, here in Table 4, a comparative analysis has been given for better understanding.

Table 4 Comparative parameters with the existing work
Full size table

5 Conclusion and future recommendations

This work highlights the design steps to construct an active-loaded differential amplifier using the DG MOSFET. Using this design process and the desired set of functional requirements, a design process that includes the respective biasing values of voltages, current, and component values has been presented. It has been validated that all design requirements have been met from testing the designed differential amplifier. The differential gain of 2 V/V was chosen to exhibit basic amplification of the differential amplifier, along with a frequency range for which the given differential gain should be valid. The common-mode output and gain values were tested, along with the resultant CMRR to assess the overall performance of the differential amplifier designed. The prototype justifies the functional requirements and proves a better design process. The frequency response and slew rate were investigated to establish the differential amplifier's performance in the frequency domain.

The future work will include the design of notable electronic subsystems to expose and improve the shortcomings of the active-loaded differential amplifier, such as differential mixer, Voltage-Controlled Oscillator (VCO), or Low Noise Amplifier (LNA). Designing these devices will introduce the need for optimization of the proposed differential amplifier, e.g., load-carrying conditions would have to be considered. The output resistance must be monitored at high frequencies, RF losses must be assessed and improved to meet functional requirements, etc. A proposed method of improving the input resistance and frequency response includes the addition of a cascade input stage-to improve the input resistance, hence improving the frequency response.