1 Introduction

The vertical vibration and pitch vibration are the key indexes to evaluate the vehicle comfort when the vehicle is running on the uneven road. However, automobile is a complex system, when the stiffness and dam** of the suspension, axle load, and wheelbase are unreasonably designed, the coupling phenomenon of front suspension and rear suspension vibration often occurs, which makes the body have obvious pitching vibration and affects the comfort and health of the driver and passenger [1,2,3,4]. The correlation analysis and decoupling design of vertical vibration and pitching vibration of vehicle body is the basis of improving comfort performance and realizing vibration control. There are more and more related studies, Zhang et al. [5] proposed a mathematical model to describe vehicle dynamics, and used state space theory to study the coupling correlation between substructures. Yang et al. [6] revealed the body pitch effect through the analysis of vibration test data at different positions of the body. Zhou et al. [7] studied the nonlinear characteristics and vibration transfer characteristics of vehicle multi-body dynamics model. The coupled vibration of the human body in transverse, vertical and pitching directions was studied by using the human body model established by Wu et al. in reference [8]. Sun et al. [9] established a mathematical model of the suspension system, and deduced the frequency response function that can evaluate the response variable according to the vibration differential equation of the suspension. The results in Ref. [10] show that the vehicle pitching performance can be improved by optimizing the length and diameter of the air suspension tube.

Vertical vibration is one of the most common vibration forms of vehicles, which can be effectively controlled through the optimization of suspension stiffness and dam**, seat optimization and other measures. Pitching vibration is a kind of vibration form which is sensitive to human body. It should be avoided in the design of vehicle dampin. However, the vehicle is a complex system, and the coupling between vertical vibration and pitching vibration often exists, which aggravates the vibration of the vehicle and reduces the comfort performance of the vehicle, sometimes causing fatigue failure of parts. At present, the research on vehicle coupled vibration is mostly concentrated in the field of theoretical modeling analysis and dynamic simulation, while there are few literatures using experimental methods to analyze vehicle coupled vibration. When the vehicle travels on uneven roads, the phenomena of axle load transfer, suspension deformation hysteresis, dam** nonlinearity, impact between components and so on often occur, the results of theoretical analysis and dynamic simulation can not accurately reflect the vehicle vibration characteristics. Therefore, it is necessary to use the experimental method to analyze the vehicle vibration coupling problem.

In order to improve the comfort performance of vehicle and provide theoretical basis for the body vibration control, the coupling phenomenon and coupling mechanism between vertical vibration and pitching vibration must be studied deeply. In the next section, the mechanism and key factors of vehicle coupling vibration are analyzed by establishing the mathematical model of vehicle coupling vibration. In Sect. 3, we present the test method for coupled vibration identification, analyze the characteristics of vibration transmission between suspensions and the law of coupled vibration. Section 4 shows the influence of difference ξ on the coupling vibration and the vibration control method.

2 Coupled vibration mechanism

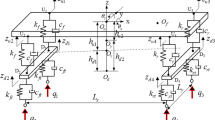
Because the road roughness excitation acts on the front and rear wheels simultaneously, the vehicle body produces vertical vibration and pitching vibration, as well as the vertical and pitching coupling vibration. In addition, the driving track of the front and rear wheels and the road excitation amplitude are the same, but there is a phase difference between the road excitations of the front and rear wheels due to the influence of the speed and wheelbase. Especially when the vehicle runs through the bump road, the coupling between vertical vibration and pitching vibration is very obvious [11, 12]. Figure 1a shows the vibration form of the body when the vehicle passes through the bump road. Zc is the vertical displacement of the center of mass C, and β is the pitch angle of the vehicle body. When Zc ≠ 0, β = 0, the vehicle does pure vertical vibration, and the vibration form often appears on random roads. When Zc = 0, β ≠ 0, the vehicle does pure pitch vibration, which is unfavorable to the body dam** design and brings serious discomfort to the driver and passenger. When Zc ≠ 0, β ≠ 0, the vehicle performs vertical and pitch coupling vibration, which makes the body vibrate more violently. Therefore, it is expected that the vibration between the front and rear suspensions is independent, and there is no coupling behavior between vertical and pitching vibrations of the body.

Fig.1
figure 1

The mechanical model of vehicle. a The vibration forms of the body. b 6-dof 1/2 vehicle mechanics model

Full size image

Figure 1b is the 1/2 vehicle mechanics model with 6-dof, The degrees of freedom are the vertical displacement Zfu of the sprung mass mfu of the front suspension, the vertical displacement Zru of the sprung mass mru of the rear suspension, the vertical displacement Zc of the center of mass and the body pitch angle β, the vertical displacement Zfd of the front suspension unsprung mass mfd, and the vertical displacement Zrd of the rear suspension unsprung mass mrd. The road roughness excitations qf and qr act on the front and rear wheels respectively, and are transmitted to the body through the front and rear suspensions, causing vertical and pitching vibrations.

Taking (Zru, β) as the generalized coordinate, the vertical vibration differential equation of the center of mass is

$$m{\ddot{z}_{c} }= c_{f} ({\dot{z}_{fd} } - {\dot{z}_{fu} } ) + k_{f} (z_{fd} - z_{fu} ) + c_{r} ({\dot{z}_{rd} } -{\dot{z}_{ru} }) + k_{r} (z_{rd} - z_{ru} )$$
(1)

where m stands for the suspension sprung mass, m = mfu + mru, cf stands for the front suspension dam**, kf stands for the front suspension stiffness, cr stands for the rear suspension dam**, and kr stands for the rear suspension stiffness.

The differential equation of body pitching vibration is

$$I_{c}\ddot{\beta} = a[c_{f} ( {\dot{z}_{fd} } - {\dot{z}_{fu} } ) + k_{f} (z_{fd} - z_{fu} )] - b[c_{r} ( {\dot{z}_{rd} } - {\dot{z}_{ru} } ) + k_{r} (z_{rd} - z_{ru} )]$$
(2)

where Ic stands for the moment of inertia of the body, a stands for the distance between the center of mass and the front axle, b stands for the distance between the center of mass and the rear axle.

According to the geometric relationship, the expression is

$$\left\{ \begin{gathered} \Delta z_{f} = z_{fu} - z_{fd} = z_{c} - a\beta \hfill \\ \Delta z_{r} = z_{ru} - z_{rd} = z_{c} + b\beta \hfill \\ \end{gathered} \right.$$
(3)

where ΔZf stands for the relative deformation of the front suspension, and ΔZr stands for the relative deformation of the rear suspension.

According to formulas (1), (2) and (3), the equation is

$$\left[ {\begin{array}{*{20}c} m & 0 \\ 0 & {I_{c} } \\ \end{array} } \right]\left\{ \begin{gathered}{\ddot{z}_{c} } \hfill \\ \ddot{\beta } \hfill \\ \end{gathered} \right\} + \left[ {\begin{array}{*{20}c} {c_{f} + c_{r} } & { - ac_{f} + bc_{r} } \\ { - ac_{f} + bc_{r} } & {a^{2} c_{f} + b^{2} c_{r} } \\ \end{array} } \right]\left\{ \begin{gathered} {\dot{z}_{c} } \hfill \\ \dot{\beta} \hfill \\ \end{gathered} \right\} + \left[ {\begin{array}{*{20}c} {k_{f} + k_{r} } & { - ak_{f} + bk_{r} } \\ { - ak_{f} + bk_{r} } & {a^{2} k_{f} + b^{2} k_{r} } \\ \end{array} } \right]\left\{ \begin{gathered} z_{c} \hfill \\ \beta \hfill \\ \end{gathered} \right\} = \left\{ \begin{gathered} 0 \hfill \\ 0 \hfill \\ \end{gathered} \right\}$$
(4)

The off-diagonal elements of the dam** matrix and stiffness matrix in Eq. (4) are not zero, and there is an elastic coupling behavior. When acf = bcr, akf = bkr, the coupling term is zero, the vertical vibration and pitch vibration do not affect each other.

According to formula (3), the equation is

$$\left\{ \begin{gathered} z_{c} = \frac{{b\Delta z_{f} + a\Delta z_{r} }}{a + b} \hfill \\ \beta = \frac{{\Delta z_{r} - \Delta z_{f} }}{a + b} \hfill \\ \end{gathered} \right.$$
(5)

Taking (ΔZf, ΔZr) as the generalized coordinate system, according to formulas (4) and (5), the equation is

$$\left[ {\begin{array}{*{20}c} {mb} & {ma} \\ { - I_{c} } & {I_{c} } \\ \end{array} } \right]\left\{ \begin{gathered}{\Delta \ddot{z}_{f} }\hfill \\ {\Delta \ddot{z}_{u} } \hfill \\ \end{gathered} \right\} + \left[ {\begin{array}{*{20}c} {c_{f} L} & {c_{r} L} \\ { - c_{f} aL} & {c_{r} bL} \\ \end{array} } \right]\left\{ \begin{gathered} {\Delta \dot{z}_{f} } \hfill \\ {\Delta \dot{z}_{r} } \hfill \\ \end{gathered} \right\} + \left[ {\begin{array}{*{20}c} {k_{f} L} & {k_{r} L} \\ { - k_{f} aL} & {k_{r} bL} \\ \end{array} } \right]\left\{ \begin{gathered} \Delta z_{f} \hfill \\ \Delta z_{r} \hfill \\ \end{gathered} \right\} = \left\{ \begin{gathered} 0 \hfill \\ 0 \hfill \\ \end{gathered} \right\}$$
(6)

where L stands for the wheelbase.

The moment of inertia of the body around the center of mass can be expressed as

$$I_{c} = m\rho^{2}_{y}$$
(7)

where \(\rho_{y}\) stands for the inertia radius.

Equation (6) can be expressed as

$$\begin{aligned} & \left[ {\begin{array}{*{20}c} {m\rho_{y}^{2} } & 0 \\ 0 & {m\rho_{y}^{2} } \\ \end{array} } \right]\left\{ \begin{gathered} {\Delta \ddot{z}_{f} } \hfill \\ {\Delta \ddot{z}_{u} } \hfill \\ \end{gathered} \right\} + \left[ {\begin{array}{*{20}c} {c_{f} (a^{2} + \rho_{c}^{2} )} & {c_{r} (\rho_{y}^{2} - ab)} \\ {c_{f} (\rho_{y}^{2} - ab)} & {c_{r} (b^{2} + \rho_{y}^{2} )} \\ \end{array} } \right]\left\{ \begin{gathered}{\Delta \dot{z}_{f} } \hfill \\ {\Delta \dot{z}_{r} } \hfill \\ \end{gathered} \right\} \\ & \quad + \left[ {\begin{array}{*{20}c} {k_{f} (a^{2} + \rho_{y}^{2} )} & {k_{r} (\rho_{y}^{2} - ab)} \\ {k_{f} (\rho_{y}^{2} - ab)} & {k_{r} (b^{2} + \rho_{y}^{2} )} \\ \end{array} } \right]\left\{ \begin{gathered} \Delta z_{f} \hfill \\ \Delta z_{r} \hfill \\ \end{gathered} \right\} = \left\{ \begin{gathered} 0 \hfill \\ 0 \hfill \\ \end{gathered} \right\} \\ \end{aligned}$$
(8)

The off-diagonal elements of the dam** matrix and stiffness matrix in Eq. (8) are not zero, ΔZf and ΔZr are coupled with each other. The vibration between the front and rear suspensions can be transmitted to each other, which is disadvantageous to the dam** performance of the vehicle. When designing the mass distribution of the vehicle, the sprung mass m is often decomposed into the front axle load mfu, the rear axle load mru and the mass center coupling mass mc. According to Fig. 1b, the expression for the three lumped masses is

$$\left\{ \begin{gathered} m_{fu} = m\frac{{\rho_{y}^{2} }}{aL} \hfill \\ m_{ru} = m\frac{{\rho_{y}^{2} }}{bL} \hfill \\ m_{c} = m\left( {1 - \frac{{\rho_{y}^{2} }}{ab}} \right) \hfill \\ \end{gathered} \right.$$
(9)

When \(\rho_{y}^{2} = ab\) in formula (9), the coupling mass \(m_{c} = 0\), the non-diagonal elements of dam** matrix and stiffness matrix in formula (8) are also zero, ΔZf and ΔZr are independent. At this time, the vibrations of the front suspension and rear suspensions are not transmitted to each other, which is beneficial to the vibration reduction performance and improves the comfort performance of the vehicle.

The expression of the pitch angle β is

$$\beta = \arctan \frac{{\left| {\Delta z_{f} - \Delta z_{u} } \right|}}{L}$$
(10)

Formula (10) shows that β is not only related to the amplitude of ΔZf and ΔZr, but also to the phase difference between ΔZf and ΔZr. When the phase difference is 180°, the pitch angle is the largest, and when the phase difference is 0, the Pitch Angle is the smallest, the pitch angle is also inversely proportional to the wheelbase. In order to realize the vibration reduction design of the vehicle, the coupling degree, amplitude and phase difference between ΔZf and ΔZr can be reduced by reasonably matching the stiffness of the front and rear suspensions without changing the wheelbase. Compared with vertical vibration, the human body is more sensitive to pitching vibration, therefore, the difference between \(\rho_{y}^{2}\) and \(ab\) is as small as possible.

3 Coupled vibration test analysis

3.1 Test description

Figure 2a shows the bench vibration test of the vehicle. The front suspension is a torsion bar spring independent suspension, and the rear suspension is a leaf spring non-independent suspension. When the front wheels (or rear wheels) excitation test is performed, the front wheels (or rear wheel) are fixed on the floating platform, and the rear wheels (or front wheel) do not do any processing, and the hydraulic cylinder drives the floating platform to perform the vibration test. When the road excitation is too large, it is easy to cause the body vibration, vertical vibration and pitching vibration are two common vibration forms. In order to simulate a vehicle passing through a single bump with a height of 50 mm and a width of 250 mm at a constant speed, sinusoidal single-pulse displacement excitation is selected for vehicle vibration test, the amplitude of excitation is 50 mm, and the excitation time is 0.0225 s.

Fig. 2
figure 2

Experimental photos of vehicle vibration test. a Vehicle vibration test-bed. b Pitching angle test of the body. c Acceleration test of front suspension. d Acceleration test of rear suspension

Full size image

To measure the pitch angle, a gyroscope was mounted on the bottom plate of the body, as shown in Fig. 2b. In order to measure the vibration acceleration of the front suspension, acceleration sensor was installed on the upper of the front suspension, as shown in Fig. 2c. Figure 2d shows the measured position of the rear suspension acceleration. The LMS test.lab acquisition system was used for the test, the frequency range was set to 0.0–30.0 Hz, and the resolution was set to 0.01. The characteristics of suspension vibration coupling and body pitch vibration were analyzed. The basic parameters of the vehicle are shown in Table 1.

Table 1 The basic parameters of the vehicle
Full size table

During the test, the vehicle was in the flameout state, so the power transmission system and the intake and exhaust system did not work. Pulse excitation was applied to the front wheels and the rear wheels respectively by the test bench. The acceleration signal of suspensions was collected directly by LMS test equipment, then the acceleration signal was processed by deburring and filtering, and the periodic vibration signal was obtained.

3.2 Test results

Figure 3a shows the vibration acceleration afu curve of the front suspension and the vibration acceleration aru curve of the rear suspensions under the excitation of the front wheels. According to the vibration data of the front suspension, the natural frequency of the front suspension is 1.49 Hz, and the peak acceleration is 14.59 m/s2. The vibration peak value of the rear suspension is 7.65 m/s2, and the vibration transmissibility of the front suspension to the rear suspension is 52.4%, that is, the coupling coefficient is 0.524. The results show that the vibration of the front suspension has a significant impact on the rear suspension.

Fig. 3
figure 3

Vibration test data. a Acceleration data under front wheel excitation. b Acceleration data under rear wheel excitation. c Pitching angle test date

Full size image

Figure 3b shows the vibration curves of the suspensions under the excitation of the rear wheels. According to the test data of the rear suspension, the natural frequency of the rear suspension is 1.76 Hz, and the peak acceleration of the aru curve is 21.61 m/s2. The vibration peak of the afu curve is 9.13 m/s2, and the vibration transmissibility of the rear suspension to front suspension is 42.3%, that is, the coupling coefficient is 0.423. The results of the test analysis show that the vibration of the rear suspension also has a significant effect on the front suspension.

Figure 3c shows the body pitch angle β curve of the vehicle body. The maximum pitch angle is 1.56° under the excitation of the front wheels, and the Z-direction displacement of the front axle relative to the rear axle is 81.7 mm. The maximum pitch angle is 1.19° under the excitation of the rear wheels and the Z-direction displacement of the rear axle relative to the front axle is 62.5 mm.

The subjective evaluation shows that the pitching feeling and impact feeling of the human body are relatively obvious, and the comfort of the vehicle is poor under the impact load condition, which has caused the driver and passengers to complain.

4 Control of vehicle coupled vibration

4.1 Influence analysis of differential ξ

Equation (9) shows that when \(\rho_{y}^{2} = ab\), the vibrations between the suspensions are independent of each other. Figure 3a, b show that the vibrations between the suspensions have obvious coupling. To reduce the degree of vibration coupling, the difference between \(\rho_{y}^{2}\) and \(ab\) needs to be reduced. Without considering dam**, according to the balance of force and moment, the dynamic equation of the center of mass is

$$\left\{ \begin{gathered} \frac{1}{2}m {\ddot{z}_{c} }+ (k_{f} + k_{r} )z_{c} + (k_{r} b - k_{f} a)\beta = 0 \hfill \\ \frac{1}{2}m\rho^{2}_{y} \ddot{\beta} + (k_{f} a^{2} + k_{r} b^{2} )\beta + (k_{r} b - k_{f} a)z_{c} = 0 \hfill \\ \end{gathered} \right.$$
(11)

The natural frequency of the body is

$$f_{y}^{2} = \frac{{2\left( {k_{f} a^{2} + k_{r} b^{2} } \right)}}{{m\rho_{y}^{2} }}$$
(12)

The pitch rotation radius of the body around the center of mass is

$$\rho_{y} = \frac{1}{{f_{y} }}\sqrt {\frac{{2\left( {k_{f} a^{2} + k_{r} b^{2} } \right)}}{m}}$$
(13)

In order to obtain the natural frequency of the vehicle body, the swing method is used in this paper. Before the test, the shock absorbers need to be removed, the rear wheels are locked, the front wheels are raised and released instantly. Figure 4 shows that the natural frequency of the front suspension ff is 1.52 Hz, the natural frequency of the rear suspension fr is 1.83 Hz, and the natural frequency of the body fc is 1.71 Hz. Therefore, according to fc and the data in Table 1, the pitch rotation radius is 1.41 m.

Fig. 4
figure 4

Natural frequency test data

Full size image

The difference ξ between \(\rho_{y}^{2}\) and \(ab\) is

$$\xi = \left| {\rho_{{_{y} }}^{2} - ab} \right| = \left| {1.99 - 1.68 \times 1.32} \right| \, = 0.23$$
(14)

Because \(\rho_{y}^{2} \ne ab\) and the difference is 0.23, the vibration between the front suspension and the rear suspension is highly coupled, which is not conducive to improving the comfort of the vehicle.

According to the formulas (12), (13) and (14), the difference ξ can also be expressed as

$$\xi = \left| {\frac{{k_{f} a^{2} + k_{r} b^{2} }}{{2\pi^{2} (k_{f} + k_{r} )}} - ab} \right|$$
(15)

Therefore, by adjusting the load distribution to change the distance a and b to obtain different values ξ. Figure 5a shows the curve of the vibration transmissibility δ between suspensions with the difference ξ, and the smaller the transmissibility ξ is, the less the vibration coupling is. The results show that when ξ ≤ 0.25, the δ has a nonlinear growth relationship with the ξ; When ξ > 0.25, the relationship between the δ and the ξ is linear. Figure 5b shows the relationship between the difference ξ and the maximum pitch angle β of the body, the smaller the maximum pitch angle is, the smaller the pitch vibration is. The results show that when ξ ≤ 0.25, the β has a linear growth relationship with the ξ; When ξ > 0.25, the relationship between the δ and the ξ is nonlinear.

Fig. 5
figure 5

Vibration test data with different ξ. a Transmissibility with different ξ. b Maximum pitching angle with different ξ

Full size image

The objective and subjective analysis shows that the vehicle comfort performance is better when the body roll angle is less than 1.0°, and the corresponding difference ξ is about 0.15. Therefore, according to Fig. 5, under the front wheel excitation, the vibration transmission rate between suspensions is controlled within 30%; Under the rear wheel excitation, the vibration transmission rate is controlled within 22%; The maximum pitch angle should be controlled within 1.0 degree.

For vehicles in the late stages of design, the position of the center of mass is difficult to change, so the difference between \(\rho_{y}^{2}\) and \(ab\) can only be narrowed by optimizing the stiffness of the front and rear suspensions.

4.2 Optimization simulation

The natural frequency and static deflection of suspension should be considered in the optimization of suspension stiffness. In order to avoid large pitching motion, the natural frequency of the front suspension should be less than that of the rear suspension, and the static deflection of the front suspension should be slightly larger than that of the rear suspension. The optimization of any mechanical system must have three elements: design variables, objective functions and constraint equations. Design variables are the key parameters affecting the objective function, objective function is a mathematical expression used to evaluate the quality of a design scheme, constraint equations are mathematical relationships used to constrain the values of design variables [13, 14].

In the paper, dynamic simulation optimization method is used to optimize the vehicle vibration analysis. The vehicle dynamics simulation model is established, as shown in Fig. 6. The model includes tire model, suspension model, the frame and the body model.

Fig. 6
figure 6

Dynamic simulation optimization method

Full size image

The design variables are suspension stiffness kf and kr, and the variation range of the variable is shown in Table 2. The objective function is \(\min \left| {\left| {a_{fu} } \right| - \left| {a_{ru} } \right|} \right|\), and the constraint equation is

$$\left\{ \begin{gathered} \frac{1}{2\pi }\sqrt {\frac{{k_{f} }}{{m_{fu} }}} = \frac{\gamma }{2\pi }\sqrt {\frac{{k_{r} }}{{m_{ru} }}} (0.9 \le \gamma \le 1) \hfill \\ \frac{{m_{fu} g}}{{k_{f} }} = \lambda \frac{{m_{ru} g}}{{k_{r} }}(1 \le \lambda \le 1.1) \hfill \\ \end{gathered} \right.$$
(16)
Table 2 The design variables
Full size table

The relationship between the optimization variable and the objective function is implicit in the virtual prototype model. Through simulation, the optimization target value of a certain set of independent variables can be obtained. In this paper, genetic algorithm is selected to optimize the model.

Through optimization calculation, the front suspension stiffness is 75 N/mm, and the rear suspension stiffness is 125 N/mm. The vehicle dynamics model was modified according to the optimized suspension stiffness, and the modal simulation was carried out, and the front suspension natural frequency is 1.62 Hz, the rear suspension natural frequency is 1.70 Hz, the rotation natural frequency about y-axis is 1.66 Hz. And the calculation result of \(\rho_{y}^{2}\) is 2.13.

The difference ξ is 0.08, the result can reduce the degree of vibration coupling between the suspensions, which is beneficial to the vibration reduction design.

Figure 7 shows the curve of suspension vibration acceleration and body pitch angle in the optimized state of suspension stiffness. The natural frequency of the front suspension is 1.60 Hz, the natural frequency of the rear suspension is 1.68 Hz, and the natural frequency of the body is 1.65 Hz, and the difference ξ is 0.11.

Fig. 7
figure 7

Vibration test data in improved state. a Acceleration data under front wheel excitation. b Acceleration data under rear wheel excitation

Full size image

Figure 7a is the vibration acceleration curve of suspensions under front wheels excitation. The peak acceleration of front suspension is 15.68 m/s2, the peak acceleration of rear suspension is 3.47 m/s2, and the coupling coefficient is 0.221. Compared with the original state, the coupling coefficient decreases by 57.8%.

Figure 7b is the vibration acceleration curve of suspensions under rear wheels excitation. The peak acceleration of front suspension is 1.94 m/s2, the peak acceleration of rear suspension is 12.34 m/s2, and the coupling coefficient is 0.157. Compared with the original state, the coupling coefficient decreases by 62.9%.

Figure 8 is the body pitch angle curve. The maximum pitch angle of the body is 0.88° under front wheels excitation, the pitch angle is decreased by 43.6% compared with the original condition. The maximum pitch angle is 0.53° under rear wheels excitation, which is 55.5% lower than the original pitch angle.

Fig. 8
figure 8

The pitching angle test date

Full size image

The results show that the degree of vibration coupling between the front suspension and the rear suspension can be significantly reduced by the reasonable matching of suspension stiffness, and the pitch angle of the body can also be effectively reduced. The subjective evaluation shows that the pitching motion and impact feeling of the human body are significantly reduced, and the comfort of the vehicle is greatly improved under the impact load condition.

5 Conclusion

The mathematical model of vehicle vertical vibration and pitching vibration is established. It is revealed theoretically that the difference ξ is the key factor that affects the coupling of front and rear suspension vibration and the vehicle body pitching vibration. Through the vibration test, the vibration law of the suspensions and the pitch vibration characteristics of the body are analyzed, and the ξ value can be effectively reduced by the reasonable matching of the stiffness of the front and rear suspensions.

Under the excitation of the front wheels, when ξ = 0.23, the suspension vibration coupling coefficient is 0.524, and the maximum body pitch angle is 1.56°; when ξ = 0.11, the suspension vibration coupling coefficient is 0.221, and the maximum body pitch angle is 0.88°. Compared with the original state, the vibration coupling coefficient of the suspension in the improved state is reduced by 57.8%, and the maximum pitch angle of the body is reduced by 43.6%.

Under the excitation of the rear wheels, when ξ = 0.23, the suspension vibration coupling coefficient is 0.423, and the maximum body pitch angle is 1.19°; when ξ = 0.11, the suspension vibration coupling coefficient is 0.157, and the maximum body pitch angle is 0.53°. Compared with the original state, the vibration coupling coefficient in the improved state is reduced by 62.9%, and the maximum pitch angle is reduced by 55.5%.

The coupling of vertical vibration and pitching vibration is analyzed in this paper. The results can provide reference for the control of this kind of vibration. But the vehicle is a complex system, the vehicle vibration also includes lateral vibration, longitudinal vibration, roll vibration and yaw vibration. Therefore, in order to reflect the Vehicle dynamics characteristics comprehensively and accurately, the multi-directional vibration coupling problem will become the focus of the future research.