1 Introduction

With the increase in human population, today's societies face a shortage of urban spaces. Hence, to solve traffic problems and to develop welfare facilities (such as subway lines, railways, etc.), the need to construct underground structures is evident [1]. Also, the underground anthropogenic cavities typically excavated in the subsoil for several purposes are commonly recognized underneath the historical city centers over the centuries [2]. However, the presence of shallow tunnels and cavities may change the ground response pattern and further affect existing buildings nearby, leading to serious geotechnical hazards for civil construction. The study of underground anomalies and their influence on surface ground motion dates back to the 1970s. There has been historical evidence that buildings in the areas with underground cavities are more likely to be damaged during destructive earthquakes [3,4,5,6]. For example, during the Abruzzo earthquake (6.IV.2009, MW = 6.3), the village of Castel Nuovo, lying on an elliptical hill about 60 m high, underwent intensive damage. Evangelista et al. [7] investigated the seismic amplification induced by the topographic effect. They confirmed that cavities significantly influenced ground motion at high frequencies. In this context, many researchers have explored the cavity or tunnel effect on seismic ground response under body waves through various methods, such as analytical methods [8,9,10], numerical simulations [11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26], and model tests [27,28,29,30]. Due to the complexity involved in wave propagation and limitations in modeling complicated systems of equations, numerical techniques are more effective compared to analytical and model tests for the parametric study of ground vibration problems [31].

Reviewing previous studies on tunnel and cavity effects on ground motion reveals that most researches have been restricted to evaluating body waves. However, it is acknowledged that the surface waves attenuate with distance more slowly than body waves, which drives higher ground strains, including horizontal and vertical components. Therefore, they may play a dominant role over body waves in the hazardous effect on structures located on or very close to the earth’s surface. Many urban areas which are settled on sedimentary basins might face important site effects such as surface waves characterized by long duration and low-frequency content, which induce high amplitude vibration in soil and tall structures. Rayleigh waves are typically generated by the interference of P and SV waves at the free surface or the edges of sedimentary basins (basin-induced surface waves) [32,33,34,35,36]. It was initially believed that R-waves from earthquakes could only be seen in far fields. However, it is now understood that they can have a considerable impact at a closer distance (within a few tens of kilometers). Awareness of these issues can help determine the realistic levels of vulnerability of existing buildings, leading to the safe design of structures on the ground [37,38,39,40,41].

In recent years, surface waves have been the subject of many analytical and numerical seismic studies in civil engineering. These researches are mostly limited to realizing the subjects like diffraction of Rayleigh waves by surface topographic features [42,43,44,45,46,47], cavity detection [48,49,50,51], evaluating bending deformation of tunnel and lining response [36, 37, 52,53,54,4 verifies the accuracy of this method. Eventually, a parametric study will evaluate the influences of the cavity burial depth, incident wave frequency, and horizontal distance of wave source from the cavity axis on the seismic ground responses.

2 Problem definition and assumptions

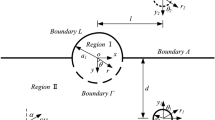
Generally, from a theoretical perspective, the problem is complex despite applying simplified assumptions such as the uniformity, isotropy, and elasticity of the soil medium, the presence of a single cavity, the circular shape geometry of the cavity, and incident harmonic waves. Because of this, most of the applied studies available in the literature provide approximate solutions, even analytically [26]. Figure 1 illustrates the geometry of the model under the incidence of Rayleigh waves. The cavity radius is indicated by “a” and the cavity depth “d” is defined as the interval between the cavity center and the ground surface. The ground response will be observed at the receiving points with specific intervals from a reference point. The manuscript describes the reference point as a position at the ground's surface above the tunnel's center.

Fig. 1
figure 1

Schematic representation of the soil-cavity model and reference point located on the ground surface to the parametric study

Full size image

To perform the parametric study, general specifications of the model and three main parameters that affect the ground response pattern, including the cavity depth, distance from the cavity axis, and dimensionless incident frequency have been introduced. For calculation convenience, these parameters are defined in dimensionless forms. First, the cavity depth ratio \((DR=d/a)\) indicates the distance between the ground surface and the cavity center (i.e., cavity depth). The distance ratio \(x/a\) indicates the horizontal distance of receiver points from the reference point. It should be noted that the results in the frequency domain can be presented in terms of dimensionless frequency. According to Eq. 1, the dimensionless frequency \(\left(\eta \right)\) [15, 66] was defined as the ratio of the total width of the scatterer (cavity diameter) to the excitation wavelength \(\left({\lambda }_{R}\right)\):

$$\eta =\frac{2a}{{\lambda }_{R}}=\frac{2af}{{C}_{R}}$$
(1)

In this Equation, “\({\lambda }_{R}\)” is the striking wavelength, “\(f\)” is the wave frequency, and “CR” is the R-wave velocity. It is important to note that when a dimensionless frequency is mentioned, it simply refers to a ratio of tunnel diameter to wavelength, which can be evaluated in the frequency domain. In this regard, five dimensionless frequencies from 0.25 to 1.5 were selected for evaluating the seismic ground response. Considering the inverse ratio, the excitation R-waves have wavelengths from 4 to 0.67 times the cavity diameter. Table 1 shows the values of the considered variables for the three dimensionless parameters involved in the problem.

Table 1 Assigned values to the dimensionless parameters in the parametric study
Full size table

3 Rayleigh wave propagation

Rayleigh waves (R-waves) are the primary surface waves that carry 2/3 of the total energy during vibration propagation. During the R-wave propagation, the particle in the medium moves in a retrograde elliptical path [67]. Indeed, Rayleigh waves are produced through the interaction of P and SV waves at the superficial ground layers, and they move more slowly than body waves. In particular, the dynamic properties of R-waves are different from other waves. For instance, the amplitude of scattered P-waves is much smaller than that of R-waves because most of R-wave motions and energies are confined to the ground surface [37]. Equation 2 represents the propagating velocity calculation formula of R-waves. R-waves are presumed to propagate along the x-axis and the coordinate system is illustrated in Fig. 1. As tunnels are long structures, a plane strain is assumed in the present study. Here is the Rayleigh equation for an elastic ground according to Zhao et al. [56]:

$${\left(\frac{{C}_{R}}{{C}_{S}}\right)}^{6}-8{\left(\frac{{C}_{R}}{{C}_{S}}\right)}^{4}+\left(24-16\frac{{{C}_{S}}^{2}}{{{C}_{P}}^{2}}\right){\left(\frac{{C}_{R}}{{C}_{S}}\right)}^{2}-16\left(1-\frac{{{C}_{S}}^{2}}{{{C}_{P}}^{2}}\right)=0$$
(2)

where \({C}_{S}=\sqrt{G/\rho }\), \({C}_{P}=\sqrt{\left(\lambda +2G\right)/\rho }\), and CR indicates the propagation velocities of S-, P-, and R-waves, respectively; λ and G are Lame constants of the soil; also, ρ is the density of the ground.

Unlike the conventional analysis under shear wave propagating upwards, numerical dynamic analysis under R-wave in the time domain is much more complicated. An analytical solution of Bath and Berkhout [68] to Lamb’s problem is implemented in this work to generate and propagate the R-wave displacement [69]. In this way, the dynamic load is simulated using a point source with a short distance from the ground surface that operates on the infinite surface and is obtained from the following equation:

$$F\left(t\right)=\frac{{F}_{b}}{\pi \left({t}^{2}+{\psi }^{2}\right)}.t$$
(3)

where “\({F}_{b}\)” modifies the value of force magnitude, “\(\psi\)” controls the frequency content of the pulse (i.e., pulse width), and “\(t\)” demonstrates time. The imaginary wave sources are positioned away from the cavities' borders to prevent singularities. Also, the vertical displacement of the R-wave is calculated from the following equations:

$${W}_{y}(t,d)=\frac{R.{F}_{b}}{(4\pi .G.{\psi }^{2}){C}_{R}}\sqrt{\frac{2\psi {C}_{R}}{d}}.\mathit{cos}(\frac{\pi }{4}-\frac{3}{2}\upsilon ).{\mathit{co}s}^\frac{3}{2}(\upsilon )$$
(4)

Given that

$$\upsilon ={\mathit{tan}}^{-1}(\frac{t-d/{C}_{R}}{\psi })$$
(5)

In these equations, “\(R\)” is a constant coefficient that relies on the type of wave. “\(G\)” is the shear modulus, “\({C}_{R}\)” is the R-wave velocity, and “\(d\)” is the distance from the wave source. To perform numerical modeling, the R-wave was generated and propagated in the model using the above equations and relevant parameters according to Table 2.

Table 2 Values of parameters that are used to generate the Rayleigh wave
Full size table

The vertical displacement of the Rayleigh wave corresponding to the time step of 0.025 s is shown in Fig. 2. As can be seen, the generated vertical component of the R-wave is applied to the system as a simple wavelet and rapid excitation. Moreover, Fig. 3 demonstrates the passage of the R-wave through the surface of the ground model.

Fig. 2
figure 2

Time history of vertical displacement and Fourier amplitude of R-wave from a solution of Lamb’s problems (dt = 0.025 s)

Full size image
Fig. 3
figure 3

A view of R-wave propagation within the model for d/a = 1.5

Full size image

4 Numerical simulation framework and verification

4.1 Numerical modeling

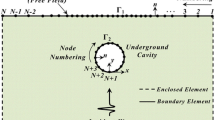
The details of a numerical modeling are presented in this part. The FEM-based ABAQUS software [70] has been used to perform numerical analysis. Figure 4 shows a 2D model of the underground cavity in a half-space medium. The quadrilateral elements assuming plane-strain conditions were employed for the meshing configuration. A simple viscoelastic model with one percent Rayleigh dam** has been used for the soil medium. The horizontal and vertical dimensions of the model were determined using sensitivity analysis as 1000 and 600 m, respectively. The dimensions of the model were chosen to be large enough to cover the deepest cavity in parametric analysis and reduce the influence of error waves in the dynamic analysis process. A circular tunnel without a lining is embedded in the model. After creating the geometry, the general mechanical properties of the model, such as density, Young’s modulus, and Poisson’s ratio were introduced. Therefore, shear wave velocity, Poisson’s ratio, and the soil density are taken into account at 150 m/s, 0.33, and 2000 kg/m3, respectively.

Fig. 4
figure 4

The numerical model of a soil-cavity system in ABAQUS

Full size image

To eliminate the reflection of waves inside the model boundaries, infinite elements are set at the sides of the main model that act as absorbing boundaries and simulate the semi-infinite condition. The infinite elements are used in conjunction with standard finite elements which model the area around the region of interest. In the Abaqus element library [70] the 4-noded plane strain infinite elements are named CINPE4 and are provided based on the works of [71, 72] for static and dynamic loading. It is noteworthy that the incident R-wave is applied to the model on the ground surface and spreads in the lateral direction. Given the sufficient height of the model, the bottom boundary is restricted in two directions of X and Y (UX = UY = 0), and a rigid boundary condition is adopted to represent bedrock in this study. Moreover, to properly propagate the waves in the model, the mesh size should be between one-tenth to one-eighth of the largest input wavelength, according to Kuhlemeyer and Lysmer’s [73] recommendations.

4.2 Verification of numerical model

In this section, the numerical model is verified by using computational approaches performed by Luco and De Barros [59] and Yu and Dravinski [60] which are based on BEM formulation. In the first case, the depth ratio and dimensionless frequency are considered as \(DR=1.5\), and \(\eta =0.5\), respectively. The radius of the cavity is considered 20 m and the appropriate mesh element size and time step were obtained at 4 m and 0.025 s. The Fourier spectrum of ground surface displacements in free-field conditions is used to normalize the receiver point's responses. Consequently, through the normalized amplitudes of horizontal and vertical displacements of receiver points, the effects of the cavity under the incident R-waves are shown in Fig. 5. In this case, the horizontal axis shows the dimensionless distance of the receiver points from the reference point. The results show that the 2D FEM modeling and the findings by Luco and De Barros [59] have reasonable level of agreement and accuracy.

Fig. 5
figure 5

Verification of horizontal and vertical displacement component of the present study with the results of Luco and De Barros (η = 0.5, d/a = 1.5)

Full size image

Furthermore, like the previous step, the accuracy of the numerical FEM model is evaluated with Yu and Dravinski [60] studies too. For this purpose, a 2D soil-cavity model with a fixed depth ratio \(DR=2\) and dimensionless frequency \(\eta =1\)  is considered. The buried depth and the cavity radius are 50 and 25 m, respectively and the wave generation source is located at a distance of 150 m from the cavity. Other parameters and soil models are selected as in the previous case. Thus, the element's dimensions and the appropriate time step for analysis are determined as 2.5 m and 0.02 s, respectively. A comparison of the obtained surface displacements around the cavity in a homogeneous half-space with the findings of Yu and Dravinski is presented in Fig. 6. As can be seen, there are appropriate agreements between the responses.

Fig. 6
figure 6

Verification of horizontal and vertical displacement component of the present study with the results of Yu and Dravinski (η = 1, d/a = 2)

Full size image

5 Wave-field patterns in time-domain

The time history or transient response is an essential aspect to evaluate the seismic effects of structures since wave scattering can be examined in the time domain [73]. Figure 7 shows the time history of normalized horizontal and vertical displacements of the ground surface with and without a buried cavity exposed to R-waves. The ground surface horizontal or vertical displacements are normalized to the maximum amplitude of incident wave motion. As a consequence, the presence of a cavity will cause more wave interference and, subsequently, more significant displacement than the free-field condition. Also, for a more accurate investigation of the ground response pattern, the normalized surface displacement amplitudes are illustrated in Fig. 8 with dimensionless distance (x/a) and wave radiation time (t). Time histories have been received from equally spaced receiver points which are located along the ground surface and both sides of the cavity between x/a =  − 5 to 5. These four graphs correspond to the two different depth ratios (d/a) of 1.5 and 4 as the most shallow and deep cavities, respectively. The synthetic seismograms clearly indicate the amplification/de-amplification patterns on the ground surface on both sides of the cavity. As demonstrated, the scattering and turbulence of ground surface motions in the shallow cavity are more significant than those in the deep case. This issue can arise from the nature of Rayleigh waves, and it does not penetrate more than its wavelength into half-space.

Fig. 7
figure 7

The horizontal and vertical components of the reference point normalized displacement in two modes with and without the cavity under the R-wave propagation (x/a = 0, DR = 1.5)

Full size image
Fig. 8
figure 8

Synthetic seismograms of normalized horizontal and vertical displacement of free surface induced by an underground cavity with depth ratios of 1.5 and 4

Full size image

Furthermore, positioning a tunnel at a shallow depth causes surface R-waves to become trapped between the tunnel and the ground surface. Increasing burial depth reduces this effect and results in less ground surface amplification. The following diagrams exhibit that the interaction of Rayleigh waves with the cavity influences more significantly the vertical component of free surface ground motion rather than the horizontal component.

6 Parametric studies in frequency domain

Although the display of results in the time domain seems to be appropriate to investigate the responses and wave propagations, the representation of amplification patterns is only possible in the transformed domains. In this regard, the amplification pattern of the ground surface is presented in terms of dimensionless frequency. This section represents the parametric analysis of Rayleigh waves scattering by two-dimensional circular cavities using FEM. The parametric analysis is carried out to see how the model's “effective parameters” change the seismic response pattern. For this purpose, the influences of the depth ratio, dimensionless incident frequency, and the distance from the cavity axis are investigated. The concept of wave amplification facilitates understanding the scatter of R-waves due to the existence of cavities. Despite the evaluation of the interrelationships between the studied parameters, the effect of these parameters is examined separately. It is worth mentioning that parametric studies are represented using normalized displacement, calculated as the ratio of the ground surface horizontal or vertical components (H or V components) to the maximum amplitude (Am) of incoming wave motion (W/Am).

6.1 Effect of depth ratio (DR)

As previously stated, the depth ratio (DR) indicates the vertical distance between the ground surface and the embedded cavity center. The ground response patterns are investigated in the frequency domains to properly evaluate the cavity depth effect. By altering the depth of the buried tunnel, the impact of the various depth ratios is investigated. Figure 9 illustrates the horizontal and vertical displacements surrounding cavities in a homogenous medium at specified receiver points. These graphs represent the ground response pattern in depth ratios of DR = 1.5, 2, 3, and 4 at constant dimensionless frequencies. As can be seen, the amplitude of the oscillations decreases with an increase in depth ratio. Actually, most energies of the surface wave concentrate near the ground surface, and it is evident that the cavity’s depth significantly affects the scattering of Rayleigh waves. R-waves become trapped in the space between the tunnel and the ground as the tunnel gets closer to the surface. This phenomenon is significant to a depth equal to or less than the R-wavelength. In other words, the trap** of scattered waves in this zone can increase the amplification of the waves.

Fig. 9
figure 9

Normalized amplitudes of the total horizontal and vertical displacements on the ground surface for different depth ratios at each constant dimensionless frequency under incident R-wave

Full size image

It is noteworthy that with a decrease in the depth ratio at each dimensionless frequency, the vertical component of the ground motion experiences both maximum amplification and maximum de-amplification. Furthermore, it can be observed that with a rising trend in the frequencies, more turbulence has occurred at ground responses. Subsequently, the change of wave frequency alters the current role of depth ratio in the amplification or de-amplification patterns. Additionally, it seems that the cavity has a greater impact on the V-components rather than the H-components.

6.2 Effects of R-wave dimensionless frequency (η)

R-waves are radiated horizontally (parallel to the surface) from the source with a constant distance to the ground surface at different dimensionless frequencies. According to Eq. (1), dimensionless frequency is defined with the cavity diameter ratio to the excitation wavelength \((2a/{\lambda }_{R})\). Figure 10 shows the free surface amplification patterns at each constant depth ratio with different dimensionless frequencies. It can be inferred that with an increasing dimensionless incident frequency, horizontal and vertical components of the ground motion decrease noticeably. Also, the amplification effect of lower frequency \(\eta =0.25\) is impressive in shallow burial depth \((DR=1.5)\), which its value reaches up to 3 in the V-component.

Fig. 10
figure 10

Normalized amplitudes of the horizontal and vertical displacements of the ground surface with different wave frequencies at each constant depth ratio for incident R-waves

Full size image

Moreover, in the frequencies of 0.5 and 0.75, the spatial position of maximum ground motion amplitude shifts towards the cavity with the increase in incident frequency. As can be seen, in the dimensionless frequency of 1, no significant amplification or de-amplification is observed. However, for frequencies greater than 1 \((\eta >1)\), the de-amplification effect is evident in the ground responses. According to Eq. (1), under wavelengths larger than the cavity diameter \((\eta <1)\), more significant responses are obtained on the ground surface. On the other hand, the presence of an underground structure reduces the stiffness of the soil medium and thus, it leads to a reduction of natural frequency. Therefore, incident seismic waves with lower frequencies lead to resonance phenomena, and consequently, amplification effects are more evident.

6.3 Effects of distance ratio (X/a)

The effect of the horizontal distance of receiver points from the reference point on the ground responses is investigated. Figures 8, 9 and 10 show that the maximum amplification of ground response over a cavity has occurred near the wave source. The amplification is decreased after passing within the cavity because of the complicated interaction of the R-waves. Meanwhile, as previously illustrated, the results reveal that for cases with distance ratios of \(x/a \le -4\) and \(x/a \ge 4\), the effect of the cavity on the amplification pattern is negligible. Moreover, the cavity acts as a barrier during the scattering of the Rayleigh waves in the transfer process. Because of the wave trap**, the amplification on the right-hand side of the cavity (\(x/a \ge 0\)) is significantly less than that on the left-hand side.

7 Concluding remarks

In this study, a series of parametric analyses were carried out to investigate the influence of a circular cavity or tunnel on the seismic ground response pattern due to Rayleigh wave propagation. The effective parameters on the ground responses were evaluated by simulating the soil-cavity system using the 2D finite element method. These include the depth of the cavity, the horizontal distance from the wave source (or cavity axis), and the frequency content of incident waves. The achieved results highlight the importance of investigating superficial amplification analyses in the presence of underground structures and surface wave propagations. The main results have been summarized as follows:

  1. 1-

    The subsurface cavity especially with a low depth ratio causes the scattering and turbulence of incident Rayleigh waves near the ground surface and leads to altering ground response compared to the free-field condition.

  2. 2-

    The cavity's influence on free surface motion decreases as the burial depth of the cavity increases. Consequently, cavities with a high depth ratio \((DR\ge 4)\), have a negligible effect on the ground displacement amplitude. This issue can arise from R-waves inherent propagation property, which penetrates as much as wavelength.

  3. 3-

    It was observed that with increasing the dimensionless frequencies, more turbulence occurs at ground responses. Furthermore, with increasing the dimensionless frequencies, the influence of depth ratio on the response amplitude has been changed and no longer follows the prior trend. This effect is more evident in vertical components.

  4. 4-

    According to observations, at each depth ratio, ground motion amplitude decreases with increasing dimensionless frequency and vice versa. This result may be because of the inherent properties of seismic waves that significantly affect the cavity with the diameters less than the incident wavelength \((\eta <1)\). Also, the reduction of soil stiffness due to the presence of cavities and, subsequently, the reduction of the natural frequency could be another reason for the amplification under low-frequency incident R-waves.

  5. 5-

    The effect of the horizontal distance of receiver points from the wave source on the ground response was investigated. It was observed that the maximum amplification occurs on the left-hand side of the cavity and near the wave radiation source. After passing the R-waves through the cavity, reducing the interaction effects leads to a decrease in the surface response.

  6. 6-

    It was observed that R-wave interaction with underground structures is the key factor that induces vertical ground motion. Moreover, during the incidence of Rayleigh waves, the presence of cavities leads to very peculiar amplification patterns at the free surface. Consequently, based on the findings of this paper, the necessity of integrating these phenomena into seismic design procedures and improving the structure design codes is more evident.

This numerical study can help to have a better understanding of the effects of surface waves' interaction with an underground cavity or tunnel as well as subsequent impacts on the free surface ground motion. Consequently, the findings may be applied for the modification of seismic microzonation guidelines and seismic design of aboveground structures built on underground spaces. It is noted that a homogeneous and visco-elastic soil model was assumed in this study. As for more detailed studies, application of nonlinear soil behavior, conducting 3D simulations, evaluations with field tests, and monitoring can be achievable goals in future investigations.