1 Introduction

The practical applications of non-Newtonian Sutterby fluid in numerous engineering sectors and industries, including gas turbines, polymer manufacture, power generators, paper manufacturing, wire drawing, glass cloth, and many others [1,2,3] have caught the interest of numerous researchers. In light of this, Hayat et al. [4] investigated the benefits of heat and mass relocation caused by Brownian diffusion and thermophoresis due to the flow of Sutterby fluid induced by a rotating disk and came to the conclusion that temperature and concentration were improved with the thermophoresis parameter. Saif-ur-Rehman et al. [5] also investigated the Sutterby fluid flow across the stretching sheet under zero mass flux conditions. They discovered that while a finer thermal conductivity parameter results in a rise in temperature distribution, a higher Sutterby fluid parameter results in a drop in the velocity field. Unlike earlier studies, Nawaz [6] concentrated on the characteristics of heat transfer in the Sutterby fluid with numerous nanoparticles, concluding that the Sutterby-nanomaterial flow experiences a stronger Lorentz force than the Sutterby hybrid nanomaterial. Additionally, Waqas et al. [7] explored the bio-convection of a Sutterby nanofluid traveling towards a wedge with activation energy and arrived at the conclusion that the Peclet number should be raised to reduce the microbe field.

In advanced technology and industry, improving the thermal efficiency of common fluids has received a lot of attention. As a result, numerous researchers have proposed various strategies from diverse perspectives to get beyond the constraints of current technologies and industries. Using solid nanoparticles (less than 100 nm in size) in ordinary fluids is a novel method for enhancing thermal efficiency. Choi and Eastman [8] were the first to use this term, and they called it nanofluid. This led Kandasamy et al. [9] investigate the heat relocation characteristics of water-based alumina, single-walled carbon nanotubes, and copper nanoparticles over a horizontal plate under the influence of chemical reaction, and they came to the conclusion that the diffusion boundary layer thickness of the water-based Cu and SWCNTs is stronger than \({\mathrm{Al}}_2{\mathrm{O}}_3\)-water with an increase in chemical reaction. Additionally, Mabood et al. [10] investigated the heat transfer properties in a sodium alginate-\({\mathrm{Fe}}_3{\mathrm{O}}_4\) nanofluid flow across a vertical spinning frame and came to the conclusion that the heat transfer rate rises with an increase in the solid volume fraction of nanoparticles. According to Singh et al. [11], a nanofluid containing 3 weight percent of nanoparticles coated with citric acid in water (\(67\%\)) results in a decrease in thermal conductivity, while a nanofluid containing 4 weight percent of oleic acid-coated nanoparticles in toluene increases thermal conductivity. Additionally, Alhajaj et al. [12] came to the conclusion that the use of \({\mathrm{Al}}_2{\mathrm{O}}_3\) nanofluid is the most suited fluid for cooling purposes in their investigation. In their study of the impact of an induced magnetic field on nanofluid flow close to the stagnation point using the Buongiorno model, Hou et al. [13] came to the conclusion that when the magnetic parameter increases, the velocity field expands while the temperature field contracts. In addition, Asjad et al. [14] evaluated heat transfer properties in the inclusion of nanoparticles in base fluid and came to the conclusion that nanoparticles with parameters Nb and Nt indicate an increase in the temperature field. Also, Jawad et al. [15] examined the heat relocation properties of \({\mathrm{Al}}_2{\mathrm{O}}_3-{\mathrm{Cu}}\) nanoparticles across a stretching sheet under the effect of radiative and Lorentz forces.

Numerous technical and contemporary industrial applications utilise fluid flows from rotating bodies, such as polymer deposition on components [16] and electrolysis procedures [17]. The formation and structure of the boundary layers in these systems close to the body’s periphery are significantly influenced by rotation. Thus, they regulate the rates of heat and mass transfer in laminar, transitional, and fully turbulent flows [18]. Conical, elliptical, disk-shaped, spherical, eccentric, and concentric systems are just a few of the possible shapes for the bodies. Several academics used this geometric flow to convey their research in a mathematical and numerical approach. Anilkumar and Roy [19] used the flow and heat characteristics across a revolving sphere while accounting for unsteady mixed convective flow as an illustration. They concluded from their research, which employed an implicit finite-difference method, that the acceleration and rotational constraints caused an increase in the surface shear stresses and the surface heat relocation. In addition, Ali et al. [20] investigated the heat and mass relocation features caused by the flow of mixed convection along a rotating sphere, and they came to the conclusion that the application of fluid wall injection resulted in growth in the velocity field along the x-component and a reduction in the temperature and concentration disseminations near the walls, while the y-direction remained relatively unchanged. More recent research by Beg et al. [21] examined the flow of nanofluid from a unsteady spinning sphere and demonstrated that the main flow is strengthened while the secondary flow is weaker with greater rotation effect. They accomplished this by utilizing the homotopy analysis technique and the notion of laminar boundary layers. Turkyilmazoglu [22] also deduced from his analysis that the flow through the revolving sphere is substantially faster than the disk itself.

However, there hasn’t been any investigation into the heat and mass transfer characteristics of the Sutterby nanofluid flow, which is caused by simultaneous quadratic convective flow, quadratic thermal radiation flux, magnetic field, and electric field. The goal of the current work is to ascertain the properties of heat transfer in quadratic convective unsteady stagnation point flow of Sutterby nanofluid over a spinning sphere. The following are some points that emphasize how innovative the current investigation is:

  1. 1.

    To enhance the existing literature [19], the non-Newtonian Sutterby nanofluid term has been added to the problem, which increases the novelty of the current work.

  2. 2.

    The flow is subjected to the combined effects of the electric field, magnetic field, and quadratic thermal radiation flux.

  3. 3.

    It is challenging to select a certain type of initial guess for numerical methods including homotopy analysis, bvp4c, spectral quasi-linearization, and finite element approaches. The universal approximation theorem [23] claims that, in contrast to these techniques, an artificial feed-forward network with one hidden layer can approximate any arbitrarily complex function with sufficient units. The resultant equations have been solved using the numerical approach Artificial Neural Networks (ANN) utilizing the JAX library in Python.

  4. 4.

    It has been researched and shown, using graphs and tables, how physical characteristics affect primary and secondary velocity, temperature, and concentration fields. Additionally, a graph illustrating the mean square error has been investigated and provided.

This paper is organized into five sections, and Sect. 2 contains the physical interpretation of the problem, mathematical modeling, similarity conversions, a non-dimensional form of the governing equation, and physical quantities. In Sect. 3, details of the numerical approach are presented. Next, the results and discussion are presented in Sect. 4. The conclusion is offered in Sect. 5, which is followed by the author’s contribution, the funding statement, the availability of data and material, conflicts of interest, ethical approval, and references.

2 Physical interpretation and modeling

2.1 Physical interpretation

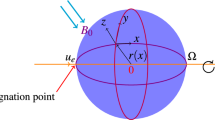
Assume that an electrically incompressible Sutterby nanofluid moves in a time-dependent quadratic convective flow around a spinning sphere while experiencing convective heating, quadratic thermal radiation, and zero mass flux conditions. The coordinate system and flow configuration are shown in Fig. 1 . The working problem is predicated on the following a few distinct hypotheses:

  • All fluid properties are assumed to be constant except the density variation in the buoyancy force term of the x-momentum equation.

  • The y-axis is perpendicular to the x- and z-axes, which are measured along the sphere’s surface and rotating axis, respectively.

  • \(T_f\) and \(C_w\) are used to represent the surface temperature and concentration, which are assumed to be constant, while \(T_{\infty }\) and \(C_{\infty }\) are used to represent the ambient temperature and concentration.

  • The consequences of the induced magnetic and electric fields are ignored under low magnetic Reynolds number assumptions.

  • The electric field \(E_{0}(t) = \frac{E_o}{\root 3 \of {t}}\) and magnetic field \(B_{0}(t) = \frac{B_0}{\sqrt{t}}\) is as considered normal to the flow.

Fig. 1
figure 1

Flow configuration

Full size image

2.2 Mathematical modeling

By taking into account the aforementioned premises, the governing equations [4, 19,20,21, 24, 25] are:

$$\begin{aligned}&\frac{\partial }{\partial x}(ru) + \frac{\partial }{\partial y}(rv) =0 \end{aligned}$$
(1)
$$\begin{aligned}&\rho _f\left[ \frac{\partial u}{\partial t} + u\frac{\partial u}{\partial x} +v\frac{\partial u}{\partial y} - \left( \frac{ w^2}{r}\right) \frac{dr}{dx}-\frac{\partial U_e}{\partial t}-U_e\frac{\partial U_e}{\partial x}\right] \nonumber \\&= \mu \bigg \{\left[ 1- \frac{\gamma ^2}{6}\frac{\partial u}{\partial y}\right] ^{^{m}} \frac{\partial ^2 u}{\partial y^2}-\frac{m \gamma ^2}{6}\left[ 1-\frac{\gamma ^2}{6}\frac{\partial u}{\partial y}\right] ^{^{m-1}}\nonumber \\&\frac{\partial u}{\partial y}\frac{\partial ^2 u}{\partial y^2}\bigg \} + \frac{{\tilde{g}}}{\rho _{f}}\left[ \tilde{\beta _o } (T - T_{\infty }) + \tilde{\beta _1}(T - T_{\infty })^2\right] \nonumber \\&\quad +\frac{\sigma _{f}}{\rho _{f}}\left[ E_o(t)B_o(t) - B_o^{2}(t)(u - U_e)\right] \end{aligned}$$
(2)
$$\begin{aligned}&\rho _{f}\left[ \frac{\partial w}{\partial t} + u\frac{\partial w}{\partial x} +v\frac{\partial w}{\partial y} - \left( \frac{ w u}{r}\right) \frac{dr}{dx}\right] \nonumber \\&= \mu \bigg \{\left[ 1- \frac{\gamma ^2}{6}\frac{\partial w}{\partial y}\right] ^{^{m}} \frac{\partial ^2 w}{\partial y^2}-\frac{m \gamma ^2}{6}\left[ 1-\frac{\gamma ^2}{6}\frac{\partial w}{\partial y}\right] ^{^{m-1}}\frac{\partial w}{\partial y}\frac{\partial ^2 w}{\partial y^2}\bigg \} \nonumber \\&\quad +\frac{\sigma _{f}}{\rho _{f}}[E_o(t)B_o(t) - B_o^{2}(t)w] \end{aligned}$$
(3)
$$\begin{aligned}&\frac{\partial T}{\partial t} + u\frac{\partial T}{\partial x} + v\frac{\partial T}{\partial y} = \alpha \frac{\partial ^2 T}{\partial y^2} \nonumber \\&\quad +\frac{48{\tilde{\sigma }}T_{\infty }^2}{3{\tilde{k}}}\left[ T\frac{\partial T}{\partial y} + (\frac{\partial T}{\partial y})^2 + T \left( \frac{\partial ^2 T}{\partial y^2}\right) \right] -\frac{32 {\tilde{\sigma }}T_{\infty }^3}{3{\tilde{k}}}\left( \frac{\partial T}{\partial y} + \frac{\partial ^2 T}{\partial y^2}\right) \nonumber \\&+{\tilde{\tau }}\left( D_{B}\frac{\partial C}{\partial y}\frac{\partial T}{\partial y} + \frac{D_{T}}{T_{\infty }}\left( \frac{\partial T}{\partial y}\right) ^{2}\right) \nonumber \\&\quad + \frac{\sigma _{f}}{\rho _{f}}\left[ (u B_o(t)- E_o(t))^2 + \left( wB_o(t)-E_o(t)\right) ^2\right] \end{aligned}$$
(4)
$$\begin{aligned}&\frac{\partial C}{\partial t} + u \frac{\partial C}{\partial x} + v\frac{\partial C}{\partial y} = D_{B}\frac{\partial ^2 C}{\partial y^2} + \frac{D_T}{T_{\infty }}\frac{\partial ^2 T}{\partial y^2} \quad \quad \end{aligned}$$
(5)

where, \({\left\{ \begin{array}{ll} \rho _{f}, \alpha , \mu , D_{B}, ((\rho c_p)_{p}, (\rho c_p)_{f} ), k, \sigma _{f} , h_f, m, \gamma , {\tilde{g}}, \tilde{\beta _0}\text { and} \tilde{\beta _1}, t, (u, v, w), \text { and} \nu _f, \\ \text {respectively, refers the density, the thermal diffusivity,the dynamic viscosity,} \\ \text {the mass diffusivity,the heat capacity, the thermal conductivity}, \\ \text { the electrical conductivity, heat transfer coefficient}, \text { power-law index}, \\ \text {material time constant, acceleration due to gravity, thermal expansion coefficient}, \\ \text { time}, \text { velocity components along (x, y z)},\\ \text {kinematic viscosity of the fluid}, {\tilde{\tau }}= \frac{(\rho c)_{p}}{(\rho c)_{f}}. \end{array}\right. }\)

2.3 Initial and boundary stipulations

Initial and boundary conditions [19,20,21] are as follows:

$$\begin{aligned}&u(t, x, y) = 0, v(t, x, y) = 0, w(t, x, y) = 0, T(t, x, y) \rightarrow T_{\infty }, \nonumber \\&C(t, x, y) \rightarrow C_{\infty }\quad \text {for} \quad t < 0 \quad \quad \quad \quad \quad \quad \nonumber \\&u(t, x, y) = 0, v(t, x, y) = 0, w(t, x, y) = r\Omega (t), T = T_{\infty } + \frac{k}{h_f}\left( \frac{\partial T}{\partial y}\right) ,\nonumber \\&C = C_w, \hbox { for y = 0 and}\ t\ge 0 \nonumber \\&u(t, x, y)\rightarrow 0, U_e(t, x, y) \rightarrow 0, T(t, x, y)\rightarrow T_{\infty } , \nonumber \\&C(t, x, y)\rightarrow C_{\infty }\quad \text {as} \quad y\rightarrow \infty \quad and\quad t\ge 0 \end{aligned}$$
(6)

2.4 Similarity conversions

The similarity metrics [19,20,21] applied in the study include:

$$\begin{aligned} {\left\{ \begin{array}{ll} \zeta = y\left( \sqrt{\frac{2}{\nu _f t}}\right) , u = \left( \frac{Ax}{t}\right) f'\left( \zeta \right) , U_e = \frac{Ax}{t}, v = - \left( \sqrt{\frac{2\nu _f}{t}}\right) Af(\zeta ), w = \left( \frac{Bx}{t}\right) g(\zeta ), \Omega (t) = \frac{B}{t},\\ T = \Theta (\zeta )\left( T_f - T_{\infty }\right) + T_{\infty }, C = \Phi (\zeta )(C_w - C_{\infty }) + C_{\infty },\quad r \approx x \end{array}\right. } \end{aligned}$$
(7)

2.5 Non-dimensional form of governing equations

The nondimensional versions of the derived governing equations are:

$$\begin{aligned}&\{\left( 1- \frac{\delta }{3}f''\right) ^m - \frac{4m \delta }{3}\left( 1 - \frac{\delta }{3}f''\right) ^{m-1}f''\} f''' + Aff''\nonumber \\&\quad -\frac{1}{2}\left( 1-f'-\frac{1}{2}\zeta f''\right) + \frac{A}{2}\left( 1 - f'^2 + \gamma _2 g^2\right) \nonumber \\&\quad +\frac{A}{2}\lambda _1 \left( \Theta -\gamma _1 \Theta ^2\right) - \left( \frac{M}{2}\right) \left( f' - E - 1\right) = 0 \nonumber \\&\left[ \left( 1 - \frac{\delta }{3}g'\right) ^{m} -\frac{4m\delta }{3}(1 - \frac{\delta }{3}g')^{m-1}g'\right] g'' \nonumber \\&\quad + A \left( fg' - f'g\right) + \frac{1}{2}\left( g + \frac{1}{2}\zeta g'\right) \nonumber \\&\quad - \left( \frac{M}{2}\right) \left( g - E\right) = 0 \nonumber \\&\left[ 1+ \frac{Rd}{4}\{3\left( 1 + \left( \Theta _t - 1\right) \Theta \right) - 2\}\right] \Theta '' + Pr \left( \frac{\zeta }{4} \Theta ' + Nb\Theta '\Phi ' + Nt\Theta '^2 \right. \nonumber \\&\quad \left. + A f \Theta '\right) +Pr Ec \left( \frac{M}{4}\right) \left[ \left( f' - E\right) ^2 + \left( g - E\right) ^2\right] = 0\nonumber \\&\Phi '' + Pr Le\left[ A f \Phi ' + \frac{\zeta }{4} \Phi ' \right] + \frac{Nt}{Nb}\Theta '' = 0 \end{aligned}$$
(8)

with

$$\begin{aligned}&f(\zeta = 0) = f'(\zeta = 0) = 0, g(\zeta = 0) = 1, \frac{\Theta '(\zeta = 0)}{Bi} = \Theta (\zeta = 0) - 1, \nonumber \\&Nb \Phi '(\zeta = 0) + Nt \Theta '(\zeta = 0) = 0, f ' (\infty ) = 1,\nonumber \\&g(\infty ) = 0, \Theta (\infty ) = \Phi (\infty ) = 0 \end{aligned}$$
(9)

where, \({\left\{ \begin{array}{ll} Gr_x = \frac{{\tilde{g}}\tilde{\beta _o} T_{\infty }(\Theta _t - 1)x^3}{\nu _f ^2} \quad \text {is Grashof number}, \quad Ec = \frac{U_e^2}{T_{\infty }(\Theta _t -1)(\rho c_p)_f}\quad \text {is Eckert number}, \quad \\ Rd = \frac{16 {\tilde{\sigma }} T_{\infty }^3}{3 {\tilde{k}}k_f} \quad \text {is quadratic thermal radiation parameter}, \quad Pr = \frac{\nu _f}{\alpha _f} \quad \text { is Prandtel number}\\ \Theta _t = \frac{T_f}{T_{\infty }} \quad \text {is temperature ratio parameter}, \quad M = \frac{\sigma _f B_o ^2}{\rho _f} \quad \text {is magnetic parameter},\\ E = \frac{E_o}{B_o U_e} \quad \text {is electric parameter}, \quad \gamma _2 = (\frac{B}{A})^2 \quad \text { is rotation parameter}, \\ Re_x = \frac{U_e x}{\nu _f} \quad \text {is Reynolds number}, \quad \lambda _1 = \frac{G_r}{Re_x^2}\quad \text {is buoyancy constraint}, \\ \gamma _1 = \frac{\tilde{\beta _1} T_{\infty }(\Theta _t - 1)}{\tilde{\beta _o}} \quad \text {is quadratic convection parameter}, \\ \quad \delta = \gamma ^2\sqrt{Re_x} \quad \text {is fluid parameter}, N_t = \frac{\tau D_T}{\alpha T_\infty }(T_f - T_\infty ) \text {is thermophoresis constraint},\\ L_e = \frac{\alpha }{D_B} \text { is Lewis number}, N_b = \frac{\tau D_B}{\alpha }(C_w - C_\infty ) \text {is Brownian motion constraint}. \end{array}\right. }\)

2.6 Physical quantities

The physical quantities [26, 27] are

$$\begin{aligned} \sqrt{ A Re_x} C_{fx}= & {} \frac{2\mu }{\rho _{f} U_{e}^{2}}\left( \frac{\partial u}{\partial y}\right) |_{y = 0} = \sqrt{8} f''(0) \end{aligned}$$
(10)
$$\begin{aligned} \sqrt{ A Re_x} C_{fz}= & {} \frac{2\mu }{\rho _{f} U_{e}^{2}}\left( \frac{\partial w}{\partial y}\right) |_{y = 0} = -\sqrt{8\gamma _2} g'(0) \end{aligned}$$
(11)
$$\begin{aligned} \sqrt{\frac{A}{Re}} Nu_{x}= & {} \frac{-x\big (\frac{\partial T}{\partial y}\big )|_{y = 0}}{k(T_{f} - T_{\infty })} = -\sqrt{2} \Theta ' (0) \end{aligned}$$
(12)
$$\begin{aligned} \sqrt{\frac{A}{Re}}Sh_{x}= & {} \frac{-x(\frac{\partial C}{\partial y})|_{y = 0}}{D_B(C_{w} - C_{\infty })} = -\sqrt{2} \Phi ' (0) \end{aligned}$$
(13)

3 Artificial neural network method

In this work, a neural network with a single input, four (4) outputs, and one hidden layer with j neurons is constructed, which is shown in Fig. 2. For each output one neural network is constructed. The outputs, \(N_n(\zeta ; w,b)\), of the proposed neural network can be expressed as,

$$\begin{aligned} N_n(\zeta ;w,b)=\sum _{j}\sigma _1\left( \zeta *w_{nj}^{h} + b_{nj}^{h}\right) *w_{nj}^{o}+b_{n}^{o}, \end{aligned}$$
(14)

where \(n=1,2,3,4\) are outputs index, \(\sigma _1:{\mathbb {R}}^{j}\rightarrow {\mathbb {R}}^{j}\) is the activation function applied to each neuron element-wise, and \(w=(w_{nj}^{h},w_{nj}^{o})\) and \(b=(b_{nj}^{h},b_{n}^{o})\), are the weights and biases of the network respectively. The symbol \(''*''\) stands for scalar product, while the letters h and o represent hidden and output layers, respectively. The neural network’s weights and biases are randomly generated first, then trained to minimize the loss function. In short, we find the neural network weights and biases that best approximate a solution, \(\{f(\zeta ), g(\zeta ), \Theta (\zeta ), \Phi (\zeta )\}\), of governing Eq. (8).

Fig. 2
figure 2

A feed-forward artificial neural network architecture with a single hidden layer and four outputs. For each output one neural network architecture with the same input is used

Full size image

Since the differential equation (8) is written in a general form we can easily convert the problem of solving the differential equations to an optimization problem [28]. The trial solutions to the problem are expressed as the neural network outputs;

$$\begin{aligned} {\bar{f}}(\zeta )= & {} N_1(\zeta ;w,b),\, {\bar{g}}(\zeta )=N_2(\zeta ;w,b),\,{\bar{\Theta }}(\zeta )\\= & {} N_3(\zeta ;w,b),\, {\bar{\Phi }}(\zeta )=N_3(\zeta ;w,b) \end{aligned}$$

Then the approximate solution \(\{{\bar{f}}(\zeta ),\, g(\zeta ),\, {\bar{\Theta }}(\zeta ),\,{\bar{\Phi }}(\zeta )\}\) to (8) can be obtained by finding the weights and biases of the neural network that minimizes the following loss function:

$$\begin{aligned} \begin{aligned} L(\zeta ;w,b)&=\frac{1}{{\tilde{m}}}\left( G_1(\zeta ;w,b)^2+G_2(\zeta ;w,b)^2\right. \\&\quad \left. +G_3(\zeta ;w,b)^2+G_4(\zeta ;w,b)^2\right. \\&\quad \left. +G_5(\zeta ;w,b)^2+G_6(\zeta ;w,b)^2\right. \\&\quad \left. +G_7(\zeta ;w,b)^2+G_8(\zeta ;w,b)^2+G_9(\zeta ;w,b)^2\right. \\&\quad \left. +G_{10}(\zeta ;w,b)^2+G_{11}(\zeta ;w,b)^2\right. \\&\quad \left. +G_{12}(\zeta ;w,b)^2+G_{13}(\zeta ;w,b)^2\right) . \end{aligned} \end{aligned}$$
(15)

where \({\tilde{m}}\) is the discretization of the domain of an input into finite points and

$$\begin{aligned} G_1(\zeta ;w,b)&=\left[ \left( 1- \frac{\delta }{3}\frac{\partial ^2 N_1}{\partial \zeta ^2}\right) ^m \right. \\&\quad \left. - \frac{4m \delta }{3}\left( 1 -\frac{\delta }{3}\frac{\partial ^2 N_1}{\partial \zeta ^2}\right) ^{m-1} \frac{\partial ^2N_1}{\partial \zeta ^2}\right] \frac{\partial ^3N_1}{\partial \zeta ^3}\\&\quad +A N_1\frac{\partial ^2N_1}{\partial \zeta ^2} -\frac{1}{2}\left( 1-\frac{\partial N_1}{\partial \zeta }-\frac{1}{2}\zeta \frac{\partial ^2N_1}{\partial \zeta ^2}\right) \\&\quad + \frac{A}{2}\left( 1 -\left( \frac{\partial N_1}{\partial \zeta }\right) ^2 + \gamma _2 N_2^2\right) \\&\quad +\frac{A}{2}\lambda _1 (N_3 -\gamma _1 N_3^2) - \left( \frac{M}{2}\right) \left( \frac{\partial N_1}{\partial \zeta } - E - 1\right) , \end{aligned}$$
Fig. 3
figure 3

\(f'(\zeta )\) and \(g(\zeta )\) against A

Full size image
Fig. 4
figure 4

\(f'(\zeta )\) and \(g(\zeta )\) against M

Full size image
$$\begin{aligned}&G_2(\zeta ;w,b) =\left[ \left( 1 - \frac{\delta }{3}\frac{\partial N_2}{\partial \zeta }\right) ^{m} \right. \\&\quad \left. -\frac{4m\delta }{3}\left( 1 - \frac{\delta }{3}\frac{\partial N_2}{\partial \zeta }\right) ^{m-1}\frac{\partial N_2}{\partial \zeta }\right] \frac{\partial ^2N_2}{\partial \zeta ^2} \\&\quad + A\left( N_1\frac{\partial N_2}{\partial \zeta } - \frac{\partial N_1}{\partial \zeta }N_2\right) \\&\quad + \frac{1}{2}\left( N_2 + \frac{1}{2}\zeta \frac{\partial N_2}{\partial \zeta }\right) - \left( \frac{M}{2}\right) (N_2 - E),\\&G_3(\zeta ;w,b) =\left[ 1+ \frac{Rd}{4}\{3(1 + (\Theta _t - 1)N_3) - 2\}\right] \frac{\partial ^2N_3}{\partial \zeta ^2} \\&\quad + Pr \left( \frac{\zeta }{4}\frac{\partial N_3}{\partial \zeta }\right. \\&\quad \left. + Nb\frac{\partial N_3}{\partial \zeta }\frac{\partial N_4}{\partial \zeta } + Nt(\frac{\partial N_3}{\partial \zeta })^2 \right. \\&\quad \left. + A N_1 \frac{\partial N_3}{\partial \zeta }\right) + Pr Ec \left( \left( \frac{M}{4}\right) \left[ \left( \frac{\partial N_1}{\partial \zeta } - E\right) ^2 + (N_2 - E)^2\right] , \right. \\&G_4(\zeta ;w,b) =\frac{\partial ^2 N_4}{\partial \zeta ^2} + Pr Le\left[ A N_1 \frac{\partial N_4}{\partial \zeta } \right. \\&\quad \left. + \frac{\zeta }{4} \frac{\partial N_4}{\partial \zeta } \right] + \frac{Nt}{Nb}\frac{\partial ^2 N_3}{\partial \zeta ^2}.\\&\text {with corresponding boundary conditions}\\&G_5(\zeta ;w,b) =N_1(0;w,b), \\&G_6(\zeta ;w,b) =\frac{\partial N_1}{\partial \zeta }(0;w,b), \\&G_7(\zeta ;w,b) =N_2(0;w,b) -1,\\&G_8(\zeta ;w,b) =\frac{\frac{\partial N_3}{\partial \zeta }(0;w,b)}{Bi} - N_3(0;w,b) + 1,\\&G_9(\zeta ;w,b) =Nb \frac{\partial N_4}{\partial \zeta }(0;w,b) + Nt \frac{\partial N_3}{\partial \zeta }(0;w,b), \\&G_{10}(\zeta ;w,b) =\frac{\partial N_1}{\partial \zeta } (\infty ;w,b)-1, \\&G_{11}(\zeta ;w,b) =N_2(\infty ; w,b), \\&G_{12}(\zeta ;w,b) =N_3(\infty ;w,b),\\&G_{13}(\zeta ;w,b) =N_4(\infty ;w,b). \end{aligned}$$

So, the problem becomes minimizing \(L(\zeta ;w,b)\) subject to w and b by choosing the hyper-parameters such as number of neurons, learning rate, momentum, activation function, which is the same as minimizing the neural network’s mean squared error (MSE) and is defined as

$$\begin{aligned} \min _{w,b}\, L(\zeta ;w,b) \end{aligned}$$
(16)

To evaluate the error, the derivatives of network outputs, \({\bar{f}}(\zeta ),\, {\bar{g}}(\zeta ), \,{\bar{\Theta }}(\zeta ),\,{\bar{\Phi }}(\zeta )\), with respect to its input were calculated. Lagaris et al. [29] have presented the automatic differentiation to compute the derivatives of a function, and the implementation is done using the JAX library in Python. The optimization can then be made via backpropagation by the gradient descent method to find the weights and biases of the NN by solving the stochastic gradient (SGD) of a loss function with respect to weights and biases. The results presented in this work were obtained using \(N = 300\) discretization points, and the neural network(NN) used consists of one hidden layer with 30 neurons and is being trained for about 20,000 epochs with a learning rate of \(5\times 10^{-3}\) and momentum = 0.99. The sigmoid activation function \(\sigma _1(x)=\frac{1}{1+e^{-x}}\) is used in all experiments.

4 Results and discussion

For various scales of values of the governing physical parameters, the ANN (Artificial Neural Network) approach is used to solve the nonlinear ordinary differential Eq. (8) subject to the boundary conditions (9). The following graphs and tabular results were made using a variety of physical parameters with values of m = 2, Rd = 0.01, Bi = 1, Le = 0.1, Ec = 0.03, Pr = 7.38, \(\Theta _t = Nt = Nb =0.1\), M = 0.1, \(\delta =0.1\), E = 0.01, A = 0.1, \(\gamma _1=0.3,\,\lambda _1 = \gamma _2 = 0.5\).

4.1 Velocity profiles

In Fig. 3, the impact of the acceleration (unsteadiness) parameter (A) on the primary and secondary velocity profiles is shown. The unsteadiness parameter increases the velocity along the x-direction (primary velocity), whereas it decreases the velocity along the z-direction (secondary velocity), as seen in Fig. 3. Physically, when \(A>0\), the momentum is redistributed and accelerates in the x-direction due to the sphere’s rotation. Figures 4 and 5 show the effects of the parameters of the magnetic field and electric field on the primary and secondary velocity. As seen in Fig. 4, an increase in the magnetic field parameters results in a main velocity increase and a secondary (rotational) direction velocity decrease. In terms of physics, the magnetic field and the Lorentz force are strongly associated, with the Lorentz force being physically inversely correlated with the magnetic field’s size. So, a low-speed flow of Sutterby nanofluid occurs in the boundary layer as a result of the Lorentz force amplifying the frictional (drag) force. However, a Coriolis force confirms the opposing influence on the Sutterby nanofluid velocity along the primary (x-direction), imposing a rise in the primary velocity. Additionally, as seen in Fig. 5, accelerating the electric field parameter speeds up the flow of Sutterby nanofluid in both the primary (x-direction) and secondary directions (z-direction). In terms of physics, the Lorentz force produced by the electric field acts as a propelling force, reducing frictional resistance and raising the fluid’s velocity. The impact of the Sutterby fluid parameter on primary and secondary velocities is seen in Fig. 6. It demonstrates how changing the Sutterby fluid parameter (\(\delta\)) causes the Sutterby nanofluid to flow in more quickly in the x-direction and more slowly in the secondary (rotational) direction. Physically, the viscidity of nanofluid increases and produces stronger resistivity forces with larger values of the Sutterby fluid parameter (\(\delta\)). Consequently, a declination in velocity occurs along the rotational (z-direction). However, due to the flow shape (a rotating sphere), this behavior is not seen along the main stream. For escalating values of rotation parameter (\(\gamma _2\)), Fig. 7 shows how primary velocity snowballs and secondary velocity decelerates. In terms of physics, the rotation becomes more intense as the values of the rotational parameters are increased, and the secondary momentum via the swirl effect contributes more to the primary momentum. The secondary flow is slowed down while the primary flow is accelerated.

Fig. 5
figure 5

e\(f'(\zeta )\) and \(g(\zeta )\) against E

Full size image
Fig. 6
figure 6

\(f'(\zeta )\) and \(g(\zeta )\) against \(\delta\)

Full size image

4.2 Temperature profiles

The impact of magnetic field (M) on the temperature field is visualized in Fig. 8. One can seen from Fig. 8 the temperature dissemination is uplifted with intensifying values of M . Physically, in the energy equation, the Lorentz force caused by a magnetic field parameter results in high Lorentz heating (Joule heating), which can be employed as an additional heat source for the flow system. Strikingly similar to the magnetic field component, the snowballing nature of \(\Theta (\zeta )\) for escalating values of \(\Theta _t\) is shown in Fig. 9. In terns of physics, the increase in \(\Theta _t\) implies a higher surface temperature than the ambient temperature, and as a result, the higher surface temperature is to blame for the wider temperature spread. The effects of the unsteadiness parameter (A), thermal Biot number (Bi), Prandtl number (Pr), and quadratic thermal radiation parameter (Rd) on the temperature transmissions, respectively, is also examined in Figs. 10, 11, 12 and 13. As shown in Fig. 10, the Sutterby nanofluid’s temperature distribution decreases as the unsteadiness parameter is increased. Physically, the shrinking of the temperature distribution with increasing snowballing values of A denotes a reduction in the size of the thermal boundary surfaces. The increased temperature and nanoparticles are then pushed to the surface of the sphere (wall) with a rising value of A as a result of the boundary layer becoming cooler. However, Fig. 11 shows that the significant convective heating brought on by the expanding thermal Biot number (Bi) results in an increase in the temperature dispersion. Physically speaking, convective heating is greatly influenced by the thermal Biot number values; a high thermal Biot number results in strong convective heating, whereas a low thermal Biot number results in weak convective heating. Additionally, as seen in Fig. 12, the outcome demonstrates that an increase in Pr results in the propagation of a reduced temperature. The Prandtl number, in terms of physics, is the ratio of momentum to thermal diffusivity. As the Prandtl number rises, momentum diffusivity tends to rise and thermal diffusivity tends to fall. A drop in the Sutterby nanofluid fluid’s temperature enforces this scenario. Furthermore, it is evident from Fig. 13 that a finer quadratic thermal radiation parameter raises the temperature of Sutterby nanofluid (\(\Theta (\zeta )\)). In terms of physics, a high value of Rd generates a lot of heat in the Sutterby nanofluid inflow zone and increases the \(\Theta (\zeta )\).

Fig. 7
figure 7

\(f'(\zeta )\) and \(g(\zeta )\) against \(\gamma _2\)

Full size image
Fig. 8
figure 8

\(\Theta (\zeta )\) against M

Full size image
Fig. 9
figure 9

\(\Theta (\zeta )\) against \(\Theta _t\)

Full size image

4.3 Concentration profiles

The effects of A, Le, Nb, Pr, Nt, and Bi in that sequence on concentration \((\Phi (\zeta ))\) is examined using the plots in Figs. 14, 15, 16, 17, 18, 19 and 20. The figures show that higher values of the acceleration (unsteadiness) parameter(see Fig. 14), Lewis number (Le), Brownian motion parameter (Nb), and Prandtl number (Pr) result in lower concentrations of Sutterby nanofluid \((\Phi (\zeta ))\). According to physical laws, the Lewis number is the product of the thermal diffusivity and mass diffusion coefficients. As the Le increases, the mass diffusion coefficient deteriorates, which lowers the concentration (see Fig. 15). The physical meaning of Nb, which is that the high in Nb is made of random motion and collision of the nanoparticles in the region of flow, also contributes to the drop in nanoparticle concentration as seen in Fig. 16. Additionally, the relationship between momentum and thermal diffusivity is the physical definition of Pr. Thus, Pr has an inverse relationship with thermal diffusivity and a direct relationship with mass diffusivity. As a result, raising Pr results in high mass diffusivity, which lowers the concentration of nanoparticles as seen in Fig. 17. While the physical interpretation of the thermophoresis parameter (Nt) is \(\frac{\tau D_{T}}{\nu _{f}} (\Theta _t - 1)\), that is, when Nt raises the resistance to mass diffusion, the concentration gradient is elevated and, as a result, the concentration distribution of Sutterby nanofluid is expanded as seen in Fig. 18. The physical description given in Fig. 11 also explains why the increase in Sutterby nanofluid concentration distribution shown in Fig. 19 is together with a rise in the thermal Biot number. Figure 20 explain the square root of the loss function (16) during the training. The root mean square error (RMSE) obtained is about \(8\times 10^{-4}\).

Fig. 10
figure 10

\(\Theta (\zeta )\) against A

Full size image
Fig. 11
figure 11

\(\Theta (\zeta )\) against Bi

Full size image
Fig. 12
figure 12

\(\Theta (\zeta )\) against Pr

Full size image

4.4 Heat transfer rate profiles

Figure 21 shows the effect of the temperature ratio parameter along with M on the local Nusselt number. As witnessed from the graph, an increment in the temperature ratio parameter led to declines in the local Nusselt number. However, as shown in Fig. 22, an increase in the thermopheric parameter Nt via M is imposed to increase the local Nusselt number. The increment in the values of the Brownian motion parameter along with the thermopheric parameter leads to a decline in the local Nusselt number, as indicated in Fig. 23. Physically, as the values of Nb increase from 0.1 to 0.4, heat is lost from the sheet as the strength of heat absorption amplifies and condenses in the thermal boundary layer thickness. Figure 24 shows that increasing the value of Pr with the thermopheric parameter Nt results in a stronger local Nusselt number.

Fig. 13
figure 13

\(\Theta (\zeta )\) against Rd

Full size image
Fig. 14
figure 14

\(\Phi (\zeta )\) against A

Full size image
Fig. 15
figure 15

\(\Phi (\zeta )\) against Le

Full size image

4.5 Solution verification

To validate our proposed numerical approach, we perform a \(f''(0)\), \(-g'(0)\), and \(-\Theta '(0)\) comparison with the works of [19], as shown in Table 1. Under limiting circumstances, we find great agreement between the present and earlier results.

4.6 Interpretation for numerical results

To explore the contributions of physical factors to skin friction (surface drag force), thermal conductivity (heat transfer rate), and mass transfer rate, Tables 2 and 3 are numerically calculated. According to Table 2, increasing the Sutterby fluid, unsteadiness, rotation, and magnetic field parameters results in an increase in the drag force (skin friction) in both the primary and secondary directions. In contrast, a rise in the electric field parameter values results in a decrease in the surface drag force in the secondary direction and an increase in the surface drag force in the primary direction. Additionally, Table 3 illustrates how \(-\Theta '(0)\) has a snowballing effect for escalating values of A, Bi, and Pr. On the other hand, a rise in the \(\Theta _t\), Rd, M, Le, Nt, and Nb results in a decrease in the \(-\Theta '(0)\). Table 3 further demonstrates that increasing Le and Nb induces an increase in the nanoparticle concentration of Sutterby nanofluid while increasing the values of Nt causes a reduction in concentration distribution because these parameters are causing the surface temperature to quickly increase and pass through the surface of the sphere. But the numerical data for the Sherwood number with rising values of \(\Theta _t\), A, Rd, Bi, M, and Pr is the opposite of the numerical data for the Nusselt number. For this reason, the numerical data for these parameters is not shown in Table 3 for the Sherwood number.

Fig. 16
figure 16

\(\Phi (\zeta )\) against Nb

Full size image
Fig. 17
figure 17

\(\Phi (\zeta )\) against Pr

Full size image
Fig. 18
figure 18

\(\Phi (\zeta )\) against Nt

Full size image
Table 1 The skin friction coefficients, heat and mass transfer rate comparison when \(M=E=\delta =\gamma _1=\Theta _t=Rd=Le=Bi=Ec=Nb=Nt=0\), Pr = 0.7
Full size table
Fig. 19
figure 19

\(\Phi (\zeta )\) against Bi

Full size image
Fig. 20
figure 20

Loss against training epochs

Full size image
Fig. 21
figure 21

Effect of \(\Theta _t\) versus M on \(-\Theta '(0)\)

Full size image
Table 2 Skin friction numerical data when \(\gamma _1 =0.3\), \(m=2, Rd=0.01, Bi=1, Le=0.1, Ec=0.03, Pr = 7.38,\) \(\Theta _t=Nt=Nb=0.1\)
Full size table
Table 3 Nusselt number and Sherwood number numerical data with \(E=0.1, m=2\), \(\delta =0.1\), \(Ec=0.03\), \(\gamma _1 =0.3\), \(\lambda _1 =\gamma _2=0.5\)
Full size table
Fig. 22
figure 22

Effect of Nt versus M on \(-\Theta '(0)\)

Full size image
Fig. 23
figure 23

Effect of Nb versus Nt on \(-\Theta '(0)\)

Full size image
Fig. 24
figure 24

Effect of Pr versus Nt on \(-\Theta '(0)\)

Full size image

5 Conclusion

Heat relocation characteristics in the time dependent quadratic convective stagnation point flow of electro-magnetic Sutterby nanofluid over a rotating sphere under the contribution of quadratic thermal radiation, convective heating and with zero mass flux conditions has been investigated in this study. The governing equations were developed using the assumptions provided in the problem statement, and the partial differential equations were then converted to ordinary differential equations using similarity conversion. The numerical approach ANN using the JAX library in Python were used in the study. The involvement of physical parameters on primary and secondary velocity, temperature and concentration fields has been studied. The major findings are shortened as under.

  1. 1.

    A growth in the values of unsteadiness parameter (A), rotation parameter (\(\gamma _2\)), magnetic field parameter (M), and Sutterby fluid parameter (\(\delta\)) increases the primarily velocity and reduces the velocity along the rotational direction.

  2. 2.

    An increment in electric field parameter (E) causes an acceleration inflow of the Sutterby nanofluid along the x-direction and rotational direction.

  3. 3.

    The intensification of \(M, Bi, \Theta _t\), and Rd increases the temperature distribution of Sutterby nanofluid.

  4. 4.

    Unsteadiness parameter (A) and Prandtl number (Pr) has similar impact on temperature dissemination.

  5. 5.

    The concentration distribution of Sutterby nanofluid is reduced with higher values of Le, A, Nb, and Pr.

  6. 6.

    The dissemination of concentration of Sutterby nanofluid is increased by finer Nt and Bi.

  7. 7.

    Increasing the unsteadiness, rotation, Sutterby fluid, and magnetic field parameters causes an increment in the surface shear stresses along the primary and secondary directions.

The current investigation is restricted to the laminar and time-dependent quadratic convective flow of incompressible Sutterby nanofluids around a rotating sphere. Additionally, the current study excludes the effects of the induced magnetic and electric fields. In the future, the phenomenon of electromagnetic induction effects on Sutterby hybrid nanofluids will be investigated using various physical geometries with different boundary conditions and novel approaches to solutions.