1 Introduction

Nanobeams have assumed a prominent role in several nano engineering structures and advanced research is instrumental in the creation of nano electromechanical systems (NEMS) and other innovations. This has led to applications that improve many aspects of life through research into nano-biomedicine, resonators, sensors, nanorobotics, etc. Vibrations of nanobeams have found expression in the field of atomic force microscopy (AFM) for scanning and manufacturing at nanoscale. The AFM was pioneered by Binnig et al. [1] and is used to scan and determine the topographical features of samples at atomic scale. The AFM is currently used in many applications including manipulation of atoms to achieve a desired structural composition of engineering materials.

The vibration characteristics of nanoscale beams can be examined within the Euler–Bernoulli framework for beams with a large aspect ratio (i.e. \(L/h > 15\)), underpinned by Eringen’s nonlocal continuum theory due to the nanoscale size of the beams as studied in a number of publications [2,3,4,5]. At macro and micro levels, classical bending theories can be used with satisfactory accuracy. When the beams reach nanoscale dimensions, modern advanced theories are employed to take the scale effects into account. These include nonlocal continuum (stress gradient) and strain gradient theories [6, 7]. The stress gradient theories include Eringen’s non-local theory (first order stress) and higher order theories like Reddy Beam Theory (RBT) and Levinson Beam Theory (LBT). Eringen’s theory postulates a unified groundwork for field equations of nonlocal continuum mechanics and provides a foundation for several stress-gradient theories [8, 9]. Higher order stress/strain gradient theories are structured to allow the transverse stress at the surface approach zero as required. Lu et al. and Gholami et al. [6, 10] investigated the strain gradient theories for nanoscale beams by considering only the local higher order strains. All these theories mentioned above provide very accurate results when benchmarked against Molecular Dynamics (MD) simulations. However, these advanced theories have an inherent hardening or softening effect on the system, meaning the frequencies can be overestimated or underestimated, when compared to molecular dynamics results. This is demonstrated in the study by Li et al. [11] which showed that with increasing nonlocal effect, the ability of the resisting compression becomes smaller leading to a hardening or softening effect on the structure of interest.

The application of flexible boundary conditions in what is termed dAFM has led to the capturing of high molecular resolution images in aqueous solutions and resolve atomic-scale surface defects as indicated in the studies by Garcı́a and Pérez [7]. The dAFM is sometimes referred to as the tap** mode AFM (TM-AFM) and was studied by Sahin et al. [8] with the inclusion of a torsional cantilever to determine and map nanomechanical changes in polymer blends. Li et al. [11] and other researchers used a variational approach to study a non-coupled system with classical and non-classical boundary conditions accounting for nonlocal strengthening and weakening effects by including torsional effects at both ends.

The inclusion of torsional effects at the boundary results in what is called a torsional probe, torsional lever or simply, a torsional cantilever [2, 3, 12, 13]. In a torsional cantilever, the clamped end is replaced with a flexible spring. At maximum spring stiffness, the boundary condition is rigid (clamped support) and at minimal spring stiffness, the beam rotates freely (pin-support). In this configuration, the flexural motion and natural frequency of the nanobeam can be altered by varying the spring stiffness. The bigger the spring stiffness, the higher the natural frequency and vice versa, similar to tuning a musical instrument. Additionally, the smaller the spring constant, the higher the tip deflection, and vice versa. This tuning effect is of particular interest and appeal for scanning samples that maybe damaged by the AFM probe tip on approach, if the probe was rigidly attached to the support [12, 13]. Furthermore, when scanning a surface, it is desirable to use a long probe in order to amplify the tip displacement and gain sensitivity. The downside is that long probes will not function optimally in a viscous fluid environment due to the viscous dam** effects [2, 3]. Therefore, using a torsional cantilever, the tip amplitude can be increased by lowering the torsional spring stiffness for a shorter beam or probe. The shorter beam in fluid environment will behave much better, with respect to dam**, than a longer beams. Basak et al. [13] have developed a model that considers the Q-factorFootnote 1 associated with dam** behaviour when torsion is applied parallel to the lengthwise direction (x-axis). On the hand, torsional cantilever can be regarded as beam loaded in torsion such that the beam undergoes an angular rotation perpendicular to the lengthwise dimension (x-axis). Sader and Yang [2, 14] studied the effects of viscous dam** and developed the relationships to quantify the Q-factor. In the former case, the torsional moment is applied in the xy-plane and in the latter case, the torsional moment is applied the yz-plane.

In the present study, the nanobeam under investigation is restrained by a torsional spring at \(x=0\) and this is to improve the sensitivity in applications involving low aspect ratio beams according Sriramshankar and Jayanth [15], whereas comparable levels of sensitivity can only be achieved by using high aspect ratio (\(L/h>15\)) beams in the case of conventional cantilevers. Furthermore, high aspect ratio beams are disadvantageous for applications in viscous mediums because of the associated dam**. In addition, rigidly mounted cantilever probe has the potential to damage to probe tip or the sample on during the sampling process. A torsional end condition at the support allows us to match the compliance of the cantilever probe to that of the sample. This is particularly important in the field of nano biosciences because most substances of interest e.g. cells, organic matter; are elastic and pliable in nature [3, 12, 13].

The classic boundary conditions for beams have been studied extensively [16, 17] at micro and macro levels. With the advent of nano materials, more research is being conducted at the nano and atomic scales. In the main, these beams are studied as individual, isolated or uncoupled systems. The present investigation couples two systems with unique frequency parameters, i.e., the beam associated with classic boundary conditions has its own unique frequencies and the spring-mass system has its own unique natural frequencies. The two sets of frequencies are consolidated into an overall system frequency, and from a consideration of all the frequencies, the motion of the tip mass can be determined. Furthermore, the two systems behave as forcing function applied by system A (beam) on system B (spring-mass) and vice versa. In essence, the beam can be regarded as a forcing function on the spring-mass system and the spring-mass system can be regarded as a forcing function on the beam due to the particular boundary conditions. This observation sets this investigation apart from recent investigations in the body of literature [16,17,18].

The solutions derived using classic theories such as the Euler–Bernoulli and Timoshenko theories cannot be applied at nanoscale and need to be modified to consider the small-scale effects. In the present investigation, the classic theories are modified by applying stress gradient theory to account for the nanoscale effects. The nanobeam carries a single degree of freedom lateral spring-mass system, comprising a longitudinal constant force spring and a concentrated mass at \(x=L\). This configuration is suitable for fine tuning the system frequencies by altering the boundary conditions, in order, to decrease or increase the frequencies and generate a desired response at the tip mass (sha**/scanning tool). The manipulation of nano samples or structures at nanoscale, i.e. removal or addition of atoms or molecules leads to changes in the mechanical behaviour of nanomaterials. The beam and spring-mass can operate as a hammer and chisel, and both the depth of penetration and force can be adjusted by tuning the elastic restraints. The longitudinal spring provides a constant axial load that is directed in the horizontal direction for small deflections, in conformity with the theories mentioned [19,20,21]. The vibration frequencies contain information about the dynamic behaviour of the entire system, i.e.: displacements of the tip of the beam, the magnitude of the mass attached to the tip, as well as velocities and accelerations [22, 23].

In Sect. 2, we consider modelling of the coupled system by presenting the fourth (4th) order nonlocal continuum differential equations of the motion for the beam, the second (2nd) order differential equations for the spring-mass system, the moment and shear force equations. In Sect. 3, we derive the buckling equation due to axial load and determine the fundamental buckling frequency. In Sect. 4, we present the boundary conditions (displacement, moments and shear force) and use these to solve for the characteristic equations. In Sect. 5, the frequency equations for various configurations that can be generated by varying the relevant parameters. Section 6 is the generation of the natural frequencies; a discussion of results and Sect. 7 is the conclusion of the investigation.

2 Nanobeam with a spring–mass and axial load at x = L

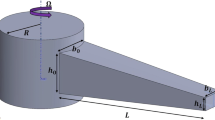
The present study involves a nanobeam which is restrained by a torsional spring \(\left({k}_{1}\right)\) at the boundary \(x=0\) and is modelled as a cantilever with a flexible restraint at the boundary \(x=L\) as shown in Fig. 1a and 1b. The stiffness of the torsional spring can be adjusted to simulate an elastic beam support with the spring exerting a varying torsional force. At the free end of the beam \(x=L\), a time-dependent axial load \(N\left(x,t\right)\) is applied in compression (+ ve) or tension (− ve). A single degree of freedom spring-mass system is attached at \(x=L\) (Fig. 1). The lateral linear spring stiffness \(\left({k}_{2}\right)\) can be varied to control the frequency of the spring-mass system, and consequently the frequency of the entire system. The pertinent information needed to achieve the desired penetration depth is contained in the consolidated frequencies of vibration.

Fig. 1
figure 1

Elastically restrained beam with concentrated axial load and spring-mass attached at free end

Full size image

The diagrams in Fig. 1 are simplified in Fig. 2 to indicate the tip displacement of the nanobeam structure and the tip-mass. The displacement of the beam is indicated by \(w\left(x,t\right)\), where \(w\left(x,t\right)\) contains the temporal domain and the modal domain functions which include the sum of an infinite number of modes in the modal domain.

Fig. 2
figure 2

Deflection of the beam with constant axial load and spring-mass attached at free end

Full size image

The displacement of the tip-mass is indicated by \(z\left(t\right)\) and is dependent on time and the position of the spring-mass system along the length of the beam \(0<x<L\). The amplitude of vibration of the tip-mass is \({z}_{o}\) and is coupled to the beam displacement. Attached to the free end of the beam at \(x=L\) is a sculpting/scanning tool which can be modelled as a mass with a sharp tip. The mass is attached to the beam by means of a linear spring \(\left({k}_{2}\right)\) such that the center of gravity of the tip mass coincides with the tip of the beam. Figure 3a shows the dAFM tip approaching the sample and Fig. 3b shows the dAFM interacting with the sample in a viscous medium.

Fig. 3
figure 3

Nanobeam probe with spring-mass approaching sample of interest a sample in open air, b stubby probe in viscous fluid medium

Full size image

During the scanning process, a contact force is produced between the tip mass and the sample to be profiled. The force results in the acceleration of the mass and combined with the distance, a vibration frequency can be extrapolated. The spring-mass system is excited by the displacement of the tip of the nanobeam during motion, generating a multiplicative effect on the displacement of the mass at the appropriate frequency. To proceed with the solution, the constitutive relation of stress–strain for the beam based on nonlocal theory of elasticity can be expressed as,

$${\sigma }_{xx}-\overline{\mu }\frac{{\partial }^{2}{\sigma }_{xx}}{{\partial x}^{2}}=E{\mathcal{E}}_{xx}$$
(1)

where \(E\) is the effective Young’s modulus, \({\mathcal{E}}_{xx}\) is the longitudinal strain, \(\overline{\mu }={e}_{o}{l}_{i}\) is the small-scale parameter with \({e}_{o}\) denoting a material constant and \({l}_{i}\) the characteristic length which are determined using Molecular Dynamics (MD) simulations. This constant \(\overline{\mu }\) indicates the extent of the effect on the molecular properties at nanoscale in the stress-gradient terms. The small scaling parameter,\({e}_{o}\), which a function of atomic structure, chirality and frequency is determined experimentally by matching of the dispersion curves via nonlocal theory for plane wave and lattice dynamics. The characteristic length (\({l}_{i}\)) is a function of the small length scales such as lattice spacing between individual atoms, surface properties, grain size, etc. The nonlocal expression for moment \(M\left(x\right)\) is given by,

$$ M\left( x \right)-\bar{\mu }\frac{{\partial ^{2} M\left( x \right)}}{{\partial x^{2} }} = EI\frac{{\partial ^{2} w}}{{\partial x^{2} }} $$
(2)

where \(I\) is the effective moment of inertia. The equation of motion for a nonlocal nanobeam undergoing transverse vibrations subject to varying axial load \(N\left(x,t\right)\) and varying cross-sectional area \(A(x)\) is given by Reddy [22] and can be expressed as,

$$EI\frac{{\partial }^{4}w\left(x,t\right)}{{\partial x}^{4}}-\left(1-\overline{\mu }\frac{{\partial }^{2}w\left(x,t\right)}{{\partial x}^{2}}\right)\cdot N\left(x,t\right)\frac{{\partial }^{2}w\left(x,t\right)}{{\partial x}^{2}}+\left(1-\overline{\mu }\frac{{\partial }^{2}w\left(x,t\right)}{{\partial x}^{2}}\right)\cdot \rho A\left(x\right)\frac{{\partial }^{2}w\left(x,t\right)}{{\partial t}^{2}}=F(x,t)$$
(3)

where \(\rho \) is the density and \(\text{A}\) is the cross-sectional area of the nanobeam. The externally applied load \(F\left(x,t\right)\) is zero during free vibration. The transverse spring \(\left({k}_{2}\right)\) is not included in the equation of motion but is introduced via the boundary condition of the beam at \(x=L\). The 2nd order differential equation of motion, including a forcing function, for the spring mass system is given by,

$${M}_{T}\frac{{\partial }^{2}z\left(t\right)}{{\partial t}^{2}} +{k}_{2}z\left(t\right)= {k}_{2}w\left(L,t\right)$$
(4)

The equation of motion of the tip mass is given by Eq. (4) and the two systems in Eqs. (3) and (4) are coupled through the motion of the tip \(w\left(L,t\right)\).

Forces and moments acting on an infinitesimal section beam are shown in Fig. 4. In Fig. 4, Q(x,t) the shear force and N(x,t) the axial load is referred to as forces Q and \({\text{N}}\) acting on the nanobeam with \({{\rho}}\) and \({\text{A}}\) denoting the density and the cross-sectional area of the nanobeam. By taking the sum of the forces in the longitudinal and transverse directions and moments about the center of the element, the governing equations of motion are derived as,

Fig. 4
figure 4

Infinitesimal section of beam showing forces and moments for a beam displaced from equilibrium position

Full size image
$$M=-EI\frac{{\partial }^{2}w\left(x,t\right)}{{\partial x}^{2}}+\overline{\mu }\left[N\frac{{\partial }^{2}w\left(x,t\right)}{{\partial x}^{2}} -\rho A\frac{{\partial }^{2}w\left(x,t\right)}{{\partial t}^{2}}\right]$$
(5)
$$Q=EI\frac{{\partial }^{3}w\left(x,t\right)}{{\partial x}^{3}}+N\frac{\partial w\left(x,t\right)}{\partial x}-\overline{\mu }\left[N\frac{{\partial }^{3}w\left(x,t\right)}{{\partial x}^{3}} -\rho A\frac{{\partial }^{3}w\left(x,t\right)}{\partial x{\partial t}^{2}}\right]$$
(6)

Using Eqs. (5) and (6), and incorporating the nonlocal effects as given by the non-local parameter (\(\overline{\mu }={e}_{o}{l}_{i}\)), the equation of motion for a nonlocal nanobeam with constant axial load, uniform cross-section and zero external load in transverse free vibration is derived as,

$$EI\frac{{\partial }^{4}w\left(x,t\right)}{{\partial x}^{4}}+N\frac{{\partial }^{2}w\left(x,t\right)}{{\partial x}^{2}}-\overline{\mu }N\frac{{\partial }^{4}w\left(x,t\right)}{{\partial x}^{4}}-\rho A\frac{{\partial }^{2}w\left(x,t\right)}{{\partial t}^{2}}+\overline{\mu }\rho A\frac{{\partial }^{4}w\left(x,t\right)}{{\partial x}^{2}{\partial t}^{2}}=0$$
(7)

3 Critical buckling load due axial load

The axial load can act both in compression and tension and the magnitude of the force in compression should be limited in order prevent buckling failure. The magnitude of the axial load can be expressed by expressing the applied load (\(N\)) in terms of the critical buckling load (\({N}_{cr}\)) of the nanobeam, i.e.,

$${N=k\cdot N}_{cr}$$
(8)

where \(k\) is the axial load fraction and allows for the axial load to be selected in a given range. In the present study the values of \(k\) are taken as, \(k=+0.8,+0.4, 0 ,-0.4,-0.8\). To determine the critical buckling load of the system, the equation of motion Eq. (7) is written below with the time-dependent terms set to zero to obtain the buckling equation given by,

$$EI\frac{{d}^{4}w\left(x\right)}{{dx}^{4}}+N\frac{{d}^{2}w\left(x\right)}{{dx}^{2}} -\overline{\mu }N \frac{{d}^{4}w\left(x\right)}{{dx}^{4}} =0$$
(9)

Equation (9) is a 4th order differential equation which can be reduced to a 2nd order differential equation by integrating twice with respect to x. After integrating twice, we derive an equation with two integration constants, \(E\) and \(F\) given by,

$$\left(EI-\overline{\mu }N\right)\frac{{\partial }^{2}w\left(x\right)}{{\partial x}^{2}}+Nw\left(x\right)=Ex+F$$
(10)

The LHS side of Eq. (10) has a homogeneous solution of the form,

$$\frac{{\partial }^{2}w\left(x\right)}{{\partial x}^{2}}+{\lambda }^{2}w\left(x\right)=0$$
(11a)
$${\lambda }^{2}=\frac{N}{\left(EI-\overline{\mu }N\right)} , N=\frac{{\lambda }^{2}}{\left(1+\overline{\mu }{\lambda }^{2}\right)}EI$$
(11b)

The solution for the second order differential Eq. (11a) has two parts, namely; a homogenous solution and a particular solution which are determined using the boundary conditions. The final solution is the sum of the homogenous and particular solutions and can be expressed as,

$$w\left(x\right)=A sin\left(\lambda x\right)+B cos\left(\lambda x\right)+\frac{1}{{\lambda }^{2}}\left(Ex+F\right)$$
(12)

The constants, \(A\), \(B\), \(E\) and \(F\) can be determined from the displacement and moment boundary conditions at \(x=0\) which are given by,

$${\left.w\left(x\right)=0 \right|}_{x=0}$$
(13)
$${\left.EI\frac{{d}^{2}w\left(x\right)}{{dx}^{2}}-\overline{\mu }N\frac{{d}^{2}w\left(x\right)}{{dx}^{2}}-{k}_{1}\frac{dw\left(x\right)}{dx}=0\right|}_{x=0}$$
(14)

and the moment and shear forces at \(x=L\), viz.

$${\left.EI\frac{{d}^{2}w\left(x\right)}{{dx}^{2}}-\overline{\mu }N\frac{{d}^{2}w\left(x\right)}{{dx}^{2}}=0 \right|}_{x=L}$$
(15)
$${\left.EI\frac{{d}^{3}w\left(x\right)}{{dx}^{3}}-\overline{\mu }N\frac{{d}^{3}w\left(x\right)}{{dx}^{3}}-N\frac{dw\left(x\right)}{dx}=0\right|}_{x=L}$$
(16)

After inserting the general solution into the boundary conditions, only three constants can be determined and the fourth constant is set to unity, and this results in a transcendental equation with roots corresponding to the various buckling modes. The lowest root of the transcendental equation gives the critical buckling load with the transcendental equation for the torsional cantilever given by,

$$-\frac{\mathrm{sin}\left(\lambda L\right)}{{k}_{1}}+\gamma \mathrm{cos}\left(\lambda L\right)=0$$
(17)

The solution given by \(\lambda =0\) is a trivial solution and therefore the transcendental equation is solved numerically to determine the non-trivial solutions. When \({k}_{1}\to 0\), the transcendental equation corresponds to that of a simply supported beam, i.e., \(\mathrm{sin}\left(\lambda L\right)=0\). When \({k}_{1}\to \infty \), the equation applies to a cantilever beam, i.e., \(\mathrm{cos}\left(\lambda L\right)=0\) as derived in Reddy [23]. The 1st root of the equation is substituted into Eq. (11b) to obtain the critical buckling load of the system (\({N}_{cr}\)), as indicated in the diagram shown in Fig. 5.

Fig. 5
figure 5

Characteristic graph for the buckling of nanobeam for torsional spring constant ratio: \({{\varvec{k}}}_{1}\) = 101, 101.5, 102 and 105. ① graph for \({{\varvec{k}}}_{1}\) = 105 and ② graph for \({{\varvec{k}}}_{1}\) = 101

Full size image

The graph in Fig. 5 shows the critical buckling frequency for the first (1st) and second (2nd) buckling modes for varying torsional spring constants \({k}_{1}\) = 101 (moderate stiffness), \({k}_{1}\) = 101.5 and 102 (intermediate stiffness) and \({k}_{1}\) = 105 (completely rigid). It is noted that for the moderately stiff case (\({k}_{1}\) = 101), the buckling frequency is minimal and as the stiffness of the spring increases, the buckling frequency increases. When the spring is completely rigid (\({k}_{1}\) = 105), the buckling frequency parameter (\({\lambda }^{2}\)) has its maximum value. The roots of the four curves in Fig. 5 are inserted into Eq. (11b) to determine the critical buckling load (\({N}_{cr}\)). The critical load can then be used to solve the homogenous differential equation (Eq. 11a) and the constants \(A\), \(B\), \(E\) and \(F\) in Eq. (12).

4 Method of solution for the governing equations

Solution of the governing Eq. (7) is obtained by eigenfunction expansion of the displacement function as,

$$w\left(x,t\right)={\sum }_{n=1}^{\infty }{X}_{n}\left(x\right){T}_{n}\left(t\right)$$
(18a)
$${z}_{L}\left(t\right)={\sum }_{n=1}^{\infty }{z}_{o}{T}_{n}\left(t\right)$$
(18b)
$${\ddot{T}}_{n}\left(t\right)+{\omega }_{n}^{2}{T}_{n}\left(t\right)=0$$
(18c)

Inserting Eq. (18a) into Eq. (7) and using Eq. (18c), the differential equation of motion in the modal domain is obtained. For the spring-mass, after inserting Eq. (18b) into Eq. (4) and using Eq. (18c), the equation of motion of the tip mass is reduced to the modal domain. The natural frequency \({\omega }_{n}\) is the frequency of the \({n}^{th}\) mode of vibration which is directly related to the frequency parameter \({a}_{n}^{4}\). The differential equation in the modal mode becomes,

$${P}_{n}\cdot {X}^{{^{\prime}}{^{\prime}}{^{\prime}}{^{\prime}}}+{Q}_{n}\cdot {X}^{{^{\prime}}{^{\prime}}}-{R}_{n}\cdot X=0$$
(19a)

where,

$${P}_{n}= 1-\mu {\beta }^{2}$$
(19b)
$${Q}_{n}=\mu {a}_{n}^{4}+{\beta }^{2}$$
(19c)
$${R}_{n}={a}_{n}^{4}$$
(19d)

and,

$$ \mu = \frac{{\bar{\mu }}}{{EI}}L,\;\beta ^{2} = \frac{N}{{EI}}L^{2}, \;N = k \cdot N_{{cr}}, \;N_{{cr}} = \frac{{EI}}{{L^{2} }}\left( {\frac{{\pi ^{2} }}{{4 + \bar{\mu }\pi ^{2} }}} \right) $$
$${a}_{n}^{4}=\frac{\rho A{\omega }_{n}^{2}}{EI} ,\; {a}_{n}=\frac{{R}_{n}}{L}$$

The 2nd order differential equation of motion of the tip-mass can also be written in the modal domain and the modal displacement of the system is,

$${M}_{T}\frac{{\partial }^{2}z\left(t\right)}{{\partial t}^{2}} = {k}_{2}\left(w\left(L,t\right) -z\left(t\right)\right)$$
(20a)

Let the compression of the spring, \( {\text{z}}_{{\text{L}}} {\text{(t)}} \), be represented by the difference in the displacement of the tip of the beam (\(w\left(L,t\right)\)) and the tip-mass (\(z\left(t\right)\)) as represented in Fig. 2.

$${z}_{L}(t)=w\left(L,t\right)-z\left(t\right)$$
$$ \therefore\quad z\left( t \right) = w\left( {L,t} \right) - z_{L} (t) $$

Substituting \(z(t)\) into Eq. (20a) and using Eqs. (18a), (18b) and (18c),

$${M}_{T}\frac{{\partial }^{2}\left(w\left(L,t\right)- {z}_{L}(t)\right)}{{\partial t}^{2}} + {k}_{2}\cdot {z}_{L}(t)=0$$
$${-M}_{T}\frac{{\partial }^{2}{z}_{L}(t)}{{\partial t}^{2}} + {k}_{2}\cdot {z}_{L}(t)={-M}_{T}\frac{{\partial }^{2}w\left(L,t\right)}{{\partial t}^{2}}$$
$${z}_{o}=\frac{{{-a}_{n}^{4}X}_{n}\left(L\right)}{\left( {a}_{k}^{4}-{a}_{n}^{4}\right)}$$
(20b)

where,

$${a}_{n}^{4}=\frac{{\omega }_{n}^{2}\rho A }{EI}{\kappa }_{2}= \frac{{k}_{2}}{EI}{a}_{k}^{4}=\frac{{\kappa }_{2}}{\eta }\eta =\frac{{M}_{T}}{\rho A}$$

where \({a}_{k}^{4}\) is frequency parameter for the spring-mass system; \({\kappa }_{2}\) and \(\eta \) represent the linear spring constant ratio and the tip-mass ratio, respectively.

The frequency parameter \({a}_{n}^{4}\) is associated with the circular frequency \({\omega }_{n}\) of vibration, \(\mu \) and \({\beta }^{2}\) are the constants corresponding to the small-scale parameter and axial load, respectively. The general solutions of Eq. (19a) is given by,

$${X}_{n}\left(x\right)={A}_{n}\mathrm{cos}{(p}_{2n}x)+{B}_{n}\mathrm{sin}{(p}_{2n}x)+{C}_{n}\mathrm{cosh}{(p}_{1n}x)+{D}_{n}\mathrm{sinh}{(p}_{1n}x)$$
(21)

where the wave numbers \({p}_{1n}\) and \({p}_{2n}\) are given by,

$${p}_{1n}=\sqrt{\frac{Q+\sqrt{{Q}^{2}+4PR}}{2P}} , {p}_{2n}=\sqrt{\frac{Q-\sqrt{{Q}^{2}+4PR}}{2P}}$$
(22)

After substituting \(P\), \(Q\) and \(R\) from Eqs. (19b), (19c) and (19d) into Eq. (22), the following two equations are obtained.

$${p}_{1n}=\sqrt{\frac{{\beta }^{2}+\mu {a}_{n}^{4}}{2\left({1-\beta }^{2}\mu \right)}+\frac{1}{2}\sqrt{\frac{({{\beta }^{2} )}^{2}+4{a}_{n}^{4}-2{\beta }^{2}\mu {a}_{n}^{4}+{\mu }^{2}{a}_{n}^{8}}{{\left({1-\beta }^{2}\mu \right)}^{2}}}}$$
(23)
$${p}_{2n}=\sqrt{\frac{{\beta }^{2}+\mu {a}_{n}^{4}}{2\left({1-\beta }^{2}\mu \right)}-\frac{1}{2}\sqrt{\frac{(-{{\beta }^{2} )}^{2}+4{a}_{n}^{4}-2{\beta }^{2}\mu {a}_{n}^{4}+{\mu }^{2}{a}_{n}^{8}}{{\left(1- {\beta }^{2}\mu \right)}^{2}}}}$$
(24)

The constants \({p}_{1n}\) and \({p}_{2n}\) are the roots of the characteristic equation of the differential equation given by Eq. (19a). The first and second terms in Eq. (19a) contain the axial load ratio \({\beta }^{2}\) which is implicitly included in \(P\) and \(Q\) in Eq. (22) as shown in Eqs. (23) and (24). For the differential equation to have real roots, the square root \(\sqrt{{Q}^{2}+4PR}\) must be positive and the external square root must also be a real number. Since the axial load ratio \({\beta }^{2}\) can be both positive (compressive) or negative (tensile), we must observe the critical limits of the values of the axial load ratio \({\beta }^{2}\) to avoid complex numbers in the results. Moreover, \(\left({1-\beta }^{2}\mu \right)\ne 0\) since this would lead to the ratio in the square root to tend to infinity. Furthermore, if the internal square root in Eq. (24) is positive, the first term under the square root must be greater than the second term and positive in order to avoid imaginary roots.

The constants \({A}_{n}\), \({B}_{n}\), \({C}_{n}\) and \({D}_{n}\) are determined from the boundary conditions where the boundary conditions at \(x=0\) are zero displacement and moment and can be expressed as

$$w\left(x\right)=0$$
(25a)
$$EI\frac{{\partial }^{2}w\left(x,t\right)}{{\partial x}^{2}}+\overline{\mu }\left[N\frac{{\partial }^{2}w\left(x,t\right)}{{\partial x}^{2}} -\left(\rho A\right)\frac{{\partial }^{2}w\left(x,t\right)}{{\partial t}^{2}}\right]-{\kappa }_{1}\frac{\partial w\left(x,t\right)}{\partial \mathrm{x}}=0$$
(25b)

where \({\kappa }_{1}\) is the torsional spring constant. Using Eqs. (18a) and (18c), the moment boundary conditions can the transformed and written in the modal mode given in Eqs. (26a) and (26b) as,

$${\left.X\left(x\right)=0 \right|}_{x=0}$$
(26a)
$${\left.\left(1-\mu {\beta }^{2}\right){X}^{{^{\prime}}{^{\prime}}}+\mu {a}_{n}^{4} X- {\kappa }_{1}{X}^{^{\prime}}=0\right| }_{x=0}$$
(26b)

At the free end, taking into consideration the small-scale effect, tip mass, the linear spring and axial load, the moment and shear boundary condition at \(x=L\) can be expressed as,

$$EI\frac{{\partial }^{2}w\left(x,t\right)}{{\partial x}^{2}}+\overline{\mu }\left[N\frac{{\partial }^{2}w\left(x,t\right)}{{\partial x}^{2}} -\left(\rho A\right)\frac{{\partial }^{2}w\left(x,t\right)}{{\partial t}^{2}}\right]=0$$
(27a)
$$EI\frac{{\partial }^{3}w\left(x,t\right)}{{\partial x}^{3}}-N\frac{\partial w\left(x,t\right)}{\partial x}+\overline{\mu }\left[N\frac{{\partial }^{3}w\left(x,t\right)}{{\partial x}^{3}} -\left(\rho A\right)\frac{{\partial }^{3}w\left(x,t\right)}{\partial x{\partial t}^{2}}\right]={F}_{L}\left(L,t\right)$$
(27b)

where \({F}_{L}\left(L,t\right)={k}_{2}\cdot {z}_{L}\left(t\right)\) is the force due to the spring-mass system and \({k}_{2}\) is the linear spring constant. The displacement \({z}_{L}\left(t\right)\) is computed from the combination of Eqs. (18b) and (20b). Equation (20) is the eigenfunction expansion solution of Eq. (4) and is used to represent \({z}_{L}\left(t\right)\) in the shear boundary at the free end. Using Eqs. (18a), (18b), (18c) and (20b) in the moment and shear boundary conditions given by Eq. (27a) and (27b), the transformed boundaries are written in the modal mode as,

$${\left.\left(1-\mu {\beta }^{2}\right){X}^{{^{\prime}}{^{\prime}}}+\mu {a}_{n}^{4} X=0\right|}_{x=L}$$
(28a)
$${\left. \left(1-\mu {\beta }^{2}\right){X}^{{^{\prime}}{^{\prime}}{^{\prime}}}+\left({\mu a}_{n}^{4}+{\beta }^{2}\right){X}^{^{\prime}}-\frac{{a}_{n}^{4}\eta }{\left(1-\frac{{a}_{n}^{4}}{{a}_{k}^{4}}\right)}X=0\right|}_{x=L}$$
(28b)

where \(\eta \) is the dimensionless tip-mass ratio which can be expressed as, \(\eta ={M}_{T}/\rho A\), and \({M}_{T}\) is the tip-mass. For practical purposes, the tip-mass ratio is specified as \(\eta =0.1\) or 10% of the mass of the nanobeam in the numerical results section. Substituting Eq. (21) into the boundary condition Eq. (25a), we obtain

$${A}_{n}+{C}_{n}=0$$
(29)

The general solution Eq. (21) can now be expressed as,

$${X}_{n}\left(x\right)={B}_{n}\mathrm{ sin}{(p}_{2n}x)+{D}_{n}\mathrm{ sin}{\mathrm{h}(p}_{1n}x)+{C}_{n} \left[\mathrm{cos}({p}_{2n}x)-\mathrm{cosh}{(p}_{1n}x)\right]$$
(30)

Substituting Eq. (30) into Eq. (25b) gives

$${B}_{n}=\frac{{C}_{n}}{{\kappa }_{1}}\left(\frac{{p}_{1n}^{2}}{{p}_{2}}+{p}_{2n}\right)\mu {\beta }^{2}+ \frac{{C}_{n}}{{\kappa }_{1}}\left(\frac{{p}_{1n}^{2}}{{p}_{2}}+{p}_{2n}\right)-\frac{{p}_{1n}}{{p}_{2n}}{D}_{n}$$
(31)

and substituting \({B}_{n}\) in Eq. (31) into Eq. (30) gives the general solution expressed in terms of constants \({C}_{n}\) and \({D}_{n}\) alone. This result can be substituted into the moment boundary conditions Eq. (28a) at \(x=L\) to obtain

$${C}_{n}\cdot {\Gamma }_{1n}+{D}_{n}\cdot {\Gamma }_{2n}=0$$
(32)

where,

$$ \begin{aligned} \Gamma _{{1n}} = & - \mu {\text{sin}}\left( {p_{2} L} \right)a_{n}^{4} p_{1}^{2} + \beta ^{2} \mu ^{2} {\text{sin}}\left( {p_{2} L} \right)a_{n}^{4} p_{1}^{2} - \mu {\text{sin}}\left( {p_{2} L} \right)a_{n}^{4} p_{2}^{2} \\ & \; + \beta ^{2} \mu ^{2} {\text{sin}}\left( {p_{2} L} \right)a_{n}^{4} p_{2}^{2} + {\text{sin}}\left( {p_{2} L} \right)p_{1}^{2} p_{2}^{2} - 2\beta ^{2} \mu {\text{sin}}\left( {p_{2} L} \right)p_{1}^{2} p_{2}^{2} \\ \; + \beta ^{4} \mu ^{2} {\text{sin}}\left( {p_{2} L} \right)p_{1}^{2} p_{2}^{2} + {\text{sin}}\left( {p_{2} L} \right)p_{2}^{4} - 2\beta ^{2} \mu {\text{sin}}\left( {p_{2} L} \right)p_{2}^{4} \\ \; + \beta ^{4} \mu ^{2} {\text{sin}}\left( {p_{2} L} \right)p_{2}^{4} + \mu {\text{cos}}\left( {p_{2} L} \right)a_{n}^{4} p_{2} \kappa _{1} - \mu {\text{cosh}}\left( {p_{1} L} \right)a_{n}^{4} p_{2} \kappa _{1} \\ \; - {\text{cosh}}\left( {p_{1} L} \right)p_{1}^{2} p_{2} \kappa _{1} + \beta ^{2} \mu {\text{cosh}}\left( {p_{1} L} \right)p_{1}^{2} p_{2} \kappa _{1} - {\text{cos}}\left( {p_{2} L} \right)p_{2}^{3} \kappa _{1} \\ \; + \beta ^{2} \mu {\text{cos}}\left( {p_{2} L} \right)p_{2}^{3} \kappa _{1} \\ \end{aligned} $$

and,

$${\Gamma }_{2n}=\left(\mu \mathrm{sin}\left({p}_{2}L\right){a}_{n}^{4}{p}_{1}-\mu \mathrm{sinh}\left({p}_{1}L\right){a}_{n}^{4}{p}_{2}-\mathrm{sinh}\left({p}_{1}L\right){p}_{1}^{2}{p}_{2}+{\beta }^{2}\mu \mathrm{sinh}\left({p}_{1}L\right){p}_{1}^{2}{p}_{2}-\mathrm{sin}\left({p}_{2}L\right){p}_{1}{p}_{2}^{2}+{\beta }^{2}\mu \mathrm{sin}\left({p}_{2}L\right){p}_{1}{p}_{2}^{2}\right){\kappa }_{1}$$

where \({\Gamma }_{1n}\) and \({\Gamma }_{1n}\) are the constants introduced by applying the moment condition Eq. (27a). After substituting Eq. (30) into the shear boundary condition Eq. (28b) at \(x=L\), the transformed equation can be expressed as,

$${C}_{n}\cdot {\Gamma }_{3n}+{D}_{n}\cdot {\Gamma }_{4n}=0$$
(33)

where,

$${\Gamma }_{3n} =\left({a}_{k}^{4}-{a}_{n}^{4}\right){p}_{2}\left(\frac{\eta \mathrm{cos}\left({p}_{2}L\right){a}_{k}^{4}{a}_{n}^{4}}{\left({a}_{k}^{4}-{a}_{n}^{4}\right)}-\frac{\eta \mathrm{cosh}\left({p}_{1}L\right){a}_{k}^{4}{a}_{n}^{4}}{\left({a}_{k}^{4}-{a}_{n}^{4}\right)}-{\beta }^{2}\mathrm{sinh}\left({p}_{1}L\right)-\mu \mathrm{sinh}\left({p}_{1}L\right){a}_{n}^{4}{p}_{1}-\mathrm{sinh}\left({p}_{1}L\right){p}_{1}^{3}+{\beta }^{2}\mu \mathrm{sinh}\left({p}_{1}L\right){p}_{1}^{3}-{\beta }^{2}\mathrm{sin}\left({p}_{2}L\right){p}_{2}-\mu \mathrm{sin}\left({p}_{2}L\right){a}_{n}^{4}{p}_{2}+\mathrm{sin}\left({p}_{2}L\right){p}_{2}^{3}-{\beta }^{2}\mu \mathrm{sin}\left({p}_{2}L\right){p}_{2}^{3}-\frac{{\beta }^{2}\mathrm{cos}\left({p}_{2}L\right){p}_{1}^{2}}{{\kappa }_{1}}+\frac{{\beta }^{4}\mu \mathrm{cos}\left({p}_{2}L\right){p}_{1}^{2}}{{\kappa }_{1}}-\frac{\mu \mathrm{cos}\left({p}_{2}L\right){a}_{n}^{4}{p}_{1}^{2}}{{\kappa }_{1}}+\frac{{\beta }^{2}{\mu }^{2}\mathrm{cos}\left({p}_{2}L\right){a}_{n}^{4}{p}_{1}^{2}}{{\kappa }_{1}}-\frac{\eta \mathrm{sin}\left({p}_{2}L\right){a}_{k}^{4}{a}_{n}^{4}{p}_{1}^{2}}{\left({a}_{k}^{4}-{a}_{n}^{4}\right){p}_{2}{\kappa }_{1}}+\frac{{\beta }^{2}\eta \mu \mathrm{sin}\left({p}_{2}L\right){a}_{k}^{4}{a}_{n}^{4}{p}_{1}^{2}}{\left({a}_{k}^{4}-{a}_{n}^{4}\right){p}_{2}{\kappa }_{1}}-\frac{\eta \mathrm{sin}\left({p}_{2}L\right){a}_{k}^{4}{a}_{n}^{4}{p}_{2}}{\left({a}_{k}^{4}-{a}_{n}^{4}\right){\kappa }_{1}}+\frac{{\beta }^{2}\eta \mu \mathrm{sin}\left({p}_{2}L\right){a}_{k}^{4}{a}_{n}^{4}{p}_{2}}{\left({a}_{k}^{4}-{a}_{n}^{4}\right){\kappa }_{1}}-\frac{{\beta }^{2}\mathrm{cos}\left({p}_{2}L\right){p}_{2}^{2}}{{\kappa }_{1}}+\frac{{\beta }^{4}\mu \mathrm{cos}\left({p}_{2}L\right){p}_{2}^{2}}{{\kappa }_{1}}-\frac{\mu \mathrm{cos}\left({p}_{2}L\right){a}_{n}^{4}{p}_{2}^{2}}{{\kappa }_{1}}+\frac{{\beta }^{2}{\mu }^{2}\mathrm{cos}\left({p}_{2}L\right){a}_{n}^{4}{p}_{2}^{2}}{{\kappa }_{1}}+\frac{\mathrm{cos}\left({p}_{2}L\right){p}_{1}^{2}{p}_{2}^{2}}{{\kappa }_{1}}-\frac{2{\beta }^{2}\mu \mathrm{cos}\left({p}_{2}L\right){p}_{1}^{2}{p}_{2}^{2}}{{\kappa }_{1}}+\frac{{\beta }^{4}{\mu }^{2}\mathrm{cos}\left({p}_{2}L\right){p}_{1}^{2}{p}_{2}^{2}}{{\kappa }_{1}}+\frac{\mathrm{cos}\left({p}_{2}L\right){p}_{2}^{4}}{{\kappa }_{1}}-\frac{2{\beta }^{2}\mu \mathrm{cos}\left({p}_{2}L\right){p}_{2}^{4}}{{\kappa }_{1}}+\frac{{\beta }^{4}{\mu }^{2}\mathrm{cos}\left({p}_{2}L\right){p}_{2}^{4}}{{\kappa }_{1}}\right)$$

and,

$${\Gamma }_{4n}=-\eta \mathrm{sin}\left({p}_{2}L\right){a}_{k}^{4}{a}_{n}^{4}{p}_{1}+\eta \mathrm{sinh}\left({p}_{1}L\right){a}_{k}^{4}{a}_{n}^{4}{p}_{2}-{\beta }^{2}\mathrm{cos}\left({p}_{2}L\right){a}_{k}^{4}{p}_{1}{p}_{2}+{\beta }^{2}\mathrm{cosh}\left({p}_{1}L\right){a}_{k}^{4}{p}_{1}{p}_{2}+{\beta }^{2}\mathrm{cos}\left({p}_{2}L\right){a}_{n}^{4}{p}_{1}{p}_{2}-{\beta }^{2}\mathrm{cosh}\left({p}_{1}L\right){a}_{n}^{4}{p}_{1}{p}_{2}-\mu \mathrm{cos}\left({p}_{2}L\right){a}_{k}^{4}{a}_{n}^{4}{p}_{1}{p}_{2}+\mu \mathrm{cosh}\left({p}_{1}L\right){a}_{k}^{4}{a}_{n}^{4}{p}_{1}{p}_{2}+\mu \mathrm{cos}\left({p}_{2}L\right){a}_{n}^{8}{p}_{1}{p}_{2}-\mu \mathrm{cosh}\left({p}_{1}L\right){a}_{n}^{8}{p}_{1}{p}_{2}+\mathrm{cosh}\left({p}_{1}L\right){a}_{k}^{4}{p}_{1}^{3}{p}_{2}-{\beta }^{2}\mu \mathrm{cosh}\left({p}_{1}L\right){a}_{k}^{4}{p}_{1}^{3}{p}_{2}-\mathrm{cosh}\left({p}_{1}L\right){a}_{n}^{4}{p}_{1}^{3}{p}_{2}+{\beta }^{2}\mu \mathrm{cosh}\left({p}_{1}L\right){a}_{n}^{4}{p}_{1}^{3}{p}_{2}+\mathrm{cos}\left({p}_{2}L\right){a}_{k}^{4}{p}_{1}{p}_{2}^{3}-{\beta }^{2}\mu \mathrm{cos}\left({p}_{2}L\right){a}_{k}^{4}{p}_{1}{p}_{2}^{3}-\mathrm{cos}\left({p}_{2}L\right){a}_{n}^{4}{p}_{1}{p}_{2}^{3}+{\beta }^{2}\mu \mathrm{cos}\left({p}_{2}L\right){a}_{n}^{4}{p}_{1}{p}_{2}^{3}$$

where \({\Gamma }_{3n}\) and \({\Gamma }_{4n}\) are the constants introduced by applying the shear boundary condition Eq. (28b) at \(x=L\). The results from the moment and shear boundary conditions given in Eqs. (32) and (33) can be expressed in matrix form as,

$$\left[\begin{array}{cc}{\Gamma }_{1n}& {\Gamma }_{2n}\\ {\Gamma }_{3n}& {\Gamma }_{4n}\end{array}\right]\left[\begin{array}{c}{C}_{n}\\ {D}_{n}\end{array}\right]=\left[\begin{array}{c}0\\ 0\end{array}\right]$$
(34)

and the characteristic equation can be obtained from the determinant of Eq. (34) as,

$${\Gamma }_{1n}\cdot {\Gamma }_{4n}-{\Gamma }_{2n}\cdot {\Gamma }_{3n}=0$$
(35)

The characteristic Eq. (35) can be solved numerically to compute the roots where \({\kappa }_{1}\), \({\kappa }_{2}\), \(\eta \), \(a_{n}^{4}\), \({\beta }^{2}\), \(\mu \) and \({a}_{k}^{4}\) are the independent dimensionless constants for the nanobeam and the spring-mass system.

5 Frequency equations for arbitrary boundary conditions

The structure shown in Fig. 1 has a torsional spring (\({\kappa }_{1}\)) at \(x=0\). When the spring constant approaches zero \(\left({\kappa }_{1}\to 0\right)\), the restraint at \(x=0\) behaves as that of a pin support where there is zero resisting moment and the nanobeam spins freely. When the spring constant is not zero (\({\kappa }_{1}\ne 0\)), there is a resisting moment at the boundary, and consequently the torsional spring influences the vibrations (frequencies) of the system. On the other hand, when the spring constant approaches infinity \(\left({\kappa }_{1}\to \infty \right)\), the support is rigid, and the boundary condition corresponds to that of a cantilever (built-in) beam. In Eq. (26b) and (31), when \({\kappa }_{1}\to \infty \) the first two terms vanish, and consequently the boundary condition is zero slope (\({X}^{^{\prime}}(0)=0\)) which is consistent with the fixed end slope of a cantilever beam. At \(x=L\), a tip mass is attached to the beam by means of a transverse linear spring. When the linear spring constant is zero\(\left({\kappa }_{2}\to 0\right)\), the effect of the tip mass is not realized at the tip of the beam and therefore the tip-mass has no influence on the natural frequencies.

However, as the linear spring constant increases \(\left({\kappa }_{2}\to \infty \right)\), the effect of the tip-mass becomes more pronounced and when \({\kappa }_{2}\) is extremely large, the tip-mass is rigidly attached to the tip of the nanobeam. By varying the torsional spring constant, linear spring constant and tip-mass ratio, we derive the classic boundary conditions shown in Table 1. The frequency equation for the total system including torsional spring and spring-mass is given below in Eq. (39). By applying the limiting values in Table 1 the following characteristic equations are derived for the boundary conditions.

Table 1 Classical boundary condition derived from the system
Full size table
  1. (i)

    Clamped-Free (CF) with constant axial load:

    $$\mathrm{sinh}\left({p}_{1}L\right)\mathrm{sin}\left({p}_{2}L\right)\left(\frac{2{\beta }^{2}}{{p}_{1}{p}_{2}}-\frac{{p}_{2}}{{p}_{1}}+\frac{{p}_{1}}{{p}_{2}}\right)+\mathrm{cosh}\left({p}_{1}L\right)\mathrm{cos}\left({p}_{2}L\right)\left({\beta }^{2}\left(\frac{1}{{p}_{2}^{2}}-\frac{1}{{p}_{1}^{2}}\right)-2\right)-{\beta }^{2}\left(\frac{1}{{p}_{2}^{2}}+\frac{1}{{p}_{1}^{2}}\right)-\frac{{p}_{2}^{2}}{{p}_{1}^{2}}-\frac{{p}_{1}^{2}}{{p}_{2}^{2}}=0$$
    (36)
  2. (ii)

    Simply supported-Free (SF):

    $$\frac{1}{{\kappa }_{1}}\left(\left({p}_{2}+\frac{{p}_{1}^{2}}{{p}_{2}}\right)\mathrm{cosh}\left({p}_{1}L\right)\mathrm{sin}\left({p}_{2}L\right)+\left(-\frac{{p}_{2}^{2}}{{p}_{1}}-{p}_{1}\right)\mathrm{sinh}\left({p}_{1}L\right)\mathrm{cos}\left({p}_{2}L\right)\right) +\left(\frac{{p}_{1}}{{p}_{2}}-\frac{{p}_{2}}{{p}_{1}}\right)\mathrm{sinh}\left({p}_{1}L\right)\mathrm{sin}\left({p}_{2}L\right)-2\mathrm{cosh}\left({p}_{1}L\right)\mathrm{cos}\left({p}_{2}L\right)-\frac{{p}_{2}^{2}}{{p}_{1}^{2}}-\frac{{p}_{1}^{2}}{{p}_{2}^{2}} =0$$
    (37)
  3. (iii)

    Clamped-Simply supported (CS):

    $$\frac{1}{{\kappa }_{1}\eta }\left(-\frac{{p}_{1}{p}_{2}^{3}\mathrm{cosh}\left({p}_{1}L\right)\mathrm{sin}\left({p}_{2}L\right)}{{a}_{n}^{4}}-\frac{{p}_{1}^{3}{p}_{2}\mathrm{cosh}\left({p}_{1}L\right)\mathrm{sin}\left({p}_{2}L\right)}{{a}_{n}^{4}}\right)+\frac{1}{{\kappa }_{1}\eta }\left(\frac{{p}_{2}^{4}\mathrm{sinh}\left({p}_{1}L\right)\mathrm{cos}\left({p}_{2}L\right)}{{a}_{n}^{4}}+\frac{{p}_{1}^{2}{p}_{2}^{2}\mathrm{sinh}\left({p}_{1}L\right)\mathrm{cos}\left({p}_{2}L\right)}{{a}_{n}^{4}}\right)+\frac{1}{{\kappa }_{1}\eta }\left(\frac{{p}_{1}^{3}{p}_{2}\mathrm{cosh}\left({p}_{1}L\right)\mathrm{sin}\left({p}_{2}L\right)}{{a}_{k}^{4}}-\frac{{p}_{2}^{4}\mathrm{sinh}\left({p}_{1}L\right)\mathrm{cos}\left({p}_{2}L\right)}{{a}_{k}^{4}}-\frac{{p}_{1}^{2}{p}_{2}^{2}\mathrm{sinh}\left({p}_{1}L\right)\mathrm{cos}\left({p}_{2}L\right)}{{a}_{k}^{4}}\right)+\frac{1}{\eta {a}_{n}^{4}}\left(\left({p}_{2}^{3}-{p}_{1}^{2}{p}_{2}\right)\mathrm{sinh}\left({p}_{1}L\right)\mathrm{sin}\left({p}_{2}L\right)+2{p}_{1}{p}_{2}^{2}\mathrm{cosh}\left({p}_{1}L\right)\mathrm{cos}\left({p}_{2}L\right)+\frac{{p}_{2}^{4}}{{p}_{1}}+{p}_{1}^{3}\right)+\frac{1}{\eta {a}_{k}^{4}}\left(\left({p}_{1}^{2}{p}_{2}-{p}_{2}^{3}\right)\mathrm{sinh}\left({p}_{1}L\right)\mathrm{sin}\left({p}_{2}L\right)-2{p}_{1}{p}_{2}^{2}\mathrm{cosh}\left({p}_{1}L\right)\mathrm{cos}\left({p}_{2}L\right)-\frac{{p}_{2}^{4}}{{p}_{1}}-{p}_{1}^{3}\right)+\frac{1}{{\kappa }_{1}}\left(\frac{{p}_{2}^{3}\mathrm{sinh}\left({p}_{1}L\right)\mathrm{sin}\left({p}_{2}L\right)}{{p}_{1}^{2}}+2{p}_{2}\mathrm{sinh}\left({p}_{1}L\right)\mathrm{sin}\left({p}_{2}L\right)+\frac{{p}_{1}^{2}\mathrm{sinh}\left({p}_{1}L\right)\mathrm{sin}\left({p}_{2}L\right)}{{p}_{2}}\right)+\left(\frac{{p}_{2}}{{p}_{1}}+\frac{{p}_{1}}{{p}_{2}}\right)\mathrm{cosh}\left({p}_{1}L\right)\mathrm{sin}\left({p}_{2}L\right)-\left(\frac{{p}_{2}^{2}}{{p}_{1}^{2}}+1\right)\mathrm{sinh}\left({p}_{1}L\right)\mathrm{cos}\left({p}_{2}L\right)=0$$
    (38)
  4. (iv)

    Torsional cantilever with spring mass system and axial load:

    $$\frac{1}{{\kappa }_{1}}\left(\mathrm{cosh}\left({p}_{1}L\right)\mathrm{sin}\left({p}_{2}L\right)\left(\frac{{p}_{2}^{3}{a}_{n}^{4}{\beta }^{2}}{{p}_{1}^{4}{a}_{k}^{4}}-\frac{{p}_{2}^{3}{\beta }^{2}}{{p}_{1}^{4}}+\frac{{p}_{2}{a}_{n}^{4}{\beta }^{2}}{{p}_{1}^{2}{a}_{k}^{4}}-\frac{{p}_{2}{\beta }^{2}}{{p}_{1}^{2}}+\frac{{p}_{2}^{3}{a}_{n}^{4}}{{p}_{1}^{2}{a}_{k}^{4}}-\frac{{p}_{2}^{3}}{{p}_{1}^{2}}+\frac{{p}_{2}{a}_{n}^{4}}{{a}_{k}^{4}}-{p}_{2}\right)\right)+\frac{1}{{\kappa }_{1}}\left(\mathrm{sinh}\left({p}_{1}L\right)\mathrm{cos}\left({p}_{2}L\right)\left(\frac{{p}_{2}^{2}{a}_{n}^{4}{\beta }^{2}}{{p}_{1}^{3}{a}_{k}^{4}}-\frac{{p}_{2}^{2}{\beta }^{2}}{{p}_{1}^{3}}+\frac{{a}_{n}^{4}{\beta }^{2}}{{p}_{1}{a}_{k}^{4}}-\frac{{\beta }^{2}}{{p}_{1}}-\frac{{p}_{2}^{4}{a}_{n}^{4}}{{p}_{1}^{3}{a}_{k}^{4}}+\frac{{p}_{2}^{4}}{{p}_{1}^{3}}-\frac{{p}_{2}^{2}{a}_{n}^{4}}{{p}_{1}{a}_{k}^{4}}+\frac{{p}_{2}^{2}}{{p}_{1}}\right)\right)+\mathrm{cosh}\left({p}_{1}L\right)\mathrm{cos}\left({p}_{2}L\right)\left(-\frac{{p}_{2}^{2}{a}_{n}^{4}{\beta }^{2}}{{p}_{1}^{4}{a}_{k}^{4}}+\frac{{p}_{2}^{2}{\beta }^{2}}{{p}_{1}^{4}}+\frac{{a}_{n}^{4}{\beta }^{2}}{{p}_{1}^{2}{a}_{k}^{4}}-\frac{{\beta }^{2}}{{p}_{1}^{2}}-\frac{2{p}_{2}^{2}{a}_{n}^{4}}{{p}_{1}^{2}{a}_{k}^{4}}+\frac{2{p}_{2}^{2}}{{p}_{1}^{2}}\right)+\frac{1}{{a}_{k}^{4}}\left(\frac{{p}_{2}^{2}{a}_{n}^{4}{\beta }^{2}}{{p}_{1}^{4}}-\frac{{a}_{n}^{4}{\beta }^{2}}{{p}_{1}^{2}}-\frac{{p}_{2}^{4}{a}_{n}^{4}}{{p}_{1}^{4}}-{a}_{n}^{4}\right)+\frac{1}{{a}_{k}^{4}}\left(\mathrm{sinh}\left({p}_{1}L\right)\mathrm{sin}\left({p}_{2}L\right)\left(\frac{2{p}_{2}{a}_{n}^{4}{\beta }^{2}}{{p}_{1}^{3}}-\frac{{p}_{2}^{3}{a}_{n}^{4}}{{p}_{1}^{3}}+\frac{{p}_{2}{a}_{n}^{4}}{{p}_{1}}\right)\right)+\mathrm{sinh}\left({p}_{1}L\right)\mathrm{sin}\left({p}_{2}L\right)\left(-\frac{2{p}_{2}{\beta }^{2}}{{p}_{1}^{3}}+\frac{{p}_{2}^{3}}{{p}_{1}^{3}}-\frac{{p}_{2}}{{p}_{1}}\right)-\frac{{p}_{2}^{2}{\beta }^{2}}{{p}_{1}^{4}}+\frac{{\beta }^{2}}{{p}_{1}^{2}}+\frac{1}{{\kappa }_{1}}\left(\mathrm{sinh}\left({p}_{1}L\right)\mathrm{sin}\left({p}_{2}L\right)\left(\frac{{p}_{2}^{3}\eta {a}_{n}^{4}}{{p}_{1}^{5}}+\frac{2{p}_{2}\eta {a}_{n}^{4}}{{p}_{1}^{3}}+\frac{\eta {a}_{n}^{4}}{{p}_{1}{p}_{2}}\right)\right)+\mathrm{sinh}\left({p}_{1}L\right)\mathrm{cos}\left({p}_{2}L\right)\left(-\frac{{p}_{2}^{2}\eta {a}_{n}^{4}}{{p}_{1}^{5}}-\frac{\eta {a}_{n}^{4}}{{p}_{1}^{3}}\right)+\mathrm{cosh}\left({p}_{1}L\right)\mathrm{sin}\left({p}_{2}L\right)\left(\frac{{p}_{2}\eta {a}_{n}^{4}}{{p}_{1}^{4}}+\frac{\eta {a}_{n}^{4}}{{p}_{1}^{2}{p}_{2}}\right)+\frac{{p}_{2}^{4}}{{p}_{1}^{4}}+1=0$$
    (39)

The above characteristic equations (Eqs. 36–39) above are for classic local beam and the small-scale effects are implicitly included in the relevant constants. The small-scale effects are taken into consideration in the nonlocal characteristic equation, Eq. (35). The natural frequencies of the system \({R}_{n}\) are obtained by making a substitution, \({a}_{n}={R}_{n}/L\), into Eq. (35). The values of \({R}_{n}\) are the dimensionless natural frequencies which are used in the numerical results section. When \({\kappa }_{1}\to \infty \), the torsional spring becomes rigid, and the boundary condition behaves like that of a cantilevered beam. The classic cantilever configuration can be obtained by setting the mass equal to zero and the fundamental natural frequency of the system is \({R}_{1}=\) 1.8750 which corresponds to the results obtained by Magrab [17], i.e., \({R}_{1}=\) 0.5969π. Furthermore, when \({\kappa }_{2}\to \infty \), the linear spring is rigid and the system behaves like a cantilevered beam with concentrated tip mass because the center of gravity of the attached mass coincides with the tip of the beam, see Fig. 6.

Fig. 6
figure 6

Fundamental frequency plotted against the axial load (\({\beta }^{2}\)) and the small-scale parameter (\(\mu \)) for different values of \({\kappa }_{1}\) and \({\kappa }_{2}\), with the tip mass ratio \(\eta = 0\).1

Full size image

6 Discussion of Numerical Results: fundamental frequencies for arbitrary boundary conditions

Elastic boundary conditions allow us to simulate different configurations by altering the stiffness of the supports. In previous publications, Moutlana and Adali [24] presented results pertaining to the vibrations of the of cantilever nanobeams, were the elastic restraint at the tip of the beam is used to model an external load. Further works was conducted by including additional elastic restraint and observing the effect of varying stiffness on the displacement of the tip mass [18]. In Fig. 6, and in the subsequent plots, the torsional spring stiffness ratio is varied for a range of \({\kappa }_{1}=\) 101, 101.5, 102 and 103 and the linear spring stiffness is chosen for a range of \({\kappa }_{2}=\) 103 with the tip-mass kept constant at \(\eta =\) 0.1 or 10% of the beam mass. In Fig. 6, the bottom most contour represents \({\kappa }_{1}=\) 101 which is the lowest stiffness ratio for the torsional spring and the upper most contour plot represents \({\kappa }_{1}=\) 103, which is a rigid support.

It was noted here that the natural frequencies increase with increasing torsional spring ratio and the lowest \({R}_{1}=\) 0.6873 occurs at the maximum compressive load \({\beta }^{2}=\)+ 0.8, minimum spring stiffness \({\kappa }_{1}=\) 103 and \({\kappa }_{2}=\) 10 with the small-scale parameter set equal to zero (\(\mu =\) 0). When the small-scale parameter increases steadily to \(\mu =0.6\), the frequency of the system increases. This change is reasonably mild when the axial load is compressive (+ \(0.4\le {\beta }^{2}\le \)+ 0.8) but is more pronounced when the load is tensile \({\beta }^{2}\le \) 0.

In Fig. 6, the 2D contour plots are presented for parameters of interest, i.e., \({\beta }^{2}=\) -0.8, 0 and + 0.8, tip-mass ratio \(\eta =0\).1, and the spring constant ratios are varied over a range of 101 \(\le {\kappa }_{1}\) and \({\kappa }_{2}\le \) 103. In Fig. 7a, it is noted that the contours are approximately linear with respect to the linear spring ratio (\({\kappa }_{2}\)), due to the fact that when the linear spring ratio is constant and the torsional spring constant (\({\kappa }_{1}\)) is varied, the changes in the natural frequency are minimal at best and close to null. This indicates that the axial load dominates the dynamics when it reaches a value close to the critical buckling load. Further to that, in Eqs. (23) and (24) we note that if frequency parameter of the nanobeam is zero (\({a}_{n}^{4}=\) 0—null dynamic motion) and the small-scale parameter is zero (\(\mu =\) 0), the wave numbers, \({p}_{1}\) and \({p}_{2}\) are non-zero and are given by,

Fig. 7
figure 7

Contour plots for torsional (\({\kappa }_{1}\)) vs. linear spring (\({\kappa }_{2}\)) with axial load (\({\beta }^{2}\)) and small scale-effects (\(\mu \))

Full size image
$${p}_{1n}=\sqrt{\frac{{\beta }^{2}}{2\left(1\right)}+\frac{1}{2}\sqrt{\frac{({{\beta }^{2} )}^{2}}{{\left(1 \right)}^{2}}}}\,{\mathrm{or}}\, p_{1n}=\sqrt{\frac{{\beta }^{2}}{2}+\frac{{\beta }^{2}}{2}}=\beta $$
(40)
$${p}_{2n}=\sqrt{\frac{{\beta }^{2}}{2\left(1\right)}-\frac{1}{2}\sqrt{\frac{(-{{\beta }^{2} )}^{2}}{{\left(1 \right)}^{2}}}}\, {\mathrm{or}}\,p_{2n}=\sqrt{\frac{{\beta }^{2}}{2}-\frac{{-\beta }^{2}}{2}}=\beta $$
(41)

This shows that for a non-zero compressive axial load, the wave numbers are non-zero (\({p}_{1n}\ne \) 0 and \({p}_{2n}\ne \) 0) for a zero-frequency parameter (\({a}_{n}^{4}=\) 0). This implies that the low order vibrations below the critical value of the wave numbers are suppressed, and unable to be exited for a nanobeam under axial compressive load. Liu et al. [21] studied transverse free vibrations and stability of axially moving nanoplates based on nonlocal elasticity theory and found that the small-scale parameter has a significant effect on the stability of vibrations, and the tendency to increase or decrease the natural frequency depends on the boundary conditions [16,17,18].

If the above conditions, with respect to the frequency and small-scale parameter are met, and the axial load is zero (\({\beta }^{2}=\) 0), the characteristic equation for determining the natural frequencies (Eq. 35) vanishes. Earlier in the text, it was noted that \(\left({1-\beta }^{2}\mu \right)\ne 0\) or \({\beta }^{2}\ne 1/\mu \) and that the term under the square root in Eqs. (23) and (24) needs to be positive to avoid imaginary roots. Therefore, in the selection of the axial load, one needs to pay special attention to the range of values of all relevant parameters selected to obtain meaningful results.

Figure 6 shows the frequencies of a nanobeam under compressive axial load and small-scale parameter \(\mu =\) 0.6 and it is noted that in the presence of nonlocal effects, the frequencies tend to increase. At maximum torsional spring ratio (\({\kappa }_{2}=\) 103), the natural frequencies are maximum, and the small-scale effects have a stiffening effect on the nanobeam as observed by Reddy and Wang [23]. For zero axial load ratio (\({\beta }^{2}=0\)) in Fig. 7b and maximum torsional and linear spring ratio (\({\kappa }_{1}={10}^{3}\) and \({\kappa }_{2}={10}^{3}\)), the system behaves like a cantilever beam with a concentrated tip-mass (\(\eta =0.1\)) and the values of the natural frequencies are widely published, \({R}_{1}=\) 1.7227 [9, 16, 17] as indicated in the plot. As expected, when the torsional spring ratio increases\(\left({\kappa }_{1}\to \infty \right)\), the frequencies increase and in Fig. 7e, a further increase in the frequencies is attributed to the small-scale parameter. In Figs. 7c and f, the nanobeam is under tensile load and the frequencies are higher than the ones in the other two instances (\({\beta }^{2}=\) + 0.8 and 0). When the axial load is compressive, the linear transverse spring has minimal effect on the natural frequencies. This means that the spring mass system has an insignificant effect on the frequencies when the axial load \({\beta }^{2}=\) + 0.8. This can be observed in Fig. 7a and d by noticing that the slope for compressive loads in the graphs tends to zero (\(\Delta {\kappa }_{2}/\Delta {\kappa }_{1}\to 0\)).

Furthermore, it is noted from Fig. 7a–f that the small-scale parameter (\(\mu \)) has an influence on the natural frequencies. Figure 7a–c shows the natural frequencies of the system without consideration of the small-scale parameter (\(\mu =0\)). Under this condition, the beam behaves like a classic Euler–Bernoulli beam and we note the natural frequency of \({R}_{1}=\) 1.7227 for maximum spring constants (\({\kappa }_{1}{, \kappa }_{2}\to \infty \)) for tip-mass ratio of \(\eta =0\) and axial load \({\beta }^{2}=\) 0. Figure 7d–f shows the natural frequencies for a non-zero small-scale parameter (\(\mu =0.6\)). From the graphs, we note an increase in the natural frequencies of approximately 10%, 9% and 8% for axial load ration \({\beta }^{2}=\) + 0.8, 0 and − 0.8, respectively. The increase in the natural frequencies indicates a stiffening effect caused by the inclusion of the small-scale effects in the formulation. It is further noted that the effects of the small-scale diminish when the axial load ratio is tensile.

The spring-mass system can be isolated as shown in Fig. 8. This represents a single degree of freedom system and the frequencies for different combinations of linear spring constant and tip mass ratio are tabulated in Table 2.

Fig. 8
figure 8

Spring-mass system at x = L

Full size image
Table 2 Frequency parameter (ak) of the spring-mass system
Full size table

The frequencies of the beam are directly coupled to the frequencies of the spring-mass system and the data in Table 2 shows the pertinent details about the vibration characteristics of the entire system. Equation (20) can be rearranged and written in the form below where the left-hand side represents the ratio of the displacement of the mass from its equilibrium position to the displacement of the tip of the beam.

$$\frac{{z}_{o}}{{X}_{n}\left(L\right)}=\left(\frac{{a}_{n}^{4}}{{a}_{k}^{4}-{a}_{n}^{4}}\right)$$
(42)

It is clear from the relationship in Eq. (42) that this ratio depends entirely on the frequency parameters \({a}_{n}^{4}\) of the beam and the frequency parameters \({a}_{k}^{4}\) of the single degree of freedom system. Therefore, information about the sample penetration depth can be obtained using the frequencies in Figs. 6 and 7 and Table 2. It is noted that when the rigidity of the linear spring increases \(\left({\kappa }_{2}\to \infty \right)\), the ratio is non-zero meaning that the tip-mass moves in synch with the nanobeam tip displacement given by

$$\frac{{z}_{0}}{{X}_{n}\left(L\right)}=\frac{1}{{a}_{k}^{4}}\left(\frac{{a}_{n}^{4}}{1-{a}_{n}^{4}/{a}_{k}^{4}}\right)$$

after factoring out \({a}_{k}^{4}\), and substituting \({a}_{k}^{4}={\kappa }_{2}/\eta \), we obtain

$$\frac{{z}_{0}}{{X}_{n}\left(L\right)}=\frac{1}{{\kappa }_{2}/\eta }\left(\frac{{a}_{n}^{4}}{1-{a}_{n}^{4}/\left({\kappa }_{2}/\eta \right)}\right)$$
$$\frac{{z}_{0}}{{X}_{n}\left(L\right)}=\frac{\eta }{{\kappa }_{2}}\left(\frac{{a}_{n}^{4}}{1-{\eta a}_{n}^{4}/{\kappa }_{2}}\right)$$

Therefore, \({F}_{L}\left(L,t\right)={k}_{2}\cdot {z}_{L}\left(t\right)\) in Eq. (27b) can be written as

$${F}_{L}\left(L,t\right)={\kappa }_{2}\cdot \frac{\eta }{{\kappa }_{2}}\left(\frac{{a}_{n}^{4}}{1-{\eta a}_{n}^{4}/{\kappa }_{2}}\right){X}_{n}\left(L\right)$$

which can be expressed as

$${F}_{L}\left(L,t\right)=\frac{\eta {a}_{n}^{4}{X}_{n}\left(L\right)}{1-\left({\eta a}_{n}^{4}\right)/{\kappa }_{2}}$$

When \(\left({\kappa }_{2}\to \infty \right)\), the second term in the denominator vanishes and the shear boundary condition Eq. (27b) reduces to that of a beam with tip mass in concurrence with the References [9, 17, 18]. To achieve the maximum tip-mass deflection, the transverse spring constant ratio \({\kappa }_{2}\) must be small. For example, we can achieve more than double the additional tip-mass deflection by allowing \({\kappa }_{2}\to 1\) and at maximum torsional spring ratio, and that was demonstrated by Moutlana and Adali [18]. This means that the penetration depth in nano manufacturing using dynamic atomic force microscopy (dAFM) can be controlled. Lastly, if \({a}_{k}^{4}<{a}_{n}^{4}\) in Eq. (42), the denominator is negative, and consequently the displacement ratio is negative which indicated that the tip of the nanobeam motion is out of synch with the tip-mass displacement (i.e., they move in opposite directions).

Equation (42) articulates the relation between the frequency parameter an of the beam and the frequency parameter ak of the single degree of freedom system. The form of the equation shows that if the denominator on the right-hand side is equal to zero (an = ak), this entire term tends to infinity, i.e. \({a}_{n}^{4}/({a}_{k}^{4}-{a}_{n}^{4})\to \infty \). When this occurs, the term on the left-hand side must be infinite by necessity. Either the numerator tends to infinity, or the denominator tends to zero in the limit. When displacement of the mass from the equilibrium \(z\left(t\right)\) is infinite, the system undergoes the phenomenon called resonance, which should be avoided in manufacturing tools. When plotting the characteristic equation, the resonance frequencies of the whole system can be identified, and this information is key to the design of nano electromechanical systems.

7 Conclusions

In the present paper, axial load, spring-mass system, small-scale and torsional end condition effects on the fundamental frequency are investigated for a nanobeam. The nanobeam is elastically restrained and carries a tip mass attached via a linear spring to the end of the beam. The solution for the beam is obtained analytically by expanding the deflection in terms of its eigenfunctions and solving the resulting characteristic equation numerically. Furthermore, the characteristic equations are presented for parametric studies of the effect of support elasticity and tip mass on the fundamental frequencies of the nanobeam.

It is observed that the boundary conditions may lead to an increase or decrease of the fundamental frequency depending on the support flexibility. Boundary conditions can be expressed in terms of a torsional spring at \(x=0\), and linear spring and tip mass at \(x=L\). The classical boundary conditions correspond to setting the torsional and linear spring constants to zero \(\left({\kappa }_{\mathrm{1,2}}\to 0\right)\) or infinity \(\left({\kappa }_{\mathrm{1,2}}\to \infty \right)\). It was observed that low torsional spring stiffness leads to a decrease in the fundamental frequency and high torsional spring stiffness to an increase in the fundamental frequency, as the small-scale parameter increases. The rates of decrease and increase depend on the relative values of the spring constants. The effect of the large tip mass on the frequencies is to lower the natural frequencies as observed in these investigations [17, 24].

The lowering of the natural frequencies can be mitigated by a tensile load. The higher tensile load tends to increase the natural frequencies of the system and the rate of increase of the frequencies are lower for small torsional spring constant ratio. When the axial load is compressive, the linear transverse spring has minimal effect on the natural frequencies, and this is observed by noting that the slope for compressive loads in the graphs tends to zero (\(\Delta {\kappa }_{2}/\Delta {\kappa }_{1}\to 0\)). The small-scale parameter shows a stiffening effect on the system leading to higher natural frequencies, in the same way that the tensile axial load would behave. In the system under consideration, it is noted that the small-scale effects are reduced by the increase in tensile load.

After some reflection one can conclude that, the limitation of this study is that the beams under consideration can be further reduced in size. At nanoscale, the bulk to surface volume ratio could be high, meaning that the mass of the atoms at the surface are a fraction of the entire nanobeam. However, when the thickness of the nanobeam is reduced, e.g. a nano-beam made up of 4 layers of atoms (pico-dimensions), the bulk to surface volume are on the same order. When bulk to surface volume ratio approaches unity (\({V}_{bulk}/{V}_{surface}\to 1\)), the atoms on the surface are exposed to the environment (air or fluid) and to the atoms on the inside of the nanobeams, whilst the atoms on the inside are exposed to surface atoms and adjacent atoms. In such configurations, we need to consider the surface energies since these will be on the same order of magnitude as the bulk energies. This will have an impact on the frequencies of vibration and will be explored by augmenting incorporating Gurtin–Murdoch surface elasticity theory into the formulation of the equations of motion.