1 Introduction

The airborne Canine distemper disease caused by Canine morbillivirus had a substantial impact on a European country’s wild and domestic animals over the last two centuries [1]. The disease is common in many animals [2,3,4]. However, it reduced the African wild dog population, particularly to the verge of extinction [5]. The disease is fatal primarily in wild dogs due to its fast spread through high social interactions [6, 7]. Several intervention measures can control the disease epidemic, but understanding the disease-spreading dynamics through mathematical models is always a prime research interest. This theoretical concept can help to identify the natural infection corridor and its control through several model parameters. The reports on the past outbreaks identified some of the natural corridors of the infection for Canine distemper in Wild dogs. The airborne CDV produces tiny buds in the infected individuals that explode after systematic dysfunction, mixes into the air, and enters into a healthy individual upon infection [2]. The histopathological study on wild dogs introduced to Catskill, New York from Namibia in 1981 confirmed the modes as mentioned earlier of Canine distemper infection [8]. A notable mass death in wild dogs reduced their population in 2001 in Tanzania through the confirmed infection modes. The IUCN enlists this African wild dog as an endangered species due to various stresses acting on it. Lindsey and Woodroffe [9,10,11], and Flacke [12] revealed that habitat destruction, human persecution, and other diseases such as rabies, CPV (Canine parvovirus) along with the Canine distemper, lowered the African wild dog abundance to less than 5500. However, the canine distemper disease poses more threat over the other mentioned stresses as the disease repeatedly reemerged since the first reported outbreak in 1967 [5, 7, 13].

Despite the substantial evidence in the literature indicating the CDV as one of the critical detrimental causes for the wild dog population, there is a major lacuna in mathematical modeling on the CDV epidemic. [14] first portrayed the entire scenario of the spreading of CDV with the consortium of the mathematical modeling. Later [15] proposed a model with intervention measures on the concerned epidemic applicable to captive animals only. So the few models so far failed to identify the control of the disease through its natural immunity.

Based on the lacunae, this article aims to answer the following questions—(a) What is the most sensitive natural modulator to subdue the disease spread in Adults? (b) Which sub-population (adults or pups) is responsible for controlling the disease? (c) What is the most effective natural regulator to increase the recovered population?

To meet these objectives, we develop a five compartmental model. We formulate the model based on natural corridors of CDV infection. The transmission of the disease can occur from both infected adults and pups to susceptible adults and pups. There is evidence of vertical transmission through the placenta or milking in dogs[16]. Mostly, this vertical transmission is studied on domestic dogs. Since both are canids belonging to the same tribes, their transmission mechsanisms are similar. So, the wild dogs can also show such vertical transmission (mother to pups transmission). Since the disease is airborne and the incubation and recovery period are negligible concerning the maturation period, we assume all the newborns from infected adults are also infected. The Adults’ mortality rate is much less, but the mortality rate in infected pups is very high naturally[17]. Note that, surviving infected pups can still mature into adults. Since their maturation time is short for the pups (12-14 months), the maturation rate is high for the pups of African wild dogs [18]. The maturation rate may vary as the maturation time varies. The variation in maturation rate can also be due to disruption in endocrine system. Endocrine disruptive chemicals are often present in environment. For example, Talpade et al. [19] and Koestel et al. [20] showed that Bisphenol A disrupts endocrine system of dogs and affects sperm production and many other physiological activities. Such health problems eventually leads to lower maturation into sexually active adults. Their study was focused on the pet dogs and their food source. However, Talpade et al. [19] noted water, air and dust as a source of such endocrine disruptors. As another canid, african wild dog may also suffer from endocrine disruption from exposure to water, dust, and air with endocrine disruptors. Thus their maturation rate into adult may vary based on environmental exposure to endocrine disruptors. We believe that this model can help to identify reasonable management measures to control the disease epidemics in the wild.

The next two subsections discusses the history of Canine Distemper disease and application of the CDV models. The second section discusses model formulation. The third section discusses dynamic properties of the model. The fourth section analyses the sensitivity of model parameters. The fifth section deals with numerical simulation of the model. The sixth section discusses the control strategies. The final and seventh section concludes the finding of the research.

2 History of the disease outbreak

Detailed documentation of the Canine distemper outbreaks can separate the African wild dog population’s declining pattern due to the disease and other stresses. The separation of disease-induced population decline from the other reduction is necessary to simulate an epidemiological model. The first well-recorded outbreak of Wild dogs’ disease was from 1967 to 1968 [5]. There was another outbreak of the canine distemper among captive dogs in the Masai Mara in 1991, but all the African wild dogs sampled in 1989 and 1990 were seronegative [21]. So the transmission might have been from any other animals.

Fig. 1
figure 1

Geographical niche of Canine distemper for our models’ application throughout the Globe as generated using Bioclim, general additive, and MaxEnt niche-modelling framework and methods as per Naimi[22]. The distribution shows that although the CDV affect Wild dog population in Africa, it has potential to spread among the animal populations in Asia, Europe, Australia, South and North America. The model is based environment-CDV interaction and data from Global biodiversity information facility, World Climate Data Base, and future climate prediction data of Climatic Research Unit

Full size image
Table 1 Timeline of the outbreaks of Canine Distemper (CD) disease in the African Wild Dogs
Full size table

The disease report in 2000 may not be the cause of the population reduction as only two dogs of a pack in Tanzania became infected. On the other hand, [23] reports the death of all juveniles and male wild dogs in two weeks in 1994 belonging to a pack of twelve individuals from Chobe National Park in northern Botswana. The disease spread rapidly in the other breeding packs in 2001. On December 21, 2000, deaths peaked from January 30 to February 6, 2001, when 15 wild dogs died. The last death record was on February 13, 2001. 49 of the 52 animals died during this outbreak [13]. To the best of our knowledge, the last documented report for the CDV infection was in the Serengeti ecosystem, Tanzania, in 2007 [7]. We enlist all the outbreaks of the CDV in the African wild dogs in the Table 1.

2.1 Potential area for applying the CDV model

Based on the literature, African Wild Dogs are the major victim of the CDV. However, Dhole (Indian Wild Dogs), and many other animals are affected by CDV outside Africa. Figure 1 shows the area with potential to face CDV attack on wild population based on niche-modelling framework [22].

3 Model formulation

A multidimensional model is key to understand the epidemiology of a diseased population under ecological and evolutionary contexts if the state variables of the model represents the populations age structure and social interactions [24, 25]. We propose a deterministic ordinary differential equation model to predict the dynamics of Canine Distemper disease transmission. The disease transmission rates are different in pups than the adults due to different exposures [26]. So, we divide the wild dog population (N(t)) majorly into adults and pups. Further, we divide each of the adults and pups into susceptible, infected, and recovered compartments. The maturation time of pups into adults is less than their recovery time [27,28,29].

Hence, we neglect recovered pups in our model. Therefore, our model comprises of five mutually disjoint compartments: susceptible adults (\(A_S\)), infected adults (\(A_I\)), recovered adults (\(A_R\)), susceptible pups (\(P_S\)), infected pups (\(P_I\)). In other words, the dog population in the model is \(N(t)=A_S(t)+A_I(t)+A_R(t)+P_S(t)+P_I(t)\) at a given time point t.

The neuropathological symptoms-based diagnosis has confirmed re-emergence of the canine-distemper disease in recovered wild dogs [30]. However, only after all individuals being infected and recovered, a small un-vaccinated population may gain herd immunity against canine distemper for a long term [31]. Hence, the possible recovered dogs’ immunity loss motivates us to consider the ’SIRS’ type model for a large wild dog population. The susceptible adult dogs may come to the concerned population at a rate of \(\lambda \) from other habitats. Some susceptible pups mature into adult susceptible at a rate of a. Also, previously recovered dogs may become susceptible again at a rate of \(\epsilon \) after immunity loss. The airborne CDV may infect a susceptible adult at \(\alpha _1\) rate in the close presence of an infected adult and at \(\alpha _2\) rate in the presence of an infected pup. Considering a natural mortality rate of d in adult susceptible, we describe the adult susceptibles’ growth rate as-

$$\begin{aligned} \frac{dA_S}{dt}= & {} \lambda + a P_S + \epsilon A_R - \alpha _1 A_S A_I\nonumber \\&- \alpha _2 A_S P_I -d A_S . \end{aligned}$$
(1)

The susceptible adults and recovered adults give birth to susceptible pups at b and r rates, respectively, after mating with a noninfected wild dog. The susceptible pups get infected at the rate of \(\phi _1\) and \(\phi _2\) upon contact with infected pups and adults, respectively. The pups’ natural mortality rates are as same as adults. Therefore the growth rate of the susceptible pups is-

$$\begin{aligned} \frac{dP_S}{dt} = b A_S + r A_R - \phi _1 P_S P_I - \phi _2 P_S A_I - a P_S - d P_S . \end{aligned}$$
(2)

As mentioned earlier, the infected adults may come from susceptible adults upon infection in the population. Also, some infected pups mature into infected adults at a \(\beta \) rate. We assume the recovery rate of infected adults is \(\gamma \). Due to disease, the infected adults die at a \(\mu _1\) rate in addition to its natural death rate. So the growth rate of infected adults is-

$$\begin{aligned} \frac{dA_I}{dt}= & {} \alpha _1 A_I A_S + \alpha _2 A_S P_I \nonumber \\&+ \beta P_I - \gamma A_I - \mu _1 A_I - d A_I. \end{aligned}$$
(3)

We assume that the infected adults give birth to infected pups at a rate of \(\phi _3\). Also, the infected pups come from susceptible pups, as mentioned above. An infected pup either matures into a recovered adult at a rate of \(\delta \) or dies. Like infected adults, the infected pups also have an additional disease-induced mortality rate \(\mu _2\) along with natural mortality. Therefore the growth rate of infected pups is-

$$\begin{aligned} \frac{dP_I}{dt}= & {} \phi _1 P_S P_I + \phi _2 P_S A_I \nonumber \\&+ \phi _3 A_I - \beta P_I - \delta P_I - \mu _2 P_I - d P_I. \end{aligned}$$
(4)

Here \(A_S=A_S(0)>0,P_S=P_S(0)>0,A_I=A_I(0)>0,P_I=P_I(0)>0,A_R=A_R(0)>0\). For the simplicity of calculation, we consider \(p^*=a+d; \quad q^*=\gamma +d+\mu _1; \quad s^*=\beta +\delta +d+\mu _2; \quad t^*=d+\epsilon \).

Fig. 2
figure 2

Schematic diagram of the proposed model

Full size image
Table 2 Collected rate of parameters for the model
Full size table

In our model, the recovered population increases both from the recovery of infected adults, and infected pups return to susceptible after immunity loss and die at the natural death rate. Therefore the growth rate of recovered adults is-

$$\begin{aligned} \frac{dA_R}{dt} = \delta P_I + \gamma A_I - \epsilon A_R - d A_R . \end{aligned}$$
(5)

So, our final proposed model is-

$$\begin{aligned} \frac{dA_S}{dt}\,=\,& {} \lambda + a P_S + \epsilon A_R - \alpha _1 A_S A_I - \alpha _2 A_S P_I -d A_S, \nonumber \\ \frac{dP_S}{dt}\,=\,& {} b A_S + r A_R - \phi _1 P_S P_I - \phi _2 P_S A_I - a P_S - d P_S, \nonumber \\ \frac{dA_I}{dt}\,=\,& {} \alpha _1 A_I A_S + \alpha _2 A_S P_I + \beta P_I - \gamma A_I - \mu _1 A_I - d A_I, \nonumber \\ \frac{dP_I}{dt}\,=\,& {} \phi _1 P_S P_I + \phi _2 P_S A_I + \phi _3 A_I - \beta P_I - \delta P_I - \mu _2 P_I - d P_I, \nonumber \\ \frac{dA_R}{dt}\,=\,& {} \delta P_I + \gamma A_I - \epsilon A_R - d A_R . \end{aligned}$$
(6)

The proposed mathematical model ( system Eq. 6) is visualized in Fig. 2 for better understanding. The ecological meaning of the parameters are represented in the Table 2.

4 Dynamical properties of the model

Theorem 1

The closed and bounded region D (\(\subset \mathbf{R} ^{5+}\)) is positively invariant and globally attracting for the proposed model (system Eq. 6) irrespective of any non-negative initial conditions, where \(D=\{(A_S,P_S,A_I,P_I,A_R)\in \mathbf{R} ^5:0\le N \le Z\}\) with \(Z=max\{\frac{\lambda }{d-m},N(0)\}.\)

Proof

The proposed model can be written in the following form: \(\frac{dX}{dt} = AX+B\),where \(X=(A_S,P_S,A_I,P_I,A_R)^T\),

$$\begin{aligned} A= \left[ {\begin{array}{ccccc} -(\alpha _1 A_I + \alpha _2 P_I+d) &{} a &{} 0 &{} 0 &{} \epsilon \\ b &{} -(\phi _1 P_I + \phi _2 A_I + p^*) &{} 0 &{} 0 &{} r\\ \alpha _1 A_I &{} 0 &{} -q^* &{} \alpha _2 A_S+\beta &{} 0\\ 0 &{} \phi _1 P_I+ \phi _2 A_I &{} \phi _3 &{} -s^* &{} 0\\ 0 &{} 0 &{} \gamma &{} \delta &{} -t^* \end{array} } \right] \end{aligned}$$

and \(B = \begin{pmatrix} \lambda \\ 0 \\ 0 \\ 0 \\ 0 \end{pmatrix}\).

Here, \(p^*=a+d\),\(q^*=\gamma +d+\mu _1\), \(s^*=\beta +\delta +d+\mu _2\),\( t^*=d+\epsilon \). B is a positive vector. A(X) is a Metzler matrix \(\forall X~\in \mathbf{R} ^5\). All off-diagonal entries of A(X) are non-negative. The system is positively invariant in \(\mathbf{R} ^5\) for \(B\ge 0\). Starting from its initial state any trajectory of the system is stuck in \(\mathbf{R} ^5\) forever.

We sum up all population growth rate as

$$\begin{aligned} \frac{dN(t)}{dt}= & {} \lambda +b A_S+r A_R + \phi _3 A_I - \mu _2 P_I\nonumber \\&-\mu _1 A_I-d N \end{aligned}$$
(7)

to check the total growth rate of wild dogs. It is clear that the Eq. 7 implies that \(\frac{dN}{dt}\le \lambda + b A_S +r A_R - d N\). Let

\(m=max\{b,r,\phi _3\}\); then,

\(\frac{dN}{dt}\le \lambda + m A_S + m A_R + m A_I - d N\) or,

\(\frac{dN}{dt}\le \lambda + m N - m(P_S+P_I) - d N\) or,

\(\frac{dN}{dt}\le \lambda - (d-m) N\),      where \(d>m\). The natural death rate (d) is lower than sum of birth rates \(b+ r+ \phi _3 \), but it must be greater than any single birth rate to maintain the population sustainability. Otherwise the wild dogs would have repopulate any empty habitat exponentially. Hence,

$$\begin{aligned} 0 \le N(t) \le \frac{\lambda }{d-m} + \left( N(0) - \frac{\lambda }{d-m}\right) ~e^{-(d-m)t} \end{aligned}$$

Therefore, as \(t~ \rightarrow ~\infty \), \(0 \le N(t) \le \frac{\lambda }{d-m}\) for any \(t > 0\), \(0 \le N(t) \le Z\), where \(Z ~= ~max~\{\frac{\lambda }{d-m}, N(0)\}\). Hereby we accomplish the proof of boundedness. \(\square \)

4.1 Equilibrium analysis

Sometimes it is quite impossible to enumerate the closed-form expression of the non-linear dynamical system. Then the stability analysis of the equilibrium points became the critical component in nurturing the system’s long-term behavior. This proposition is also applicable for our proposed model (system Eq. 6) as the analytical expression of each population size is not tractable. So, we evaluate the equilibrium points of the system Eq. (6). Mathematically the system Eq. (6) may have several fixed points. However, from the context of epidemiological consideration, we select two equilibrium points, i.e., the Disease-free equilibrium point (henceforth, DFE) and the endemic equilibrium points.

  1. 1.

    We express the disease equilibrium point by \(E_0 =(e_1,e_2,0,0,0)\), where, \(e_1=\frac{\lambda (a+d)}{d(a+d)-ab}\)and \(e_2=\frac{\lambda b}{d(a+d)-ab}\). Note that the DFE is always feasible in any epidemiological system so it’s feasibility is trivial.

  2. 2.

    Another fixed point be endemic equilibrium point: \(E(A_S^*,P_S^*,A_I^*,P_I^*,A_R^*)\). The feasibility of the equilibrium point is given in the following stability analysis.

4.2 Stability analysis

4.2.1 Basic reproduction number

The basic reproduction number (henceforth, BRN) is a crucial measure in epidemiology to understand the virulence of the disease. This BRN is defined by the rate at which new infections occur, i.e., the average number of cases produced due to secondary infections. Thus, BRN can measure the maximum reproductive potential of an infectious disease. The BRN, usually denoted by \(R_0\), provides a threshold condition for the stability of equilibrium points in any epidemic system. The BRN is most useful to understand any disease at the beginning of its epidemic [33, 25].

Numerous methods are available to evaluate the analytical form of BRN, viz., (i) Jacobian approach, (ii) Next-generation approach, (iii) The Castiloll-Chavez, Feng, and Huang approach [34]. However, the most popular method in the enumeration of BRN is the approach of the “Next Generation Matrix” (henceforth, NGM) method due to its ecological relevance. Generations in epidemiology are defined as the waves of secondary infection that arise from each of the previous infections. Thus, the number of secondary infections can be viewed as the first generation in any epidemiological system. As an instance, If \(R_i\) indicates the reproduction number of the \(i^{th}\) generation, then \(R_0\) is simply the number of infections generated by the index case, i.e., the generation zero (0). Kee** these things in mind P. den Driessche [35] proposes the NGM approach to evaluate the BRN.

The construction of the reproduction number with the NGM method comprises the development of two essential matrices denoted by F and V. Here the matrices F, V account for the “new” infections and disease transfer between the infected compartments, respectively. In our case, i.e., for the proposed model the two matrices can be defined as

$$ \begin{aligned} F = \begin{bmatrix} \alpha _1 e_1 &{} \alpha _2 e_1\\ \phi _2 e_2 &{} \phi _1 e_2 \end{bmatrix} \& ~ V = \begin{bmatrix} q^* &{} -\beta \\ -\phi _3 &{} s^* \end{bmatrix} \end{aligned}$$

where, \(e_1=\frac{\lambda (a+d)}{d(a+d)-ab}\) ; \(e_2=\frac{\lambda b}{d(a+d)-ab}\) ; \(q^*=\gamma +d+\mu _1\) ; \(s^*=\beta +\delta +d+\mu _2\).

Note that the inverse of the matrix V consists of the property of Z sign pattern, i.e., the off-diagonal entries are either negative or zero. So, the BRN can be obtained from the following equation

$$\begin{aligned} R_0~=~\rho (F V^{-1}), \end{aligned}$$

where \(\rho \) indicates the spectral radius, i.e., the dominant eigen value of the matrix \(F V^{-1}\) . Thus,

$$\begin{aligned} FV^{-1}=\left[ {\begin{array}{cc} {}\frac{e_1 (s^* \alpha _1 + \phi _3 \alpha _2)}{q^* s^* - \phi _3 \beta } &{} \frac{e_1 (\beta \alpha _1 + q^* \alpha _2)}{q^* s^* - \phi _3\beta }\\ {}\frac{e_2 (s^* \phi _2 + \phi _1 \phi _3)}{q^* s^* - \phi _3 \beta } &{} {}\frac{e_2 (q^* \phi _1 + \beta \phi _2)}{q^* s^* - \phi _3 \beta }\\ \end{array} } \right] \end{aligned}$$

Let \(\lambda _1\) and \(\lambda _2\) be two eigen values of the matrix \(FV^{-1}\) with

$$\begin{aligned}&\lambda _1\\&\quad = \frac{{\begin{array}{l} {e_1(\alpha _1s^*+\alpha _2 \phi _3)+e_2(\phi _2 \beta +\phi _1q^*)}\\ \qquad +\sqrt{{\begin{array}{l} {[e_1(\alpha _1 s^*+\alpha _2 {}\phi _3)-e_2(\phi _2 \beta +\phi _1 q^*)]^2}\\ \qquad { + 4e_1e_2(\alpha _1\beta +\alpha _2 q^*)(\phi _2 s^*+\phi _1\phi _3)} \end{array}}}\end{array}}}{2(q^* s^* - \phi _3 \beta )} \\&\lambda _2\\&\quad = \frac{{\begin{array}{l} {e_1(\alpha _1s^*+\alpha _2 \phi _3)+e_2(\phi _2 \beta +\phi _1q^*)}\\ \qquad -\sqrt{{\begin{array}{l} {[e_1(\alpha _1 s^*+\alpha _2\phi _3)-e_2(\phi _2 \beta +\phi _1 q^*)]^2 }\\ \qquad {+ 4e_1e_2(\alpha _1\beta +\alpha _2 q^*)(\phi _2 s^*+\phi _1\phi _3)} \end{array}}}\end{array}}}{2(q^* s^* - \phi _3 \beta )} \end{aligned}$$

Without loss generality, let us consider \(\lambda _1\) as the dominant eigenvalue of the matrix \(FV^{-1}\). So the analytical expression of BRN is given by,

$$\begin{aligned}&R_0 \nonumber \\&\quad =\frac{{\begin{array}{l} {e_1(\alpha _1 s^*+\alpha _2\phi _3)+e_2(\phi _2 \beta +\phi _1q^*)}\\ \qquad +\sqrt{{\begin{array}{l} {[e_1(\alpha _1 s^*+\alpha _2\phi _3)-e_2(\phi _2 \beta +\phi _1 q^*)]^2}\\ \qquad {+ 4e_1e_2(\alpha _1\beta +\alpha _2 q^*)(\phi _2 s^*+\phi _1\phi _3)} \end{array}}}\end{array}}}{2(q^* s^* - \phi _3 \beta )} \end{aligned}$$
(8)

4.2.2 Local stability of the disease free equilibrium point

Theorem 2

For our proposed model, the disease-free equilibrium(\(E_0\)) is locally asymptotically stable if \(R_0<1\) and unstable if \(R_0>1\).

Proof

Jacobian at the disease free equilibrium point(\(E_0\)).

$$\begin{aligned} J(E_0)=\left[ {\begin{array}{ccccc} -d &{} a &{} -\alpha _1 e_1 &{} -\alpha _2 e_1 &{} \epsilon \\ b &{} - p^* &{} -\phi _2 e_2 &{} -\phi _1 e_2 &{} r\\ 0 &{} 0 &{} \alpha _1 e_1 - q^* &{} \alpha _2 e_1 + \beta &{} 0\\ 0 &{} 0 &{} \phi _2 e_2 + \phi _3 &{} \phi _1 e_2 - s^* &{} 0\\ 0 &{} 0 &{} \gamma &{} \delta &{} -t^*\\ \end{array} } \right] \end{aligned}$$

Eigenvalues of \(J_{E_0}\) are \(-t^*\) and other four are given by the roots of the equation

$$\begin{aligned} {}\psi ^4 + S_1 \psi ^3 + S_2 \psi ^2 + S_3 \psi + S_4 = 0 \end{aligned},$$
(9)

where

\(S_1 = - (\alpha _1 e_1 - q^* + \phi _1 e_2 - s^*) + (d+p^*)\),

\(S_2 = (\alpha _1 e_1 - q^*)(\phi _1 e_2 - s^*) - (\alpha _2 e_1 + \beta )(\phi _2 e_2 + \phi _3) - (d+p^*)(\alpha _1 e_1 - q^* + \phi _1 e_2 - s^*)\),

\(S_3 = (\alpha _1 e_1 - q^*)(\phi _1 e_2 - s^*)(d+p^*) - (\alpha _2 e_1 + \beta )(\phi _2 e_2 + \phi _3)(d+p^*) - (dp^*+ab)(\alpha _1 e_1 - q^* + \phi _1 e_2 - s^*)\),

\(S_4 = -(\alpha _2 e_1 + \beta )(\phi _2 e_2 + \phi _3)(dp^*+ab) + (\alpha _1 e_1 - q^*)(\phi _1 e_2 - s^*)(dp^*+ab)\). Clearly, all roots of Eq. (9) are either negative or have negative real parts if \(R_0<1\). Hence, the disease free equilibrium point (\(E_0\)) is locally asymptotically stable if \(R_0<1\) and unstable if \(R_0>1\).

Remark 1

In our model (system Eq. 6), a \(R_0<1\) implies that a small inflow of infected wild dog populations into packs would not generate a massive outbreak. As a result, the persistence of the disease decreasing in time.

4.2.3 Global stability of the disease free equilibrium point

Theorem 3

The DFE (\(E_0\)) point in our proposed model becomes globally asymptotically stable for \(R_0 < 1\).

Proof

The system Eq. (6) can be written in the following form using theorem of as per [36] [37]

$$\begin{aligned} \frac{dX}{dt} = T(X,I), \qquad \\ \frac{dI}{dt} = U(X,I), \qquad U(X,0) = 0, \end{aligned}$$

where \(X=[A_S,P_S,A_R]\) and \(I=[A_I,P_I]\) denote the uninfected and infected compartments, respectively. \(E_0=(X^*,0)\) denotes the disease-free equilibrium of this system.

Now, we will show the two conditions of Castillo-Chavez theorem [36]. \( T(X,0)=\left[ {\begin{array}{c} {}\lambda +a P_S+\epsilon A_R-d A_S\\ b A_S+r A_R-a P_S-d P_S\\ -d A_R -\epsilon A_R\\ \end{array} } \right] \)

Solving the ODEs by equating both sides, we get

$$\begin{aligned} A_R(t)= & {} A_R(0) e^{-(d+\epsilon )t}\\ A_S(t)= & {} \left[ \frac{\lambda }{d}+\frac{a}{d}P_S(t)+\frac{\epsilon }{d}A_R(t)\right] \\&- \left[ \frac{\lambda }{d}+\frac{a}{d}P_S(0)+\frac{\epsilon }{d}A_R(0) - A_S(0)\right] e^{-dt}\\ P_S(t)= & {} \left[ \frac{b}{a+d}A_S(t)+\frac{r}{a+d} A_R(t)\right] \\&- \left[ \frac{b}{a+d} A_S(0)+\frac{r}{a+d} A_R(0)-P_S(0)\right] e^{-(a+d)t} \end{aligned}$$

Thus,   \(\lim _{t\rightarrow \infty } A_R = 0\) Let, \(\lim _{t\rightarrow \infty } A_S = m \) and \(\lim _{t\rightarrow \infty } P_S = n\). Solving above equations, we get

$$\begin{aligned} m = \frac{\lambda }{d}+(\frac{a}{d}) n,\\ n = (\frac{b}{a+d}) m. \end{aligned}$$

Solving above equations we get,    \(m=\frac{\lambda (a+d)}{d(a+d)-ab} = e_1\) and \(n=\frac{b\lambda }{d(a+d)-ab} = e_2\). Therefore, \(\lim _{t\rightarrow \infty } A_S = m = e_1 \) and \(\lim _{t\rightarrow \infty } P_S = n = e_2\). Hence the system Eq. (6) satisfy the first condition.

$$\begin{aligned} \frac{dI}{dt} = U(X,I), \end{aligned}$$

where, \(U(X,I)=\begin{bmatrix} \alpha _1 A_S A_I+\alpha _2 A_S P_I+\beta P_I-q^* A_I\\ \phi _1 P_S P_I+\phi _2 P_S A_I+\phi _3 A_I - s^* P_I \end{bmatrix}\). Now, we can write U(X, I) in the form of :   \(U(X,I) = AI -\hat{U}(X,I)\), where, \(A=\left[ {\begin{array}{cc} {}\alpha _1 A_S - q^* &{} \alpha _2 A_S+\beta \\ {}\phi _2 P_S+\phi _3 &{} \alpha _1 P_S - s^*\\ \end{array} } \right] \), and \(\hat{U}(X,I)=\left[ {\begin{array}{c} 0\\ 0 \end{array} } \right] \)

Here, matrix A is a M-matrix because the off-diagonal entries of A are non-negative and \(\hat{U}(X,I) = 0.\) Hence, the system Eq. (6) also satisfy the second condition. So, our disease free equilibrium point(\(E_0\))is globally asymptotically stable for \(R_0 < 1\). This completes the proof □.

4.2.4 Existence of the endemic equilibrium point

For system Eq. (6), an endemic equilibrium point \(E(A_S^*,P_S^*,A_I^*,P_I^*,A_R^*)\). From the equilibrium equations of our proposed model (system Eq. 6), we have

\(A_S^* = \frac{Y_1 - Y_2 P_S}{Y_3 + Y_4P_S}\),

\(A_I^* = \frac{X_1 P_S^2 + X_2 P_S + X_3}{X_4 P_S^2 + X_5 P_S + X_6}\),

\(P_I^* = \frac{W_1 P_S^3 + W_2 P_S^2 + W_3 P_S + W_4}{(W_5 - W_6 P_S)(X_4 P_S^2 + X_5 P_S + X_6)}\),

\(A_R^* = \frac{Z_1 P_S^3 + Z_2 P_S^2 + Z_3 P_S + Z_4}{(Z_5 - Z_6 P_S)(X_4 P_S^2 + X_5 P_S + X_6)},\) with \(X_1 = p^* t^* \phi _1 (\alpha _1 \phi _1 - \alpha _2 \phi _2) - b t^* \phi _1 (\beta \phi _2 + q^* \phi _1)\),

\(X_2 = p^* t^* s^* (\alpha _2 \phi _2 - \alpha _1 \phi _1) - p^* t^* \phi _1 (\alpha _1 s^* + \alpha _2 \phi _3) + b t^* \phi _1 (q^*s^* - \beta \phi _3) + b t^* s^* (\beta \phi _2 + q^* \phi _1)\),

\(X_3 = p^* t^* s^* (\alpha _1 s^* + \alpha _2 \phi _3) - t^* s^* b (q^* s^* - \beta \phi _3)\),

\(X_4 = r(\alpha _2 \phi _2 - \alpha _1 \phi _1)(\delta \phi _2 - \gamma \phi _1) - t^* \phi _1 \phi _2 (\alpha _1 s^* + \alpha _2 \phi _3) - t^* \phi _1 \phi _3 (\alpha _2 \phi _2 - \alpha _1 \phi _1)+ \) \( t^* \phi _1 \phi _2 (\alpha _1 s^* + \alpha _2 \phi _3) - t^* \phi _2 s^* (\alpha _2 \phi _2 - \alpha _1 \phi _1)\),

\(X_5 = r(\delta \phi _3 + \gamma s^*)(\alpha _2 \phi _2 - \alpha _1 \phi _1) + r(\delta \phi _2 - \gamma \phi _1)(\alpha _1 s^* + \alpha _2 \phi _3) - t^* \phi _1 \phi _3 (\alpha _1 s^* + \alpha _2 \phi _3) - t^* \phi _2 s^* (\alpha _1 s^* + \alpha _2 \phi _3)\),

\(X_6 = r(\delta \phi _3 + \gamma s^*)(\alpha _1 s^* + \alpha _2 \phi _3)\),

\(Y_1 = q^* s^* - \beta \phi _3\),       \(Y_2 = \beta \phi _2 + q^* \phi _1\),       \(Y_3 = \alpha _1 s^* + \alpha _2 \phi _3\),       

\(Y_4 = \alpha _2 \phi _2 - \alpha _1 \phi _1\),

\(Z_1 = (\delta \phi _2 - \gamma \phi _1)X_1\),       \(Z_2 = X_2(\delta \phi _2 - \gamma \phi _1) + X_1(\delta \phi _3 + \gamma s^*)\),       \(Z_3 = X_3(\delta \phi _2 - \gamma \phi _1) + X_2(\delta \phi _3 + \gamma s^*)\),

\(Z_4 = X_3(\delta \phi _3 + \gamma s^*)\),       \(Z_5 = t^*s^*\),       \(Z_6 = t^*\phi _1\),       \(W_1 = \phi _2 X_1\),       \(W_2 = \phi _2 X_2 + \phi _3 X_1\),

\(W_3 = \phi _2 X_3 + \phi _3\),       \(W_4 = X_3 \phi _3\),       \(W_5 = s^*\),       \(W_6 = \phi _1\).

Now, from equilibrium equations using above values of \(A_S\),\(A_I\),\(P_I\),\(A_R\), we get the following equations of \(P_S\):

$$\begin{aligned} A_1 P_S^6 + A_2 P_S^5 + A_3 P_S^4 + A_4 P_S^3 + A_5 P_S^2 + A_6 P_S + A_7 = 0 \end{aligned}$$
(10)

The expression of the coefficients are in Appendix A.1. By applying the Descartes’ rule of signs on the Eq. (10), we listed the unique positive root of this equation in Table 3.

Table 3 Descartes’ rule of signs for unique endemic point
Full size table

4.3 Local Stability of the Endemic equilibrium

The Jacobian matrix of our system Eq. (6), evaluated at the endemic point E, is -

$$\begin{aligned} J(E)=\left[ {{\begin{array}{ccccc} -d-\alpha _1 A_I^* - \alpha _2 P_I^* &{} a &{} -\alpha _1 A_S^* &{} -\alpha _2 A_S^* &{} \epsilon \\ b &{} -\phi _1 P_I^* - \phi _2 A_I^* - p^* &{} -\phi _2 P_S^* &{} -\phi _1 P_S^* &{} r\\ \alpha _1 A_I^* + \alpha _2 P_I^* &{} 0 &{} \alpha _1 A_S^* - q^* &{} \alpha _2 A_S^* + \beta &{} 0\\ 0 &{} \phi _1 P_I^* + \phi _2 A_I^* &{} \phi _2 P_S^* + \phi _3 &{} \phi _1 P_S^* - s^* &{} 0\\ 0 &{} 0 &{} \gamma &{} \delta &{} -t^*\\ \end{array}} } \right] \end{aligned}$$

Now, we will write Jacobian in this way

$$\begin{aligned} J(E)=\left[ {\begin{array}{ccccc} J_{11} &{} J_{12} &{} J_{13} &{} J_{14} &{} J_{15}\\ J_{21} &{} J_{22} &{} J_{23} &{} J_{24} &{} J_{25}\\ J_{31} &{} 0 &{} J_{33} &{} J_{34} &{} 0\\ 0 &{} J_{42} &{} J_{43} &{} J_{44} &{} 0\\ 0 &{} 0 &{} J_{53} &{} J_{54} &{} J_{55}\\ \end{array} } \right] \end{aligned},$$

where \(J_{11} = -d-\alpha _1 A_I^* - \alpha _2 P_I^*,\) \(J_{12} = a,\) \(J_{13} = -\alpha _1 A_S^*\),       \(J_{14} = -\alpha _2 A_S^*\),       \(J_{15} = \epsilon \),

\(J_{21} = b\),       \(J_{22} = -\phi _1 P_I^* - \phi _2 A_I^* - p^*\),       \(J_{23} = -\phi _2 P_S^*\),       \(J_{24} = -\phi _1 P_S^*\),       \(J_{25} = r\),

\(J_{31} = \alpha _1 A_I^* + \alpha _2 P_I^*\),       \(J_{33} = \alpha _1 A_S^* - q^*\),       \(J_{34} = \alpha _2 A_S^* + \beta \),

\(J_{42} = \phi _1 P_I^* + \phi _2 A_I^*\),       \(J_{43} = \phi _2 P_S^* + \phi _3,\) \(J_{44} = \phi _1 P_S^* - s^*,\)

\(J_{53} = \gamma \),       \(J_{54} = \delta \),       \(J_{55} = -t^*\). The corresponding characteristic equation of the endemic equilibrium point (E) is

$$\begin{aligned} \rho ^5 + B_1 \rho ^4 + B_2 \rho ^3 + B_3 \rho ^2 + B_4 \rho + B_5 = 0 \end{aligned}$$
(11)

The expression of the coefficients are in Appendix A.2.

Using the Routh-Hurtwitz condition, all roots of the Eq. (11) are either negative or have a negative real part if and only if following conditions hold

$$\begin{aligned} \Delta _1 = B_1> 0,~~~\Delta _2= \begin{vmatrix} B_1&1 \\ B_3&B_2\\ \end{vmatrix}> 0,~~~\Delta _3= \begin{vmatrix} B_1&1&0\\ B_3&B_2&B_1\\ B_5&B_4&B_3 \end{vmatrix}> 0,\\ \Delta _4= \begin{vmatrix} B_1&1&0&0\\ B_3&B_2&B_1&1\\ B_5&B_4&B_3&B_2\\ 0&0&B_5&B_4 \end{vmatrix}> 0, ~~\text{ and }~~B_5 > 0. ~~~~~~~~~~~~~~~~~~~~~~~~ \end{aligned}$$

Or,

\(B_1 > 0\),      \((B_1 B_2 - B_3) > 0\), \(B_1 (B_2 B_3 - B_1 B_4) - (B_3^2 - B_1 B_s) > 0\),

\(-B_1 B_5 B_2^2 + 2B_1 B_4 B_5 + B_1 B_2 B_3 B_4 - B_1^2 B_4^2 + B_2 B_3 B_5 - B_5^2 - B_3^2 B_4 > 0\),

\(B_5 > 0\).

Only upon satisfying the conditions 3.3, the endemic equilibrium point E is locally asymptotically stable.

4.4 Global Stability of the Endemic equilibrium point

Theorem 4

The Endemic equilibrium E is Globally asymptotically stable inside the region of attraction D if the following six (\(1-6\)) conditions are satisfied:

  1. 1.

    \(k_1 \alpha _1 A_S^* + k_2 \phi _2 P_S^* \le k_1 q^*\)

  2. 2.

    \(k_1 \beta P_I^* + k_2 p^* P_S^* \le k_1 \epsilon A_R^*\)

  3. 3.

    \(k_1 \alpha _2 A_S^* + k_2 \phi _1 P_S^* + k_1 \beta \le k_1 \beta \frac{A_I^*}{A_I}\)

  4. 4.

    \(k_1 \epsilon + k_2 r \le k_1 \epsilon \frac{A_S^*}{A_S} + k_2 r \frac{P_S^*}{P_S}\)

  5. 5.

    \(\epsilon \frac{A_R^*}{A_S} + a \frac{P_S^*}{P_S} \le a \frac{P_S}{A_S}\)

  6. 6.

    \(b A_S \le p^* P_S\)

Remark

Note that the construction of the Lyapunov function and to show the global stability criteria involved routine mathematics. However, the problem becomes messy due to lengthy, complex, and untractable equations associated with the proof. For better readability and understanding of the text, we have included the proof in the main manuscript.

Proof

Let us construct a Lyapunov function \(V(A_S,P_S,A_I,P_I,A_R)\), such that \( V\ge 0 \) and at a point \(E^*(A_S^*,P_S^*,A_I^*,P_I^*,A_R^*)\), \(V(A_S^*,P_S^*,A_I^*,P_I^*,A_R^*)=0\);

Then, \(V(A_S,P_S,A_I,P_I,A_R) = k_1(A_S - A_S^* -A_S^*\ln \frac{A_S}{A_S^*}) + k_2(P_S - P_S^* -P_S^*\ln \frac{P_S}{P_S^*}) + k_3(A_I - A_I^* -A_I^*\ln \frac{A_I}{A_I^*}) + k_4(P_I - P_I^* -P_I^*\ln \frac{P_I}{P_I^*}) + k_5(A_R - A_R^* -A_R^*\ln \frac{A_R}{A_R^*})\); Differentiating with respect to t, we get

\(\frac{dV}{dt} = k_1(1 - \frac{A_S^*}{A_S})\frac{dA_S}{dt} + k_2(1 - \frac{P_S^*}{P_S})\frac{dP_S}{dt} + k_3(1 - \frac{A_I^*}{A_I})\frac{dA_I}{dt} + k_4(1 - \frac{P_I^*}{P_I})\frac{dP_I}{dt} + k_5(1 - \frac{A_R^*}{A_R})\frac{dA_R}{dt} \);

\(\implies \) \(\frac{dV}{dt} = k_1(1 - \frac{A_S^*}{A_S})[a(P_S - P_S^*)+\epsilon (A_R - A_R^*)\)

\(- \alpha _1 A_S A_I \)

\(+ \alpha _1 A_S^* A_I^* - \alpha _2 A_S P_I \)

\(+ \alpha _2 A_S^* P_I^* - d(A_S -A_S^*) ]\)

\(+ k_2(1 - \frac{P_S^*}{P_S})\)

\([bA_S + rA_R - \phi _1 P_S P_I - \phi _2 P_S A_I - p^* P_S^* ]\)

\( +k_3(1 - \frac{A_I^*}{A_I})[\alpha _1 A_S A_I\)

\(+ \alpha _2 A_S P_I +\beta P_I -q^* A_I] + k_4(1 - \frac{P_I^*}{P_I})\left[ \phi _1 P_S P_I + \phi _2 P_S A_I + \phi _3 A_I - s^* P_I \right] + k_5(1 - \frac{A_R^*}{A_R})\left[ \delta P_I + \gamma A_I - t^* A_R\right] \);

\(\implies \) \(\frac{dV}{dt} = -\frac{k_1 d}{A_S}(A_S - A_S^*)^2\)

\( +\frac{k_1 a}{A_S}(A_S P_S - A_S P_S^* - A_S^* P_S + A_S^* P_S^*)\)

\(+ \frac{k_1 \epsilon }{A_S}(A_S A_R - A_S A_R^* - A_S^* A_R +A_S^* A_R^*)\)

\( - k_1 \alpha _1 A_I (A_S - A_S^*) + \frac{k_1\alpha _1}{A_S}A_S^* A_I^* (A_S - A_S^*)\)

\( - k_1 \alpha _2 P_I (A_S- A_S^*) \)

\(+ \frac{k_1 \alpha _2}{A_S} A_S^* P_I^* (A_S - A_S^*)\)

\( + \frac{k_2 b}{P_S}A_S (P_S - P_S^*) \)

\(+ \frac{k_2 r}{P_S} A_R (P_S - P_S^*) - k_2 \phi _1 P_I (P_S - P_S^*) \)

\(- k_2 \phi _2 A_I (P_S - P_S^*) - k_2 p^* (P_S - P_S^*) + k_3 \alpha _1 A_S(A_I - A_I^*) \)

\(+ \frac{k_3 \alpha _2}{A_I} A_S P_I (A_I - A_I^*) \)

\(+ \frac{k_3 \beta }{A_I} P_I (A_I - A_I^*) - k_3 q^* (A_I - A_I^*) \)

\(+ k_4 \phi _1 P_S (P_I - P_I^*) + \frac{k_4 \phi _2}{P_I} A_I P_S (P_I - P_I^*) \)

\( + \frac{k_4 \phi _3}{P_I}A_I(P_I - P_I^*) - s^* k_4(P_I - P_I^*) \)

\(+ \frac{k_5 \delta }{A_R}P_I(A_R - A_R^*) \)

\(+\frac{k_5 \gamma }{A_R}A_I(A_R - A_R^*) - k_5 t^*(A_R - A_R^*)\);

\(\implies \) \(\frac{dV}{dt} = - k_1 d\frac{(A_S - A_S^*)^2}{A_S} + k_1 a P_S - k_1 a P_S^* - \frac{k_1 a}{A_S} A_S^* P_S \)

\( + \frac{k_1 a}{A_S}A_S^* P_S^* + k_1 \epsilon A_R - k_1 \epsilon A_R^* \)

\( -\frac{k_1 \epsilon }{A_S}A_R A_S^* + \frac{k_1 \epsilon }{A_S}A_R^* A_S^* - k_1 \alpha _1 A_S A_I + k_1 \alpha _1 A_S^* A_I + k_1 \alpha _1 A_S^* A_I^* \)

\(- \frac{k_1 \alpha _1}{A_S} A_S^{*^2} A_I^* - k_1 \alpha _2 A_S P_I + k_1 \alpha _2 A_S^* P_I + k_1 \alpha _2 A_S^* P_I^*\)

\(- \frac{k_1 \alpha _2}{A_S} A_S^{*^2} P_I^* + k_2 b A_S \)

\(-\frac{k_2 b}{P_S} A_S P_S^* + k_2 r A_R - \frac{k_2 r}{P_S}P_S^* A_R\)

\(- k_2 \phi _1 P_S P_I + k_2 \phi _1 P_S^* P_I - k_2 \phi _2 A_I P_S + k_2 \phi _2 P_S^* A_I \)

\( - k_2 p^* P_S + k_2 p^* P_S^* + k_3 \alpha _1 A_S A_I - k_3 \alpha _1 A_S A_I^* + k_3 \alpha _2 A_S P_I\)

\( - k_3 \alpha _2 A_S P_I \frac{A_I^*}{A_I} + k_3 \beta P_I - k_3 \beta P_I \frac{A_I^*}{A_I} - k_3 q^* A_I \)

\(+ k_3 q^* A_I^* + k_4\phi _1 P_S P_I \)

\(- k_4 \phi _1 P_S P_I^* + k_4 \phi _2 P_S A_I - k_4\phi _2 P_S A_I \frac{P_I^*}{P_I} \)

\(+ k_4 \phi _3 A_I - k_4 \phi _3A_I \frac{P_I^*}{P_I} \)

\(- k_4 s^* P_I + k_4 s^* P_I^* + k_5 \delta P_I \)

\(- k_5 \delta P_I \frac{A_R^*}{A_R} \)

\(+ k_5 \gamma A_I\)

\(- k_5 \gamma A_I \frac{A_R^*}{A_R} - k_5 t^* A_R + k_5 t^*A_R^*\);

We consider \(k_1 = k_3\) and \(k_2 = k_4\).

\(\implies \)

\(\frac{dV}{dt} = -\frac{k_1 d}{A_S}(A_S - A_S^*)^2 + k_1 a P_S - k_1 a P_S^* \)

\(- k_1 a P_S^* \frac{A_S^* P_S}{A_S P_S^*} + k_1 a P_S \frac{A_S^* P_S^*}{A_S P_S} \)

\(+ k_1 \epsilon A_R - k_1 \epsilon A_R^* - k_1 \epsilon A_R^* \frac{A_S^* A_R}{A_S A_R^*} \)

\(+k_1 \epsilon A_R \frac{A_S^* A_R^*}{A_S A_R} + k_1 \alpha _1 A_S^* A_I + k_1 \alpha _1 A_S^* A_I^* \)

\(- k_1 \alpha _1 \frac{A_S^{*^2}A_I^*}{A_S} + k_1\alpha _2 A_S^* P_I + k_1 \alpha _2 A_S^* P_I^* \)

\(- k_1 \alpha _2 \frac{A_S^{*^2}P_I^*}{A_S} + k_2 b A_S\)

\( - k_2 b A_S^* \frac{A_S P_S^*}{A_S^* P_S} + k_2 r A_R - k_2 r A_R^* \frac{P_S^* A_R}{P_S A_R^*} \)

\(+ k_2 \phi _1 P_S^* P_I + k_2\phi _2 P_S^* A_I - k_2 p^* P_S \)

\( + k_2 p^* P_S^* - k_1 \alpha _1A_S A_I^* - k_1 \alpha _2 A_S^* P_I^* \frac{A_S P_I A_I^*}{A_S^* P_I^* A_I} \)

\(+ k_1 \beta P_I - k_1 \beta P_I^* \frac{P_I A_I^*}{P_I^* A_I} - k_1 q^* A_I \)

\(+ k_1 q^* A_I^* - k_2 \phi _1 P_S P_I^* - k_2 \phi _2 P_S^* A_I^* \frac{P_S A_I P_I^*}{P_S^* A_I^* P_I}\)

\(+ k_2 \phi _3 A_I - k_2 \phi _3 A_I^* \frac{A_I P_I^*}{A_I^* P_I} - k_2 s^* P_I \)

\(+ k_2 s^* P_I^* + k_5 \delta P_I - k_5 \delta P_I^* \frac{P_I A_R^*}{P_I^* A_R} \)

\( + k_5 \gamma A_I - k_5 \gamma A_I^* \frac{A_I A_R^*}{A_I^* A_R} - k_5 t^* A_R + k_5 t^* A_R^*\)

Again, we consider, \(k_2 \phi _3 A_I^* = k_1 \alpha _2 A_S^* P_I^*\) and \(k_5 t^* A_R^* = k_1 \alpha _2 A_S^* P_I^*\).

\(\implies \)

\(\frac{dV}{dt} = - \frac{k_1 d (A_S -A_S^*)^2}{A_S} + K_1 \alpha _1 A_S^* A_I^* (2 - \frac{A_S^*}{A_S} - \frac{A_S}{A_S^*}) + k_1 \alpha _2 A_S^* P_I^* (3 - \frac{A_S^*}{A_S} - \frac{A_S P_I A_I^*}{A_S^* P_I^* A_I} - \frac{A_I P_I^*}{A_i^* P_I}) + k_1 a P_S - k_1 a P_S^* - k_1 a P_S^* \frac{A_S^* P_S}{A_S P_S^*} + k_1 a P_S \frac{A_S^* P_S^*}{A_S P_S} + k_1 \epsilon A_R - k_1 \epsilon A_R^* - k_1 \epsilon A_R^* \frac{A_S^* A_R}{A_S A_R^*} + k_1 \epsilon A_R \frac{A_S^* A_R}{A_S A_R} + k_1 \alpha _1 A_S^* A_I + k_1 \alpha _2 A_S^* P_I + k_2 b A_S - k_2 b A_S^* \frac{A_S P_S^*}{A_S^* P_S} + k_2 r A_R - k_2 r A_R^* \frac{P_S^* A_R}{P_S A_R^*} + k_2 \phi _1 P_S^* P_I + k_2 \phi _2 P_S^* A_I - k_2 p^* P_S + k_2 p^* P_S^* + k_1 \beta P_I - k_1 \beta P_I^* \frac{P_I A_I^*}{P_I^* A_I} - k_1 q^* A_I + k_1 \beta P_I^* - k_2 \phi _1 P_S P_I^* - k_2 \phi _2 P_S^* A_I^* \frac{P_S A_I P_I^*}{P_S^* A_I^* P_I} + k_2 \phi _3 A_I - k_2 s^* P_I + k_2 s^* P_I^* + k_5 \delta P_I - k_5 \delta P_I^* \frac{P_I A_R^*}{P_I^* A_R} +k_5 \gamma A_I - k_5 \gamma A_I^* \frac{A_I A_R^*}{A_I^* A_R} - k_5 t^* A_R\).

Let, \(A = \frac{k_1 d (A_S -A_S^*)^2}{A_S}\),   \(B =K_1 \alpha _1 A_S^* A_I^* (2 - \frac{A_S^*}{A_S} - \frac{A_S}{A_S^*})\) and

\(C = k_1 \alpha _2 A_S^* P_I^* (3 - \frac{A_S^*}{A_S} - \frac{A_S P_I A_I^*}{A_S^* P_I^* A_I} - \frac{A_I P_I^*}{A_I^* P_I})\).

\(\implies \)

\(\frac{dV}{dt} = - A + B + C - k_1 a P_S - k_1 a P_S^* - k_1 a \frac{A_S^* P_S}{A_S} + k_1 a \frac{A_S^* P_S^*}{P_S} + k_1 \epsilon A_R - k_1 \epsilon A_R^* - k_1 \epsilon \frac{A_S^* A_R}{A_S} + k_1 \epsilon \frac{A_S^* A_R^*}{A_S} + k_1 \alpha _1 A_S^* A_I + k_1 \alpha _2 A_S^* P_I + k_2 b A_S - k_2 b \frac{P_S^* A_S}{P_S} + k_2 r A_R - k_2 r \frac{P_S^* A_R}{P_S} + k_2 \phi _1 P_S^* P_I + k_2 \phi _2 P_S^* A_I - k_2 p^* P_S + k_2 p^* P_S^* + k_1 \beta P_I - k_1 \beta \frac{A_I^* P_I}{A_I} - k_1 q^* A_I + k_1 \beta P_I^*\)

Now, let \(k_1 a = k_2 p^*\).

\(\implies \)

\(\frac{dV}{dt} = - A+B+C - k_1 a \frac{A_S^* P_S}{A_S} + k_1 a \frac{A_S^* P_S^*}{P_S} + k_1 \epsilon A_R - k_1 \epsilon A_R^* - k_1 \epsilon \frac{A_S^* A_R}{A_S} + k_1 \epsilon \frac{A_S^* A_R^*}{A_S} + k_1 \alpha _1 A_S^* A_I + k_1 \alpha _2 A_S^* P_I + k_2 b A_S - k_2 b \frac{P_S^* A_S}{P_S} + k_2 r A_R - k_2 r \frac{P_S^* A_R}{P_S} + k_2 \phi _1 P_S^* P_I + k_2 \phi _2 P_S^* A_I - k_2 p^* P_S + k_2 p^* P_S^* + k_1 \beta P_I - k_1 \beta \frac{A_I^* P_I}{A_I} - k_1 q^* A_I + k_1 \beta P_I^*\).

\(\implies \)

\(\frac{dV}{dt} = - A + B + C + A_I (k_1 \alpha _1 A_S^* + k_2 \phi _2 P_S^*\)

\( - k_1 q^*) \)

\(+ \left( k_1 \beta P_I^* + k_2p^* P_S^* - k_1 \epsilon A_R^* \right) \)

\(+ P_I \left( k_1 \alpha _2A_S^* + k_2 \phi _1 P_S^* + k_1 \beta - k_1 \beta \frac{A_I^*}{A_I}\right) \)

\(+ A_R \left( k_1 \epsilon + k_2 r - k_1 \epsilon \frac{A_S^*}{A_S} - k_2 r \frac{P_S^*}{P_S} \right) \)

\( + k_1 A_S^*\left( \epsilon \frac{A_R^*}{A_S} + a \frac{P_S^*}{P_S} - a \frac{P_S}{A_S}\right) + k_2 \left( b A_S - p^* P_S \right) - k_2 b \frac{P_S^8 A_S}{P_S}\).

The first term above is clearly negative and for the second term, we consider \(x_1 = \frac{A_S^*}{A_S}\), \(X_2 = \frac{A_S}{A_S^*}\). Then we get \(\frac{A_S^*}{A_S} + \frac{A_S}{A_S^*} \ge 2\) [A.M \(\ge \) G.M ]. For third term we again consider \(x_1 = \frac{A_S^*}{A_S} , x_2 = \frac{A_S P_S A_I^*}{A_S^* P_I^* A_I}, x_3 = \frac{A_I P_I^*}{A_I^* P_I}\) and then applying A.M \(\ge \) G.M, we get \(\frac{A_S^*}{A_S} + \frac{A_S P_I A_I^*}{A_S^* P_I^* A_I} + \frac{A_I P_I^*}{A_I^* P_I} \ge 3\).

Therefore, \(\frac{dV}{dt} \le 0\).

4.4.1 Bifurcation Analysis

The qualitative change of the equilibrium points in any non-linear dynamical system with the alteration of the parameter values is termed as Bifurcation analysis. This method helps to describe the variation of the ecological state due to the change of equilibrium magnitudes. Here we propose a theorem expressing the bifurcation analysis for our system Eq. (6).

Theorem 5

The proposed model shows a transcritical bifurcation with respect to the parameter \(\alpha _2\) if the following conditions hold:

  1. 1.

    \(2\alpha _1 w_1 w_3 (v_3-v_1)+2\alpha _2^* w_1 w_4 (v_3 - v_1)+2\phi _1 w_2 w_4(v_4 - v_2)+2\phi _2 w_2 w_3 (v_4 - v_2) < 0\)

  2. 2.

    \(w_4 e_1(v_3 - v_1)>0\)

Proof

To study transcritical bifurcation for our proposed, we use the theorem in [38]. In our case, let \(\alpha _2\) be the bifurcation parameter and using \(R_0=1\), we have \(\alpha _2 = \alpha _2^*\). A is the Jacobian matrix at the disease free equilibrium point.

$$\begin{aligned} A=\left[ {\begin{array}{ccccc} -d &{} a &{} -\alpha _1 e_1 &{} -\alpha _2^* e_1 &{} \epsilon \\ b &{} -p^* &{} -\phi _2 e_2 &{} -\phi _1 e_2 &{} r\\ 0 &{} 0 &{} \alpha _1 e_1 -q^* &{} \alpha _2^* e_1+\beta &{} 0\\ 0 &{} 0 &{} \phi _2 e_2+\phi _3 &{} \phi _1 e_2-s^* &{} 0\\ 0 &{} 0 &{} \gamma &{} \delta &{} -t^*\\ \end{array} } \right] \end{aligned}$$

Now, let \(w=(w_1,w_2,w_3,w_4,w_5)^t\) be the right eigen vector of A.

Then \(Aw=0w \quad \) implies that

$$\begin{aligned}&-d w_1 + a w_2 - \alpha _1 e_1 w_3 - \alpha _2^* e_1 w_4 + \epsilon w_5 = 0 \end{aligned}$$
(12)
$$\begin{aligned}&b w_1 - p^* w_2 - \phi _2 e_2 w_3 - \phi _1 e_2 w_4 + r w_5 = 0 \end{aligned}$$
(13)
$$\begin{aligned}&(\alpha _1 e_1 - q^*) w_3 + (\alpha _2^* e_1 + \beta ) w_4 =0 \end{aligned}$$
(14)
$$\begin{aligned}&(\phi _2 e_2 + \phi _3) w_3 + (\phi _1 e_2 -s^*) w_4 = 0 \end{aligned}$$
(15)
$$\begin{aligned}&\gamma w_3 + \delta w_4 - t^* w_5 = 0 \end{aligned}$$
(16)

From Eqs. (14) and (15), we get

\(w_3 = - \frac{\alpha _2^* e_1 + \beta }{\alpha _1 e_1 - q^*} w_4\)

\(w_5 = \frac{{\delta (\alpha _1 e_1 - q^*)-\gamma (\alpha _2^* e_1 + \beta )}}{t^*(\alpha _1 e_1 -q^*)} w_4\) Multiplying Eq. (12) by b and 13 by d, then adding Eqs. (12 and 13), we get \(w_2\)

\(=\left[ \frac{{\begin{array}{l} {t^*(\alpha _1 e_1 -q^*)}\\ \quad {(b \alpha _2^* e_1 + d \phi _1 e_2)}\\ \qquad {+\gamma (b\epsilon + r d)(\alpha _2^* e_1 +\beta )}\\ \quad {-t^*(\alpha _2^* e_1 + beta)(b \alpha _1 e_1 + d \phi _2 e_2)}\\ \qquad \qquad {-\delta (b \epsilon + r d)(\alpha _1 e_1 -q^*)} \end{array}}}{t^*(\alpha _1 e_1 - q^*)(ab-dp^*)}\right] w_4\)

Multiplying Eq. (12) by \(p^*\) and 13 by a, then adding Eqs. (12) and (13), we get

\(w_1\)

\(=\left[ \frac{{\begin{array}{l} {t^*(\alpha _1 e_1 -q^*)(\alpha _2^* e_1 p^* + \phi _1 e_2a)}\\ \quad {+\gamma (\alpha _2^*e_1 +\beta )(p^* \epsilon + ar)}\\ \qquad {-t^*(\alpha _2^* e_1 + \beta )(\alpha _1 e_1 p^*}\\ \qquad \qquad {+\phi _2 e_2 a)-\delta (\alpha _1 e_1 - q^*)(p^* \epsilon + ar)} \end{array}}}{t^*(\alpha _1 e_1 - q^*)(ab-dp^*)}\right] w_4\)

Again, let \(v=(v_1,v_2,v_3,v_4,v_5)\) be the left eigen vector of A. Then, \(vA=0A\), \(\implies \) \((vA)^t=0\), \(\implies \) \(A^t v^t=0\). Now the transpose of the matrix A is

$$\begin{aligned} A^t=\left[ {\begin{array}{ccccc} -d &{} b &{} 0 &{} 0 &{} 0\\ a &{} -p^* &{} 0 &{} 0 &{} 0\\ -\alpha _1 e_1 &{} -\phi _2 e_2 &{} \alpha _1 e_1 -q^* &{} \phi _2 e_2+\phi _3 &{} \gamma \\ -\alpha _2^* e_1 &{} -\phi _1 e_2 &{} \alpha _2^* e_1+\beta &{} \phi _1 e_2-s^* &{} \delta \\ \epsilon &{} r &{} 0 &{} 0 &{} -t^*\\ \end{array} } \right] \end{aligned}$$

Here, \(A^t v^t=0\) implies that

$$\begin{aligned}&-d v_1 + b v_2 = 0 \end{aligned}$$
(17)
$$\begin{aligned}&av_1 - p^* v_2 = 0 \end{aligned}$$
(18)
$$\begin{aligned}&-\alpha _1 e_1 v_1 - \phi _2 e_2 v_2 + (\alpha _1 e_1 - q^*) v_3 \nonumber \\&+(\phi _2 e_2 + \phi _3) v_4 + \gamma v_5 = 0 \end{aligned}$$
(19)
$$\begin{aligned}&-\alpha _2^* e_1 v_1 - \phi _1 e_2 v_2 + (\alpha _2^* e_1 + \beta ) v_3\nonumber \\&+ (\phi _1 e_2 - s^*) v_4 + \delta v_5 =0 \end{aligned}$$
(20)
$$\begin{aligned}&\epsilon v_1 + r v_2 - t^* v_5 = 0 \end{aligned}$$
(21)

From Eqs. (17 and 21), we get

\(v_1=\frac{b}{d} v_2\), and

\(v_5=\frac{b \epsilon +r d}{t^* d}v_2\). Now, multiplying Eq. (19) by \((\alpha _2^* e_1 + \beta )\) and Eq. (20) by \((\alpha _1 e_1 - q^*)\), and subtracting Eq. (20) from Eq. (19), we get

\(v_4=\)

\({\left[ \frac{{\begin{array}{l} {t^*be_1(\alpha _1 \beta + \alpha _2^* q^*)+t^*d \phi _2 e_2(\alpha _2^* e_1+ \beta )}\\ \quad {-t^*d \phi _1 e_2(\alpha _1 e_1 -q^*)+(b\epsilon +rd)\{\delta (\alpha _1 e_1 - q^*)-\gamma (\alpha _2^* e_1 +\beta )\}} \end{array}}}{{\normalsize t^*d\{(\phi _2 e_2+\phi _3)(\alpha _2^* e_1+\beta )-(\phi _1 e_2 - s^*)(\alpha _1 e_1 - q^*)\}}}\right] v_2}\)

Multiplying Eq. (19) by \((\phi _1 e_2 - s^*)\) and Eq. (20) by \((\phi _2 e_2 +\phi _3)\), and subtracting Eq. (20) from (19), we derive

\(v_3=\)

\({\left[ \frac{{\begin{array}{l} {t^*b\{\alpha _2^*e_1(\phi _2 e_2 + \phi _3)-\alpha _1 e_1(\phi _1 e_2 - s^*)\}}\\ \quad {+t^*be_2(\phi _1 \phi _3 + \phi _2 s^*)+(b\epsilon +rd)\{\gamma (\phi _1 e_2 - s^*)-\delta (\phi _2 e_2 + \phi _3)\}} \end{array}}}{{\normalsize t^*d\{(\phi _2 e_2+\phi _3)(\alpha _2^* e_1+\beta )-(\phi _1 e_2 - s^*)(\alpha _1 e_1 - q^*)\}}}\right] v_2}\)

Therefore,

\(w=(w_1,w_2,w_3,w_4,w_5)^t\)

Where,

\(w_1=t^*(\alpha _1 e_1 - q^*)(\alpha _2^* e_1 p^* + \phi _1 e_2 a)+\gamma (\alpha _2^* e_1 +\beta )(p^* \epsilon + a r)-t^*(\alpha _2^* e_1 + \beta )(\alpha _1 e_1 p^* + \phi _2 e_2 a)-\delta (\alpha _1 e_1 - q^*)(p^* \epsilon + a r)\);

\(w_2=t^*(\alpha _1 e_1 - q^*)(b \alpha _2^* e_1 + d \phi _1 e_2)+\gamma (b \epsilon + r d)(\alpha _2^* e_1 + \beta )-t^*(\alpha _2^* e_1 + beta)(b \alpha _1 e_1 + d \phi _2 e_2)-\delta (b \epsilon + r d)(\alpha _1 e_1 - q^*)\);

\(w_3=-t^*(ab-dp^*)(\alpha _2^* e_1 + \beta )\);

\(w_4=t^*(\alpha _1 e_1 - q^*)(ab-dp^*)\);

\(w_5=\delta (\alpha _1 e_1 - q^*)(ab-dp^*)-\gamma (\alpha _2^* e_1 + \beta )(ab-dp^*)\); and

\(v=(v_1,v_2,v_3,v_4,v_5)\)

where,

\(v_1=t^*b\{(\phi _2 e_2+\phi _3)(\alpha _2^* e_1+\beta )-(\phi _1 e_2 - s^*)(\alpha _1 e_1 - q^*)\}\);

\(v_2=t^*d\{(\phi _2 e_2+\phi _3)(\alpha _2^* e_1+\beta )-(\phi _1 e_2 - s^*)(\alpha _1 e_1 - q^*)\}\);

\(v_3=t^*b\{\alpha _2^* e_1(\phi _2 e_2 + \phi _3)-\alpha _1 e_1(\phi _1 e_2 - s^*)\}+t^*b e_2(\phi _1 \phi _3 + \phi _2 s^*)+(b\epsilon +rd)\{\gamma (\phi _1 e_2 - s^*)-\delta (\phi _2 e_2 + \phi _3)\}\);

\(v_4=t^*b e_1(\alpha _1 \beta + \alpha _2^* q^*)+t^*d \{ \phi _2 e_2(\alpha _2^* e_1 + \beta )-\phi _1 e_2(\alpha _1 e_1 - q^*)\}+(b\epsilon +rd)\{\delta (\alpha _1 e_1 - q^*)-\gamma (\alpha _2^* e_1 +\beta )\}\);

\(v_5=(b \epsilon +r d) \{(\phi _2 e_2+\phi _3)(\alpha _2^* e_1+\beta )-(\phi _1 e_2 - s^*)(\alpha _1 e_1 - q^*)\}\);

For sake of simplicity, we consider \(x_1=A_S,\quad x_2=P_S,\quad ,x_3=A_I,\quad x_4=P_I,\quad ,x_5=A_R\)

Then,

\(f_1=\lambda + a x_2 + \epsilon x_5 - \alpha _1 x_1 x_3 - \alpha _2 x_1 x_1 -d x_1\);

\(f_2=b x_1 + r x_5 - \phi _1 x_2 x_4 - \phi _2 x_2 x_3 - a x_2 - d x_2\);

\(f_3=\alpha _1 x_3 x_1 + \alpha _2 x_1 x_4 + \beta x_4 - \gamma x_3 - \mu _1 x_3 - d x_3\);

\(f_5=\delta x_4 + \gamma x_3 - \epsilon x_5 - d x_5\);

\(f_5=\delta x_4 + \gamma x_3 - \epsilon x_5 - d x_5\);

Now, the coefficients a and b are calculated as follows using the theorem of Castillo-Chavez and Song [38].

In order to find the values of a and b, we have to calculate all the partial derivatives.

\(\frac{\delta ^2 f_1}{\delta x_4 \delta \alpha _2}=-e_1,\quad \frac{\delta ^2 f_3}{\delta x_4 \delta \alpha _2}=e_1,\quad \)

\(\frac{\delta ^2 f_1}{\delta x_1 \delta x_3}=-\alpha _1, \quad \frac{\delta ^2 f_1}{\delta x_1 \delta x_4}=-\alpha _2^*,\quad \frac{\delta ^2 f_1}{\delta x_3 \delta x_1}=-\alpha _1,\quad \)

\(\frac{\delta ^2 f_1}{\delta x_4 \delta x_1}=-\alpha _2^*, \quad \frac{\delta ^2 f_2}{\delta x_2 \delta x_3}=-\phi _2, \)

\(\quad \frac{\delta ^2 f_2}{\delta x_2 \delta x_4}=-\phi _1,\quad \)

\(\frac{\delta ^2 f_2}{\delta x_3 \delta x_2}=-\phi _2,\quad \frac{\delta ^2 f_2}{\delta x_4 \delta x_2}=-\phi _1,\quad \frac{\delta ^2 f_3}{\delta x_1 \delta x_3}=\alpha _1,\quad \frac{\delta ^2 f_3}{\delta x_1 \delta x_4}=\alpha _2^*, \)

\( \quad \frac{\delta ^2 f_3}{\delta x_3 \delta x_1}=\alpha _1,\quad \frac{\delta ^2 f_3}{\delta x_4 \delta x_1}=\alpha _2^*,\quad \)

\(\frac{\delta ^2 f_4}{\delta x_2 \delta x_3}=\phi _2,\quad \frac{\delta ^2 f_4}{\delta x_2 \delta x_4}=\phi _1,\quad \frac{\delta ^2 f_4}{\delta x_3 \delta x_2}=\phi _2,\quad \frac{\delta ^2 f_4}{\delta x_4 \delta x_2}=\phi _1\)

and all other

partial derivatives are zero. Putting these all values in a and b, we get

\(a=2\alpha _1 w_1 w_3 (v_3-v_1)+2\alpha _2^* w_1 w_4 (v_3 - v_1)+2\phi _1 w_2 w_4(v_4 - v_2)+2\phi _2 w_2 w_3 (v_4 - v_2)\) and \(b=w_4 e_1(v_3 - v_1)\)

Now we can say that our proposed system undergoes transcritical bifurcation for the parameter \(\alpha _2\), if \(a>0\) and \(b<0\) using Castilo-chavez theorem as proven above.

5 Sensitivity Analysis

Sensitivity analysis (henceforth, SA) is a vital tool in mathematical modeling to characterize the influence of the input parameters. This method comprises two techniques, i.e., first, the Uncertainty analysis (henceforth, UA), and second the SA. Based on the structure of the model, one can distinguish UA into two parts, viz., (i) epistemic, (ii) aleatory [39]. The first one describes the uncertainty in the deterministic system, and that of the second one is for stochastic dynamics. Since our proposed model (system Eq. 6) explains the deterministic scenario, so we choose the epistemic approach. Numerous methods are available to delineate the UA viz., response surface process, differential analysis, etc., but [39] illustrate the most parsimonious approach to conduct the UA and SA. The author applies two techniques, (i) Monte Carlo (henceforth, MC) simulation and (ii) Latin-Hyper Cube sampling (henceforth, LHS), to perform the UA. It is worthy of mentioning that the uncertainty analysis follows the sensitivity analysis.

The goal of SA is to recognize those inputs such as the initial conditions, parameter values, etc., that would certainly influence the uncertainty analysis, hence the model outcomes. Sensitivity analysis can also be distinguished in the local and global sense. The local SA is generally applied when the input factors such as the model parameters and initial population sizes are known with a small level of uncertainty. The partial derivative approach is the best one to describe the local SA [40]. Nevertheless, in most ecological problems, the input of the model parameters and initial sizes are often unknown, which provides a biased result for the local SA. In this connection, one needs to perform the global SA followed by the methods of [39]. The author describes two methods, (i) the partial rank correlation coefficient (henceforth, PRCC) and (ii) the e-Fast algorithm to conduct global SA. Here we follow the first method, i.e., the PRCC approach to perform the global SA for our model ( system Eq. 6). The detailed procedure to perform the global SA is mentioned in the article of [39].

The motto of SA in case of our dynamical system (Eq. 6) is to identify the ecological parameters that would certainly affect the basic reproduction number (\(R_0\)). According to the protocol mentioned by the author we calculate the PRCC of the parameters a, \(\alpha _1\), \(\alpha _2\), d, b, \(\phi _1\), \(\phi _2\), \(\phi _3\), \(\beta \), \(\gamma \), \(\mu _2\), \(\delta \), \(\mu _1\), \(\epsilon \), \(\lambda \), r with respect to \(R_0\). Note that we initially perform the LHS protocol in conducting the UA, where we consider the parameter values from a biologically feasible region. The bar diagram in Fig. 3 represent the measure of correlation between \(R_0\) and the other model parameters. Infection rate of susceptible pups \((P_S)\) in contact to infected pups \((P_I)\), i.e., \(\phi _1\) stands to be the most correlated and henceforth most sensitive parameter in the enumeration of BRN (\(R_0\)).

Fig. 3
figure 3

Sensitivity analysis is performed on the basic reproduction number \((R_0)\) based on our proposed model with the Latin Hypercube Sampling (LHS) method where the number of sample size is 1000. The value of the input (model) parameters are listed in the Table 2. The asterisk (*) sign indicates the PRCC of the corresponding parameters have a significant difference from zero with 5% level of accuracy. The figure projects that the model parameter \(\phi _1\) has the highest positive correlation with \(R_0\)

Full size image

6 Numerical simulations

This section is devoted to the verification of analytical results by rigorous numerical simulation using MATLAB. First, we examine the behaviour of the system near \(R_0=1\). As found in the global stability results of the disease free equilibrium, it is expected that the disease will die out for \(R_0 < 1\). However, to perform the numerical simulation we take parameters from Table 2 and initial conditions are taken as \(A_S(0)=5000\), \(P_S(0)=100\), \(A_I(0)=1\), \(P_I(0)=1\) and \(A_R(0)=0\).

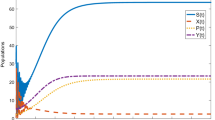
All the parameters are fixed except \(\alpha _2\). The time series solutions of the compartments are depicted in Fig. 4(A) when \(R_0<1\) (\(\alpha _2 = 9 \times 10^{-4}\)) and in Fig. 4(B) when \(R_0>1\) (\(\alpha _2 = 3 \times 10^{-3}\)). It can be observed that the equilibrium approaches disease free state when \(R_0=0.8555<1\) and the disease becomes endemic whenever \(R_0=1.3979>1\). The corresponding equilibrium values for \(R_0=0.8555\) are (61.03, 80.51, 0.00, 0.00, 0.00) and (46.02, 54.78, 6.93, 1.87, 3.59) for \(R_0=1.3979\). Therefore, the analytical results for stability of DFE is verified.

Fig. 4
figure 4

Time evolution of the populations when (A) \(R_0 < 1\) and (B) \(R_0 > 1\). Parameter values are taken from Table 2 except in (A) we take \(\alpha _2 = 0.0009\)

Full size image

Now, to examine the transcritical bifurcation at \(R_0=1\), we draw bifurcation diagrams with respect to the infected adults and pups. As we focused on the parameter \(\alpha _2\) as a bifurcation parameter, we vary \(10^{-5} \le \alpha _2 \le 5 \times 10^{-3}\) only and all other parameters are fixed. The fixed parameters are taken from Table 2 and the initial conditions are taken as \(A_S(0)=5000\), \(P_S(0)=100\), \(A_I(0)=1\), \(P_I(0)=1\) and \(A_R(0)=0\). The bifurcation diagrams with respect to \(A_I(t)\) and \(P_I(t)\) are shown in Fig. 5(A) and Fig. 5(B), respectively. We observe that the transcritical bifurcation occurs at \(R_0=1\) as shown analytically. This confirms that \(R_0\) is a sharp threshold for the proposed model. In other words, the infected dog populations will die out if one maintain \(R_0<1\) for a sufficiently large period of time.

Fig. 5
figure 5

Transcritical bifurcation diagrams with respect to the basic reproduction number for A equilibrium density of \(A_I\) and B equilibrium density of \(P_I\)

Full size image

Further, we examine the global stability of the endemic equilibrium point numerically. To perform the numerical simulation we take parameters values from Table 2. The endemic equilibrium \(E(A_S^*, P_S^*, A_I^*, P_I^*, A_R^*)\) is found to be (46.02, 54.78, 6.93, 1.87, 3.59) for this parameter set. Further, the conditions for the global asymptotic stability of the equilibrium are satisfied for this particular parameter set. It is shown that the endemic equilibrium is globally asymptotically stable inside the region D in \(A_S-A_I-P_I\) and \(P_S-A_I-P_I\) spaces (see Fig. 6). From the figures it is also observed that the solutions that originate inside the region D, approach the points \((A_S^*, A_I^*, P_I^*)\) and \((P_S^*, A_I^*, P_I^*)\) in Fig. 6(A) and Fig. 6(B) respectively. Thus, the numerical simulations also confirm that the endemic equilibrium is globally asymptotically stable in the \(A_S-A_I-P_I\) and \(P_S-A_I-P_I\) spaces. Furthermore, we can show the global asymptotic stability of the endemic equilibrium in other spaces by proceeding similarly.

Fig. 6
figure 6

Global stability of the endemic equilibrium in A \(A_S\) - \(A_I\) - \(P_I\) and B)\(P_S\) - \(A_I\) - \(P_I\) spaces

Full size image

7 Control strategies

The Canine distemper disease in wild dogs is a major concern for naturalist, conservation biologist and environmental policy makers. Our SIRS epidemiological model is useful to forecast the disease spread over time. Unlike existing models, this model focuses on natural controls rather than intervention measures. Since the model is conceptually developed from the interactive structure of African Wild dogs, the parameters of the model represent specific ecological aspects of African wild dogs. Introducing control strategies based on the parameters and their corresponding ecological aspects is a common practice in epidemiology [41, 42]. This bridge between the natural aspects and parameters makes the model easier to implement in wild.

For example, if a policy focuses on the reintroduction of Wild dogs in an area, predicting the change in disease outbreak is plausible through tuning the \(\lambda \) parameters of the model. Similarly, the disease dynamics can be monitored and control through 15 eco-sociological paths enlisted in table 2 through parameter tuning using this model. Among the 15 parameters, \(\phi _1\) is the most sensitive as per our study. However, this study provides an order of parameters opening several combinations of parametric set to control the disease outbreak based on the local and global scenario. The policymakers can choose the feasible parameters they can control based on the ranking we provide through sensitivity analysis to drive a wild population from endemic equilibrium to disease-free equilibrium.

We find the disease free equilibrium is both locally and globally stable. Therefore, once the wild dog population achieves disease-free equilibrium, the population can withstand threats of new emergence of this disease for a long term. Since, under six conditions provided in theorem 4, the endemic equilibrium is globally stable too, conservation strategists must focus on disrupting these criteria based on feasibility. For example, Adding more Adult susceptible to break six conditions of global stability is a simple way to destabilize the endemic equilibrium. Sterilization of adult susceptible to control birth rate of pups is another option to destabilize the endemic equilibrium. Since selective sterilization of wild dog population is harder than introducing adult wild dogs, the introduction of susceptible seems to be more logical in terms of strategy development in a diseased population. The transcritical-bifurcation analysis reveals regulation of infection rate of Susceptible adults in contact with infected pups is the key to transform the endemic to disease-free equilibrium. Although, theoretically sound, this regulation may turn out to be impractical during implementation. One way to lower the infection rate is monitoring the mobility of reintroduced adult susceptible dogs by fencing and confining them in the breeding ground where the infected pups are less. Such isolation techniques may work only in Sanctuaries or small conserved lands as it requires cost-intensive man power.

7.1 Strategy I: Isolation

In this section, we examine the effects of isolating infected dogs, a potential preventive strategy against canine distemper disease. Some existing literature already indicates the necessity of isolating infected dogs in domestic or captive environment. The isolation strategy in other wild animals is also a common prevention strategy [43]. Thus, quantifying the effects of isolating adult and pups is an important issue. It is assumed that infected adults and infected pups are isolated from the system at constant rates \(\xi _1\) and \(\xi _2\) respectively. After incorporating the isolation in the model, the modified system of equations take the following form

$$\begin{aligned} \frac{dA_S}{dt}= & {} \lambda + a P_S + \epsilon A_R - \alpha _1 A_S A_I - \alpha _2 A_S P_I -d A_S, \nonumber \\ \frac{dP_S}{dt}= & {} b A_S + r A_R - \phi _1 P_S P_I - \phi _2 P_S A_I - a P_S - d P_S, \nonumber \\ \frac{dA_I}{dt}= & {} \alpha _1 A_I A_S + \alpha _2 A_S P_I + \beta P_I - \gamma A_I - \mu _1 A_I - (d+\xi _1) A_I, \nonumber \\ \frac{dP_I}{dt}= & {} \phi _1 P_S P_I + \phi _2 P_S A_I + \phi _3 A_I - \beta P_I \nonumber \\&- \delta P_I - \mu _2 P_I - (d + \xi _2) P_I, \nonumber \\ \frac{dA_R}{dt}= & {} \delta P_I + \gamma A_I - \epsilon A_R - d A_R . \end{aligned}$$
(22)
Fig. 7
figure 7

Effect of isolating infected adults and pups

Full size image

We vary the parameters \(\xi _1\) and \(\xi _2\) in the range [0, 0.1] while doing numerical simulations. For different levels of isolation rates, the reduction in \(A_I\) and \(P_I\) are depicted in Fig. 7. We observe that \(\xi _1\) is more effective than \(\xi _2\) in reducing the number of infected adult dog population. On the other hand, \(\xi _2\) is more effective than \(\xi _1\) in reducing the number of infected pups.

Further, to quantify the effects of isolation more precisely, we calculate the percentage reduction of adult and pups infected dogs in the 50 days projection period. We use the following basic formula

$$\begin{aligned} {\text {Percentage reduction}= {\frac{\text {Baseline cases} -\text {Cases with control}}{\text {Baseline cases}}\times 100}.} \end{aligned}$$

The percentage reduction for both infected populations are reported in Table 4. From observed values in percentage reduction, it can be reinforced that \(\xi _1\) is more effective in reduction of canine distemper cases of infected adults. Maximum value of \(\xi _1\) (=0.1) can reduce infected adult cases upto 65.63%. The reason behind this observation may be that the transmission coefficient of infected adults is greater than the transmission coefficient of infected pups. Maximum value of \(\xi _2\) (=0.1) can reduce pups infection by 47.98%. However, it is also observed that when both infected populations are isolated at a moderate level (=0.05), the percentage reduction in both infected populations show competitive results. Thus, we recommend moderate isolation of both infected populations since it is effective as well as more feasible.

Table 4 Percentage reduction in total number of infected adult and pups for different levels of isolation
Full size table

Although cost-intensive, isolating infected adults and pups from the wild is a possible solution to control the disease outbreak. Especially, if the contaminated zone is smaller in size, isolation strategy may work better than birth controlling. So we modified the proposed model to incorporate isolation terms. The modified model (system Eq. 22) can predict the disease dynamics better than the first proposed model under various isolation rates. The numerical simulation of the modified model also shows that the isolation of both infected adults and pups together brings down the disease. Isolation of only adults still allows the susceptible pups to be in contact with the infected pups and thus producing more secondary infection in pups. Therefore, isolating pups is more important than isolating adults. There is a broad prospect of studying the disease dynamics with various intervention measures with complicated forms based on the proposed model. Nonetheless, this proposed model set a framework to address epidemiological complications to manage disease outbreak in wild animals.

7.2 Strategy II: Birth control and reintroduction

The sensitivity analysis of BRN for parameters through PRCC reveals that \(\phi _{1}\), b, and \(\alpha _1\) have highest PRCC with BRN in decreasing order among 10 significantly correlated parameters. Controlling \(\phi _1\) or infection rate of susceptible pups in contact to infected pups is thus the most effective way to lower the BRN. However, this control measure is a cost-intensive strategy requiring selective isolation of pups via manual survey. Especially an infected pup and a susceptible pup may belong to the care of same mother. So isolating pups may make them vulnerable to other diseases without the nurture from their mothers. On the other hand, controlling \(\alpha _{1}\) is a relatively easier strategy than the aforementioned one. Lowering \(\alpha _{1}\) or the infection rate of susceptible adults to infected adults also requires selective isolation of infected adults. However, infected adults produce infected pups; their isolation do not separate pups from their mothers. Therefore, the scientific choice which is implacable seems to be regulating the parameter with second highest b, i.e., birth rate of susceptible pups from susceptible adults. Lowering b means reducing the birth rate of susceptible pups by preventing the mating rate of Susceptible adults in infected areas. Reducing the birth rate of an endangered species may apparently incur the extinction risk of the population but re-introduction of the adults from other areas eliminates the chance of extinction. Since, the birth controlling is limited to the diseased area only, other areas can still produce enough pups to be matured into adults and transferred during reintroduction. Note that the wild-dog population suffers from inbreeding depression, improvising their immunity. Lowering the b and increasing \(\lambda \) together can reduce this improvisation in a synergistic fashion. The increment in \(\lambda \) is possible through reintroducing the susceptible in the wild area where the disease is found. This reintroduction will increase the birth-rate of susceptible pups relative to the birth rate of infected pups. Infected pups spread the disease more efficiently than others through interactions. The relative low abundance of infected pups can result in less interaction with infected pups, leading to reduced production of secondary infections. Thus, the disease can be controlled through birth control and reintroduction.

8 Conclusion

Epidemiological model can predict the dynamics of Canine Distemper disease, which is a major threat to wild dog population. The proposed epidemiological model provides insight to the path of disease outbreak through parameters. This article derive control strategies from the proposed model based on the parameters. The two major strategies we proposed are isolation strategy and birth-control-reintroduction strategy. This article concludes that a moderate isolation rate of infected adults and pups can reduce the disease significantly. The birth-control and reintroduction strategy diminishes the disease by reducing the infected pups and interaction with them. Finally, the outcome of this study can be imposed in the practical field by the conservation policy makers.