1 Introduction

Air spray guns were widely used in many industries such as automobile, aero-space, aircraft, ship, and furniture, due to its good atomization performance [1,

Fig. 1
figure 1

Geometry of three-nozzle

Full size image

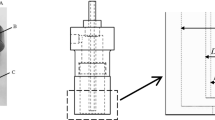
The spraying schematic diagram and coordinate system definition of three-nozzle are shown in Fig. 2. The shape of coating film is elliptical under the action of sha** air flow. The intersection of the center axis of three-nozzle and the target surface is the origin of coordinate system. The X-axis and Y-axis are parallel to the short and long axis of elliptical coating film. The Z-axis is along the center axis of three-nozzle.

Fig. 2
figure 2

Definition of coordinate system

Full size image

2.2 Computational domain and grid

ICEM software was used to create the computational domain and generate unstructured grid for three-nozzle. Figure 3 shows the computational domain and unstructured grid. Considering the complex structure of three-nozzle and the area of elliptical coating film, the size of computational domain was set to 600 × 200 × 210 mm3. Three-nozzle is located in the center of lower surface. The upper surface is the target. The spraying distance is 200 mm. Due to the complex structure of three-nozzle and fast airflow velocity in the region near the nozzle, local grid refinement method was applied in this paper. In order to accurately describe the effect of air flow on paint droplets and improve the calculation accuracy, a higher grid resolution was adopted in the region near the nozzle. In order to increase the calculation speed and save computing resources, a lower grid resolution was used in the region far from the nozzle.

Fig. 3
figure 3

Computational domain and grid: a calculation domain; b overall unstructured grid; c grid at section x = 0

Full size image

2.3 Methods and initial conditions

The spraying process of three-nozzle can be regard as a gas–liquid two-phase flow field. In this paper, Euler–Lagrange method was used to model the two-phase flow field. The software platform for simulation is ANSYS-Fluent. The finite volume method was used to simulate the spraying process. Coupled solver and second-order upwind scheme were used to calculate the three-dimensional compressible airflow. The standard k-ε model was used to calculate the turbulent transport process. DPM model was used to track the trajectory of discrete phase. TAB model was used to describe the secondary breakup process of paint droplets. The turbulent diffusion of paint droplets in the gas flow field can be simulated by calculating the trajectories of a large number of representative particles with the help of stochastic tracking model. Euler wall film model was used to calculate the coating film thickness distribution on the workpiece.

The motion equation of discrete phase is:

$$\frac{{du_{p} }}{dt} = F_{D} \left( {u - u_{p} } \right) + F_{G}$$
(1)

in which \({F}_{D}\left(u-{u}_{p}\right)\) is the drag force; \({F}_{G}\) is the gravity force; \({u}_{p}\) is the velocity of droplet; \(u\) is the instantaneous velocity of air; which is obtained by adding the local average velocity and the pulsating velocity caused by turbulence.

Since the density of air is much smaller than that of droplets, the virtual force and Saffman force can be ignored. Since the mass flow of paint is generally small, the interaction force between droplets can be ignored. The droplet trajectory can be obtained by integrating the motion equation of discrete phase.

Due to the complexity of atomization, many researchers have not studied the process of jet atomization. Rather, it is assumed that the paint has been completely atomized at a position very close to the nozzle. The velocity and size distribution of droplets are obtained through experiments. In order to avoid dependence on experiment, simplified inlet boundary conditions are used for both continuous and discrete phase. The discrete phase is directly added at the position of paint hole. All paint holes were set as mass inlets, with a mass flow rate of 1 × 10–3 kg/s and an initial velocity of 50 m/s [23]. Atomizing air holes, sha** air holes, and assisting air holes were set as pressure inlets. The surface of three-nozzle and target surface were set as walls. The other boundaries were set as pressure outlets, with a static pressure of 0 MPa. The main parameters and material properties of three-nozzle are shown in Tables 1 and 2.

Table 1 Application parameters used in the simulations
Full size table
Table 2 The properties of the liquid and gas
Full size table