1 Introduction

Carbon capture and storage (CCS) technologies have been developed as an exceptional solution to reduce CO2 emissions from fossil fuel utilization, especially CO2 emissions from power plants and industrial processes. The transportation of liquid CO2 is a fundamental stage of the CCS technological processes [1]. The decompression of liquified CO2 from tanks or pipelines is a continuing concern in terms of the safe transport and storage of CO2. A container filled with liquified CO2 may fail due to projectile impact, corrosion, or overheating. Under some circumstances, liquid CO2 depressurization may lead to rapid phase change with explosive boiling and the creation of blast waves. If the container fails catastrophically with a sizable multiphase mixture rapid outburst to the environment, it can be characterized as boiling liquid expanding vapor explosion (BLEVE) [2]. In such explosions, serious hazards arise from generated pressure loads and discharge of considerable CO2 volume to the surroundings, in addition to dangerous flying fragments [3]. Therefore, there is a need for profound insights into process safety and risk assessment to protect against, avoid, and mitigate such devastating incidence. It is crucial to study the fundamental processes of rapid phase transition and evaporation, estimate the strength of the generated pressure waves, and determine the factors that affect these processes.

Attempts to specify the conditions promoting a BLEVE incident have been proposed in the published literature. Reid's superheat limit theory [4, 5] suggested the factors that produce BLEVE. According to this theory, a liquid crossing the saturation line after the decrease in pressure becomes superheated in the metastable state. It remains in this state between saturation and spinodal curves until it reaches the superheated limit temperature(SLT). BLEVE is more likely to occur whenever the liquid temperature exceeds the SLT and approaches the spinodal line. Depending on the depressurization rate, the liquid attains a high degree of superheating (DOS). In addition, evaporation must be rapid and induced by homogeneous nucleation in the liquid bulk. However, other studies have mentioned that explosive evaporation could occur even when the liquid temperature has not exceeded the SLT [6, 7]. When a liquid CO2 depressurizes, a rarefaction wave propagates through the liquid, followed by an evaporation wave. The two-phase mixture formed behind the evaporation wave flows toward the atmospheric pressure side. As a result, it compresses the gas ahead and, in certain conditions, produces a shock wave. The vapor/liquid contact surface moves behind the shock wave into the surroundings [8, 9].

Different types of shock tubes have established their capability and effectiveness in small-scale experiments to measure the properties related to analogous phenomena. Such devices are used to study pressure-driven transient phenomena that involve considerable energy transformation due to pressure change. Several experimental studies aiming to describe the front propagating behind the incident shock or evaporation waves have been carried out on vertical laboratory-scale test devices with various fluids [10,11,12,13,14]. Several tests have been performed on larger horizontal tubes and pipes [15,16,17]. Almost all of these studies were conducted in constant cross-sectional vessels and mainly used the one-membrane burst method. This paper emphasizes experiments that include decompression from the top of vertical containers, divergent cross-sectional vessels, and double-diaphragm bursting mechanisms.

Chaves [18] performed experiments on two ducts with a constant and diverging cross-section to study the evaporation wave evolution during the depressurization of liquids with high specific heat. The study found that the splitting of the expansion wave is a restricted thermodynamic incident and is not dependent on the geometry. Zabelinskii et al. [19] tested the leading shock front shape in a gas (explosive mixture diluted with cold hydrogen) employing a horizontal shock tube with a conical passage between high and low-pressure parts. According to the study's outcome, the diverging cross-sectional passageway resulted in the retention of heterogeneities on the wavefront surface.

Various diaphragm rupturing methods have been developed and introduced to examine sudden decompression procedures in shock tubes. Hill [10] implemented a typical rupture method using knife blades prompted by a pneumatic cylinder to cut aluminum foil diaphragm sets between low- and high-pressure reservoirs. In the study on boiling development during the depressurization of superheated liquid in a column, Das et al. [13] employed a four-bladed cutter placed adjacent to and over a plastic diaphragm and covered by an air chamber. The diaphragm swells to touch the blades and is punctured when the pressure falls due to a vacuum pump in the air chamber. A remarkable study on explosive vaporization of superheated liquids was introduced by Reinke [20]: the moveable flange method. A brass sheet was pressed between the flanges from the bottom side and the two-ring flange from the top. The outer flange had a sharp edge, and the diaphragm was fixed to the next bottom flange. An inner ring, which could move up and down, pressed the diaphragm in a smaller circle. Lifting the mobile flange's ring increased the force on the diaphragm surface due to the increased area under load, and subsequently, the diaphragm ruptured.

Recently, a different method presented by Dewangan et al. [14] applied a Nichrome heating wire to heat and rupture the plastic diaphragm fixed between two flanges. Li et al. [21] questioned which factors influenced the promotion of boiling liquid expanding vapor explosion (BLEVE) by heating dry ice in a cylindrical vessel sealed with a burst disk. The container’s pressure increased as the dry ice liquefied and evaporated until the point where the disk exploded. Stotz et al. [16] demonstrated a double-diaphragm shock tube to investigate atomized liquids and the associated combustion processes. The 12-m long horizontal installation consisted of three tubular parts: driver, driven, and buffer zones. The two diaphragms ruptured by the pressure quickly decreasing in the buffer section.

Over recent years, the depressurization of liquified CO2, the associated evaporation, and the developed pressure waves have been studied at the University of South-Eastern Norway (USN). Wei Ke [22] conducted experiments on BLEVE by using cylindrical plastic tubes filled with dry ice. The pressure rose by heating the test tube. Then, the pressure was vented with the help of a pneumatic piston. The tube exploded when it could not withstand the increasing pressure, and CO2 splashed out. The progression of the evaporation waves during the decompression of liquid CO2 was analyzed by Tosse et al. [23]. A transparent polycarbonate tube was utilized as a high-pressure unit, and Mylar sheets were utilized as a membrane ruptured by a pneumatically driven needle. Hansen et al. [24] broadly studied the rapid depressurization of CO2 utilizing three different vertical apparatuses, two of which were described above. The third setup consisted of a stainless steel rectangular duct filled with liquid CO2 to a specified level. Sudden decompression was performed by rupturing the aluminum diaphragm with a pneumatically driven cross-shaped knife.

One major issue in the previous CO2 depressurization experiments was that the two-phase flow behind the evaporation wave was not instantaneously released from the test section. This is because the ducts' constant cross-sectional area, especially with more minor opening exits, did not allow the prompt release of the rapidly expanded two-phase mixture. In turn, the analysis of the evaporation process was complicated, and there may have been shock attenuation effects. In addition, the decompression in the previous test sections was performed by rupturing the diaphragms with an actuated knife or needle, which was fixed above the test duct. This arrangement disturbed the exploded multiphase flow and subsequently imprecisely captured its behavior. As a continuation of this research activity, this project seeks to expand prior research by providing results and analysis of expansion wave dynamics in a new vessel design.

The present work focuses on a divergent cross-sectional area, as opposed to previous work. The divergent cross-section will significantly enhance fluid expansion as the rarefaction wave propagates toward a smaller area. The experimental setup should identify whether the phase transfer rate and the metastable state following the rarefaction wave are independent of fluid expansion (the degree of superheating). This setup has three characteristic features. The vessel test section has a conical-shaped body (i.e., divergent cross section). The test section is sealed by a double-membrane, where a slip-on flange positioned between the two membranes constitutes a medium-pressure section (MPS). The rupturing of membranes could either be achieved by increasing or decreasing the pressure in the MPS. Although few types of research with rapid phase transition have been carried out on double-membrane apparatus, the difference in rupturing mechanisms by increasing and decreasing the MPS has not been discussed. This paper compares these two methods of rupturing membranes and how the rupture mechanism influences the waves. The focus here is on the rupture stages, the wave pattern, and the device performance.

2 Design description of the double-membrane test rig

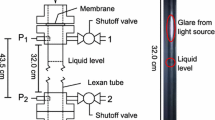
The double-membrane conical rig is designed to carry out small-scale experiments to investigate the sudden release of liquified CO2 and the associated underlying processes of rapid phase transition. It is a modified apparatus of shock tube type. The existing double-membrane system consists of two pressurized CO2 sections: a high-pressure conical vessel (i.e., test section) and a medium-pressure slip-on flange. The conical vessel is reinforced on the aluminum structure and fastened together with the two slip-on flanges. The two aluminum diaphragms have different thicknesses. Figure 1 shows a sketch and an image of the rig.

Fig. 1
figure 1

Schematic drawing of the double-diaphragm conical arrangement, its main dimensions, and a magnified MPS sketch on the left-hand side. An image of the conical vessel fastened with the two flanges on the right-hand side

Full size image

2.1 High-pressure conical vessel

The conical part of the vessel was made of stainless steel AISI 316 and was welded to a slip-on flange (pressure class 1500 lb) with a full penetrating weld. The flange facilitates carrying the diaphragm gaskets underneath the load and firmly attaches the other parts to the vessel. The vessel has a total height of 383 mm, a volume of 480·103 mm3, and solid sidewalls with a thickness of 18.67 mm. The vessel wall is inclined at an angle of 4° and has an inner surface with an average roughness (Ra) of 3.2 μm. The conical vessel's upper orifice has a diameter of 90.7 mm. The vessel has a flat surface circular bottom (diameter 9.37 mm) to avoid excessively high stress that could arise from evaporation waves that descend just after the diaphragm ruptures. The tapered vessel bottom was strengthened with a cube-shaped block from the same material with a side of 70 mm. There are two openings for CO2. Inflow in the bottom and outflow from the top of the vessel's wall, and each opening equipped with ¼ʺ NPT fittings. Additionally, there are 12 threaded holes, six for pressure sensors on one vessel's side and the other six for temperature sensors on the opposite side. The distance between the sensors' holes is 50 mm.

2.2 Medium-pressure section

A slip-on flange is utilized as a medium-pressure section installed above the vessel. The MPS has a cylindrical cross section with a diameter of 90 mm, a depth of 80 mm, and a volume of 510·103 mm3. The slip-on flange is fabricated from stainless steel ASME B 16.5 (pressure class 1500 lbs). It is modified by drilling an inlet/outlet opening through its thick-disk sidewall. Additionally, two additional openings were drilled for fitting pressure and temperature sensors. O-ring grooves were machined to guarantee tight sealing. The inlet/outlet opening is equipped with a ½" NPT fitting and connected to a pneumatic three-way valve by a ½ʺ flexible metal hose that facilitates the slip-on flange's movement to replace the diaphragm. This arrangement enabled a controlled pressure relief unit. Another slip-on flange is positioned on the top of the MPS flange and opens to atmospheric conditions. This flange is used to keep the diaphragm pressed between the two flanges. The pressurized sections, the diaphragms, and the second slip-on flange are tightly held together by eight bolts. Figure 1 is a diagram of the double-diaphragm conical arrangement with a magnified MPS schematic, its main dimensions, and sensor positions used in the experimental setup on the left-hand side. Figure 1 also includes an image of the conical vessel fastened with the two flanges on the right-hand side.

2.3 Diaphragm material and employment

Two thin diaphragm sets are tightly attached to separate the high-pressure conical vessel from the MPS flange bottom opening (high-Pressure diaphragm / HP diaphragm) and the MPS flange top opening from the surrounding atmosphere (medium-Pressure diaphragm / MP diaphragm). The diaphragm is critical in shock tube employment, so the material and thickness are central features to consider. Aluminum has proven its compatibility in shock tube CO2 tests due to fast crack propagation, and aluminum does not create small and diverse fragments during rupturing.

The diaphragms were designed as circular pieces cut from blank, natural smooth aluminum sheets. In addition, the sheets have different thicknesses and were manufactured by Alfer Aluminium (manufacturer art. number: 4001116382741). Three plate thicknesses of 0.3, 0.5, and 0.8 mm were used to form diaphragm sets. An empirical method was applied to determine the optimal combination of thicknesses for the operating conditions (pressure difference between HPS, MPS, and atmospheric pressure section). A series of tests were conducted for this purpose. The tests demonstrated that the best thickness combination for the diaphragm separating the conical vessel from the MPS flange (HP diaphragm) is 1.5–1.6 mm. For the diaphragm between the MPS and atmospheric flanges (MP diaphragm), 1.4–1.5 mm is best. Two gaskets are applied to each diaphragm to prevent any leaks from the membrane. The gasket types are Tesnit BA-GL and Centurion. Both are made of glass, aramid fibers, and nitrile binder. The gaskets are approved for use with CO2, pressure up to 30 MPa, and temperatures up to 450 °C.

3 Diaphragms rupturing methods and wave patterns

In this double membrane arrangement, the diaphragms rupture either by increasing or decreasing the pressure in the medium-pressure section. Therefore, the pneumatic three-way valve has a prime role in controlling the swift pressure build-up or release in the MPS. Increasing or decreasing the pressure in the MPS occurs by triggering the three-way control valve, adjusting the opening-closing duration, and regulating the necessary amount of CO2 entering or evacuating from the MPS.

3.1 Diaphragm rupture induced by increasing the pressure in MPS

An increase in the MPS pressure higher than the bursting pressure (the maximum pressure that the diaphragm can withstand) results in the upper diaphragm rupture, which first separates the two flanges. By opening the first diaphragm, pressure in the flange section falls to atmospheric in milliseconds. Then, the second diaphragm ruptures following the increased pressure difference. Figure 2a shows the shape of the conical vessel and the two slip-on flanges fastened to the top of the vessel. Additionally, the steps of diaphragm rupture occur by increasing the pressure in the MPS during the decompression of gaseous and liquid CO2.

Fig. 2
figure 2

Schematic drawing of the structure and stages of diaphragm rupture during the depressurization of liquified CO2 from the conical vessel. Increasing a and decreasing b the pressure in MPS

Full size image

When the MP diaphragm ruptures, and due to the sudden air compression in the section with atmospheric pressure, a shock wave is generated and propagates outward in the chamber's space. Simultaneously, a rarefaction wave travels downward until it hits the second diaphragm, and then the wave is reflected upwards. Rupture of the diaphragm separating the conical vessel from the mid-section flange generates a second shock wave that propagates through the MPS toward the chamber space, followed by the vapor/liquid interface. A rarefaction wave moves downward through the liquid to the vessel's bottom side, while an evaporation wave travels behind it in the downward direction. Figure 3a shows a graphical representation of the wave pattern in the depressurization sections of liquified CO2 from the conical vessel caused by increasing the pressure in the MPS.

Fig. 3
figure 3

Illustrative graph of wave patterns in the vertical y-axis of the conical vessel during liquified CO2 depressurization caused by increasing pressure in the MPS (a), and decreasing (b) the pressure in the MPS: 1- first shock wave; 2-first rarefaction wave (Fan); 3-first rarefaction wave (fan) reflection; 4-s shock wave; 5-contact surface; 6-s rarefaction wave (fan); 7-evaporation wave; 8-s rarefaction wave (fan) reflection; 9-bottom evaporation waves reflection; 10-first shock wave reflection; 11-contact surface reflection; 12-first shock wave reflection's bottom reflection; 13- bottom wave reflection

Full size image

3.2 Diaphragm rupture prompted by decreasing the pressure in the MPS

When the pressure promptly falls to atmospheric pressure in the MPS, the diaphragm separating the conical vessel from the mid-flange ruptures first due to its failure to withstand the higher pressure difference. Then, the diaphragm between the flanges ruptures following the continuous higher difference in pressure. Figure 2 (b) shows the stages of diaphragm rupture in the double-membrane scheme by decreasing the MPS pressure and during CO2 depressurization in the conical vessel.

Once the diaphragm placed between the vessel and the flange ruptures, a shock wave is formed and moves upward in the MPS. Concurrently, a rarefaction wave emerges and travels down through the liquid CO2, followed by an evaporation wave. The shock wave and the contact surface propagating behind it hit the upper diaphragm and are then reflected downward. Consequently, the rupturing of the HP diaphragm generates a new shock wave that propagates outward toward the chamber's space together with the vapor–liquid contact surface moving behind it. Figure 3b illustrates the waves' pattern for the decreasing pressure method during the depressurization of the liquified CO2 in the conical vessel.

4 Experimental setup and procedure

The experimental system consists of three components. (1) the conical vessel and its accessories in the double-membrane composition; (2) the auxiliary rectangular duct installation; and (3) the control, supply, and data acquisition systems. The double-diaphragm configuration is fixed on an aluminum structure. Above it, there is an atmospheric chamber with a volume of 0.338 m3. The chamber's space is covered by polycarbonate sheets on all six faces, with a vent from one side on the top. Figure 4 shows a sketch of the experimental setup.

Fig. 4
figure 4

Graphical illustration of the constituent components of the experimental installation

Full size image

Industrial-grade two cylinders gaseous and liquid CO2 supply the HP and MP sections separately. One line supplies the conical vessel and the rectangular duct, and the second line connects to the medium-pressure flange. The gaseous cylinder is equipped with a regulator and a control valve, while the cylinder that supplies liquid CO2 is equipped with a dip-tube and two control valves.

One of the vital parameters to know in the conical vessel experiments is the volume liquid fraction (LVF). An auxiliary structure is constructed to observe the liquid height in the opaque conical vessel. This structure includes a high-pressure rectangular duct with a glass window connected by a pipe net to the HP vessel, and CO2 is supplied to the cylinders through four pneumatic valves. The first valve connects the CO2 cylinders to the conical vessel inlet, and the second controls the flow between the conical vessel and the rectangular duct. The other two valves control the CO2 flow to the conical vessel and duct outlet pipe, which is connected to a regulator and control valve before CO2 exhaust. Before filling, the vessel is flushed two or three times with pressurized CO2 gas at 10 bars. The MPS is primarily filled with CO2 gas until the pressure reaches 26–28 bar, which is approximately half the pressure in the conical vessel (approximately 52–56 bar). The conical section is filled with liquid CO2 to a selected level by viewing the rectangular duct's liquid height. It takes 5–7 min to stabilize the liquid level and obtain liquid/vapor equilibrium in the conical vessel. Then, the conical vessel is disconnected from the rectangular duct by closing the control valve between the vessel and the duct.

Four Kulite (XTM-190-2000G) pressure transducers are mounted on the vessel wall. The distances between these transducers are 50, 100, and 100 mm from the bottom. Besides, these transducers have a pressure range of 0–70 bar and a natural frequency of 410 kHz. A sensor of the same type is attached to the MPS wall to measure the MPS pressure. A Kulite (XTM-190-100G) sensor is mounted in the middle of the vertical chamber's side to measure the overpressure after diaphragm rupture. This sensor has a pressure range of 0–3.5 bar, measuring the overpressure up to 7 bars, and has a natural frequency of 95 kHz. Both transducer types have a piezoresistive sensor as a sensing element and accuracy of approximately ± 1%. To determine the temperature variations in the vessel during CO2 decompression, three K-type thermocouple temperature sensors were installed on the vessel wall. These temperature sensors are on the side opposite the pressure transducers. The spacing between two adjacent transducers was 150 and 100 mm measured from the bottom to the top. A Photron Fastcam SA-1 high-speed camera, which has a sample rate of 5000 frames per second, captures the emergence and evolution of multiphase release after diaphragm rupture. The illumination system installed on the chamber's opposite sides consists of three LED panels (CE & RoHS, one 80 W, and two 38 W).

5 Results and discussion

A series of tests were conducted by opening then closing the three-way valve for various time durations. The times were 0.3, 0.5, 0.8, 1, and 1.5 s. The objective was to draw a comparison between the rupture methods. In addition, two sets of diaphragm thickness combinations (MP/HP diaphragms), 1.5/1.6 and 1.4/1.5 mm, and different liquid volume fractions (LVFs), 42 and 52%, were used. The experiments were carried out under identical initial conditions in the chamber where the temperature and pressure were atmospheric (T = 19–23 °C and P approximately 0.1 MPa), and the same atmospheric temperature range was maintained in the vessel and MPS. However, the pressure inside the conical vessel was 5.2–5.5 MPa, and the pressure in the MPS was 2.6–2.8 MPa.

5.1 Comparison of rupturing methods

Figure 5 shows the pressure readings in the conical vessel for i) increasing and ii) decreasing the MPS pressure. The conditions for the two diaphragms to rupture when decreasing the MPS pressure were the following: diaphragm thickness combination 1.4/1.5, 52% LVF, and valve opening/closing duration of 0.8 s. When the HP-diaphragm ruptured, i.e., a decrease in MPS pressure, a primary shock wave propagated upward followed by the contact surface. When the shock wave reached the MP diaphragm, the wave was reflected, resulting in an increased pressure difference. This pressure difference consequently caused the MP-diaphragm to rupture. The reflection of the first shock wave is shown in the enlarged sectors a, b, d, f, g, and i in Fig. 5 (the blue curves). The fluctuations that were observed on the MPS pressure fall lines can also be explained as the effect of the reflections of the compression waves hitting the MP diaphragm and the reflections of the expansion waves propagating downwards through the liquid. In the enlarged sectors c, e, and h in Fig. 5, the first pressure drop is due to increasing the pressure in the lines, and the following oscillations are due to HP diaphragm bulge after MP diaphragm rupturing.

Fig. 5
figure 5

Change in pressure transducer recordings inside the conical vessel, from top to bottom (P1 to P4), during the CO2 depressurization by increasing (Incr. P line) and decreasing the pressure in the MPS (Drop. P line). Enlarged segments (c), (e) and (h) show the oscillations due to HP diaphragm rupture, and (a), (b), (d), (f), (g) and (i) show fluctuations due to wave reflection

Full size image

The pressure histories were drawn with reference to the vessel height to clarify the effect of the mentioned wave reflections on the rarefaction and evaporation wave propagation inside the vessel. Every synchronized pressure–time line starts at the corresponding transducer location, as shown in Fig. 6. The pressure–time lines' first and second pressure drop trajectories correspond to the rarefaction and evaporation wave paths, respectively. On the decreasing pressure in the MPS lines, the observed slight fluctuations on the second plateaus were caused by the reflected waves from the MPS. This process slows evaporation wave propagation, as seen from the comparison of the plateau time durations in Fig. 6. The evaporation wavefront velocities were calculated along two height regions (185–85 mm) and (85–35 mm), as shown in Fig. 6. The results indicate that for increasing pressure in the MPS method, the evaporation wavefront propagated with a mean velocity of 59.98 ± 0.4 m/s, while for the decreasing pressure method, the wave's mean velocity was 39.92 ± 2.56 m/s.

Fig. 6
figure 6

Diagram vessel height vs. time for pressure readings during 25 ms of liquified CO2 depressurization by increasing (left) and decreasing (right) the pressure in the MPS. This shows the wave trajectories of rarefaction (RW) and evaporation (EW)

Full size image

Figure 7 illustrates the pressure change in the MPS (PMPS) and overpressure generated in the chamber space (PCHS) during CO2 decompression from the conical vessel after the pressure surged in the MPS (Incr. P line), and the pressure fell (Drop. P line). Overpressure was measured, appointing atmospheric pressure as the reference pressure.

Fig. 7
figure 7

Pressure variation in the MPS (PMPS) and overpressure variation in the chamber space (PCHS) during the time of CO2 depressurization by increasing (Incr. P line) and decreasing the pressure (Drop. P line)in the MPS

Full size image

The time duration between diaphragm ruptures in the bursting method when increasing the MPS pressure is shorter than that when decreasing the pressure. A possible explanation is that in the former technique, due to the extended pressure variation between the HP diaphragm sides, only this diaphragm needs to burst as the MP diaphragm is already ruptured by a sudden MPS pressure increase. However, in the latter technique, rupturing both diaphragms is required. Two reflection waves are propagated in the opposite direction of the incident shock and contact surface. Subsequently, the travel of these waves through the MPS slowed down, as shown in magnified parts (j) and (k) in Fig. 7. The time duration between the pressure drop in the MPS and the HP diaphragm rupture is 200.5 ms for the increasing pressure test and 5740 ms for the decreasing pressure test.

The effect of reflected compression waves and encountered reflection of the expansion waves when decreasing the MPS pressure slowed the diaphragm rupture. It also weakened the intensity of the generated shock wave after the MP diaphragm ruptured. This behavior can be observed from the overpressure peaks in Fig. 7, which were 12 kPa after the MP diaphragm ruptured by decreasing the MPS pressure. Furthermore, they were 33 and 29 kPa after the MP and HP diaphragms ruptured, respectively, when increasing the MPS pressure.

When increasing the pressure in the MPS, the MP diaphragm ruptures before the HP diaphragm. Then, the MPS gas expands rapidly close to atmospheric pressure before the HP diaphragm rupture initiates the depressurization process inside the HP vessel. The volume of the MPS is thought to have an insignificant effect on the consequent process. When lowering the pressure in the MPS, the bottom diaphragm will rupture and cause an expansion of fluid from the HP vessel into the MPS before the top diaphragm ruptures. In this case, the state in the HP vessel will depend on the MPS volume. Moreover, an increase in the MPS volume results in a prolonged time between diaphragm rupture and subsequently influences the expansion wave behavior. Regardless of the MPS volume, the duration between diaphragm rupture is still higher for the decreasing MPS pressure technique than for the increasing MPS pressure technique unless the vented opening has the same diameter for both methods.

5.2 Rupturing mechanism

The diaphragm rupture mechanism depends on considerations such as the pressure required for prompt rupturing, the time duration of the gas entering or leaving the MPS, and the diaphragm disk layer durability and hardness. However, to regulate these factors, it is essential to completely open the diaphragm area under load and prevent multiphase flow disturbance. Regardless of the rupturing method, the bursting mechanism was initiated when the diaphragm layers began bulging due to CO2 filling. Subsequently, the circular cross-sectional edge weakens due to the maximum strain applied. By increasing the pressure difference between its surfaces, the diaphragm starts to crack in one spot along the circumference and then stretches to remove the entire underloaded cross-section in the case of increasing the pressure in the MPS. In the case of pressure decrease in MPS, a cut is made circularly while leaving a small portion on one side. The images in Fig. 8 show the crack trajectory on the loaded diaphragm circumference after rupturing by decreasing pressure in the MPS. Furthermore, the residual ring after the diaphragm loaded area was removed because of increased pressure in the MPS. This rupturing mechanism emphasizes that diaphragm bursting does not occur immediately [25], making the multiphase flow start as a jet and grow until it occupies the vessel orifice cross section.

Fig. 8
figure 8

The left and middle images show circular tracks on the bulged diaphragm circumference after the HP diaphragms were ruptured by MPS pressure relief. The right image shows the remaining ring after the bulged loaded section was entirely removed by the HP diaphragm rupturing when increasing MPS pressure

Full size image

Figure 9 shows cropped images from the high-speed video captured during the experiment with LVF of 52% and 1.5/1.6 diaphragm sets. It shows the development of the multiphase flow and rocketed diaphragm parts after bursting due to the increasing pressure in the MPS. The top series illustrates the MP diaphragm rupture and release from the MPS, whereas the bottom series displays the HP diaphragm rupture and the release from the HP vessel.

Fig. 9
figure 9

High-speed images of the evolution of multiphase flow and the ruptured diaphragm fragments after diaphragm bursting. The time step between two images was 0.56 ms in both sequences

Full size image

As the upper diaphragm bursts first by increasing the MPS pressure and its cross-section under the increased pressure is entirely broken and opened, there is a free path for the upcoming shock wave and multiphase flow. No reflection occurs. This implies that the reflected compression wave does not influence the processes inside the conical vessel.

The velocity of the ruptured diaphragms in the chamber is estimated by processing the high-speed videos. The designated approach was to visually track the rocketed diaphragm positions upward after rupturing for 860 mm (the inner vertical distance in the chamber space).

All videos were recorded within 1.79 s at 5400 frames per second (fps) and a resolution of 576 × 1024 pixels. Trajectory tracking was performed with a 0.91 mm/px pixel height conversion. Calculating the velocity of the ruptured slices from the MP diaphragm gives 118–123 m/s, and for the HP diaphragm, it gives 127–132 m/s. As shown in Fig. 9, the ruptured diaphragm fragments, indicated by small arrows on the upper image sequence, proceed with nearly identical velocity as the multiphase flow proceeds. The time step between the pictures on each line is 0.56 ms, and the time between the upper and lower image sequences is 1.68 ms.

6 Conclusions

A double-diaphragm vertical conical rig for studying decompression of liquified CO2 from a diverging cross-sectional vessel is described. The paper also highlights the characteristic features of the test setup. This setup includes a slip-on flange as a medium-pressure section, and the method of rupturing the diaphragms is either a pressure increase or decrease in the medium-pressure section (MPS). A series of experiments were carried out on this setup to compare its performance when applying the two diaphragm rupturing methods.

This paper focuses on the sequence and mechanism of diaphragm rupturing and the generated wave pattern. The conditions included different liquid volume fractions in the conical vessel, different three-way valve opening/closing durations (this valve controls the entry or evacuation of gas in the MPS), and different diaphragm thicknesses.

The experimental results indicate that the rupture caused by increasing the MPS pressure has no reflected compression wave complications in the MPS or test vessel. This is because the MP diaphragm ruptures firstly, the underloaded diaphragm sections are entirely removed. When the pressure in the MPS decreases, the compression waves are reflected back into the vessel, which slows evaporation wave propagation. This evaporation wave slowing, in turn, reduces the phase transition rate. Furthermore, the time between diaphragm bursting when increasing the MPS pressure is shorter than that when decreasing the pressure. In addition, increasing the pressure in the MPS offers more operating simplicity and reliability. These operational analyses suggest that increasing the MPS pressure is a more feasible technique to conduct CO2 depressurization tests on this installation for the conditions compared.

Finally, a potential weakness to consider is that the pressure drop in the MPS was performed by evacuating the gas from the MPS through a ½" opening. The evacuation rate could be too slow to attain a higher pressure difference between the vessel and the MPS. The limited dimensions of the slip-on flange used as the MPS excluded a larger opening.