1 Introduction

Batch production forms a pillar of the chemical and pharmaceutical industry. As it involves discontinuous processes, the corresponding production scheduling is characterized by a large number of discrete decisions, especially in plants where dozens of different product types run. Finding an ideal schedule often marks a bottleneck when it comes to value creation, optimization of internal processes and compliance with supply chain demands.

Scheduling models in the process industry are typically realized through mixed-integer programming (MIP) [1]. Though it basically enables a mathematical solver to search and find good quality solutions, providing an acceptable computational performance remains a challenge regarding practical application. In order to cope with that issue, an integral and tailored approach becomes necessary. Several improvement strategies, specifically in batch scheduling, have been reported over the last decades [2]. The aim of the presented work is to develop and assess a method that not only enhances an existing model but considers further boundary conditions to offer a more detailed representation of the real-word production process. The use case was taken from an actively operating plant of the chemical industry. A decomposition approach based upon previous research consolidates the final algorithm (see also Sect. 1). In addition, a novel strategy utilizing capabilities of the Gurobi MIP solver [3] will be introduced. It should be noted that the authors do not claim to present the most efficient or powerful model in that area of research. However, the paper describes a new approach to cope with resource-demanding batch scheduling models that was successfully leveraged in a real-word application. It was developed based on a preexisting model [4], which did not meet performance requirements and the full scope of boundary conditions in practice.

This paper describes the regarded chemical plant in Sect. 2. An overview of literature connected to batch scheduling problems is given in Sect. 3. Afterwards, the original MILP model is presented in Sect. 4, alongside its weaknesses that prevent practical applicability. A review of the existing model reveals the possibility for simplification and reduced problem size, which is executed in Sect. 5. The final model scope is outlined in Sect. 6 through introduction of remaining features by stating corresponding constraints in mathematical form. Finally, Sect. 7 presents an integral algorithm that merges several different approaches into one method, which builds the foundation for a practically applicable tool and high-quality solutions. Further findings throughout the novel procedure indicate areas for future research. Section 8 contains a summary and outlook.

2 Problem statement

Along continuous processes, batch production forms a pillar of manufacturing in chemical industries. Each batch marks a finite quantity of material, which undergoes discrete alteration steps (reactions) in different units (reactors) of the production facility. The product can then be traced and measured precisely in terms of quality and possible defects. Various arrangement types for reactors, pipes and other equipment exist in practice, allowing for varying production conditions (see also [5]).

The plant subject to this paper, consisting of two nearly identical, parallel production lines with two reactors each, is operated with several dozens of different product types (Fig. 1). Due to the variety of batches in total plus fluctuating orders, demands and portfolio, the facility can be considered a multi-product plant, which normally operates all week long and around the clock. The units are arranged in cascade connection so that once products were dosed into the first reactor of a line, no material flow will be conveyed to or received from units of the opposite line. Moreover, some products can only be run on either of the parallel units, whereas others may use both. Between batches, diverse cleansing mechanisms take place which vary based on successor and predecessor. Like residence times for different products, the duration of a cleansing step depends on the batch sequence. Furthermore, a basic distinction can be identified as major and minor cleansing. While the latter is characterized by decoupled processes for the reactors, a major cleansing requires that the washing fluid is given into the first unit. When the washing ends, it must be immediately transferred to the second reactor, where the respective cleansing is then started. A zero-wait policy is enforced at all reaction stages. Due to the nature of the process, a product immediately leaves a unit as soon as the all alteration tasks are finished. The transport duration can be considered insignificantly little. There are some forbidden sequences concerning different product types. Although this constraint must always be met, very few combinations are affected which usually forms no challenges regarding feasible solutions.

Fig. 1
figure 1

Scheme of the investigated plant

Full size image

At the end of both production lines, there is a tank which stores some finished products, yet only for duration of filling it into a transport container. Generally, this third vessel is disregarded for the batch scheduling since the corresponding occupancy time ends before a successor product can be injected. A special case scenario where it must not be neglected comprises certain products which are collected by tankers at certain dates and times. Affected batches will be put into the vessel subsequent to the completion of the reactions, where it remains until it is filled into a carriage. Therefore, no second product meant to be conveyed to the tank at the end of line 1 or 2 must be inserted within that interval. The capacity regarding how many batches of the same product can be retained at a time may vary, but shall have no impact on the scheduling.

Unlike other comparable scenarios reported in literature, the regarded case involves due dates only for designated batches. Many target products can be shifted up and down the time line arbitrarily. Therefore, the bottleneck of this optimization problem is to achieve high quality results rather than purely feasible solutions.

3 Literature review

Mendéz, Grossmann et. al. have been actively contributing to the area of batch scheduling optimization, especially mixed-integer approaches. Their work from 2008 [6] and 2006 [7] provide a detailed overview not only on solution strategies but also profound classifications of corresponding models.

In order to decrease complexity, non-monolithic methods are usually preferred over models that incorporate separable tasks into one optimization. Trautmann [8] showed a decomposition approach that divides the problem into batching (number and size) and batch scheduling, resulting in a reduced number of decision variables. Earlier, Rodriguez et. al. [9] had applied another bi-level strategy, considering time windows for each production event. Subsequently, the proper scheduling makes use of a mixed-integer linear program (MILP) and involves the predefined time slots, leading to a condensed model.

Multi-level optimization is a characteristic of hierarchical production planning, where scheduling tasks are split into several subproblems in order to reduce the respective model size. A common approach is to develop a more coarse arrangement on the higher level, which returns constraints imposed on a dependent at a lower level to tighten the solution space. Franck et. al. [10] display a comprehensive hierarchical approach that contains several aspects described in this section so far. The resource-constrained task is divided based on organizational planning stages regarding different time horizons, resource categories and items to be scheduled. From the highest level to fine planning, which comprises the actual batch scheduling, each subproblem imposes new conditions on the one below, though some feedback upstream is included as well. Omar and Teo [11] report a schedule optimization of a multi-product batch plant using a hierarchical structure with three levels. The problem described in this publication is more closely oriented towards the job sequencing and provides an analysis of the experienced computational performance.

Günther [12] presented a problem decomposition that the author refers to as block scheduling. The fundamental idea arises through the understanding that a natural sequence prevails when the scheduling task aims for minimizing total changeover costs, which directly correlates with minimization of makespan. Based on that, products are assigned to groups describing batches of minor reciprocal changeovers. In the following, blocks, each representing one family, are scheduled with continuous time representation in a way that major setup times exist only between different product families. The sequence within a family must be defined beforehand and shall be based on the user’s experience and requirements. However, this technique can only be applied if the modeling data offers the possibility for a related structure.

A step-wise approach to an optimum solution is found in Kopano et al. [13]. Utilizing a benchmark problem of the pharmaceutical industry, a decomposition strategy is applied to split products into clusters that allow a group-wise scheduling in reasonable time through a MIP. Once a batch has been added to the group, an optimization is performed that assumes previously inserted products as fixed in terms of unit allocation and sequence. However, the timing can change so that the new product may be scheduled between preexisting ones. The second step comprises the improvement of the constructed solution, which starts with a reordering of a partially fixed model. Unit allocation cannot be altered, yet sequential and timing decision still offer better outcomes than in the constructive method. Afterwards, some products are given the freedom to be reinserted, meaning that these can be shifted arbitrarily, though the remaining batches are still bound to their current position time- and unit-wise. The improvement procedure is iteratively executed until it reaches a stop** criteria or does not display any further enhancement alternatively. The construction-improvement method was adapted in several papers with strong practical orientation. Basán et. al. [14] presented a practical implementation for the shipbuilding industry. Rather than addressing batches, the authors apply the tool on block erections as a principle of lean manufacturing. Apostolos et. al. [15] contribute with an application in consumer goods manufacturing.

Lastly, Klotz and Newman [16] provide a more general overview on difficulties in large-scale MIP models, decoupled from scheduling problems. Most importantly, common characteristics of weak performance are outlined and suggestions made to tackle these issues.

Naturally, publications on batch scheduling of the past decades cover more than what is outlined here. The authors decided to include those papers that led to the procedure developed throughout this work. An important factor to consider is that due to the unique and complex nature of many industrial scheduling problems, extensive research may be required to either obtain an appropriate solution algorithm from literature, or to develop one from scratch. This is emphasized on by Herrmann [17]. The publication of Baker [18] describes how generic tools (like integer programming solvers) have become competitive to an extend that they can be utilized as benchmark for comparison against novel or enhanced strategies. This is especially true considering outdated performance results based on advanced hard- and software capabilities.

Unlike former approaches, we seek to combine extended decomposition for constructing and improving a solution as well as separated models for different components of the production plant. In addition, instead of utilizing rule-based meta-heuristics, our algorithm shall leverage solver warmstarts and adjusted parameter settings to cope with finding and enhancing results plus minimizing the MILP gap. All in all, the model is meant to facilitate a real-world problem, with a strong focus on value creation and rewarding application.

4 Reference model

4.1 Scope

The initial model was developed by Krellner [4] to serve as a benchmark and draft planning tool. It comprises the batch scheduling step only, size and number of batches are determined separately in advance. Furthermore, only the proper sequencing of products is reflected, additional constraints such as due dates and others mentioned in Sect. 2 have been disregarded. According to Mendéz et. al. [6], the model can be classified as shown in Table 1. Specifying these four criteria provides an overview on its characteristics. Time and event representation are interconnected and determine how discrete jobs are handled and scheduled by the optimization. Material flows within the production facility are described through the material balances aspect. Generally, the authors distinguish between network flow equations and lots. The latter is used for the given problem and assumes batch number and size as given beforehand.

Table 1 Classification of the scheduling model (based on [7])
Full size table

The input data comprises selected products i and the number of batches to be produced \(p_{i}\). Based upon those quantities, the maximum number of events t shall be consolidated to \(t_{\max}\) per production line in a preprocessing step.

4.2 Formulation

Both integer-restricted variables are binaries. The state of occupancy per unit and event is represented by \(x_{t, i}^{L,R}\). A changeover will be expressed by \(s_{t,i,j}^{L,R}\). The remaining assumes continuous values and most of them are used to express the timing and duration of the events. Both \({\rm tr}_{t}^{L,R}\) and \(ts_{t}^{L,R}\) are auxiliaries that represent residual times and cleansing duration, respectively. The time marking an event’s completion \({\rm tt}_{t}^{L,R}\) states the only variable that directly contributes to the objective function. A major cleansing mechanism is indicated through the binary parameter \({\rm TSL}_{i,j}=1\).

Objective

$$\begin{aligned} \min \ {\rm tt}_{t_{\max}}^{1,2} + {\rm tt}_{t_{\max}}^{2,2} + 0.5 \cdot \varepsilon \end{aligned}$$
(1)

Absolute completion time difference

$$\begin{aligned} - \varepsilon \le {\rm tt}_{t_{\max}}^{2,2} - {\rm tt}_{t_{\max}}^{1,2} \end{aligned}$$
(2)
$$\begin{aligned} \varepsilon \ge {\rm tt}_{t_{\max}}^{2,2} - {\rm tt}_{t_{\max}}^{1,2} \end{aligned}$$
(3)

Reactor occupancy

$$\begin{aligned} \forall L \ \forall R \ \forall t : \sum _{i} x_{t,i}^{L,R} \le 1 \end{aligned}$$
(4)

Product demands

$$\begin{aligned} \forall L \ \forall R \ \forall i \notin \ P_{\rm double} : \sum _{t} \ x_{t,i}^{L,R} = p_{i} \end{aligned}$$
(5)
$$\begin{aligned} \forall R \ \forall i \in P_{\rm double} : \sum _{L} \sum _{t} x_{t,i}^{L,R} = p_{i} \end{aligned}$$
(6)

Forbidden sequences

$$\begin{aligned} \forall L \ \forall R \ \forall t>1 \ \forall i, \ j \in F_{i,j}: x_{t-1,i}^{L,R} + x_{t,j}^{L,R} \le 1 \end{aligned}$$
(7)

Transfer to second stage

$$\begin{aligned} \forall L \ \forall t \ \forall i : x_{t,i}^{L,1} - x_{t,i}^{L,2} = 0 \end{aligned}$$
(8)

Consecutive events

$$\begin{aligned} \forall L \ \forall R \ \forall t>1 : \sum _{i} x_{t,i}^{L,R} \le \sum _{i} x_{t-1,i}^{L,R} \end{aligned}$$
(9)

Batch changeovers

$$\begin{aligned}&\forall L \ \forall R \ \forall t<t_{\max} \ \forall i \ \forall j: 0.5 \cdot (x_{t,i}^{L,R} + x_{t+1,j}^{L,R}) - s_{t,i,j}^{L,R} \ge 0 \end{aligned}$$
(10)
$$\begin{aligned}&\forall L \ \forall R \ \forall t<t_{\max} \ \forall i \ \forall j: 0.5 \cdot (x_{t,i}^{L,R} + x_{t+1,j}^{L,R}) - s_{t,i,j}^{L,R} - 0.5 \le 0 \end{aligned}$$
(11)

Last event

$$\begin{aligned} \forall L \ \forall R \ \forall i \ \forall j: s_{t_{\max},i,j}^{L,R} = 0 \end{aligned}$$
(12)

Setup time

$$\begin{aligned} \forall L \ \forall R \ \forall t: ts_{t}^{L,R} \ge \sum _{i} \sum _{j} s_{t,i,j}^{L,R} \cdot TS_{i,j}^{R} \end{aligned}$$
(13)

Reactor time

$$\begin{aligned} \forall L \ \forall R \ \forall t: {\rm tr}_{t}^{L,R} = ts_{t}^{L,R} + \sum _{i} \sum _{j} s_{t,i,j}^{L,R} \cdot {\rm TR}_{i,j}^{R} \end{aligned}$$
(14)

Zero-wait

$$\begin{aligned} \forall L \ \forall t: {\rm tt}_{t}^{L,2} - {\rm tr}_{t}^{L,2} = {\rm tt}_{t}^{L,2} - ts_{t}^{L,1} \end{aligned}$$
(15)

First event completion

$$\begin{aligned}&\forall L : {\rm tt}_{1}^{L,1} - {\rm tr}_{1}^{L,1} \ge 0 \end{aligned}$$
(16)
$$\begin{aligned}&\forall L : {\rm tt}_{1}^{L,2} - {\rm tr}_{1}^{L,2} \ge {\rm tt}_{1}^{L,1} \end{aligned}$$
(17)

Event completion

$$\begin{aligned}&\forall L \ \forall t>1 : {\rm tt}_{t}^{L,1} - {\rm tr}_{t}^{L,1} - {\rm tt}_{t - 1}^{L,1} \ge 0 \end{aligned}$$
(18)
$$\begin{aligned}&\forall L \ \forall t>1 : {\rm tt}_{t}^{L,2} - {\rm tr}_{t}^{L,2} - {\rm tt}_{t - 1}^{L,2} - TB \ge 0 \end{aligned}$$
(19)

Setup mechanism

$$\begin{aligned}&\forall L \ \forall t>1 : {\rm tt}_{t}^{L,1} - ts_{t}^{L,1} - {\rm tt}_{t - 1}^{L,2} \nonumber \\&\quad + {\rm BigM} \cdot \sum _{i} \sum _{j} s_{t,i,j}^{L,1} \cdot {\rm TSL}_{i,j} \ge 0 \end{aligned}$$
(20)
$$\begin{aligned}&\forall L \ \forall t>1 : {\rm tt}_{t}^{L,1} \ge {\rm tt}_{t}^{L,2} - ts_{t}^{L,2} \nonumber \\&\quad - {\rm BigM} \cdot (1-\sum _{i} \sum _{j} s_{t,i,j}^{L,2} \cdot {\rm TSL}_{i,j}) \end{aligned}$$
(21)
$$\begin{aligned}&\forall L \ \forall t>1 : {\rm tt}_{t}^{L,1} \le {\rm tt}_{t}^{L,2} - ts_{t}^{L,2}\nonumber \\&\quad + {\rm BigM} \cdot (1-\sum _{i} \sum _{j} s_{t,i,j}^{L,2} \cdot {\rm TSL}_{i,j}) \end{aligned}$$
(22)

Note that the model contains further auxiliary parameters that represent diverse changeover and setup details occurring between batches. These impact the reactor time \({\rm tr}_{t}^{L,R}\) and, thus, the event completion \(ts_{t}^{L,R}\). For the sake of simplicity, only the washing fluid is considered here through \(ts_{t}^{L,R}\), since it is connected to the changeover mechanism \({\rm TSL}_{i,j}\).

4.3 Evaluation

The model was designed in close collaboration with the target plant. Therefore, a scheduling tool should be capable of providing good results for 30 to 45 product batches within an hour. Table 2 shows how the model performed up to a size where no feasible solution was found (Intel\(\circledR\) Core\(^{\mathrm{TM}}\) i5-6300U DualCore 3.0 GHz, 16 GB RAM, Gurobi version 9.0.2)

Table 2 Performance of the reference model
Full size table
Fig. 2
figure 2

Gantt chart representation

Full size image

Up to 21 batches, the model finishes with a fairly low MILP gap after one hour of computation. Note that with an increasing number of products, the remaining gap grows to an extend that significantly better, not yet uncovered solutions are likely to exist. Eventually, the scope reached a magnitude at 36 batches that makes it impossible for the optimization to find a feasible result at all.

Clearly, this does not suffice the planner’s requirements regarding the speed at which results are output. Regardless of the computation time to solve the MILP, a significant portion is spent on building the model. In addition, crucial boundary conditions have not been implemented yet. It is also worth mentioning that existing papers have demonstrated better results for even more batches and stages and in similar scenarios, without applying any complex solution strategy. For instance, the benchmark model in Kopanos et al. [13] is capable of solving up to 336 batches (60 distinct products) within 3600 seconds. Interestingly, it particularly struggles to cope with conditions that apply to the present work as well, namely makespan minimization and zero-wait transfer. As the variable and constraint formulation itself appears to be a weakness to begin with, alternate mathematical expressions were investigated first. This also complies to suggestions given by Klotz and Newman [16].

5 Reformulation of variables and constraints

5.1 Idea

An analysis of the given production conditions revealed the opportunity for two decisive simplifications. Firstly, as a zero-wait policy is imposed on all products, the time for a batch to be produced can be consolidated into a constant number across all involved reactors. A Gantt-chart representation of a simple product sequence is displayed in Fig. 2. Secondly, it was found that in a sequence of items along the timeline, the exact positioning of a batch is only impacted by its direct predecessor or successor. Rather than utilizing multiple model variables and parameters to reflect complex changeover mechanisms, the gap between end time of one product and start time of the next can be expressed by a single number.

Fig. 3
figure 3

Visualization of changeover costs

Full size image

So called changeover costs are defined and assigned to each sequential combination of batches. Although the chosen reference point may vary, the costs shall describe the offset between the start of the second and the completion of the first product due to zero-wait policy (Fig. 3). For reasons of practicability, the changeover cost values can be stored in a table or matrix. The MILP model will later access these parameters for optimization. The content of the matrix must be calculated in a separate step and before the actual solution process. As a consequence, the formation of changeover costs \(T_{{\rm ch},i,j}\) can be conducted once and independent from the scheduling tasks itself, which offers time savings. Only if products, cleansing mechanisms or other related circumstances are subject to changes, the matrix creation should be rerun. The approach comprises a distinction of different cases based on the relation of reaction and setup times between two batches A and B, plus the underlying changeover mechanism.

5.2 Formulation

As the consideration of processes in individual reactors becomes obsolete, index R shall be dropped for all affected variables. In addition, the binary for changeovers is altered to \(s_{c,i,j}^{L}\), with c being a specific changeover between event \(t = c\) and \(t + 1\). Furthermore, variables that describe residual times \({\rm tr}_{t}^{L,R}\), cleansing durations \(ts_{t}^{L,R}\) and changeover mechanisms \({\rm TSL}_{i,j}\) are no longer required, as they are summarized into the new variable for changeover costs \(z_{c}^{L}\). Consequently, all related, originally existing constraints will be replaced by an expression that simply accesses the parameter \({T_{\rm ch},i,j}\) in equation 35. Therefore, both variables and constraints can be erased without interfering with the validity of the model. For the visual output in, e.g. a Gantt-chart, the actual cleansing and reaction times can be generated in a postprocessing outside the MILP, which entails negligible computation efforts.

Objective

$$\begin{aligned} \min \ {\rm tt}_{t_{\max}}^{1} + {\rm tt}_{t_{\max}}^{2} + 0.5 \cdot \varepsilon \end{aligned}$$
(23)

Absolute completion time difference

$$\begin{aligned}&- \varepsilon \le {\rm tt}_{t_{\max}}^{2} - {\rm tt}_{t_{\max}}^{1} \end{aligned}$$
(24)
$$\begin{aligned}&\varepsilon \ge {\rm tt}_{t_{\max}}^{2} - {\rm tt}_{t_{\max}}^{1} \end{aligned}$$
(25)

Reactor occupancy

$$\begin{aligned} \forall L \ \forall t : \sum _{i} x_{t,i}^{L} \le 1 \end{aligned}$$
(26)

Consecutive events

$$\begin{aligned} \forall L \ \forall t > 1 \ : \sum _{i} x_{t,i}^{L} \le x_{t-1,i}^{L} \end{aligned}$$
(27)

Product demands

$$\begin{aligned} \forall L \ \forall i \notin P_{\rm double} \ : \sum _{t} x_{t,i}^{L} = p_{i} \end{aligned}$$
(28)
$$\begin{aligned} \forall L \ \forall i \in P_{\rm double} \ : \sum _{L} \sum _{t} x_{t,i}^{L} = p_{i} \end{aligned}$$
(29)

Batch changeovers

$$\begin{aligned}&\forall L \ \forall R \ \forall c \ \forall i \ \forall j: 0.5\cdot (x_{c,i}^{L} + x_{c+1,j}^{L}) - s_{t,i,j}^{L} \ge 0 \end{aligned}$$
(30)
$$\begin{aligned}&\forall L \ \forall R \ \forall c \ \forall i \ \forall j: 0.5\cdot (x_{c,} + x_{c+1,j}^{L}) - s_{t,i,j}^{L} - 0.5 \le 0 \end{aligned}$$
(31)

Forbidden sequences

$$\begin{aligned} \forall L \ \forall t>1 \ \forall i, \ j \in F_{i,j}: x_{t-1,i}^{L} + x_{t,j}^{L} \le 1 \end{aligned}$$
(32)

First event completion

$$\begin{aligned} \forall L \ \forall t,\ t=1: \sum _{i} x_{t,i}^{L} \sum _{R} {\rm TR}_{i,R} \le {\rm tt}_{t}^{L} \end{aligned}$$
(33)

Event completion

$$\begin{aligned} \forall L \ \forall t ,\ t>1: \sum _{i} x_{t,i}^{L} \sum _{R} {\rm TR}_{i,R} + {\rm tt}_{t-1,i}^{L} + z_{t-1}^{L} \le {\rm tt}_{t}^{L} \end{aligned}$$
(34)

Changeover offset

$$\begin{aligned} \forall L \ \forall c: \ z_{c}^{L} = \sum _{i} \sum _{j} s_{t,i,j}^{L} \cdot {T_{\rm ch},i,j} \end{aligned}$$
(35)

5.3 Evaluation

Unlike the original model, the reformulated version enables to find feasible solutions within the favored time period. Additionally, the built time could be decreased considerably (Table 3). One reason certainly lies in the model size, which is less than 50 % compared to the initial model regarding the number of variables and constraints.

Table 3 Model performance after reformulation
Full size table

6 Extended model

The model shall now be complemented with the features outlined in the problem statement (Sect. 2). Note that this requires the insertion of several novel variables.

6.1 Critical production dates

Both earliest start date and due date for a batch can be optionally selected.

Due date

$$\begin{aligned} \forall L \ \forall i \in P_{l} \ \forall t: \ {\rm tt}_{t}^{L} - {\rm BigM} \cdot (1-x_{t,i}^{L}) \le x_{t,i}^{L} \cdot T_{l,i} \end{aligned}$$
(36)

Earliest start

$$\begin{aligned} \forall L \ \forall i \in P_{e} \ \forall t: \ {\rm tt}_{t}^{L} - {\rm BigM} \cdot (1-x_{t,i}^{L}) \ge x_{t,i}^{L} \cdot T_{l,e} \end{aligned}$$
(37)

6.2 Maintenance slots

Maintenance slots are meant to block certain components of the production facility, preventing batches from being processed during predefined intervals. A planner should have the flexibility to either shut down single units or entire production lines. In order to implement these forbidden intervals in linear form, the variable \(d_{{\rm sd},t}^{L}\) is introduced, which expresses whether the end time of an event t occurs later (\(d_{{\rm sd},t}^{L} = 1\)) or earlier (\(d_{{\rm sd},t}^{L} = 0\)) than a shutdown sd.

The closure of a whole line or the first unit is realized as follows.

Shutdown production line

$$\begin{aligned}&\forall L \ \forall {\rm sd} \in {\rm SD}_{L} \ \forall t: \ \nonumber \\&\quad d_{{\rm sd},t}^{L} \cdot {\rm BigM} + T_{l,{\rm sd}} - {\rm tt}_{t}^{L} \ge 0 \end{aligned}$$
(38)
$$\begin{aligned}&\forall L \ \forall {\rm sd} \in {\rm SD}_{L} \ \forall t: \nonumber \\&\quad \ (1 - d_{{\rm sd},t}^{L}) \cdot {\rm BigM} - T_{l,{\rm sd}} + {\rm tt}_{t}^{L} \ge 0 \end{aligned}$$
(39)
$$\begin{aligned}&\forall L \ \forall {\rm sd} \in {\rm SD}_{L} \ \forall t: \nonumber \\&\quad \ {\rm tt}_{t}^{L} \le T_{e,{\rm sd}} + {\rm BigM} \cdot d_{{\rm sd},t}^{L} \end{aligned}$$
(40)
$$\begin{aligned}&\forall L \ \forall {\rm sd} \in {\rm SD}_{L} \ \forall t: \nonumber \\&\quad \ {\rm tt}_{t}^{L} - \sum _{i} x_{t,i}^{L} \cdot \sum _{R} {\rm TR}_{i,R} \ge T_{l,{\rm sd}} - {\rm BigM} \cdot (1 - d_{{\rm sd},t}^{L}) \end{aligned}$$
(41)

Shutdown first unit

$$\begin{aligned}&\forall L \ \forall {\rm sd} \in {\rm SD}_{L,1} \ \forall t: \ d_{{\rm sd},t}^{L} \cdot {\rm BigM} \nonumber \\&\quad + T_{l,{\rm sd}} - ({\rm tt}_{t}^{L} - \sum _{i} (x_{t,i}^{L} \cdot {\rm TR}_{i,2})) \ge 0 \end{aligned}$$
(42)
$$\begin{aligned}&\forall L \ \forall {\rm sd} \in {\rm SD}_{L,1} \ \forall t: \ (1 - d_{{\rm sd},t}^{L})) \cdot {\rm BigM} \nonumber \\&\quad - T_{l,{\rm sd}} + {\rm tt}_{t}^{L} - \sum _{i} (x_{t,i}^{L} \cdot {\rm TR}_{i,2}) \ge 0 \end{aligned}$$
(43)
$$\begin{aligned}&\forall L \ \forall {\rm sd} \in {\rm SD}_{L,1} \ \forall t: \ {\rm tt}_{t}^{L} - \sum _{i} (x_{t,i}^{L} \cdot {\rm TR}_{i,2}) \le T_{e,{\rm sd}} \nonumber \\&\quad + {\rm BigM} \cdot d_{{\rm sd},t}^{L}) \end{aligned}$$
(44)
$$\begin{aligned}&\forall L \ \forall {\rm sd} \in {\rm SD}_{L,1} \ \forall t: \ {\rm tt}_{t}^{L} - \sum _{i} x_{t,i}^{L} \cdot \sum _{R} {\rm TR}_{i,R} \ge T_{l,{\rm sd}}\nonumber \\&\quad - {\rm BigM} \cdot (1 - d_{{\rm sd},t}^{L})) \end{aligned}$$
(45)

The remaining option is to block the second reactor for production processes. In contrast to other features, that entails an event occurring in the second reactor only. On a real-world schedule, it can be handled easily by e.g. planning with single-stage product during the shutdown period. However, as an event time \({\rm tt}_{t}^{L}\) cannot be directly assigned to a specific product, a novel variable \(r_{2,t}^{L}\) is required to decide whether a reaction in the second reactor takes place or not.

Shutdown second unit

$$\begin{aligned}&\forall L \ \forall {\rm sd} \in {\rm SD}_{L,2}\ \forall t: \nonumber \\&\quad \ r_{2,t}^{L} \cdot {\rm BigM} \ge \sum _{i} (x_{t,i}^{L} \cdot {\rm TR}_{i,2}) \end{aligned}$$
(46)
$$\begin{aligned}&\forall L \ \forall {\rm sd} \in {\rm SD}_{L,2}\ \forall t: \nonumber \\&\quad \ r_{2,t}^{L} \le {\rm BigM} \cdot \sum _{i} (x_{t,i}^{L} \cdot {\rm TR}_{i,2}) \end{aligned}$$
(47)
$$\begin{aligned}&\forall L \ \forall {\rm sd} \in {\rm SD}_{L,2}\ \forall t: \nonumber \\&\quad \ d_{{\rm sd},t}^{L} \cdot {\rm BigM} + T_{l,{\rm sd}} - ({\rm tt}_{t}^{L} - \sum _{i} (x_{t,i}^{L} \cdot {\rm TR}_{i,2})) \ge 0 \end{aligned}$$
(48)
$$\begin{aligned}&\forall L \ \forall {\rm sd} \in {\rm SD}_{L,2}\ \forall t: \ (1 - d_{{\rm sd},t}^{L}) \cdot {\rm BigM} \nonumber \\&\quad - T_{l,{\rm sd}} + {\rm tt}_{t}^{L} - \sum _{i} (x_{t,i}^{L} \cdot {\rm TR}_{i,2}) \ge 0 \end{aligned}$$
(49)
$$\begin{aligned}&\forall L \ \forall {\rm sd} \in {\rm SD}_{L,2}\ \forall t: \ {\rm tt}_{t}^{L} \le T_{e,{\rm sd}}\nonumber \\&\quad + {\rm BigM} \cdot (1 + d_{{\rm sd},t}^{L} - r_{2,t}^{L}) \end{aligned}$$
(50)
$$\begin{aligned}&\forall L \ \forall {\rm sd} \in {\rm SD}_{L,2}\ \forall t: \ {\rm tt}_{t}^{L} - \sum _{i} (x_{t,i}^{L} \cdot {\rm TR}_{i,2}) \nonumber \\&\quad \ge T_{l,{\rm sd}} - {\rm BigM} \cdot (2 - d_{{\rm sd},t}^{L} - r_{2,t}^{L}) \end{aligned}$$
(51)

6.3 Tanker products with temporary storage

A tanker product in PT blocks the completion of a tanker affected product in \({\rm PT}_{a}\) for the time span between finishing the tanker product and its pick-up date, which is equal to a due date \(T_{t,i}\). Similar to the modeling of maintenance slots, the binary variable \(n_{i,j}^{L}\) indicates if a product of \({\rm PT}_{a}\) is scheduled before or after a product of PT. Unlike a predefined shutdown, the arrangement of a tanker product is subject to optimization as well.

$$\begin{aligned}&\forall L \ \forall i \in {\rm PT} \ \forall j \in {\rm PT}_{a}, \ i \ne j: \ \sum _{t} x_{t,i}^{L} \cdot t\nonumber \\&\quad - \sum _{t}( x_{t,j}^{L} \cdot t) - (1 - n_{i,j}^{L}) \cdot {\rm BigM} \le 0 \end{aligned}$$
(52)
$$\begin{aligned}&\forall L \ \forall i \in {\rm PT} \ \forall j \in {\rm PT}_{a}, \ i \ne j: \ \sum _{t} x_{t,i}^{L} \cdot t \nonumber \\&\quad - \sum _{t}( x_{t,j}^{L} \cdot t) + n_{i,j}^{L} \cdot {\rm BigM} \ge 0 \end{aligned}$$
(53)
$$\begin{aligned}&\forall L \ \forall t \in \forall t \ \forall i \in {\rm PT} \ \forall j \in {\rm PT}_{a}, \ i \ne j: \ {\rm BigM} \cdot (3 - \sum _{t} x_{t,i}^{L} \nonumber \\&\quad - x_{t,j}^{L} - n_{i,j}^{L}) + {\rm tt}_{t}^{L} \ge T_{l,i} \end{aligned}$$
(54)

So far, producing multiple batches \(p_{i}\) could be realized by having an equal index for the targeted product i, and equations 28 plus 29. However, the position of batches that occur more than once along the schedule is not unambiguously defined, which raises an issue when it comes to specifying \(n_{i,j}^{L}\). All batches of a product type \({\rm PT}_{a}\) must be distinguishable if at least one product of PT belongs to the same scheduling execution. Though the realization can be done easily by allocating a unique index i to each batch in a preprocessing, the consequences for the model size should not be disregarded. Considering that fundamental binary variables as \(x_{t,j}^{L}\) and \(s_{t,i,j}^{L}\) were defined for all product indices, this range is significantly extended when equal products are split into single entities per batch. Multi-line products are especially concerned, as the increase in complexity will be seen on both production lines.

6.4 Campaigns

In some cases, more than one batch of a product type should be produced successively as a campaign, regardless whether it may impact the makespan negatively. A campaign shall be determined as \({\rm CP}_{i,p}\) with i being the product type and p the number of batches to be created.

Campaign products

$$\begin{aligned} \forall {\rm CP}_{i,p}: \ \sum _{L} \sum _{c} \sum _{i\in {\rm CP}_{i,p}} \ \sum _{j\in {\rm CP}_{i,p}} s_{t,i,j}^{L} = p - 1 \end{aligned}$$
(55)

7 Integrated algorithm

In order to validate results plus analyse the model performance, input conditions have been defined depending on the number of batches to be produced. Table 4 contains data that exceeds the planners regular demands in every column, so the model applicability is guaranteed. Note that the number of special constraints, such as tanker products, due dates and campaigns are scaled to the total set of products. They are distributed randomly across all batches, but with respect to the relation between single and multi-line products. Campaigns account for the lower number of distinct products to maintain the incremental increase of total batches.

Table 4 Model input data for testing purposes
Full size table

Despite the novel model, which enables to schedule 45 batches within an hour (Table 3), considering the additional constraints leads to further issues. Not a single feasible solution was found by the MILP solver even for the minimum requirements of 30 products (see also Sect. 4.3). Consequently, a reformulation alone does not suffice for achieving acceptable performance, but must be complemented by an additional strategy. In the following, a novel approach shall demonstrate how batch scheduling models can be realized using decomposition and solver capabilities such as warmstart and hyperparameter optimization.

7.1 Separation of parallel production lines

Two characteristics make the use case stand out against comparable instances found in the literature. Firstly, only two parallel production lines exist, limiting the positioning decisions for the solver decisively. Secondly, it is assumed that only 1/3 of all batch types can be produced in arbitrary reactor cascades, the majority does not offer the opportunity of switching to the alternate one.

Pursuing that idea further, the option to solve the production lines separately was investigated. As a first step, only those batches with fixed path allocation shall be optimized, disregarding all multi-line products. Afterwards, a heuristic is utilized to assign all remaining batches, aiming for balanced end times of both lines, which corresponds to the minimization of makespan for the entire plant. The characteristics of that method may vary depending on how precise the heuristic allocates multi-line batches, which in return demands a more complex implementation. Alternatively, the increase of makespan per added product may be estimated based on its regular production time and an average changeover duration.

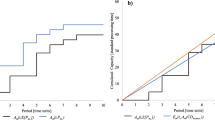
Experimental studies in Table 5 reveal that the performance improvement is significant. A feasible solution was not only found for all tested inputs, yet each MILP could be completely solved to a gap of zero. The main reason lies in the reduced solution space, or in other words, the eliminated degrees of freedom for multi-line products to be switched between different alternate paths. It should be kept in mind that the total schedule still consists of both production lines combined, therefore, the number of batches per line is lower than in the overall scope.

Table 5 Performance for separate production line optimization
Full size table

7.2 Stepwise solution approach

The idea introduced in the following section is founded on the assumption that a final solution can be generated gradually. Rather than applying a single optimization on the entire set of products, it was investigated whether an incremental increase of the model size and complexity could be realized based on the problem’s nature and the capabilities of the Gurobi solver software (Fig. 4).

Firstly, a partial but valid solution shall be found for all critical batches that do not allow an arbitrary sequencing (step 1). It applies to all products with timing constraints like due and earliest start dates, but also to those affected by tanker-induced storage conflicts. All related batches should be optimized in a first step, and due to the reduced scope, a first feasible solution is found within an acceptable period.

Next, the introduced decomposition strategy for separate production lines accesses the result information of the previous MILP model, and adds all remaining single-line products to their respective path (step 2). A initial warmstart solution can be generated, which serves as a basis for a re-optimization. The outcome comprises two separate schedules, each holding a schedule for one production line.

Now, only unassigned multi-line products are left to be arranged. The mentioned heuristic approach should aim to allocate these batches in a way that the completion time of the parallel is balanced. Once again, a first feasible warmstart can be leveraged to improve both schedules, in combination a complete schedule is formed (step 3). However, before concluding the result, it was shown that a last overall optimization of the entire plant enables to further reduce the total makespan (step 4). Starting off with what has been achieved so far, a final MILP run searches for any better solution and mitigates possible weaknesses that arose through decomposition and limited precision of the heuristic.

Considering the limited computational resources of one hour, a maximum time period for each stage of the algorithm is needed. A proposition is given in Table 6. Here, the right-hand column refers to a maximum solution time that each model is given. In total, the entire algorithm should not exceed 3600 seconds. A large portion must be given to the first step that is supposed to find a first valid incumbent. Single-line optimizations complete significantly faster and, thus, demand less resources. In many cases, these submodels are fully solved before the maximum allowable time is reached. The remaining resources are invested in the final re-scheduling across both production lines. The termination thresholds do not account for deviations if a model is solved earlier. Likewise, the time buffer for auxiliary processes should be deemed a rough estimate. As a result, the overall schedule optimization may finish before, but never later than the targeted hour.

Note that the method shown in Fig. 4 can be regarded as a fundamental concept for step-wise model execution and decomposition of production lines. For the subjected real-word production plant, given certain input conditions, some simplifications can be implemented. For instance, if no multi-line products are intended for a planning cycle, each production line can be optimized individually, leading to a significant performance gain.

Fig. 4
figure 4

Stepwise optimization procedure

Full size image
Table 6 Distribution of computation time for 4-stage approach
Full size table

7.2.1 Warmstarting with incomplete starting solutions

It should be noted that the usability of warmstarts in mathematical programs assumes that a solver software provides this feature in the first place. Furthermore, some can handle partially defined input variables and inherently complement them to a integral solution if possible. Gurobi falls under this sort of programs, which comes in handy for the task in the present work. Figure 4 illustrates where new batches are added to an existing schedule, namely stages 2 and 3. No warmstart information is conveyed from the previous step, so that the solver inevitably deals with incomplete starting vectors. However, experiments showed that no starting solution could be derived from the last optimization by simply inserting additional variables and constraints without any initial information.

In order to provide the missing warmstart data, a method is introduced which makes use of the fact that joined products may be arranged in arbitrary sequence. They may be timed subsequent to the last batch of the preexisting schedule. The challenge entailed by this procedure emerges from the variety of model variables that a newly inserted item creates. Not only sequencing variables must be defined, but also continuous values for the event finish time, extra binaries for shutdowns and more. Rather than searching for an algorithm that determines all missing data towards a complete starting solution, a specification of key variables suffices to let the Gurobi solver establish a valid warmstart in a split second. For the present case, only the binaries relevant for the sequencing, namely \(x_{t,i}^{L}\) and \(s_{t,i,j}^{L}\) were imposed.

7.2.2 Adjusting solver parameters

Each stage of the method shown in Fig. 4 aims for certain optimization goal. While sole purpose of the first step is to find an initial feasible solution, the actual result quality is of less importance. Conversely, subsequent MILP models should generate better outcomes, especially the final optimization as it will conclude the scheduling process. Since the model sizes increase gradually as more items are added to the scope, the progress of finding better objective values decelerates. The focus of a mathematical solver can be shifted by adjusting its parameter based on the respective target. Gurobi offers a wide range of modification possibilities for various purposes, such as the concentration on uncovering feasible solutions. In fact, this strategy in addition to the outlined decomposition enabled solving complex schedules in the first place. It is worth mentioning that phase 1 of the algorithm forms a bottleneck of the task, as soon as a single feasible solution was found here, the following warmstart procedure can always complement the product arrangement until a final result becomes available.

In order to speed up the search for enhanced objectives for both separated and combined production lines, a modification of solver parameters towards heuristic methods turned out to be beneficial. The observed behavior revealed that better solutions are derived from the initial warmstart quickly. Note that this focus does not necessarily lead to a global optimum eventually. Running the final stage without parameter adjustments and no limit to computation time generated better solutions in comparison. However, it took the solver several days to actually beat what the presented method produced within an hour.

The drawback of emphasizing on heuristic strategies becomes visible through a significant remaining MILP gap. In other words, it does not serve for an assessment whether the final solution is close or far from the global optimum. Additional models with parameters aiming for a proof of optimality may be inserted downstream (Table 7). Analogously, both separated and combined production lines may be subject to these optimization stages. For practical applications, it should be omitted since no further gain for the objective value will be obtained.

Table 7 Distribution of computation time for 6-stage approach
Full size table

Note that multiple solvers come with a tuning tool used to determine ideal parameters for a specific model. Apart from that, related work can be found in literature. Hutter et al. [19] proposed an iterative parameter configuration method, treating it as a black box algorithm due to proprietary solver algorithms. The research of Sorrell [20] is fully dedicated to finding ideal settings, including screening procedures for those features that are relevant. A recent and more practical example is given in Ishihara and Limmer [21]. The authors aim to optimize solver parameters for an electric vehicle charging problem. In the present work, each stage of the solution algorithm requires distinct parameter modifications for pursuing either a single feasible solution, an objective improvement or the minimization of the MILP gap. In addition, it was observed that fully optimized settings strongly depend on the configuration of the input data, such as the total number of batches and the occurrence of related constraints. Finding robust correlations in between appears to be a promising area for further investigation.

7.2.3 Parallel computing

Looking at Fig. 4, there are multiple submodels which are solved simultaneously and fully independently. In order to speed up the computation at theses stages, it was investigated whether the parallel execution of computations offers benefits performance-wise. To the best of the authors’ knowledge, literature on that particular subject is scarce. Gil and Araya [22] realized a parallel implementation for a stochastic MILP in hydrothermal generation, which accelerates the gap convergence. Winger [23] submitted a patent describing a system for parallel handling of multiple MILP’s in the area of load management. The vast majority of publications addresses solver-internal parallelization. An overview can be viewed in Ralphs [24]. Note that Gurobi belongs to the type of optimization software that inherently makes use of all available threads, so that parallelization is in fact applied to single MILP’s already. This also suggests that multiple concurrently started models will need to share resources, which can be supported by adjusting the “Threads” parameter of the solver, specifically assigning half of the given processing power to each of the optimizations.

Multiple comparisons of parallel versus sequential solving approaches were conducted. Through a variation of input data, it was observed that larger concurrent models exhibit a tendency to output equal objectives up to 20 % faster. After all, an improvement could not be accomplished consistently throughout all tested variations. Several cases ended up having deteriorated results in comparison to sequential model execution. The underlying reason can be found in the slower solution improvement progress due to reduced number of threads. A reliable correlation between input data settings and effectiveness of parallel MILP computing could not be determined. After all, since the performance benefit in several cases was found to be substantial, further investigation with comparable problems is recommended.

7.3 Model comparison and evaluation

The precedence outlined in this paper is strongly tailored for a particular use case. However, a benchmark becomes available if the initial model is taken into account. A comparison regarding the original state of work without additional constraints between the first model (Sect. 4), the reformulation (Sect. 5) and the final solution algorithm (Sect. 7) can be viewed in Table 8. Each was given 3600 s for computation. Here, the method of Fig. 4 is applied by passing the step of finding a first feasible, since no critical products are to be scheduled. As mentioned before, the original model fails to handle 36 batches and more. Although the reformulation copes with a significantly extended number of input products, it is consistently outperformed by the novel solution strategy. More importantly, the introduced stepwise approach enables the realization of more complex boundary conditions and a viable utilization at the target plant, although it lacks a benchmark for comparison. Note that the reformulated single-step model finds valid schedules when decreasing the product number further, the reduced scope, however, does not suffice practical requirements.

Table 8 Model comparison
Full size table

Following the structure in Table 4 embodying all relevant constrains, schedules up to 45 batches could be solved within an hour (Table 9). For a larger input data, observations showed that no first feasible solution was obtained in the first stage of the algorithm within the maximum allowable time. Shifting computational resources displayed in Table 6 towards step 1 facilitates an extension of the number of batches to some point, yet poses a crucial limitation to the model capabilities. Given the restrained time span for optimization, negative effects on solution quality emerge as an inevitable consequence.

Table 9 Modeling results for input data in Table 4 and procedure in Table 6
Full size table

Evidently, the procedure of Fig. 4 and Table 6, respectively, appears to be incapable of finding an adequate lower bound to reduce MILP gap for the integral scheduling problem. A similar behavior was monitored when additionally investing in proving that a discovered solution is optimal (Table 7). Nonetheless, an alternate approach to assess the result utilizes the optimality proof for decomposed production lines (steps 5a and 5b). First, due to the significant performance improvement for single-line scheduling, the subproblems are either solved completely, or to a small gap at the least (< 5 %). Secondly, the result can be analysed to check if parallel units are balanced regarding occupancy. Moving multi-line batch to the opposite line should not obviously decrease the makespan. If both criteria are met, the schedule should be considered close to the global optimum and, hence, to be of high quality.

8 Summary and outlook

The presented solution strategy tackles performance issues of a rather specialized scheduling problem based on a real-world chemical plant. It has been shown that a condensed model did not suffice for a reasonable production scope, which called for an alternate approach. Splitting the set of batches into critical and non-critical items, plus limitation of some products to be restrained to one line enabled to derive a decomposed algorithm as it was described. A finished submodel conveys its solution to the successor optimization, where it is consolidated as a MILP warmstart. Added batches are provided with sequential starting variables only, the Gurobi solver is able to derive a feasible schedule, which allows a focus on improving the initial result. Furthermore, solver parameters can be adjusted to shift the optimization efforts on either finding a solution, its enhancement or the proof of optimality at the respective stage in the algorithm. Optimal settings of these modifications appears to be related to the input data.

This paper joins a series of related literature that cites the groundwork of Kopanos et. al [13]. Although the plant structure of this use case may be less sophisticated in terms of production units and number of batches, more complex boundary conditions make the iterative heuristic approaches less applicable for the scheduling model. Emphasis is laid upon the solver being able to cope with smaller, decomposed optimization steps. It can be displayed how the novel procedure succeeds the initial model whilst maintaining the event-based time representation. Some findings are premised upon certain features of the use case. Considering reactor arrangements of greater complexities, more production lines or interdependencies between parallel routes, scalability of the presented model should be analysed carefully. After all, it is worth mentioning that a slightly adapted but strongly resembling approach was successfully utilized for a similar facility which takes into account material flow between different production lines.

We encourage the reader to review if the described procedure is applicable to other manufacturing processes as well, and how it performs respectively. Moreover, further research on some emerging findings is advised. Particularly, uncovering more solid correlations between input data of a model and ideal solver parameter settings may provide additional performance improvements. Even stop** criteria such as maximum computation times hold optimization potential: For example, when focusing on heuristics to gain better solutions, the progress tends to level off at some point. First observations indicate that this point is reached later if the scheduling task becomes more sophisticated. The potential of parallel computing of independent and subsequently merged MILPs is yet to be consolidated. Given that a corresponding procedure is applicable in the model, concurrent optimizations could outperform a sequential solution approach. The positive effect has been discovered in the present work, though it currently comes with some uncertainty. An comprehensive investigation on conditions for a successful realization is advised.