1 Introduction

The operation of transmission lines at high voltage level, above 500-kV, has been embraced by the developed countries as a standard [1,2,3,4,5]. A reliable power supply is an essential part of any nation thriving toward economic growth and national development. Nigeria, being the giant of Africa and home to the largest economy in Africa as of 2014 [6], cannot boast of a steady power supply due to the state of the power sector operations. It is no longer news that the national power system has been identified with frequent outages. This advertently caused the cost of living to increase as citizens now have to consider the cost of running their private generators. Furthermore the negative role it plays in industrial and economic development has to be considered. Industries and companies refrain from production activities in the nation because of the outrageous cost of running their power sources. This has also caused some of the existing industries to collapse due to the unavailability of electricity thereby resulting in the loss of jobs in those industries and further increase in the hardship faced by the populace of this country [7].

Over the years, there have been reforms in the power sector to curb the many deficiencies which the power sector experiences. Notable progress has been made in the generating sector after the deregulation of the generating wing of PHCN. Regardless of that, the problem of power outages and unavailability of consistent power still plague innocent citizens. The reason is that the grid's weak infrastructure is characterized by high line losses and unbalance of reactive power between generation and load center due to forced outages and system disturbances [8,9,10,11], and cannot support the effective transmission of power to the areas where it is needed for utilization. The Nigerian power transmission system currently utilizes a 330-kV grid for power transmission across the country. The network is more of radial nature, and its infrastructure comprises effective 31 buses, 6,000 MW total installed power generation capacity, and 4,889.2 km length of transmission lines [12, 13]. Several losses have already occurred in the existing grid inferring the inadequacy of the current transmission to deal effectively with the generation. The nation currently suffers the problem of under capacity and poor transmission due to the huge losses experienced on our transmission lines [14,15,16].

In light of this observed challenges, the major objective of the ongoing reform is to expand the existing grid network to a proposed mesh structure and increase the number of buses to a total of 49 buses; 32 buses from existing 330-kV plus 17 buses of the proposed 750-kV. However, this expansion remains a proposed one because no technical analysis shows its viability The rapid increase in the demand for electricity as a result of population growth, industrial development and rise in consumer electrical appliances has necessitated the step** up of generation and demands similar of the transmission capabilities of the grid network to deliver quality power supply to the consumers. The present Nigerian transmission grid network is prone to evacuating and dispatching reliable and quality electricity supply and maintaining an operational standard of security to prevent any collapses [17]. Moreover, there are ever-increasing power demands and restrictions on land and space to build more transmission corridors globally [18]. All the above-aforementioned reasons set the platform for the modification of power system analysis of a 750-kV transmission line and integration to the grid to support the increase in generation and demand by citizens.

The power system analysis of the 750-kV transmission grid integrated into existing 330-kV involves the load-flow analysis and the contingency analysis for system security and reliability. The load-flow analysis of this system serves as an important tool in determining the results that are necessary for planning, design and operating of power system under steady state The power-flow solution is therefore used to evaluate the bus voltage, branch current, real power flow, reactive power flow for specified generation and load conditions. The idea behind this research work is that at 750-kV, the current through the transmission lines would be less thus a decline in the losses experienced across the transmission lines [19]. This research will show the comparison between the load-flow analysis of the 330-kV grid and the 750-kV integrated into the grid. The resulting data obtained from the outcome will be used to infer the appropriate solution for the advancement and modification of the existing transmission grid for maximum efficiency and continuous sustainable energy supply.

2 Methodology adopted for the work

The test system for this research work is a proposed 750-kV transmission grid. The grid is an integrated system comprising the existing 330-kV grid and the selected identified regions to upgrade to the 750-kV transmission voltage. Thirteen buses have been identified for the transmission voltage level upgrade to reduce the cost. The various locations of the upgraded buses are shown on the Nigerian site plan map of Fig. 1. These buses have been selected for an upgrade because they are positioned in critical areas within the grid’s topology, transforming the existing radial structure to a ring one. A step-wise approach has been applied to upgrade this system due to the cost of implementing upgrading all the buses to 750 kV at once. In an attempt to ring the entire grid with the proposed thirteen buses mapped out from the super grid, two more lines were added: Mambilla–Jalingo and Jalingo—Gombe. This is in anticipation of power that will soon be evacuated from the Mambilla Hydropower plant, which is expected to be completed by 2018. Thus, the name and distance of every line as mapped out from the supper grid map are presented in Table 1. The transmission line data for the 16 lines of the upgraded 750-kV shown in Table 1 are calculated from the first principle, while the bus and generator data of the existing 330-kV grid were used as obtained from PHCN.

Fig. 1
figure 1

Map of the Nigerian 750-kV grid [20]

Full size image
Table 1 Line name and length as mapped out from super grid map
Full size table

The single-line diagram of the upgraded 750-kV lines, as presented in Table 1, is shown in Fig. 1. The integration of this upgraded 750-kV grid with the existing 330-kV grid is illustrated in Fig. 2.

Fig. 2
figure 2

Single-line diagram of the proposed upgraded 750-kV Nigerian transmission Grid

Full size image

2.1 Load-flow analysis of the integrated Nigerian 750-kV transmission system

To carry out any comparative analysis between the integrated 750-kV system that formed a new network with the existing 330-kV system and the existing 330-kV grid system, it is necessary to perform the load-flow analysis of the system first. It is essential because the load-flow results are required for loss of generating unit, loss of transmission line, or failure of any single component [21]. The load-flow analysis is used to evaluate bus voltages, branch currents, and real and reactive power flow under steady-state balanced conditions. For this research work, load-flow analysis based on the Newton–Raphson technique was performed using Power World Simulator on run mode. The simulation software was used to determine the bus voltages, real and reactive power flow losses on the various lines under normal conditions for the 330-kV and the 750-kV integrated grids.

The real and reactive power losses obtained were also verified using the MATLAB software to show the authenticity of the results obtained from the simulation of the network.

2.2 Newton–Raphson method

This method is a successive approximation procedure which is based on an initial estimate of the unknown and the use of Taylor’s series expansion.

For a typical bus of power system, the net current entering bus I is given by Eq. (1).

$${\mathrm{\rm I}}_{i}={V}_{i}\sum_{j=0}^{n}{y}_{ij}-\sum_{j=1}^{n}{y}_{ij}{V}_{j j\ne i}$$
(1)

In terms of bus admittance matrix, this equation becomes

$${\mathrm{\rm I}}_{i}=\sum_{j=1}^{n}{Y}_{ij}{V}_{j j\ne i}$$
(2)

Expressing the above equation in polar form results in Eq. (3).

$$\mathrm{Ii}=\sum_{j=1}^{n}|{Y}_{ij}||{V}_{j}|\angle {\theta }_{ij}-{\delta }_{j}$$
(3)

Complex power is obtained from Eqs. (4) and (5)

$${P}_{i}-{jQ}_{i}={V}_{i}^{*}{I}_{i}$$
(4)
$${{\varvec{P}}}_{{\varvec{i}}}-{{\varvec{j}}{\varvec{Q}}}_{{\varvec{i}}}=\left|{{\varvec{V}}}_{{\varvec{i}}}\right|\mathbf{\angle }-{{\varvec{\delta}}}_{{\varvec{i}}}\sum_{{\varvec{j}}=1}^{{\varvec{n}}}\left|{{\varvec{Y}}}_{{\varvec{i}}{\varvec{j}}}\right|\left|{{\varvec{V}}}_{{\varvec{j}}}\right|\mathbf{\angle }{{\varvec{\theta}}}_{{\varvec{i}}{\varvec{j}}}+{{\varvec{\delta}}}_{{\varvec{j}}}$$
(5)

The real and imaginary powers are respectively given by Eqs. (6) and (7).

$${P}_{i}=\sum_{j=1}^{n}{|V}_{i}|\left|{V}_{j}\right|\left|{Y}_{ij}\right|\mathrm{cos}\left({\theta }_{ij}-{\delta }_{i}+{\delta }_{j}\right)$$
(6)
$${Q}_{i =}-\sum_{j=1}^{n}{|V}_{i}|\left|{V}_{j}\right|\left|{Y}_{ij}\right|\mathrm{sin}\left({\theta }_{ij}-{\delta }_{i}+{\delta }_{j}\right)$$
(7)

The matrix form of Newton–Raphson method is given as shown in Eq. (8)

$$\left[\begin{array}{c}\Delta P\\\Delta Q\end{array}\right]=\left[\begin{array}{cc}{J}_{1}& {J}_{2}\\ {J}_{3}& {J}_{4}\end{array}\right]\left[\begin{array}{c}\Delta \delta \\\Delta |V|\end{array}\right]$$
(8)

where; \(\Delta P\) and \(\Delta Q\) are respectively the real and reactive power mismatch, \(\Delta \left|V\right|\) and \(\Delta \delta\) are respectively bus voltage magnitude and angle, J1 through J4 are called Jacobian sub-matrices.

The Jacobian sub matrices can be obtained from Eqs. (9) and (10).

$$\frac{{\partial P}_{i}}{{\partial \delta }_{j}}=-\left|{V}_{i}\right|\left|{V}_{j}\right|\left|{Y}_{ij}\right|\mathrm{sin}\left({\theta }_{ij}-{\delta }_{i}+{\delta }_{j}\right)$$
(9)
$$\frac{{\partial P}_{i}}{{\partial \delta }_{j}}=\sum_{j\ne i}|{V}_{i}||{V}_{j}||{Y}_{ij}|\mathrm{cos}\left({\theta }_{ij}-{\delta }_{i}+{\delta }_{j}\right)$$
(10)

2.3 Calculations of the transmission line data for 750-kV lines

The determination of the line parameters is carried out using the per-unit system. Typical base value of 1,000 MVA was adopted for the 750-kV transmission grid system using Eq. (11).

$${V}_{base}={V}_{line}=750 kV$$
$${Z}_{base}=\frac{{\left({V}_{base}\right)}^{2}}{{MVA}_{base}}$$
(11)

Thus, the impedance and admittance base values are obtained respectively as shown in Eqs. (12) and (13), respectively.

$${Z}_{base}=\frac{{\left(\mathrm{750,000}\right)}^{2}}{1000\times {10}^{6}}$$
$${Z}_{base}=562.5\Omega$$
$${Y}_{base}=\frac{1}{{Z}_{base}}$$
(12)
$${Y}_{base}=\frac{1}{562.5}$$
$${Y}_{base}=1.709\times {10}^{-3 }Siemens$$
(13)

The computation of per-unit values for resistance, reactance and susceptance are respectively obtained using Eqs. (14), (15) and (16), respectively.

$${R}_{p.u}=\frac{{R}_{actual value}}{{Z}_{base}};$$
(14)
$${R}_{p.u}=\frac{0.01507}{562.5};$$
$${R}_{p.u}=0.00002679\frac{pu}{km};$$
$${X}_{p.u}=\frac{{X}_{actual value}}{{Z}_{base}};$$
(15)
$${X}_{p.u}=\frac{0.2771}{562.5}$$
$${X}_{p.u}=0.0004926 pu/km$$
$${B}_{p.u}=\frac{{B}_{actual value}}{{Y}_{base}};$$
(16)
$${B}_{p.u}=\frac{4.2\times {10}^{-6}}{1.709\times {10}^{-3 }};and$$
$$B\_(p.u)=0.002458 pu/km$$

The calculated per-unit values of the resistance, reactance, and susceptance were used to multiply the individual line lengths to generate the line parameters for the proposed 750-kV, as shown in Table 2

Table 2 Generated transmission line parameters for upgraded 750-kV grid with 1000 KVA base value
Full size table

2.4 Power world simulator

Power world simulator (PWS) is the software used in this research work for simulation purposes. Both load-flow analysis and contingency analysis were carried out using this software. PWS is very user-friendly, and it is interactive simulation software. The simulator allows full-colored animated one-line diagrams with zooming and panning capability, which helps to increase the user’s understanding. Load-flow simulation was carried out on the existing 330-kV and the integrated 750-kV super grid. The results obtained from both simulations served as the basis for comparison in terms of MW and MVar losses, and the number of voltages violated buses in the grid.

2.5 Load-flow simulation of the existing 330-kV transmission grid

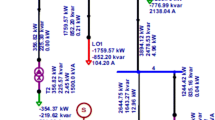
To carry out load flow using the PWS, the single-line diagram of the existing 330-kV grid was drawn in the edit mode of the simulator. The main simulation was done in the run mode and the run mode executed in the simulation using N-R iterative method in order to obtain bus voltages, phase angles, real and reactive power flows, and line losses. The results were obtained after inputting line data, load data and generator data obtained from PHCN into the dialogue box of the PWS in edit mode. For this simulation, Egbin was set as the slack bus and it was used to simulate the load flow of the existing grid. Figure 3 shows the existing grid in the run mode of the power world program. The simulation of the network obtained the unknown bus angles and voltage levels at each bus.

Fig. 3
figure 3

Single line diagram of the integrated 750-kV Nigerian transmission Super Grid

Full size image

2.6 Load-flow simulation of the 330-kV and integrated 750-kV transmission grid

In executing the load-flow simulation of the 750-kV transmission grid, a similar method was used as that of the 330-kV grid. The 750-kV grid integrated to the existing 330-kV was redrawn in the edit mode of the power world simulator as shown in Fig. 4. The line, bus and generator data were entered in the edit mode of the simulator. The main simulation was done in the run mode and the run mode executed for the simulation using N-R iterative method in order to obtain bus voltages, phase angles, real and reactive power flows, and line losses. The edit mode of the load-flow simulation is as presented in Fig. 5. The simulation of the network obtained the unknown bus angles and voltage levels at each bus.

Fig. 4
figure 4

Integrated 750-kV super grid in power world simulator (run mode)

Full size image
Fig. 5
figure 5

Existing 330-kV transmission grid in the run mode of the PWS

Full size image

MATLAB was used to verify the losses recorded from the load-flow simulation of both the existing Nigerian 330-kV and the integrated 750-kV grids using the power world simulator. The simulation was done by imputing the same load and transmission line data for the 330-kV and 750-kV grids used on power world simulator into a MATLAB script developed to perform load-flow analysis and print total losses.

2.7 Power system contingency analysis

Contingencies are characterized as possibly harmful disruptions that happen during the steady-state operation of a power system. A power system operating in its normal mode is prone to experiencing contingencies such as sudden loss of line or generator, sudden increase or decrease in power demand. These contingencies cause transmission line overloading or bus voltage violations. It represents an important tool to study the effect of components outages in power system security during operation and planning [22].

The contingency that analyses the model failure events of all credible outages, one after the other in sequence have been studied and executed on the power systems. It is also important for this research because it shows how both the 330-kV and integrated systems will respond to the given outage conditions, thus, providing validation for the integrated 750-kV and a foundation for the implementation of the system in the Nigerian national grid. This research used a simple contingency format to analyze the new test system and the existing 330-kV system. The contingency analysis implored was a simple single-line contingency analysis. The simulation was carried out using the PWS. The contingency analysis sequence of execution can be described in a simple way by the following flowchart.

3 Result analysis and discussion

In this section, the load-flows and contingency analysis results that were carried out on both the existing 330-kV and the configured new network (i.e., with the 750-kV integrated power line grid) are compared and analyzed. Thus, the load-flow results obtained for unknown bus angle, voltage magnitude, and real and reactive power losses at each bus using MATLAB and PWS in run-mode were analyzed and discussed for performance evaluation. Also, the simple single-line contingency analysis results employed in the study were analyzed and discussed to provide validation for the integrated 750-kV and a foundation for the implementation of the system in the Nigerian national grid.

3.1 Load-flow analysis of the existing 330-kV

The load-flow analysis of the existing grid using the power world simulator produced the values of the bus voltage magnitudes, voltage angles, and real and reactive power flow losses on the various lines under normal conditions. The graphical representations of the results of voltage profile, real and reactive power losses are shown in Figs. 6, 7 and 8, respectively.

Fig. 6
figure 6

Contingency analysis flow-chart

Full size image
Fig. 7
figure 7

Voltage profile of the existing 330-kV grid

Full size image
Fig. 8
figure 8

Real power loss on the existing 330-kV grid

Full size image

The analysis of Fig. 6 shows that 11 buses had voltage violations under steady-state operation. These buses include Birinin-Kebbi; Akangba; Katampe; Onitsha; New Heaven; Alaoji; Shiroro; Kano; Kaduna; Jos; and Gombe, with the bus at Gombe recording the lowest voltage of 0.36pu.

Also, Fig. 7 showed that 14 power lines recorded losses higher than 4 MW with critical value along line 20–19, representing okapi to Onitsha that recorded 50.71 MW in real power losses. These lines include following: 2–4; 4–6; 8–14; 10–14; 14–19; 14–17; 20–19; 22–23; 24–4; 24–12; 25–26; 26–24; 27–28; and 27–26. Also, the total real and reactive power losses recorded were 251.7 MW and 277.4Mvar, respectively.

3.2 Load-flow analysis of integrated 750-kV super grid (new model)

The load-flow analysis of the new model using the Power Word Simulator produced the values of the bus voltage magnitudes, voltage angles, and real and reactive power flow losses on the various lines under normal conditions. Figure 9 shows the voltage profile of the N-R in PWS load-flow with bus voltage violations at Birnin-Kebbi, New Heaven, Alaoji, Kano, Gombe, Jalingo and Mambilla buses. The real, and reactive power losses are graphically represented in Figs. 10 and 11, respectively. The analysis of the results showed that under steady-state operation, 7 buses were slightly below the specified voltage tolerance, with the bus at New Heaven recorded the lowest voltage of 0.883pu.

Fig. 9
figure 9

Reactive power loss of existing 330-kV grid

Full size image
Fig. 10
figure 10

Voltage profile of 750-kV super gird

Full size image
Fig. 11
figure 11

Real power loss of the integrated 750-kV super Grid

Full size image

Analysis of Fig. 10 showed that 8 lines recorded losses higher than 4 MW and these lines include 1–2; 3–5; 8–10; 14–17; 20–19; 22–23; 24–3; and 26–4 with critical value also along line 20–19 i.e., line from Okapi to Onitsha that recorded 50.87 MW in real power losses. This shows that the model with 750-kV super grid was able to reduce the number of lines with loses greater than 4 MW. The integrated 750-kV super grid recorded a 78.44-MW difference in real power loses and 1123.79Mvar in reactive power losses between the existing 330-kV grid.

Also, the total real and reactive power losses recorded were 173.21 and − 846.39 Mvar respectively. These show that the combined new model of 330-kV and 750-kV super grid was able to reduce the real power losses by 30.2% as shown in Fig. 12 and the reduction in the reactive power losses shows shortages in reactive power. While Fig. 13 shows the combined real power losses of 330-kV and 750-kV transmission line.

Fig. 12
figure 12

Reactive power loss of integrated 750-kV super grid

Full size image
Fig. 13
figure 13

The combined real power losses of 330-kV and 750-kV transmission line

Full size image

3.3 Loss verification using MATLAB

Table 3 shows a side-by-side comparison of the total losses obtained when the load-flow analysis was simulated in both the PWS and MATLAB software. The result in Table 3 validates the authenticity of the losses recorded using the Power World Simulator. The Real Power Loss differences between 330-kV and 750-kV grids were 78.44 MW and 69.74 MW in PWS and MATLAB, respectively. This shows that they are within the same range. The percentage loss differences between both grids were also similar with 30.2% and 37.87% in PWS and MATLAB, respectively. This validates that loss reduction will occur in the integrated 750-kV Super Grid.

Table 3 Loss comparison between MATLAB and power world simulator (PWS)
Full size table

3.4 Contingency analysis results

Tables 4 and 5 show the results of single-line contingency analysis carried out on the existing 330-kV grid and the combined 330-kV grid integrated with 750-kV super grid respectively. The contingency results were evaluated by subjecting the various lines to a single contingency analysis to examine the effect of loss of any single line on the network. The analysis of the results in Tables 4 and 5 show the following:

Table 4 Contingency results for 330-kV grid
Full size table
Table 5 Contingency records for integrated 750-kV super grid
Full size table

When the existing 330-kV was subjected to contingency analysis, a total of 201 voltage violations with 2 unsolved cases were recorded as shown in Table 4

The integrated 750-kV super grid responded better to the single-line contingency analysis by recording only 70 voltage violations with 0 unsolved case as presented in Table 5.

4 Conclusion and recommendation

So far, it has been established that the present Nigerian 330-kV power grid is characterized by lower power availability to consumers. This is a consequence of some identified poor power qualities like power losses, voltage violations, and network topology. These reasons set the platform for the motivation to develop a new network system combining the existing 330-kV grid and some buses selected for upgrade to 750-kV super grid integrated to the existing 330-kV grid to transform the existing radial structure to a ring topology at a reasonable cost. The performance outcome of the power system analysis revealed a significant improvement in the voltage profile of voltage violated buses in the existing 330-kV grid. There was also a considerable reduction in transmission line losses by 30.2% compared to the existing 330-kV grid. With losses more significant than 4 MW, the total number of power lines was also reduced from 14 to 7 lines with the new network. There was also a reduction in voltage violation after single-line contingency analysis from 201 violations in the existing grid to 70 violations with zero unsolved cases for the new network. Based on the performance evaluation results obtained, it is highly recommended to extend the upgrade to all the buses of the existing 330-kV grid to 750-kV super grid based on the performance evaluation results obtained in this research work. Moreover, future research needs to be carried out on the dynamic thermal rating (DTR) system, integration and analysis of probabilistic peak demand matching by battery energy storage, and impacts of the dynamic thermal rating on wind-integrated power networks to increase the reliability enhancement of the modified model.