1 Introduction

Detecting damages in structures such as buildings, aircraft, vehicles or pipelines is one of the aspects that have been studied and analyzed in every branch of engineering to avoid breakdowns, malfunctions or deficiencies that could lead to risks of accidents or high unforeseen economic costs [1,2,3]. To prevent this, several approaches are necessary such as visual inspection with highly specialized operators, preventive maintenance, and exclusive techniques for damage detection. For this reason, at present, it is necessary to corroborate the integrity of both public and private structures to ensure their safety. Thus, different experimental techniques have been used to evaluate deformation in structures such as digital holographic interferometry to learn to what extent the beam is deformed at the load and how much it can withstand [4], o the experimental research about mechanical properties of the high-strength steel S960 QL and its welded joints, carried out in fatigue-testing equipment at the laboratory level [5]. An important example occurs in the oil industry, which makes use of pipelines for the supply and transport of hydrocarbons in a liquid or gaseous state, requiring that such pipelines must be in optimal conditions for their use, therefore it is necessary to analyze their structure to detect possible failures or leaks that could endanger both personnel and distribution.

It is important to highlight that the mentioned analysis requires an extensive inspection process and, in some cases, demands for material to be analyzed, which is submitted to certain tests that affect its proper functioning or even cause the total loss of it, this type of analysis is known as destructive testing. Since it is very costly and there are some inconveniences when performing structural analysis by the tests or destructive tests, alternative methods are required, which do not interfere with regular activities, nor affect or damage the element to be analyzed. These methods are known as non-destructive tests, such as the magnetic memory method, eddy currents, and active vision using light scattering.

The optical NDT methods provide higher sensitivity and resolution for high precision applications, however, requires a high cost of implementation and have better penetration on most of dry non-metallic or insolating materials [6].

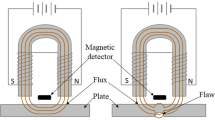
The advantage of the Magnetic Memory Method (MMM) over other non-destructive testing methods that apply magnetism, such as Magnetic Particle Testing, is that MMM does not require the artificial magnetization of the element to be tested [2, 7], but rather makes use of its residual magnetic field for the detection of faults or anomalies. This occurs in structures of a ferromagnetic nature. Another advantage of this method is the capacity not only to detect the superficial anomalies but also the internal ones that the element or structure can have. Magnetoresistive sensors have the ability to detect magnetic field disturbances, which is of great importance for the detection of anomalies in ferromagnetic structures when using the MMM [8, 9]. Such distortion may be a reaction of some defect in the structure, which can be flaws, fractures, hits or dents. The advantages of this method are mainly: (a) the detection of faults in the structure by means of a non-destructive analysis [1,

Fig. 5
figure 5

FSM of robot´s behavior path

Full size image

2.2 Python simulations of the magnetic field in rectangular defect

In order to elucidate the relationship among the profiles of the magnetic field measured by the sensor and geometric characteristics of the flaws, numerical simulations were performed. In the simulations, the system was considered as formed by an ordered arrangement of magnetic moments representing the scenario of a magnetized system incorporating in the structure’s rectangular flaws of different aspect ratios. Hence, the magnetic flux density (strength of the B-field) in Teslas was determined by adding the contributions to the magnetic field of every magnetic moment (representing an average domain) at a given distance from the surface. Every dipolar contribution, being the curl of the vector potential A, reads as follows

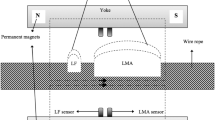
$$\vec{B}\left( {\vec{r}} \right) = \vec{\nabla } \times \vec{A} = \frac{{\mu_{0} }}{4\pi }\left[ {\frac{{3\vec{r}\left( {\vec{m} \cdot \vec{r}} \right)}}{{r^{5} }} - \frac{{\vec{m}}}{{r^{3} }}} \right]$$

where m is the magnetic moment per domain, and r is the vector going from the position of every magnetic moment in the arrangement to the position where B is evaluated. By repeating iteratively this procedure, the cartesian components of B were obtained along the profile at a given distance from the surface. The corresponding experimental counterpart was set up using a pair of permanent neodymium magnets, as shown in Fig. 6, in order to magnetize the domains in the region where the sensor came through. Figure 7 shows the array of random and ordered magnetic domains using Python. The Fig. 8, 9 and 10 shows the behavior of the magnetic field on the plate under test by using the model implemented in software and written in Python programming language and running in a workstation Dell T7910.

Fig. 6
figure 6

Magnetization of the plate to orient the magnetics domain a top view, b side view of the setup using a permanent neodymium magnet

Full size image
Fig. 7
figure 7

a array of random magnetic domains, b ordered magnetic domains on the plate AST A-27 under test

Full size image
Fig. 8
figure 8

Magnetic field X of a rectangular defect with ordered magnetic domains

Full size image
Fig. 9
figure 9

Magnetic field Y of a rectangular defect with ordered magnetic domains

Full size image
Fig. 10
figure 10

Magnetic field Z of a rectangular defect with ordered magnetic domains

Full size image