1 Introduction

The two-dimensional BBT system can be considered as the extension of the one-dimensional ball and beam system. It is widely used as an experimental device for the study of multivariable nonlinear systems. The BBT is a challenging system known to be highly unstable in open-loop and strongly coupled. It consists of a ball rolling freely on the top of a rectangular plate fixed in its centre and able to rotate around its X and Y-axis. The coordinates of the steel ball are acquired through a touch screen in real-time.

Until now, a considerable number of studies have been devoted to the motion control problem of the BBT system [8, 16, 23, 30]. It includes both, the static position control problem where the ball is stabilised at a reference position and the dynamic position control problem where the ball follows a desired trajectory. Many controllers have been suggested for studying these problems and one of the most prevalent is the classic PID controller. Nevertheless, it suffers from many limitations which were mentioned by several researchers such as an important settling time, a large overshoot [31], a low-precision [34] and others. So to ameliorate system performances, several advanced control methods have been investigated. In [8], a hierarchical fuzzy control scheme was proposed. A Fuzzy-PID controller based on Kalman filter was introduced in [13] where the PID parameters were self-tuned, and the Kalman filter was used to overcome modelling imprecision and reduce noise from sensors. In [3], an optimal nonlinear controller based on the model reference control structure was investigated. To determine optimal parameters, the invasive weed optimisation algorithm was used. In [15], in order to solve the trajectory tracking problem, an adaptive sliding mode controller was proposed. Based on the performance of static position and dynamic tracking, a comparison in [16] was carried out between Fuzzy controller, LQR, sliding mode and PID. In [27], two control approaches were presented and compared in an experimental study which are the state space feedback based on an observer and the sliding mode controller. In [12], the design of a functional observer-based feedback controller using the direct approach was presented. The controller was tested in a simulation environment. The acceptability of the simulation results has motivated the effort reported in the present paper to test the validity of the proposed controller on the BBT laboratory model in real-time. Linear functional observers (LFOs) have gained increasing interest in the past number of years, due to their potential to overcome problems related to technical constraints and high costs of sensors installation. In functional observer theory, it is not required to determine each component of the state variables, but it is sufficient to estimate a part of them, so by using a functional observer, we can ensure reducing substantially the order of the observer. This state variables partial reconstruction can be interesting and useful in many control systems and one of the widely used applications is the state feedback design where the control signal is generated as the output of the estimator. Various approaches have been proposed to provide state estimation. These approaches are essentially based on eigenvalue assignment or on the Sylvester-observer equation resolution [7]. In [21], the direct method was introduced for the first time to reconstruct a single linear functional observer and since then many studies have been carried out on functional observer design using this method [11, 18, 24]. The main advantage of this method is its simplicity as it relied on iterative derivations of the vector to be reconstructed. Besides, it is sufficient for the system to be functional observable (or functional detectable) instead of being observable (or detectable). We have to mention that the notion of functional observability (or functional detectability) is less restrictive than the observability (or the detectability) notion. In this work, the implementation of a feedback controller on a hardware platform has motivated the elaboration of the equations in a discrete-time framework. This paper is divided into six sections. Section 2 deals with the description of the experimental setup of a ball balancing table. In section 3, our focus is on the design of a state feedback control law using a functional observer. Next, section 4 describes the direct procedure for the estimation of a desired functional by a linear multifunctional observer. The 5th section is devoted to the design of the BBT system controller. In the following section, the experimental results of the proposed algorithm are presented. Finally, some conclusions are given.

2 Experimental setup description and modeling

The ball balancing table is an apparatus used to evaluate the control algorithms developed in this paper. Figures 1 and 2 show the experimental setup and its main parts.

Fig. 1
figure 1

Parts of the BBT system: 1. Power distribution box 2. NI myRIO 3. RC servos 4. Steel ball 5. 2D resistive touch sensor and controller

Full size image
Fig. 2
figure 2

Block diagram of the ball balancing table

Full size image
Fig. 3
figure 3

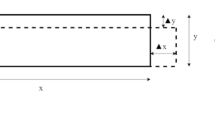
Schematic diagram of ball and plate system [1]

Full size image

The BBT physical parameters are indicated in Table 1 and Figure 3.

Table 1 BBT physical parameters [1]
Full size table

2.1 Mathematical model

To derive the coupled equations of motion, the following assumptions are taken into account:

  • All resulting frictions and torques between the ball and the plate are neglected in order to simplify the system equations.

  • The ball never loses contact with the table. This allows to avoid discontinuities in the ball position signal.

  • The ball moves freely on the plate without slip**.

The last two hypotheses impose a constraint on the rotation acceleration of the plate.

By using the Lagrangian method and the relationship between the plate angle and the motor angle, the nonlinear equations of the system for X-direction and Y-direction can be written as follows:

$$\begin{aligned} \ddot{ x } _ { b }= & {} \frac{ m _ { b } g r _ { b } ^ { 2 } r _ { M } }{ \left( m _ { b } r _ { b } ^ { 2 } + J _ { b } \right) L _ { x } } \sin \left( \vartheta _ { x } \right) \end{aligned}$$
(1)
$$\begin{aligned} \ddot{ y } _ { b }= & {} \frac{ m _ { b } g r _ { b } ^ { 2 } r _ { M } }{ \left( m _ { b } r _ { b } ^ { 2 } + V _ { b } \right) L _ { y } } \sin \left( \vartheta _ { y } \right) \end{aligned}$$
(2)

To simplify the control of such a highly nonlinear system, we can use the approximation of sine function for small angles:

$$\begin{aligned} \sin \left( \vartheta _ { x } \right) \approx \vartheta _ { x } , \sin \left( \vartheta _ { y } \right) \approx \vartheta _ { y } \end{aligned}$$
(3)

Then, the differential equations can be linearized around the operating point \((x_b=0, y_b=0)\) and the equations (1) and (2) become:

$$\begin{aligned} \ddot{ x } _ { b }= & {} \frac{ m _ { b } g r _ { b } ^ { 2 } r _ { M } }{ \left( m _ { b } r _ { b } ^ { 2 } + J _ { b } \right) L _ { x } } \vartheta _ { x } = K _ { B B T , X } \vartheta _ { x } \end{aligned}$$
(4)
$$\begin{aligned} \ddot{ y } _ { b }= & {} \frac{ m _ { b } g r _ { b } ^ { 2 } r _ { M } }{ \left( m _ { b } r _ { b } ^ { 2 } + J _ { b } \right) L _ { y } } \vartheta _ { y } = K _ { B B T , Y } \vartheta _ { y } \end{aligned}$$
(5)

with

$$\begin{aligned} K _ { B B T , X }= & {} \frac{ m _ { b } g r _ { b } ^ { 2 } r _ { M } }{ \left( m _ { b } r _ { b } ^ { 2 } + J _ { b } \right) L _ { x } } \end{aligned}$$
(6)
$$\begin{aligned} K _ { B B T , Y }= & {} \frac{ m _ { b } g r _ { b } ^ { 2 } r _ { M } }{ \left( m _ { b } r _ { b } ^ { 2 } + J _ { b } \right) L _ { Y } } \end{aligned}$$
(7)

Taking the Laplace transform of (4), we obtain the transfer function:

$$\begin{aligned} G _ { B B T , X } ( s ) = \frac{ X _ { b } ( s ) }{ \vartheta _ { x } ( s ) } = \frac{ K _ { B B T , X } }{ s ^ { 2 } } \end{aligned}$$
(8)

In Y-direction, the transfer function can be written as:

$$\begin{aligned} G _ { B B T , Y } ( s ) = \frac{ Y _ { b } ( s ) }{ \vartheta _ { y } ( s ) } = \frac{ K _ { B B T , Y } }{ s ^ { 2 } } \end{aligned}$$
(9)

As the actuator of ball balancing table is a servomotor, its transfer function, denoted by \(G_{M}(s)\), can be approximated as a first order function of the form:

$$\begin{aligned} {G_M}(s) = \frac{{{\vartheta _x}}}{{{U_X}}} = \frac{{{\vartheta _y}}}{{{U_Y}}} = \frac{{{K_M}}}{{\tau s + 1}} \end{aligned}$$
(10)

where \({U_{X}}\) and \({U_{Y}}\) are the input signals of servomotors in X and Y directions, \(K _ { M }\) is the gain and \(\tau\) is the time constant of the actuator.

The ball balancing table has a cascade structure (Figure 4), then the plant’s and actuator’s transfer matrix is:

Fig. 4
figure 4

Block diagram of the system after reduction

Full size image
$$\begin{aligned} \left( {\begin{array}{*{20}{c}} {{X_b}(s)}\\ {{Y_b}(s)} \end{array}} \right) = G_{sys}(s)\left( {\begin{array}{*{20}{c}} {{U_x}(s)}\\ {{U_y}(s)} \end{array}} \right) \end{aligned}$$
(11)

where

$$\begin{aligned}G_{sys}(s) = \left( {\begin{array}{*{20}{c}} {{G_{BBT,X}}(s) \times {G_M}(s)}&{}0\\ 0&{}{{G_{BBT,Y}}(s) \times {G_M}(s)} \end{array}} \right) \end{aligned}$$

From the transfer function matix, we can easily deduce the continuous state space representation.

2.2 Discrete state space representation

Assume that the general form of the continuous time state space model of the BBT is given by the following equation:

$$\begin{aligned} \begin{array}{l} x(t) = A_cx(t) + B_cu(t)\\ y(t) = C_cx(t)\\ \end{array} \end{aligned}$$
(12)

where the system matrix \(A_c\) is \(n \times n\), the input matrix \(B_c\) is \(n \times p\) and the output matrix \(C_c\) is \(m \times n\). To implement the numerical control calculation, this linear continuous model needs to be discretized.Then, the discrete state space equations are given by:

$$\begin{aligned} \begin{array}{l} x(k+1) = Ax(k) + Bu(k)\\ y(k) = Cx(k)\\ \end{array} \end{aligned}$$
(13)

with:

$$\begin{aligned}\left\{ {\begin{array}{*{20}{l}} {A = {e^{{A_c}T}}}\\ {B = \int _0^T {{e^{{A_c}\theta }}} {B_c}\mathrm{{d}}\theta }\\ {C = {C_c}} \end{array}} \right. \end{aligned}$$

Notations

In the whole paper, all the sampled signals are functions of the discrete-time variable k which we may write in one of three ways

\(s(kT)\mathrm{{ }} \equiv s(k)\mathrm{{ }} \equiv {s_k}\), where \(k \in \mathbb {N}\), \(k\ge k_0\) and T are a sampling interval.

3 Discrete feedback controller

In order to guarantee the asymptotic convergence of the error estimation to zero, the control loop poles are assigned by the pole placement method. The feedback control law is given as follows:

$$\begin{aligned} u(k)=N_{C} r(k)-F x(k) \end{aligned}$$
(14)

where r(k) is a two-dimensional reference input signal. F and \(N_C\) are, respectively, the state feedback gain matrix and a constant matrix that acts on the static gain [20, 25].

By replacing u(k) by its expression in (13), we obtain:

$$\begin{aligned} \begin{array}{l}{{x}(k+1)=(A-BF) x(k)+B N_{C} r(k)} \\ {y(k)=C x(k)}\end{array} \end{aligned}$$
(15)

For an external reference input r(k), the static gain \(\Gamma\) is expressed as follows:

$$\begin{aligned} \Gamma =C(B F-A)^{-1} B N_{C} \end{aligned}$$
(16)

The matrix \(N_C\) is calculated if the static gain \(\Gamma\) is determined and we can obtain:

$$\begin{aligned} N_{C}=\left[ C(B F-A)^{-1} B\right] ^{-1} \Gamma \end{aligned}$$
(17)

If the system (13) is controllable [2, 17], then the design of the pole placement controller is possible.

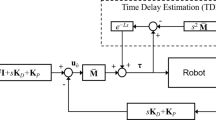
From the equation (14), it’s clear that a state observer is required to estimate the states used for the feedback. In literature, various types of state observers are used, but our focus is limited to the functional observer. The block diagram of the proposed system is shown in Figure 5.

Fig. 5
figure 5

A feedback control system with functional observer-based state feedback controller

Full size image

Next, the state observer design for discrete system is detailed step by step.

4 Discrete functional linear observers

Let us consider the problem of observing a linear functional \(\upsilon (k)\), the vector that is required to be estimated (or reconstructed):

$$\begin{aligned} \upsilon (k) = F x(k) \end{aligned}$$
(18)

where \(F \in \mathbb {R}^{(l \times n)}\).

Without loss of generality, it is assumed in this paper that:

  • F and C are matrices that have full row rank, i.e., \(\mathrm{{rank}}(F) = l\) and \(\mathrm{{rank}}(C) = m\)

  • \(\mathrm {rank} \left( {\left[ {\begin{array}{*{20}{c}} C\\ F \end{array}} \right] } \right) \mathrm{{ }} = \mathrm{{ }}m\mathrm{{ }} + \mathrm{{ }}l\).

  • The number of functions to be estimated is not greater than the difference between the number of states and the outputs of the system \(l \le n - m\). The greatest possible order for the functional observer is \(n-m\), which is the order of the Cumming-Gopinath observer [5, 10].

  • The triplet (A, C, F) is functional observable or at least functional detectable [6, 9, 14, 22]. If this condition does not hold, then it is not possible to design a functional observer for this triplet.

To reconstruct the function, \(\upsilon (k)\), the following Luenberger observer structure of order q, \(q\mathrm{{ }} \le \mathrm{{ }}(n - p)\), is proposed:

$$\begin{aligned} \begin{array}{l} z\left( k+1 \right) = Lz\left( k \right) + Vu\left( k \right) + Py\left( k \right) \\ {\hat{v}}\left( k \right) = Hz\left( k \right) + Gy\left( k \right) \end{array} \end{aligned}$$
(19)

where z(k) is the q-dimensional state vector and \({\hat{v}}\left( k \right) \in \mathbb {R}^{l}\) is the estimate of \(\upsilon (k)\). The observer matrices \(L \in \mathbb {R}^{(q \times q)}\), \(V\in \mathbb {R}^{(q \times p)}\), \(P\in \mathbb {R}^{(q \times m)}\), \(H\in \mathbb {R}^{(l \times q)}\) and \(G\in \mathbb {R}^{(l \times m)}\) are determined such that:

$$\begin{aligned} \mathop {\lim }\limits _{\mathrm{{k}} \rightarrow \infty } \left( {\upsilon \left( k \right) - {\hat{v}}\left( k\right) } \right) = 0 \end{aligned}$$
(20)

The linear functional observer structure is given in Figure 6.

Fig. 6
figure 6

Discrete linear functional observer structure

Full size image

4.1 Existence conditions

Theorem 1

The observable system (19) is an asymptotic observer of linear functional (18) if and only if there exists a \((q \times n)\) matrix T solution of the equations:

$$\begin{aligned} V= & {} T B \end{aligned}$$
(21)
$$\begin{aligned} T A - L T= & {} P C \end{aligned}$$
(22)
$$\begin{aligned} L= & {} H T +G C \end{aligned}$$
(23)

and the matrix L is Schur, namely when all the absolute value of the eigenvalues are less than one.

4.2 The direct approach to design linear functional observers

Let us define \(\nu\) as the smallest integer such that:

$$\begin{aligned} {r_\nu }= \mathrm{{rank}}\left( {{\Sigma _\nu }} \right) - \mathrm{{rank}}\left( {\left[ {\begin{array}{*{20}{c}} {F{A^{\nu }}}\\ {{\Sigma _\nu }} \end{array}} \right] } \right) = 0 \end{aligned}$$
(24)

where

$$\begin{aligned} \begin{array}{l} {\Sigma _\nu } = \left[ {\begin{array}{*{20}{c}} {C{{A}^\nu }}\\ {F{{A}^{\nu - 1}}}\\ {C{{A}^{\nu - 1}}}\\ \vdots \\ {F{{A}}}\\ {C{{A}}}\\ {F}\\ {C} \end{array}} \right] \;\mathrm{{~~if}}\;\nu > 0,\;\\ {\Sigma _\nu } = C\;for\;\;\nu = 0 \end{array} \end{aligned}$$
(25)

The hypothesis (24) can always be fulfilled using Cayley-Hamilton theorem [32] for every \(k \ge {k_0}\).

After \(\mu = 0,\mathrm{{ ~}}1,\mathrm{{~ }}2 \ldots\) phase-advanced of \(\upsilon (k) = Fx(k)\), we obtain:

$$\begin{aligned} \begin{array}{*{20}{l}} {\upsilon (k + \mu ) = F{A^\mu }x(k)} {+ F\sum \limits _{j = 0}^{\mu - 1} {{A^{\mu - 1 - j}}Bu(k + j)} } \end{array} \end{aligned}$$
(26)

From Equation (24), it can be deduced that \({F{A^\nu }}\) is a function of \({\Sigma _\nu }\). Then, there exist the matrices \({L_{C,i}},\mathrm{{ ~}}i = 0 \ldots \nu\) and \({L_{F,i}},\mathrm{{~ }}i = 0 \ldots \nu - 1\) such that:

$$\begin{aligned} \begin{array}{l} F{A^\nu } = \sum \limits _{i = 0}^\nu {{L_{C,i}}C{A^i}} + \sum \limits _{i = 0}^{\nu - 1} {{L_{F,i}}F{A^i}} \end{array} \end{aligned}$$
(27)

From the previous equation, the following linear equation can be written:

$$\begin{aligned} F(k + \nu ){A^\nu } = \Phi (k){\Sigma _\nu }(k)\end{aligned}$$
(28)

where \(\Phi\) is a \(\left( {l \times \rho } \right)\) matrix, \(\rho = m + \nu \left( {l + m} \right)\), \(\Phi\) can be written as:

$$\begin{aligned} \Phi = {\left[ {\begin{array}{*{20}{c}} {{L_{C,\nu }}}\\ {{L_{F,\nu - 1}}}\\ {{L_{C,\nu - 1}}}\\ \vdots \\ {{L_{F,0}}}\\ {{L_{C,0}}} \end{array}} \right] ^T} \end{aligned}$$
(29)

For \(\mu = \nu\), the equation (26) can be written as:

$$\begin{aligned} \begin{array}{l} \upsilon \left( {k + \nu } \right) = \sum \limits _{i = 0}^\nu {{L_{C,i}}C{A^i}x\left( k \right) } + \sum \limits _{i = 0}^{\nu - 1} {{L_{F,i}}F{A^i}x\left( k \right) } \\ \mathrm{{~~~~~~~~~~~~~~}} + F\sum \limits _{j = 0}^{\nu - 1} {{A^{\nu - 1 - j}}Bu(k + j)} \end{array}\end{aligned}$$
(30)

To eliminate the state x(k) from equation (30), let’s consider the successive shift forward of \(\upsilon \left( k \right) = F x\left( k \right)\) and \(y\left( k \right) =Cx\left( k \right)\):

  • For \(i=1\) to \(\nu -1\),

    $$\begin{aligned} \begin{array}{l} F{A^i}x(k) = \upsilon (k + i)-F\sum \limits _{j = 0}^{i - 1} {{A^{i - 1 - j}}Bu(k + j)} \end{array} \end{aligned}$$
    (31)

  • For \(i=1\) to \(\nu\),

    $$\begin{aligned} \begin{array}{l} C{A^i}x(k) = y(k + i) - C\sum \limits _{j = 0}^{i - 1} {{A^{i - 1 - j}}Bu(k + j)} \end{array} \end{aligned}$$
    (32)

By replacing (31) and (32) in (30), we get:

$$\begin{aligned} \begin{array}{l} \upsilon (k + \nu ) = \sum \limits _{i = 0}^{\nu - 1} {{L_{F,i}}} \upsilon (k + i) + \sum \limits _{i = 0}^\nu {{L_{C,i}}} y(k + i)\\ \mathrm{{~~~~~~~~~~~~~~}} + \sum \limits _{i = 0}^{\nu - 1} {{V_i}} u(k + i) \end{array}\end{aligned}$$
(33)

where for \(\nu \ge 2\) and \(j=0\) to \(\nu -2\):

$$\begin{aligned} \begin{array}{l} {V_j} = \left( {F{A^{\nu - 1 - j}} - \sum \limits _{i = j + 1}^{\nu - 1} {{L_{F,i}}F{A^{i - 1 - j}}} } \right. \\ \left. {\mathrm{{~~~~~~~~ }} - \sum \limits _{i = j + 1}^\nu {{L_{C,i}}C{A^{i - 1 - j}}} } \right) B \end{array} \end{aligned}$$
(34)

and

\(\begin{array}{l} {V_{\nu - 1}} = \left( {F - {L_{C,\nu }}C} \right) B. \end{array}\)

The equation (33) can be written as:

$$\begin{aligned}\begin{array}{*{20}{l}} {\upsilon (k) = {L_{C,\nu }}y(k) + }\\ {\;\;\;\;\;{{{\bar{q}}}^{ - 1}}\left[ {{L_{F,\nu - 1}}\upsilon (k) + {L_{F,\nu - 1}}y(k) + {V_{\nu - 1}}u(k)} \right. + }\\ {\;\;\;\;\; \vdots }\\ {\;\;\;\;\;{{{\bar{q}}}^{ - 1}}\left[ {{L_{F,1}}\upsilon (k) + {L_{C,1}}y(k) + {V_1}u(k)} \right. + }\\ {\;\;\;\;\;{{{\bar{q}}}^{ - 1}}\left. {\left[ {{L_{F,0}}\upsilon (k) + {L_{C,0}}y(k) + {V_0}u(k)} \right] \cdots } \right] } \end{array}\end{aligned}$$

where \({{\bar{q}}}\) stands for the shift forward operator and \(\bar{q}^{-1}\) for the delay operator in a discrete-time formulation.

Let us denote the vectors:

\({z_i}(k) = {{{\bar{q}}}^{ - 1}}\left[ {{L_{F,0}}\upsilon (k) + {L_{C,0}}y(k) + {V_0}u(k)} \right]\), \(\mathrm{{for}}\;i = 0\)

\({z_i}(k) = {{{\bar{q}}}^{ - 1}}\left[ {{L_{F,i}}\upsilon (k) + {L_{C,i}}y(k) + {V_i}u(k) + {z_{i - 1}}} \right]\), for \({i = 1\;\mathrm{{to}}\;\nu - 1\;}\)

With \(\upsilon (k) = {z_{\nu - 1}}(k) + {F_{C,\nu }}y(k)\), we obtain:

$$\begin{aligned} \begin{array}{*{20}{l}} {{z_0}(k + 1) = {L_{F,0}}{z_{\nu - 1}}(k) + {P_{C,0}}y(k) + {V_0}u(k)}\\ \begin{array}{l} {z_1}(k + 1) = {L_{F,1}}{z_{\nu - 1}}(k) + {P_{C,1}}y(k) + {V_1}u(k) + {z_0}(k) \end{array}\\ \vdots \\ \begin{array}{*{20}{l}} \begin{array}{l} {z_{\nu - 1}}(k + 1) = {L_{F,\nu - 1}}{z_{\nu - 1}}(k) + {P_{C,\nu - 1}}y(k)\\ \mathrm{{~~~~~~~~~~~~~~~~~~}} + {V_{\nu - 1}}u(k) + {z_{\nu - 2}}(k) \end{array} \end{array} \end{array} \end{aligned}$$
(35)

where the matrices \({P_{C,i}}\) for \(i=0\) to \(\nu - 1\) are given by:

$$\begin{aligned}{P_{C,i}} = {L_{C,i}}+ {L_{F,i}}{L_{C,\nu }}\mathrm{{ ~for~ }}i = 0\mathrm{{~ to~ }}\nu - 1\end{aligned}$$

Let us introduce the vector \(z(k) = {\left[ {\begin{array}{*{20}{c}} {z_0^T(k)}&\cdots&{z_{\nu - 1}^T(k)} \end{array}} \right] ^T}\), the input-output recurrence equation (35) can be realised as the state space observable system (19) where

$$\begin{aligned} \begin{array}{*{20}{l}} {L = \left[ {\begin{array}{*{20}{c}} {}&{}{}&{}{}&{}{}&{}{{L_{F,0}}}\\ {{I_l}}&{}{}&{}{}&{}{}&{}{{L_{F,1}}}\\ {}&{} \ddots &{}{}&{}{}&{}{}\\ {}&{}{}&{}{{I_l}}&{}{}&{}{{L_{F,\nu - 2}}}\\ {}&{}{}&{}{}&{}{{I_l}}&{}{{L_{F,\nu - 1}}} \end{array}} \right] ,V = \left[ {\begin{array}{*{20}{c}} {{V_0}}\\ {{V_1}}\\ \vdots \\ {{V_{\nu - 2}}}\\ {{V_{\nu - 1}}} \end{array}} \right] }\\ {P = \left[ {\begin{array}{*{20}{c}} {{L_{C,0}}}\\ {{L_{C,1}}}\\ \vdots \\ {{L_{C,\nu - 2}}}\\ {{L_{C,\nu - 1}}} \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} {{L_{F,0}}}\\ {{L_{F,1}}}\\ \vdots \\ {{L_{F,\nu - 2}}}\\ {{L_{F,\nu - 1}}} \end{array}} \right] {F_{C,\nu }}}\\ {H = \left[ {\begin{array}{*{20}{c}} 0&{} \cdots &{}0&{}{{I_l}} \end{array}} \right] ,G = {L_{C,\nu }}} \end{array}\end{aligned}$$
(36)

If L is a Schur matrix then the observer (19) is an asymptotic observer of \(\upsilon (k)\). Now, finding the stable functional observer depends on the resolution of the linear equation (28) and then the decomposition of \(\Phi\).

The solution set of the linear equation (28) is given by:

$$\begin{aligned} \Phi = F{A^\nu }\Sigma _\nu ^{\left[ 1 \right] } + \Omega \left( {{I_\rho } - {\Sigma _\nu }\Sigma _\nu ^{\left[ 1 \right] }} \right) \end{aligned}$$
(37)

where \(\Omega\) is an arbitrary \(\left( {l \times \rho } \right)\) matrix and \({\Sigma _\nu ^{\left[ 1 \right] }}\) is a generalized inverse of \({\Sigma _\nu }\) given by [4]:

$$\begin{aligned} \Sigma _\nu ^{\left[ 1 \right] } \in \left\{ {X \in {R^{\left( {n \times \rho } \right) }},{\Sigma _\nu }X{\Sigma _\nu } = {\Sigma _\nu }} \right\} \end{aligned}$$
(38)

For single functional observers (case \(l = 1\)), the proposed method leads to the minimum functional observer [21]. However, for multiple functional observers (case \(l > 1\)), the resulting order observer does not necessarily represent the minimum possible order. When theorem 1 is fulfilled, the order of the designed observer is \(\nu l\). The stable observer order could be even greater than n or \(n-m\). That’s why a reduction of the observer order is required to obtain a stable minimal observer.

5 Controller design for BBT system

Considering the plant’s and actuator’s modeling method in section 2. \(K _ { M }\) is determined as 100 and \(\tau\) is calculated as 0.01. After the calculations, motor transfer function is obtained as below:

$$\begin{aligned} G_{M}(s) = \frac{ 100 }{ 0.01 s + 1 } \end{aligned}$$
(39)

then the transfer function of system is given by:

$$\begin{aligned} G_{sys}=\left( {\begin{array}{*{20}{c}} {\frac{{100}}{{0.01s + 1}} \times \frac{1}{{{s^2}}}}&{}0\\ 0&{}{\frac{{100}}{{0.01s + 1}} \times \frac{{1.255}}{{{s^2}}}} \end{array}} \right) \end{aligned}$$

For the sampling period \(T=0.004s\), the discrete state space representation in the form (13) is obtained:

$$\begin{aligned}\begin{array}{l} A = \left( {\begin{array}{*{20}{c}} {0.6703}&{}0&{}0&{}0&{}0&{}0\\ {0.0033}&{}1&{}0&{}0&{}0&{}0\\ 0&{}{0.004}&{}1&{}0&{}0&{}0\\ 0&{}0&{}0&{}{0.6703}&{}0&{}0\\ 0&{}0&{}0&{}{0.0033}&{}1&{}0\\ 0&{}0&{}0&{}0&{}{0.004}&{}1 \end{array}} \right) \\ B = \left( {\begin{array}{*{20}{c}} {0.422}&{}0\\ {0.0009}&{}0\\ 0&{}0\\ 0&{}{0.422}\\ 0&{}{0.0009}\\ 0&{}0 \end{array}} \right) ,C = \left( {\begin{array}{*{20}{l}} 0&{}0&{}{78.1250}&{}0&{}0&{}0\\ 0&{}0&{}0&{}0&{}0&{}{98.0469} \end{array}} \right) \end{array}\end{aligned}$$

To start the design, we have to choose the following stable closed-loop poles:

$$\begin{aligned}Poles = \left( {\begin{array}{*{20}{l}} {0.9637 + 0.0001i}\\ {0.9637 - 0.0001i}\\ {0.9639 + 0.0001i}\\ {0.9639 - 0.0001i}\\ {0.9640 + 0.0001i}\\ {0.9640 - 0.0001i} \end{array}} \right) \end{aligned}$$

The controller gain F, which assigns the above closed-loop poles is calculated by using the pole-assignment routine. The result is :

$$\begin{aligned}F = \left( {\begin{array}{*{20}{l}} { - 0.5293}&{}{2.2909}&{}{6.9838}&{}0&{}{ - 0.0002}&{}{ - 0.0010}\\ 0&{}{ - 0.0001}&{}{ - 0.0003}&{}{ - 0.5293}&{}{2.2917}&{}{6.9879} \end{array}} \right) \end{aligned}$$

and

$$\begin{aligned}{N_C} = \left( {\begin{array}{*{20}{c}} {\mathrm{{0}}\mathrm{{.1858}}}&{}\mathrm{{0}}\\ \mathrm{{0}}&{}{\mathrm{{0}}\mathrm{{.1480}}} \end{array}} \right) \end{aligned}$$

Now, our focus is on the design of the functional observer. The first step deals with the determination of \(\nu\). From (24), \({r_1}(k)=0\) thus we deduce \(\nu =1\) and as the arbitrary matrix can be written as follows:

$$\begin{aligned} \Omega = \left( {\begin{array}{*{20}{c}} {\mathrm{{ - 0}}\mathrm{{.4}}}&{}{\mathrm{{0}}\mathrm{{.3}}}&{}{\mathrm{{ - 0}}\mathrm{{.6}}}&{}1&{}{\mathrm{{ - 0}}\mathrm{{.5}}}&{}0\\ {\mathrm{{ - 0}}\mathrm{{.4}}}&{}{0.3}&{}{\mathrm{{ - 0}}\mathrm{{.6}}}&{}1&{}{\mathrm{{ - 0}}\mathrm{{.5}}}&{}0 \end{array}} \right) \end{aligned}$$
(40)

we obtain from (37):

$$\begin{aligned} {L_{C,0}} = \left[ {\begin{array}{*{20}{r}} { - 2.5612}&{}{0.0002}\\ {0.0001}&{}{ - 2.0417} \end{array}} \right] \end{aligned}$$
(41)
$$\begin{aligned} {L_{C,1}}= & {} \left[ {\begin{array}{*{20}{r}} {2.5918}&{}{ - 0.0002}\\ { - 0.0001}&{}{2.0660} \end{array}} \right] \end{aligned}$$
(42)
$$\begin{aligned} {L_{F,0}}= & {} \left[ {\begin{array}{*{20}{l}} {0.6586}&{}0\\ 0&{}{0.6586} \end{array}} \right] \end{aligned}$$
(43)

Following (36), the second step consists in the definition of \(L=L_{F,0}\). Thus, F is asymptotically stable and we can design a second-order Luenberger asymptotically stable observer for the linear functional Fx(k). The observer parameters are obtained with the third step. Applying the formula (36), we get:

$$\begin{aligned} \begin{array}{*{20}{l}} {P = \left[ {\begin{array}{*{20}{r}} { - 0.8542}&{}{0.0001}\\ 0&{}{ - 0.6809} \end{array}} \right] }\\ {\begin{array}{*{20}{l}} {V = \left[ {\begin{array}{*{20}{l}} { - 0.2215}&{}0\\ 0&{}{ - 0.2215} \end{array}} \right] ,H = \left[ {\begin{array}{*{20}{c}} 1&{}0\\ 0&{}1 \end{array}} \right] ,}\\ {G = \left[ {\begin{array}{*{20}{r}} {2.5918}&{}{ - 0.0002}\\ { - 0.0001}&{}{2.0660} \end{array}} \right] } \end{array}} \end{array}\end{aligned}$$
(44)

6 Experimental results

Fig. 7
figure 7

The system’s experimental results are shown in Figure 7 and 8. Real-time and reference signals of the state feedback controller using the linear functional observer

Full size image
Fig. 8
figure 8

The control input of servomotors

Full size image

It is clear, in Figure 7 that the experimental output signals of the ball balancing table follow the reference trajectories with good performances. The results show also that the control law obtained by using the functional observer, allows to obtain high performances with an error which starts from the prescribed initial value and quickly goes to zero.

The motor angles provide an amplitude saturation outside the range \([ - {45^ \circ }, + {45^ \circ }]\). In this paper, the stabilization problems during the saturation period have been fulfilled experimentally according to the dynamics of the system. As a perspective of this work, the stability analysis problem for the systems with input saturation will be addressed. For several decades, the stability analysis or stabilization problems of control systems with saturation have attracted extensive attention in the research community and they still constitute an open source of both theoretical and practical problems (see, e.g., [26, 28, 29, 33, 35]).

7 Conclusion

A functional observer with a minimum order, designed for time-invariant discrete-time linear systems, was determined by applying the direct procedure. To evaluate this procedure, a state feedback controller based on a multifunctional observer is implemented in a control laboratory experiment.

Compared to full order observer, some interesting functional observer features can be deduced. On the one hand, the functional observer designer is free to choose the states to be estimated. On the other hand, the number of state variables reconstructed using a functional observer is lower than that using a full order observer. As it is mentioned in section 5, the two inputs, two outputs, sixth-order BBT system require only a second-order functional observer, while it requires a sixth-order Kalman observer or a fourth-order Cumming–Gopinath observer. Designing the minimum observer has the advantages of reducing the observer calculation time. Compared to [4], the reduction of the observer establishment time, in such a way as to allow estimating the two system states before the controller stabilizes them, is not required when using the functional observer since it needs to construct only one BBT system state. Let us note that to simplify the calculation, the model in [19] takes into consideration only the ball dynamics.

In further works, the development conditions of matrix \(\Omega\) leading to an asymptotic observer with minimal dimension as well as the extension of the direct approach to the unknown disturbance input linear observers will be considered.