Solving time-fractional Navier–Stokes equations using homotopy perturbation Elzaki transform

Abstract

In this article, a hybrid technique called homotopy perturbation Elzaki transform method has been applied to solve Navier–Stokes equation of fractional order. In the hybrid technique, homotopy perturbation method and Elzaki transform method are amalgamated. Three example problems are solved with a purpose to validate and demonstrate the efficacy of the present method. It is also demonstrated that the results obtained from the present method are in excellent agreement with the results by other methods. It is shown that the proposed method is found to be reliable, efficient and easy to implement for various related problems of science and engineering.

1 Introduction

Fractional calculus is an important branch of applied mathematics which deals with the differential and integral operators with non-integral powers. Fractional calculus has become popular due to its demonstrated wide range of application in rheology, viscoelasticity, electrochemistry, electromagnetism, fluid mechanics etc. For details, one may see the monographs of Kilbas et al. [1], some fundamental works on various aspects of fractional calculus are given by Kiryakova [2], Lakshmikantham and Vatsala [3], Miller and Ross [4] and the solutions method of differential equations of arbitrary real order and applications of the described methods in various fields are given by Podlubny [5]. In recent years, many analytical and approximate methods for solving fractional differential equations have been developed such as differential transform method [6, 7], finite difference method (FDM) [8], Adomian decomposition method (ADM) [9, 10], homotopy perturbation method (HPM) [11,12,13], Haar wavelet method (HWM) [14, 15], differential transform method (DTM) [16,17,18], variational iteration method (VIM) [19] and many others. Among all the above-listed methods, homotopy perturbation method which was first proposed by the Chinese researcher J.H. He in 1998 plays an important role. This is due to the fact that it addresses a problem directly without the need for any form of transformation, linearization and discrimination. Elzaki Transform (ET) is a new integral transform which was introduced by Tarig ELzaki in 2010. ET is modified transform of Sumudu and Laplace transforms. It is worth mentioning that there are some differential equations with variable coefficients which may not be solved by Sumudu and Laplace transforms but may easily be solved with the aid of ET. Fractional nonlinear differential equations have been solved by various authors [20] by means of the combination of ET and ADM. As regards, Klein-Gordon equations were solved by the authors [21] by amalgamation of ET and iterative method. Further, non-linear partial differential equations are also solved by different authors [22, 23] using modified HPM.

The primary equation of movement of viscous fluid flow known as the NS equation has been presented in 1822 [24]. This equation portrays a few projections which include sea streams, fluid stream in channels, bloodstream and wind current around the wings of an airship. The NS equation was first carried out in 2005 in the fractional form in [25] by El-Shahed and Salem. The classical NS equation was answered by El-Shahed and Salem [25] by means of laplace transform (LT), finite Hankel transforms (FHT) and Fourier sine transform. A nonlinear fractional NS equation was solved analytically by Kumar et al. [26] by the combination of HPM with LT algorithm. Also the same NS equation was resolved by Ragab et al. [27] and Ganji et al. [28] by adopting homotopy analysis method. ADM was adopted by Birajdar [29] and Momani et al. [30] for the solution of fractional NS equation. Sunil Kumar et al. [31] achieved the analytical result of fractional NS equation by means of ADM and LT algorithm while Chaurasia and Kumar [32] solved the similar equation by the pairing of LT with FHT. The present paper gives an exact or approximate solution for the proposed problem by using HPETM.

This article is planned as follows: some basic features of fractional calculus related to the titled problems have been presented in Sect. 2. Elzaki transform and elaborated form of the HPETM have been included in Sects. 3 and 4 respectively. In Sect. 5, three example problems are included to validate the effectiveness and exactness of the proposed method. Lastly, a conclusion is given in Sect. 6.

2 Basic features of fractional calculus

Definition 2.1

The operator $D^{\alpha }$ of order $\alpha$ in Abel–Riemann (A–R) sense is defined as [4, 5, 40]

$$D^{\alpha } u(x) = \left\{ {\begin{array}{ll} {\frac{{d^{m} }}{{dx^{m} }}u\left( x \right),} & {\alpha = m} \\ {\frac{1}{\varGamma (m - \alpha )}\frac{d}{{dx^{m} }}\int\limits_{0}^{x} {\frac{u(t)}{{(x - t)^{\alpha - m + 1} }}} dt,} & {m - 1 < \alpha < m} \\ \end{array} } \right.$$

(1)

where $m \in Z^{ + } ,\;\alpha \in R^{ + }$ and

$$D^{ - \alpha } u\left( x \right) = \frac{1}{\varGamma \left( \alpha \right)}\int\limits_{0}^{x} {\left( {x - t} \right)^{\alpha - 1} u\left( t \right)} \,dt,\,\,\,0 < \alpha \le 1$$

(2)

Definition 2.2

The A–R fractional order integration operator $J^{\alpha }$ is described as [4, 5]

$$J^{\alpha } u\left( x \right) = \frac{1}{\varGamma \left( \alpha \right)}\int\limits_{0}^{x} {\left( {x - t} \right)^{\alpha - 1} u\left( t \right)} \,dt,\;t > 0\;\alpha > 0$$

(3)

Following Podlubny [5] we may have

$$J^{\alpha } t^{n} = \frac{{\varGamma \left( {n + 1} \right)}}{{\varGamma \left( {n + \alpha + 1} \right)}}t^{n + \alpha }$$

(4)

$$D^{\alpha } t^{n} = \frac{{\varGamma \left( {n + 1} \right)}}{{\varGamma \left( {n - \alpha + 1} \right)}}t^{n - \alpha }$$

(5)

Definition 2.3

The operator $D^{\alpha }$ of order $\alpha$ in Caputo sense is defined as [5, 33, 39]

$$^{C}D^{\alpha } u(x) = \left\{ {\begin{array}{ll} {\frac{1}{{\Gamma (m - \alpha )}}\int\limits_{0}^{x} {\frac{{u^{m} (t)}}{{(x - t)^{{\alpha - m + 1}} }}} dt,} & {m - 1 < \alpha < m,} \\ {\frac{{d^{m} }}{{dt^{m} }}u\left( x \right),} & {\alpha = m} \\ \end{array} } \right.$$

(6)

Definition 2.4

[4, 5, 33, 34]:

• (a)
  $$D_{t}^{\alpha } J_{t}^{\alpha } f\left( t \right) = f\left( t \right)$$
• (b)
  $$J_{t}^{\alpha } D_{t}^{\alpha } f\left( t \right) = f\left( t \right) - \sum\limits_{k = 0}^{m} {f^{\left( k \right)} \left( {0^{ + } } \right)} \frac{{t^{k} }}{k!},\;{\text{for}}\;t > 0,\;{\text{and}}\;m - 1 < \alpha \le m,m \in N.$$

  (7)

3 Elzaki transform (ET)

The definition of modified Sumudu transform or ET of the function $f\left( t \right)$ is defined as

$$E\left[ {f\left( t \right)} \right] = F\left( q \right) = q\int\limits_{0}^{\infty } {f\left( t \right)e^{{\frac{ - t}{q}}} } dt,\;t > 0$$

(8)

The Elzaki transform is very effective and powerful method for solving integral equation which cannot be solved by the Sumudu transform method. For this, one may see the Ref. [35].

Integration by parts in Eq. (8) can be used in order to find ET of partial derivatives as follows [35].

• 1.
  $$E\left[ {\frac{{\partial f\left( {x,t} \right)}}{\partial t}} \right] = \frac{1}{q}F\left( {x,q} \right) - q\,f\left( {x,0} \right)$$
• 2.
  $$E\left[ {\frac{{\partial^{2} f\left( {x,t} \right)}}{{\partial t^{2} }}} \right] = \frac{1}{{q^{2} }}F\left( {x,q} \right) - f\left( {x,0} \right) - q\frac{{\partial f\left( {x,0} \right)}}{\partial t}$$
• 3.
  $$E\left[ {\frac{{\partial f\left( {x,t} \right)}}{\partial x}} \right] = \frac{d}{dx}F\left( {x,q} \right)$$
• 4.
  $$E\left[ {\frac{{\partial^{2} f\left( {x,t} \right)}}{{\partial x^{2} }}} \right] = \frac{{d^{2} }}{{dx^{2} }}F\left( {x,q} \right).$$

3.1 ET of Caputo fractional derivative

Theorem 1 ([36])

If $G\left( s \right)$ is the Laplace transform of $f\left( t \right)$ then ET $F\left( q \right)$ of $f\left( t \right)$ is given by

$$F\left( q \right) = qG\left( {\frac{1}{q}} \right)$$

(9)

Theorem 2 ([36])

If $F\left( q \right)$ is the ET of the function $f\left( t \right)$ then

$$E\left[ {D^{\alpha } f\left( t \right)} \right] = \frac{F\left( q \right)}{{q^{\alpha } }} - \sum\limits_{k = 0}^{n - 1} {q^{k - \alpha + 2} f^{\left( k \right)} \left( 0 \right)} ,\;n - 1 < \alpha \le n$$

(10)

4 Homotopy perturbation Elzaki transform method (HPETM)

In order to clarify the idea of HPETM, the fractional order nonlinear non-homogeneous partial differential equation with initial condition (IC) is consider as below

$$D_{t}^{\alpha } f\left( {x,y,z,t} \right) + Rf\left( {x,y,z,t} \right) + Nf\left( {x,y,z,t} \right) = g\left( {x,y,z,t,} \right),\;0 < \alpha \le 1$$

(11)

$$f\left( {x,y,z,0} \right) = h\left( {x,y,z} \right)$$

(12)

where $D_{t}^{\alpha } f\left( {x,y,z,t} \right)$ is the derivative of $f\left( {x,y,z,t} \right)$ in Caputo sense, $R,N$ are the linear and nonlinear differential operators and $g\left( {x,y,z,t} \right)$ is the source term.

Now by taking ET on both sides of Eq. (11), we have

$$E\left[ {D_{t}^{\alpha } f\left( {x,y,z,t} \right) + Rf\left( {x,y,z,t} \right) + Nf\left( {x,y,z,t} \right)} \right] = E\left[ {g\left( {x,y,z,t} \right)} \right]$$

(13)

Using differentiation property of ET, we obtain

$$E\left\{ {f\left( {x,y,z,t} \right)} \right\} = \sum\limits_{k = 0}^{n - 1} {q^{k + 2} f^{\left( k \right)} \left( 0 \right) + } q^{\alpha } \left[ {E\left\{ {g\left( {x,y,z,t} \right)} \right\} - E\left\{ {Rf\left( {x,y,z,t} \right) + Nf\left( {x,y,z,t} \right)} \right\}} \right]$$

(14)

Applying inverse Elzaki transform on both sides of Eqs. (14) and (12), we find

$$f\left( {x,y,z,t} \right) = G\left( {x,y,z,t} \right) - E^{ - 1} \left[ {q^{\alpha } \left[ {E\left\{ {Rf\left( {x,y,z,t} \right) + Nf\left( {x,y,z,t} \right)} \right\}} \right]} \right]$$

(15)

where $G\left( {x,y,z,t} \right)$ represents the term coming from initial condition and source term.

Now, by applying HPM to the Eq. (15), we get

$$f\left( {x,y,z,t} \right) = G\left( {x,y,z,t} \right) - p\left( {E^{ - 1} \left[ {q^{\alpha } \left[ {E\left\{ {Rf\left( {x,y,z,t} \right) + Nf\left( {x,y,z,t} \right)} \right\}} \right]} \right]} \right) .$$

(16)

The homotopy parameter $p$ is used to expand the solution as

$$f\left( {x,y,z,t} \right) = \sum\limits_{n = 0}^{\infty } {p^{n} f_{n} \left( {x,y,z,t} \right)}$$

(17)

and the nonlinear term is decomposed as

$$Nf\left( {x,y,z,t} \right) = \sum\limits_{n = 0}^{\infty } {p^{n} H_{n} \left( f \right)}$$

(18)

where $H_{n} \left( f \right)$ is He’s polynomials and is given by

$$H_{n} \left( {f_{0} ,f_{1} , \ldots ,f_{n} } \right) = \frac{1}{n!}\frac{\partial }{{\partial p^{n} }}\left[ {N\left( {\sum\limits_{n = 0}^{\infty } {p^{n} f_{n} } } \right)} \right].$$

(19)

Substituting Eqs. (17) and (18) in Eq. (16), we get

$$\sum\limits_{n = 0}^{\infty } {p^{n} f_{n} \left( {x,y,z,t} \right)} = G\left( {x,y,z,t} \right) - p\left( {E^{ - 1} \left[ {q^{\alpha } \left[ {E\left\{ {R\sum\limits_{n = 0}^{\infty } {p^{n} f_{n} \left( {x,y,z,t} \right)} + N\sum\limits_{n = 0}^{\infty } {p^{n} H_{n} \left( f \right)} } \right\}} \right]} \right]} \right)$$

(20)

Comparing the coefficient of equal powers of $p$ from both sides of above equation, the following equations are obtained

$$\begin{aligned} & p^{0} :f_{0} \left( {x,y,z,t} \right) = G\left( {x,y,z,t} \right), \\ & p^{1} :f_{1} \left( {x,y,z,t} \right) = E^{ - 1} \left[ {q^{\alpha } \left[ {E\left\{ {Rf_{0} \left( {x,y,z,t} \right) + H_{0} \left( f \right)} \right\}} \right]} \right] \\ &p^{2} :f_{2} \left( {x,y,z,t} \right) = E^{ - 1} \left[ {q^{\alpha } \left[ {E\left\{ {Rf_{1} \left( {x,y,z,t} \right) + H_{1} \left( f \right)} \right\}} \right]} \right] \\ \end{aligned}$$

Continuing in this manner we may find $f_{n} \left( {x,y,z,t} \right)$ and then the solution is written as

$$f\left( {x,y,z,t} \right) = f_{1} \left( {x,y,z,t} \right) + f_{2} \left( {x,y,z,t} \right) + f_{3} \left( {x,y,z,t} \right) + \cdots$$

5 Application of HPETM on NS equation

The proposed method is implemented here and then the accuracy of the HPETM is investigated for NS equation. The time fractional NS equation with constant density $\rho$ and kinematic viscosity $v = \frac{\eta }{\rho }$ is given as [24, 29]

$$\left\{ {\begin{array}{ll} {D_{t}^{\alpha } U + \left( {U.\nabla } \right)U = \rho _{0} \nabla ^{2} U - \frac{1}{\rho }\nabla \rho ,} & {\Omega \times \left( {0,T} \right)} \\ {\nabla .U = 0,} & {\Omega \times \left( {0,T} \right)} \\ {U = 0,} & {\Omega \times \left( {0,T} \right)} \\ \end{array} } \right.$$

(21)

where $U = \left( {u,v,w} \right),\,t,\,\rho$ represent the fluid vector, time and pressure respectively. $\eta$ is the dynamic viscosity while the ratio $\rho_{0} = \frac{\eta }{\rho }$ represents the kinematics viscosity. Here $\varOmega = \left( { - \pi ,\pi } \right) \times \left( { - \pi ,\pi } \right)$ is the domain with boundary $\partial \varOmega$. In Cartesian coordinate, Eq. (21) is written as

$$\left\{ \begin{aligned} & D_{t}^{\alpha } u + u\frac{\partial u}{\partial x} + v\frac{\partial u}{\partial y} + w\frac{\partial u}{\partial z} = \rho_{0} \left( {\frac{{\partial^{2} u}}{{\partial x^{2} }} + \frac{{\partial^{2} u}}{{\partial y^{2} }} + \frac{{\partial^{2} u}}{{\partial z^{2} }}} \right) - \frac{1}{\rho }\frac{\partial p}{\partial x}, \\ & D_{t}^{\alpha } v + u\frac{\partial v}{\partial x} + v\frac{\partial v}{\partial y} + w\frac{\partial v}{\partial z} = \rho_{0} \left( {\frac{{\partial^{2} v}}{{\partial x^{2} }} + \frac{{\partial^{2} v}}{{\partial y^{2} }} + \frac{{\partial^{2} v}}{{\partial z^{2} }}} \right) - \frac{1}{\rho }\frac{\partial p}{\partial y}, \\ & D_{t}^{\alpha } w + u\frac{\partial w}{\partial x} + v\frac{\partial w}{\partial y} + w\frac{\partial w}{\partial z} = \rho_{0} \left( {\frac{{\partial^{2} w}}{{\partial x^{2} }} + \frac{{\partial^{2} w}}{{\partial y^{2} }} + \frac{{\partial^{2} w}}{{\partial z^{2} }}} \right) - \frac{1}{\rho }\frac{\partial p}{\partial z}, \\ \end{aligned} \right.$$

(22)

If the value of $p$ is known then all the values of $g_{1} = - \frac{1}{\rho }\frac{\partial p}{\partial x},\,g_{2} = - \frac{1}{\rho }\frac{\partial p}{\partial y}$ and $g_{3} = - \frac{1}{\rho }\frac{\partial p}{\partial z}$ can be determined.

5.1 Numerical examples

Example 1

From Eq. (22), 2-dimensional NS equation of fractional order with $g_{1} = - g_{2} = g$ may be written as

$$\begin{aligned} & D_{t}^{\alpha } u + u\frac{\partial u}{\partial x} + v\frac{\partial u}{\partial y} = \rho_{0} \left( {\frac{{\partial^{2} u}}{{\partial x^{2} }} + \frac{{\partial^{2} u}}{{\partial y^{2} }}} \right) + g, \\ & D_{t}^{\alpha } v + u\frac{\partial v}{\partial x} + v\frac{\partial v}{\partial y} = \rho_{0} \left( {\frac{{\partial^{2} v}}{{\partial x^{2} }} + \frac{{\partial^{2} v}}{{\partial y^{2} }}} \right) - g, \\ \end{aligned}$$

(23)

with IC [37]

$$u\left( {x,y,0} \right) = - \sin \left( {x + y} \right),\,v\,\left( {x,y,0} \right) = \sin \left( {x + y} \right) .$$

(24)

Applying ET on both sides of Eq. (23) with IC (24), we get

$$E\left\{ {u\left( {x,y,t} \right)} \right\} = - q^{2} \sin \left( {x + y} \right) + q^{\alpha } E\left[ {\rho_{0} \left( {\frac{{\partial^{2} u}}{{\partial x^{2} }} + \frac{{\partial^{2} u}}{{\partial y^{2} }}} \right) + g - u\frac{\partial u}{\partial x} - v\frac{\partial u}{\partial y}} \right]$$

(25)

$$E\left\{ {v\left( {x,y,t} \right)} \right\} = q^{2} \sin \left( {x + y} \right) + q^{\alpha } E\left[ {\rho_{0} \left( {\frac{{\partial^{2} v}}{{\partial x^{2} }} + \frac{{\partial^{2} v}}{{\partial y^{2} }}} \right) - g - u\frac{\partial v}{\partial x} - v\frac{\partial v}{\partial y}} \right]$$

(26)

The inverse Elzaki transform of Eqs. (25) and (26) implies that

$$u\left( {x,y,t} \right) = - \sin \left( {x + y} \right) + E^{ - 1} \left[ {q^{\alpha } E\left[ {\rho_{0} \left( {\frac{{\partial^{2} u}}{{\partial x^{2} }} + \frac{{\partial^{2} u}}{{\partial y^{2} }}} \right) + g - u\frac{\partial u}{\partial x} - v\frac{\partial u}{\partial y}} \right]} \right]$$

(27)

$$v\left( {x,y,t} \right) = \sin \left( {x + y} \right) + E^{ - 1} \left[ {q^{\alpha } E\left[ {\rho_{0} \left( {\frac{{\partial^{2} v}}{{\partial x^{2} }} + \frac{{\partial^{2} v}}{{\partial y^{2} }}} \right) - g - u\frac{\partial v}{\partial x} - v\frac{\partial v}{\partial y}} \right]} \right]$$

(28)

Simplifying Eqs. (27) and (28), we get

$$u\left( {x,y,t} \right) = - \sin \left( {x + y} \right) + \frac{{gt^{\alpha } }}{{\varGamma \left( {\alpha + 1} \right)}} + E^{ - 1} \left[ {q^{\alpha } E\left[ {\rho_{0} \left( {\frac{{\partial^{2} u}}{{\partial x^{2} }} + \frac{{\partial^{2} u}}{{\partial y^{2} }}} \right) - u\frac{\partial u}{\partial x} - v\frac{\partial u}{\partial y}} \right]} \right]$$

(29)

$$v\left( {x,y,t} \right) = \sin \left( {x + y} \right) - \frac{{gt^{\alpha } }}{{\varGamma \left( {\alpha + 1} \right)}} + E^{ - 1} \left[ {q^{\alpha } E\left[ {\rho_{0} \left( {\frac{{\partial^{2} v}}{{\partial x^{2} }} + \frac{{\partial^{2} v}}{{\partial y^{2} }}} \right) - u\frac{\partial v}{\partial x} - v\frac{\partial v}{\partial y}} \right]} \right]$$

(30)

Now applying the homotopy perturbation method, we have

$$\sum\limits_{n = 0}^{\infty } {p^{n} u_{n} \left( {x,y,t} \right) = - \sin \left( {x + y} \right) + \frac{{gt^{\alpha } }}{{\varGamma \left( {\alpha + 1} \right)}} + p\left\{ {E^{ - 1} \left[ {q^{\alpha } E\left[ {\sum\limits_{n = 0}^{\infty } {p^{n} H_{n} \left( u \right)} } \right]} \right]} \right\}}$$

(31)

$$\sum\limits_{n = 0}^{\infty } {p^{n} v_{n} \left( {x,y,t} \right) = \sin \left( {x + y} \right) - \frac{{gt^{\alpha } }}{{\varGamma \left( {\alpha + 1} \right)}} + p\left\{ {E^{ - 1} \left[ {q^{\alpha } E\left[ {\sum\limits_{n = 0}^{\infty } {p^{n} H_{n} \left( v \right)} } \right]} \right]} \right\}}$$

(32)

where $H_{n} \left( u \right)$ and $H_{n} \left( v \right)$ are He’s polynomials which signifies the nonlinear terms.

$$\left\{ \begin{aligned} & H_{n} \left( u \right) = p\left[ {\rho_{0} \left( {\frac{{\partial^{2} u}}{{\partial x^{2} }} + \frac{{\partial^{2} u}}{{\partial y^{2} }}} \right) - u\frac{\partial u}{\partial x} - v\frac{\partial u}{\partial y}} \right] = 0 \\ & H_{n} \left( v \right) = p\left[ {\rho_{0} \left( {\frac{{\partial^{2} v}}{{\partial x^{2} }} + \frac{{\partial^{2} v}}{{\partial y^{2} }}} \right) - u\frac{\partial v}{\partial x} - v\frac{\partial v}{\partial y}} \right] = 0 \\ \end{aligned} \right.$$

where

$$\begin{aligned} u = & \,u_{0} + pu_{1} + p^{2} u_{2} + \cdots , \\ v = & \,v_{0} + pv_{1} + p^{2} v_{2} + \cdots , \\ \end{aligned}$$

The first few components of He’s polynomials are given as

$$\left\{ \begin{aligned} & H_{0} \left( u \right) = \rho_{0} \left( {u_{0xx} + u_{0yy} } \right) - u_{0} u_{0x} - v_{0} u_{0y} \\ & H_{0} \left( v \right) = \rho_{0} \left( {v_{0xx} + v_{0yy} } \right) - u_{0} v_{0x} - v_{0} v_{0y} \\ & H_{1} \left( u \right) = \rho_{0} \left( {u_{1xx} + u_{1yy} } \right) - u_{0} u_{1x} - u_{1} u_{0x} - v_{0} u_{1y} - v_{1} u_{0y} \\ & H_{1} \left( v \right) = \rho_{0} \left( {v_{1xx} + v_{1yy} } \right) - u_{0} v_{1x} - u_{1} v_{0x} - v_{0} v_{1y} - v_{1} v_{0y} \\ & \quad \quad \quad \quad \quad \quad \quad \vdots \\ \end{aligned} \right.$$

Using the above He’s polynomials and comparing the coefficients of same power of $p$ in Eqs. (31) and (32) we have

$$\begin{aligned} p^{0} :u_{0} \left( {x,y,t} \right) = & \, - \sin \left( {x + y} \right) + \frac{{gt^{\alpha } }}{{\varGamma \left( {\alpha + 1} \right)}} \\ v_{0} \left( {x,y,t} \right) = & \,\sin \left( {x + y} \right) - \frac{{gt^{\alpha } }}{{\varGamma \left( {\alpha + 1} \right)}} \\ \end{aligned}$$

$$\begin{aligned} p^{1} :u_{1} \left( {x,y,t} \right) = & \,E^{ - 1} \left[ {q^{\alpha } E\left[ {H_{0} \left( u \right)} \right]} \right] = 2\rho_{0} \sin \left( {x + y} \right)\frac{{t^{\alpha } }}{{\varGamma \left( {\alpha + 1} \right)}} \\ v_{1} \left( {x,y,t} \right) = & \,E^{ - 1} \left[ {q^{\alpha } E\left[ {H_{0} \left( v \right)} \right]} \right] = - 2\rho_{0} \sin \left( {x + y} \right)\frac{{t^{\alpha } }}{{\varGamma \left( {\alpha + 1} \right)}} \\ \end{aligned}$$

$$\begin{aligned} p^{2} :u_{2} \left( {x,y,t} \right) = & \,E^{ - 1} \left[ {q^{\alpha } E\left[ {H_{1} \left( u \right)} \right]} \right] = - 4\rho_{0}^{2} \sin \left( {x + y} \right)\frac{{t^{2\alpha } }}{{\varGamma \left( {2\alpha + 1} \right)}} \\ v_{2} \left( {x,y,t} \right) = & \,E^{ - 1} \left[ {q^{\alpha } E\left[ {H_{1} \left( v \right)} \right]} \right] = 4\rho_{0}^{2} \sin \left( {x + y} \right)\frac{{t^{2\alpha } }}{{\varGamma \left( {2\alpha + 1} \right)}} \\ \end{aligned}$$

So the solution $u\left( {x,y,t} \right)$ and $v\left( {x,y,t} \right)$ are written as

$$u\left( {x,y,t} \right) = u_{0} \left( {x,y,t} \right) + u_{1} \left( {x,y,t} \right) + u_{2} \left( {x,y,t} \right) + \cdots = - \sin \left( {x + y} \right)e^{{ - 2\rho_{0} t^{\alpha } }} + \frac{{gt^{\alpha } }}{{\varGamma \left( {\alpha + 1} \right)}}$$

(33)

$$v\left( {x,y,t} \right) = v_{0} \left( {x,y,t} \right) + v_{1} \left( {x,y,t} \right) + v_{2} \left( {x,y,t} \right) + \cdots = \sin \left( {x + y} \right)e^{{ - 2\rho_{0} t^{\alpha } }} - \frac{{gt^{\alpha } }}{{\varGamma \left( {\alpha + 1} \right)}}$$

(34)

For $g = 0,\,\alpha = 1$ Eqs. (33) and (34) reduce to

$$\left\{ \begin{aligned} u\left( {x,y,t} \right) = & \, - \sin \left( {x + y} \right)e^{{ - 2\rho_{0} t}} \\ v\left( {x,y,t} \right) = & \,\sin \left( {x + y} \right)e^{{ - 2\rho_{0} t}} \\ \end{aligned} \right.$$

(35)

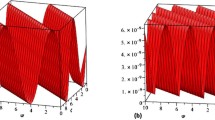
This solution is in good agreement with [37]. The plots of Eq. (35) are depicted in Figs. 1, 2, 3 and 4, for different values of $\alpha = 1,\,\,0.2,\,\,0.4,\,0.6$, $\rho_{0} = 0.5\,,t = 3$. The comparison plots of $U_{0} ,U_{1} ,U_{2} ,U_{3} ,U_{4}$ and $V_{0} ,V_{1} ,V_{2} ,V_{3} ,V_{4}$ with their exact solution (35) for $\alpha = 1$ are depicted in Fig. 5 and solution plots of Example 1 are given in Fig. 6 for different values of $\alpha$.

Fig. 1

Solution plots of Eq. (35) for $\rho_{0} = 0.5,\;t = 3,\;\alpha = 1$ and $g = 0$

Fig. 2

Solution plots of Eq. (35) for $\rho_{0} = 0.5,\;t = 3,\;\alpha = 0.2$ and $g = 0$ (Example 1)

Fig. 3

Solution plots of Eq. (35) for $\rho_{0} = 0.5,\;t = 3,\;\alpha = 0.4$ and $g = 0$ (Example 1)

Fig. 4

Solution plots of Eq. (35) for $\rho_{0} = 0.5,\;t = 3,\;\alpha = 0.6$ and $g = 0$ (Example 1)

Fig. 5

Comparison of the approximate solution $U_{0} ,U_{1} ,U_{2} ,U_{3} ,U_{4}$ and $V_{0} ,V_{1} ,V_{2} ,V_{3} ,V_{4}$ with their exact solution (35) for $\rho_{0} = 0.5,\,x = \frac{\pi }{4},\,y = \frac{\pi }{4}$ (Example 1)

Fig. 6

Solution plots of Eq. (35) for different values of $\alpha$ (Example 1)

Example 2

Consider the NS Eq. (23) with IC [37]

$$u\left( {x,y,0} \right) = - e^{x + y} ,\;v\left( {x,y,0} \right) = e^{x + y}$$

(36)

Applying ET on both sides of Eq. (23) subject to IC (36), we get

$$E\left\{ {u\left( {x,y,t} \right)} \right\} = - q^{2} e^{x + y} + q^{\alpha } E\left[ {\rho_{0} \left( {\frac{{\partial^{2} u}}{{\partial x^{2} }} + \frac{{\partial^{2} u}}{{\partial y^{2} }}} \right) + g - u\frac{\partial u}{\partial x} - v\frac{\partial u}{\partial y}} \right]$$

(37)

$$E\left\{ {v\left( {x,y,t} \right)} \right\} = q^{2} e^{x + y} + q^{\alpha } E\left[ {\rho_{0} \left( {\frac{{\partial^{2} v}}{{\partial x^{2} }} + \frac{{\partial^{2} v}}{{\partial y^{2} }}} \right) - g - u\frac{\partial v}{\partial x} - v\frac{\partial v}{\partial y}} \right]$$

(38)

The inverse Elzaki transform of Eqs. (37) and (38) implies that

$$u\left( {x,y,t} \right) = - e^{x + y} + E^{ - 1} \left[ {q^{\alpha } E\left[ {\rho_{0} \left( {\frac{{\partial^{2} u}}{{\partial x^{2} }} + \frac{{\partial^{2} u}}{{\partial y^{2} }}} \right) + g - u\frac{\partial u}{\partial x} - v\frac{\partial u}{\partial y}} \right]} \right]$$

(39)

$$v\left( {x,y,t} \right) = e^{x + y} + E^{ - 1} \left[ {q^{\alpha } E\left[ {\rho_{0} \left( {\frac{{\partial^{2} v}}{{\partial x^{2} }} + \frac{{\partial^{2} v}}{{\partial y^{2} }}} \right) - g - u\frac{\partial v}{\partial x} - v\frac{\partial v}{\partial y}} \right]} \right]$$

(40)

Simplifying Eqs. (39) and (40), we get

$$u\left( {x,y,t} \right) = - e^{x + y} + \frac{{gt^{\alpha } }}{{\varGamma \left( {\alpha + 1} \right)}} + E^{ - 1} \left[ {q^{\alpha } E\left[ {\rho_{0} \left( {\frac{{\partial^{2} u}}{{\partial x^{2} }} + \frac{{\partial^{2} u}}{{\partial y^{2} }}} \right) - u\frac{\partial u}{\partial x} - v\frac{\partial u}{\partial y}} \right]} \right]$$

(41)

$$v\left( {x,y,t} \right) = e^{x + y} - \frac{{gt^{\alpha } }}{{\varGamma \left( {\alpha + 1} \right)}} + E^{ - 1} \left[ {q^{\alpha } E\left[ {\rho_{0} \left( {\frac{{\partial^{2} v}}{{\partial x^{2} }} + \frac{{\partial^{2} v}}{{\partial y^{2} }}} \right) - u\frac{\partial v}{\partial x} - v\frac{\partial v}{\partial y}} \right]} \right]$$

(42)

Now applying HPM, we have

$$\sum\limits_{n = 0}^{\infty } {p^{n} u_{n} \left( {x,y,t} \right) = - e^{x + y} + \frac{{gt^{\alpha } }}{{\varGamma \left( {\alpha + 1} \right)}} + p\left\{ {E^{ - 1} \left[ {q^{\alpha } E\left[ {\sum\limits_{n = 0}^{\infty } {p^{n} H_{n} \left( u \right)} } \right]} \right]} \right\}}$$

(43)

$$\sum\limits_{n = 0}^{\infty } {p^{n} v_{n} \left( {x,y,t} \right) = e^{x + y} - \frac{{gt^{\alpha } }}{{\varGamma \left( {\alpha + 1} \right)}} + p\left\{ {E^{ - 1} \left[ {q^{\alpha } E\left[ {\sum\limits_{n = 0}^{\infty } {p^{n} H_{n} \left( v \right)} } \right]} \right]} \right\}}$$

(44)

where $H_{n} \left( u \right)$ and $H_{n} \left( v \right)$ are He’s polynomials that denotes the nonlinear terms and are given as

$$\left\{ \begin{aligned} H_{n} \left( u \right) = & \,p\left[ {\rho_{0} \left( {\frac{{\partial^{2} u}}{{\partial x^{2} }} + \frac{{\partial^{2} u}}{{\partial y^{2} }}} \right) - u\frac{\partial u}{\partial x} - v\frac{\partial u}{\partial y}} \right] = 0 \\ H_{n} \left( v \right) = & \,p\left[ {\rho_{0} \left( {\frac{{\partial^{2} v}}{{\partial x^{2} }} + \frac{{\partial^{2} v}}{{\partial y^{2} }}} \right) - u\frac{\partial v}{\partial x} - v\frac{\partial v}{\partial y}} \right] = 0 \\ \end{aligned} \right.$$

where

$$\begin{aligned} u = & \,u_{0} + pu_{1} + p^{2} u_{2} + \cdots , \\ v = & \,v_{0} + pv_{1} + p^{2} v_{2} + \cdots , \\ \end{aligned}$$

The first few components of He’s polynomials are given by

$$\left\{ \begin{aligned} & H_{0} \left( u \right) = \rho_{0} \left( {u_{0xx} + u_{0yy} } \right) - u_{0} u_{0x} - v_{0} u_{0y} \\ & H_{0} \left( v \right) = \rho_{0} \left( {v_{0xx} + v_{0yy} } \right) - u_{0} v_{0x} - v_{0} v_{0y} \\ & H_{1} \left( u \right) = \rho_{0} \left( {u_{1xx} + u_{1yy} } \right) - u_{0} u_{1x} - u_{1} u_{0x} - v_{0} u_{1y} - v_{1} u_{0y} \\ & H_{1} \left( v \right) = \rho_{0} \left( {v_{1xx} + v_{1yy} } \right) - u_{0} v_{1x} - u_{1} v_{0x} - v_{0} v_{1y} - v_{1} v_{0y} \\ & \quad \quad \quad \quad \quad \quad \quad \vdots \\ \end{aligned} \right.$$

Using the above He’s polynomials and comparing the coefficients of same power of $p$ in Eqs. (43) and (44) we have

$$\begin{aligned} p^{0} :u_{0} \left( {x,y,t} \right) = & \, - e^{x + y} + \frac{{gt^{\alpha } }}{{\varGamma \left( {\alpha + 1} \right)}} \\ v_{0} \left( {x,y,t} \right) = & \,e^{x + y} - \frac{{gt^{\alpha } }}{{\varGamma \left( {\alpha + 1} \right)}} \\ \end{aligned}$$

$$\begin{aligned} p^{1} :u_{1} \left( {x,y,t} \right) = & \,E^{ - 1} \left[ {q^{\alpha } E\left[ {H_{0} \left( u \right)} \right]} \right] = - 2\rho_{0} e^{x + y} \frac{{t^{\alpha } }}{{\varGamma \left( {\alpha + 1} \right)}} \\ v_{1} \left( {x,y,t} \right) = & \,E^{ - 1} \left[ {q^{\alpha } E\left[ {H_{0} \left( v \right)} \right]} \right] = 2\rho_{0} e^{x + y} \frac{{t^{\alpha } }}{{\varGamma \left( {\alpha + 1} \right)}}\, \\ \end{aligned}$$

$$\begin{aligned} p^{2} :u_{2} \left( {x,y,t} \right) = & \,E^{ - 1} \left[ {q^{\alpha } E\left[ {H_{1} \left( u \right)} \right]} \right] = - 4\rho_{0}^{2} e^{x + y} \frac{{t^{2\alpha } }}{{\varGamma \left( {2\alpha + 1} \right)}} \\ v_{2} \left( {x,y,t} \right) = & \,E^{ - 1} \left[ {q^{\alpha } E\left[ {H_{1} \left( v \right)} \right]} \right] = 4\rho_{0}^{2} e^{x + y} \frac{{t^{2\alpha } }}{{\varGamma \left( {2\alpha + 1} \right)}} \\ \end{aligned}$$

Then the solution $u\left( {x,y,t} \right)$ and $v\left( {x,y,t} \right)$ are given as

$$u\left( {x,y,t} \right) = u_{0} \left( {x,y,t} \right) + u_{1} \left( {x,y,t} \right) + u_{2} \left( {x,y,t} \right) + \cdots = - e^{x + y} e^{{2\rho_{0} t^{\alpha } }} + \frac{{gt^{\alpha } }}{{\varGamma \left( {\alpha + 1} \right)}}$$

(45)

$$v\left( {x,y,t} \right) = v_{0} \left( {x,y,t} \right) + v_{1} \left( {x,y,t} \right) + v_{2} \left( {x,y,t} \right) + \cdots = e^{x + y} e^{{2\rho_{0} t^{\alpha } }} - \frac{{gt^{\alpha } }}{{\varGamma \left( {\alpha + 1} \right)}}$$

(46)

For $g = 0,\,\alpha = 1$ Eqs. (45) and (46) reduce to

$$\left\{ \begin{aligned} u\left( {x,y,t} \right) = & \, - e^{{x + y + 2\rho_{0} t}} \\ v\left( {x,y,t} \right) = & \,e^{{x + y + 2\rho_{0} t}} \\ \end{aligned} \right.$$

(47)

This solution is same as the solution solved in [29]. The behavior of the solution (47) are depicted in Figs. 7, 8 and 9 for different values of $\alpha = 1,\,0.4,0.8$, $\rho_{0} = 0.5\,,t = 0.05$. The comparison plots of $U_{0} ,U_{1} ,U_{2} ,U_{3} ,U_{4}$ and $V_{0} ,V_{1} ,V_{2} ,V_{3} ,V_{4}$ with their exact solution (47) for $\alpha = 1$ are depicted in Fig. 10 and solution of plots of Example 2 for different values of $\alpha$ are illustrated in Fig. 11

Fig. 7

Solution plots of Eq. (47) for $\rho_{0} = 0.5,\;t = 0.05,\;\alpha = 1$ and $g = 0$ (Example 2)

Fig. 8

Solution plots of Eq. (47) for $\rho_{0} = 0.5,\;t = 0.05,\;\alpha = 0.4$ and $g = 0$ (Example 2)

Fig. 9

Solution plots of Eq. (47) for $\rho_{0} = 0.5,\;t = 0.05,\;\alpha = 0.8$ and $g = 0$ (Example 2)

Fig. 10

Comparison of the approximate solution $U_{0} ,U_{1} ,U_{2} ,U_{3} ,U_{4}$ and $V_{0} ,V_{1} ,V_{2} ,V_{3} ,V_{4}$ with their exact solution (47) for $\rho_{0} = 0.5,\,x = \frac{\pi }{4},\,y = \frac{\pi }{4}$ (Example 2)

Fig. 11

Solution plots of Eq. (47) for different values of $\alpha$ (Example 2)

Example 3

Finally let us consider 3-dimensional NS Eq. (22) with $g_{1} = g_{2} = g_{3} = 0$ with IC [37]

$$u\left( {x,y,z,0} \right) = - \,0.5x + y + z,\;v\left( {x,y,z,0} \right) = x - 0.5y + z,\;w\left( {x,y,z,0} \right) = x + y - 0.5z$$

(48)

Applying ET on both sides of Eq. (22) subject to IC (48), we have

$$E\left\{ {u\left( {x,y,z,t} \right)} \right\} = q^{2} \left( { - 0.5x + y + z} \right) + q^{\alpha } E\left[ {\rho_{0} \left( {\frac{{\partial^{2} u}}{{\partial x^{2} }} + \frac{{\partial^{2} u}}{{\partial y^{2} }} + \frac{{\partial^{2} u}}{{\partial z^{2} }}} \right) - u\frac{\partial u}{\partial x} - v\frac{\partial u}{\partial y} - w\frac{\partial u}{\partial z}} \right]$$

(49)

$$E\left\{ {v\left( {x,y,z,t} \right)} \right\} = q^{2} \left( {x - 0.5y + z} \right) + q^{\alpha } E\left[ {\rho_{0} \left( {\frac{{\partial^{2} v}}{{\partial x^{2} }} + \frac{{\partial^{2} v}}{{\partial y^{2} }} + \frac{{\partial^{2} v}}{{\partial z^{2} }}} \right) - u\frac{\partial v}{\partial x} - v\frac{\partial v}{\partial y} - w\frac{\partial v}{\partial z}} \right]$$

(50)

$$E\left\{ {w\left( {x,y,z,t} \right)} \right\} = q^{2} \left( {x + y - 0.5z} \right) + q^{\alpha } E\left[ {\rho_{0} \left( {\frac{{\partial^{2} w}}{{\partial x^{2} }} + \frac{{\partial^{2} w}}{{\partial y^{2} }} + \frac{{\partial^{2} w}}{{\partial z^{2} }}} \right) - u\frac{\partial w}{\partial x} - v\frac{\partial w}{\partial y} - w\frac{\partial w}{\partial z}} \right]$$

(51)

The inverse Elzaki transform of Eqs. (49)–(51) implies that

$$u\left( {x,y,z,t} \right) = \left( { - 0.5x + y + z} \right) + E^{ - 1} \left[ {q^{\alpha } E\left[ {\rho_{0} \left( {\frac{{\partial^{2} u}}{{\partial x^{2} }} + \frac{{\partial^{2} u}}{{\partial y^{2} }} + \frac{{\partial^{2} u}}{{\partial z^{2} }}} \right) - u\frac{\partial u}{\partial x} - v\frac{\partial u}{\partial y} - w\frac{\partial u}{\partial z}} \right]} \right]$$

(52)

$$v\left( {x,y,z,t} \right) = \left( {x - 0.5y + z} \right) + E^{ - 1} \left[ {q^{\alpha } E\left[ {\rho_{0} \left( {\frac{{\partial^{2} v}}{{\partial x^{2} }} + \frac{{\partial^{2} v}}{{\partial y^{2} }} + \frac{{\partial^{2} v}}{{\partial z^{2} }}} \right) - u\frac{\partial v}{\partial x} - v\frac{\partial v}{\partial y} - w\frac{\partial v}{\partial z}} \right]} \right]$$

(53)

$$w\left( {x,y,z,t} \right) = \left( {x + y - 0.5z} \right) + E^{ - 1} \left[ {q^{\alpha } E\left[ {\rho_{0} \left( {\frac{{\partial^{2} w}}{{\partial x^{2} }} + \frac{{\partial^{2} w}}{{\partial y^{2} }} + \frac{{\partial^{2} w}}{{\partial z^{2} }}} \right) - u\frac{\partial w}{\partial x} - v\frac{\partial w}{\partial y} - w\frac{\partial w}{\partial z}} \right]} \right]$$

(54)

Now applying the homotopy perturbation method we obtain

$$\sum\limits_{n = 0}^{\infty } {p^{n} u_{n} \left( {x,y,z,t} \right) = \left( { - 0.5x + y + z} \right) + p\left\{ {E^{ - 1} \left[ {q^{\alpha } E\left[ {\sum\limits_{n = 0}^{\infty } {p^{n} H_{n} \left( u \right)} } \right]} \right]} \right\}}$$

(55)

$$\sum\limits_{n = 0}^{\infty } {p^{n} v_{n} \left( {x,y,z,t} \right) = \left( {x - 0.5y + z} \right) + p\left\{ {E^{ - 1} \left[ {q^{\alpha } E\left[ {\sum\limits_{n = 0}^{\infty } {p^{n} H_{n} \left( v \right)} } \right]} \right]} \right\}}$$

(56)

$$\sum\limits_{n = 0}^{\infty } {p^{n} w_{n} \left( {x,y,z,t} \right) = \left( {x + y - 0.5z} \right) + p\left\{ {E^{ - 1} \left[ {q^{\alpha } E\left[ {\sum\limits_{n = 0}^{\infty } {p^{n} H_{n} \left( w \right)} } \right]} \right]} \right\}}$$

(57)

where $H_{n} \left( u \right)$, $H_{n} \left( v \right)$ and $H_{n} \left( w \right)$ are He’s polynomials that represents the nonlinear terms as

$$\left\{ \begin{aligned} H_{n} \left( u \right) = & \,p\left[ {\rho_{0} \left( {\frac{{\partial^{2} u}}{{\partial x^{2} }} + \frac{{\partial^{2} u}}{{\partial y^{2} }} + \frac{{\partial^{2} u}}{{\partial z^{2} }}} \right) - u\frac{\partial u}{\partial x} - v\frac{\partial u}{\partial y} - w\frac{\partial u}{\partial z}} \right] = 0 \\ H_{n} \left( v \right) = & \,p\left[ {\rho_{0} \left( {\frac{{\partial^{2} v}}{{\partial x^{2} }} + \frac{{\partial^{2} v}}{{\partial y^{2} }} + \frac{{\partial^{2} v}}{{\partial z^{2} }}} \right) - u\frac{\partial v}{\partial x} - v\frac{\partial v}{\partial y} - w\frac{\partial v}{\partial z}} \right] = 0 \\ H_{n} \left( w \right) = & \,p\left[ {\rho_{0} \left( {\frac{{\partial^{2} w}}{{\partial x^{2} }} + \frac{{\partial^{2} w}}{{\partial y^{2} }} + \frac{{\partial^{2} w}}{{\partial z^{2} }}} \right) - u\frac{\partial w}{\partial x} - v\frac{\partial w}{\partial y} - w\frac{\partial w}{\partial z}} \right] = 0 \\ \end{aligned} \right.$$

where

$$\begin{aligned} u = & \,u_{0} + pu_{1} + p^{2} u_{2} + \cdots , \\ v = & \,v_{0} + pv_{1} + p^{2} v_{2} + \cdots , \\ w = & \,w_{0} + pw_{1} + p^{2} w_{2} + \cdots , \\ \end{aligned}$$

The first few components of He’s polynomials are given as

$$\left\{ \begin{aligned} & H_{0} \left( u \right) = \rho_{0} \left( {u_{0xx} + u_{0yy} + u_{0zz} } \right) - u_{0} u_{0x} - v_{0} u_{0y} - w_{0} u_{0z} \\ & H_{0} \left( v \right) = \rho_{0} \left( {v_{0xx} + v_{0yy} + v_{0zz} } \right) - u_{0} v_{0x} - v_{0} v_{0y} - w_{0} v_{0z} \\ & H_{0} \left( w \right) = \rho_{0} \left( {w_{0xx} + w_{0yy} + w_{0zz} } \right) - u_{0} w_{0x} - v_{0} w_{0y} - w_{0} w_{0z} \\ & H_{1} \left( u \right) = \rho_{0} \left( {u_{1xx} + u_{1yy} + u_{1zz} } \right) - u_{0} u_{1x} - u_{1} u_{0x} - v_{0} u_{1y} - v_{1} u_{0y} - w_{0} u_{1z} - w_{1} u_{0z} \\ & H_{1} \left( v \right) = \rho_{0} \left( {v_{1xx} + v_{1yy} + v_{1zz} } \right) - u_{0} v_{1x} - u_{1} v_{0x} - v_{0} v_{1y} - v_{1} v_{0y} - w_{0} v_{1z} - w_{1} v_{0z} \\ & H_{1} \left( w \right) = \rho_{0} \left( {w_{1xx} + w_{1yy} + w_{1zz} } \right) - u_{0} w_{1x} - u_{1} w_{0x} - v_{0} w_{1y} - v_{1} w_{0y} - w_{0} w_{1z} - w_{1} w_{0z} \\ & \quad \quad \quad \quad \quad \quad \quad \;\; \vdots \\ \end{aligned} \right.$$

Using the above He’s polynomials and comparing the coefficients of same power of $p$ in Eqs. (55)–(57) we have

$$\begin{aligned} p^{0} :u_{0} \left( {x,y,z,t} \right) = & \,\left( { - 0.5x + y + z} \right) \\ v_{0} \left( {x,y,z,t} \right) = & \,\left( {x - 0.5y + z} \right) \\ w_{0} \left( {x,y,z,t} \right) = & \,\left( {x + y - 0.5z} \right) \\ \end{aligned}$$

$$\begin{aligned} p^{1} :u_{1} \left( {x,y,z,t} \right) = & \,E^{ - 1} \left[ {q^{\alpha } E\left[ {H_{0} \left( u \right)} \right]} \right] = - \,\left( {2.25x} \right)\frac{{t^{\alpha } }}{{\varGamma \left( {\alpha + 1} \right)}} \\ v_{1} \left( {x,y,z,t} \right) = & \,E^{ - 1} \left[ {q^{\alpha } E\left[ {H_{0} \left( v \right)} \right]} \right] = -\, \left( {2.25y} \right)\frac{{t^{\alpha } }}{{\varGamma \left( {\alpha + 1} \right)}}\, \\ w_{1} \left( {x,y,z,t} \right) = & \,E^{ - 1} \left[ {q^{\alpha } E\left[ {H_{0} \left( w \right)} \right]} \right] = -\, \left( {2.25z} \right)\frac{{t^{\alpha } }}{{\varGamma \left( {\alpha + 1} \right)}} \\ \end{aligned}$$

$$\begin{aligned} p^{2} :u_{2} \left( {x,y,z,t} \right) = & \,E^{ - 1} \left[ {q^{\alpha } E\left[ {H_{1} \left( u \right)} \right]} \right] = \left( { - \,2.25x + 4.5y + 4.5z} \right)\frac{{t^{2\alpha } }}{{\varGamma \left( {2\alpha + 1} \right)}} \\ v_{2} \left( {x,y,z,t} \right) = & \,E^{ - 1} \left[ {q^{\alpha } E\left[ {H_{1} \left( v \right)} \right]} \right] = \left( {4.5x - 2.25y + 4.5z} \right)\frac{{t^{2\alpha } }}{{\varGamma \left( {2\alpha + 1} \right)}} \\ w_{2} \left( {x,y,z,t} \right) = & \,E^{ - 1} \left[ {q^{\alpha } E\left[ {H_{1} \left( w \right)} \right]} \right] = \left( {4.5x + 4.5y - 2.25z} \right)\frac{{t^{2\alpha } }}{{\varGamma \left( {2\alpha + 1} \right)}} \\ \end{aligned}$$

$$\begin{aligned} p^{3} :u_{3} \left( {x,y,z,t} \right) = & \,E^{ - 1} \left[ {q^{\alpha } E\left[ {H_{2} \left( u \right)} \right]} \right] = - \,\left( {20.25 + 5.0625\frac{{\varGamma \left( {2\alpha + 1} \right)}}{{\left( {\varGamma \left( {\alpha + 1} \right)} \right)^{2} }}} \right)\frac{{xt^{3\alpha } }}{{\varGamma \left( {3\alpha + 1} \right)}} \\ v_{3} \left( {x,y,z,t} \right) = & \,E^{ - 1} \left[ {q^{\alpha } E\left[ {H_{2} \left( v \right)} \right]} \right] = - \left( {20.25 + 5.0625\frac{{\varGamma \left( {2\alpha + 1} \right)}}{{\left( {\varGamma \left( {\alpha + 1} \right)} \right)^{2} }}} \right)\frac{{yt^{3\alpha } }}{{\varGamma \left( {3\alpha + 1} \right)}} \\ w_{3} \left( {x,y,z,t} \right) = & \,E^{ - 1} \left[ {q^{\alpha } E\left[ {H_{21} \left( w \right)} \right]} \right] = -\, \left( {20.25 + 5.0625\frac{{\varGamma \left( {2\alpha + 1} \right)}}{{\left( {\varGamma \left( {\alpha + 1} \right)} \right)^{2} }}} \right)\frac{{zt^{3\alpha } }}{{\varGamma \left( {3\alpha + 1} \right)}} \\ \end{aligned}$$

So the solutions $u\left( {x,y,z,t} \right)$, $v\left( {x,y,z,t} \right)$ and $w\left( {x,y,z,t} \right)$ are given as

$$\begin{aligned} & u\left( {x,y,z,t} \right) = u_{0} \left( {x,y,z,t} \right) + u_{1} \left( {x,y,z,t} \right) + u_{2} \left( {x,y,z,t} \right) + u_{3} \left( {x,y,z,t} \right) \cdots = \left( { - 0.5x + y + z} \right) + - \left( {2.25x} \right)\frac{{t^{\alpha } }}{{\varGamma \left( {\alpha + 1} \right)}} + \\ & \quad \left( { - 2.25x + 4.5y + 4.5z} \right)\frac{{t^{2\alpha } }}{{\varGamma \left( {2\alpha + 1} \right)}} + - \left( {20.25 + 5.0625\frac{{\varGamma \left( {2\alpha + 1} \right)}}{{\left( {\varGamma \left( {\alpha + 1} \right)} \right)^{2} }}} \right)\frac{{xt^{3\alpha } }}{{\varGamma \left( {3\alpha + 1} \right)}} + \cdots \\ \end{aligned}$$

(58)

$$\begin{aligned} & v\left( {x,y,z,t} \right) = v_{0} \left( {x,y,z,t} \right) + v_{1} \left( {x,y,z,t} \right) + v_{2} \left( {x,y,z,t} \right) + v_{3} \left( {x,y,z,t} \right) \cdots = \left( {x - 0.5y + z} \right) + - \left( {2.25y} \right)\frac{{t^{\alpha } }}{{\varGamma \left( {\alpha + 1} \right)}} + \\ & \quad \left( {4.5x - 2.25y + 4.5z} \right)\frac{{t^{2\alpha } }}{{\varGamma \left( {2\alpha + 1} \right)}} + - \left( {20.25 + 5.0625\frac{{\varGamma \left( {2\alpha + 1} \right)}}{{\left( {\varGamma \left( {\alpha + 1} \right)} \right)^{2} }}} \right)\frac{{yt^{3\alpha } }}{{\varGamma \left( {3\alpha + 1} \right)}} + \cdots \\ \end{aligned}$$

(59)

$$\begin{aligned} & w\left( {x,y,z,t} \right) = w_{0} \left( {x,y,z,t} \right) + w_{1} \left( {x,y,z,t} \right) + w_{2} \left( {x,y,z,t} \right) + w_{3} \left( {x,y,z,t} \right) \cdots = \left( {x + y - 0.5z} \right) + - \left( {2.25z} \right)\frac{{t^{\alpha } }}{{\varGamma \left( {\alpha + 1} \right)}} + \\ & \quad \left( {4.5x + 4.5y - 2.25z} \right)\frac{{t^{2\alpha } }}{{\varGamma \left( {2\alpha + 1} \right)}} + - \left( {20.25 + 5.0625\frac{{\varGamma \left( {2\alpha + 1} \right)}}{{\left( {\varGamma \left( {\alpha + 1} \right)} \right)^{2} }}} \right)\frac{{zt^{3\alpha } }}{{\varGamma \left( {3\alpha + 1} \right)}} + \cdots \\ \end{aligned}$$

(60)

For $\,\alpha = 1$ Eqs. (58)–(60) reduce to

$$\begin{aligned} u\left( {x,y,z,t} \right) = & \,\left( { - 0.5x + y + z} \right)\left( {1 + 2.25t^{2} + 2.25^{2} t^{4} + \cdots } \right) - 2.25xt\left( {1 + 2.25t^{2} + \cdots } \right) = \frac{ - 0.5x + y + z - 2.25xt}{{1 - 2.25t^{2} }} \\ v\left( {x,y,z,t} \right) = & \,\left( {x - 0.5y + z} \right)\left( {1 + 2.25t^{2} + 2.25^{2} t^{4} + \cdots } \right) - 2.25yt\left( {1 + 2.25t^{2} + \cdots } \right) = \frac{x - 0.5y + z - 2.25yt}{{1 - 2.25t^{2} }} \\ w\left( {x,y,z,t} \right) = \, & \left( {x + y - 0.5z} \right)\left( {1 + 2.25t^{2} + 2.25^{2} t^{4} + \cdots } \right) - 2.25zt\left( {1 + 2.25t^{2} + \cdots } \right) = \frac{x + y - 0.5z - 2.25zt}{{1 - 2.25t^{2} }} \\ \end{aligned}$$

(61)

This solution is same as solution solved in [38]. The plots of Eq. (61) are depicted in Fig. 12 for $\alpha = 1,$ $\rho_{0} = 0.5\,,\,t = 0.1$ and the comparison plots of $U_{0} ,\,U_{1} ,\,U_{2} ,U_{3}$, $V_{0} ,\,V_{1} ,\,V_{2} ,V_{3}$ and $W_{0} ,\,W_{1} ,\,W_{2} ,W_{3}$ with their exact solution (61) for $\alpha = 1$ are depicted in Fig. 13.

Fig. 12

Solution plots of Eq. (61) for $t = 0.1$ and $\alpha = 1$ (Example 3)

Fig. 13

Comparison of the approximate solution $U_{0} ,\,U_{1} ,\,U_{2} ,U_{3}$, $V_{0} ,\,V_{1} ,\,V_{2} ,V_{3}$ and $W_{0} ,\,W_{1} ,\,W_{2} ,W_{3}$ with their exact solution (61) for $\rho_{0} = 0.5,\,x = \frac{\pi }{4},\,y = \frac{\pi }{4},z = \frac{\pi }{4}$ (Example 3)

6 Conclusion

In this paper, HPETM is applied for solution of time-fractional NS equations with IC. HPETM provides the solution in term of convergent series. Three example problems are addressed in order to validate and test the efficacy of the proposed method. One may see that the obtained results are in excellent agreement with HPM [28] and ADM [29]. The major benefit of this method over HPM and ADM is that this is a powerful and effective method in finding the analytical and approximate solutions for fractional order nonlinear partial differential equations in place of Adomian’s polynomials.