1 Introduction

Repetitive heavy duties tasks can produce muscle fatigue, cause joint and posture disorders as mentioned, for example, in [1,2,3]. Robotic solutions have been proposed to assist workers who perform tasks that require muscular effort, as reported, for example, in [4,5,6]. There is a wide range of several types of exoskeletons specifically de-signed for various assistive tasks. Exoskeletons can be classified as aimed at the upper or lower limbs. They can be wearable or be fixed to an external frame. They can be active or passive. They can provide some gravity balancing either via software or hardware solutions. Each exoskeleton’s class has specific features to fit for specific applications. Asgari et al. [7], for example, propose a wearable exoskeleton with a mechanism that supports the upper limb and particularly the shoulder. Similarly, de Book et al. [8] present the Exo4Work exoskeleton for assisting both upper limbs in overhead working scenarios. Upper limb exoskeletons require careful attention to their own weight, which should be kept to a minimum. Moreover, the weight distribution of a wearable exoskeleton needs to be carefully addressed, since it can significantly affect the natural motions of a human, resulting in negative side effects, especially in terms of undesired bending/torsions on the spine and overloads of the lower limbs.

Masud et al. [9] propose an upper-body exoskeleton with a fixed base frame that is attached to a chair. A user can sit on that chair and perform various tasks. Similarly, Gull et al. [10] propose an upper limb exoskeleton that is fixed to the frame of a wheelchair. All the reaction forces are acting on the fixed frame. Accordingly, the use of a fixed frame avoids the side effects that are due to exoskeleton’s own weight. However, the fixed frame typically is bulky and introduces limitations on the portability and on the user's motion ranges. These drawbacks often make exoskeletons with fixed frames unpractical in activities of daily life within human shared environments. Active exoskeletons require actuators (often DC motors) and power supplies (often DC batteries). An evaluation of the effect of an active industrial exoskeleton on muscle activity has been presented in [11] with reductions of the back muscle activity up to 12%–15%. Pasqual et al., [12], proposed an upper extremity exoskeleton robot for lift assistance (ArmX), which provides power assistance during lifting operations. However, active exoskeletons require external power supplies or heavy and expansive batteries. Accordingly, several researchers have investigated solutions for passive exoskeletons.

Passive exoskeletons usually are based on a passive mechanism that provides support to workers by redistributing the workloads and/or by providing some sort of gravity balancing without requiring motors or batteries, such as outlined in [13]. In this context, an example of passive upper-limb exoskeleton is presented in [14]. This exoskeleton allows to reduce the prevalence of musculoskeletal disorders when performing repetitive holding tasks. However, passive exoskeletons usually provide positive effects only in a limited operation range while negative side effects often occur outside their operation range. Their own weight plays a significant role for most exoskeletons. A gravity balancing can be achieved by means of hardware solutions such as cables, pulleys, springs, counter masses, and rigid linkages, as proposed in [15]. Also, several control algorithms have been proposed for active exoskeletons for providing some sort of virtual gravity compensation such as reported in [16, 17]. However, the proposed gravity compensation strategies are usually limited to a limb and not to the whole body. This can cause discomfort and pain.

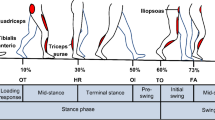
The interaction between robotic and human systems in the healthcare area has been studied for decades, an example shown in Fig. 1, which has been proposed in the references [18,19,20,21,22]. In [23], the authors propose to minimize the interaction force between human and mechanism by structural optimization and the development of a mathematical model of the human arm. Experimental results showed that the human–machine interaction force is reduced. In [24] a new mechanism is proposed for an exoskeletal hip joint of 3 DoF with five rotating joints and two prismatic. The authors also investigate joint movements and propose a new robotic articulation to eliminate the forces of interaction and misalignment between the system and the human body. Figure 1 shows a summary study of the vast thorough research reported in the state of the art, with the most relevant aspects of the exoskeleton types previously researched highlighted. These characteristics have been grouped considering the realization with the type of exoskeleton. Table 1 has been designed, which presents a broad summary of the several types of exoskeletons with their respective characteristics.

Fig. 1
figure 1

Analysis of the main characteristics of exoskeleton

Full size image
Table 1 Examples of exoskeletons’ characteristics
Full size table

In this paper, a novel design for a passive upper-limb exoskeleton using a novel magnetic self-locking mechanism and a specially designed load balancing mechanism for weight relief is proposed. The proposed mechanism can be utilized when performing repetitive tasks such as maintaining a position while drilling, painting, or hammering. The document is structured as follows: Sect. 2 defines the design requirements by identifying the specific characteristics of the intended application; Sect. 3 describes the main steps of mechanism design; Sect. 4 focuses on the proposed approach for balancing of the spine by including multibody dynamics simulations to test the feasibility and effectiveness of the proposed balancing system; Sect. 5 describes the proposed novel locking mechanism allowing to hold any position of the spine; and Sect. 6 describes the experimental characterization of the proposed mechanism, is completely passive and capable of self-locking without requiring a dedicated control, motor, or power supply, thereby making it feasible for long repetitive and laborious tasks.

2 Methodology and Requirements Design

The methodology for the development of this research project was based on the W model proposed in [25], the process of designing a product created by Asimow [26] and the experimental design methodology [27]. The diagram representing the methodological process is shown in Fig. 2. The development of the methodology is defined by three areas of interest: types of passive and active exoskeletons, energy saving strategies and drive and balance mechanisms. Considering each of the areas mentioned above, the design parameters to be fulfilled by the design during the proposed task are proposed.

Fig. 2
figure 2

Methodological process

Full size image

The shoulder joint is one of the most injured in the human body during exhausting tasks due to its limited range of motion and untrained muscles. Normally, such tasks involve the use of tools that add weight and external forces that worsen the working conditions. Therefore, relieving the weight and balancing the human arm during tasks that involve the shoulder can prevent illness and injury, as pointed out in [28]. Drilling, painting, and hammering tasks are part of the scenarios where exoskeletons can provide valuable assistance. A drilling task has been chosen as proof of concept to test the proposed system, as proposed in Fig. 3. To understand the design requirements for the proposed solution, a preliminary biomechanical analysis must be taken into consideration. Thus, a test scenario has been herewith proposed to estimate the torque needed at the shoulder joint, the elbow joint and the wrist joint to maintain the arm posture during a task using a drill of 1.20 kg as shown in Fig. 3. The average of the human arm characteristics and the acting forces are presented in Table 2, as based on [28, 29].

Fig. 3
figure 3

Upper limb free body diagram

Full size image
Table 2 Primary features of an average human arm (adapted from [28, 29])
Full size table

The torques to maintain the needed position can be computed using the equilibrium equations, Eqs. (1) to (5), with reference to the free body model in Fig. 3 schematic. The free-body diagram of the upper limb along with the stresses and torques acting throughout the drilling operation. The shoulder joint has been taken into consideration at β = 40 deg and the elbow joint at α = 10 deg. The mentioned torques can be calculated by the equilibrium equations as referring to the scheme in Fig. 3 as:

$$0 = \tau_{1a } - W_4 cos\left( \alpha \right)\left( {L_1 } \right) - W_1 cos\left( \alpha \right)\left( {L_1 /2} \right)$$
(1)
$$0 = R_{y1 } - W_1 - W_4$$
(2)
$$0 = \tau_{2a } - W_2 cos\left( \alpha \right)\left( {L_2 /2} \right) - \tau_{1a } - R_{y1} cos\left( \alpha \right)\left( {L_2 } \right)$$
(3)
$$0 = R_{y2} - R_{y1 } - W_2$$
(4)
$$0 = \tau_{3a } - W_3 cos\left( \beta \right)\left( {L_3 /2} \right) - \tau_{2a } - R_{y2} cos\left( \beta \right)\left( {L_3 } \right)$$
(5)

where:

  • \(\tau_{1a{ }}\) is the torque required from the wrist.

  • \(\tau_{2a{ }}\) is the torque required from the forearm.

  • \(\tau_{3a{ }}\) is the torque required from the arm.

  • \(R_{y1{ }}\) are the reaction forces acting along y-axis at the wrist.

  • \(R_{y2{ }}\) are the reaction forces acting along y-axis at the elbow.

  • \(W_1\) is the weight of the hand.

  • \(W_2\) is the weight of the forearm.

  • \(W_3\) is the weight of the arm.

  • \(W_4\) is the weight of the drill.

  • \(L_1\) is the length of the hand.

  • \(L_2\) is the length of the forearm.

  • \(L_3\) is the length of the arm.

  • \(\alpha\) is the elbow joint angle.

  • \(\beta\) is the shoulder joint angle.

Using Eqs. (1) to (5), it can be calculated the required torque at the wrist \(\tau_{1a } = 2.24 {\text{Nm}}\), the required torque at the elbow \(\tau_{2a} = 12.44 {\text{Nm}}\) and the required torque at the shoulder joint \(\tau_{3a } = 29.85 {\text{Nm}}\). The calculation of these values is obtained by considering as input data the values in Table 2 in terms of the average arm dimensions and acting forces at each body part. A similar approach was proposed, for example, in [30]. This can include a compensation technique similar to the one proposed in [31]. The introduced parameters are fundamental and have been used to conduct a formal analysis to determine the practicability of the proposed mechanism and its behavior and performance.

3 Mechanism Design

3.1 A Proposed Mechanism

The proposed novel design ExoM-S (Magnetic-Spring Exoskeleton) is composed of a passive mechanical chain that is symmetrical to the sagittal plane. A horizontal translational joint (\(\Delta_1\)) is connected in series with three revolute joints (\(\theta_2 ,{ }\theta_3 ,{ }\theta_4\)) with mutually perpendicular and parallel axes, as in Fig. 4. In addition, another translational joint (\(\Delta_2\)) allows relative motion between the mechanism and the End-Effector (EE). The first joint (\(\theta_2\)) that allows abduction and adduction must be aligned with the anatomical axis of the human shoulder, while the second joint (\(\theta_3\)) has a vertical axis that is not coupled to any specific biological axis. The action of \(\theta_3\), combined with the horizontal slider \(\Delta_1\), allows the passive motion of the glenohumeral joint. The third revolute joint (\(\theta_4\)) allows the flexion and extension of the human shoulder. The passive translational joint (\(\Delta_2\)) has been included to absorb any undesired longitudinal translational reaction force that can be generated at the human arm-mechanism interface. Two repositionable elastic straps are located on the shoulders, to fix and adapt to various human anthropometric sizes. In addition, a back support structure is positioned on the rear part. An adjustable belt connects the device with the user’s body in the lower part of the waist and an adjustable EE bracelet allows the forearm to be fixed to the mechanism. The back structure is made of a molded aluminum frame covered by elastic material. The mechanism sizes are based on the average anthropomorphic sizes of a human male [28].

Fig. 4
figure 4

A scheme of the PRRRP exoskeleton mechanism with reference frames

Full size image

3.2 A Kinematic Model

ExoM-S is characterized by a 5-DoFs (Degrees of Freedom) PRRRP (P-Prismatic; R-Revolute) kinematic chain (Fig. 4) that allows self-alignment of the axes of the device with the anatomical axes of the shoulder and elbow, minimizing the transfer of unwanted forces to the user’s musculoskeletal system. Figure 4 shows the CAD design of the proposed mechanism allowing the upper limbs to generate abduction and adduction movements. Furthermore, the proposed mechanism counteracts the passive translation movements of the glenohumeral joint that occur during abducting, bending and extension movements of the arm.

3.3 A Static Analysis

A static analysis has been conducted to compute the torques acting at exoskeleton joints. The models in Figs. 5 show the main torques acting on the exoskeleton at a given configuration of the joint 4 (indicated by \(\theta_4\)). Namely, Fig. 5(a) shows a scheme of the exoskeleton alone while Fig. 5(b) shows the exoskeleton as attached to the human upper limb. The torque \(\tau_{E1{ }}\) on the joint \(\theta_4\) without the arm sited in the exoskeleton can be calculated using Eq. (6). Similarly, it is possible to determine the torque \(\tau_{c1{ }}\) acting on the joint \(\theta_4\) with the arm sited in the proposed mechanism using Eqs. (7–9).

Fig. 5
figure 5

Static analysis of the ExoM-S joint \(\theta_4\); a Mechanical system without human arm, b Human mockup wearing the exoskeleton

Full size image

Static equations for the joint \(\theta_4\) can be defined as:

$$\sum^\tau_ = 0 = \left[ {L_{E1} x W_{E1} } \right] = \tau_{E1 }$$
(6)
$$\tau_{c1 } = \tau_{E1 } + \tau_{3a }$$
(7)
$$\sum^\tau_ = 0 = \tau_{c1 } - \tau_{s1 }$$
(8)
$$\tau_{c1 } = \tau_{s1 }$$
(9)

where \(L_{E1}\) is the distance between the centre of mass and the joint \(\theta_4 ,\) \(W_{E1}\) is the weight of the link \(E1\), and \(\tau_{s1{ }}\) is the torque required by the passive joint \(\theta_4\) to maintain the posture.

With the same concept, the torque needed at \(\theta_2\) to maintain the posture has been computed at a pivotal moment, the joints \(\theta_2\) and \(\Delta_1\) support the whole weight of the exoskeleton and the human arm. Figures 6(a) and (b) show the forces and torques acting while holding a static position without the human and with the human wearing the exoskeleton, respectively. Equations (10–11) have been used to compute the torques \(\tau_{E12{ }}\) and \(\tau_{E3{ }}\) in function to the joint \(\theta_2\) and \(\Delta_1\). In addition, the torques acting along the mechanism, including the human arm torque, have been analyzed, in Fig. 7(a) and (b). Similarly, the torque \(\tau_{Et{ }}\) and \(\tau_{t{ }}\) on the joint \(\theta_2\) with the arm can be calculated using the following equations:

$$\sum^\tau_ = 0 = \left[ {L_{E1} x W_{E1} } \right] + \left[ {L_{E2} x W_{E2} } \right] = \tau_{E12 }$$
(10)
$$\sum^\tau_ = 0 = \left[ {L_{E3} x W_{E3} } \right] = \tau_{E3 }$$
(11)
$$\tau_{Et } = \tau_{3a } + \tau_{E12 } + \tau_{E3 }$$
(12)
$$\sum^\tau_ = 0 = \tau_{t } - \tau_{Et }$$
(13)
$$\tau_t = \tau_{Et }$$
(14)

where \(\tau_t\) is the torque produced at the mechanism's central revolute point (\(\theta_2\) and \(\Delta_1\)).

Fig. 6
figure 6

Static analysis of the ExoM-S without the human arm; a Torques produced at the links E1 and E2, b Torque produced at the link E3

Full size image
Fig. 7
figure 7

Static analysis in the joints \(\theta_2\) and \(\Delta_1\) of the mechanism with a human mockup wearing in the exoskeleton; a Torques produced at the links E1 and E2, b Torque produced at the link E3

Full size image

4 A Balancing Procedure

To improve the performance of the proposed mechanism allowing better posture maintenance and load distribution together with weight relief, a balance procedure has been proposed. Figure 8 illustrates the ExoM-S with the balancing mechanism that consists in a cable connected to a pulley that is free to move. The pulley is connected to the moving link connected to the spine and the exoskeleton’s arm. The cable is directly connected to a bracelet wrap** the user’s leg. The leg is used as a fixed frame to distribute the force along the mechanism from the arm to the spine up to the leg and make the dynamic balancing procedure work.

Fig. 8
figure 8

ExoM-S with the balancing system mechanism

Full size image

A multibody dynamic simulation has been carried out to test the feasibility of the proposal using the CAD in Fig. 9. Two simulation modes of 10 s have been planned with and without the balancing system. Referring to Fig. 9(a), the ExoM-S prototype without the balancing mechanism can fit into a box of about (532.00 × 372.00 × 361.00) mm with an approximate weight of 2.23 kg. Figure 9(b) shows the ExoM-S with the balancing mechanism.

Fig. 9
figure 9

ExoM-S CAD model; a without balancing system, b with balancing

Full size image

The simulation studies have been conducted applying a force of 86.15 N on the bracelet simulating the weight of the arm and the operating drill. Several materials have been chosen for the parts acting in the multibody dynamic simulation which characteristics are detailed in Table 3: the bracelets of the arm and leg is in ABS the rope are in nylon the links and the tensioner on the leg bracelet is in Aluminum alloy and the posture corset is in Polyester.

Table 3 Chosen materials properties features
Full size table

Several multibody simulations have been performed considering the Earth gravity and the possible collision between the bodies. It is fundamental to compute shaking forces with and without the balancing system mechanism to understand the performance of the balancing system.

Figure 10 shows the reference axis of the point aligned to the shoulder that has been used to compute the shaking forces with and without the balancing system. Figure 11 shows the shaking forces without the balancing system. Analyzing the plot, looking at the shaking forces, it can be noticed that the mechanism it is not balanced along the Y and Z axis, and it is oscillating. The peaks at 2.30 s show the collision of the exoskeleton’s arm with the posture corset. The oscillation finishes at 3.90 s when the link is totally inclined due to the continuous applied force. The shaking forces along the X-axes have a range of -0.17 N to 0.45 N with a mean of -0.05 N; the shaking forces along Y-axes have a range of -64.57 N to 6.13 N with a mean of -30.96 N; the shaking forces along Z-axes have a range of -12.45 N to 27.31 N with a mean of 12.45 N.

Fig. 10
figure 10

A scheme with reference axes used to compute the shaking forces with and without the balancing system

Full size image
Fig. 11
figure 11

Shaking forces computation without balancing system

Full size image

Figure 12 shows the shaking forces with the balancing system. Analyzing the plot, looking at the shaking forces, it can be noticed that the balancing system mechanism works properly. The shaking forces along the X-axes have a range of 0.31 N to 0.32 N with a mean of 0.31 N; the shaking forces along Y-axes have a range of 0.01 N to 0.02 N with a mean of 0.01 N; the shaking forces along Z-axes have a range of 17.02 N to 17.52 N with a mean of 17.06 N. It is important to notice that the shaking forces, especially the previously unbalanced one, are now balanced and neglectable. In addition, the trend of the plots is flat, showing that the balancing system is working properly. The shaking forces along X and Y axis are almost zero while, as expected, on the Z-axes the only force that is acting is the weight of the mechanism since Z-axes are the axes along which the gravity force is acting. In addition, for a complete characterization of the balancing system performance, the movement of the oscillating link on the back of the posture corset has been computed.

Fig. 12
figure 12

Shaking forces computation with balancing system

Full size image

Figure 13 shows the reference axes of the oscillating link revolute joint (\(\theta_2\)). Figure 14 shows the computed angular displacement of the Z-axes of the oscillating link. It can be noticed that there is a transient of settlement where the links moves 0.082 deg. After the transient movement, the link remains stable. Thus, the movement of the oscillating link is neglectable.

Fig. 13
figure 13

Oscillating link revolute joint (\(\theta_2\)) reference axes

Full size image
Fig. 14
figure 14

Oscillating link angular displacement

Full size image

After implementing the balancing system, the torque needed on the passive joint \(\theta_4\) to maintain the arm standstill during the selected task has been computed. Figure 15 shows the passive joint \(\theta_4\) and the reference axes. Figure 16 shows the torque needed to assist the wearer in maintaining the arm standstill while operating with the drill. At the beginning of the simulation there is a small transient movement in which the torque reaches 1.49 Nm, then the needed torque stabilizes at 1.32 N.

Fig. 15
figure 15

A scheme with the reference axes of the passive joint \(\theta_4\)

Full size image
Fig. 16
figure 16

Simulated torque needed by the passive joint \(\theta_4\) to keep standstill

Full size image

The balance mechanism is adjusted according to the user's height. The position of the fixed frame on the thighs is set according to the user's comfort. The cable is used to counterbalance the limb load. The user can hold any configuration including the vertical configuration with mostly the same efforts.

5 A Locking Mechanism

A magnetic-spring support has been implemented as a passive actuation system to maintain the posture at the joint \(\theta_4\) of ExoM-S while performing the planned task. The magnetic spring is based on the mechanism used to block the safety seat belt in vehicles. Therefore, when ExoM-S is used, the joint \(\theta_4\) can be locked according to the required task posture. To perform the locking procedure, the user puts the arm in the desired position and locks the joint \(\theta_4\) by applying a torque in counterclockwise direction. The mentioned procedure allows kee** a desired posture allowing the user to work without generating physical effort. When the user wants to unlock the system, they should only raise the arm less than 10 deg. Doing so, the system will automatically unlock.

The passive actuation system is based on a ratchet-gear mechanism, Fig. 17(a). When a force higher than the designed threshold force is applied, the actuation system is blocked, Fig. 17(b). This effect is caused since a centripetal force is generated, causing the mobile system in body A to lock the body B. In detail, body A has a spring (SpringG) that causes the lock to be produced, and it is also coupled to the safety tape’s axis of rotation. Body B has a spring (SpringP) that permits the system to be unlocked. The described locking mechanism is very efficient, but its performance can vary when used in repetitive cycles for long terms.

Fig. 17
figure 17

Conventional Seat belt locking mechanism: a Free motion system, b Block rotation system

Full size image

The mechanism functionality depends on the efficiency of the mechanical springs. These springs may lose their coefficient of elasticity making the braking system not working bringing to injuries. The industry standard for mechanical springs is a life cycle of about 10,000–15,000 uses, [32]. In ExoM-S working scenario, this can bring lesions and injuries. On the other hand, permanent magnet does not lose no more than 1% of its magnetic strength over a period of 100 if well maintained at temperatures that are lower than 80 °C, [33]. Thus, the mechanical spring (SpringP) of body B has been replaced with a magnetic-spring system allowing higher stability in operating cycles and longer duration. To be able to replace the mechanical spring with a magnetic-spring, the former (SpringP) has been experimentally characterized in terms of force–displacement when subjected to a compressive force, Fig. 18(a). Using the system in Fig. 17, it has been measured that when the system is blocked, the spring is compressed 5 mm. Thus, using a compression/traction machine, the mechanical spring has been compressed up to 5 mm to understand the needed force given by the spring to block the system in Fig. 16. The obtained curve of force–displacement is shown in Fig. 18(b) where it can be noted that when the spring is compressed 5 mm the spring requires a force of 5.40 N.

Fig. 18
figure 18

Force–displacement characterization; a Experimental layout, b Characterization plot

Full size image

Similarly, to the mechanical spring, to estimate the maximum force of repulsion generated by magnets, an experimental test has been carried out using two magnets configured with equal polarity and repulsive force between them. The selected magnets for the magnetic spring are of neodymium material with a diameter of 10 mm, Fig. 19(a). Using the compression/traction machine the repulsion force of the two magnets has been measured at different separation distances. Figure 19(b) shows the curve force–displacement. It is important to note that the displacement in Fig. 19(b) is the change in position of the compression/stretching machine. Thus, the mentioned displacement is inversely proportional to distance between the two magnets. According to Fig. 19(b), the two magnets can generate a repulsion force of 1.40 N. Therefore, to obtain a repulsion force of 5.40 N, a magnet arrangement to obtain a larger repulsion force is necessary.

Fig. 19
figure 19

Magnetic-spring characterization; a Experimental layout, b Characterization plot

Full size image

Since the system in Fig. 17 has a limited space to include the magnet arrangement, considering that when the magnets are too close, they do not come into contact, a maximum of one pair of 3 magnets each can be used to actuate the blocking system. Thus, since one pair of 3 magnets each magnet cannot generate the needed force of 5.40 N, it has been necessary to test experimentally the setting to check if the system can operate as needed. The choice of magnet has been carried out also as based on [33].

Figure 20 shows the ratchet-gear system with the magnetic-spring replacement. A bar has been attached to the seat belt system to simulate human arm movement. The locking device can be locked continuously at any desired locking configuration. However, the locking system takes 0.038 s to reach a full stop. The minimum velocity required to lock the system is 1.82 m/s. Accordingly, the locking device requires a rotation of 12 deg to reach a complete lock. To unlock the system the bar must be moved backward to the prior position with a counter rotation of 12 deg. The experiment showed that the system could operate correctly with the proposed magnet–spring arrangement. Although the proposed magnet–spring system with the one pair of 3 magnets each in Fig. 20 has about 4.20 N of repulsion force, having a lower force than the original mechanical spring in Fig. 17, it has a repulsion force sufficient for the seat belt system to operate correctly. It is worth noting that—using the proposed locking mechanism—the exoskeleton can hold a wide range of different configurations without requiring any change on the locking system can hold. In fact, the locking system has been designed to hold more than 250 kg by considering the worst-case scenario with a relevant safety factor.

Fig. 20
figure 20

Seat belt magnetic-spring test experimental layout; a Front view, b Back view

Full size image

6 Experimental Characterization

6.1 Prototype Description

After checking the feasibility of the novel proposed design, a prototype has been developed, Fig. 21. Two linear guides of 15 mm and 7 mm length have been chosen for the translational joins \(\Delta_1\) and \(\Delta_2\), respectively. A posture corrector with back straightening support belt has been chosen for the back-support. The links of the mechanism have been manufactured using aluminium flat bar. Comfortable fabric bracelets were used for the arm End-Effector (EE) and the leg attachment. A metal hinge has been chosen for the revolute joint \(\theta_3\). The weight of ExoM-S prototype is 1.20 kg, and its manufacturing price is less than 350 USD.

Fig. 21
figure 21

ExoM-S exoskeleton manufactured prototype. The person shown in the figure voluntarily granted permission to take and use photographs and/or digital images of him for use in this article

Full size image

6.2 Adaptability of the ExoM-S Prototype to Different Anthropometric Sizes

Important to the design of the proposed mechanism was its adaptability to various anthropomorphic sizes. To accomplish this, a postural corrector has been used as the basis for the proposed mechanism. Figure 21 shows a prototype of the proposed mechanism. Two Velcro shoulder straps that can be adjusted to accommodate various human anthropometric sizes. Figure 21 also shows a back support structure positioned on the rear portion. A belt with an adjustable length connects the device to the user's body below the waist, and an EE bracelet with an adjustable length allows the forearm to be attached to the mechanism. The back structure is comprised of an aluminium frame. The revolute joint located close to the spine is mounted on a prismatic guide, allowing it to freely adapt to the wearer's anthropometric dimensions and ensuring the mechanism's proper operation. The exoskeleton is equipped with Velcro straps that can be easily unfastened at any time in case of danger.

The adaptability of the ExoM-S prototype to different anthropometric sizes is evaluated on three users (two men and a woman). The aim is just an example to show how ExoM-S can accommodate users with different anthropometric measurements. Figure 22(a) shows the anthropometric reference sizes detailed in Table 4. Figure 22(b) shows that the prototype can be adapted for a user with a height of 170 cm and weighting of 60 kg. Figure 22(c) shows that the prototype can be adapted for a user with a height of 155 cm and a weighting of 90 kg. Figure 22(d) shows that the prototype can be adapted for a user with a height of 180 cm and a weighting of 83 kg.

Fig. 22
figure 22

Adaptability tests; a Arthrometric measures, b Man measuring 170 cm in height and weighing 60 kg, c Woman measuring 155 cm in height and weighing 90 kg, d Man measuring 180 cm in height and weighing 83 kg. People shown in the figure voluntarily granted permission to take and use photographs and/or digital images of him for use in this article

Full size image
Table 4 Anthropometric sizes referenced to people in Fig. 22
Full size table

According to the results, flexible components can adjust their dimensions and conform to the user's extremities. The cable length should also be adjusted in accordance with the user's height. The configuration of 5 DoFs that has been implemented in the prototype allows the user to generate free movements of the upper limbs without restrictions by the mechanism. The results of the experimental adaptation tests are based on user feedback; each user mentioned being comfortable with using the exoskeleton. They also mentioned that the weight of the mechanism was light and that they could move, walk, and move their upper limbs without any restriction by ExoM-S.

6.3 Testing Setup

Experiments have been carried out to estimate the human arm behavior in combination with the weight relief performance of the proposed mechanism when a user holds a drilling tool whose weight is 1.61 kg, as reported in Fig. 23a. Four experimental tests have been carried out with the following operation conditions:

Fig. 23
figure 23

a The scheme of U9C force transducer; b the installed sensor

Full size image

- The user holding the position without payload and without wearing the exoskeleton;

- The user holding the position with payload and without wearing the exoskeleton;

- The user holding the position without payload and with wearing the exoskeleton;

- The user holding the position with payload and with wearing the exoskeleton.

The aim of the experimental tests was to measure the time that the user can maintain the desired posture with the shoulder joint at θ = 90 deg about X, Y and Z axis and elbow joint at α = 10 deg about X, Y and Z axis. A U9C force transducer has been used to measure the payload acting on the arm. The most important characteristics of the U9C force transducer are:

- Capable of measuring both tensile/compressive force,

- Accuracy class 0.2,

- Nominal (rated) force range 50 N—50 KN,

- Protection class IP67,

- High rigidity, particularly suited for dynamic measurement tasks.

A bracelet support has been used to connect the arm to the force transducer.

The force measurement system was used to validate the performance of the exoskeleton in terms of physical forces and strains during a specific application that consisted of ceiling and surface drilling operations. The system was positioned at the top and centre of the test scenario (Fig. 23b). The device sampling rate used during testing was 0.02 s. Figure 24 shows the experimental layout. Figure 24(a) shows the experimental layout without the assistance of ExoM-S, while Fig. 24(b) shows experimental layout where the user is wearing ExoM-S exoskeleton.

Fig. 24
figure 24

Experimental layout: a Without the assistance of ExoM-S exoskeleton, b With the assistance of ExoM-S exoskeleton. The person shown in the figure voluntarily granted permission to take and use photographs and/or digital images of him for use in this article

Full size image

6.3.1 First Test Results (Without the Payload and Without Wearing ExoM-S)

During the first test, the user attempted to maintain the defined posture and when the user became tired, they released all his weight on the bracelet connected to the force sensor and the test was stopped. The results of the first test, without Exoskeleton assistance and without the payload, show that the user can maintain that posture for a maximum of 178 s, after this period, the user was not able to hold the defined posture and reached a different one, releasing all the weight on the bracelet, Fig. 25.

Fig. 25
figure 25

Force–Time curve obtained from the first experiment where the user tries to keep the defined posture without wearing ExoM-S

Full size image

6.3.2 Second Test Results (Without Wearing ExoM-S and Holding the Payload)

In the second experiment, the user manages to maintain the posture with the load for 71 s, as shown in Fig. 26. This indicates that the user holds for a shorter time than in the first experiment without load.

Fig. 26
figure 26

Force–Time curve obtained from the first experiment where the user tries to keep the defined posture with drill without wearing ExoM-S

Full size image

6.3.3 Third Test Results (Wearing ExoM-S Without the Payload)

Figure 27 shows the results from the third test where the user wears ExoM-S passively (without holding the payload and the exoskeleton help to maintain the posture. During the third test after 192 s, the user felt lightly tired of kee** the defined posture and involuntary motions were produced since the rest of the body could not maintain the given static posture for a long time. Therefore, after 192 s, the body motions caused postural changes that produced a non-linear variation load measured by the force sensor. After 886 s, the user felt pressure from the points \(\theta_2\), \(\Delta_1\) and at the EE and at the leg bracelet (points \(\theta_2\), \(\Delta_1\) of the exoskeleton were pointed out in, thus, the test was stopped. The results from the second test show that the user can maintain the defined posture 708 s more than the first test without exoskeleton. Although the experiment was stopped at 886 s because the user was tired of maintaining the defined posture, the force measured by the sensor did not increase exponentially because ExoM-S was supporting the weight of the arm. Indeed, the force sensor measures the maximum load when stopped the test.

Fig. 27
figure 27

Force–Time curve obtained from the third experiment where the user is wearing ExoM-S passively

Full size image

6.3.4 Fourth Test Results (Wearing ExoM-S and Holding the Payload)

During the fourth test of can observe how the user can hold the load of the drill longer time compared to test number two, in addition the support time for this scenario was 693 s, which indicates that the exoskeleton allows to help the user to maintain the desired holding posture. Figure 28 shows the results from the fourth test. After 693 s, the user felt pressure at the same points of third test (\(\theta_2\), \(\Delta_1\), EE, and the leg bracelet) and the test was stopped. The results from the fourth test show that the user can maintain the defined posture 515 s more than the first test and 622 s more than the second test.

Fig. 28
figure 28

Force–Time curve obtained from the third test using ExoM-S assistance with user participation to keep and correct the defined posture

Full size image

7 Discussion

Figure 29 shows the results of the fourth previous experimental tests in the same timeline and force value: the user holds the posture without ExoM-S and without drill; the user holds the drill without using ExoM-S; the user holds the posture using ExoM-S without the drill; and the user holds the drill using ExoM-S. Consequently, by carrying out a joint analysis of the results obtained from the four experimental tests carried out, it may be stated that:

  • The results of the third test show that the user can maintain the defined posture for 708 s longer than in the first test without an exoskeleton. Although the experiment was stopped at 886 s because the user was tired of maintaining the defined posture, the increase in performance in terms of time is calculated at 503.3%.

  • The results from the fourth test show that the user can maintain the defined posture for 622 s longer than in the second test. Furthermore, the user can maintain the defined posture for longer with a payload. Although the experiment was interrupted at 693 s because the user was tired, the force sensor never had to carry the entire payload. The increase in performance was 976%.

Fig. 29
figure 29

Force–Time curve obtained from the first, second, third and fourth test using ExoM-S assistance with user participation to keep and correct the defined posture

Full size image

Table 5 shows the strength average and time results obtained by three volunteer users. Each user has been performing multiple tests. Results of four exemplary tests are reported in Table 5 by referring to three users having different characteristic limb sizes.

Table 5 Strength average and time results obtained from three volunteer users (with different limb sizes) who performed each four tests
Full size table

A comprehensive evaluation of the experiment will be planned in future by extending the number of subjects to be evaluated, increasing the force measurement of the thigh bracelet and by adding an oxygen consumption test such as proposed for example in [34, 35]. Experimental performance techniques will be also considered as proposed, for example in [36,37,38,39].

8 Conclusions

This paper proposes a new Exoskeleton for weigh relief based on a PRRRP (P-Prismatic; R-Revolute) kinematic chain with 5 passive DoFs. The proposed exoskeleton results to be ergonomic and adjustable to the user anthropometric measures. Furthermore, ExoM-S can maintain a postural position thanks to a specifically designed blocking system that includes a passive magnetic-spring. A specific balancing system has been simulated and successfully integrated in the prototype to improve the performance of the proposed exoskeleton and reduce discomfort and pain. The proposed exoskeleton has been manufactured and experimentally evaluated while holding a drilling tasks posture. With the assistance of ExoM-S, a user held a drilling task posture significantly longer and with much less force effort than when without wearing the ExoM-S demonstrating the ExoM-S’s capability to reduce physical strain. The limitations of the proposed mechanism are a result of its design to perform repetitive and stationary repetitive tasks. Future work will improve the mechanism so that it can perform additional tasks. In moreover, the prototype's ergonomics will be enhanced to reduce the pressure points where the user experienced the most discomfort (θ2, Δ1, End-Effector (EE), and the leg bracelet). In addition, experiments will be conducted to evaluate the performance of the ExoM-S when the user's posture changes during task performance. Finally, muscle signals (Electromyography) will be analyzed to characterize the behavior of muscles while using ExoM-S.