1 Introduction

The piezoelectric ultrasonic transducer is one of the most important components in ultrasonically assisted manipulating, machining, and manufacturing processes, such as thermosonic bonding for the packaging of integrated circuit (IC) chips [1,2,3]. With the rapid development of microelectronic techniques, IC chips with high density, multilead, and fine space characteristics have been increasingly applied. For high efficiency and interconnection reliability, high-frequency piezoelectric ultrasonic transducers with a resonant frequency of more than 100 kHz are widely used [4,5,6]. In general, the ultrasonic transducers used in thermosonic bonding adopt a sandwich structure, which consists of a back slab, a piezoceramic stack, and a tapered ultrasonic horn and is responsible for transferring the mechanical vibration to the working end of the transducer and amplifying this vibration [7].

The steady-state vibration amplitude is an important performance indicator of a high-frequency ultrasonic transducer and can be used to measure the level of ultrasonic energy utilization. It is commonly sensitive to many factors, such as structural characteristics and parameters, assembly, and applied exciting voltage and frequency. Hence, a high-reliability calculation model is essential to efficiently control the steady-state vibration amplitude of ultrasonic transducers. Using the equivalent circuit of the piezoelectric ultrasonic transducer as a basis, Cai et al. [8, 9] modeled the vibration amplitude based on a bilateral capacitance compensation method. The test results proved the effectiveness of the model. By combining the equivalent kinetics model and the vibration equation, Zhou et al. [10] developed a calculation model that can obtain the vibration amplitude of ultrasonic transducers with different quality factors. For a high-power ultrasonic transducer, Saffar et al. [11] investigated the correlation between the heat caused by friction of different parts and the wave amplitude during propagation and then proposed a method for the online estimation of the vibration amplitude of the transducer. Zhao et al. [12] developed an amplitude calculation model for ultrasonic transducers by combining the piezoelectric and vibration equations.

In recent years, composite structure-based multibranch ultrasonic transducers have attracted increasing interest owing to their bright application prospect in thermosonic bonding with large energy requirements, such as heavy wire and multistrand cable bonding for battery harnesses and Insulated Gate Bipolar Transistor modules [13, 14]. Dymel et al. [15] designed a four-branch ultrasonic transducer to create Cu-Cu electrical interconnection; the results demonstrated that the resultant vibration of the dual-dimensional ultrasonic vibration can provide large ultrasonic energy, which is beneficial for bonding the workpiece with a large contact area and improving the electric interconnection reliability. Asami et al. [16] proposed a dual-branch transducer that combines a torsional and a longitudinal vibration at its working end. Schemmel et al. [17] designed a multibranch transducer that can operate under a circular or rectangular pattern. Liu et al. [18, 19] designed various multibranch ultrasonic transducers that can be used in ultrasonic motors. Given that multibranch ultrasonic transducers mechanically connect some traditional single-branch transducers in parallel or series, their resultant output presents great complexity. For efficient control, modeling the vibration amplitude of this new kind of multibrand transducer is necessary.

Our recent research proposed a new type of dual-branch cascaded composite structure-based ultrasonic transducer that possesses two groups of piezoceramic stacks [20]. Under separate excitation of either stack, both working ends of the transducer can output ultrasonic vibration. When two piezoceramic stacks are operated simultaneously, the outputs of both working ends can be enhanced due to the constructive interference of two ultrasonic waves. To promote the practical application of the newly proposed transducer, the present research developed a calculation model for its steady-state vibration amplitude.

2 New Type of Composite Structure Ultrasonic Transducer

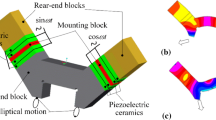
A 3D model of the newly proposed cascaded composite structure-based ultrasonic transducer is illustrated in Fig. 1. The transducer has two piezoceramic stacks, each of which involves a pair of PZT-4 rings. Two ultrasonic horns of the transducer adopt different profiles, with the left one consisting of a cylindrical section, a conical section, and a stepped section, and the right one having two cylindrical sections and two conical sections.

Fig. 1
figure 1

Cascaded composite structure-based ultrasonic transducer

Full size image

For convenience of expression, the left horn is named the stepped horn, and the right horn is the conical horn. The stack near the stepped horn is labeled as stack A, and that near the conical horn is stack B. At the center of the transducer lies a mounting clamp used to install the whole transducer on a mounting bracket during usage. The mounting clamp has two flexible parallelogram mechanisms in its connecting arms between the mounting bracket and transducer, which can offer a translation pair in the longitudinal direction of the transducer. The primary dimensional parameters of the ultrasonic transducer are marked in Fig. 1, and their values are listed in Table 1.

Table 1 Dimensional parameters of the ultrasonic transducer
Full size table

The mode analysis of the transducer is shown in Fig. 2a. The transducer can work in a longitudinal vibration mode at a frequency of 129.936 kHz. Figure 2b describes the ultrasonic energy transfer vector of the transducer under the longitudinal vibration mode. The mechanical vibration is generated by the piezoceramic stack and then magnified by the ultrasonic horn before being delivered to the two horn tips. The longitudinal vibration shape of the transducer is provided in Fig. 2c, which shows that the longitudinal vibration can be transferred to both ends along the longitudinal direction (z-axis). Meanwhile, the maximum vibration amplitude just appears at the two horn tips (working ends).

Fig. 2
figure 2

Modal analysis results, a longitudinal vibration mode, b ultrasonic energy transmission vector, and c longitudinal vibration shape of the proposed transducer

Full size image

As mentioned above, the transducer can be operated in a separate excitation of one piezoceramic stack or in a simultaneous excitation of both stacks. When operated in the longitudinal vibration mode, the transducer can be thought of as a connection of three basic structural units involving a cylindrical rod with a constant cross section (CCS), a cylindrical rod with a variable cross section (VCS), and piezo stacks.

3 Calculation Models for the Vibration Amplitude of the Structural Units

3.1 Vibration amplitude of the piezo stack

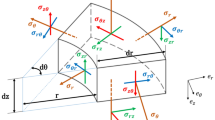
The piezoceramic stack of an ultrasonic transducer can be considered a piezo rod with an applied electric field parallel to the propagation direction of the ultrasonic wave. Figure 3 illustrates the longitudinal oscillation of a pair of piezoceramic rings under an exciting voltage of U. The current flowing through the piezoceramic rings can be calculated by \(I = 2\pi fq\), where \(f\) is the exciting frequency and \(q\) denotes the electric charge. The total thickness of the two piezo rings is labeled as \(l_{5}\)(Fig. 1), and the cross section area is represented by \(A_{5}\). \(F_{1}\) and \(F_{2}\) denote the external forces applied to the end faces, and \(\dot{\xi }_{1}\) and \(\dot{\xi }_{2}\) are the vibration velocities.

Fig. 3
figure 3

Oscillation of piezoceramic rings

Full size image

Given the electrical field is imposed along the z-axis (i.e., the longitudinal direction),\(E_{3} \ne 0\) (\(E_{3} = U/l_{5}\)), and \(E_{1} = E_{2} = 0\). Meanwhile, the stress \(T_{3} \ne 0\)(\(T_{3} = F_{1} /A_{5}\)), and those in other directions are zero, i.e.,\(T_{1} = T_{2} = T_{4} = T_{5} = T_{6} = 0\). Considering that the electrical displacement of the head face of the piezoceramic ring is evenly distributed, \(\partial D_{3} /\partial z = 0\) (where \(D_{3} = q/A_{5}\)). In this case, \(D_{3}\) and \(T_{3}\) can be selected as the independent variables, and strain \(S_{3}\) (\(S_{3} = x_{0} /l_{5}\), where \(x_{0}\) is the displacement, i.e., vibration amplitude under a harmonic excitation, along the longitudinal direction) and electric field intensity \(E_{3}\) are the dependent variables to constitute a g-type piezoelectric equation, given by

$$\left\{ {\begin{array}{*{20}c} {S_{3} = s_{33}^{D} T_{3} + g_{33} D_{3} } \\ {E_{3} = \beta_{33}^{T} D_{3} - g_{33} T_{3} } \\ \end{array} } \right.$$
(1)

where \(s_{33}^{D}\) is the elastic compliance coefficient at a constant electrical displacement, \(g_{33}\) is the piezoelectric coefficient, and \(\beta_{33}^{T}\) is the permittivity under constant stress. Equation (1) can also be written as

$$\left\{ {\begin{array}{*{20}c} {\frac{{x_{0} }}{{l_{5} }} = \frac{{s_{33}^{D} }}{{A_{5} }}F_{1} + \frac{1}{{2\pi fA_{5} }}g_{33} } \\ {\frac{U}{{l_{5} }} = \frac{1}{{2\pi fA_{5} }}\beta_{33}^{T} - \frac{{F_{1} }}{{A_{5} }}g_{33} } \\ \end{array} } \right.$$
(2)

Thus, the steady-state vibration amplitude \(x_{0}\) of the piezoceramic stack under harmonic excitation can be expressed as follows:

$$x_{0} = - \frac{{s_{33}^{D} }}{{g_{33} }}U + \left( {\frac{{s_{33}^{D} l_{5} \beta_{33}^{T} }}{{2\pi fA_{5} g_{33} }} + \frac{{l_{5} g_{33} }}{{2\pi fA_{5} }}} \right)I$$
(3)

3.2 Vibration Equations of VCS and CCS Rods

A VCS cylindrical rod under longitudinal vibration is illustrated in Fig. 4, where \(l_{i}\) denotes its length, \(F_{1}\) and \(F_{2}\) denote the external forces applied to the large and small ends, respectively; \(\dot{\xi }_{1}\) and \(\dot{\xi }_{2}\) represent vibration velocities, and \(A_{1}\) and \(A_{2}\) are the sectional areas of the large and small ends, respectively.

Fig. 4
figure 4

Longitudinal vibration of VCS cylindrical rod

Full size image

The vibration equation of a VCS rod can be given by

$$\frac{{\partial^{2} \xi }}{{\partial z^{2} }} + \frac{1}{A(x)}\frac{\partial A(z)}{{\partial z}}\frac{\partial \xi }{{\partial z}} + K^{2} \xi = 0$$
(4)

where \(A(z)\) is a sectional area function, \(K = {\omega \mathord{\left/ {\vphantom {\omega c}} \right. \kern-0pt} c}\) is the wavenumber (\(\omega\) is the angular frequency), and \(c = \sqrt {{E \mathord{\left/ {\vphantom {E \rho }} \right. \kern-0pt} \rho }}\) is the equivalent sound velocity of the ultrasonic wave in the VCS rod. \(E\) and \(\rho\) are Young’s modulus and density of the rod, respectively. Given that the CCS rod can be thought of as a special case of a VCS rod (\(A(z){ = }A_{1} = A_{2} = A\)), its vibration equation can be written based on Eq. (4) as

$$\frac{{\partial^{2} \xi }}{{\partial z^{2} }} + K^{2} \xi = 0$$
(5)

The solution of the above equation can be written as

$$\xi (z) = C_{1} \cos (kz) + C_{2} \sin (kz)$$
(6)

where \(C_{1}\) and \(C_{2}\) are defined as displacement coefficients.

3.3 Vibration Transfer Equations of CCS and VCS Rods

Given the displacement continuous condition and the force equilibrium conditions at the interface between sections, we obtain

$$\left\{ \begin{gathered} \xi \left( {l_{i}^{r} } \right) = \xi \left( {l_{i + 1}^{l} } \right) \hfill \\ E_{i} A_{i} \frac{{\partial \xi \left( {l_{i}^{r} } \right)}}{\partial z} = E_{i + 1} A_{i + 1} \frac{{\partial \xi \left( {l_{i + 1}^{l} } \right)}}{\partial z} \hfill \\ \end{gathered} \right.$$
(7)

where \(i = 1,2, \cdots ,9\) corresponds to every section of the transducer, and \(E_{i}\) is the elasticity modulus of the ith section. The superscript \(r\) in \(l_{i}^{r}\) represents the right end of the ith section. Similarly, \(l\) in \(l_{i + 1}^{l}\) denotes the left end of the (i + 1)th section. Referring to Eq. (7), a group of equations can be developed as shown below:

$$\left\{ \begin{gathered} \xi_{2}^{l} = C_{11} \cos \left( {k_{1} l_{1} } \right) + C_{12} \sin \left( {k_{1} l_{1} } \right) \hfill \\ E_{2} A_{2} k_{2} C_{22} = E_{1} A_{1} k_{1} \left[ { - C_{11} \sin \left( {k_{1} l_{1} } \right) + C_{12} \cos \left( {k_{1} l_{1} } \right)} \right] \hfill \\ \xi_{3}^{l} = C_{21} \cos \left( {k_{2} l_{2} } \right) + C_{22} \sin \left( {k_{2} l_{2} } \right) \hfill \\ E_{3} A_{3} k_{3} C_{32} = E_{2} A_{2} k_{2} \left[ { - C_{21} \sin \left( {k_{2} l_{2} } \right) + C_{22} \cos \left( {k_{2} l_{2} } \right)} \right] \hfill \\ \xi_{4}^{l} = C_{31} \cos \left( {k_{3} l_{3} } \right) + C_{32} \sin \left( {k_{3} l_{3} } \right) \hfill \\ E_{4} A_{4} k_{4} C_{42} = E_{3} A_{3} k_{3} \left[ { - C_{31} \sin \left( {k_{3} l_{3} } \right) + C_{32} \cos \left( {k_{3} l_{3} } \right)} \right] \hfill \\ \xi_{5}^{l} = C_{41} \cos \left( {k_{4} l_{4} } \right) + C_{42} \sin \left( {k_{4} l_{4} } \right) \hfill \\ E_{5} A_{5} k_{5} C_{52} = E_{4} A_{4} k_{4} \left[ { - C_{41} \sin \left( {k_{4} l_{4} } \right) + C_{42} \cos \left( {k_{4} l_{4} } \right)} \right] \hfill \\ \xi_{6}^{r} = C_{72} \cos \left( {k_{7} l_{7} } \right) + C_{71} \sin \left( {k_{7} l_{7} } \right) \hfill \\ E_{6} A_{6} k_{6} C_{62} = E_{7} A_{7} k_{7} \left[ { - C_{72} \sin \left( {k_{7} l_{7} } \right) + C_{71} \cos \left( {k_{7} l_{7} } \right)} \right] \hfill \\ \xi_{7}^{r} = C_{82} \cos \left( {k_{8} l_{8} } \right) + C_{81} \sin \left( {k_{8} l_{8} } \right) \hfill \\ E_{7} A_{7} k_{7} C_{72} = E_{8} A_{8} k_{8} \left[ { - C_{82} \sin \left( {k_{8} l_{8} } \right) + C_{81} \cos \left( {k_{8} l_{8} } \right)} \right] \hfill \\ \xi_{8}^{r} = C_{92} \cos \left( {k_{9} l_{9} } \right) + C_{91} \sin \left( {k_{9} l_{9} } \right) \hfill \\ E_{8} A_{8} k_{8} C_{82} = E_{9} A_{9} k_{9} \left[ { - C_{92} \sin \left( {k_{9} l_{9} } \right) + C_{91} \cos \left( {k_{9} l_{9} } \right)} \right] \hfill \\ \xi_{9}^{r} = C_{102} \cos \left( {k_{10} l_{10} } \right) + C_{101} \sin \left( {k_{10} l_{10} } \right) \hfill \\ E_{9} A_{9} k_{9} C_{92} = E_{10} A_{10} k_{10} \left[ { - C_{102} \sin \left( {k_{10} l_{10} } \right) + C_{101} \cos \left( {k_{10} l_{10} } \right)} \right] \hfill \\ \end{gathered} \right.$$
(8)

When a matrix representation is adopted, the equations corresponding to every section of the stepped horn can be written as

$$\left[ \begin{gathered} C_{j1} \hfill \\ C_{j2} \hfill \\ \end{gathered} \right] = {\varvec {T}}_{i} \left[ \begin{gathered} C_{i1} \hfill \\ C_{i2} \hfill \\ \end{gathered} \right] = \left[ {\begin{array}{*{20}c} {\cos \left( {k_{i} l_{i} } \right)} & {\sin \left( {k_{i} l_{i} } \right)} \\ { - \frac{{E_{i} S_{i} k_{i} }}{{E_{j} S_{j} k_{j} }}\sin \left( {k_{i} l_{i} } \right)} & {\frac{{E_{i} S_{i} k_{i} }}{{E_{j} S_{j} k_{j} }}\cos \left( {k_{i} l_{i} } \right)} \\ \end{array} } \right]\left[ \begin{gathered} C_{i1} \hfill \\ C_{i2} \hfill \\ \end{gathered} \right]$$
(9)

where \(i = 1, \cdots ,4\) and \(j = i + 1\). \({\varvec {T}}_{i}\) is a transfer coefficient matrix.

Similarly, the vibration transfer equations of all sections of the conical horn can be written as

$$\left[ \begin{gathered} C_{n1} \hfill \\ C_{n2} \hfill \\ \end{gathered} \right] = {\varvec {T}}_{i} \left[ \begin{gathered} C_{i2} \hfill \\ C_{i1} \hfill \\ \end{gathered} \right] = \left[ {\begin{array}{*{20}c} {\cos \left( {k_{i} l_{i} } \right)} & {\sin \left( {k_{i} l_{i} } \right)} \\ { - \frac{{E_{i} S_{i} k_{i} }}{{E_{j} S_{j} k_{j} }}\sin \left( {k_{i} l_{i} } \right)} & {\frac{{E_{i} S_{i} k_{i} }}{{E_{j} S_{j} k_{j} }}\cos \left( {k_{i} l_{i} } \right)} \\ \end{array} } \right]\left[ \begin{gathered} C_{i2} \hfill \\ C_{i1} \hfill \\ \end{gathered} \right]$$
(10)

where \(i = 7, \cdots ,10\) and \(n = i - 1\). Thus,

$$\left[ \begin{gathered} C_{51} \hfill \\ C_{52} \hfill \\ \end{gathered} \right] = {\varvec {T}}\left[ \begin{gathered} C_{11} \hfill \\ C_{12} \hfill \\ \end{gathered} \right] = {\varvec {T}}_{4} \cdot {\varvec {T}}_{3} \cdot {\varvec {T}}_{2} \cdot {\varvec {T}}_{1} = \left[ {\begin{array}{*{20}c} {T_{a} } & {T_{b} } \\ {T_{c} } & {T_{d} } \\ \end{array} } \right]\left[ \begin{gathered} C_{11} \hfill \\ C_{12} \hfill \\ \end{gathered} \right]$$
(11)
$$\left[ \begin{gathered} C_{51} \hfill \\ C_{52} \hfill \\ \end{gathered} \right] = {\varvec {T}}\left[ \begin{gathered} C_{102} \hfill \\ C_{101} \hfill \\ \end{gathered} \right] = {\varvec {T}}_{6} \cdot {\varvec {T}}_{7} \cdot {\varvec {T}}_{8} \cdot {\varvec {T}}_{9} \cdot {\varvec {T}}_{10} = \left[ {\begin{array}{*{20}c} {T_{a1} } & {T_{b1} } \\ {T_{c1} } & {T_{d1} } \\ \end{array} } \right]\left[ \begin{gathered} C_{102} \hfill \\ C_{101} \hfill \\ \end{gathered} \right]$$
(12)

The VCS section of the proposed transducer, such as Num. 3, 9, and 10 in Fig. 2, can be viewed as a connection of a series of CCS rods, as shown in Fig. 5. Therefore, according to Eqs. (9)–(12), we can obtain the vibration transfer equation of the VCS section and the coefficient matrix.

Fig. 5
figure 5

Equivalent transformation of VCS rod

Full size image

3.4 Calculation model for vibration amplitude output

According to Eq. (6), the vibration amplitude functions of the two working ends of the transducer can be expressed as

$$\xi_{1} (z_{1} ) = C_{11} \cos \left( {k_{1} z_{1} } \right) + C_{12} \sin \left( {k_{1} z_{1} } \right)$$
(13)
$$\xi_{10} (z_{10} ) = C_{102} \cos \left( {k_{10} z_{10} } \right) + C_{12} \sin \left( {k_{10} z_{10} } \right)$$
(14)

During the design of the ultrasonic transducer, the total length of the transducer is set equal to two wavelengths, as shown in Fig. 2c, to ensure that the transducer can produce its maximum vibration outputs at the two tips. Therefore, according to Eqs. (13)–(14), the maximum outputs can be calculated by

$$\max \left( {\xi_{1} (z_{1} )} \right) = \left. {\xi_{1} (z_{1} )} \right|_{{z_{1} = 0}} = C_{11}$$
(15)
$$\max \left( {\xi_{10} (z_{10} )} \right) = \left. {\xi_{10} (z_{10} )} \right|_{{z_{10} = 0}} = C_{102}$$
(16)

Furthermore, the vibration amplitude function of the two output ends of the transducer can also be written as

$$\xi_{1} (z) = \sqrt {C_{11}^{2} + C_{12}^{2} } \sin (k_{1} z_{1} + \beta_{1} )$$
(17)
$$\xi_{10} (z_{10} ) = \sqrt {C_{101}^{2} + C_{102}^{2} } \sin (k_{10} z_{10} + \beta_{10} )$$
(18)

where \(\beta_{1} = \arctan ({{C_{12} } \mathord{\left/ {\vphantom {{C_{12} } {C_{11} }}} \right. \kern-0pt} {C_{11} }})\) and \(\beta_{10} = \arctan ({{C_{101} } \mathord{\left/ {\vphantom {{C_{101} } {C_{102} }}} \right. \kern-0pt} {C_{102} }})\). From Eqs. (15)-(18), we can obtain \(\sqrt {C_{11}^{2} + C_{12}^{2} } = C_{11}\) and \(\sqrt {C_{101}^{2} + C_{102}^{2} } = C_{102}\). Thus, \(C_{12} = C_{101} = 0\). Therefore,

$$C_{51} = T_{a} C_{11} = T_{a1} C_{102}$$
(19)
$$C_{52} = T_{c} C_{11} = T_{c1} C_{102}$$
(20)

When the piezoceramic stack A operates under separate excitation, its vibration equation can be given by

$$\xi_{5} (z_{5} ) = C_{51} \cos \left( {k_{5} z_{5} } \right) + C_{52} \sin \left( {k_{5} z_{5} } \right)$$
(21)

Given \(x_{0}\) in Eq. (3) can also be calculated by

$$x_{0} = \left. {\xi_{5} \left( {z_{5} } \right)} \right|_{{z_{5} = 0}} - \left. {\xi_{5} \left( {z_{5} } \right)} \right|_{{z_{5} = l_{5} }}$$
(22)

Thus, the following equations can be achieved:

$$\begin{gathered} x_{0} = C_{11} M_{r} = C_{11} \left[ {T_{a} - T_{a} \cos \left( {k_{5} l_{5} } \right) - T_{c} \sin \left( {k_{5} l_{5} } \right)} \right] \hfill \\ x_{0} = C_{102} M_{l} = C_{102} \left[ {T_{a1} - T_{a1} \cos \left( {k_{5} l_{5} } \right) - T_{c1} \sin \left( {k_{5} l_{5} } \right)} \right] \hfill \\ \end{gathered}$$
(23)

By combining Eqs. (23) and (3), we can calculate the maximum steady-state vibration amplitude of the two working ends of the transducer

$$C_{11} = - \frac{{s_{33}^{D} }}{{g_{33} M_{r} }}U + \frac{1}{{M_{r} }}\left( {\frac{{s_{33}^{D} l_{5} \beta_{33}^{T} }}{{2\pi fA_{5} g_{33} }} + \frac{{l_{5} g_{33} }}{{2\pi fA_{5} }}} \right)I$$
(24)
$$C_{102} = - \frac{{s_{33}^{D} }}{{g_{33} M_{l} }}U + \frac{1}{{M_{l} }}\left( {\frac{{s_{33}^{D} l_{5} \beta_{33}^{T} }}{{2\pi fA_{5} g_{33} }} + \frac{{l_{5} g_{33} }}{{2\pi fA_{5} }}} \right)I$$
(25)

In light of the above analysis, relevant prediction models are easy to construct when only stack B is used.

4 Performance of the Calculation Model

The composite structure ultrasonic transducer was fabricated to test the performance of the developed calculation models, and a photo of the prototype is shown in Fig. 6. An experimental system was then developed, and a sample experimental scene is shown in Fig. 7. An ultrasonic signal generator and a power amplifier were combined to excite the transducer. During trials, the transducer was installed on a mounting bracket fixed on a vibration isolation platform, and the vibration amplitude signals of the two working ends were measured using a laser Doppler vibrometer (Vector-speed, OPTOMET GmbH) and sampled by a signal acquisition device (USB6366, NI Inc.) with a sampling rate of 2 MHz. The true root-mean-square values of the exciting voltage and the current of the piezoceramic stacks were also measured.

Fig. 6
figure 6

Prototype of the proposed ultrasonic transducer

Full size image
Fig. 7
figure 7

Photo of the experimental system

Full size image

Before the exciting trials, the resonant frequency of the transducer was measured using an Impedance Analyzer of PV80A (Bei**g Band ERA Co., Ltd.), and the results are shown in Fig. 8. The resonant frequency corresponds to the minimum of the impedance curve. The transducer has a resonant frequency of 129.928 kHz when piezoceramic stack A is connected to the analyzer (Fig. 8a) and 129.420 kHz when stack B is connected (Fig. 8b).

Fig. 8
figure 8

a Impedance- and phase-frequency curves of the transducer: a the piezoceramic stack A is excited individually, and b stack B is excited individually

Full size image

On the basis of the measured resonant frequencies, a series of exciting experiments were carried out using five exciting voltage levels from 10 Vp-p to 18 Vp-p with an increment of 2 V. When piezoceramic stack A was excited, the vibration amplitude signals of the two horn tips were measured, and the results are shown in Fig. 9. The outputs of the stepped horn are displayed in Fig. 9a, and those of the conical horn are illustrated in Fig. 9b. The steady-state vibration amplitude of both ends increases with the exciting voltage.

Fig. 9
figure 9

Vibration amplitude of two ultrasonic horns of the transducer under different exciting voltages when only piezoceramic stack A is excited: a stepped horn and b conical horn

Full size image

Figure 10 displays the vibration response of two working ends when the piezoceramic stack B operates under a separate excitation condition. Figure 10a shows the vibration amplitude outputs of the stepped horn and (b) illustrates the vibration outputs of the conical horn. The same change tendency can be observed when the exciting voltage increases.

Fig. 10
figure 10

Vibration amplitude of two ultrasonic horns of the transducer under different exciting voltages when only the piezoceramic stack B is excited: a stepped horn and b conical horn

Full size image

The steady-state vibration amplitude values can be extracted from the measured vibration amplitude signals, and a series of calculation values were obtained from Eqs. (24) and (25). Comparison in Fig. 11 shows a good agreement between the calculated and measured results. The deviation analysis results are listed in Table 2. The maximum deviation between the calculated and measured results is 0.0221 μm, the minimum deviation is 0.0013 μm, the average deviation is 0.0097 μm, and the standard deviation is 0.0046 μm. These values demonstrated that the developed calculation models are effective and reliable.

Fig. 11
figure 11

Comparison between the calculated and measured results, a and b steady-state vibration amplitude of the two working ends of the transducer when only the piezoceramic stack A is excited, and c and d those of the transducer when only the piezoceramic stack B is excited

Full size image
Table 2 Error analysis of the calculated and measured results
Full size table

5 Conclusions

The new composite structure-based ultrasonic transducer has a wide application prospect in thermosonic bonding for the packaging of IC chips. This research aimed to develop a calculation model for the steady-state vibration amplitude output of the newly proposed dual-branch cascaded composite structure ultrasonic transducer in our previous work. The steady-state amplitude of the piezoceramic stack was derived from the piezoelectric equation. The vibration transfer matrices of the stepped and conical horns were constructed by combining the vibration equation with the displacement continuous condition and force equilibrium condition between different sections of the transducer. Calculation models for the steady-state vibration amplitude of the two working ends of the proposed ultrasonic transducer were then established while focusing on the exciting voltage, current, and resonance frequency. For the evaluation of the performance of the developed calculation models, the proposed ultrasonic transducer was fabricated, and an experimental system was set up and used for a series of resonance excitation trials. The vibration amplitude signals of the stepped and conical horns and the exciting voltage and current were measured, and the steady-state vibration amplitude under different excitation conditions was calculated using the developed calculation models. Comparison between the calculated and measured results showed that the maximum deviation is 0.0221 μm, the minimum deviation is 0.0013 μm, the average deviation is 0.0097 μm, and the standard deviation is 0.0046 μm. These values manifested that the developed calculation models are effective and have good calculation accuracy, laying a good foundation for the control of the newly proposed ultrasonic transducer.