1 Introduction

Shale gas is receiving a growing attention in Sichuan basin of southwestern China recently. The thickness of the Silurian Longmaxi (LMX) Formation shale ranges from 65 to 516 m, which consists of graptolite-rich transgressive shales and suggests an ideal horizon for exploration and development (Chen et al. 2011; Liu et al. 2011). However, wellbore stability has significantly affected the Rig-site process and economic consume in LMX formation that is characterized by high elastic and strength anisotropy (Chen et al. 2011; Liu et al. 2011; Zhang et al. 2017b). According to previous drilling experience and related research (Westergaard 1940; Seth et al. 1968a, b), it is necessary to recognize the influence of anisotropy on shale instability.

Borehole stability analysis contains two parts, near wellbore stress distribution and rock strength criterion. Investigation on instability of well was first carried out based on the assumption of linear elastic and isotropic by Bradley (Bradley 1979), but this model didn’t consider the influence of elastic anisotropy nor strength anisotropy on wellbore stability, which brought various hazards in drilling operation, especially, for wells drilled in bedding layers (Økland et al. 1998; Zhang et al. 2013; Zhang et al. 2017a, b; Aadnøy et al. 2019). The strength of shales owning transverse isotropy characteristic, behaves direction-dependent. (Willson et al. 2007; Lee et al. 2012; Amadei et al. 2012; Huang et al. 2012a, b; Alqahtani et al. 2013; Zhang et al. 2015; Bautmans et al. 2018; Iferobia et al. 2019). Jaeger (Jaeger 1960) reported the plane of weakness model for shale firstly, which demonstrated that strength of shale depends on two components namely intact rock matrix strength and strength of bedding plane. The plane of weakness model proposed based on the well-known Mohr–Coulomb criterion has been applied to wellbore instability analysis by many researchers (Borsetto et al. 1984; Chenevert et al. 2001; Ghorbani et al. 2009; Bai et al. 2013; Ismael et al. 2017).

Except for anisotropic strength, elastic anisotropy is another important characteristic for borehole stability in shales. The elastic anisotropy is caused not only by bedding plane, but also the existence of natural fractures (Amadei 1984; Ong et al. 1993; Abousleiman et al. 1995). Previous studies taking shales as isotropic medium made the predicted mud weight lower than collapse pressure, due to the increasing of circumferential stress induced by elastic anisotropy (Ding et al. 2018; Aadnoy 1989; Zhang et al. 2021a, b; Ren et al. 2023; Yin et al. 2022). Lu et al. (2013) discovered that porous flow in fractures aggravated wellbore instability, but their works ignored the effect of elastic anisotropic on borehole stress distribution. Wellbore stress distribution in layered shales was established firstly by Lekhnitskii (1963), then the influence of other factors such as temperature (Ewy et al. 2005; Zhang et al. 2015; Gao et al. 2017), pore pressure (Ekbote et al. 2000; Ghassemi et al. 2002; Huang et al. 2012a, b; Zhou et al. 2018), seepage (Nagel et al. 2013; Kanfar et al. 2015; Dokhani et al. 2016) on wellbore stability was reached with elastic anisotropy considered.

Another important aspect for wellbore stability in shales is water, shale is rich in clay minerals which have a strong chemical reaction with water, so oil-based mud is widely used. But oil-based mud has comparatively high price and is harmful to environment, the development of shale gas by water—based drilling fluid is very promising. Before the develo** of a favorable water-based drilling fluid for shale, the impact of water on shale structure and mechanics should be analyzed. The wellbore stability model proposed by Dokhani et al. (2016) implanted the interaction of aqueous fluids with clay minerals, however, the shale formation was considered as isotropic medium. Liu et al. (2016) revealed the strength anisotropy, elastic anisotropy induced by bedding planes and natural fractures, while in terms of the strength anisotropy, the strength of shale predicted by single plane strength criterion has a low accuracy.

In conclusion, the elastic anisotropy, strength anisotropy and hydration should be assessed in wellbore stability analysis in shale reservoir. Besides, the effect of natural fractures on wellbore stresses should also be considered. In this study, the strength of LMX shales with various moisture content and bedding plane orientations in the reference is fitted by three anisotropic strength criteria, then a novel borehole stability model considering the impact of elastic anisotropy introduced by sedimentation effect and natural fractures located in the bedding plane is proposed. The obtaining of a more precise collapse pressure for shale formation is conducive to improve practical drilling efficiency in the field.

2 Anisotropic strength of shale with different water absorption

2.1 Review of layered rock failure criterion

It is well-known that strength of shale is characterized by anisotropic, although many researchers have put enormous efforts into modeling the strength of transversely isotropic medium, no unified assessment has emerged yet. The existing anisotropic strength model can be categorized into three types, mathematical and empirical criteria (Saeidi et al. 2014), continuous and discontinuous criteria (Fjær et al. 2014). In view of anisotropic strength curve with various orientations, anisotropic strength criteria can be divided into three types, i.e., shoulder, U and undulatory type (Ramamurthy 1993; Tien et al. 2001). The type of discontinuous criteria can reveal the distinction between rock matrix failure and bedding plane failure (Fjær et al. 2014). While layered shales have a sophisticated failure mechanism which jump between the bedding planes and rock matrix (Ambrose et al. 2014). Results predicted by discontinuous criteria always have a larger deviation in the transition zone between rock matrix failure and bedding plane failure. The failure criteria for anisotropic shale should be selected carefully, three kinds of criteria are reviewed in this work, the Jaeger’s plane of weakness model belongs to mathematical-discontinuous-shoulder type, the plane of patchy weakness model belongs to mathematical-discontinuous-undulatory type, the Pariseau’s model belongs to mathematical-continuous-U type (Hoek and Brown 1980; He et al. 2016; Zhu et al. 2019).

2.1.1 Jaeger’s plane of weakness model

The single plane of weakness model was first proposed by Jaeger (1960) based on Mohr conception, which is most widely used to predict shale strength. The failure model for rock matrix is given in Eq. (1),

$$\sigma_{1} - \sigma_{3} = 2\left( {S_{o} + \sigma_{3} \tan \phi_{o} } \right)\left( {\sqrt {1 + \tan^{2} \phi_{o} } + \tan \phi_{o} } \right)$$
(1)

In which, So cohesion, MPa; friction angle ϕo is the internal friction angle, °. The failure model for bedding plane is shown as Eq. (2),

$$\tau_{{\text{m}}} = \frac{{\sigma_{{\text{m}}} \sin \phi_{{{\text{bp}}}} + S_{{{\text{bp}}}} \cos \phi_{{{\text{bp}}}} }}{{\sin \left( {2\beta - \phi_{{{\text{bp}}}} } \right)}}$$
(2)

where σm is the mean normal stress, σ m = (σ1 + σ3)/2, MPa; τm is the maximum shear stress on bedding plane, τm = (σ1-σ3)/2, MPa; σ1 is maximum principal stress, MPa; σ3 is minimum principal stress, MPa; Sbp is the cohesion of bedding plane, MPa; ϕbp is the internal friction angle of bedding plane, °; β is angle between the maximum principal stress and normal of the bedding plane, °.

2.1.2 Plane of patchy weakness model

The plane of patchy weakness model (Fjær et al. 2013 and 2014) is extended on the conception of Jaeger’s plane of weakness, which holds that the plane of weakness contains some weak patches. A lower loading force will cause a higher local stress, consequently, the global failure of shale rocks occurs at a lower external stress. The model for intrinsic rock and plane of weak patchy failure strength are followed as Eqs. (3) and (4),

$$\sigma_{1} - \sigma_{3} = 2\left( {1 - \eta \sin^{2} 2\beta } \right)\frac{{S_{o} \cos \phi_{o} + \sigma_{3} \sin \phi_{o} }}{{1 - \sin \phi_{o} }}$$
(3)
$$\sigma_{1} - \sigma_{3} = 2\left( {1 - \eta \sin^{2} 2\beta } \right)\frac{{S_{{{\text{bp}}}} \cos \phi_{{{\text{bp}}}} + \sigma_{3} \sin \phi_{{{\text{bp}}}} }}{{\sin 2\beta \cos \phi_{{{\text{bp}}}} - \left( {\cos 2\beta + 1} \right)\sin \phi_{{{\text{bp}}}} }}$$
(4)

In which, \(\eta\) is a dimensionless parameter that represents the property of weak patchy. For the case, no weak patches exist in the bedding plane, \(\eta\) is zero, the model degrades to single plane weak plane criterion.

2.1.3 Pariseau’s model

Pariseau’s model (Pariseau 1968) satisfying the symmetry requirements for the transversely isotropic medium, is an extensive form of Drucker–Prager model. The anisotropic strength with variational bedding orientations predicted by this criterion is continuous and smooth, besides, the model can reveal the strength difference between isotropic plane and anisotropic plane. Pariseau’s model is expressed by Eq. (5),

$$\sigma_{1} = \sigma_{3} + \frac{{1 + \sigma_{3} \left( {U + 2V} \right)}}{{\sqrt {F\sin^{4} \beta + G\left( {\cos^{4} \beta + \cos^{2} 2\beta } \right) + 0.25M\sin^{2} 2\beta } - U\cos^{2} \beta - V\sin^{2} \beta }}$$
(5)

where F, G, M, U and V are rock property parameters determined by laboratory experiments.

2.2 Analysis of experimental results

Once the strength criterion is determined, strength parameters should be calculated carefully based on experimental data. In this paper, shale strength conducted by Zhang in reference (Liu et al. 2022) is cited, data fitting approach presented by Ambrose et al. (2014) is adopted to determine the strength parameters, wherein the parameters are selected to provide a global minimum magnitude for the root-mean-squared error that shows as Eq. (6),

$${\text{RMSE}} = \sqrt {\sum\nolimits_{i = 1}^{N} {\left( {\sigma_{i}^{test} - \sigma_{i}^{predict} } \right)/N} }$$
(6)

where N is the tested sample number, \(\sigma_{i}^{test}\) and \(\sigma_{i}^{predict}\) are experimental failure strength, and the predicted failure strength for the sample labeled i, respectively, MPa; the range of those strength parameters is refined step by step in MATLAB, the optimum parameters with least RMSE that can be found iteratively. The brief computed process is described in reference (Tien 2001).

The experimental strength datasets (Zhang et al. 2020) are shown in Figs. 1, 2 and 3, where they have been fitted to the plane of weakness model, weakness Patchiness model and Pariseau’s model, respectively. The strength data indicated that shale with β = 0° has the maximum strength, minimum strength is encountered at about β = 60°, the strength of shale with β = 0° and β = 90° have a prominent difference. Besides, all samples showed increased strength at higher confining pressure, but reduced strength with higher moisture content. The failure of anisotropic rock depends not only on the hydrostatic pressure and relative angle from the axial loading to the normal vector of the bedding plane, but also on the water content, those affecting factors should be considered in doing rock engineering analysis.

Fig. 1
figure 1

Experimental data with different moisture content fitted by plane of weakness model

Full size image
Fig. 2
figure 2

Experimental data with different moisture content fitted by plane of patchy weakness model

Full size image
Fig. 3
figure 3

Experimental data with different moisture content fitted by Pariseau’s model

Full size image

By comparing the failure lines in Figs. 1, 2 and 3, we can find that, the plane of weakness model does capture some essential features of the experimental observations, but predicts reduced strength in a narrower region than the experimental strength of shale with slightly higher inclination; while the weak patchy plane model predicts smaller strength than the plane of weakness model with a wide range of bedding plane dip** angle β, which conforms to the experimental phenomenon. The Pariseau’s model consists of a single expression for all angles between the load and the normal direction of bedding plane, the failure envelopes predicted by which shows a smoothly varying transition for distinct failure patterns. Besides, the Pariseau’s model can fit the strength data better than the two previous anisotropic strength criteria, because it can pick up the significant differences between β = 0° and β = 90°, whereas the model of plane of weakness and weak patchy plane predict the same results for β = 0° and β = 90°.

To access the predictable ability of these three criteria on shale strength, the parameter RMSE is calculated and summarized in Table 1. It is found that Pariseau’s model possesses a lower RMSE than the other two models, which conforms Pariseau’s model can predict shale strength reasonably well.

Table 1 Prediction error of different strength criteria
Full size table

3 State of stresses around a borehole

3.1 Compliance matrix of transversely isotropic medium

Assuming shale is porous elastic medium, the relationship of its stress and stain is represented by Hooke law, where A is the compliance tensor of transversely isotropic shale.

$${{\varvec{\upvarepsilon}}} = {\mathbf{A\sigma }}$$
(7)

In which, \({{\varvec{\upvarepsilon}}}\) is strain tensor, \({{\varvec{\upsigma}}}\) is stress tensor, A is compliance tensor. When the borehole axis is perpendicular to the bedding plane, the compliance tensor Abp can be expressed as Eq. (8),

$${\mathbf{A}}_{{{\mathbf{bp}}}} = \left[ {\begin{array}{*{20}c} {1/E_{{\text{h}}} } & { - \nu_{{\text{h}}} /E_{{\text{h}}} } & { - \nu_{{\text{v}}} /E_{{\text{v}}} } & 0 & 0 & 0 \\ { - \nu_{{\text{h}}} /E_{{\text{h}}} } & {1/E_{{\text{h}}} } & { - \nu_{{\text{v}}} /E_{{\text{v}}} } & 0 & 0 & 0 \\ { - \nu_{{\text{v}}} /E_{{\text{v}}} } & { - \nu_{{\text{v}}} /E_{{\text{v}}} } & {1/E_{{\text{v}}} } & 0 & 0 & 0 \\ 0 & 0 & 0 & {\frac{{E_{{\text{v}}} \left( {1 + 2v_{{\text{v}}} } \right) + E_{{\text{h}}} }}{{E_{{\text{h}}} E_{{\text{v}}} }}} & 0 & 0 \\ 0 & 0 & 0 & 0 & {\frac{{E_{{\text{v}}} \left( {1 + 2v_{{\text{v}}} } \right) + E_{{\text{h}}} }}{{E_{{\text{h}}} E_{{\text{v}}} }}} & 0 \\ 0 & 0 & 0 & 0 & 0 & {\frac{{2\left( {1 + v_{{\text{h}}} } \right)}}{{E_{{\text{h}}} }}} \\ \end{array} } \right]$$
(8)

where Eh (GPa) and vh are elastic modulus and Poisson’s ratio in the isotropic plane, Ev (GPa) and vv are elastic modulus and Poisson’s ratio in the normal of isotropic plane. Except for transversely elasticity of rock matrix of shale, the deformation induced by natural fractures should be considered (Amadei 2012; Wu et al. 1988). The influence of fractures on the elastically stress–strain behavior of rock can be studied on the conception of equivalent anisotropic continuum, correspondingly, the compliance tensor Anf (Goodman 1976; Amadei 2012; Zhu et al. 1992) induced by natural fractures can be accessed by Eq. (9),

$${\mathbf{A}}_{{{\mathbf{nf}}}} = \left[ {\begin{array}{*{20}c} 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & {1/e_{n} d} & { - \tan \omega /e_{{\text{s}}} d} & { - \tan \omega /e_{{\text{s}}} d} & 0 \\ 0 & 0 & { - \tan \omega /e_{{\text{s}}} d} & {1/e_{{\text{s}}} d} & 0 & 0 \\ 0 & 0 & { - \tan \omega /e_{{\text{s}}} d} & 0 & {1/e_{{\text{s}}} d} & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 \\ \end{array} } \right]$$
(9)

where en is secant normal stiffness, GPa; es is unit shear stiffness, GPa; \(\omega\) is the dilation angle representing the normal displacement caused by a discontinuous shear deformation, deg; d is distance between bedding planes, m. As the borehole axis is perpendicular to bedding plane, the compliance matrix in Eq. (7) can be expressed as follows,

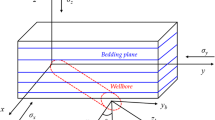
$${\mathbf{A = A}}_{{{\mathbf{bd}}}} {\mathbf{ + A}}_{{{\mathbf{nf}}}}$$
(10)

When the borehole axis is not perpendicular to bedding plane, as shown in Fig. 4, the coordinate transformation for the compliance tensor from BPCS to BCS should be done. Five coordinate systems should be defined, which are global coordinate system (GCS), in-situ stress coordinate system (ICS), borehole coordinate system (BCS), polar coordinate system (PCS), and bedding plane coordinate system (BPCS), respectively, as shown in Fig. 5, αs is azimuth of maximum horizontal in-situ stress, βs is inclination of vertical in-situ stress, αb and βb are well azimuth and inclination, αbp and βbp are is bedding plane azimuth and inclination. θ is borehole circumferential angle measured between the direction of Xb counter clock-wisely.

Fig. 4
figure 4

Relative angle between the borehole axis and bedding plane of shale formation

Full size image
Fig. 5
figure 5

Reference coordinate systems

Full size image

Assume that \(\left( {{\mathbf{x}}_{{\mathbf{b}}} ,{\mathbf{y}}_{{\mathbf{b}}} ,{\mathbf{z}}_{{\mathbf{b}}} } \right)\) and \(\left( {{\mathbf{x}}_{{{\mathbf{bp}}}} ,{\mathbf{y}}_{{{\mathbf{bp}}}} ,{\mathbf{z}}_{{{\mathbf{bp}}}} } \right)\) are the rectangular axes of BCS and BPCS in GCS, which are expressed as the Eqs. (11) and (12).

$$\left[ \begin{gathered} {\mathbf{x}}_{{\mathbf{b}}} \hfill \\ {\mathbf{y}}_{{\mathbf{b}}} \hfill \\ {\mathbf{z}}_{{\mathbf{b}}} \hfill \\ \end{gathered} \right] = \left[ {\begin{array}{*{20}l} {\cos \alpha_{b} \cos \beta_{b} ,\sin \alpha_{b} \cos \beta_{b} , - \sin \beta_{b} } \hfill \\ { - \sin \alpha_{b} ,\cos \alpha_{b} ,0} \hfill \\ {\cos \alpha_{b} \sin \beta_{b} ,\sin \alpha_{b} \sin \beta_{b} ,\cos \beta_{b} } \hfill \\ \end{array} } \right]$$
(11)
$$\left[ \begin{gathered} {\mathbf{x}}_{{{\mathbf{bp}}}} \hfill \\ {\mathbf{y}}_{{{\mathbf{bp}}}} \hfill \\ {\mathbf{z}}_{{{\mathbf{bp}}}} \hfill \\ \end{gathered} \right] = \left[ {\begin{array}{*{20}l} {\cos \alpha_{bp} \cos \beta_{bp} ,\sin \alpha_{bp} \cos \beta_{bp} , - \sin \beta_{bp} } \hfill \\ { - \sin \alpha_{b} ,\cos \alpha_{b} ,0} \hfill \\ {\cos \alpha_{bp} \sin \beta_{bp} ,\sin \alpha_{bp} \sin \beta_{bp} ,\cos \beta_{bp} } \hfill \\ \end{array} } \right]$$
(12)

Consequently, the relative angle between each two vectors can be reached, Eq. (13) give an example for the calculation process of vector Xb and Xbp.

$$\begin{aligned} \cos \left( {{\mathbf{x}}_{{\mathbf{b}}} ,{\mathbf{x}}_{{{\mathbf{bp}}}} } \right) & = \frac{{{\mathbf{x}}_{{\mathbf{b}}} \cdot {\mathbf{x}}_{{{\mathbf{bp}}}} }}{{\left| {{\mathbf{x}}_{{\mathbf{b}}} } \right| \cdot \left| {{\mathbf{x}}_{{{\mathbf{bp}}}} } \right|}} \\ & = \cos \alpha_{b} \cos \beta_{b} \cos \alpha_{bp} \cos \beta_{bp} \\ & \quad + \sin \alpha_{b} \cos \beta_{b} \sin \alpha_{bp} \cos \beta_{bp} \\ & \quad + \sin \beta_{b} \sin \beta_{bp} \\ \end{aligned}$$
(13)

In order to express conveniently, the cosines of each two vectors are expressed as follows,

$$\begin{array}{*{20}c} {l_{1} = \cos \left( {{\mathbf{x}}_{{\mathbf{b}}} ,{\mathbf{x}}_{{{\mathbf{bp}}}} } \right),} & {l_{2} = \cos \left( {{\mathbf{x}}_{{\mathbf{b}}} ,{\mathbf{y}}_{{{\mathbf{bp}}}} } \right),} & {l_{3} = \cos \left( {{\mathbf{x}}_{{\mathbf{b}}} ,{\mathbf{z}}_{{{\mathbf{bp}}}} } \right),} \\ {m_{1} = \cos \left( {{\mathbf{y}}_{{\mathbf{b}}} ,{\mathbf{x}}_{{{\mathbf{bp}}}} } \right),} & {m_{2} = \cos \left( {{\mathbf{y}}_{{\mathbf{b}}} ,{\mathbf{y}}_{{{\mathbf{bp}}}} } \right),} & {m_{3} = \cos \left( {{\mathbf{y}}_{{\mathbf{b}}} ,{\mathbf{z}}_{{{\mathbf{bp}}}} } \right),} \\ {n_{1} = \cos \left( {{\mathbf{z}}_{{\mathbf{b}}} ,{\mathbf{x}}_{{{\mathbf{bp}}}} } \right),} & {n_{2} = \cos \left( {{\mathbf{z}}_{{\mathbf{b}}} ,{\mathbf{y}}_{{{\mathbf{bp}}}} } \right),} & {n_{3} = \cos \left( {{\mathbf{z}}_{{\mathbf{b}}} ,{\mathbf{z}}_{{{\mathbf{bp}}}} } \right),} \\ \end{array}$$
(14)

The transformation matrix (Lekhnitskii 1963) for transversely isotropic compliance tensor from BPCS to BCS is shown as Eq. (15),

$${\text{Q}} = \left[ {\begin{array}{*{20}c} {l_{1}^{2} } & {l_{2}^{2} } & {l_{3}^{2} } & {l_{2} l_{3} } & {l_{1} l_{3} } & {l_{1} l_{2} } \\ {m_{1}^{2} } & {m_{2}^{2} } & {m_{3}^{2} } & {m_{2} m_{3} } & {m_{1} m_{3} } & {m_{1} m_{2} } \\ {n_{1}^{2} } & {n_{2}^{2} } & {n_{3}^{2} } & {n_{2} n_{3} } & {n_{1} n_{3} } & {n_{1} n_{2} } \\ {2m_{1} n_{1} } & {2m_{2} n_{2} } & {2m_{3} n_{3} } & {m_{2} n_{3} + m_{3} n_{2} } & {m_{1} n_{3} + m_{3} n_{1} } & {m_{2} n_{1} + m_{1} n_{2} } \\ {2l_{1} n_{1} } & {2l_{2} n_{2} } & {2l_{3} n_{3} } & {l_{2} n_{3} + l_{3} n_{2} } & {l_{1} n_{3} + l_{3} n_{1} } & {l_{2} n_{1} + l_{1} n_{2} } \\ {2l_{1} m_{1} } & {2l_{2} m_{2} } & {2l_{3} m_{3} } & {l_{2} m_{3} + l_{3} m_{2} } & {l_{1} m_{3} + l_{3} m_{1} } & {l_{2} m_{1} + l_{1} m_{2} } \\ \end{array} } \right]$$
(15)

The new compliance tensor with arbitrary relative angle between wellbore axis and bedding planeis expressed as Eq. (16),

$${\mathbf{B = QAQ}}^{{\mathbf{T}}}$$
(16)

3.2 Stress tensors superposition

3.2.1 Stress induced by in-situ stress

When a borehole is excavated, in-situ stress will concentrate around wellbore, coordinate system transformations are required to transform the in-situ stress from ICS to GCS, then to BCS, finally the near wellbore stress caused by in-situ stress in BSC is calculated as Eq. (17),

$${{\varvec{\upsigma}}}_{{\mathbf{i}}} = {\mathbf{B}} \times {\mathbf{E}}^{{\mathbf{T}}} \times {{\varvec{\upsigma}}}_{{{\mathbf{ics}}}} \times {\mathbf{E}} \times {\mathbf{B}}^{{\mathbf{T}}}$$
(17)

with

$${\mathbf{E}} = \left[ {\begin{array}{*{20}l} {\cos \alpha_{s} \cos \beta_{s} } \hfill & {\sin \alpha_{s} \cos \beta_{s} } \hfill & {\sin \beta_{s} } \hfill \\ { - \sin \alpha_{s} } \hfill & {\cos \alpha_{s} } \hfill & 0 \hfill \\ { - \cos \alpha_{s} sin\beta_{s} } \hfill & { - \sin \alpha_{s} sin\beta_{s} } \hfill & {\cos \beta_{s} } \hfill \\ \end{array} } \right]$$
(18)
$${\mathbf{B}} = \left[ {\begin{array}{*{20}l} {\cos \alpha_{b} \cos \beta_{b} } \hfill & {\sin \alpha_{b} \cos \beta_{b} } \hfill & {\sin \beta_{b} } \hfill \\ { - \sin \alpha_{b} } \hfill & {\cos \alpha_{b} } \hfill & 0 \hfill \\ { - \cos \alpha_{b} sin\beta_{b} } \hfill & { - \sin \alpha_{b} sin\beta_{b} } \hfill & {\cos \beta_{b} } \hfill \\ \end{array} } \right]$$
(19)

where the rotation matrix for transformation from ICS to GCS can be expressed as Eq. (18), the rotation matrix for transformation from GCS to BCS can be expressed as Eq. (19), \({{\varvec{\upsigma}}}_{{{\text{ics}}}} = \left[ {\upsigma _{{\text{H}}} ,0,0;\;0,\upsigma _{{\text{h}}} ,0;\;0,0,\upsigma _{{\text{v}}} } \right]\) is in-situ stress matrix, \({{\varvec{\upsigma}}}_{{\text{i}}} = \left[ {\sigma_{xx,i} ,\sigma_{yy,i} ,\sigma_{zz,i} ,\tau_{xy,i} ,\tau_{xz,i} ,\tau_{yz,i} } \right]\) is stress components around wellbore in BCS.

3.2.2 Stress induced by anisotropy

The components of stress concentration caused by transversely isotropic plane was given by Lekhnitskii (1968) firstly as,

$$\left\{ {\begin{array}{*{20}l} {\sigma_{xx,a} = 2{\text{Re}} \left[ {\xi_{1}^{2} \phi_{1}^{^{\prime}} \left( {z_{1} } \right) + \xi_{2}^{2} \phi_{2}^{^{\prime}} \left( {z_{2} } \right) + \chi_{3} \xi_{3}^{2} \phi_{3}^{^{\prime}} \left( {z_{3} } \right)} \right]} \hfill \\ {\sigma_{yy,a} = 2{\text{Re}} \left[ {\phi_{1}^{^{\prime}} \left( {z_{1} } \right) + \phi_{2}^{^{\prime}} \left( {z_{2} } \right) + \chi_{3} \phi_{3}^{^{\prime}} \left( {z_{3} } \right)} \right]} \hfill \\ {\tau_{xy,a} = - 2{\text{Re}} \left[ {\xi_{1} \phi_{1}^{^{\prime}} \left( {z_{1} } \right) + \xi_{2} \phi_{2}^{^{\prime}} \left( {z_{2} } \right) + \chi_{3} \xi_{3} \phi_{3}^{^{\prime}} \left( {z_{3} } \right)} \right]} \hfill \\ {\tau_{xz,a} = 2{\text{Re}} \left[ {\chi_{1} \xi_{1} \phi_{1}^{^{\prime}} \left( {z_{1} } \right) + \chi_{2} \xi_{2} \phi_{2}^{^{\prime}} \left( {z_{2} } \right) + \xi_{3} \phi_{3}^{^{\prime}} \left( {z_{3} } \right)} \right]} \hfill \\ {\tau_{yz,a} = - 2{\text{Re}} \left[ {\chi_{1} \phi_{1}^{^{\prime}} \left( {z_{1} } \right) + \chi_{2} \phi_{2}^{^{\prime}} \left( {z_{2} } \right) + \phi_{1}^{^{\prime}} \left( {z_{3} } \right)} \right]} \hfill \\ {\sigma_{zz,a} = - \left( {B_{31} \sigma_{xx,a} + B_{32} \sigma_{yy,a} + B_{34} \tau_{yz,a} + B_{35} \tau_{xz,a} + B_{36} \tau_{xy,a} } \right)/B_{33} } \hfill \\ \end{array} } \right.$$
(20)

In which, \(\left[ {\sigma_{xx,a} ,\sigma_{yy,a} ,\sigma_{zz,a} ,\tau_{xy,a} ,\tau_{xz,a} ,\tau_{yz,a} } \right]\) are the stress components induced by elastic anisotropy at wellbore wall. Bij is defined in the anisotropic compliance matrix in BCS, Re is the real component of a complex number, \(\xi_{i} ,\chi_{i}\) and \(\phi_{i}^{^{\prime}} \left( {z_{i} } \right)\) are expressed in the following equations.

$$f\left( \xi \right) = I_{4} \left( \xi \right)I_{2} \left( \xi \right) - I_{3}^{2} \left( \xi \right) = 0$$
(21)

with

$$\left\{ {\begin{array}{*{20}l} {I_{4} \left( \xi \right) = \beta_{11} \xi^{4} - 2\beta_{16} \xi^{3} + \left( {2\beta_{12} + \beta_{66} } \right)\xi^{2} - 2\beta_{26} \xi + \beta_{22} } \hfill \\ {I_{3} \left( \xi \right) = \beta_{15} \xi^{3} - \left( {\beta_{14} + \beta_{56} } \right)\xi^{2} + \left( {\beta_{25} + \beta_{46} } \right)\xi - \beta_{24} } \hfill \\ {I_{2} \left( \xi \right) = \beta_{55} \xi^{2} - 2\beta_{45} \xi^{2} + \beta_{44} } \hfill \\ \end{array} } \right.$$
(22)

where \(\xi_{i}\) (i = 1,2,3) are the three positive roots of Eq. (21), and has six roots that can be real or complex conjugates. \(\beta_{ij}\) is called reduced strain coefficient as shown in Eq. (23),

$$\begin{array}{*{20}l} {\beta_{ij} = B_{ij} - \frac{{B_{i3} B_{j3} }}{{B_{33} }}} \hfill & {\left( {i,j = 1,2,4,5,6} \right)} \hfill \\ \end{array}$$
(23)

The complex parameter \(\chi_{i}\) can be obtained by Eq. (24),

$$\chi_{1} = - \frac{{I_{3} \left( {\xi_{1} } \right)}}{{I_{2} \left( {\xi_{1} } \right)}},\quad \chi_{2} = - \frac{{I_{3} \left( {\xi_{2} } \right)}}{{I_{2} \left( {\xi_{2} } \right)}},\quad \chi_{3} = - \frac{{I_{3} \left( {\xi_{3} } \right)}}{{I_{4} \left( {\xi_{3} } \right)}}$$
(24)

After rigorous mathematical derivation, \(\phi_{i}^{^{\prime}} \left( {z_{i} } \right)\) is determined,

$$\left\{ {\begin{array}{*{20}l} {\phi_{1}^{^{\prime}} \left( {z_{1} } \right) = \left[ {D^{^{\prime}} \left( {\chi_{2} \chi_{3} - 1} \right) + E^{^{\prime}} \left( {\xi_{2} - \chi_{2} \chi_{3} \xi_{3} } \right) + F^{^{\prime}} \chi_{3} \left( {\xi_{2} - \xi_{3} } \right)} \right]/2G_{1} } \hfill \\ {\phi_{2}^{^{\prime}} \left( {z_{2} } \right) = \left[ {D^{^{\prime}} \left( {1 - \chi_{1} \chi_{3} } \right) + E^{^{\prime}} \left( {\chi_{1} \chi_{3} \xi_{3} - \xi_{1} } \right) + F^{^{\prime}} \chi_{3} \left( {\xi_{1} - \xi_{3} } \right)} \right]/2G_{2} } \hfill \\ {\phi_{3}^{^{\prime}} \left( {z_{3} } \right) = \left[ {D^{^{\prime}} \left( {\chi_{1} - \chi_{2} } \right) + E^{^{\prime}} \left( {\xi_{1} \chi_{2} - \xi_{2} \chi_{1} } \right) + F^{^{\prime}} \chi_{3} \left( {\xi_{2} - \xi_{1} } \right)} \right]/2G_{3} } \hfill \\ \end{array} } \right.$$
(25)

with

$$\left\{ {\begin{array}{*{20}l} {D^{^{\prime}} = \left( {p_{w} - \sigma_{xx,i} } \right)\cos \theta - \tau_{xy,i} \sin \theta - i\left( {p_{w} - \sigma_{xx,i} } \right)\sin \theta - i\tau_{xy,i} \cos \theta } \hfill \\ {E^{^{\prime}} = - \left( {p_{w} - \sigma_{yy,i} } \right)sin\theta + \tau_{xy,i} co{\text{s}} \theta - i\left( {p_{w} - \sigma_{yy,i} } \right)\cos \theta - i\tau_{xy,i} sin\theta } \hfill \\ {F^{^{\prime}} = - \tau_{xz,i} co{\text{s}} \theta - \tau_{yz,i} \sin \theta + i\tau_{xz,i} \sin \theta - i\tau_{yz,i} co{\text{s}} \theta } \hfill \\ {G_{k} = \left( {\xi_{k} \cos \theta - \sin \theta } \right)\left[ {\xi_{2} - \xi_{1} + \chi_{2} \chi_{3} \left( {\xi_{1} - \xi_{3} } \right) + \chi_{1} \chi_{3} \left( {\xi_{3} - \xi_{2} } \right)} \right]} \hfill \\ \end{array} } \right.$$
(26)

where Pw is mud pressure in the well, MPa.

3.2.3 Pore pressure in anisotropic formation

Generally, the Biot coefficient is taken as constant variable for the facility of calculation in drilling engineering, but in shale reservoir, Biot coefficient is significantly affected by the high degrees of rock anisotropy and fractures and can’t be regarded as constant. Cheng et al. (1997) presented the Biot coefficient for poroelastic anisotropic formation,

$$\alpha_{i} = \left\{ {\begin{array}{*{20}l} {1 - \frac{{\sum\nolimits_{j = 1}^{3} {M_{ij} } }}{{3K_{s} }},\quad i = 1,2,3} \hfill \\ { - \frac{{\sum\nolimits_{j = 1}^{3} {M_{ij} } }}{{3K_{s} }},\quad i = 4,5,6} \hfill \\ \end{array} } \right.$$
(27)

where \(\alpha_{i}\) is Biot coefficient, Ks is grain solid bulk modulus, GPa; \(M_{ij}\) are drained coefficients in the stiffness matrix M = (B)−1. Therefore, the effective stress at wellbore can be achieved by superimposing the stress components induced by in-situ stress, elastic anisotropic created by foliation and discontinuous, and anisotropic pore pressure, as shown in Eq. (28),

$$\left\{ {\begin{array}{*{20}l} {\sigma_{x,eff} = \sigma_{xx,i} + \sigma_{xx,a} - \alpha_{1} p_{{\text{p}}} } \hfill \\ {\sigma_{y,eff} = \sigma_{yy,i} + \sigma_{yy,a} - \alpha_{2} p_{{\text{p}}} } \hfill \\ {\tau_{xy,eff} = \tau_{xy,i} + \tau_{xy,a} - \alpha_{6} p_{{\text{p}}} } \hfill \\ {\tau_{xz,eff} = \tau_{xz,i} + \tau_{xz,a} - \alpha_{5} p_{{\text{p}}} } \hfill \\ {\tau_{yz,eff} = \tau_{yz,i} + \tau_{yz,a} - \alpha_{4} p_{{\text{p}}} } \hfill \\ {\sigma_{z,eff} = \sigma_{zz,i} + \sigma_{zz,a} - \alpha_{3} p_{{\text{p}}} } \hfill \\ \end{array} } \right.$$
(28)

Then transform the wellbore wall stress tensor from BCS to PCS, the stress components in polar coordinate system of plain stress condition are expressed as,

$$\left\{ {\begin{array}{*{20}l} {\sigma_{r} = \sigma_{x,eff} \cos^{2} \theta + \sigma_{y,eff} \sin^{2} \theta + \tau_{xy,eff} \sin 2\theta } \hfill \\ {\sigma_{\theta } = \sigma_{x,eff} \sin^{2} \theta + \sigma_{y,eff} \cos^{2} \theta - \tau_{xy,eff} \sin 2\theta } \hfill \\ {\tau_{r\theta } = - 0.5\sigma_{x,eff} \sin 2\theta + 0.5\sigma_{y,eff} \sin 2\theta + \tau_{xy,i} \cos 2\theta } \hfill \\ {\tau_{\theta z} = \tau_{yz,eff} \cos \theta - \tau_{xz,eff} \sin \theta } \hfill \\ {\tau_{re} = \tau_{yz,eff} \sin \theta + \tau_{xz,eff} \cos \theta } \hfill \\ {\sigma_{z} = \sigma_{z,eff} } \hfill \\ \end{array} } \right.$$
(29)

3.3 Borehole collapse pressure model

The failure strength is generally described in terms of three principal components, so the effective stress at wellbore wall should be transformed to principal stress pattern,

$$\left\{ {\begin{array}{*{20}l} {\sigma_{1,2} = \left( {\sigma_{\theta } + \sigma_{z} } \right)/2 \pm \sqrt {\left( {\sigma_{\theta } + \sigma_{z} } \right)^{2} + 4\tau_{\theta z}^{2} } /2} \hfill \\ {\sigma_{3} = \sigma_{r} } \hfill \\ \end{array} } \right.$$
(30)

Besides, anisotropic strength contains a relative angle measured between the axial loading direction and bedding plane normal. Based on space geometry theory, the angle between the maximum principal stress at angular positions of borehole wall with normal direction of bedding plane can be determined by Eq. (31),

$$\beta_{{\text{i}}} = \arccos \frac{{{\mathbf{nN}}}}{{\left| {\mathbf{n}} \right|\left| {\mathbf{N}} \right|}}$$
(31)

where n is vector of bedding plane normal, N is vector of maximum principal stress at angular positions of borehole wall, they can be expressed by Eq. (32) and (33),

$${\mathbf{n}} = \left[ {{\text{cos}}\alpha_{{{\text{bp}}}} {\text{sin}}\beta_{{{\text{bp}}}} {\text{,sin}}\alpha_{{{\text{bp}}}} {\text{sin}}\beta_{{{\text{bp}}}} ,\cos \beta_{{{\text{bp}}}} } \right]$$
(32)
$${\mathbf{N}} = \left[ {\begin{array}{*{20}l} {{\text{cos}}\alpha_{{\text{b}}} \cos \beta_{{\text{b}}} \sin \theta - \sin \alpha_{{\text{b}}} \cos \theta + \cos \alpha_{{\text{b}}} \sin \beta_{{\text{b}}} \cos \gamma } \hfill \\ {\sin \alpha_{{\text{b}}} \cos \beta_{{\text{b}}} \sin \theta + \cos \alpha_{{\text{b}}} \cos \theta + \sin \alpha_{{\text{b}}} \sin \beta_{{\text{b}}} \cos \gamma } \hfill \\ {\cos \beta_{{\text{b}}} cos\gamma - \sin \beta_{{\text{b}}} \sin \theta } \hfill \\ \end{array} } \right]$$
(33)

with

$$\gamma = 0.5\arctan \left[ {2\tau_{\theta z} /\left( {\sigma_{\theta } - \sigma_{z} } \right)} \right]$$
(34)

By substituting Eqs. (30) and (31) into a selected anisotropic strength model, the collapse pressure of layered shale can be calculated. In consideration of periodicity and symmetry of the circumferential angle, its range is restricted to 0–180° with a given increment 2° in the subsequent analysis. The wellbore inclination is defined as an increase from 0° to 90° with a given increment 5°, azimuth is defined as an increase from 0° to 360° with a given increment 10°, then the critical mud pressure is obtained for the variable circumferential angle with a given array (\(\alpha_{b} ,\beta_{b}\)) by newton iteration algorithm in MATLAB, thereinto, the maximum mud pressure under a given (\(\alpha_{b} ,\beta_{b}\)) condition can be achieved.

4 Collapse pressure analysis

The LMX shale located in lower Silurian, CN block in Sichuan basin, is used for a field example of wellbore collapse pressure analysis. The well depth is 6200 m, overburden in-situ stress is 136.4 MPa, maximum horizontal in-situ stress is 155 MPa (N150°E), minimum horizontal in-situ stress is 117.8 MPa, formation pressure is 82.46 MPa, the in-situ stress is of typical strike-slip faulting regime. The angle of bedding azimuth and inclination are supposed to be N 150° E and 1.2°, respectively. Strength parameters embedding in Pariseau’s Model with different moisture contents in Fig. 3 are adopted.

4.1 Comparative analysis of elastic isotropy and anisotropy case

Some researchers held that elastically anisotropic parameters didn’t have prominent influence on collapse pressure (Aadnøy 1988 and 1989; Chen et al. 2002), more common viewpoint thought that the anisotropy of shale should be considered to evaluated the near wellbore stress. In this paper, a comparison between elastically isotropic case and elastically anisotropic case is conducted, combining with a continuous strength criterion. In order to conduct a comparison of elastic anisotropy and anisotropy effects on wellbore collapse pressure, the Young modulus and Poisson’s Ratio parallel and perpendicular to the isotropic plane i.e. (Ev, vv, Eh, vh) in compliance tensor should be determined. The mechanical parameters inputted in this observation are summarized in Table 2.

Table 2 Elastically anisotropic parameters used for sensitivity analysis
Full size table

According to document research, the Young modulus and Poisson’s Ratio of shale with β = 0° are 28 GPa and 0.15, respectively. Based on strength parameters determined by tested data of first group shale, the collapse pressure can be calculated, as shown in Fig. 6, polar plots of collapse pressure as a function of well trajectory are accessed on different cases. The concentric circles denote increasing inclination, and the outer circle correspond to the borehole azimuth, which is measured clock wisely from North, the pink line is the direction of maximum horizontal in-situ stress. In Fig. 6a, Jaeger’s plane of weakness model is adopted, in which the Coulomb parameters are determined from Fig. 1a, and the elastic parameters are set to be equal, the shale formation is simplified to isotropy, parameters used in Fig. 6b are same with Fig. 6a except for the more reasonable strength model of Pariseau is adopted, the comparison of results predicted by these two different anisotropic strength criteria can be carried out. Meanwhile, the Young Modulus of isotropic plane is defined as twice that of vertical to isotropic plane in Fig. 6c, the other parameters used are the same as these chosen for Fig. 6b, so the different induced by elasticity anisotropy can be studied.

Fig. 6
figure 6

Polar plots of collapse pressure predicted by different strength criteria

Full size image

The polar plots in Fig. 6 are symmetrical because bedding plane is aligned with horizontal principal stress, the little difference of collapse pressure along minimum horizontal in-situ stress results from the dip** angle of bedding plane. The polar plot determined by Jaeger’s weak plane criterion indicates that the most stable drilling direction is parallel to the maximum horizontal principal stress with a relative higher inclination, as well as that predicted by Pariseau’s model.

In Fig. 6a, the well drilled in the direction of horizontal minimum principal stress with high inclinations is observed to be the most unstable well trajectory, the collapse pressure range from 69.45 to 87.8 MPa. In Fig. 6b, the central area corresponding to relatively lower inclination is observed to be unstable, which is very different from the results predicted by the plane of weakness model.

In Fig. 6c, the collapse pressure fluctuation range of horizontal wells is severe, however, on the other area, the collapse pressures maintain almost the same with that in Fig. 6b, the collapse pressure only decreased by 0.55 MPa. It indicates that the anisotropy of elastic parameters has insignificant impact on the collapse pressure. This viewpoint had been reported by many researchers (Aadnøy 1988; Chen et al. 2002; Vahid et al. 2011; Liu et al. 2016), but the difference of bedding occurrence and in-situ regime may reach a totally opposite conclusion.

4.2 Impact of water absorption on collapse pressure

In drilling operation, the contact of water with shale formation will result in strength loss and crack propagation because of chemical reactions. Characteristic of shale is not only controlled by bedding plane orientations, but also controlled by water content markedly. The influence of moisture content on polar plot of collapse pressure is shown as Fig. 7.

Fig. 7
figure 7

Polar plots of collapse pressure with different moisture content

Full size image

The polar plots of collapse pressure for different moisture content show the same trend as a function of well trajectory, but collapse pressure increases with the increasing of water content. The maximum collapse pressure is 89.9 MPa in Fig. 7a, after the shale soaked in water for 24 h and 48 h, the maximum collapse pressures are 93 MPa with an increment about 3.1 MPa, and 96.25 MPa with an increment about 6.35 MPa, respectively. Invasion of drilling fluid is even worse in drilling field than in-door tests because of high pressure and high temperature. The collapse pressure of horizontal well drilled in horizontal minimum in-situ stress is much larger than the well drilled in horizontal maximum in-situ stress, this is different from isotropic formation. The interaction of shale and drilling fluid is one of the critical factors controlling wellbore stability of shale formation. Methods to minimize fluid intrusion into bedding planes, such as the appropriate use of plugging materials, optimizing attack angle of wellbore axis and bedding plane, should be considered in the following wells drilled in shale reservoirs.

5 Conclusion

Three different types of anisotropic strength criteria are reviewed and fitted to strength shale with different confining pressures, bedding plane orientations and water content published in the literature. Then, the best-fit parameters contained in the anisotropic strength models are determined by a new fitting approach, which gives complete prediction of the test data. Researches show that, Jaeger’s plane of weakness model captures the general trend quiet well, but the weak planes seem to have an impact on strength even outside the range of bedding plane orientations where the predicted shear slippage on bedding plane will occur. Although plane of weak patchy model predicts a wider range of reduced strength and captures the transition zone where the mixed failure occurred, it fails to explain the difference of shale strength measured perpendicular and parallel to bedding plane. The Pariseau’ model can conquer these shortcomings, and match the experimental data quiet well with the lowest RMSE. The prediction accuracy of shale strength is improved by 33.04% using Pariseau’s model, but it has not yet been used in stability analysis of well drilled in shale formation.

Then, the wellbore stress model considering compliance incremental tensor induced by natural fractures is adopted, combining with Pariseau’ model, the impact of water content, strength and elastic anisotropy on wellbore stability are performed. The main discoveries are as follows, the polar plot predicted by Pariseau’ model is very different from that predicted by weak plane criterion, the most unstable drilling area shifts from northeast and southwest to the central area corresponding to relatively lower inclination. Elastic anisotropy leads to a severe fluctuation for horizontal wells, while on the other trajectories, the anisotropy of elastic parameters has insignificant impact on the collapse pressure. Furthermore, the collapse pressure only decreased by 0.55 MPa with considering the anisotropy of elastic parameters, the strength criteria have a distinct influence. Compared with the results predicted by Jæger’s plane of weakness, the collapse pressure increased by 8.55 MPa using Pariseau’ model. The collapse pressures with different water content show the same variation trend as a function of well trajectory, but the values of mud pressure increase with the increasing of water content. For example, collapse pressure for the vertical wellbore increased by 6.35 MPa after two hours of contacting with water.