Abstract
We determine the cohomology groups of the quartic and hyperelliptic loci inside the moduli space of genus three curves with symplectic level two structure as representations of the symmetric group \(S_7\) together with their mixed Hodge structures by means of making equivariant point counts over finite fields and via purity arguments. This determines the weighted Euler characteristic of the whole moduli space of genus three curves with level two structure.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Let n be a positive integer and let C be a curve. A level n structure on C is a basis for the n-torsion of the Jacobian of C. The purpose of this paper is to study the cohomology of the moduli space \(\mathscr {M}_{3}[2]\) of genus 3 curves with symplectic level 2 structure.
A genus 3 curve which is not hyperelliptic is embedded as a plane quartic via its canonical linear system. The corresponding locus in \(\mathscr {M}_{3}[2]\) is called the quartic locus and it is denoted \(\mathscr {Q}[2]\). A plane quartic with level 2 structure is specified, up to isomorphism, by an ordered septuple of points in general position in \(\mathbb {P}^{2}\), up to the action of  (see Sect. 3, especially Theorem 3.2). This identification will be the basis for our investigation of \(\mathscr {Q}[2]\).
(see Sect. 3, especially Theorem 3.2). This identification will be the basis for our investigation of \(\mathscr {Q}[2]\).
Our main focus will be on \(\mathscr {Q}[2]\) but we will also consider its complement in \(\mathscr {M}_{3}[2]\), i.e. the hyperelliptic locus \(\mathscr {H}_{3}[2]\). The spaces \(\mathscr {M}_{3}[2]\), \(\mathscr {Q}[2]\) and \(\mathscr {H}_{3}[2]\) are all defined over  , a fact which gives us the flexibility to consider them over the complex numbers as well as over finite fields of characteristic different from 2. In the present paper, the latter viewpoint will be the central one and the computations will be carried out via point counts over finite fields (see Sects. 6, 7). By virtue of Lefschetz trace formula (see Sect. 4), such point counts give cohomological information in the form of Euler characteristics. However, we shall see (in Proposition 5.3 resp. Sect. 7) that both \(\mathscr {Q}[2]\) and \(\mathscr {H}_{3}[2]\) satisfy certain strong purity conditions which allow us to deduce information about the individual cohomology groups, in the form of Poincaré polynomials, from these Euler characteristics.
, a fact which gives us the flexibility to consider them over the complex numbers as well as over finite fields of characteristic different from 2. In the present paper, the latter viewpoint will be the central one and the computations will be carried out via point counts over finite fields (see Sects. 6, 7). By virtue of Lefschetz trace formula (see Sect. 4), such point counts give cohomological information in the form of Euler characteristics. However, we shall see (in Proposition 5.3 resp. Sect. 7) that both \(\mathscr {Q}[2]\) and \(\mathscr {H}_{3}[2]\) satisfy certain strong purity conditions which allow us to deduce information about the individual cohomology groups, in the form of Poincaré polynomials, from these Euler characteristics.
The group  acts on \(\mathscr {M}_{3}[2]\) as well as on \(\mathscr {Q}[2]\) and \(\mathscr {H}_{3}[2]\) by changing level structures. The cohomology groups thus become
acts on \(\mathscr {M}_{3}[2]\) as well as on \(\mathscr {Q}[2]\) and \(\mathscr {H}_{3}[2]\) by changing level structures. The cohomology groups thus become  -representations and our computations will therefore be equivariant. However, the action of
-representations and our computations will therefore be equivariant. However, the action of  is rather subtle on \(\mathscr {Q}[2]\) when \(\mathscr {Q}[2]\) is identified with the space of septuples of points in general position in \(\mathbb {P}^{2}\). On the other hand, the action of the symmetric group \(S_7\) on seven elements is very clear and we will therefore restrict our attention to this subgroup. The main results are presented in Tables 2 and 5 where we give the cohomology groups of \(\mathscr {Q}[2]\) and \(\mathscr {H}_{3}[2]\) as representations of \(S_7\). In particular, we obtain the following.
is rather subtle on \(\mathscr {Q}[2]\) when \(\mathscr {Q}[2]\) is identified with the space of septuples of points in general position in \(\mathbb {P}^{2}\). On the other hand, the action of the symmetric group \(S_7\) on seven elements is very clear and we will therefore restrict our attention to this subgroup. The main results are presented in Tables 2 and 5 where we give the cohomology groups of \(\mathscr {Q}[2]\) and \(\mathscr {H}_{3}[2]\) as representations of \(S_7\). In particular, we obtain the following.
Theorem 1.1
The Poincaré polynomial of \(\mathscr {Q}[2]\) is

Theorem 1.2
The Poincaré polynomial of \(\mathscr {H}_{3}[2]\) is

The present paper may to a large extent be seen as a level 2 analogue of Looijenga [25] and many results, for instance Propositions 1.1 and 1.2, have counterparts in [25] and [19]. Our paper also builds heavily on the work of Dolgachev and Ortland [14], especially the description of \(\mathscr {Q}[2]\) in terms of configurations of points in the projective plane, and van Geemen, whose results are unpublished by himself but can be found in [14]. It may also be of interest to compare the present paper to the work of Bergström [3, 4], and Bergström and Tommasi [5] which also investigate cohomological questions about moduli spaces of low genus curves via point counts. Although there are many similarities, a key difference between the works mentioned above and the present paper is that in previous works the most refined information is obtained for compactifications of the various moduli spaces under investigation, and compactness is used in an essential way, whereas in the present paper we obtain the strongest information for “open” moduli spaces. There are also several other works which answer representation theoretic questions about the cohomology groups of various spaces, e.g. [10, 13, 22, 23]. It should also be mentioned that our results are an essential ingredient in the article [7] where further information about the action of  on the cohomology \(\mathscr {M}_{3}[2]\) and \(\mathscr {Q}[2]\) is obtained via quite different methods.
on the cohomology \(\mathscr {M}_{3}[2]\) and \(\mathscr {Q}[2]\) is obtained via quite different methods.
2 Symplectic level structures
Let \(K\) be an algebraically closed field of characteristic not equal to 2 and let C be a smooth and irreducible curve of genus g over \(K\). The 2-torsion part  of the Jacobian of C is isomorphic to \(( \mathbb {Z}/2\mathbb {Z})^{2g}\) as an abelian group and the Weil pairing is a nondegenerate and alternating bilinear form on
of the Jacobian of C is isomorphic to \(( \mathbb {Z}/2\mathbb {Z})^{2g}\) as an abelian group and the Weil pairing is a nondegenerate and alternating bilinear form on  .
.
Definition 2.1
A symplectic level two structure on a curve C is an ordered basis \((D_1, \ldots , D_{2g})\) of  such that the Weil pairing has matrix
such that the Weil pairing has matrix
with respect to this basis. Here, \(I_g\) denotes the  identity matrix (note that the matrix of the pairing takes a somewhat simpler form than in general since
identity matrix (note that the matrix of the pairing takes a somewhat simpler form than in general since  is a vector space over a field of characteristic 2).
is a vector space over a field of characteristic 2).
For more information about the Weil pairing and level structures, see e.g. [2] or [20]. Since we shall only consider symplectic level structures we shall refer to symplectic level structures simply as level structures.
A tuple \((C,D_1,\ldots , D_{2g})\) where C is a smooth irreducible curve and \((D_1, \ldots , D_{2g})\) is a level 2 structure on C is called a curve with level 2 structure. Let \((C',D'_1, \ldots ,D'_{2g})\) be another curve with level 2 structure. An isomorphism of curves with level 2 structures is an isomorphism of curves \(\phi :C \rightarrow C'\) such that \(\phi ^*(D'_i)=D_i\) for \(i=1, \ldots , 2g\). We denote the moduli space of genus g curves with level 2 structure by \(\mathscr {M}_{g}[2]\). We remark that we shall consider these moduli spaces as coarse spaces and not as stacks. The group  acts on \(\mathscr {M}_{g}[2]\) by changing level structures.
acts on \(\mathscr {M}_{g}[2]\) by changing level structures.
A concept closely related to level 2 structures is that of theta characteristics.
Definition 2.2
Let C be a smooth and irreducible curve and let \(K_C\) be its canonical class. An element  such that \(2 \theta = K_C\) is called a theta characteristic. We denote the set of theta characteristics of C by \(\Theta (C)\).
such that \(2 \theta = K_C\) is called a theta characteristic. We denote the set of theta characteristics of C by \(\Theta (C)\).
Let C be a curve of genus g. Given two theta characteristics \(\theta _1\) and \(\theta _2\) on C, we obtain an element  by taking the difference \(\theta _1 -\theta _2\). Conversely, given a theta characteristic \(\theta \) and a 2-torsion element D, we obtain a new theta characteristic as \(\theta '=\theta +D\). More precisely we have that \(\Theta (C)\) is a
by taking the difference \(\theta _1 -\theta _2\). Conversely, given a theta characteristic \(\theta \) and a 2-torsion element D, we obtain a new theta characteristic as \(\theta '=\theta +D\). More precisely we have that \(\Theta (C)\) is a  -torsor and the set
-torsor and the set  is a vector space of dimension \(2g+1\) over the field \(\mathbb {Z}/2\mathbb {Z}\) of two elements.
is a vector space of dimension \(2g+1\) over the field \(\mathbb {Z}/2\mathbb {Z}\) of two elements.
Definition 2.3
An ordered basis \(A=(\theta _1, \ldots , \theta _{2g+1})\) of theta characteristics of the vector space \(\widetilde{\Theta }(C)\) is called an ordered Aronhold basis if the expression
only depends on the number of elements in A that is required to express \(\theta \) for any theta characteristic \(\theta \).
Proposition 2.4
Let C be a smooth and irreducible curve. There is a bijection between the set of ordered Aronhold bases on C and the set of level 2 structures on C.
For a proof of Proposition 2.4 as well as a more thorough treatment of theta characteristics and Aronhold bases we refer to [21] and [26, Section 3.3].
Proposition 2.4 provides a more geometric way to think about level 2 structures. In the case of a plane quartic curve, which shall be the case of most importance to us, we point out that each theta characteristic occurring in an Aronhold basis is cut out by a bitangent line. Thus, in the case of plane quartics one can think of ordered Aronhold bases as ordered sets of bitangents (although not every ordered set of bitangents constitute an ordered Aronhold basis).
3 Plane quartics
Let \(K\) be an algebraically closed field of characteristic not equal to 2 and let C be a smooth and irreducible curve of genus g over \(K\). If C is not hyperelliptic it is embedded into \(\mathbb {P}^{\, g-1}\) via its canonical linear system. Thus, a non-hyperelliptic curve of genus 3 is embedded into \(\mathbb {P}^{2}\) and by the genus-degree formula we see that the degree of the image is 4. We therefore refer to the corresponding locus in \(\mathscr {M}_{3}\), the moduli space of curves of genus 3, as the quartic locus and denote it by \(\mathscr {Q}\). It is the complement of the hyperelliptic locus, \(\mathscr {H}_{3}\). Similarly, we denote the complement of the hyperelliptic locus in \(\mathscr {M}_{3}[2]\) by \(\mathscr {Q}[2]\). Clearly, the action of  on \(\mathscr {M}_{3}[2]\) restricts to an action on \(\mathscr {Q}[2]\).
on \(\mathscr {M}_{3}[2]\) restricts to an action on \(\mathscr {Q}[2]\).
The purpose of this section is to give an explicit, combinatorial description of \(\mathscr {Q}[2]\). This description will be in terms of points in general position. Intuitively, a set of n points in the projective plane is in general position if there is no “unexpected” curve passing through all of them. In our case, this is made precise by the following definition.
Definition 3.1
Let \((P_1, \ldots , P_7)\) be a septuple of points in \(\mathbb {P}^{2}\). We say that the septuple is in general position if there is no line passing through any three of the points and no conic passing through any six of them. We denote the moduli space of septuples of points in general position up to projective equivalence by \(\mathscr {P}^2_7\).
Let \(T=(P_1, \ldots , P_7)\) be a septuple of points in general position in the projective plane and let  be the net of cubics passing through T. If we let \(F_0\), \(F_1\) and \(F_2\) be generators for
be the net of cubics passing through T. If we let \(F_0\), \(F_1\) and \(F_2\) be generators for  , then the equation
, then the equation

describes a plane sextic curve \(S_T\) with double points precisely at \(P_1, \ldots , P_7\). By the genus-degree formula we see that \(S_T\) has geometric genus 3 and it turns out that its smooth model is not hyperelliptic. Moreover, if we let  be a resolution of the singularities, then \(D_i = \rho ^{-1}(P_i)\) is a theta characteristic and \((D_1, \ldots , D_7)\) is an ordered Aronhold basis.
be a resolution of the singularities, then \(D_i = \rho ^{-1}(P_i)\) is a theta characteristic and \((D_1, \ldots , D_7)\) is an ordered Aronhold basis.
The following result can be found in [14] where it is attributed to van Geemen.
Theorem 3.2
Sending a septuple \(T=(P_1, \ldots , P_7)\) of points in general position in the projective plane to \((C_T, D_1, \ldots , D_7)\) gives an  -equivariant isomorphism
-equivariant isomorphism
Remark 3.3
Even though [14] only considers the case \(K= \mathbb {C}\), the proof only relies on the theory of geometrically marked Del Pezzo surfaces of degree 2. This theory is the same over any algebraically closed field of characteristic different from 2, see [24, Section III.3].
It should be pointed out that while the action of  is clear on \(\mathscr {Q}[2]\) its action on \(\mathscr {P}^2_7\) is much more subtle. However, we can at least plainly see the symmetric group
is clear on \(\mathscr {Q}[2]\) its action on \(\mathscr {P}^2_7\) is much more subtle. However, we can at least plainly see the symmetric group  acting on \(\mathscr {P}^2_7\) by permuting points.
acting on \(\mathscr {P}^2_7\) by permuting points.
Remark 3.4
Since it is not at all obvious at first glance that the group \(S_7\) embeds into  we say a few words about how this can be seen. It is not harder to see the embedding of the larger group \(S_8\) and we begin by explaining this embedding. Recall that \(S_8\) has a presentation given by generators \(\sigma _i\), \(i=1, \ldots , 7\), and relations
we say a few words about how this can be seen. It is not harder to see the embedding of the larger group \(S_8\) and we begin by explaining this embedding. Recall that \(S_8\) has a presentation given by generators \(\sigma _i\), \(i=1, \ldots , 7\), and relations

One should think about \(\sigma _i\) as the transposition of i and \(i+1\).
Let u be a vector in the six-dimensional vector space V over \(\mathbb {Z}/2\mathbb {Z}\) on which  acts and let b denote the symplectic bilinear form. The transvection
acts and let b denote the symplectic bilinear form. The transvection

is then an element in  . Let \(x_1, x_2,x_3, y_1,y_2,y_3\) be a symplectic basis of V (i.e. a basis such that
. Let \(x_1, x_2,x_3, y_1,y_2,y_3\) be a symplectic basis of V (i.e. a basis such that  ). The embedding of \(S_8\) can now be given explicitly as
). The embedding of \(S_8\) can now be given explicitly as
An embedding of \(S_7\) into  is now given via its natural embedding into \(S_8\). We also remark that all embedded copies of \(S_8\) and \(S_7\) in
is now given via its natural embedding into \(S_8\). We also remark that all embedded copies of \(S_8\) and \(S_7\) in  are conjugate.
are conjugate.
4 Lefschetz trace formula
We are interested in the spaces \(\mathscr {M}_{3}[2]\), \(\mathscr {Q}[2]\) and \(\mathscr {H}_{3}[2]\) and in particular we want to know their cohomology. The Lefschetz trace formula provides a way to obtain cohomological information about a space via point counts over finite fields.
Let p be a prime number, let \(n\geqslant 1\) be an integer and let \(q=p^n\). Also, let \(\mathbb {F}_{q}\) denote a finite field with q elements, let \(\mathbb {F}_{q^m}\) denote a degree m extension of \(\mathbb {F}_{q}\) and let \(\overline{\mathbb {F}}_{q}\) denote an algebraic closure of \(\mathbb {F}_{q}\). Let X be a scheme defined over \(\mathbb {F}_{q}\) and let \(F\) denote its geometric Frobenius endomorphism. Finally, let l be a prime number different from p and let  denote the k-th compactly supported étale cohomology group of X with coefficients in \(\mathbb {Q}_l\).
denote the k-th compactly supported étale cohomology group of X with coefficients in \(\mathbb {Q}_l\).
Let \(\Gamma \) be a finite group acting on X by rational automorphisms (i.e. automorphisms over \(\mathbb {F}_{q}\)). Then each cohomology group  is a \(\Gamma \)-representation. The Lefschetz trace formula allows us to obtain information about these representations by counting the number of fixed points of \(F\sigma \) for different \(\sigma \in \Gamma \).
is a \(\Gamma \)-representation. The Lefschetz trace formula allows us to obtain information about these representations by counting the number of fixed points of \(F\sigma \) for different \(\sigma \in \Gamma \).
Theorem 4.1
(Lefschetz trace formula) Let X be a separated scheme of finite type over \(\mathbb {F}_{q}\) with Frobenius endomorphism \(F\) and let \(\sigma \) be a rational automorphism of X of finite order. Then

where \(\overline{X}{}^{F\sigma }\) denotes the fixed point set of \(F\sigma \) in  .
.
For a proof, see [11, Rapport – Théorème 3.2].
Remark 4.2
This theorem is usually only stated in terms of \(F\). To get the above version one simply applies the “usual” theorem to the twist of X by \(\sigma \), i.e. by descending from \(\overline{X}\) via \(F\sigma \) instead of F. For more details, see e.g. [12, Section 3].
Remark 4.3
If \(\Gamma \) is a finite group acting on X by rational automorphisms and \(\sigma \in \Gamma \), then \(|\overline{X}{}^{F\sigma }|\) will only depend on the conjugacy class of \(\sigma \) in \(\Gamma \).
Let \(R(\Gamma )\) denote the representation ring of \(\Gamma \) and let the compactly supported \(\Gamma \)-equivariant Euler characteristic of \(\overline{X}\) be defined as the virtual representation

We also introduce the following notation:

Note in particular that  is the ordinary Euler characteristic of \(\overline{X}\). By character theory,
is the ordinary Euler characteristic of \(\overline{X}\). By character theory,  is completely determined by computing
is completely determined by computing  for a representative \(\sigma \) of each conjugacy class of \(\Gamma \). This motivates the following definition.
for a representative \(\sigma \) of each conjugacy class of \(\Gamma \). This motivates the following definition.
Definition 4.4
Let X be a separated scheme of finite type over \(\mathbb {F}_{q}\) with Frobenius endomorphism \(F\) and let \(\Gamma \) be a finite group acting on X by rational automorphisms. The determination of \(|X^{F\sigma }|\) for all \(\sigma \in \Gamma \) is then called a \(\Gamma \)-equivariant point count of X over \(\mathbb {F}_{q}\).
5 Minimal purity
Let X be a separated scheme of finite type over the finite field \(\mathbb {F}_{q}\) and let \(\Gamma \) be a group acting on X by rational automorphisms. We define the compactly supported \(\Gamma \)-equivariant Poincaré polynomial of X as

As for the Euler characteristic, we introduce the notation

In the previous section we saw that equivariant point counts give equivariant Euler characteristics. Poincaré polynomials contain more information (namely the cohomological grading) and are therefore more desirable to obtain but are typically more complicated to compute. However, if X satisfies a certain purity condition one can recover the Poincaré polynomial from the Euler characteristic. See also [3,4,5, 8] where similar phenomena for compact spaces have been exploited.
Definition 5.1
(Dimca and Lehrer [13]) Let X be an irreducible and separated scheme of finite type over \(\overline{\mathbb {F}}_{q}\) with Frobenius endomorphism \(F\) and let l be a prime not dividing q. The scheme X is called minimally pure if \(F\) acts on  by multiplication by
by multiplication by  .
.
A pure dimensional and separated scheme X of finite type over \(\overline{\mathbb {F}}_{q}\) is minimally pure if for any collection \(\{X_1, \ldots , X_r\}\) of irreducible components of X, the irreducible scheme  is minimally pure.
is minimally pure.
Examples of minimally pure varieties include complements of arrangements of hyperplanes and hypertori, toric varieties and quotients of reductive groups by maximal tori. For more examples, see [13, 22, 23].
Thus, if X is minimally pure and \(\sigma \) is a rational automorphism of X of finite order, then  . Therefore, a term
. Therefore, a term  in \(|\overline{X}{}^{F\circ \sigma }|\) can only come from
in \(|\overline{X}{}^{F\circ \sigma }|\) can only come from  and we can determine the \(\Gamma \)-equivariant Poincaré polynomial of X via the relation
and we can determine the \(\Gamma \)-equivariant Poincaré polynomial of X via the relation

If we recall that q is a prime power and, in particular, an integer and we see that the above formula indeed yields an integer (as it should). On the other hand we may view the above expression as a polynomial in q. We then see that the point count is polynomial and that the coefficients of this polynomial are given by the values of the characters of the representations  .
.
5.1 Minimal purity of \(\mathscr {Q}[2]\)
We shall now show that that the moduli space \(\mathscr {Q}[2]\) is minimally pure. Let \(C \subset \mathbb {P}^2\) be a plane quartic, let \(P \in C\) be a point and let  denote the tangent line of C at P. We say that P is a bitangent point if
denote the tangent line of C at P. We say that P is a bitangent point if

for some point Q that might coincide with P. If \(P \ne Q\) we say that P is a genuine bitangent point. We denote the moduli space of plane quartics with level 2 structure marked with a bitangent point by  and we denote the moduli space of plane quartics with level 2 structure marked with a genuine bitangent point by
and we denote the moduli space of plane quartics with level 2 structure marked with a genuine bitangent point by  . The space
. The space  is an open subvariety of
is an open subvariety of  and its complement
and its complement  is the moduli space of plane quartics with level 2 structure marked with a hyperflex point. We denote the latter space by
is the moduli space of plane quartics with level 2 structure marked with a hyperflex point. We denote the latter space by  .
.
Lemma 5.2
(Looijenga [25, Proposition 1.18, Lemma 3.6])  is minimally pure.
is minimally pure.
Proposition 5.3
\(\mathscr {Q}[2]\) is minimally pure.
Proof
A plane quartic has 28 bitangents so the morphism

forgetting the marked bitangent point, is finite of degree  . Thus, the map
. Thus, the map

is multiplication with  . In particular, the map
. In particular, the map

is injective. Since \(F\) acts on  by multiplication by \(q^{k-6}\), the same is true on the subspace
by multiplication by \(q^{k-6}\), the same is true on the subspace  and we conclude that \(\mathscr {Q}[2]\) is minimally pure. \(\square \)
and we conclude that \(\mathscr {Q}[2]\) is minimally pure. \(\square \)
Since \(\mathscr {Q}[2]\) is isomorphic to \(\mathscr {P}^2_7\), we may compute the cohomology of \(\mathscr {Q}[2]\) as a representation of \(S_7\) by making \(S_7\)-equivariant point counts of \(\mathscr {P}^2_7\).
6 Equivariant point counts
In this section we shall perform an \(S_7\)-equivariant point count of \(\mathscr {P}^2_7\). This amounts to the computation of \(|( \mathscr {P}^2_7)^{F\sigma } |\) for one representative \(\sigma \) of each of the fifteen conjugacy classes of \(S_7\). The computations will be rather different in the various cases but at least the underlying idea will be the same. Throughout this section we shall work over a finite field \(\mathbb {F}_{q}\) where q is odd.
Let U be a subset of \(( \mathbb {P}^{2}(\overline{\mathbb {F}}_{q}) )^7\) and interpret each point of U as an ordered septuple of points in \(\mathbb {P}^{2}(\overline{\mathbb {F}}_{q})\). Define the discriminant locus\(\Delta \subset U\) as the subset consisting of septuples which are not in general position. If U contains the subset of \(( \mathbb {P}^{2}(\overline{\mathbb {F}}_{q}) )^7\) consisting of all septuples which are in general position, then

An element of  is completely specified by where it takes four points in general position. Therefore, the action of
is completely specified by where it takes four points in general position. Therefore, the action of  on U is free and we have the simple relation
on U is free and we have the simple relation

We shall choose the set U in such a way that counting fixed points of \(F\sigma \) in U is easy. We shall therefore focus on the discriminant locus.
The discriminant locus can be decomposed as
where \(\Delta _\mathsf{l}\) consists of septuples where at least three points lie on a line and \(\Delta _\mathsf{c}\) consists of septuples where at least six points lie on a conic. The computation of \(|\Delta ^{F\sigma }|\) will consist of the following three steps:
the computation of \(|\Delta _\mathsf{l}^{F\sigma }|\),
the computation of \(|\Delta _\mathsf{c}^{F\sigma }|\),
the computation of
 .
.
We can then easily determine \(|\Delta ^{F\sigma }|\) via the principle of inclusion and exclusion.
Lemma 6.1
Let \(C \subset \mathbb {P}^{2}\) be a smooth conic over a field k and let \(P \in \mathbb {P}^{2}\) be a point such that n tangent lines of C pass through P. Then \(n \leqslant 2\) or  .
.
Proof
The line \(P^{\vee }\) in the dual projective plane intersects the dual conic \(C^{\vee }\) in n points. The dual conic \(C^{\vee }\) is smooth if the characteristic of k is not 2 and we conclude that n can be at most 2. \(\square \)
One can, of course, also see this via a direct computation.
Lemma 6.2
Let \(C \in \mathbb {P}^2\) be a smooth, \(\mathbb {F}_{q}\)-rational conic and let P be an \(\mathbb {F}_{q}\)-rational point lying on precisely one tangent line L to C. Then P is a point on C.
Proof
We first observe that L must be \(\mathbb {F}_{q}\)-rational since otherwise L and \(FL\) would be two distinct tangent lines passing through P. Let \(Q \in C\) be the point of tangency of L and assume \(Q \ne P\). If \(L'\) is another tangent to C, then \(L'\) cannot pass through Q since if that was the case the quadratic curve \(L \cup L'\) would intersect C with multiplicity at least 5, contradicting Bezout’s theorem.
Now consider the set S of \(\mathbb {F}_{q}\)-rational tangents of C different from L. We have \(|S|=q\). By the above observation we have that none of the elements passes through Q and, by assumption, none of them passes through P. Since the number of \(\mathbb {F}_{q}\)-rational points of L different from P and Q is \(q-1\), the pigeon hole principle gives that there must be a point R on L such that two of the elements of S pass through R. But now R is a point with three tangents of C passing through it which is impossible by Lemma 6.1. We conclude that \(P=Q\) and that P is a point on C. \(\square \)
The above results justify the following definition, which will be useful in the analysis of  . See also Fig. 1 for motivation of the terminology.
. See also Fig. 1 for motivation of the terminology.
Definition 6.3
Let C be a smooth conic over \(\mathbb {F}_{q}\) and let \(P \in \mathbb {P}^{2}(\mathbb {F}_{q})\). We then say that
P is on the \(\mathbb {F}_{q}\)-inside of C if there is no \(\mathbb {F}_{q}\)-tangent to C passing through P,
P is on C if there is precisely one \(\mathbb {F}_{q}\)-tangent to C passing through P,
P is on the \(\mathbb {F}_{q}\)-outside of C if there are two \(\mathbb {F}_{q}\)-tangents to C passing through P.
Recall that the natural action of \(S_7\) on a septuple \((P_1, \ldots , P_7)\) is given by
Thus, a septuple is fixed by \(F\sigma \) if and only if  for \(i=1,\ldots ,7\). This is the motivation for the following definition.
for \(i=1,\ldots ,7\). This is the motivation for the following definition.
Definition 6.4
Let X be an \(\mathbb {F}_{q}\)-scheme with Frobenius endomorphism \(F\) and let \(Z \subset X_{\overline{\mathbb {F}}_{q}}\) be a subscheme. We say that Z is a strict\(\mathbb {F}_{q^m}\)-subscheme if Z is an \(\mathbb {F}_{q^m}\)-subscheme which is not defined over \(\mathbb {F}_{q^n}\) for any \(n<m\).
If Z is a strict \(\mathbb {F}_{q^m}\)-subscheme, the m-tuple \((Z, \ldots , F^{m-1}Z)\) is called a conjugatem-tuple. Let r be a positive integer and let  be a partition of r. An r-tuple \((Z_1, \ldots , Z_r)\) of closed subschemes of X is called a conjugate\(\lambda \)-tuple if it consists of \(\lambda _1\) conjugate 1-tuples, \(\lambda _2\)-conjugate 2-tuples and so on. We denote the set of conjugate \(\lambda \)-tuples of \(\overline{\mathbb {F}_{q}}\)-points of X by \(X(\lambda )\).
be a partition of r. An r-tuple \((Z_1, \ldots , Z_r)\) of closed subschemes of X is called a conjugate\(\lambda \)-tuple if it consists of \(\lambda _1\) conjugate 1-tuples, \(\lambda _2\)-conjugate 2-tuples and so on. We denote the set of conjugate \(\lambda \)-tuples of \(\overline{\mathbb {F}_{q}}\)-points of X by \(X(\lambda )\).
We shall sometimes drop the adjective “conjugate” and simply write “\(\lambda \)-tuple”. Since the conjugacy class of an element in \(S_7\) is given by its cycle type, we want to count the number of conjugate \(\lambda \)-tuples in both U and \(\Delta \) for each partition of 7.
We now recall a number of basic results regarding point counts. We begin by noting that the number of conjugate \(\lambda \)-tuples of hyperplanes in  is equal to the number of conjugate \(\lambda \)-tuples of points in
is equal to the number of conjugate \(\lambda \)-tuples of points in  . We also recall that
. We also recall that

and that

A slightly less elementary result is that the number of smooth conics defined over \(\mathbb {F}_{q}\) is

To see this, note that there is a \(\mathbb {P}^{5}\) of conics. Of these there are \(q^2+q+1\) double \(\mathbb {F}_{q}\)-lines,  intersecting pairs of \(\mathbb {F}_{q}\)-lines and
intersecting pairs of \(\mathbb {F}_{q}\)-lines and  conjugate pairs of \(\mathbb {F}_{q^2}\)-lines while the remaining conics are smooth. Finally, recall that a smooth conic is rational and thus has \(q+1\) points.
conjugate pairs of \(\mathbb {F}_{q^2}\)-lines while the remaining conics are smooth. Finally, recall that a smooth conic is rational and thus has \(q+1\) points.
We are now ready for the task of counting the number of conjugate \(\lambda \)-tuples for each element of \(S_7\).
Remark 6.5
Since \(\mathscr {P}^2_7\) is minimally pure, equation (6.1) gives that \(|( \mathscr {P}^2_7)^{F\sigma } |\) is a monic polynomial in q of degree six so it is in fact enough to make counts for six different finite fields and interpolate. This is however hard to carry out in practice, even with a computer, as soon as \(\lambda \) contains parts of large enough size (where “large enough” means 3 or 4). However, one can always obtain partial information which provides important checks for our computations and for partitions entirely with parts at most 2 we have been able to obtain the entire polynomials also via computer counts. This fact might help to convince the reader of the validity of our results since these cases are by far the hardest to do by hand.
6.1 The case \(\lambda = [7]\)
For \(\lambda =[7]\), a conjugate \(\lambda \)-tuple is a septuple \((P_1, \ldots , P_7)\) such that \(FP_i=P_{i+1}\) for \(i=1,\ldots ,6\) and \(FP_7=P_1\). In this case, we simply take U as the subset of \((\mathbb {P}^{2})^7\) of pairwise distinct points. We then have
The main observation is the following.
Lemma 6.6
If \((P_1, \ldots , P_7)\) is a \(\lambda \)-tuple with three of its points on a line, then all seven points lie on a line defined over \(\mathbb {F}_{q}\).
Proof
Suppose that the set  is contained in the line L. Then L is either defined over \(\mathbb {F}_{q}\) or is a strict \(\mathbb {F}_{q^7}\)-line. If there is an \(1 \leqslant r \leqslant 6\) such that
is contained in the line L. Then L is either defined over \(\mathbb {F}_{q}\) or is a strict \(\mathbb {F}_{q^7}\)-line. If there is an \(1 \leqslant r \leqslant 6\) such that  we must have
we must have  and the result follows. For instance,
and the result follows. For instance,
- (i)
if S is of the form \(S=\{P_i,P_{i+1},P_{i+2}\}\), then
 ,
, - (ii)
if S is of the form \(S=\{P_i,P_{i+2},P_{i+4}\}\), then
 ,
, - (iii)
if S is of the form \(S=\{P_i,P_{i+1},P_{i+4}\}\), then
 .
.
However, if S is not of the above form we have  for all \(1 \leqslant r \leqslant 6\) and the above method fails.
for all \(1 \leqslant r \leqslant 6\) and the above method fails.
We show how to argue in the case \(S={P_1,P_2,P_4}\), the other cases are analogous. We assume that L is a strict \(\mathbb {F}_{q^7}\)-line and derive a contradiction. Since L is a strict \(\mathbb {F}_{q^7}\)-line, the points \(P_1,P_2,P_3\) and \(P_6\) must be in general position (otherwise we could find a triple of type (i)–(iii) on a line among these points, which would imply that L is defined over \(\mathbb {F}_{q}\)). Let \(L_{i,j}\) denote the line between \(P_i\) and  and define
and define
Since \(P_1,P_2,P_3\) and \(P_6\) are in general position, the points \(Q_1,Q_2\) and \(Q_3\) do not lie on a line.
Since \(P_1,P_2\) and \(P_4\) lie on a line we have \(P_4 \in L_{1,2}\). We have  and
and  so
so  . But since \(P_2 \in L_{1,2}\) we must have
. But since \(P_2 \in L_{1,2}\) we must have  . We thus have \(P_4 \in L_{1,2}\) and \(P_4 \in L_{3,6}\) so \(P_4=Q_1\). By analogous arguments one shows that \(P_5 =Q_3\) and \(P_7 =Q_2\). But we now have that \(\{Q_1,Q_2,Q_3\}=\{P_4,P_5,P_7\}=F^3 S\) so the points \(Q_1,Q_2\) and \(Q_3\) lie on the line \(F^3 L\). This contradiction establishes the claim. \(\square \)
. We thus have \(P_4 \in L_{1,2}\) and \(P_4 \in L_{3,6}\) so \(P_4=Q_1\). By analogous arguments one shows that \(P_5 =Q_3\) and \(P_7 =Q_2\). But we now have that \(\{Q_1,Q_2,Q_3\}=\{P_4,P_5,P_7\}=F^3 S\) so the points \(Q_1,Q_2\) and \(Q_3\) lie on the line \(F^3 L\). This contradiction establishes the claim. \(\square \)
Lemma 6.7
If \((P_1, \ldots , P_7)\) is a \(\lambda \)-tuple with six of its points on a smooth conic, then all seven points lie on a smooth conic defined over \(\mathbb {F}_{q}\).
Proof
Suppose that the set \(S=\{P_{i_1}, \ldots , P_{i_6}\}\) lies on a smooth conic C. We have  and since a conic is defined by any five points on it we have \(FC=C\). Hence, we have that C is defined over \(\mathbb {F}_{q}\) and that all seven points lie on C. \(\square \)
and since a conic is defined by any five points on it we have \(FC=C\). Hence, we have that C is defined over \(\mathbb {F}_{q}\) and that all seven points lie on C. \(\square \)
We conclude that \(\Delta _\mathsf{l}^{F\sigma }\) and \(\Delta _\mathsf{c}^{F\sigma }\) are disjoint. We obtain \(|\Delta _\mathsf{l}^{F\sigma }|\) by first choosing an \(\mathbb {F}_{q}\)-line L and then picking a \(\lambda \)-tuple on L. We thus have

To obtain \(|\Delta _\mathsf{c}|\) we first choose a smooth conic C and then a conjugate \(\lambda \)-tuple on C. We thus have

Equation (6.1) now gives

6.2 The case \(\lambda = [1,6]\)
For \(\lambda =[1,6]\) we can take a conjugate \(\lambda \)-tuple as a septuple \((P_1, \ldots , P_7)\) such that \(FP_i=P_{i+1}\) for \(i=1,\ldots ,5\), \(FP_6=P_1\) and \(FP_7 =P_7\). Also in this case we take U as the subset of \((\mathbb {P}^{2})^7\) of pairwise distinct points. We then have

The main observation is the following.
Lemma 6.8
If a \(\lambda \)-tuple has three points on a line, then either
- (1)
the first six points of the \(\lambda \)-tuple lie on an \(\mathbb {F}_{q}\)-line or,
- (2)
the first six points lie on two conjugate \(\mathbb {F}_{q^2}\)-lines, the \(\mathbb {F}_{q^2}\)-lines contain three \(\mathbb {F}_{q^6}\)-points each and these triples are interchanged by \(F\), or,
- (3)
the first six points lie pairwise on three conjugate \(\mathbb {F}_{q^3}\)-lines which intersect in \(P_7\).
Proof
Suppose that  lie on a line L. Then L is either defined over \(\mathbb {F}_{q},\mathbb {F}_{q^2},\mathbb {F}_{q^3}\) or \(\mathbb {F}_{q^6}\). One easily checks that for each of the \(\left( {\begin{array}{c}7\\ 3\end{array}}\right) =35\) possible choices of S there is an integer \(1 \leqslant r \leqslant 3\) such that
lie on a line L. Then L is either defined over \(\mathbb {F}_{q},\mathbb {F}_{q^2},\mathbb {F}_{q^3}\) or \(\mathbb {F}_{q^6}\). One easily checks that for each of the \(\left( {\begin{array}{c}7\\ 3\end{array}}\right) =35\) possible choices of S there is an integer \(1 \leqslant r \leqslant 3\) such that  so L is defined over \(\mathbb {F}_{q},\mathbb {F}_{q^2}\) or \(\mathbb {F}_{q^3}\), i.e. we are in one of the three cases above. \(\square \)
so L is defined over \(\mathbb {F}_{q},\mathbb {F}_{q^2}\) or \(\mathbb {F}_{q^3}\), i.e. we are in one of the three cases above. \(\square \)
Let \(\Delta _{\mathsf{l},i}\) be the subset of \(\Delta _\mathsf{l}\) corresponding to case (i) in Lemma 6.8. The set \(\Delta _{\mathsf{l},1}^{F\sigma }\) is clearly disjoint from \(\Delta _{\mathsf{l},2}^{F\sigma }\) and \(\Delta _{\mathsf{l},3}^{F\sigma }\).
Lemma 6.9
If six of the points of a \(\lambda \)-tuple \((P_1, \ldots , P_7)\) lie on a smooth conic, then \(P_1, \ldots , P_6\) lie on the conic and the conic is defined over \(\mathbb {F}_{q}\).
Proof
Suppose \(S=\{P_{i_1}, \ldots , P_{i_6}\}\) lie on a smooth conic C. Then \(|FS \cap S| \geqslant 5\) so \(FC=C\). Let \(P \in S\) be an \(\mathbb {F}_{q^6}\)-point. Then we have  . \(\square \)
. \(\square \)
Since a smooth conic does not contain a line, we have that \(\Delta _\mathsf{c}\) only intersects \(\Delta _{\mathsf{l},3}\), see Fig. 2.
We compute \(|\Delta _{\mathsf{l},1}^{F\sigma }|\) by first choosing an \(\mathbb {F}_{q}\)-line L and then a strict \(\mathbb {F}_{q^6}\) point on L. Finally we choose an \(\mathbb {F}_{q}\)-point \(P_7\) anywhere. We thus have

To obtain \(|\Delta _{\mathsf{l},2}^{F\sigma }|\) we first choose a strict \(\mathbb {F}_{q^2}\)-line, L. There are \(q^4-q\) such lines and once a line L is chosen, the other line must be \(FL\). We then choose a strict \(\mathbb {F}_{q^6}\)-point \(P_1\) on L. The points \(P_2=FP_1, \ldots , P_6=F^5 P_1\) will then be the rest of our conjugate sextuple and there are \(q^6-q^2\) choices. We now have two \(\mathbb {F}_{q^2}\)-lines with three of our six \(\mathbb {F}_{q^6}\)-points on each so all that remains is to choose an \(\mathbb {F}_{q}\)-point anywhere we want in one of \(q^2+q+1\) ways. Hence,

To count \(|\Delta _{\mathsf{l},3}^{F\sigma }|\) we first choose an \(\mathbb {F}_{q}\)-point \(P_7\) in \(q^2+q+1\) ways. There is a \(\mathbb {P}^{1}\) of lines through \(P_7\) and we want to choose a strict \(\mathbb {F}_{q^3}\)-line L through P. There are \(q^3-q\) choices. Finally, we choose one of the strict \(\mathbb {F}_{q^6}\)-points \(P_1\) on L in one of \(q^6-q^3\) possible ways. We thus have

In order to finish the computation of \(\Delta _\mathsf{l}\), we need to compute \(\bigl |\Delta _{\mathsf{l},2}^{F\sigma } \cap \Delta _{\mathsf{l},3}^{F\sigma }\bigr |\). We first choose a pair of conjugate \(\mathbb {F}_{q^2}\)-lines in  ways. These lines intersect in an \(\mathbb {F}_{q}\)-point and we choose \(P_7\) away from this point in one of \(q^2+q\) ways. We then choose a strict \(\mathbb {F}_{q^3}\)-line through \(P_7\) in one of \(q^3-q\) ways. This line intersects the two \(\mathbb {F}_{q^2}\)-lines in two distinct points which clearly must have \(\mathbb {F}_{q^6}\) as their minimal field of definition. We choose one of them to become \(P_1\) in one of two ways. Thus, in total we have
ways. These lines intersect in an \(\mathbb {F}_{q}\)-point and we choose \(P_7\) away from this point in one of \(q^2+q\) ways. We then choose a strict \(\mathbb {F}_{q^3}\)-line through \(P_7\) in one of \(q^3-q\) ways. This line intersects the two \(\mathbb {F}_{q^2}\)-lines in two distinct points which clearly must have \(\mathbb {F}_{q^6}\) as their minimal field of definition. We choose one of them to become \(P_1\) in one of two ways. Thus, in total we have

To compute \(|\Delta _\mathsf{c}^{F\sigma }|\) we first choose a smooth conic C in \(q^5-q^2\) ways. There are then \(q^6-q^3-q^2+q\) ways of choosing a conjugate sextuple on C. Finally, we choose \(P_7\) anywhere we want in \(q^2+q+1\) ways. We thus see that

It remains to compute the size of the intersection between \(\Delta _\mathsf{l}^{F\sigma }\) and \(\Delta _\mathsf{c}^{F\sigma }\). To do this, we begin by choosing a smooth conic C in \(q^5-q^2\) ways and then an \(\mathbb {F}_{q}\)-point \(P_7\) not on C in \(q^2+q+1-(q+1)=q^2\) ways. There are \(q^3-q\) strict \(\mathbb {F}_{q^3}\)-lines passing through \(P_7\). All of these intersect C in two, not necessarily strict, \(\mathbb {F}_{q^6}\)-points since, by Lemma 6.1, these lines cannot be tangent to C. More precisely, choosing any of the \(q^3-q\) strict \(\mathbb {F}_{q^3}\)-points Q of C gives a strict \(\mathbb {F}_{q^3}\)-line through Q and \(P_7\), and since every such line cuts C in exactly two points we conclude that there are precisely  strict \(\mathbb {F}_{q^3}\)-lines through P intersecting C in two strict \(\mathbb {F}_{q^3}\)-points. Thus, the remaining
strict \(\mathbb {F}_{q^3}\)-lines through P intersecting C in two strict \(\mathbb {F}_{q^3}\)-points. Thus, the remaining
strict \(\mathbb {F}_{q^3}\)-lines through \(P_7\) will intersect C in two strict \(\mathbb {F}_{q^6}\)-points. If we pick such a line and label one of the intersection points as \(P_1\) we obtain an element in \(\Delta _\mathsf{l}^{F\sigma } \cap \Delta _\mathsf{c}^{F\sigma }\). Hence,

We now conclude that
6.3 The case \(\lambda =[2,5]\)
For \(\lambda =[2,6]\) we can take a conjugate \(\lambda \)-tuple as a septuple \((P_1, \ldots , P_7)\) such that \(FP_i=P_{i+1}\) for \(i=1,\ldots ,4\), \(FP_5=P_1\), \(FP_6 =P_7\) and \(FP_7=P_6\). Also in this case we take U as the subset of \((\mathbb {P}^{2})^7\) of pairwise distinct points. We then have

The main observation is the following.
Lemma 6.10
If \((P_1, \ldots , P_7)\) is a \(\lambda \)-tuple with three of its points on a line, then all five \(\mathbb {F}_{q^5}\)-points lie on a line defined over \(\mathbb {F}_{q}\). If six of the points lie on a smooth conic C, then all seven points lie on C and C is defined over \(\mathbb {F}_{q}\).
Proof
The proof is very similar to the proofs of Lemmas 6.6 and 6.7 and is therefore omitted. \(\square \)
There are \(q^{10}+q^5-q^2-q\) conjugate quintuples whereof  lie on a line. We may thus choose a conjugate quintuple whose points do not lie on a line in \(q^{10}-q^7-q^6+q^3\) ways. This quintuple defines a smooth conic C. By Lemma 6.10, it is enough to choose a conjugate pair outside C in order to obtain an element of
lie on a line. We may thus choose a conjugate quintuple whose points do not lie on a line in \(q^{10}-q^7-q^6+q^3\) ways. This quintuple defines a smooth conic C. By Lemma 6.10, it is enough to choose a conjugate pair outside C in order to obtain an element of  of the desired type. Since there are \(q^4-q\) conjugate pairs of which \(q^2-q\) lie on C there are \(q^4-q^2\) remaining choices. We thus obtain
of the desired type. Since there are \(q^4-q\) conjugate pairs of which \(q^2-q\) lie on C there are \(q^4-q^2\) remaining choices. We thus obtain

6.4 The case 
The computation in this case is very similar to that of the case \(\lambda =[2,5]\) and we therefore simply state the result:

6.5 The case 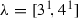
For \(\lambda =[3,4]\) we can take a conjugate \(\lambda \)-tuple as a septuple \((P_1, \ldots , P_7)\) such that \(F\) permutes the tuples \((P_1, P_2, P_3, P_4)\) and \((P_5,P_6,P_7)\) cyclically. Also in this case we take U as the subset of \((\mathbb {P}^{2})^7\) of pairwise distinct points. We then have

The main observation is the following.
Lemma 6.11
If a conjugate \(\lambda \)-tuple has three points on a line, then either
- (1)
the four \(\mathbb {F}_{q^4}\)-points lie on an \(\mathbb {F}_{q}\)-line, or
- (2)
the three \(\mathbb {F}_{q^3}\)-points lie on an \(\mathbb {F}_{q}\)-line.
Proof
It is easy to see that if three \(\mathbb {F}_{q^4}\)-points lie on a line, then all four \(\mathbb {F}_{q^4}\)-points lie on that line and even easier to see the corresponding result for three \(\mathbb {F}_{q^3}\)-points.
Suppose that two \(\mathbb {F}_{q^4}\)-points \(P_i\) and  and an \(\mathbb {F}_{q^3}\)-point P lie on a line L. Since \(F^4P_i=P_i\) and
and an \(\mathbb {F}_{q^3}\)-point P lie on a line L. Since \(F^4P_i=P_i\) and  we see that \(F^4L=L\). Thus, \(F^4P=FP \ne P\) lies on L. Repeating this argument again, with \(FP\) in the place of P, shows that also \(F^2P\) lies on L. We are thus in case (2).
we see that \(F^4L=L\). Thus, \(F^4P=FP \ne P\) lies on L. Repeating this argument again, with \(FP\) in the place of P, shows that also \(F^2P\) lies on L. We are thus in case (2).
If we assume that two \(\mathbb {F}_{q^3}\)-points and an \(\mathbb {F}_{q^4}\)-point lie on a line, then a completely analogous argument shows that all four \(\mathbb {F}_{q^4}\)-points lie on that line. \(\square \)
We decompose \(\Delta _\mathsf{l}^{F\sigma }\) as
where \(\Delta _{\mathsf{l},1}\) consists of tuples with the four \(\mathbb {F}_{q^4}\)-points on a line and \(\Delta _{\mathsf{l},2}\) consists of tuples with the three \(\mathbb {F}_{q^3}\)-points on a line. The computations of \(|\Delta _{\mathsf{l},1}|,|\Delta _{\mathsf{l},2}|\) and  are straightforward and we get
are straightforward and we get

so

To compute \(|\Delta _\mathsf{c}^{F\sigma }|\) we start by noting that if six of the points of a \(\lambda \)-tuple lie on a smooth conic C, then all seven points lie on C and C is defined over \(\mathbb {F}_{q}\). Thus, the problem consists of choosing a smooth conic C over \(\mathbb {F}_{q}\) and then picking a \(\lambda \)-tuple on C. We thus have

Since no three points on a smooth conic lie on a line, we conclude that the intersection  is empty. We thus obtain
is empty. We thus obtain

6.6 The case \(\lambda =[1,2,4]\)
For \(\lambda =[1,2,4]\) we can take a conjugate \(\lambda \)-tuple as a septuple \((P_1, \ldots , P_7)\) such that \(F\) permutes the tuple \((P_1, P_2, P_3, P_4)\) cyclically, transposes the points \(P_5\) and \(P_6\) and fixes the point \(P_7\). Also in this case we take U as the subset of \((\mathbb {P}^{2})^7\) of pairwise distinct points. We then have

We have the following trivial decomposition of \(\Delta _\mathsf{l}^{F\sigma }\):

where
\(\Delta _{\mathsf{l},1}\) consists of \(\lambda \)-tuples with three strict \(\mathbb {F}_{q^4}\)-points lying on a line,
\(\Delta _{\mathsf{l},2}\) consists of \(\lambda \)-tuples with two strict \(\mathbb {F}_{q^4}\)-points and a strict \(\mathbb {F}_{q^2}\)-point lying on a line,
\(\Delta _{\mathsf{l},3}\) consists of \(\lambda \)-tuples with two strict \(\mathbb {F}_{q^4}\)-points and the \(\mathbb {F}_{q}\)-point lying on a line,
\(\Delta _{\mathsf{l},4}\) consists of \(\lambda \)-tuples with a strict \(\mathbb {F}_{q^4}\)-point and two strict \(\mathbb {F}_{q^2}\)-points lying on a line,
\(\Delta _{\mathsf{l},5}\) consists of \(\lambda \)-tuples with a strict \(\mathbb {F}_{q^4}\)-point, a strict \(\mathbb {F}_{q^2}\)-point and an \(\mathbb {F}_{q}\)-point lying on a line, and,
\(\Delta _{\mathsf{l},6}\) consists of \(\lambda \)-tuples with the two strict \(\mathbb {F}_{q^2}\)-points and the \(\mathbb {F}_{q}\)-point lying on a line.
This decomposition is of course naive and is not very nice to work with since none of the possible intersections are empty and the reader can surely think of many other decompositions which, a priori, look more promising. However, the more “clever” approaches we have tried have turned out to be quite hard to work with in practice. The positive thing about the above decomposition is that most intersections are rather easily handled and that quadruple intersections (and higher) all consist of tuples where all seven points lie on an \(\mathbb {F}_{q}\)-line.
The two slightly more complicated sets in the above list are \(\Delta _{\mathsf{l},2}\) and \(\Delta _{\mathsf{l},3}\). We shall therefore comment a bit about the computations involving them.
The set \(\Delta _{\mathsf{l},2}\) splits into three disjoint subsets
where
\(\Delta _{\mathsf{l},2}^1\) consists of \(\lambda \)-tuples such that the four strict \(\mathbb {F}_{q^4}\)-points and the two strict \(\mathbb {F}_{q^2}\)-points lie on an \(\mathbb {F}_{q}\)-line, or,
\(\Delta _{\mathsf{l},2}^2\) consists of \(\lambda \)-tuples such that the two strict \(\mathbb {F}_{q^4}\)-points and the strict \(\mathbb {F}_{q^2}\)-point lie on a strict \(\mathbb {F}_{q^2}\)-line L (and the other two strict \(\mathbb {F}_{q^4}\)-points and the second strict \(\mathbb {F}_{q^2}\)-point lie on \(FL\)), or,
\(\Delta _{\mathsf{l},2}^3\) consists of \(\lambda \)-tuples such that the four strict \(\mathbb {F}_{q^4}\)-points and the two strict \(\mathbb {F}_{q^2}\)-points are intersection points of four conjugate \(\mathbb {F}_{q^4}\)-lines.
The sets \(\Delta _{\mathsf{l},2}^2\) and \(\Delta _{\mathsf{l},2}^3\) are illustrated in Fig. 3. The cardinality of \(\Delta _{\mathsf{l},2}^1\) is easily computed to be  . To get the cardinality of \(\Delta _{\mathsf{l},2}^2\), we first choose a strict \(\mathbb {F}_{q^2}\)-line L in one of \(q^4-q\) ways and then a strict \(\mathbb {F}_{q^4}\)-point \(P_1\) on L in one of \(q^4-q^2\) ways. This determines all the four \(\mathbb {F}_{q^4}\) points since they must be \(P_2=FP_1\),
. To get the cardinality of \(\Delta _{\mathsf{l},2}^2\), we first choose a strict \(\mathbb {F}_{q^2}\)-line L in one of \(q^4-q\) ways and then a strict \(\mathbb {F}_{q^4}\)-point \(P_1\) on L in one of \(q^4-q^2\) ways. This determines all the four \(\mathbb {F}_{q^4}\) points since they must be \(P_2=FP_1\),  and
and  . We must now decide if \(P_5\) should lie on L or \(FL\). We then choose a strict \(\mathbb {F}_{q^2}\)-point on the chosen line. The lines L and \(FL\) both contain \(q^2+1\) points defined over \(\mathbb {F}_{q^2}\) of which precisely one is defined over \(\mathbb {F}_{q}\) (namely the point \(L \cap FL\)). Hence, there are \(q^2\) choices for \(P_5\). It now only remains to choose \(P_7\) in one of \(q^2+q+1\) ways. We thus have
. We must now decide if \(P_5\) should lie on L or \(FL\). We then choose a strict \(\mathbb {F}_{q^2}\)-point on the chosen line. The lines L and \(FL\) both contain \(q^2+1\) points defined over \(\mathbb {F}_{q^2}\) of which precisely one is defined over \(\mathbb {F}_{q}\) (namely the point \(L \cap FL\)). Hence, there are \(q^2\) choices for \(P_5\). It now only remains to choose \(P_7\) in one of \(q^2+q+1\) ways. We thus have

It remains to compute \(|\Delta _{\mathsf{l},2}^3|\). We first choose an \(\mathbb {F}_{q^2}\)-point \(P_5\) not defined over \(\mathbb {F}_{q}\) in one of \(q^4-q\) ways. There are \(q^4-q^2\) lines L strictly defined over \(\mathbb {F}_{q^4}\) through \(P_5\) and we choose one of them. We thus get four \(\mathbb {F}_{q^4}\)-lines which intersect in the two \(\mathbb {F}_{q^2}\)-points \(P_5\) and \(P_6\) as well as in four strict \(\mathbb {F}_{q^4}\)-points. We choose one of these to become \(P_1\) and the labels of the other three points are then given. However, we could as well have chosen the line \(F^2L\) and ended up with the same four \(\mathbb {F}_{q^4}\)-points. We therefore must divide by 2. Finally, we choose any of the \(q^2+q+1\)\(\mathbb {F}_{q}\)-points to become \(P_7\). We thus have

The set \(\Delta _{\mathsf{l},3}^{F\sigma }\) splits into two disjoint subsets
where
\(\Delta _{\mathsf{l},3}^1\) consists of \(\lambda \)-tuples such that the four strict \(\mathbb {F}_{q^4}\)-points and the \(\mathbb {F}_{q}\)-point lie on an \(\mathbb {F}_{q}\)-line, and,
\(\Delta _{\mathsf{l},3}^2\) consists of \(\lambda \)-tuples such that there are two conjugate \(\mathbb {F}_{q^2}\)-lines intersecting in the \(\mathbb {F}_{q}\)-point, each \(\mathbb {F}_{q^2}\)-line containing two of the strict \(\mathbb {F}_{q^4}\)-points.
To compute \(|\Delta _{\mathsf{l},3}^1|\) we first choose an \(\mathbb {F}_{q}\)-line L, then a conjugate quadruple and an \(\mathbb {F}_{q}\)-point on L and finally a conjugate pair of \(\mathbb {F}_{q^2}\)-points anywhere. Hence

To compute \(|\Delta _{\mathsf{l},3}^2|\) we first choose an \(\mathbb {F}_{q^2}\)-line L not defined over \(\mathbb {F}_{q}\), then an \(\mathbb {F}_{q^4}\)-point \(P_4\) not defined over \(\mathbb {F}_{q^2}\) on L and finally a pair of conjugate \(\mathbb {F}_{q^2}\)-points anywhere. We thus have

We now consider the intersection \(\Delta _{\mathsf{l},2} \cap \Delta _{\mathsf{l},3}\). The decompositions above yield a decomposition

The intersection \(\Delta _{\mathsf{l},2}^1 \cap \Delta _{\mathsf{l},3}^1\) consists of configurations where all seven points lie on an \(\mathbb {F}_{q}\)-line. There are

such \(\lambda \)-tuples. Both the intersections \(\Delta _{\mathsf{l},2}^1 \cap \Delta _{\mathsf{l},3}^2\) and \(\Delta _{\mathsf{l},2}^2 \cap \Delta _{\mathsf{l},3}^1\) are empty.
To compute the cardinality of \(\Delta _{\mathsf{l},2}^2 \cap \Delta _{\mathsf{l},3}^2\) we first choose a strict \(\mathbb {F}_{q^2}\)-line L in one of \(q^4-q\) ways and then a strict \(\mathbb {F}_{q^4}\)-point \(P_1\) on L in one of \(q^4-q^2\) ways. We must now decide if \(P_5\) should lie on L or \(FL\). We then choose a strict \(\mathbb {F}_{q^2}\)-point on the chosen line in one of \(q^2\) ways. We are now sure to have a tuple in \(\Delta _{\mathsf{l},2}^2\). To make sure that the tuple also lies in \(\Delta _{\mathsf{l},3}^2\) we have no choice but to put \(P_7\) at the intersection of L and \(FL\). There are thus

elements in the intersection \(\Delta _{\mathsf{l},2}^2 \cap \Delta _{\mathsf{l},3}^2\).
The intersection \(\Delta _{\mathsf{l},2}^3 \cap \Delta _{\mathsf{l},3}^1\) is empty so there is only one intersection remaining. As explained in the computation of \(|\Delta _{\mathsf{l},2}^3|\), there are  ways to obtain four strict \(\mathbb {F}_{q^4}\)-points and two strict \(\mathbb {F}_{q^2}\)-points which are the intersection points of four conjugate \(\mathbb {F}_{q^4}\)-lines. We now note that there are precisely six lines through pairs of points among the four strict \(\mathbb {F}_{q^4}\)-points. Four of these lines are of course the four \(\mathbb {F}_{q^4}\)-lines. The remaining two lines are defined over \(\mathbb {F}_{q^2}\) and therefore intersect in an \(\mathbb {F}_{q}\)-point. To obtain a tuple in \(\Delta _{\mathsf{l},3}^2\) we have no choice but to choose \(P_7\) as this intersection point. Therefore, there are
ways to obtain four strict \(\mathbb {F}_{q^4}\)-points and two strict \(\mathbb {F}_{q^2}\)-points which are the intersection points of four conjugate \(\mathbb {F}_{q^4}\)-lines. We now note that there are precisely six lines through pairs of points among the four strict \(\mathbb {F}_{q^4}\)-points. Four of these lines are of course the four \(\mathbb {F}_{q^4}\)-lines. The remaining two lines are defined over \(\mathbb {F}_{q^2}\) and therefore intersect in an \(\mathbb {F}_{q}\)-point. To obtain a tuple in \(\Delta _{\mathsf{l},3}^2\) we have no choice but to choose \(P_7\) as this intersection point. Therefore, there are

elements in the intersection \(\Delta _{\mathsf{l},2}^3 \cap \Delta _{\mathsf{l},3}^2\).
The remaining computations are rather straightforward and one obtains

We now turn to \(\Delta _\mathsf{c}\). We have that if six points of a conjugate \(\lambda \)-tuple lie on a smooth conic C, then the four \(\mathbb {F}_{q^4}\)-points and the two \(\mathbb {F}_{q^2}\)-points lie on C and C is defined over \(\mathbb {F}_{q}\). Thus, the computation of \(|\Delta _\mathsf{c}|\) consists of choosing a smooth conic C defined over \(\mathbb {F}_{q}\), choosing a strict \(\mathbb {F}_{q^4}\)-point and a strict \(\mathbb {F}_{q^2}\)-point on C and finally choosing an \(\mathbb {F}_{q}\)-point anywhere. We thus have

It remains to investigate the intersection \(\Delta _\mathsf{l} \cap \Delta _\mathsf{c}\). Since a smooth conic cannot contain three collinear points, we only have nonempty intersection between \(\Delta _\mathsf{c}^{F\sigma }\) and the sets \(\Delta _{\mathsf{l},3}^2\) and \(\Delta _{\mathsf{l},6}\).
To compute  we first choose a smooth conic C, then a conjugate quadruple on C and finally a pair of conjugate \(\mathbb {F}_{q^2}\)-points on C. The \(\mathbb {F}_{q}\)-point is then uniquely defined as the intersection point of the two \(\mathbb {F}_{q^2}\)-lines through pairs of the four strict \(\mathbb {F}_{q^4}\)-points. We thus have
we first choose a smooth conic C, then a conjugate quadruple on C and finally a pair of conjugate \(\mathbb {F}_{q^2}\)-points on C. The \(\mathbb {F}_{q}\)-point is then uniquely defined as the intersection point of the two \(\mathbb {F}_{q^2}\)-lines through pairs of the four strict \(\mathbb {F}_{q^4}\)-points. We thus have

The same construction as above works for the intersection \(\Delta _{\mathsf{l},6} \cap \Delta _\mathsf{c}^{F\sigma }\) if we remember that we now have some choice for the \(\mathbb {F}_{q}\)-point since it can lie anywhere on the line through the two \(\mathbb {F}_{q^2}\)-points. We thus have

The only thing that remains to compute is the cardinality of the triple intersection \(\Delta _{\mathsf{l},3}^2 \cap \Delta _{\mathsf{l},6} \cap \Delta _\mathsf{c}^{F\sigma }\). We first assume that the \(\mathbb {F}_{q}\)-point is on the \(\mathbb {F}_{q}\)-outside of a smooth conic C containing the other six points. We first choose C in \(q^5-q^2\) ways. There are  ways to choose two \(\mathbb {F}_{q}\)-points P and Q on C. Intersecting the tangents
ways to choose two \(\mathbb {F}_{q}\)-points P and Q on C. Intersecting the tangents  and \(T_QC\) gives an \(\mathbb {F}_{q}\)-point \(P_7\) which will clearly lie on the \(\mathbb {F}_{q}\)-outside of C. Hence, there are precisely
and \(T_QC\) gives an \(\mathbb {F}_{q}\)-point \(P_7\) which will clearly lie on the \(\mathbb {F}_{q}\)-outside of C. Hence, there are precisely  ways to choose an \(\mathbb {F}_{q}\)-point on the \(\mathbb {F}_{q}\)-outside of C.
ways to choose an \(\mathbb {F}_{q}\)-point on the \(\mathbb {F}_{q}\)-outside of C.
We now want to choose an \(\mathbb {F}_{q}\)-line through \(P_7\) intersecting C in two \(\mathbb {F}_{q^2}\)-points. There are \(q+1\)\(\mathbb {F}_{q}\)-lines through \(P_7\) of which two are tangent to C. These tangent lines contain an \(\mathbb {F}_{q}\)-point of C each so there are \(q-1\) remaining \(\mathbb {F}_{q}\)-points on C. Picking such a point gives a line through this point, \(P_7\) and one further point on C. We thus see that exactly  of the \(\mathbb {F}_{q}\)-lines through \(P_7\) intersect C in two conjugate \(\mathbb {F}_{q^2}\)-points. We label one of them as \(P_5\).
of the \(\mathbb {F}_{q}\)-lines through \(P_7\) intersect C in two conjugate \(\mathbb {F}_{q^2}\)-points. We label one of them as \(P_5\).
We shall now choose a conjugate pair of \(\mathbb {F}_{q^2}\)-lines through \(P_7\) intersecting C in four \(\mathbb {F}_{q^4}\)-points. There are \(q^2-q\) conjugate pairs of \(\mathbb {F}_{q^2}\)-lines through \(P_7\). No \(\mathbb {F}_{q^2}\)-line through \(P_7\) is tangent to C so each \(\mathbb {F}_{q^2}\)-line through \(P_7\) will intersect C in two points. The conic C contains \(q^2-q\) points which are defined over \(\mathbb {F}_{q^2}\) but not \(\mathbb {F}_{q}\). Picking such a point gives a line through this point and \(P_7\) as well as one further \(\mathbb {F}_{q^2}\)-point not defined over \(\mathbb {F}_{q}\). Thus, there are  lines obtained in this way. Typically, such a line will be defined over \(\mathbb {F}_{q^2}\) but not \(\mathbb {F}_{q}\). We saw above that the number of such lines which are defined over \(\mathbb {F}_{q}\) is precisely
lines obtained in this way. Typically, such a line will be defined over \(\mathbb {F}_{q^2}\) but not \(\mathbb {F}_{q}\). We saw above that the number of such lines which are defined over \(\mathbb {F}_{q}\) is precisely  . Thus, there are precisely
. Thus, there are precisely
\(\mathbb {F}_{q^2}\)-lines, not defined over \(\mathbb {F}_{q}\), which intersect C in two strict \(\mathbb {F}_{q^2}\)-points. Thus, the remaining
\(\mathbb {F}_{q^2}\)-lines must intersect C in two strict \(\mathbb {F}_{q^4}\)-points. Picking such a line and labeling one of the points \(P_1\) gives a configuration belonging to \(\Delta _{\mathsf{l},3}^2 \cap \Delta _{\mathsf{l},6} \cap \Delta _\mathsf{c}^{F\sigma }\) and we thus see that there are

such configurations with \(P_7\) on the \(\mathbb {F}_{q}\)-outside of C.
We now assume that \(P_7\) is on the \(\mathbb {F}_{q}\)-inside of C. We first choose C in one of \(q^5-q^2\) ways. Since the number of \(\mathbb {F}_{q}\)-points is \(q^2+q+1\) and \(q+1\) of these lie on C the number of \(\mathbb {F}_{q}\)-points not on C is precisely \(q^2\). We just saw that  of these lie on the \(\mathbb {F}_{q}\)-outside of C so there must be
of these lie on the \(\mathbb {F}_{q}\)-outside of C so there must be

\(\mathbb {F}_{q}\)-points which lie on the \(\mathbb {F}_{q}\)-inside of C.
Since \(P_7\) now lies on the \(\mathbb {F}_{q}\)-inside of C, every \(\mathbb {F}_{q}\)-line through \(P_7\) will intersect C in two points. Exactly  will intersect C in two \(\mathbb {F}_{q}\)-points so the remaining
will intersect C in two \(\mathbb {F}_{q}\)-points so the remaining  will intersect C in two conjugate \(\mathbb {F}_{q^2}\)-points. We pick such a pair of points and label one of them \(P_5\).
will intersect C in two conjugate \(\mathbb {F}_{q^2}\)-points. We pick such a pair of points and label one of them \(P_5\).
We now choose a conjugate pair of \(\mathbb {F}_{q^2}\)-lines through \(P_7\) intersecting C in a conjugate quadruple of \(\mathbb {F}_{q^4}\)-points. The number of \(\mathbb {F}_{q^2}\)-lines, not defined over \(\mathbb {F}_{q}\), through \(P_7\) is \(q^2-q\). Two of these are tangent to C so, using ideas similar to those above, we see that
of these lines intersect C in points strictly defined over \(\mathbb {F}_{q^2}\). Hence, the remaining
lines intersect C in two \(\mathbb {F}_{q^4}\)-points which are not defined over \(\mathbb {F}_{q^2}\). If we pick one of these points to become \(P_1\) we end up with a configuration in \(\Delta _{\mathsf{l},3}^2 \cap \Delta _{\mathsf{l},6} \cap \Delta _\mathsf{c}^{F\sigma }\). We thus have

such configurations with \(P_7\) on the inside of C. One may note that the expression above actually is the same as the expression when \(P_7\) was on the outside, but this will not always be the case in this type of decomposition. We thus have

and finally

6.7 The case 
For  we can take a conjugate \(\lambda \)-tuple as a septuple \((P_1, \ldots , P_7)\) such that \(F\) permutes the tuple \((P_1, P_2, P_3, P_4)\) cyclically and fixes each of the points \(P_5,P_6\) and \(P_7\). In this case we take U as the subset of \((\mathbb {P}^{2})^7\) consisting of pairwise distinct points such that the last three of the points are not collinear. Thus, \(U^{F\sigma }\) consists of a conjugate quadruple and three \(\mathbb {F}_{q}\)-points not on a line. We then have
we can take a conjugate \(\lambda \)-tuple as a septuple \((P_1, \ldots , P_7)\) such that \(F\) permutes the tuple \((P_1, P_2, P_3, P_4)\) cyclically and fixes each of the points \(P_5,P_6\) and \(P_7\). In this case we take U as the subset of \((\mathbb {P}^{2})^7\) consisting of pairwise distinct points such that the last three of the points are not collinear. Thus, \(U^{F\sigma }\) consists of a conjugate quadruple and three \(\mathbb {F}_{q}\)-points not on a line. We then have

We can decompose \(\Delta _\mathsf{l}^{F\sigma }\) into a disjoint union as
where \(\Delta _{\mathsf{l},1}\) consists of septuples such that all four \(\mathbb {F}_{q^4}\)-points lie on a \(\mathbb {F}_{q}\)-line and \(\Delta _{\mathsf{l},2}\) consists of septuples such that the \(\mathbb {F}_{q^2}\)-line through \(P_1\) and \(P_3\) intersects the \(\mathbb {F}_{q^2}\)-line through \(P_2\) and \(P_4\) in \(P_5,P_6\) or \(P_7\).
To compute \(|\Delta _{\mathsf{l},1}|\) we simply choose a \(\mathbb {F}_{q}\)-line L, a conjugate quadruple on L and finally place the three \(\mathbb {F}_{q}\)-points in such a way that they do not lie on a line. This can be done in

ways. To compute \(|\Delta _{\mathsf{l},2}|\) we first choose \(P_5\), \(P_6\) or \(P_7\) then a \(\mathbb {F}_{q^2}\)-line L not defined over \(\mathbb {F}_{q}\) through this point. Finally, we choose a \(\mathbb {F}_{q^4}\)-point \(P_1\) which is not defined over \(\mathbb {F}_{q^2}\) on L and make sure that the final two \(\mathbb {F}_{q}\)-points are not collinear with the first. This can be done in

ways. This gives that

We now turn to investigate \(\Delta _{c}\). It is not hard to see that if six of the points lie on a smooth conic C, then the four \(\mathbb {F}_{q^4}\)-points must lie on that conic and C must be defined over \(\mathbb {F}_{q}\). We thus choose a smooth conic C over \(\mathbb {F}_{q}\) and a conjugate quadruple on C. Then we choose \(P_5,P_6\) or \(P_7\) to possibly not lie on C and place the other two on C. Finally, we place the final \(\mathbb {F}_{q}\)-point anywhere except on the line through the other two \(\mathbb {F}_{q}\)-points. This gives the number

However, we have now counted the configurations where all seven points lie on a smooth conic three times. There are

such configurations and it thus follows that

We now turn to the intersection \(\Delta _{l}^{F\sigma } \cap \Delta _{c}^{F\sigma } =\Delta _{\mathsf{l},2} \cap \Delta _{c}^{F\sigma }\). We begin by choosing one of the \(\mathbb {F}_{q}\)-points \(P_5\), \(P_6\) and \(P_7\) to not lie on the conic C. We call the chosen point P and the remaining two points \(P_i\) and  where \(i<j\). We now have three disjoint possibilities:
where \(i<j\). We now have three disjoint possibilities:
- (i)
the point P may lie on the \(\mathbb {F}_{q}\)-outside of C with one of the tangents through P also passing through \(P_i\),
- (ii)
the point P may lie on the \(\mathbb {F}_{q}\)-outside of C with none of the tangents through P passing through \(P_i\),
- (iii)
the point P may lie on the \(\mathbb {F}_{q}\)-inside of C.
We consider the three cases (i)–(iii) separately.
(i). We begin by choosing a smooth conic C over \(\mathbb {F}_{q}\) in one of \(q^5-q^2\) ways and a \(\mathbb {F}_{q}\)-point P on the \(\mathbb {F}_{q}\)-outside of C in one of \(\frac{1}{2}(q+1)q\) ways. By equation (6.2), there are now \(q^2-1\) ways to choose \(P_1\). Since we require \(P_i\) to lie on a tangent to C which passes through P, we only have 2 choices for \(P_i\). Finally, we may choose  as any of the q remaining points on C. We thus have
as any of the q remaining points on C. We thus have

possibilities in this case.
(ii). Again, we begin by choosing a smooth conic C over \(\mathbb {F}_{q}\) in one of \(q^5-q^2\) ways and a \(\mathbb {F}_{q}\)-point P on the \(\mathbb {F}_{q}\)-outside of C in one of  ways. We then choose \(P_1\) on C in one of \(q^2-1\) ways. The point \(P_i\) should now not lie on a tangent to C which passes through P so we have \(q-1\) choices. Since the line between P and \(P_i\) is not a tangent to C, there is one further intersection point between this line and C. Since \(P,P_i\) and
ways. We then choose \(P_1\) on C in one of \(q^2-1\) ways. The point \(P_i\) should now not lie on a tangent to C which passes through P so we have \(q-1\) choices. Since the line between P and \(P_i\) is not a tangent to C, there is one further intersection point between this line and C. Since \(P,P_i\) and  should not be collinear, we must take
should not be collinear, we must take  away from this point and \(P_i\) and we thus have \(q-1\) possible choices. Hence, we have
away from this point and \(P_i\) and we thus have \(q-1\) possible choices. Hence, we have

possibilities in this case.
(iii). We start by choosing a smooth conic C over \(\mathbb {F}_{q}\) in \(q^5-q^2\) ways and then a point P on the \(\mathbb {F}_{q}\)-inside of C in  ways. We continue by using equation (6.3) to see that we have \(q^2-1\) choices for \(P_1\). We now choose \(P_i\) as any of the \(\mathbb {F}_{q}\)-points on C and thus have \(q+1\) choices. Finally, we may choose
ways. We continue by using equation (6.3) to see that we have \(q^2-1\) choices for \(P_1\). We now choose \(P_i\) as any of the \(\mathbb {F}_{q}\)-points on C and thus have \(q+1\) choices. Finally, we may choose  as any \(\mathbb {F}_{q}\)-point on C, except in the intersection of C with the line through \(P_i\) and P. Hence, we have \(q-1\) choices. We thus have
as any \(\mathbb {F}_{q}\)-point on C, except in the intersection of C with the line through \(P_i\) and P. Hence, we have \(q-1\) choices. We thus have

possibilities in this case. We conclude that

and, finally,

6.8 The case \(\lambda =[1,3^2]\)
For \(\lambda =[1,3^2]\) we can take a conjugate \(\lambda \)-tuple as a septuple \((P_1, \ldots , P_7)\) such that \(F\) permutes the tuples \((P_1, P_2, P_3)\) and \((P_4,P_5,P_6)\) cyclically and fixes the point \(P_7\). In this case we take U as the subset of \((\mathbb {P}^{2})^7\) consisting of pairwise distinct points. We then have

We shall also denote the second triple of strict \(\mathbb {F}_{q^3}\)-points by \((Q_1,Q_2,Q_3)\) and the \(\mathbb {F}_{q}\)-point by R.
We decompose \(\Delta _\mathsf{l}^{F\sigma }\) as

where
\(\Delta _{\mathsf{l},1}\) consists of \(\lambda \)-tuples such that the points \(P_1,P_2\) and \(P_3\) lie on an \(\mathbb {F}_{q}\)-line,
\(\Delta _{\mathsf{l},2}\) consists of \(\lambda \)-tuples such that the points \(P_1,P_2\) and \(P_3\) are the intersection points of a conjugate triple of \(\mathbb {F}_{q^3}\)-lines with each of the lines containing one of the points \(Q_1,Q_2\) and \(Q_3\),
\(\Delta _{\mathsf{l},3}\) consists of \(\lambda \)-tuples such that the points \(Q_1,Q_2\) and \(Q_3\) are the intersection points of a conjugate triple of \(\mathbb {F}_{q^3}\)-lines with each of the lines containing one of the points \(P_1,P_2\) and \(P_3\),
\(\Delta _{\mathsf{l},4}\) consists of \(\lambda \)-tuples such that the points \(Q_1,Q_2\) and \(Q_3\) lie on an \(\mathbb {F}_{q}\)-line, and
\(\Delta _{\mathsf{l},5}\) consists of \(\lambda \)-tuples such that the point R is the intersection of three conjugate \(\mathbb {F}_{q^3}\)-lines with each of the \(\mathbb {F}_{q^3}\)-lines containing one of the points \(P_1,P_2\) and \(P_3\) and one of the points \(Q_1,Q_2\) and \(Q_3\) (Fig. 4).
We investigate each of the cases separately.
6.8.1 \(\Delta _{{l},1}\) and \(\Delta _{{l},4}\)
The cardinalities of \(\Delta _{\mathsf{l},1}\) and \(\Delta _{\mathsf{l},4}\) are obviously the same so we only make the computation for \(\Delta _{\mathsf{l},1}\). We thus choose an \(\mathbb {F}_{q}\)-line L, a conjugate \(\mathbb {F}_{q^3}\)-tuple \(P_1,P_2,P_3\) on L, a conjugate \(\mathbb {F}_{q^3}\)-tuple \(Q_1,Q_2,Q_3\) anywhere except equal to the other \(\mathbb {F}_{q^3}\)-tuple and, finally, an \(\mathbb {F}_{q}\)-point anywhere. We thus get

6.8.2 \(\Delta _{{l},2}\) and \(\Delta _{{l},3}\)
The cardinalities of \(\Delta _{\mathsf{l},2}\) and \(\Delta _{\mathsf{l},3}\) are of course also the same. To compute \(|\Delta _{\mathsf{l},2}|\) we first choose a conjugate triple of lines, \(L,FL,F^2 L\), which do not intersect in a point. There are \(q^6+q^3-q^2-q\) conjugate triples of lines of which  intersect in a point. There are thus \(q^6-q^5-q^4+q^3\) possible triples. We give the label \(P_1\) to the point \(L \cap FL\) which determines the labels of the other two intersection points. We must now choose if \(Q_1\) should lie on \(L,FL\) or \(F^2 L\) and then place \(Q_1\) on the chosen line. There are
intersect in a point. There are thus \(q^6-q^5-q^4+q^3\) possible triples. We give the label \(P_1\) to the point \(L \cap FL\) which determines the labels of the other two intersection points. We must now choose if \(Q_1\) should lie on \(L,FL\) or \(F^2 L\) and then place \(Q_1\) on the chosen line. There are  ways to do this. Finally, we choose any \(\mathbb {F}_{q}\)-point. We thus have
ways to do this. Finally, we choose any \(\mathbb {F}_{q}\)-point. We thus have

6.8.3 \(\Delta _{{l},5}\)
We first choose an \(\mathbb {F}_{q}\)-point R anywhere and then a conjugate triple of lines, \(L,FL\), \(F^2L\) through R. We then choose a point \(P_1\) somewhere on L in \(q^3\) ways. We must now decide if \(Q_1\) should lie on \(L,FL\) or \(F^2L\) and then pick a point on the chosen line in one of \(q^3-1\) ways. We thus see that

We must now compute the cardinalities of the different intersections. Firstly, note that the intersection between \(\Delta _{\mathsf{l},1}\) and \(\Delta _{\mathsf{l},2}\) is empty. Secondly, the size of the intersection of \(\Delta _{\mathsf{l},1}\) and \(\Delta _{\mathsf{l},3}\) is equal to that of the intersection of \(\Delta _{\mathsf{l},2}\) and \(\Delta _{\mathsf{l},4}\). To obtain \(|\Delta _{\mathsf{l},1} \cap \Delta _{\mathsf{l},3}|\) we first choose a conjugate triple of lines, \(L,FL,F^2L\), which do not intersect in a point and label the intersection \(L \cap FL\) by \(Q_1\). We then choose an \(\mathbb {F}_{q}\)-line \(L'\) and thus get three strict \(\mathbb {F}_{q^3}\)-points \(L' \cap L\), \(L' \cap FL\) and \(L' \cap F^2L\). We label one of these by \(P_1\). We may now choose any \(\mathbb {F}_{q}\)-point to become R. We thus see that that

When we consider the intersection between \(\Delta _{\mathsf{l},1}\) and \(\Delta _{\mathsf{l},4}\) we must distinguish between the cases where the two triples of strict \(\mathbb {F}_{q^3}\)-points lie on the same line and when they do not. A simple computation then gives

We continue by observing that  . To compute \(|\Delta _{\mathsf{l},1} \cap \Delta _{\mathsf{l},5}|\) we first choose an \(\mathbb {F}_{q}\)-point R and then a conjugate \(\mathbb {F}_{q^3}\)-tuple of lines \(L,FL,F^2L\) through R. We continue by choosing an \(\mathbb {F}_{q}\)-line \(L'\) not through R in one of \(q^2\) ways and then label \(L' \cap L\), \(L' \cap FL\) or \(L' \cap F^2L\) by \(Q_1\). Finally, we choose one of the remaining \(q^3-1\) points of L to become \(P_1\). Hence,
. To compute \(|\Delta _{\mathsf{l},1} \cap \Delta _{\mathsf{l},5}|\) we first choose an \(\mathbb {F}_{q}\)-point R and then a conjugate \(\mathbb {F}_{q^3}\)-tuple of lines \(L,FL,F^2L\) through R. We continue by choosing an \(\mathbb {F}_{q}\)-line \(L'\) not through R in one of \(q^2\) ways and then label \(L' \cap L\), \(L' \cap FL\) or \(L' \cap F^2L\) by \(Q_1\). Finally, we choose one of the remaining \(q^3-1\) points of L to become \(P_1\). Hence,

The sets \(\Delta _{\mathsf{l},2}\) and \(\Delta _{\mathsf{l},3}\) do not intersect and neither do the sets \(\Delta _{\mathsf{l},3}\) and \(\Delta _{\mathsf{l},4}\). Hence, there are only two intersections left, namely the one between \(\Delta _{\mathsf{l},2}\) and \(\Delta _{\mathsf{l},5}\) and the one between \(\Delta _{\mathsf{l},3}\) and \(\Delta _{\mathsf{l},5}\). These have equal cardinalities. To compute  we first choose a conjugate triple of lines, \(L,FL,F^2L\), which do not intersect in a point and label the intersection \(L \cap FL\) by \(Q_1\). We then choose an \(\mathbb {F}_{q}\)-point R. The lines between R and the points \(Q_1,Q_2\) and \(Q_3\) intersect the lines \(L,FL\) and \(F^2L\) in three points and we label one of them by \(P_1\). We thus have
we first choose a conjugate triple of lines, \(L,FL,F^2L\), which do not intersect in a point and label the intersection \(L \cap FL\) by \(Q_1\). We then choose an \(\mathbb {F}_{q}\)-point R. The lines between R and the points \(Q_1,Q_2\) and \(Q_3\) intersect the lines \(L,FL\) and \(F^2L\) in three points and we label one of them by \(P_1\). We thus have

There is only one triple intersection, namely between \(\Delta _{\mathsf{l},1},\Delta _{\mathsf{l},4}\) and \(\Delta _{\mathsf{l},5}\). To compute the size of this intersection we first choose an \(\mathbb {F}_{q}\)-point R and then a conjugate triple of lines, \(L,FL,F^2L\) through R. We then choose an \(\mathbb {F}_{q}\)-line \(L'\) not through R and label the intersection \(L \cap L'\) by \(P_1\). Finally, we choose another \(\mathbb {F}_{q}\)-line \(L''\) and label one of the intersections  ,
,  and
and  by \(Q_1\). This shows that
by \(Q_1\). This shows that

We now turn to the computation of \(|\Delta _\mathsf{c}|\). If six points of a \(\lambda \)-tuple lie on a smooth conic C, then both of the conjugate triples must lie on C and C must be defined over \(\mathbb {F}_{q}\). Hence, to obtain \(|\Delta _\mathsf{c}|\) we only have to choose a smooth \(\mathbb {F}_{q}\)-conic C, two conjugate triples on C and an \(\mathbb {F}_{q}\)-point anywhere. We thus have that

Since the sets \(\Delta _{\mathsf{l},1},\Delta _{\mathsf{l},2},\Delta _{\mathsf{l},3}\) and \(\Delta _{\mathsf{l},4}\) all require three of the \(\mathbb {F}_{q^3}\)-points to lie on a line, they will have empty intersection with \(\Delta _\mathsf{c}\). This is however not true for the set \(\Delta _{\mathsf{l},5}\). To obtain such a configuration we first choose a smooth conic C and an \(\mathbb {F}_{q}\)-point R. Now choose an \(\mathbb {F}_{q^3}\)-point \(P_1\) on C which is not defined over \(\mathbb {F}_{q}\) in one of \(q^3-q\) ways. Since both C and R are defined over \(\mathbb {F}_{q}\) we know that any tangent to C which passes through R must be defined over \(\mathbb {F}_{q^2}\). Hence, the line through R and \(P_1\) will intersect C in \(P_1\) and one point more. We label this point with \(Q_1,Q_2\) or \(Q_3\). We thus have

We now obtain

6.9 The case 
For  we can take a conjugate \(\lambda \)-tuple as a septuple \((P_1, \ldots , P_7)\) such that \(F\) permutes the tuple \((P_1, P_2, P_3)\) cyclically and transposes the pairs \((P_4,P_5)\) and \((P_6,P_7)\). In this case we take U as the subset of \((\mathbb {P}^{2})^7\) consisting of pairwise distinct points. We then have
we can take a conjugate \(\lambda \)-tuple as a septuple \((P_1, \ldots , P_7)\) such that \(F\) permutes the tuple \((P_1, P_2, P_3)\) cyclically and transposes the pairs \((P_4,P_5)\) and \((P_6,P_7)\). In this case we take U as the subset of \((\mathbb {P}^{2})^7\) consisting of pairwise distinct points. We then have

We can decompose \(\Delta _\mathsf{l}^{F\sigma }\) as
where \(\Delta _{\mathsf{l},1}\) consists of septuples such that the three strict \(\mathbb {F}_{q^3}\)-points lie on a line and \(\Delta _{\mathsf{l},2}\) consists of septuples such that the four strict \(\mathbb {F}_{q^2}\)-points lie on a line.
We have

and

The cardinality of the intersection is easily computed to be

This allows us to compute \(|\Delta _\mathsf{l}^{F\sigma }|\).
We have that if six of the points of a \(\lambda \)-tuple lie on a smooth conic C, then all seven points lie on C and C is defined over \(\mathbb {F}_{q}\). We thus have that \(\Delta _\mathsf{c}^{F\sigma }\) is disjoint from \(\Delta _\mathsf{l}^{F\sigma }\). We also see that

so,

6.10 The case 
For  we can take a conjugate \(\lambda \)-tuple as a septuple \((P_1, \ldots , P_7)\) such that \(F\) permutes the tuple \((P_1, P_2, P_3)\) cyclically, transposes the pair \((P_4,P_5)\) and fixes \(P_6\) and \(P_7\). In this case we take U as the subset of \((\mathbb {P}^{2})^7\) consisting of pairwise distinct points. We then have
we can take a conjugate \(\lambda \)-tuple as a septuple \((P_1, \ldots , P_7)\) such that \(F\) permutes the tuple \((P_1, P_2, P_3)\) cyclically, transposes the pair \((P_4,P_5)\) and fixes \(P_6\) and \(P_7\). In this case we take U as the subset of \((\mathbb {P}^{2})^7\) consisting of pairwise distinct points. We then have

We shall use the notation \(P_1,P_2,P_3\) for the conjugate triple, \(Q_1,Q_2\) for the conjugate pair and use \(R_6\) and \(R_7\) to denote the two \(\mathbb {F}_{q}\)-points.
We decompose \(\Delta _\mathsf{l}^{F\sigma }\) as
where \(\Delta _{\mathsf{l},1}\) consists of \(\lambda \)-tuples such that the three strict \(\mathbb {F}_{q^3}\)-points lie on an \(\mathbb {F}_{q}\)-line and \(\Delta _{\mathsf{l},2}\) consists of \(\lambda \)-tuples such that the two conjugate \(\mathbb {F}_{q^2}\)-points and one of the \(\mathbb {F}_{q}\)-points lie on an \(\mathbb {F}_{q}\)-line.
We have

We decompose \(\Delta _{\mathsf{l},2}\) as
where \(\Delta _{\mathsf{l},2}^i\) consists of tuples such that the line through the two \(\mathbb {F}_{q^2}\)-points passes through \(R_i\). We have

We now turn to the double intersections. We have

and

Finally, we compute the cardinality of the intersection of all three sets

This allows us to compute \(\Delta _\mathsf{l}\).
If six points of a \(\lambda \)-tuple lie on a smooth conic C, then the three \(\mathbb {F}_{q^3}\)-points and the two \(\mathbb {F}_{q^2}\)-points lie on C and C is defined over \(\mathbb {F}_{q}\). Thus, to compute \(|\Delta _\mathsf{c}^{F\sigma }|\) we begin by choosing a smooth conic C over \(\mathbb {F}_{q}\). We then choose a conjugate triple and a conjugate pair of \(\mathbb {F}_{q^2}\)-points on C. Then, we choose either \(R_6\) or \(R_7\) and place the chosen point on C. Finally, we place the remaining point anywhere we want. We thus obtain the number

However, in the above we have counted the configurations where all seven points lie on the conic twice. We thus have to take away

in order to obtain \(|\Delta _\mathsf{c}^{F\sigma }|\).
It only remains to compute the cardinality of the intersection  . We only have nonempty intersection between the set \(\Delta _\mathsf{c}^{F\sigma }\) and the set \(\Delta _{\mathsf{l},2}\). To compute the cardinality of this intersection, we only have to make sure to choose the point \(R_6\) (resp. \(R_7\)) on the line through the two \(\mathbb {F}_{q^2}\)-points. Hence, we have
. We only have nonempty intersection between the set \(\Delta _\mathsf{c}^{F\sigma }\) and the set \(\Delta _{\mathsf{l},2}\). To compute the cardinality of this intersection, we only have to make sure to choose the point \(R_6\) (resp. \(R_7\)) on the line through the two \(\mathbb {F}_{q^2}\)-points. Hence, we have

and, therefore,

This gives us

6.11 The case 
For  we can take a conjugate \(\lambda \)-tuple as a septuple \((P_1, \ldots , P_7)\) such that \(F\) permutes the tuple \((P_1, P_2, P_3)\) cyclically and fixes the points \(P_4, P_5, P_6\) and \(P_7\). In this case we take U as the subset of \((\mathbb {P}^{2})^7\) consisting of pairwise distinct points such that the last four points lie in general position. We then have
we can take a conjugate \(\lambda \)-tuple as a septuple \((P_1, \ldots , P_7)\) such that \(F\) permutes the tuple \((P_1, P_2, P_3)\) cyclically and fixes the points \(P_4, P_5, P_6\) and \(P_7\). In this case we take U as the subset of \((\mathbb {P}^{2})^7\) consisting of pairwise distinct points such that the last four points lie in general position. We then have

We shall denote the four \(\mathbb {F}_{q}\)-points by \(Q_1,Q_2,Q_3\) and \(Q_4\).
A septuple in \(\Delta _\mathsf{l}^{F\sigma }\) will have the three strict \(\mathbb {F}_{q^3}\)-points on an \(\mathbb {F}_{q}\)-line. Thus, to compute the size of \(\Delta _\mathsf{l}^{F\sigma }\) we only need to place the four \(\mathbb {F}_{q}\)-points in general position, choose \(\mathbb {F}_{q}\)-line L and place the conjugate \(\mathbb {F}_{q^3}\)-tuple on L. We thus have,

A septuple in \(\Delta _\mathsf{c}^{F\sigma }\) will have the three strict \(\mathbb {F}_{q^3}\)-points on a smooth conic C defined over \(\mathbb {F}_{q}\). Thus, to compute \(|\Delta _\mathsf{c}^{F\sigma }|\), we first choose a smooth conic C defined over \(\mathbb {F}_{q}\) and then a conjugate triple on C. We then choose one of the points \(Q_1,Q_2,Q_3\) and \(Q_4\) to possibly not lie on C. Call this point Q. We then place the other three points on C. These three points define three lines which, in total, contain \((q+1)+q+(q-1)=3q\) points. As long as we choose Q away from these points, the four \(\mathbb {F}_{q}\)-points will be in general position. We thus obtain

However, we have counted the septuples with all seven points on a smooth conic four times. We thus need to take away

Since \(\Delta _\mathsf{l}^{F\sigma }\) and \(\Delta _\mathsf{c}^{F\sigma }\) are disjoint we are done and conclude that

6.12 The case \(\lambda =[1,2^3]\)
For \(\lambda =[1,2^3]\) we can take a conjugate \(\lambda \)-tuple as a septuple \((P_1, \ldots , P_7)\) such that \(F\) transposes the pairs \((P_1, P_2),(P_3,P_4)\) and \((P_5,P_6)\) and fixes the point \(P_7\). In this case we take U as the subset of \((\mathbb {P}^{2})^7\) consisting of pairwise distinct points such that the first six points have no three points on a line. We then have

We shall denote the three conjugate pairs of \(\mathbb {F}_{q^2}\)-points by \(P_1,P_2,Q_1,Q_2\) and \(R_1,R_2\) and the \(\mathbb {F}_{q}\)-point by O.
We decompose \(\Delta _\mathsf{l}^{F\sigma }\) as
where \(\Delta _{\mathsf{l},1}\) consists of those septuples where two conjugate \(\mathbb {F}_{q^2}\)-points and the \(\mathbb {F}_{q}\)-point lie on an \(\mathbb {F}_{q}\)-line and \(\Delta _{\mathsf{l},2}\) consists of those septuples where two conjugate \(\mathbb {F}_{q^2}\)-lines, containing two \(\mathbb {F}_{q^2}\)-points each, intersect in the point defined over \(\mathbb {F}_{q}\).
The set \(\Delta _{\mathsf{l},1}\) naturally decomposes into three equally large, but not disjoint, subsets:
the set \(\Delta _{\mathsf{l},1}^a\) where \(P_1,P_2\) and O lie on an \(\mathbb {F}_{q}\)-line,
the set \(\Delta _{\mathsf{l},1}^b\) where \(Q_1,Q_2\) and O lie on an \(\mathbb {F}_{q}\)-line, and
the set \(\Delta _{\mathsf{l},1}^c\) where \(R_1,R_2\) and O lie on an \(\mathbb {F}_{q}\)-line.
Similarly, the set \(\Delta _{\mathsf{l},2}\) decomposes into six disjoint and equally large subsets:
the two sets \(\Delta _{\mathsf{l},2}^{P_1,Q_i}\) where the line through the points \(P_1\) and \(Q_i\) also passes through the point O,
the two sets \(\Delta _{\mathsf{l},2}^{P_1,R_i}\) where the line through the points \(P_1\) and \(R_i\) also passes through the point O, and
the two sets \(\Delta _{\mathsf{l},2}^{Q_1,R_i}\) where the line through the points \(Q_1\) and \(R_i\) also passes through the point O.
The cardinalities of these sets are easily computed to be

and

To compute  we note that if we place the three pairs of conjugate \(\mathbb {F}_{q^2}\)-points so that no three lie on a line, then the line through \(P_1\) and \(P_2\) and the line through \(Q_1\) and \(Q_2\) will intersect in an \(\mathbb {F}_{q}\)-point. By choosing this point as O we obtain an element of
we note that if we place the three pairs of conjugate \(\mathbb {F}_{q^2}\)-points so that no three lie on a line, then the line through \(P_1\) and \(P_2\) and the line through \(Q_1\) and \(Q_2\) will intersect in an \(\mathbb {F}_{q}\)-point. By choosing this point as O we obtain an element of  . We now see that
. We now see that

To compute  we first choose a conjugate pair \(Q_1,Q_2\) and then a conjugate pair of \(\mathbb {F}_{q^2}\)-points \(R_1,R_2\) which do not lie on the line through \(Q_1\) and \(Q_2\). We now only have one choice for O. We choose an \(\mathbb {F}_{q}\)-line L through O. There are two possibilities: either L will pass through the intersection point P of the line through \(Q_1\) and \(R_2\) and the line through \(Q_2\) and \(R_1\) or it will not. If L passes through P, then we have \(q^2-q\) possible choices for \(P_1\) and \(P_2\) on L. Otherwise, we only have \(q^2-q-2\) choices. Hence
we first choose a conjugate pair \(Q_1,Q_2\) and then a conjugate pair of \(\mathbb {F}_{q^2}\)-points \(R_1,R_2\) which do not lie on the line through \(Q_1\) and \(Q_2\). We now only have one choice for O. We choose an \(\mathbb {F}_{q}\)-line L through O. There are two possibilities: either L will pass through the intersection point P of the line through \(Q_1\) and \(R_2\) and the line through \(Q_2\) and \(R_1\) or it will not. If L passes through P, then we have \(q^2-q\) possible choices for \(P_1\) and \(P_2\) on L. Otherwise, we only have \(q^2-q-2\) choices. Hence

The only nonempty triple intersection is \(\Delta _{\mathsf{l},1}^a \cap \Delta _{\mathsf{l},1}^b \cap \Delta _{\mathsf{l},1}^c\). A computation very similar to the one for  gives
gives

This finishes the investigation of \(\Delta _\mathsf{l}^{F\sigma }\).
We now turn to \(\Delta _\mathsf{c}^{F\sigma }\). If six points of a \(\lambda \)-tuple lie on a smooth conic C, then the six \(\mathbb {F}_{q^2}\)-points lie on C and C is defined over \(\mathbb {F}_{q}\). Since no three points of a smooth conic can lie on a line, we shall obtain an element of \(\Delta _\mathsf{c}^{F\sigma }\) simply by choosing a smooth conic C, three conjugate pairs on C and, finally, an \(\mathbb {F}_{q}\)-point anywhere. We thus have

We shall now compute the cardinality of the intersection between \(\Delta _\mathsf{l}\) and \(\Delta _\mathsf{c}\). The intersections with the cases \(\Delta _{\mathsf{l},1}^a,\Delta _{\mathsf{l},1}^b\), and \(\Delta _{\mathsf{l},1}^c\) are easily handled — we simply choose a smooth conic with three conjugate pairs on it and then place O on the line through the right conjugate pair. We thus get

The intersections with the sets  and \(\Delta _{\mathsf{l},2}^{Q_1,R_i}\) are just as simple. Once we have chosen our conic C and our conjugate pairs we have only one choice for O. Hence,
and \(\Delta _{\mathsf{l},2}^{Q_1,R_i}\) are just as simple. Once we have chosen our conic C and our conjugate pairs we have only one choice for O. Hence,

An analogous argument shows that

The remaining intersections are quite a bit harder than the previous ones. We begin by considering the intersection  , but the other intersections of this type are completely analogous and have the same size.
, but the other intersections of this type are completely analogous and have the same size.
We first consider the case when O is on the \(\mathbb {F}_{q}\)-outside of C. There are \(q+1\) lines through O. Of these, precisely two are tangents and  intersect C in \(\mathbb {F}_{q}\)-points. Thus, the remaining
intersect C in \(\mathbb {F}_{q}\)-points. Thus, the remaining  lines will intersect C in two conjugate \(\mathbb {F}_{q^2}\)-points. We thus pick one of these lines and label one of the intersection points by \(P_1\).
lines will intersect C in two conjugate \(\mathbb {F}_{q^2}\)-points. We thus pick one of these lines and label one of the intersection points by \(P_1\).
Picking an \(\mathbb {F}_{q^2}\)-point not defined over \(\mathbb {F}_{q}\) on C will typically define an \(\mathbb {F}_{q^2}\)-line through O which is not defined over \(\mathbb {F}_{q}\). However, some of these choices will give \(\mathbb {F}_{q}\)-lines and we saw above that the number of such \(\mathbb {F}_{q}\)-lines is  . Thus, the number of \(\mathbb {F}_{q^2}\)-lines, not defined over \(\mathbb {F}_{q}\), intersecting C in two strict \(\mathbb {F}_{q^2}\)-points is
. Thus, the number of \(\mathbb {F}_{q^2}\)-lines, not defined over \(\mathbb {F}_{q}\), intersecting C in two strict \(\mathbb {F}_{q^2}\)-points is
We pick one such line, label one of the intersection points \(Q_1\) and the other intersection point \(R_1\). This gives us a configuration of the desired type. Hence, the number of tuples in  with O on the \(\mathbb {F}_{q}\)-outside of C is
with O on the \(\mathbb {F}_{q}\)-outside of C is

We now turn to the case when O is on the \(\mathbb {F}_{q}\)-inside of C. Of the \(q+1\) lines defined over \(\mathbb {F}_{q}\) which pass through O,  will now intersect C in \(\mathbb {F}_{q}\)-points and equally many in conjugate \(\mathbb {F}_{q^2}\)-points. We thus pick a line that intersects C in two conjugate \(\mathbb {F}_{q^2}\)-points and label one of them by \(P_1\).
will now intersect C in \(\mathbb {F}_{q}\)-points and equally many in conjugate \(\mathbb {F}_{q^2}\)-points. We thus pick a line that intersects C in two conjugate \(\mathbb {F}_{q^2}\)-points and label one of them by \(P_1\).
We now want to pick an \(\mathbb {F}_{q^2}\)-line through O which is not defined over \(\mathbb {F}_{q}\) and which intersects C in two \(\mathbb {F}_{q^2}\)-points that are not defined over \(\mathbb {F}_{q}\). To obtain such a line we pick an \(\mathbb {F}_{q^2}\)-point which is not defined over \(\mathbb {F}_{q}\) on C. However, two such points define tangents to C which pass through O and  of the lines obtained in this way are actually defined over \(\mathbb {F}_{q}\). We thus have
of the lines obtained in this way are actually defined over \(\mathbb {F}_{q}\). We thus have
choices. We pick such a line and label the intersection points by \(Q_1\) and \(R_1\). Hence, the number of tuples in  with O on the \(\mathbb {F}_{q}\)-inside of C is
with O on the \(\mathbb {F}_{q}\)-inside of C is

This finishes the computation of  ,
,  and
and  .
.
The only remaining intersection is  which we shall handle in a way similar to that above. Fortunately, much of the work has already been done. To start, if O is on the \(\mathbb {F}_{q}\)-outside of C, then there are
which we shall handle in a way similar to that above. Fortunately, much of the work has already been done. To start, if O is on the \(\mathbb {F}_{q}\)-outside of C, then there are  lines though O which are defined over \(\mathbb {F}_{q}\) and intersect C in conjugate pairs of \(\mathbb {F}_{q^2}\)-points. Thus, there are
lines though O which are defined over \(\mathbb {F}_{q}\) and intersect C in conjugate pairs of \(\mathbb {F}_{q^2}\)-points. Thus, there are

ways to pick three lines and label the intersection points with \(P_1\) and \(P_2\), \(Q_1\) and \(Q_2\) and \(R_1\) and \(R_2\). Hence, the number of \(\lambda \)-tuples in  with O on the outside of C is
with O on the outside of C is

Similarly, if O lies on the \(\mathbb {F}_{q}\)-inside of C we have seen that there are  lines through O which are defined over \(\mathbb {F}_{q}\) and which intersect C in a pair of conjugate \(\mathbb {F}_{q^2}\)-points. Thus, there are
lines through O which are defined over \(\mathbb {F}_{q}\) and which intersect C in a pair of conjugate \(\mathbb {F}_{q^2}\)-points. Thus, there are

ways to pick three lines and label the intersection points with \(P_1\) and \(P_2\), \(Q_1\) and \(Q_2\) and \(R_1\) and \(R_2\). Hence, the number of \(\lambda \)-tuples in  with O on the inside of C is
with O on the inside of C is

We finally obtain

6.13 The case 
For  we can take a conjugate \(\lambda \)-tuple as a septuple \((P_1, \ldots , P_7)\) such that \(F\) fixes the points \(P_1,P_2\) and \(P_3\) and transposes the pairs \((P_4, P_5)\) and \((P_6,P_7)\). In this case we take U as the subset of \((\mathbb {P}^{2})^7\) consisting of pairwise distinct points such that the first five points lie in general position. We then have
we can take a conjugate \(\lambda \)-tuple as a septuple \((P_1, \ldots , P_7)\) such that \(F\) fixes the points \(P_1,P_2\) and \(P_3\) and transposes the pairs \((P_4, P_5)\) and \((P_6,P_7)\). In this case we take U as the subset of \((\mathbb {P}^{2})^7\) consisting of pairwise distinct points such that the first five points lie in general position. We then have

We shall denote the \(\mathbb {F}_{q}\)-points by \(P_1,P_2\) and \(P_3\) and the two conjugate pairs of \(\mathbb {F}_{q^2}\)-points by \(Q_1,Q_2\) and \(R_1,R_2\).
The set \(\Delta _\mathsf{l}^{F\sigma }\) can be decomposed as
where
\(\Delta _{\mathsf{l},1}\) consists of tuples such that the line through \(R_1\) and \(R_2\) also passes through \(P_1,P_2\) or \(P_3\),
\(\Delta _{\mathsf{l},2}\) consists of tuples such that the points \(R_1\) and \(R_2\) lie on the line through \(Q_1\) and \(Q_2\), and
\(\Delta _{\mathsf{l},3}\) consists of tuples such that a line through \(Q_1\) and one of the points \(P_1,P_2\) and \(P_3\) also contains \(R_1\) or \(R_2\).
The set \(\Delta _{\mathsf{l},1}\) decomposes as a union of the sets \(\Delta _{\mathsf{l},1}^1,\Delta _{\mathsf{l},1}^2\) and \(\Delta _{\mathsf{l},1}^3\) consisting of tuples with the line through \(R_1\) and \(R_2\) passing through \(P_1,P_2\) and \(P_3\), respectively. Similarly, the set \(\Delta _{\mathsf{l},3}\) is the union of the six sets \(\Delta _{\mathsf{l},3}^{i,j}\), \(i=1,2\), \(j=1,2,3\), where \(\Delta _{\mathsf{l},3}^{i,j}\) contains all tuples such that \(Q_1,R_i\) and  lie on a line.
lie on a line.
The cardinalities of the above sets are easily computed to be

The cardinality of \(\Delta _{\mathsf{l},1}^i \cap \Delta _{\mathsf{l},1}^j\), \(i \ne j\), is also easily computed

There is only nonempty intersection between the set \(\Delta _{\mathsf{l},1}^i\) and the set \(\Delta _{\mathsf{l},3}^{j,k}\) if \(k \ne i\). We then place the first five points in general position and choose an \(\mathbb {F}_{q}\)-line through \(P_k\) which does not pass through \(P_i\) in one of q ways. This gives a tuple of the desired form. We thus see that

We also have nonempty intersection between the sets \(\Delta _{\mathsf{l},3}^{1,i}\) and the set \(\Delta _{\mathsf{l},3}^{2,j}\) where \(i \ne j\). Such a configuration is actually given by specifying the first five points in general position since we must then take \(R_1\) as the intersection point of the line between \(Q_1\) and \(P_i\) and the line between \(Q_2\) and  and similarly for \(R_2\). Hence,
and similarly for \(R_2\). Hence,

The set \(\Delta _{\mathsf{l},2}\) cannot intersect any of the other sets since this would require \(Q_1\) and \(Q_2\) to lie on a line through one of the \(\mathbb {F}_{q}\)-points. It is thus time to consider the triple intersections.
Since \(P_1,P_2\) and \(P_3\) do not lie on a line we have that the intersection of \(\Delta _{\mathsf{l},1}^1,\Delta _{\mathsf{l},1}^2\) and \(\Delta _{\mathsf{l},1}^3\) is empty. We thus only have two types of triple intersections, namely  and
and  where, of course, i, j and k are assumed to be distinct.
where, of course, i, j and k are assumed to be distinct.
An element of  is specified by choosing the first five points in general position. The point \(R_r\) must then be chosen as the intersection point of the line between \(P_i\) and
is specified by choosing the first five points in general position. The point \(R_r\) must then be chosen as the intersection point of the line between \(P_i\) and  and the line between \(Q_1\) and \(P_s\) and similarly for \(FR_r\). We thus have
and the line between \(Q_1\) and \(P_s\) and similarly for \(FR_r\). We thus have

To compute the cardinality of the intersection  we first choose two \(\mathbb {F}_{q}\)-points
we first choose two \(\mathbb {F}_{q}\)-points  and \(P_k\). We then choose a conjugate pair of \(\mathbb {F}_{q^2}\)-lines through each of these points. The intersections of these lines give four \(\mathbb {F}_{q^2}\)-points which we only have one way to label with \(Q_1,Q_2,R_1\) and \(R_2\). We must now place the point \(P_i\) somewhere on the line L through \(R_1\) and \(R_2\). The line through \(P_i\) and \(P_k\) intersects L in one \(\mathbb {F}_{q}\)-point and the line through \(Q_1\) and \(Q_2\) intersects L in another. Thus, we have \(q-1\) choices for \(P_i\). We thus see that
and \(P_k\). We then choose a conjugate pair of \(\mathbb {F}_{q^2}\)-lines through each of these points. The intersections of these lines give four \(\mathbb {F}_{q^2}\)-points which we only have one way to label with \(Q_1,Q_2,R_1\) and \(R_2\). We must now place the point \(P_i\) somewhere on the line L through \(R_1\) and \(R_2\). The line through \(P_i\) and \(P_k\) intersects L in one \(\mathbb {F}_{q}\)-point and the line through \(Q_1\) and \(Q_2\) intersects L in another. Thus, we have \(q-1\) choices for \(P_i\). We thus see that

This completes the investigation of \(\Delta _\mathsf{l}^{F\sigma }\).
If a smooth conic C contains six of the points, then C contains both the conjugate \(\mathbb {F}_{q^2}\)-pairs and C is defined over \(\mathbb {F}_{q}\). Thus, to compute \(|\Delta _\mathsf{c}^{F\sigma }|\) we first choose a smooth conic C over \(\mathbb {F}_{q}\) and then pick one of the points \(P_1,P_2\) and \(P_3\) to possibly lie outside C. We call the chosen point P. We then place the other two points and the two \(\mathbb {F}_{q^2}\)-pairs on C. Finally, we must place P somewhere to make \(P_1,P_2,P_3\), \(Q_1\) and \(Q_2\) lie in general position. Hence, we must choose P away from the line through the two other \(\mathbb {F}_{q}\)-points and away from the line through \(Q_1\) and \(Q_2\). This gives us

However, in the above we have counted the configurations where all seven points lie on C three times. We must therefore take away

in order to obtain \(|\Delta _\mathsf{c}^{F\sigma }|\).
The intersection \(\Delta _{\mathsf{l},2} \cap \Delta _\mathsf{c}^{F\sigma }\) is empty but the intersections of \(\Delta _\mathsf{c}^{F\sigma }\) with the other sets in the decomposition of \(\Delta _\mathsf{l}^{F\sigma }\) are not. To compute  we shall first assume that \(P_i\) lies on the \(\mathbb {F}_{q}\)-outside of C. Of the \(q+1\) lines through \(P_i\) which are defined over \(\mathbb {F}_{q}\) we have that two are tangent to C and
we shall first assume that \(P_i\) lies on the \(\mathbb {F}_{q}\)-outside of C. Of the \(q+1\) lines through \(P_i\) which are defined over \(\mathbb {F}_{q}\) we have that two are tangent to C and  intersect C in two \(\mathbb {F}_{q}\)-points. Thus, there are
intersect C in two \(\mathbb {F}_{q}\)-points. Thus, there are  lines left which must intersect C in a pair of conjugate \(\mathbb {F}_{q^2}\)-points. We pick such a line and label the intersection points by \(R_1\) and \(R_2\) in one of two ways. We shall now place the other two \(\mathbb {F}_{q}\)-points on C. There are
lines left which must intersect C in a pair of conjugate \(\mathbb {F}_{q^2}\)-points. We pick such a line and label the intersection points by \(R_1\) and \(R_2\) in one of two ways. We shall now place the other two \(\mathbb {F}_{q}\)-points on C. There are  ways to choose two \(\mathbb {F}_{q}\)-points on C of which
ways to choose two \(\mathbb {F}_{q}\)-points on C of which  pairs lie on an \(\mathbb {F}_{q}\)-line through \(P_i\). There are thus
pairs lie on an \(\mathbb {F}_{q}\)-line through \(P_i\). There are thus  pairs which do not lie on a line through \(P_i\) and, since there are two ways to label each pair, we thus have \(q^2+1\) choices for the two \(\mathbb {F}_{q}\)-points. Finally, we shall place \(Q_1\) and \(Q_2\) somewhere on C but we have to make sure that the points \(P_1,P_2,P_3\), \(Q_1\) and \(Q_2\) are in general position. Since the lines between \(P_i\) and the other two \(\mathbb {F}_{q}\)-points intersect C only in \(\mathbb {F}_{q}\)-points, the only thing that might go wrong when choosing \(Q_1\) and \(Q_2\) is that the line through \(Q_1\) and \(Q_2\) might also go through \(P_i\). As seen above, there are exactly \(q-1\) choices for \(Q_1\) and \(Q_2\) for which this happens, so the remaining \(q^2-q-(q-1)=q^2-2q+1\) choices will give a configuration of the desired type. We thus have that the number of elements in
pairs which do not lie on a line through \(P_i\) and, since there are two ways to label each pair, we thus have \(q^2+1\) choices for the two \(\mathbb {F}_{q}\)-points. Finally, we shall place \(Q_1\) and \(Q_2\) somewhere on C but we have to make sure that the points \(P_1,P_2,P_3\), \(Q_1\) and \(Q_2\) are in general position. Since the lines between \(P_i\) and the other two \(\mathbb {F}_{q}\)-points intersect C only in \(\mathbb {F}_{q}\)-points, the only thing that might go wrong when choosing \(Q_1\) and \(Q_2\) is that the line through \(Q_1\) and \(Q_2\) might also go through \(P_i\). As seen above, there are exactly \(q-1\) choices for \(Q_1\) and \(Q_2\) for which this happens, so the remaining \(q^2-q-(q-1)=q^2-2q+1\) choices will give a configuration of the desired type. We thus have that the number of elements in  such that \(P_i\) lies on the \(\mathbb {F}_{q}\)-outside of C is
such that \(P_i\) lies on the \(\mathbb {F}_{q}\)-outside of C is

We now assume that \(P_i\) lies on the \(\mathbb {F}_{q}\)-inside of C. We proceed similarly to the above. First we observe that the number of \(\mathbb {F}_{q}\)-lines through \(P_i\) is \(q+1\) of which half intersect C in two \(\mathbb {F}_{q}\)-points and half intersect C in conjugate pairs of \(\mathbb {F}_{q^2}\)-points. We choose a line which intersects C in two conjugate \(\mathbb {F}_{q^2}\)-points and label the intersection points by \(R_1\) and \(R_2\). We now choose an \(\mathbb {F}_{q}\)-point  on C in one of \(q+1\) ways. The line through \(P_i\) and
on C in one of \(q+1\) ways. The line through \(P_i\) and  intersects C in another \(\mathbb {F}_{q}\)-point and we choose the final \(\mathbb {F}_{q}\)-point away from this intersection point and
intersects C in another \(\mathbb {F}_{q}\)-point and we choose the final \(\mathbb {F}_{q}\)-point away from this intersection point and  . Finally, we shall place the points \(Q_1\) and \(Q_2\) on C in a way so that the points \(P_1,P_2,P_3,Q_1\) and \(Q_2\) are in general position. As above, the only thing that might go wrong is that the line through \(Q_1\) and \(Q_2\) might go through \(P_i\) and there are precisely \(q+1\) choices for \(Q_1\) and \(Q_2\) for which this happens. Thus, there are \(q^2-q-(q+1)=q^2-2q-1\) valid choices for \(Q_1\) and \(Q_2\). Hence, there are
. Finally, we shall place the points \(Q_1\) and \(Q_2\) on C in a way so that the points \(P_1,P_2,P_3,Q_1\) and \(Q_2\) are in general position. As above, the only thing that might go wrong is that the line through \(Q_1\) and \(Q_2\) might go through \(P_i\) and there are precisely \(q+1\) choices for \(Q_1\) and \(Q_2\) for which this happens. Thus, there are \(q^2-q-(q+1)=q^2-2q-1\) valid choices for \(Q_1\) and \(Q_2\). Hence, there are

elements in  such that \(P_i\) lies on the \(\mathbb {F}_{q}\)-inside of C.
such that \(P_i\) lies on the \(\mathbb {F}_{q}\)-inside of C.
To compute the intersection  we note that if we place
we note that if we place  on the \(\mathbb {F}_{q}\)-outside of C and then choose two \(\mathbb {F}_{q}\)-points on C and two conjugate \(\mathbb {F}_{q^2}\)-points \(Q_1\) and \(Q_2\) on C such that \(P_1,P_2,P_3\), \(Q_1\) and \(Q_2\) are in general position, then we must choose \(R_i\) as the other intersection point of C with the line through \(Q_1\) and
on the \(\mathbb {F}_{q}\)-outside of C and then choose two \(\mathbb {F}_{q}\)-points on C and two conjugate \(\mathbb {F}_{q^2}\)-points \(Q_1\) and \(Q_2\) on C such that \(P_1,P_2,P_3\), \(Q_1\) and \(Q_2\) are in general position, then we must choose \(R_i\) as the other intersection point of C with the line through \(Q_1\) and  . We may thus use constructions analogous to those above to see that there are
. We may thus use constructions analogous to those above to see that there are

elements in  with
with  on the \(\mathbb {F}_{q}\)-outside of C and
on the \(\mathbb {F}_{q}\)-outside of C and

elements with  on the \(\mathbb {F}_{q}\)-inside of C.
on the \(\mathbb {F}_{q}\)-inside of C.
We may now put all the pieces together to obtain

6.14 The case 
For  we can take a conjugate \(\lambda \)-tuple as a septuple \((P_1, \ldots , P_7)\) such that \(F\) fixes the points \(P_1,P_2,P_3,P_4\) and \(P_5\) and transposes the pair \((P_6,P_7)\). In this case we take U as the subset of \((\mathbb {P}^{2})^7\) consisting of pairwise distinct points such that the first five points lie in general position. We then have
we can take a conjugate \(\lambda \)-tuple as a septuple \((P_1, \ldots , P_7)\) such that \(F\) fixes the points \(P_1,P_2,P_3,P_4\) and \(P_5\) and transposes the pair \((P_6,P_7)\). In this case we take U as the subset of \((\mathbb {P}^{2})^7\) consisting of pairwise distinct points such that the first five points lie in general position. We then have

We shall denote the conjugate pair of \(\mathbb {F}_{q^2}\)-points by \(Q_1,Q_2\).
If three points of a conjugate \(\lambda \)-tuple in \(U(\lambda )\) lie on a line, then \(Q_1\) and \(Q_2\) lie on a line passing through one of the \(\mathbb {F}_{q}\)-points. There are
\(\mathbb {F}_{q}\)-lines passing through \(P_1,P_2,P_3,P_4\) or \(P_5\) (or possibly two of them). Each of these lines contain \(q^2-q\) conjugate pairs of \(\mathbb {F}_{q^2}\)-points and no conjugate pair lies on two such lines. We thus have

If six of the points of a conjugate \(\lambda \)-tuple lie on a smooth conic C, then C is defined over \(\mathbb {F}_{q}\) and contains \(Q_1\) and \(Q_2\). Therefore, to compute the cardinality of \(\Delta _\mathsf{c}^{F\sigma }\) we first choose a smooth conic C defined over \(\mathbb {F}_{q}\) and one of the points \(P_1,P_2,P_3,P_4\) or \(P_5\) to possibly lie outside C. We call the chosen point P. Then, we choose four \(\mathbb {F}_{q}\)-points and a conjugate pair on C. Finally, we choose P away from the six lines through pairs of the other four \(\mathbb {F}_{q}\)-points. We thus get

In the above we have counted the \(\lambda \)-tuples with all seven points on a conic five times. We therefore must take away

in order to obtain \(|\Delta _\mathsf{c}^{F\sigma }|\).
To compute the size of the intersection \(\Delta _\mathsf{l}^{F\sigma } \cap \Delta _\mathsf{c}^{F\sigma }\) we shall decompose this set into a disjoint disjoint union of five subsets \(A_i\), \(i=1,\ldots , 5\), where \(A_i\) consists of those tuples where \(P_i\) does not lie on the conic C through the other six points. Each of the sets \(A_i\) is then decomposed further into a union of the sets \(A_i^{\mathrm {out}}\) and \(A_i^{\mathrm {in}}\) where \(A_{i}^{\mathrm {out}}\) consists of those tuples with \(P_i\) on the \(\mathbb {F}_{q}\)-outside of C and \(A_i^{\mathrm {in}}\) consists of those with \(P_i\) on the \(\mathbb {F}_{q}\)-inside of C. Finally, we shall decompose \(A_i^{\mathrm {out}}\) into a union of the three disjoint subsets:
the set \(A_{i,0}^{\mathrm {out}}\) consisting of \(\lambda \)-tuples such that the tangent lines to C passing through \(P_i\) do not pass through any of the other points of the \(\lambda \)-tuple,
the set \(A_{i,1}^{\mathrm {out}}\) consisting of \(\lambda \)-tuples such that exactly one of the tangent lines to C passing through \(P_i\) pass through one of the other points of the \(\lambda \)-tuple,
the set \(A_{i,2}^{\mathrm {out}}\) consisting of \(\lambda \)-tuples such that both the tangent lines to C passing through \(P_i\) passes through another point of the \(\lambda \)-tuple.
To compute \(|A_i^{\mathrm {out}}|\), we first choose a smooth conic C defined over \(\mathbb {F}_{q}\) in \(q^5-q^2\) ways and then a point \(P_i\) outside C in  ways. As seen many times before, there are exactly
ways. As seen many times before, there are exactly  lines through \(P_i\) which are defined over \(\mathbb {F}_{q}\) and which intersect C in a conjugate pair of points. We pick such a line and label the points \(Q_1\) and \(Q_2\) in one of two ways. From this point on, the computations are a little bit different for the three subsets of \(A_i^{\mathrm {out}}\).
lines through \(P_i\) which are defined over \(\mathbb {F}_{q}\) and which intersect C in a conjugate pair of points. We pick such a line and label the points \(Q_1\) and \(Q_2\) in one of two ways. From this point on, the computations are a little bit different for the three subsets of \(A_i^{\mathrm {out}}\).
The subset\(A_{i,0}^{\mathrm {out}}\). We shall now pick the other four \(\mathbb {F}_{q}\)-points of the \(\lambda \)-tuple. Since we should not pick points whose tangents pass through \(P_i\), we have \(q-1\) choices for the first point. For the second point, we should stay away from the tangent points, the first point and the other intersection point of C and the line through \(P_i\) and the first point. Hence, we have \(q-3\) choices. In a similar way, we see that we have \(q-5\) choices for the third point and \(q-7\) for the fourth. Hence,

The subset\(A_{i,1}^{\mathrm {out}}\). We begin by choosing one of the four \(\mathbb {F}_{q}\)-points to lie on a tangent to C passing through \(P_i\) and then we pick the tangent it should lie on. For the first of the remaining three points we now have \(q-1\) choices and, similarly to the above case, we have \(q-3\) choices for the second and \(q-5\) for the third. Thus,

The subset\(A_{i,2}^{\mathrm {out}}\). We begin by choosing two of the four \(\mathbb {F}_{q}\)-points to lie on tangents to C passing through \(P_i\) and then we pick which point should lie on which tangent. For the first of the remaining two points we now have \(q-1\) choices and we then have \(q-3\) choices for the second. Thus,

It remains to compute \(|A_i^{\mathrm {in}}|\). We first choose a smooth conic C defined over \(\mathbb {F}_{q}\) in \(q^5-q^2\) ways and then a point \(P_i\) on the inside of C in  ways. We have already seen that there now are
ways. We have already seen that there now are  lines passing through \(P_i\) which are defined over \(\mathbb {F}_{q}\) and which intersect C in a conjugate pair of points. We thus pick such a line and label the intersection points by \(Q_1\) and \(Q_2\). Since any \(\mathbb {F}_{q}\)-line through \(P_i\) will intersect C in precisely two points, we have \((q+1)(q-1)(q-3)(q-5)\) choices for the remaining four \(\mathbb {F}_{q}\)-points of the \(\lambda \)-tuple. We thus see that
lines passing through \(P_i\) which are defined over \(\mathbb {F}_{q}\) and which intersect C in a conjugate pair of points. We thus pick such a line and label the intersection points by \(Q_1\) and \(Q_2\). Since any \(\mathbb {F}_{q}\)-line through \(P_i\) will intersect C in precisely two points, we have \((q+1)(q-1)(q-3)(q-5)\) choices for the remaining four \(\mathbb {F}_{q}\)-points of the \(\lambda \)-tuple. We thus see that

We now conclude that

6.15 The case \(\lambda =[1^7]\)
Since we shall almost exclusively be interested in objects defined over \(\mathbb {F}_{q}\), we shall often omit the decoration “\(\mathbb {F}_{q}\)”. For instance, we shall simply write “point” to mean “\(\mathbb {F}_{q}\)-point”. Let \(U \subset (\mathbb {P}^{2})^7\) be the subset consisting of septuples of pairwise distinct points such that the first four points lie in general position. We thus have

The following notation will be quite convenient.
Definition 6.12
If P and Q are two points in \(\mathbb {P}^2\), then the line through P and Q shall be denoted \(P Q\).
Since we shall often want to stay away from lines through two of the first four points we define

We note that \(\mathscr {S}^{F\sigma }\) contains
points.
6.15.1 The set \(\Delta _{{l}}\)
The set \(\Delta _\mathsf{l}\) decomposes into a disjoint union of three sets
where
the points of \(\Delta _{\mathsf{l},1}\) are such that at least one of the points \(P_5,P_6\) or \(P_7\) lies in \(\mathscr {S}\),
the points of \(\Delta _{\mathsf{l},2}\) are such that one of the lines
 , \(5 \leqslant i < j \leqslant 7\), contains one of the points \(P_1,P_2,P_3\) and \(P_4\), but \(\{P_5,P_6,P_7\} \cap \mathscr {S} = \varnothing \), and
, \(5 \leqslant i < j \leqslant 7\), contains one of the points \(P_1,P_2,P_3\) and \(P_4\), but \(\{P_5,P_6,P_7\} \cap \mathscr {S} = \varnothing \), andthe points of \(\Delta _{\mathsf{l},3}\) are such that the three points \(P_5,P_6\) and \(P_7\) lie on a line which does not pass through \(P_1,P_2,P_3\) or \(P_4\).
We shall consider the three subsets separately.
The set\(\Delta _{\mathsf{l},1}\). For each subset \(I \subset \{5,6,7\}\), let \(\Delta _{\mathsf{l},1}(I)\) denote the set of points in \(\Delta _{\mathsf{l},1}\) such that \(P_i \in \mathscr {S}\) for all \(i \in I\). We can then decompose \(\Delta _{\mathsf{l},1}\) further as
Clearly,  .
.
A typical element of  is illustrated in Fig. 5. To compute
is illustrated in Fig. 5. To compute  we first place the first four points in general position, then choose \(P_i\) as any point in \(\mathscr {S}\) and finally place the remaining two points anywhere. Hence
we first place the first four points in general position, then choose \(P_i\) as any point in \(\mathscr {S}\) and finally place the remaining two points anywhere. Hence

Similarly, we have

and

This allows us to compute \(|\Delta _{\mathsf{l},1}|\) as

The set\(\Delta _{\mathsf{l},2}\). Let  , \(r \in \{1,2,3,4\}\) and let
, \(r \in \{1,2,3,4\}\) and let  be the subset of points in \(\Delta _{\mathsf{l},2}\) such that
be the subset of points in \(\Delta _{\mathsf{l},2}\) such that  . We also define
. We also define

A typical element of  is illustrated in Fig. 6. To obtain an element of
is illustrated in Fig. 6. To obtain an element of  we first place \(P_1,P_2,P_3\) or \(P_4\) in general position. There are \(q+1\) lines through \(P_r\) of which three are contained in \(\mathscr {S}\). We choose
we first place \(P_1,P_2,P_3\) or \(P_4\) in general position. There are \(q+1\) lines through \(P_r\) of which three are contained in \(\mathscr {S}\). We choose  as one of the remaining \(q-2\) lines. Note that
as one of the remaining \(q-2\) lines. Note that  will not pass through any of the points
will not pass through any of the points
Hence,  will intersect \(\mathscr {S}\) in \(P_r\) and three further points. There are thus \(q-3\) ways to choose \(P_i\) and then \(q-4\) ways to choose
will intersect \(\mathscr {S}\) in \(P_r\) and three further points. There are thus \(q-3\) ways to choose \(P_i\) and then \(q-4\) ways to choose  . Finally, there are
. Finally, there are

choices for the seventh point. We thus have

We have counted some tuples several times. To begin with, the points of
have been counted three times. There are

of these. Further, the sets  and
and  will intersect if \(r \ne s\) and \(j \ne k\). A typical element is illustrated in Fig. 7.
will intersect if \(r \ne s\) and \(j \ne k\). A typical element is illustrated in Fig. 7.
To compute  we begin by choosing \(P_1,P_2,P_3\) and \(P_4\) in general position and continue by choosing \(P_i\) outside \(\mathscr {S}\) in one of \(q^2-5q+6\) ways. This gives us two lines \(P_i P_r\) and \(P_i P_s\) which intersect \(\mathscr {S}\) in four points each. We choose
we begin by choosing \(P_1,P_2,P_3\) and \(P_4\) in general position and continue by choosing \(P_i\) outside \(\mathscr {S}\) in one of \(q^2-5q+6\) ways. This gives us two lines \(P_i P_r\) and \(P_i P_s\) which intersect \(\mathscr {S}\) in four points each. We choose  on \(P_i P_r\) away from \(P_i\) and \(\mathscr {S}\) in \(q-4\) ways and similarly for \(P_{k}\). This gives
on \(P_i P_r\) away from \(P_i\) and \(\mathscr {S}\) in \(q-4\) ways and similarly for \(P_{k}\). This gives

Finally, we must compute the cardinality of the triple intersection
where r, s and t are distinct. A typical element of the intersection is illustrated in Fig. 8.
This is where we have to pay for the awkward requirement that \(P_5,P_6\) and \(P_7\) should not be in \(\mathscr {S}\). We shall view \(\Delta _{\mathsf{l},2}^r(\{5,6\}) \cap \Delta _{\mathsf{l},2}^s(\{5,7\}) \cap \Delta _{\mathsf{l},2}^t(\{6,7\})\) as an open subset of the set \(T^{r,s,t}\) consisting of tuples such that
the line \(P_5 P_6\) passes through \(P_r\), \(P_5 P_7\) passes through \(P_s\) and \(P_6 P_7\) passes through \(P_t\) but,
we allow \(P_5,P_6\) and \(P_7\) to lie in \(\mathscr {S}\), but,
we do not allow the lines
 , \(5 \leqslant i < j \leqslant 7\) to be contained in \(\mathscr {S}\).
, \(5 \leqslant i < j \leqslant 7\) to be contained in \(\mathscr {S}\).
The complement of  in \(T^{r,s,t}\) can be decomposed into a union of three subsets \(T^{r,s,t}_i\), \(i=5,6,7\), consisting of those tuples with \(P_i\) in \(\mathscr {S}\).
in \(T^{r,s,t}\) can be decomposed into a union of three subsets \(T^{r,s,t}_i\), \(i=5,6,7\), consisting of those tuples with \(P_i\) in \(\mathscr {S}\).
We begin with the computation of \(|T^{r,s,t}|\). To obtain such a tuple, we begin by choosing a line \(L_r\) through \(P_r\) in \(q-2\) ways. We shall then choose a line \(L_s\) through \(P_s\). There are however two cases that may occur. Typically, the intersection point \(P_5=L_r \cap L_s\) will lie outside \(\mathscr {S}\) but for one choice of \(L_s\) it will lie in \(\mathscr {S}\). The situation is illustrated in Fig. 9.
There are \(q-3\) ways to choose \(L_s\) so that \(L_r \cap L_s\) lies outside \(\mathscr {S}\). When we choose the line \(L_t\) through \(P_t\) we must make sure that \(L_t\) is not contained in \(\mathscr {S}\) and that \(L_t\) does not pass through \(L_r \cap L_s\), since we want to end up with three distinct intersection points. We thus have \(q-3\) choices. On the other hand, if we choose \(L_s\) as the one line making the intersection point \(L_r \cap L_s\) lie in \(\mathscr {S}\) we only need to make sure that \(L_t\) is not contained in \(\mathscr {S}\) and we thus have \(q-2\) choices. Hence, we see that

We now turn to the computation of \(|T^{r,s,t}_i|\), \(i=5,6,7\). We then begin by choosing a line \(L_r\) through \(P_r\) in \(q-2\) ways. The line \(L_s\) through \(P_s\) is then completely determined since we must have \(P_i \in \mathscr {S}\). This gives us \(q-2\) choices for the final line \(L_t\) through \(P_t\). Hence,

We now turn to the computation of  , \(5 \leqslant i < j \leqslant 7\). As above, we begin by choosing a line \(L_r\) through \(P_r\) in \(q-2\) ways. Since \(P_i\) must lie in \(\mathscr {S}\) we have only one choice for \(L_s\). Since
, \(5 \leqslant i < j \leqslant 7\). As above, we begin by choosing a line \(L_r\) through \(P_r\) in \(q-2\) ways. Since \(P_i\) must lie in \(\mathscr {S}\) we have only one choice for \(L_s\). Since  we see that we now have precisely one choice for \(L_t\) also. Hence,
we see that we now have precisely one choice for \(L_t\) also. Hence,

We now consider  . It turns out that once the four points \(P_1,P_2,P_3\) and \(P_4\) have been placed in general position, there is precisely one such tuple. The situation is illustrated in Fig. 10.
. It turns out that once the four points \(P_1,P_2,P_3\) and \(P_4\) have been placed in general position, there is precisely one such tuple. The situation is illustrated in Fig. 10.
This finally allows us to compute

The set\(\Delta _{\mathsf{l},3}\). Recall the definition of the three points \(Q_1,Q_2\) and \(Q_3\) from equation (6.4). Using these three points we may decompose \(\Delta _{\mathsf{l},3}\) into a disjoint union of the following subsets:
\(\Delta _{\mathsf{l},3}(\{Q_r,Q_s\})\) consisting of those tuples of \(\Delta _{\mathsf{l},3}\) where \(P_5,P_6\) and \(P_7\) lie on the line \(Q_r Q_s\), \(1 \leqslant r < s \leqslant 3\), and,
\(\Delta _{\mathsf{l},3}(\{Q_r\})\) consisting of those tuples of \(\Delta _{\mathsf{l},3}\) with \(P_5,P_6\) and \(P_7\) on a line through \(Q_r\), \(1 \leqslant r \leqslant 3\), which does not pass through any of the other \(Q_i\), and
\(\Delta _{\mathsf{l},3}(\varnothing )\) consisting of those tuples of \(\Delta _{\mathsf{l},3}\) with \(P_5,P_6\) and \(P_7\) on a line which does not pass through \(Q_1,Q_2\) or \(Q_3\).
We begin by considering \(\Delta _{\mathsf{l},3}(\{Q_r,Q_s\})\). The line \(Q_r Q_s\) contains \(q+1\) points of which four lie in \(\mathscr {S}\). There are thus \(q-3\) choices for \(P_5\), \(q-4\) choices for \(P_6\) and \(q-5\) choices for \(P_7\). Hence,

We continue with \(|\Delta _{\mathsf{l},3}(\{Q_r\})|\). There are \(q+1\) lines through \(Q_r\) of which two are contained in \(\mathscr {S}\) and two are the lines through the other two \(Q_i\). Hence, there are \(q-3\) choices for a line L though \(Q_r\). The line L intersects \(\mathscr {S}\) in five points so we have \(q-4\) choices for \(P_5\), \(q-5\) choices for \(P_6\) and \(q-6\) choices for \(P_7\). We conclude that

To compute \(|\Delta _{\mathsf{l},3}(\varnothing )|\) we begin by choosing a line L which does not pass through any of the points \(P_1\), \(P_2\), \(P_3\), \(P_4\), \(Q_1\), \(Q_2\) and \(Q_3\). There are \(q^2+q+1\) lines in \(\mathbb {P}^2\), of which \(q+1\) passes through \(P_i\), \(i=1,2,3,4\). There is exactly one line through each pair of these points so there are

lines which do not pass through \(P_1,P_2,P_3\) and \(P_4\). Of the \(q+1\) lines through \(Q_i\), \(i=1,2,3\), precisely two have been removed above and the line  passes through both \(Q_i\) and
passes through both \(Q_i\) and  . Hence, we have
. Hence, we have

choices for L.
The line L intersects \(\mathscr {S}\) in six points. We therefore have \(q-5\) choices for \(P_5\), \(q-6\) choices for \(P_6\) and \(q-7\) choices for \(P_7\). Hence,

We now add everything together to obtain

and, finally,

6.15.2 The set \(\Delta _{c}\)
We decompose \(\Delta _\mathsf{c}^{F\sigma }\) as
where \(\Delta _{\mathsf{c},1}\) consists of tuples where six points lie on a smooth conic C with one of the points \(P_1,P_2,P_3\) or \(P_4\) possibly outside C and \(\Delta _{\mathsf{c},2}\) consists of tuples where six points lie on a smooth conic C with one of the points \(P_5,P_6\) or \(P_7\) possibly outside the conic C.
To obtain an element of \(\Delta _{\mathsf{c},1}\) we first choose one of the points \(P_1,P_2,P_3\) and \(P_4\) and call it P. Then we choose a smooth conic C in \(q^5-q^2\) ways and place all of the seven points except P on C in

ways. There are three lines through pairs of points in  which together contain 3q points. These lines do not contain \(P_5,P_6\) and \(P_7\) so we have
which together contain 3q points. These lines do not contain \(P_5,P_6\) and \(P_7\) so we have

choices for P. Multiplying everything together we obtain

which is almost \(|\Delta _{\mathsf{c},1}|\) except that we have counted the tuples where all seven points lie on C four times.
To obtain an element of \(\Delta _{\mathsf{c},2}\) we first choose \(P_5,P_6\) and \(P_7\) and call the chosen point P. We then choose a smooth conic C and place all but the chosen points on C. Finally, we place P anywhere in \(\mathbb {P}^2\) except at the six chosen points. In this way we obtain the number

which is almost equal to \(|\Delta _{\mathsf{c},2}|\) except that we have counted the tuples with all seven points on C three times.
We now want to compute the number of tuples with all seven points on a smooth conic C. We thus choose a smooth conic C and place all seven points on it in

ways. We thus have

6.15.3 The set \(\Delta _{l} \cap \Delta _{c}\)
We introduce the filtration  where
where
the set \(\mathscr {F}_1\) consists of tuples such that at least one line contains three points of the tuple,
the set \(\mathscr {F}_2\) consists of tuples such that at least two lines contain three points of the tuple,
the set \(\mathscr {F}_3\) consists of tuples such that at least three lines contain three points of the tuple.
The strategy will be to compute the numbers:

and thereby obtain the desired cardinality.
Since the points \(P_1,P_2,P_3\) and \(P_4\) are assumed to constitute a frame, we must do things a little bit differently depending on whether the point not on the conic is one of these four or not. We therefore make further subdivisions.
The subsets with\(P_5,P_6\)or\(P_7\)not on the conic. We shall denote the subsets in question by  and, similarly
and, similarly

To compute \(N_1^{5,6,7}\), we first choose one of the points \(P_5,P_6\) or \(P_7\) to be the point P not on the smooth conic C and call the remaining two points \(P_i\) and  . We then choose C in \(q^5-q^2\) ways and choose two points among
. We then choose C in \(q^5-q^2\) ways and choose two points among  and call them \(R_1\) and \(R_2\). There are
and call them \(R_1\) and \(R_2\). There are  ways to place \(R_1\) and \(R_2\) on C and there are then \(q-1\) ways to place P on the line \(R_1 R_2\). Finally, we place the remaining four points on C in
ways to place \(R_1\) and \(R_2\) on C and there are then \(q-1\) ways to place P on the line \(R_1 R_2\). Finally, we place the remaining four points on C in  ways. Multiplying everything together we obtain
ways. Multiplying everything together we obtain

In order to compute \(N_2^{5,6,7}\), we first choose one of the points \(P_5,P_6\) or \(P_7\) to be the point P not on the smooth conic C and call the remaining two points \(P_i\) and  . We then choose C in \(q^5-q^2\) ways and choose two unordered pairs of unordered points among
. We then choose C in \(q^5-q^2\) ways and choose two unordered pairs of unordered points among  . This can be done in
. This can be done in  ways. We call the points of the first pair \(R_1\) and \(R_2\) and those of the second \(O_1\) and \(O_2\). There are
ways. We call the points of the first pair \(R_1\) and \(R_2\) and those of the second \(O_1\) and \(O_2\). There are  ways to place
ways to place  on C and the point P is then completely determined as \(P=R_1 R_2 \cap O_1 O_2\). Thus
on C and the point P is then completely determined as \(P=R_1 R_2 \cap O_1 O_2\). Thus

The computation of \(N_3^{5,6,7}\) is slightly more complicated since we need to subdivide into two subcases depending on if P is on the outside or on the inside of C. We call the two corresponding numbers \(N_{3,\mathrm {out}}^{5,6,7}\) and \(N_{3,\mathrm {in}}^{5,6,7}\).
To compute \(N_{3,\mathrm {out}}^{5,6,7}\) we first choose one of the points \(P_5,P_6\) or \(P_7\) to be the point P not on the smooth conic C. We proceed by choosing the smooth conic C in \(q^5-q^2\) ways and then the point P on the outside of C in  ways. We now place \(P_1\) at one of the \(q-1\) points of C whose tangent does not pass through P and choose one of the remaining five points as the other intersection point in \(C \cap P_1 P\). There are now four remaining points
ways. We now place \(P_1\) at one of the \(q-1\) points of C whose tangent does not pass through P and choose one of the remaining five points as the other intersection point in \(C \cap P_1 P\). There are now four remaining points  and \(P_{l}\) to place on C. We place \(P_i\) at one of the \(q-3\) remaining points of C whose tangent does not pass through P and choose one of the remaining three points as the other intersection point in \(C \cap P_i P\). There are now two points \(P_r\) and \(P_s\) to place on C. We place \(P_r\) at one of the \(q-5\) possible points and the point \(P_s\) is then determined. We thus have
and \(P_{l}\) to place on C. We place \(P_i\) at one of the \(q-3\) remaining points of C whose tangent does not pass through P and choose one of the remaining three points as the other intersection point in \(C \cap P_i P\). There are now two points \(P_r\) and \(P_s\) to place on C. We place \(P_r\) at one of the \(q-5\) possible points and the point \(P_s\) is then determined. We thus have

We proceed by computing \(N_{3,\mathrm {in}}^{5,6,7}\). We first choose one of the points \(P_5,P_6\) or \(P_7\) to be the point P not on the smooth conic C. We proceed by choosing the smooth conic C in \(q^5-q^2\) ways and then the point P on the outside of C in  ways.
ways.
We now place \(P_1\) at one of the \(q+1\) points of C whose tangent does not pass through P and choose one of the remaining five points as the other intersection point in \(C \cap P_1 P\). There are now four remaining points  and \(P_l\) to place on C. We place \(P_i\) at one of the \(q-1\) remaining points of C and choose one of the remaining three points as the other intersection point in \(C \cap P_i P\). There are now two points \(P_r\) and \(P_s\) to place on C. We place \(P_r\) at one of the \(q-3\) possible points and the point \(P_s\) is then determined. We now see that
and \(P_l\) to place on C. We place \(P_i\) at one of the \(q-1\) remaining points of C and choose one of the remaining three points as the other intersection point in \(C \cap P_i P\). There are now two points \(P_r\) and \(P_s\) to place on C. We place \(P_r\) at one of the \(q-3\) possible points and the point \(P_s\) is then determined. We now see that

The subsets with\(P_1,P_2,P_3\)or\(P_4\)not on the conic. We shall denote the subsets in question by \(\mathscr {F}_i^{1,2,3,4}\) and, similarly

In order to compute \(N_1^{1,2,3,4}\), we first choose one of the points \(P_1,P_2,P_3\) or \(P_4\) to be the point P not on the smooth conic C and call the remaining three points \(P_r,P_s\) and \(P_t\). We continue by choosing a smooth conic C in \(q^5-q^2\) ways.
We first assume that P lies on a line \(R_1 R_2\) where \(\{R_1, R_2 \} \subset \{P_5,P_6,P_7\}\). We therefore choose the two points in three ways and call the remaining point \(P_i\). We then place \(R_1\) and \(R_2\) on C in  ways. We continue by choosing the three points \(P_r,P_s\) and \(P_t\) on C in
ways. We continue by choosing the three points \(P_r,P_s\) and \(P_t\) on C in  ways. The lines \(P_r P_s,P_r P_t\) and \(P_s P_t\) intersect the line \(R_1 R_2\) in three distinct points so there are \(q-4\) ways to choose the point P on \(R_1 R_2\) but away from these three points and \(R_1\) and \(R_2\). Finally, we place \(P_i\) at one of the \(q-4\) remaining points of C. Multiplying everything together we get
ways. The lines \(P_r P_s,P_r P_t\) and \(P_s P_t\) intersect the line \(R_1 R_2\) in three distinct points so there are \(q-4\) ways to choose the point P on \(R_1 R_2\) but away from these three points and \(R_1\) and \(R_2\). Finally, we place \(P_i\) at one of the \(q-4\) remaining points of C. Multiplying everything together we get

We now assume that P lies on a line \(a b\) with \(a \in \{P_1,P_2,P_3,P_4\}\) and \(b \in \{P_5,P_6,P_7\}\). We thus first choose a as one of the points in \(\{P_r,P_s,P_t\}\) and the point b as one of the points \(\{P_5,P_6,P_7\}\) and place a and b on C in one of  ways. We then place the remaining two points, c and d, of \(\{P_1,P_2,P_3,P_4\}\) on C in
ways. We then place the remaining two points, c and d, of \(\{P_1,P_2,P_3,P_4\}\) on C in  ways. The line \(c d\) intersects \(a b\) in a point outside of C so there are \(q-2\) ways to choose P on \(a b\) but away from this intersection point and a and b. Finally, we place the remaining two points of \(\{P_5,P_6,P_7\}\) on C in one of
ways. The line \(c d\) intersects \(a b\) in a point outside of C so there are \(q-2\) ways to choose P on \(a b\) but away from this intersection point and a and b. Finally, we place the remaining two points of \(\{P_5,P_6,P_7\}\) on C in one of  ways. Multiplying everything together we obtain
ways. Multiplying everything together we obtain

We now add the two answers above together to get

To compute \(N_2^{1,2,3,4}\), we first choose one of the points \(P_1,P_2,P_3\) or \(P_4\) to be the point P not on the smooth conic C and call the remaining three points \(P_r,P_s\) and \(P_t\). We continue by choosing a smooth conic C in \(q^5-q^2\) ways.
We first assume that P lies on two lines \(R_1 R_2\) and \(O_1 O_2\) where \(\{R_1, O_1 \} \subset \{P_5,P_6,P_7\}\) and \(\{R_2,O_2\} \subset \{P_r,P_s,P_t\}\). We now choose two points among \(\{P_5,P_6,P_7\}\) in three ways and choose two points among \(\{P_r,P_s,P_t\}\) in three ways and rename the remaining two points to \(P_u\) and \(P_v\). There are now two possible ways to label the four chosen points \(R_1,R_2,O_1\) and \(O_2\) in such a way that \(\{R_1,O_1\} \subset \{P_5,P_6,P_7\}\) and \(\{R_2,O_2\} \subset \{P_r,P_s,P_t\}\) and we choose one of them. We then place the four points \(R_1,R_2,O_1\) and \(O_2\) on the conic C in  ways. The point P is now given as \(P=R_1 R_2 \cap O_1 O_2\) and no matter how we place \(P_u\) and \(P_v\), the three lines \(P_r P_s,P_r P_t\) and \(P_s P_t\) will not go through P. We can now multiply everything together to obtain
ways. The point P is now given as \(P=R_1 R_2 \cap O_1 O_2\) and no matter how we place \(P_u\) and \(P_v\), the three lines \(P_r P_s,P_r P_t\) and \(P_s P_t\) will not go through P. We can now multiply everything together to obtain

The other possibility is that P lies on two lines \(R_1 R_2\) and \(R_3 b\) where \(\{R_1,R_2,R_3\}\) is the set \(\{P_5,P_6,P_7\}\) and \(b \in \{P_r,P_s,P_t\}\). We thus choose b in three ways and rename the remaining two points in \(\{P_r,P_s,P_t\}\) to \(P_u\) and \(P_v\). From now on, we must differentiate between when P is on the outside and on the inside of C.
First, we choose P on the outside of C in  ways. We then choose b as a point on C whose tangent does not pass through P in \(q-1\) ways. We then choose one of the points \(P_5,P_6\) and \(P_7\) to become the second intersection point in \(C \cap b P\). Then, we place the remaining two points among \(\{P_5,P_6,P_7\}\) on C such that the line through them passes through P in \(q-3\) ways. There are now \(q-5\) ways to choose \(P_u\) and \(P_v\) such that the line \(P_u P_v\) will pass through P. Thus, the remaining
ways. We then choose b as a point on C whose tangent does not pass through P in \(q-1\) ways. We then choose one of the points \(P_5,P_6\) and \(P_7\) to become the second intersection point in \(C \cap b P\). Then, we place the remaining two points among \(\{P_5,P_6,P_7\}\) on C such that the line through them passes through P in \(q-3\) ways. There are now \(q-5\) ways to choose \(P_u\) and \(P_v\) such that the line \(P_u P_v\) will pass through P. Thus, the remaining  choices must give \(P_u\) and \(P_v\) such that none of the lines \(P_r P_s,P_r P_t\) and \(P_s P_t\) will contain P. We may now multiply everything together to obtain
choices must give \(P_u\) and \(P_v\) such that none of the lines \(P_r P_s,P_r P_t\) and \(P_s P_t\) will contain P. We may now multiply everything together to obtain

Now we choose P on the inside of C in one of  ways. We then choose b as a point on C whose tangent does not pass through P in \(q+1\) ways. We then choose one of the points \(P_5,P_6\) and \(P_7\) to become the second intersection point in \(C \cap b P\). Then, we place the remaining two points among \(\{P_5,P_6,P_7\}\) on C such that the line through them passes through P in \(q-1\) ways. There are now \(q-3\) ways to choose \(P_u\) and \(P_v\) such that the line \(P_u P_v\) will pass through P. Thus, the remaining
ways. We then choose b as a point on C whose tangent does not pass through P in \(q+1\) ways. We then choose one of the points \(P_5,P_6\) and \(P_7\) to become the second intersection point in \(C \cap b P\). Then, we place the remaining two points among \(\{P_5,P_6,P_7\}\) on C such that the line through them passes through P in \(q-1\) ways. There are now \(q-3\) ways to choose \(P_u\) and \(P_v\) such that the line \(P_u P_v\) will pass through P. Thus, the remaining  choices must give \(P_u\) and \(P_v\) such that none of the lines \(P_r P_s,P_r P_t\) and \(P_s P_t\) will contain P. We may now multiply everything together to obtain
choices must give \(P_u\) and \(P_v\) such that none of the lines \(P_r P_s,P_r P_t\) and \(P_s P_t\) will contain P. We may now multiply everything together to obtain

We may now add everything together to get

Finally, we need to compute \(N_3^{1,2,3,4}\). We begin by choosing one of the points \(P_1,P_2,P_3\) or \(P_4\) to be the point P not on the smooth conic C and call the remaining three points \(P_r,P_s\) and \(P_t\). We continue by choosing a smooth conic C in \(q^5-q^2\) ways.
Here, we only have the possibility that P lies on three lines \(R_1 O_1,R_2 O_2\) and \(R_3 O_3\) where \(\{R_1,R_2,R_3\} = \{P_5,P_6,P_7\}\) and \(\{O_1,O_2,O_3\}=\{P_r,P_s,P_t\}\). However, we must take care of the case that P is on the outside of C and the case that P is on the inside of C separately. We call the corresponding numbers \(N_{3,\mathrm {out}}^{1,2,3,4}\) and \(N_{3,\mathrm {in}}^{1,2,3,4}\).
We begin by computing \(N_{3,\mathrm {out}}^{1,2,3,4}\). We thus choose the point P as a point on the outside of C in  ways. We begin by placing \(P_5\) at one of the points of C whose tangent does not pass through P in \(q-1\) ways. We label the second intersection point of \(C \cap P_5 P\) with \(P_r,P_s\) or \(P_t\) and call the remaining two points \(P_u\) and \(P_v\). We then place \(P_6\) at one of the \(q-3\) remaining points of C whose tangent does not pass through P and then choose one of the points \(P_u\) and \(P_v\) to become the other intersection point of \(C \cap P_6 P\). Finally, we place \(P_7\) at one of the remaining \(q-5\) points and label the other point of \(C \cap P_7 P\) in the only possible way. We thus have
ways. We begin by placing \(P_5\) at one of the points of C whose tangent does not pass through P in \(q-1\) ways. We label the second intersection point of \(C \cap P_5 P\) with \(P_r,P_s\) or \(P_t\) and call the remaining two points \(P_u\) and \(P_v\). We then place \(P_6\) at one of the \(q-3\) remaining points of C whose tangent does not pass through P and then choose one of the points \(P_u\) and \(P_v\) to become the other intersection point of \(C \cap P_6 P\). Finally, we place \(P_7\) at one of the remaining \(q-5\) points and label the other point of \(C \cap P_7 P\) in the only possible way. We thus have

We now turn to computing \(N_{3,in}^{1,2,3,4}\). We thus choose the point P as a point on the inside of C in  ways. We begin by placing \(P_5\) at one of the points of C whose tangent does not pass through P in \(q+1\) ways. We label the second intersection point of \(C \cap P_5 P\) with \(P_r,P_s\) or \(P_t\) and call the remaining two points \(P_u\) and \(P_v\). We then place \(P_6\) at one of the \(q-1\) remaining points of C and then choose one of the points \(P_u\) and \(P_v\) to become the other intersection point of \(C \cap P_6 P\). Finally, we place \(P_7\) at one of the remaining \(q-3\) points and label the other point of \(C \cap P_7 P\) in the only possible way. We now see that
ways. We begin by placing \(P_5\) at one of the points of C whose tangent does not pass through P in \(q+1\) ways. We label the second intersection point of \(C \cap P_5 P\) with \(P_r,P_s\) or \(P_t\) and call the remaining two points \(P_u\) and \(P_v\). We then place \(P_6\) at one of the \(q-1\) remaining points of C and then choose one of the points \(P_u\) and \(P_v\) to become the other intersection point of \(C \cap P_6 P\). Finally, we place \(P_7\) at one of the remaining \(q-3\) points and label the other point of \(C \cap P_7 P\) in the only possible way. We now see that

and we get

We now obtain

and, finally,

This concludes the equivariant point count of \(\mathscr {Q}[2]\). In Sect. 8 we provide a summary of the results of the computations.
7 The hyperelliptic locus
Up to this point we have almost exclusively discussed plane quartics. We shall now briefly turn our attention to the other type of genus 3 curves — the hyperelliptic curves. There are many possible ways to approach the computation of the cohomology of \(\mathscr {H}_{3}[2]\). Our choice is by means of equivariant point counts as in the previous section.
Recall that a hyperelliptic curve C of genus g is determined, up to isomorphism, by \(2g+2\) distinct points on \(\mathbb {P}^1\), up to projective equivalence and that any such collection S of \(2g+2\) points determines a double cover \(\pi :C \rightarrow \mathbb {P}^{1}\) branched precisely over S (and C is thus a hyperelliptic curve). Moreover, if we pick \(2g+2\) ordered points \(P_1, \ldots , P_{2g+2}\) on \(\mathbb {P}^{1}\), the curve C also attains a level 2 structure. In the genus 3 case, we get eight points \(Q_i=\pi ^{-1}(P_i)\) which determine \(\left( {\begin{array}{c}8\\ 2\end{array}}\right) =28\) odd theta characteristics  , \(i <j\) and \(\{Q_1+Q_8, \ldots ,Q_7+Q_8\}\) is an ordered Aronhold basis, see [2, Appendix B.32–33] and [21], and an ordered Aronhold basis determines a level 2 structure.
, \(i <j\) and \(\{Q_1+Q_8, \ldots ,Q_7+Q_8\}\) is an ordered Aronhold basis, see [2, Appendix B.32–33] and [21], and an ordered Aronhold basis determines a level 2 structure.
However, not all level 2 structures on the hyperelliptic curve C arise from different orderings of the points. Nevertheless, there is an intimate relationship between the moduli space \(\mathscr {H}_{g}[2]\) of hyperelliptic curves with level 2 structure and the moduli space \(\mathscr {M}_{0,2g+2}\) of \(2g+2\) ordered points on \(\mathbb {P}^{1}\) given by the following theorem which can be found in [14, Theorem VIII.1].
Theorem 7.1
Each irreducible component of \(\mathscr {H}_{g}[2]\) is isomorphic to the moduli space \(\mathscr {M}_{0,2g+2}\) of \(2g+2\) ordered points on the projective line.
Dolgachev and Ortland [14] pose the question whether the irreducible components of \(\mathscr {H}_{g}[2]\) also are the connected components or, in other words, if \(\mathscr {H}_{g}[2]\) is smooth. In the complex case, the question was answered positively by Tsuyumine in [29] and later, by a shorter argument, by Runge in [28]. Using the results of [1], the argument of Runge carries over word for word to an algebraically closed field of positive characteristic different from 2.
Theorem 7.2
If \(g \geqslant 2\), then each irreducible component of \(\mathscr {H}_{g}[2]\) is also a connected component.
We have a natural action of \(S_{2g+2}\) on the space \(\mathscr {M}_{0,2g+2}\). Since different orderings of the points correspond to different symplectic level 2 structures, \(S_{2g+2}\) sits naturally inside  and, in fact, for \(g=3\) and for even g it is a maximal subgroup, see [15]. With Theorems 7.1 and 7.2 at hand, the following slight generalization of a corollary in [14, p. 145] is clear.
and, in fact, for \(g=3\) and for even g it is a maximal subgroup, see [15]. With Theorems 7.1 and 7.2 at hand, the following slight generalization of a corollary in [14, p. 145] is clear.
Corollary 7.3
Let \(g \geqslant 2\) and let \(X_{[\tau ]} = \mathscr {M}_{0,2g+2}\) for each left coset  . Then
. Then

and the group  acts transitively on the set of connected components \(X_{[\tau ]}\) of \(\mathscr {H}_{g}[2]\). In particular, there are
acts transitively on the set of connected components \(X_{[\tau ]}\) of \(\mathscr {H}_{g}[2]\). In particular, there are

connected components of \(\mathscr {H}_{g}[2]\).
Remark 7.4
As pointed out in [28], the argument to prove the corollary stated in [14] is not quite correct in full generality as it is given there. However, it is enough to prove the result for \(g=3\) and for even g, and in [28] it is explained how to obtain the full result.
Let us now, once and for all, choose a set T of representatives of  . If we denote the elements of \(X_{[\text {id}]}\) by x, then any element in \(X_{[\tau ]}\) can be written as \(\tau x\) for some \(x \in X_{[\text {id}]}\). Let \(\alpha \) be any element of
. If we denote the elements of \(X_{[\text {id}]}\) by x, then any element in \(X_{[\tau ]}\) can be written as \(\tau x\) for some \(x \in X_{[\text {id}]}\). Let \(\alpha \) be any element of  . Then
. Then
for some \(\sigma \in S_{2g+2}\) and some \(\tau ' \in T\). Since the Frobenius commutes with the action of  we have that
we have that
if and only if

But the Frobenius acts on each of the components of \(\mathscr {H}_{g}[2]\) so we see that \(F \alpha (\tau x)=\tau x\) if and only if \(\tau ' = \tau \) and \(F \sigma x = x\).
We now translate the above observation into more standard representation theoretic vocabulary. Define a class function \(\psi \) on \(S_{2g+2}\) by
and define a class function \(\widehat{\psi }\) on  by setting
by setting
for any  . By the above observation we have that
. By the above observation we have that

where
In other words, \(\widehat{\psi }\) is the class function \(\psi \) induced from \(S_{2g+2}\) up to  . Thus, to make an \(S_{2g+2}\)-equivariant point count of \(\mathscr {H}_{g}[2]\) we can make an \(S_{2g+2}\)-equivariant point count of \(\mathscr {M}_{0,2g+2}\) and then use the representation theory of \(S_{2g+2}\) and
. Thus, to make an \(S_{2g+2}\)-equivariant point count of \(\mathscr {H}_{g}[2]\) we can make an \(S_{2g+2}\)-equivariant point count of \(\mathscr {M}_{0,2g+2}\) and then use the representation theory of \(S_{2g+2}\) and  in order to first induce the class function up to
in order to first induce the class function up to  and then restrict it down again to \(S_{2g+2}\). Once this is done, we can obtain the \(S_{2g+1}\)-equivariant point count by restricting from \(S_{2g+2}\) to \(S_{2g+1}\).
and then restrict it down again to \(S_{2g+2}\). Once this is done, we can obtain the \(S_{2g+1}\)-equivariant point count by restricting from \(S_{2g+2}\) to \(S_{2g+1}\).
Compared to Q[2], the \(S_8\)-equivariant point count of \(\mathscr {H}_{3}[2]\) is very easy. We first compute the number of \(\lambda \)-tuples of \(\mathbb {P}^1\) for each partition of \(\lambda \) of 8 and then divide by  in order to obtain \(|\mathscr {M}_{0,8}^{F\sigma }|\), where \(\sigma \) is a permutation in \(S_8\) of cycle type \(\lambda \). The result is given in Table 3. Once this is done, we induce up to
in order to obtain \(|\mathscr {M}_{0,8}^{F\sigma }|\), where \(\sigma \) is a permutation in \(S_8\) of cycle type \(\lambda \). The result is given in Table 3. Once this is done, we induce up to  in order to obtain the
in order to obtain the  -equivariant cohomology of \(\mathscr {H}_{3}[2]\). The results are given in Table 4. Finally, we restrict to \(S_7\) to get the results of Tables 5 and 6. The computations present no difficulties whatsoever.
-equivariant cohomology of \(\mathscr {H}_{3}[2]\). The results are given in Table 4. Finally, we restrict to \(S_7\) to get the results of Tables 5 and 6. The computations present no difficulties whatsoever.
It is not very hard to see that \(\mathscr {M}_{0,n}\) is isomorphic to the complement of a hyperplane arrangement. One way to see this is to start by placing the first three points at 0, 1 and \(\infty \). Then \(\mathscr {M}_{0,n}\) is isomorphic to  , where
, where  is the subset of points where at least two coordinates are equal. Thus, \(\mathscr {H}_{3}[2]\) is minimally pure and by the results of Sect. 5 we can deduce the cohomology of \(\mathscr {H}_{3}[2]\) from the equivariant point counts. In Sect. 8 we provide a summary of the results of the computations. We also mention that the equivariant cohomology of \(\mathscr {M}_{0,n}\) and \(\overline{\mathscr {M}}_{0,n}\) have been computed for all \(n \geqslant 3\) in [18] and later by many others, e.g. Gaiffi [17], Kisin and Lehrer [22] and Robinson and Whitehouse [27]. Thus, using Corollary 7.3, the cohomology of \(\mathscr {H}_{g}[2]\) is in principle known (up to our understanding of the representation theory of
is the subset of points where at least two coordinates are equal. Thus, \(\mathscr {H}_{3}[2]\) is minimally pure and by the results of Sect. 5 we can deduce the cohomology of \(\mathscr {H}_{3}[2]\) from the equivariant point counts. In Sect. 8 we provide a summary of the results of the computations. We also mention that the equivariant cohomology of \(\mathscr {M}_{0,n}\) and \(\overline{\mathscr {M}}_{0,n}\) have been computed for all \(n \geqslant 3\) in [18] and later by many others, e.g. Gaiffi [17], Kisin and Lehrer [22] and Robinson and Whitehouse [27]. Thus, using Corollary 7.3, the cohomology of \(\mathscr {H}_{g}[2]\) is in principle known (up to our understanding of the representation theory of  ). For instance, the Poincaré polynomial of \(\mathscr {H}_{g}[2]\) is
). For instance, the Poincaré polynomial of \(\mathscr {H}_{g}[2]\) is

8 Summary of computations
We summarize the computations related to \(\mathscr {Q}[2]\) in Table 1. Also recall that the Poincaré polynomial of \(\mathscr {Q}[2]\) is given in Theorem 1.1. In Table 2 we give the cohomology of \(\mathscr {Q}[2]\) as a representation of \(S_7\). The rows correspond to the cohomology groups and the columns correspond to the irreducible representations of \(S_7\). The symbol \(s_{\lambda }\) denotes the irreducible representation of \(S_7\) corresponding to the partition \(\lambda \) and a number n in row \(H^k\) and column \(s_{\lambda }\) means that \(s_{\lambda }\) occurs in \(H^k\) with multiplicity n.
Tables 3, 4 and 5 give equivariant point counts for various spaces and groups related to the equivariant point count of \(\mathscr {H}_{3}[2]\) and in Table 6 we give the cohomology groups of \(\mathscr {H}_{3}[2]\) as representations of \(S_7\). Recall that the Poincaré polynomial of \(\mathscr {H}_{3}[2]\) is given in Theorem 1.2.
We mention that since both \(H^k(\mathscr {Q}[2],\mathbb {C})\) and \(H^k(\mathscr {H}_{3}[2],\mathbb {C})\) are of pure Tate type (k, k), see [7], we have that their full mixed Hodge structure can be determined from Theorems 1.1 and 1.2. More precisely, replacing t by \(uv^2\) in the polynomials gives the corresponding Poincaré–Serre polynomials. Here u encodes the cohomological degree and v encodes the Hodge weight.
9 The total moduli space
By adding the results of \(\mathscr {Q}[2]\) and \(\mathscr {H}_{3}[2]\) we find the \(S_7\)-equivariant point count of \(\mathscr {M}_{3}[2]\).
Theorem 9.1
The \(S_7\)-equivariant point count of \(\mathscr {M}_{3}[2]\) is given by

Note in particular that the representations in the coefficients of each power of q occur with the same sign, except in the constant term where \(s_7\) occurs with coefficient 1 while all others occur with negative coefficients. Thus, in contrast with \(\mathscr {Q}[2]\) and \(\mathscr {H}_{3}[2]\), we cannot have that \(H^k(\mathscr {M}_{3}[2],\mathbb {C})\) is pure of Tate type (k, k). Moreover, Looijenga [25] shows that \(H^k(\mathscr {M}_{3},\mathbb {C})\) is pure of Tate type  for some i which is sometimes different from k. In our case, neither this weaker purity holds.
for some i which is sometimes different from k. In our case, neither this weaker purity holds.
To go a bit further in the investigation of the cohomology of \(\mathscr {M}_{3}[2]\), we recall the following result.
Lemma 9.2
(Looijenga [25]) Let X be a rational homology manifold (see [9]) of pure dimension and let \(Y \subset X\) be a hypersurface. Then there is a Gysin exact sequence of mixed Hodge structures

Recall that \(H^{k} (\mathscr {Q}[2],\mathbb {C})\) and \(H^{k} (\mathscr {H}_{3}[2],\mathbb {C})\) are both pure of Tate type (k, k). Thus, if we apply Lemma 9.2 to \(X=\mathscr {M}_{3}[2]\), \(Y=\mathscr {H}_{3}[2]\) and  we have that the long exact sequence splits into four term sequences
we have that the long exact sequence splits into four term sequences

where \(\mathrm {gr}_{2i}^WH^{k} (X,\mathbb {C})\) denotes the weight 2i graded quotient of \(H^{k} (X,\mathbb {C})\) (which in this case is of Tate type  ). We may thus conclude the following.
). We may thus conclude the following.
Proposition 9.3
The cohomology group \(H^{k} (\mathscr {M}_{3}[2],\mathbb {C})\) consists of one part of Tate type \((k-1,k-1)\) and one part of Tate type (k, k).
Moreover, let \(m^k_X(\lambda )\) denote the multiplicity of \(s_{\lambda }\) in \(H^{k} (X)\) and let \(n^k(\lambda )= m^k_{\mathscr {Q}[2]}(\lambda ) - m^{k-2}_{\mathscr {H}_{3}[2]}(\lambda )\). If \(n^k(\lambda )\geqslant 0\), then \(s_{\lambda }\) occurs with multiplicity at least \(n^k(\lambda )\) in \(W_kH^{k} (\mathscr {M}_{3}[2])\) and if \(n^k(\lambda ) \leqslant 0\), then \(s_{\lambda }\) occurs with multiplicity at least  in \(W_kH^{k+1} (\mathscr {M}_{3}[2])\). Thus, Tables 2 and 6 provide explicit bounds for the cohomology groups of \(\mathscr {M}_{3}[2]\). We note that a sharper bound for the dimension of \(H^{7} (\mathscr {M}_{3}[2],\mathbb {C})\) than that obtained here can be found in recent work of Fullarton and Putman [16]. However, the observation above gives bounds for all cohomology groups.
in \(W_kH^{k+1} (\mathscr {M}_{3}[2])\). Thus, Tables 2 and 6 provide explicit bounds for the cohomology groups of \(\mathscr {M}_{3}[2]\). We note that a sharper bound for the dimension of \(H^{7} (\mathscr {M}_{3}[2],\mathbb {C})\) than that obtained here can be found in recent work of Fullarton and Putman [16]. However, the observation above gives bounds for all cohomology groups.
References
Andreatta, F.: The small Schottky–Jung locus in positive characteristics different from two. Ann. Inst. Fourier (Grenoble) 53(1), 69–106 (2003)
Arbarello, E., Cornalba, M., Griffiths, P.A., Harris, J.: Geometry of Algebraic Curves, vol I. Grundlehren der Mathematischen Wissenschaften, vol. 267. Springer, New York (1985)
Bergström, J.: Cohomology of moduli spaces of curves of genus three via point counts. J. Reine Angew. Math. 622, 155–187 (2008)
Bergström, J.: Equivariant counts of points of the moduli spaces of pointed hyperelliptic curves. Doc. Math. 14, 259–296 (2009)
Bergström, J., Tommasi, O.: The rational cohomology of \(\overline{\cal{M}}_4\). Math. Ann. 338(1), 207–239 (2007)
Bergvall, O.: Cohomology of Arrangements and Moduli Spaces. Ph.D. thesis, Stockholms Universitet (2016)
Bergvall, O.: Equivariant cohomology of moduli spaces of genus three curves with level two structure. Geom. Dedicata (2018). https://doi.org/10.1007/s10711-018-0407-5
van den Bogaart, T., Edixhoven, B.: Algebraic stacks whose number of points over finite fields is a polynomial. In: van der Geer, G., Moonen, B., Schoof, R. (eds.) Number Fields and Function Fields—Two Parallel Worlds. Progress in Mathematics, vol. 239, pp. 39–49. Birkhäuser, Boston (2005)
Borel, A.: Seminar on Transformation Groups. Annals of Mathematics Studies, vol. 46. Princeton University Press, Princeton (1960)
Das, R.: The space of cubic surfaces equipped with a line (2018). ar**v:1803.04146
Deligne, P.: Cohomologie Étale. Séminaire de Géométrie Algébrique du Bois-Marie SGA 4 1/2. Lecture Notes in Mathematics, vol. 569. Springer, Berlin (1977)
Deligne, P., Lusztig, G.: Representations of reductive groups over finite fields. Ann. Math. 103(1), 103–161 (1976)
Dimca, A., Lehrer, G.I.: Purity and equivariant weight polynomials. In: Lehrer, G. (ed.) Algebraic Groups and Lie Groups. Australian Mathematical Society Lecture Series, vol. 9, pp. 161–181. Cambridge University Press, Cambridge (1997)
Dolgachev, I., Ortland, D.: Point Sets in Projective Spaces. Astérisque, vol. 165. Société Mathématique de France, Paris (1988)
Dye, R.: Symmetric groups as maximal subgroups of orthogonal and symplectic groups over the field of two elements. J. London Math. Soc. s2–20(2), 227–237 (1979)
Fullarton, N., Putman, A.: The high-dimensional cohomology of the moduli space of curves with level structures (2016). ar**v:1610.03768 (to appear in J. Eur. Math. Soc.)
Gaiffi, G.: The actions of \(S_{n+1}\) and \(S_n\) on the cohomology ring of a Coxeter arrangement of type \(A_{n-1}\). Manuscripta Math. 91(1), 83–94 (1996)
Getzler, E.: Operads and moduli spaces of genus \(0\) Riemann surfaces. In: Dijkgraaf, R., Faber, C., van der Geer, G. (eds.) The Moduli Space of Curves. Progress in Mathematics, vol. 129, pp. 199–230. Birkhäuser, Boston (1995)
Getzler, E., Looijenga, E.: The hodge polynomial of \(\cal M\it _{3,1}\) (1999). ar**v:math/9910174
Griffiths, P., Harris, J.: Principles of Algebraic Geometry. Wiley, Hoboken (1978)
Gross, B.H., Harris, J.: On some geometric constructions related to theta characteristics. In: Hida, H., Ramakrishnan, D., Shahidi, F. (eds.) Contributions to Automorphic Forms, Geometry and Number Theory, pp. 279–311. The Johns Hopkins University Press, Baltimore (2004)
Kisin, M., Lehrer, G.I.: Equivariant Poincaré polynomials and counting points over finite fields. J. Algebra 247(2), 435–451 (2002)
Kisin, M., Lehrer, G.: Eigenvalues of Frobenius and Hodge numbers. Pure Appl. Math. Q. 2(2), 497–518 (2006)
Kollár, J.: Rational Curves on Algebraic Varieties. Ergebnisse der Mathematik und ihrer Grenzgebiete, vol. 32. Springer, Berlin (1996)
Looijenga, E.: Cohomology of \(\cal{M}_3\) and \(\cal{M}_3^1\). In: Bödigheimer, C.-F., Hain, R.M. (eds.) Map** Class Groups and Moduli Spaces of Riemann Surfaces. Contemporary Mathematics, vol. 150, pp. 205–228. American Mathematical Society, Providence (1993)
Ritzenthaler, C.: Problèmes arithmétiques relatifs à certaines familles de courbes sur les corps finis. Ph.D. thesis, Université Paris Diderot—Paris 7 (2003)
Robinson, A., Whitehouse, S.: The tree representation of \(\Sigma _{n+1}\). J. Pure Appl. Algebra 111(1–3), 245–253 (1996)
Runge, B.: Level-two-structures and hyperelliptic curves. Osaka J. Math. 34(1), 21–51 (1997)
Tsuyumine, S.: Thetanullwerte on a moduli space of curves and hyperelliptic loci. Math. Z. 207(1), 539–568 (1991)
Acknowledgements
This paper is based on parts of my thesis [6] written at Stockholms Universitet. I would like to thank my advisors Carel Faber and Jonas Bergström for their help as well as Dan Petersen for useful comments on an early version of this paper. I also want to thank the anonymous referees for many improvements.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Bergvall, O. Equivariant cohomology of the moduli space of genus three curves with symplectic level two structure via point counts. European Journal of Mathematics 6, 262–320 (2020). https://doi.org/10.1007/s40879-019-00332-9
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40879-019-00332-9


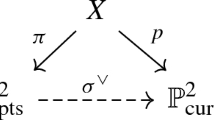

 .
.
 ,
, ,
, .
.

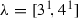








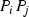 ,
, 






 ,
, 

