Introduction

In the past few decades, many mathematicians and physicists have been concerned with interface problems. It is interesting to explore the ways to solve them. So many numerical methods have been presented to solve these problems.

Interface problems occur in several applications such as dynamical systems [1], fluid mechanics [2], electromagnetic wave propagation [3, 4]. Recently, many researchers have studied numerical methods for solving interface problems such as immersed finite element method [5,6,7], RKHS methods for 1-D interface problems [8, 9], high-order difference potentials methods [10].

Fractional differential equations (FDEs) occupy a very important area because the important of their applications in many fields of science and engineering [11]. Riemann–Liouville and Caputo were the first to investigate the generalization of ordinary integral and differential operators into fractional derivatives. The fractional-order differential equations offer a logical framework for studying real-world problems such as Rubella disease modal [12], waste water modal [13], economic growth model [14], diffusion processes [15], coronavirus disease and Covid-19 models sense [16, 17], in [18] the authors solve the system of nonlinear fractional order PDEs involving of power law kernel using hybrid analytical technique. On the other hand there is some work on a new method for solving fractional PDEs in [19]. In [20,21,22] some fractional differential equations with decay kernel are disscused. Since it is difficult to find exact solutions in closed forms for most differential equations of fractional order, so approximations and numerical techniques will be used, for more see [23,24,25].

The hypothesis of the reproducing kernel Hilbert space (RKHS) and its reproducing kernel function (RKF) have important applications in numerical analysis. The researchers applied the RKHS to develop several numerical techniques for solving different types of differential and integral equations, in [26] the authors introduce the solution the ABC- fractional Riccati and Bernoulli equations by using RKHS method. To explain the important of (RKF), (RKHS) you can read more details from Reproducing kernel for solving mixed type singular time-fractional partial integrodifferential equations [27], singularly perturbed boundary value problems with a delay [28], strongly nonlinear Duffing oscillators [29], integrodifferential systems with two-points periodic boundary conditions [30], Bagley–Torvik and Painlevé equations of fractional order [31], fuzzy fractional differential equations in presence of the Atangana–Baleanu–Caputo differential operators [32], time-fractional Tricomi and Keldysh equations [33], ABC–Fractional Volterra integro-differential equations [34], the Atangana–Baleanu fractional Van der Pol dam** model [35], time-fractional partial differential equations subject to Neumann boundary conditions [36], singular integral equation with cosecant kernel [37]. In this paper, a new numerical method is proposed for solving 1-D interface problems of fractional order. The method is based on the reproducing kernel functions and the shooting method. In the first step, the boundary value problems are converted to the initial value problem with interface conditions by the shooting method, thereafter the reproducing kernel method is applied for solving the new initial value problems. In addition, we carefully study the effectiveness of this method by solving some numerical examples.

By using a modification of the RKHS method, we try to find an approximate solution to our problem, but we cannot use the RKF-based techniques to solve fractional interface problems directly because of the interface point conditions. Therefore, the main challenge here is to construct an effective and accurate numerical method to solve the 1-D fractional interface problem.

In our work, we consider the following 1-D fractional interface problem

$$ \left\{ {\begin{array}{*{20}c} {D^{\alpha } \vartheta \left( \xi \right) + y_{1} \vartheta \left( \xi \right) = f_{1} \left( \xi \right), 0 < \xi < z,} \\ {D^{\alpha } \vartheta \left( \xi \right) + y_{2 } \vartheta \left( \xi \right) = f_{2} \left( \xi \right), z < \xi < 1} \\ {\vartheta \left( 0 \right) = \beta_{0} ,\vartheta \left( 1 \right) = \beta_{1} .} \\ \end{array} } \right.,1 < \alpha \le 2, $$
(1)

and with the interface conditions on \( z\):

$$ \left\{ {\begin{array}{*{20}c} {\vartheta \left( {z^{ + } } \right) = x_{1} \vartheta \left( {z^{ - } } \right) + \gamma_{0 } ,} \\ {\vartheta^{\prime}\left( {z^{ + } } \right) = x_{2} \vartheta^{\prime}\left( {z^{ - } } \right) + \gamma_{1 } .} \\ \end{array} } \right. $$
(2)

where \( y_{1} ,y_{2 }\) are sufficiently smooth functions defined in \( \left( {0,z} \right), \left( {z,1} \right) \) respectively and \(\vartheta\) is an unknown function that will be determined. The operator \(D^{\alpha }\) has the following formula:

$$ D^{\alpha } \vartheta \left( \xi \right) = \frac{1}{{\Gamma \left( {n - \alpha } \right)}}\mathop \int \limits_{0}^{\xi } \left( {\xi - \tau } \right)^{{\left( {n - 1 - \alpha } \right)}} \vartheta^{(n)} \left( \tau \right)d\tau , \qquad 0 < \tau < \xi , 1 < \alpha \le 2. $$
(3)

is called the Caputo fractional derivative operator of order \( \alpha\) of a function \(\vartheta \left( \xi \right)\).

Let and \( f\left( \xi \right) = \left\{ {\begin{array}{*{20}c} {f^{1} \left( \xi \right), 0 < \xi < z} \\ {f_{2} \left( \xi \right), z < \xi < 1.} \\ \end{array} } \right.\)

Then (1) can be written as

(4)

Preliminaries

In this section, we present some basic definitions, results and observations of the shooting method and the reproducing kernel Hilbert spaces that will be required in the sequel to understand the necessary literature and develop our main results.

Shooting Method

In numerical analysis, the shooting method is a technique for converting the boundary value problem to an equivalent initial value problem. Then, an initial value problem is solved via a trial-and-error approach. This technique is called a "shooting" method, by analogizing it to the procedure of shooting an object at a stationary target. Roughly speaking, we shoot out trajectories in different directions until we find a trajectory that has the desired boundary value.

For the utilization of the shooting method: Firstly, we need to reduce the boundary value problem to a system of initial value problems, and we need to assume a guess value at the lower bound of the interval. After these, the solution goes on like the solution of a system of differential equations.

Let us consider a second-order boundary value problem:

$$ \left\{ {\begin{array}{*{20}l} {\vartheta ^{\prime\prime}\left( \xi \right) = f\left( {\xi ,\vartheta ,\vartheta ^{\prime}} \right),} \hfill & {\alpha \le \xi \le \beta } \hfill \\ {\vartheta \left( \alpha \right) = \gamma ,} \hfill & {\vartheta \left( \beta \right) = \eta .} \hfill \\ \end{array} } \right. $$
(5)

At first, we reduce the second-order (BVP) of the equation to a system of a first-order (IVP). The second-order ODE is transformed into a system of two first-order ODEs as:

$$ \left\{ {\begin{array}{*{20}l} {\frac{{d\vartheta }}{{d\xi }} = \vartheta ^{\prime} = x = f_{1} \left( {\xi ,\vartheta ,x} \right),} \hfill & {\vartheta \left( \alpha \right) = \gamma ,} \hfill \\ {\frac{{dx}}{{d\xi }} = \vartheta '' = f_{2} \left( {\xi ,\vartheta ,x} \right),} \hfill & {\vartheta \left( \beta \right) = \omega .} \hfill \\ \end{array} } \right. $$
(6)

In the wake of choosing the \(\hbar\) step size, we use one of the known methods like Euler, Runge–Kutta, etc. to solve these equations. The first numerical result of the BVP is then obtained, which is subject to the first guess value \( \omega . \) If the solution is close enough to the other bound \( \eta\), it is valid; otherwise, the method will resume with another guess. Instead of making the third guess arbitrary after the first two, we can utilize interpolation to get the third and if necessary, the subsequent guesses [38]. Note that the interpolation is given by

$$ \vartheta \left( 0 \right) = {\text{G}}_{1} + \frac{{({\text{G}}_{2} - {\text{G}}_{1} )}}{{({\text{B}}_{2} - {\text{B}}_{1} )}}\left( {{\text{D}} - {\text{B}}_{1} } \right). $$
(7)

where: G1: First guess at the initial slope; G2: Second guess at the initial slope; B1: Final result at endpoint (using G1); B2: Second result at endpoint (using G2); D: The desired value at the endpoint.

Reproducing Kernel Hilbert Spaces

We present some fundamental definitions and theorems, which account for a significant part of the study of RKHSs.

Definition 2.2.1

Let \({\text{M }}\) be a nonempty set, the function \( \psi : M \times M \to {\mathbb{C}}\) is called a reproducing kernel function to Hilbert space \({\text{H }}\) iff

  1. (a)
    $$ \psi \left( {.,\xi } \right) \in H,\forall \xi \in M, $$
  2. (b)

    \(\left\langle {\varphi \left( . \right),\psi \left( {.,\xi } \right)} \right\rangle_{H} = \varphi \left( \xi \right)\) for all \( \varphi \in H \) and for all \(\xi \in M.\)

The second condition is called the reproducing property (the value of the function \(\varphi { }\) at the point \(\xi\) is reproduced by the inner product of \(\varphi { }\) with \( \psi \left( {.,\xi } \right) \)), where the function \(\psi { }\) is called the reproducing kernel function of \(H{ }\) that has some important properties such as being unique, symmetric, and positive definite.

Definition 2.2.2

The function space \( W_{2}^{1} \left[ {a,b} \right] \) is defined by:

\(W_{2}^{1} \left[ {a,b} \right] = \left\{ {\vartheta |\vartheta \; is\; absolutely\; continuous\; function \;and \;\vartheta^{\prime} \in L^{2} \left[ {a,b} \right]} \right\}\), with the inner product:

$$ \left\langle {\vartheta ,v} \right\rangle_{{W_{2}^{1} }} = \vartheta \left( a \right)v\left( a \right) + \mathop \int \limits_{a}^{b} \vartheta ^{\prime}\left( \xi \right)v^{\prime}\left( \xi \right)d\xi $$
(8)

and the norm:

$$ \left\| \vartheta \right\|_{{{\text{W}}_{2}^{1} }} = \sqrt {\left\langle {\vartheta ,\vartheta } \right\rangle_{{{\text{W}}_{2}^{1} }} } ,{ }where{ }\vartheta ,{\text{v}} \in {\text{W}}_{2}^{1} \left[ {{\text{a}},{\text{b}}} \right]. $$
(9)

Definition 2.2.3

The function space \( W_{2}^{2} \left[ {a,b} \right] \) is defined by:

\(W_{2}^{2} \left[ {a,b} \right] = \big\{ {\vartheta |\vartheta , \vartheta^{\prime} are \;absolutely\; continuous\;functions\;and\;\vartheta^{\prime\prime} \in L^{2} \left[ {a,b} \right],\vartheta ( a )}\)

\({ = 0} \big\}\), with the inner product:

$$ \left\langle {\vartheta ,v} \right\rangle_{{W_{2}^{2} }} = \vartheta \left( a \right)v\left( a \right) + \vartheta \left( b \right)v\left( b \right) + \mathop \int \limits_{a}^{b} \vartheta^{\prime\prime}\left( \xi \right)v^{\prime\prime}\left( \xi \right)d\xi $$
(10)

and the norm:

$$ \left\| \vartheta \right\|_{{{\text{W}}_{2}^{2} }} = \sqrt {\left\langle {\vartheta ,\vartheta } \right\rangle_{{{\text{W}}_{2}^{2} }} } ,{ }where{ }\,\,\vartheta ,{{v}} \in {\text{W}}_{2}^{2} \left[ {{\text{a}},{\text{b}}} \right]. $$
(11)

Definition 2.2.4

The function space \(W_{2}^{3} \left[ {a,b} \right]\) is defined by:

$$ W_{2}^{3} \left[ {a,b} \right] = \left\{ {\vartheta |\vartheta , \;\vartheta^{\prime},\; \vartheta^{\prime\prime}\;are\; absolutely \;continuous\; functions\; and\; \vartheta^{\prime \prime \prime } \in L^{2} \left[ {a,b} \right]\quad \vartheta \left( a \right) = \vartheta ^{\prime}\left( a \right) = 0 } \right\}, $$

with the inner product:

$$ \left\langle {\vartheta ,v} \right\rangle _{{W_{2}^{3} }} = \vartheta \left( a \right)v\left( a \right) + \vartheta ^{\prime } \left( a \right)v^{\prime } \left( a \right) + \vartheta ^{{\prime \prime }} \left( a \right)v^{{\prime \prime }} \left( a \right) + \int\limits_{a}^{b} {\vartheta ^{{\prime \prime \prime }} \left( \xi \right)v^{{\prime \prime \prime }} \left( \xi \right)d\xi } $$
(12)

and the norm:

$$ \left\| \vartheta \right\|_{{{\text{W}}_{2}^{3} }} = \sqrt {\left\langle {\vartheta ,\vartheta } \right\rangle_{{{\text{W}}_{2}^{3} }} } ,{ }where{ }\vartheta ,{\text{v}} \in {\text{W}}_{2}^{3} \left[ {{\text{a}},{\text{b}}} \right]. $$
(13)

Theorem 2.2.1

The space \(W_{2}^{3} \left[ {a,b} \right] \) is a complete reproducing kernel space and its reproducing kernel function \( {\grave{O}}_{\xi } \) is given by.

$$ {\mathcal{Q}}_{\xi } \left( \eta \right) = {\mathcal{Q}}\left( {\xi ,\eta } \right) = \left\{ {\begin{array}{*{20}l} {q_{1} \left( {\xi ,\eta } \right),~} \hfill & {~a \le \eta \le \xi \le b,} \hfill \\ {q_{1} \left( {\eta ,\xi } \right),~} \hfill & {a \le \xi < \eta \le b.} \hfill \\ \end{array} } \right. $$
(14)

where:

$$ q_{1} \left( {\xi ,\eta } \right) = \frac{ - 1}{{120}}\left( {a - \eta } \right)^{2} \left( {6a^{3} - 3a^{2} \left( {5\xi + \eta + 10} \right) + 2a\left( {5\xi^{2} + 5\xi \left( {\eta + 6} \right) - \eta^{2} } \right) - 10\xi^{2} \left( {\eta + 3} \right) + 5\xi \eta^{2} - \eta^{3} } \right). $$

Definition 2.2.5

The function space \( W_{2}^{3} \left[ {a,b} \right] \) is defined by:

\( \bar{W}_{2}^{3} \left[ {a,b} \right] = \left\{ \vartheta |\vartheta ,~\vartheta ^{\prime } ,~\vartheta ^{{\prime \prime }} \;are~\;absolutely~\;continuous\;~functions\;~and\;~\vartheta ^{{\prime \prime \prime }} \in \right.\break\left. L^{2} \left[ {a,b} \right],\vartheta (a) = \vartheta (b) = 0 \right\} \) with the inner product:

$$ \left\langle {\vartheta ,v} \right\rangle _{{\bar{W}_{2}^{3} }} = \vartheta \left( a \right)v\left( a \right) + \vartheta ^{\prime}\left( a \right)v^{\prime}\left( a \right) + \vartheta \left( b \right)v\left( b \right) + \int\limits_{a}^{b} {\vartheta ^{{\prime \prime \prime }} \left( \xi \right)v^{{\prime \prime \prime }} \left( \xi \right)d\xi } $$
(15)

and the norm:

$$ \left\| \vartheta \right\|_{{{\overline{\text{W}}}_{2}^{3} }} = \sqrt {\left\langle {\vartheta ,\vartheta } \right\rangle_{{{\overline{\text{W}}}_{2}^{3} }} } ,where{ }\vartheta ,{\text{v}} \in {\overline{\text{W}}}_{2}^{3} \left[ {{\text{a}},{\text{b}}} \right]. $$
(16)

Theorem 2.2.2

The space \(\overline{W}_{2}^{3} \left[ {a,b} \right]\) is a complete reproducing kernel space and its reproducing kernel function \(\overline{{\grave{O}} }_{\xi }\) is given by.

$$ \`O _{\xi } \left( \eta \right) = \bar{\`O }\left( {\xi ,\eta } \right) = \left\{ {\begin{array}{*{20}l} {q_{2} \left( {\xi ,\eta } \right),} \hfill & {a \le \eta \le \xi \le b,} \hfill \\ {q_{2} \left( {\eta ,\xi } \right),~~} \hfill & {a \le \xi < \eta \le b.} \hfill \\ \end{array} } \right. $$
(17)

where

$$ \begin{aligned} q_{2} \left( {\xi ,\eta } \right) &= \frac{1}{{120\left( {a - b} \right)^{2} }}\left( {a - \eta } \right)( - 4a^{4} \left( {b - \xi } \right)\left( {b - \eta } \right) - 6b^{3} \xi^{2} \eta + a^{3} \left( {b - \xi } \right)\left( {b - \eta } \right)(6b + 7\xi + 3\eta ) \hfill \\ & \quad + \xi^{2} \eta \left( { - 120 + \xi^{3} + \eta^{3} } \right) - 3a^{2} \left( {b - \eta } \right)(\xi \eta \left( { - 3\xi + \eta } \right) + 2b^{2} \left( {2\xi + \eta } \right) - b(4\xi^{2} - \xi \eta + \eta^{2} )) \hfill \\ & \quad - 5b\xi \left( { - 24\eta + \xi^{3} \eta + \xi \left( { - 24 + \eta^{3} } \right)} \right) + b^{2} \left( {10\xi^{3} \eta - \eta^{4} + 5\xi \left( { - 24 + \eta^{3} } \right)} \right) + a(6b^{3} \xi (\xi + 2\eta) \hfill \\ & \quad - b^{2} \left( { - 120 + 10\xi^{3} + 12\xi^{2} \eta + 15\xi \eta^{2} + \eta^{3} } \right) + \xi \left( { - \xi^{4} + \xi \eta^{3} - 2\eta \left( { - 60 + \eta^{3} } \right)} \right) \hfill \\ & \quad + b\left( { - 120\xi + 5\xi^{4} + 15\xi^{2} \eta^{2} + 2\eta \left( { - 60 + \eta^{3} } \right)} \right)) \hfill \\ \end{aligned} $$
(18)

Proof

By definition 2.2.5, we have

\( \begin{aligned} & \bar{\vartheta }_{1} \left( \xi \right) - \mathop \sum \limits_{{k = 0}}^{1} \frac{{\bar{\vartheta }_{1}^{{\left( k \right)}} \left( 0 \right)}}{{k!}}\left( {\xi - 0} \right)^{k} + y_{1} \frac{1}{{\Gamma \left( \alpha \right)}}\mathop \int \limits_{0}^{\xi } \left( {\xi - t} \right)^{{\alpha - 1}} \bar{\vartheta }_{1} \left( t \right)dt \\ & \quad \quad \quad = \frac{1}{{\Gamma \left( \alpha \right)}}\mathop \int \limits_{0}^{\xi } \left( {\xi - t} \right)^{{\alpha - 1}} \bar{f}_{1} \left( t \right)dt. \\ \end{aligned} \)

then by applying the integration by parts three times for the third scheme of the right-hand, we obtain

$$ \begin{aligned} \left\langle {\vartheta ,{\grave{O}}_{\xi } } \right\rangle_{{W_{2}^{3} }} = & \vartheta \left( a \right){\grave{O}}_{\xi } \left( a \right) + \vartheta^{\prime}\left( a \right){\grave{O}}_{\xi }^{^{\prime}} \left( a \right) + \vartheta \left( b \right){\grave{O}}_{\xi } \left( b \right) \\ & \quad + \vartheta^{\prime\prime}\left( b \right){\grave{O}}_{\xi }^{\prime \prime \prime } \left( b \right) - \vartheta^{\prime\prime}\left( a \right){\grave{O}}_{\xi }^{\prime \prime \prime } \left( a \right) - \vartheta^{\prime}\left( b \right){\grave{O}}_{\xi }^{\left( 4 \right)} \left( b \right) + \vartheta^{\prime}\left( a \right){\grave{O}}_{\xi }^{\left( 4 \right)} \left( a \right) \\ & \quad + \vartheta \left( b \right){\grave{O}}_{\xi }^{\left( 5 \right)} \left( b \right) - \vartheta \left( a \right){\grave{O}}_{\xi }^{\left( 5 \right)} \left( a \right) - \mathop \int \limits_{a}^{b} \vartheta \left( \eta \right){\grave{O}}_{\xi }^{\left( 6 \right)} \left( \eta \right)d\eta . \\ \end{aligned} $$

Note that the reproducing property is \(\left\langle {\vartheta \left( \eta \right),{\grave{O}}_{\xi } \left( \eta \right)} \right\rangle_{{\overline{W}_{2}^{3} }} = \vartheta \left( \xi \right),\)

Since \(\vartheta \left( \eta \right), {\grave{O}}_{\xi } \left( \eta \right) \in \overline{W}_{2}^{3} \left[ {a,b} \right]\), we have.

  1. (1)

    \({\grave{O}}_{\xi } \left( a \right) - {\grave{O}}_{\xi }^{\left( 5 \right)} \left( a \right) = 0,\)

  2. (2)

    \({\grave{O}}_{\xi }^{^{\prime}} \left( a \right) + {\grave{O}}_{\xi }^{\left( 4 \right)} \left( a \right) = 0,\)

  3. (3)

    \({\grave{O}}_{\xi } \left( b \right) + O@_{\xi }^{\left( 5 \right)} \left( b \right) = 0,\)

  4. (4)

    \({\grave{O}}_{\xi }^{\prime \prime \prime } \left( b \right) = 0,\)

  5. (5)

    \({\grave{O}}_{\xi }^{\prime \prime \prime } \left( a \right) = 0,\)

  6. (6)

    \({\grave{O}}_{\xi }^{\left( 4 \right)} \left( b \right) = 0.\)

Thus, we need to solve the BVP \(-{\grave{O}}_{\xi }^{\left( 6 \right)} \left( \eta \right) = \delta \left( {\xi - \eta } \right)\) subject to the conditions (1–6).

When \(\xi \ne \eta\), we know \({\grave{O}}_{\xi }^{\left( 6 \right)} \left( \eta \right) = 0\).

Consequently, we attain

$$ {\grave{O}}_{\xi } \left( \eta \right) = \left\{ {\begin{array}{*{20}c} {\mathop \sum \limits_{j = 0}^{5} c_{j} \left( \xi \right)\eta^{j} , a \le \eta \le \xi \le b,} \\ {\mathop \sum \limits_{j = 0}^{5} d_{j} \left( \xi \right)\eta^{j} , a \le \xi < \eta \le b.} \\ \end{array} } \right. $$

Since \( {\grave{O}}_{\xi }^{\left( 6 \right)} \left( \eta \right) = \delta \left( {\xi - \eta } \right)\), we have \({\grave{O}}_{{\xi^{ + } }}^{\left( k \right)} \left( \xi \right) = {\grave{O}}_{{\xi^{ - } }}^{\left( k \right)} \left( \xi \right), k = 0,1,2,3,4,\) \({\grave{O}}_{{\xi^{ + } }}^{\left( 5 \right)} \left( \xi \right) - {\grave{O}}_{{\xi^{ - } }}^{\left( 5 \right)} \left( \xi \right) = - 1\).

The unknown coefficients \(c_{j} \left( \xi \right)\) and \(d_{j} \left( \xi \right) \left( {j = 0,1,2,3,4,5} \right)\) can be found by using Mathematica 12, hence (18) is obtained.

Solution of Problem (1)

In this section, we consider the 1-D fractional interface problem (1) with the interface conditions (2). We solve the problem (1) on intervals \( \left( {0,{\text{z}}} \right){ }\) and \( \left( {{\text{z}},1} \right){ }\) by using the shooting method and RKHSs, respectively.

Now we apply the shooting method to (1) then we have

(19)

On \(\left( {0,{\text{z}}} \right),{ }\) we get

$$ D^{\alpha } \vartheta_{1} \left( \xi \right) + y_{1} \vartheta_{1} \left( \xi \right) = f_{1} \left( \xi \right),\vartheta_{1} \left( 0 \right) = \beta_{0} ,\vartheta_{1} ^{\prime}\left( 0 \right) = \sigma_{1} . $$
(20)

We discuss Eq. (20) with homogeneous conditions, that is,

$$ D^{\alpha } \overline{\vartheta }_{1} \left( \xi \right) + y_{1} \overline{\vartheta }_{1} \left( \xi \right) = \overline{f}_{1} \left( \xi \right), \overline{\vartheta }_{1} \left( 0 \right) = 0, \overline{\vartheta }_{1} ^{\prime}\left( 0 \right) = 0. $$
(21)

where

\(\vartheta_{1} \left( \xi \right) = \overline{\vartheta }_{1} \left( \xi \right) + \delta_{1} \left( \xi \right)\), \(\overline{f}_{1} \left( \xi \right) = f_{1} \left( \xi \right) - L\delta_{1} \left( \xi \right)\) and \(\delta_{1} \left( \xi \right) = \beta_{0} + \sigma_{1} \xi .\)

By applying the Riemann–Liouville fractional integral operator of the order \(\alpha\) of both sides of Eq. (21), we have

$$ \overline{\vartheta }_{1} \left( \xi \right) - \mathop \sum \limits_{k = 0}^{1} \frac{{\overline{\vartheta }_{1}^{\left( k \right)} \left( 0 \right)}}{k!}\left( {\xi - 0} \right)^{k} + y_{1} \frac{1}{\Gamma \left( \alpha \right)}\mathop \int \limits_{0}^{\xi } \left( {\xi - t} \right)^{\alpha - 1} \overline{\vartheta }_{1} \left( t \right)dt = \frac{1}{\Gamma \left( \alpha \right)}\mathop \int \limits_{0}^{\xi } \left( {\xi - t} \right)^{\alpha - 1} \overline{f}_{1} \left( t \right)dt. $$
(22)

But since \(\overline{\vartheta }_{1}^{\left( j \right)} \left( 0 \right) = 0, j = 0,1\) then we have

$$ \overline{\vartheta }_{1} \left( \xi \right) = \overline{F}_{1} \left( {\xi ,\overline{\vartheta }_{1} \left( \xi \right)} \right) $$
(23)

where \( \overline{F}_{1} \left( {\xi ,\overline{\vartheta }_{1} \left( \xi \right)} \right) = \frac{1}{{{\Gamma }\left( \alpha \right)}}\mathop \int \limits_{0}^{\xi } \left( {\xi - t} \right)^{\alpha - 1} \overline{f}_{1} \left( t \right)dt - {\text{y}}_{1} \frac{1}{{{\Gamma }\left( {\upalpha } \right)}}\mathop \int \limits_{0}^{{\upxi }} \left( {{\upxi } - {\text{t}}} \right)^{{{\upalpha } - 1}} \overline{\vartheta }_{1} \left( {\text{t}} \right){\text{dt}}.\)

Choose a countable dense subset \(\left\{ {\xi_{1} ,\xi_{2} , \ldots ,\xi_{N} } \right\}\) in \(\left( {0,z} \right)\), we define

$$ \psi_{j} \left( \xi \right) = \left. {{\grave{O}} \left( {\xi ,\eta } \right)} \right|_{{\eta = \xi_{j} }} , j = 1,2, \ldots ,N. $$
(24)

The solution of (21) can be written as

$$ \overline{\vartheta }_{1,N} \left( \xi \right) = \mathop \sum \limits_{j = 1}^{N} d_{j} \psi_{j} \left( \xi \right), $$
(25)

where \( \left\{ {d_{j} } \right\}_{j = 1}^{N}\) are constants to be determined. Therefore, the solution of (21) is given by

$$ \vartheta_{1,N} \left( \xi \right) = \overline{\vartheta }_{1,N} \left( \xi \right) + \delta_{1} \left( \xi \right). $$
(26)

Because of the uniformed convergence of \(\vartheta_{1,N} \left( \xi \right)\) and its derivative, utilizing those states in the interface point, \(\vartheta_{1,N} \left( \xi \right)\) could provide an exact close estimation of the values of \(\vartheta \left( {z^{ + } } \right), \vartheta^{\prime}\left( {z^{ + } } \right).\)

Now the problem (19) on \(\left( {{\text{z}},1} \right){ }\) can be written as

$$ \left\{ {\begin{array}{*{20}l} {D^{\alpha } \vartheta _{2} \left( \xi \right) + y_{2} \vartheta _{2} \left( \xi \right) = f_{2} \left( \xi \right)~,} \hfill \\ {\vartheta _{2} \left( z \right) = x_{1} \vartheta _{{1,N}} \left( {z^{ - } } \right) + \gamma _{0} ,~\vartheta '_{2} \left( z \right) = x_{2} \vartheta '_{{1,N}} \left( {z^{ - } } \right) + \gamma _{1} ~.} \hfill \\ \end{array} } \right. $$
(27)

Toward utilizing the manner for solving the problem (20), we get \(\vartheta_{2,N} \left( \xi \right)\) to the problem (19) on \(\left( {z,1} \right).\) So we have an approximate solution to the problem (19), which is given by

$$ \vartheta_{N} \left( \xi \right) = \left\{ {\begin{array}{*{20}c} {\vartheta_{1,N} \left( \xi \right) \xi \in \left( {0,z} \right), } \\ {\vartheta_{2,N} \left( \xi \right) \xi \in \left( {z,1} \right). } \\ \end{array} } \right. $$
(28)

Applications

In this part, we introduce some applications to solve 1-D interface problems of fractional order.

Example 1

Consider the following problem [8]:

$$ \gamma D^{\alpha } \vartheta \left( \xi \right) = 12\xi^{2} , \gamma = \left\{ {\begin{array}{*{20}c} {1, \xi \in \left( {0,\frac{1}{2}} \right), \alpha \in \left( {1,2} \right].} \\ {2, \xi \in \left( {\frac{1}{2},1} \right), } \\ \end{array} } \right. $$

subject to the boundary and interface conditions:

$$ \vartheta \left( 0 \right) = 0, \vartheta \left( 1 \right) = \frac{17}{{32}}, \vartheta \left( {\frac{1}{2}^{ + } } \right) = \vartheta \left( {\frac{1}{2}^{ - } } \right), \vartheta ^{\prime}\left( {\frac{1}{2}^{ + } } \right) = \vartheta ^{\prime}\left( {\frac{1}{2}^{ - } } \right). $$

As \(\alpha = 2\), the exact solution is

$$ \vartheta \left( \xi \right) = \left\{ {\begin{array}{*{20}c} {\xi^{4} , \xi \in \left( {0,\frac{1}{2}} \right).} \\ {\frac{1}{2}\left( {\xi^{4} + \frac{1}{16}} \right), \xi \in \left( {\frac{1}{2},1} \right).} \\ \end{array} } \right. $$

After the initial conditions have been homogenized, choose.

$$ \xi_{j} = \left\{ {\begin{array}{*{20}c} {\frac{j}{2N} , \xi \in \left( {0,\frac{1}{2}} \right),} \\ {\frac{1}{2} + \frac{j - 1}{{2\left( {N - 1} \right)}}, \xi \in \left( {\frac{1}{2},1} \right),} \\ \end{array} } \right.for j = 1,2, \ldots ,N. $$

Then we apply the RKHS method with \(N = 50\), Table 1 which describes the exact and approximate solutions of \( \vartheta \left( \xi \right) \) for \( \alpha = 2\) and approximate solutions for different values of \(\alpha\).

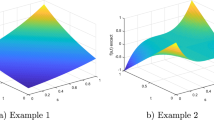
Table 1 Numerical results for \(\vartheta (\xi )\) in Example 1
Full size table

The graph in Fig. 1a represents the exact and approximate solution \(\vartheta \left( \xi \right)\) when \(\alpha = 2. \) In Fig. 1b, graphs of the approximate solutions of \(\vartheta \left( \xi \right)\) are plotted for different values of \(\alpha\). It is clear from Fig. 1b that the approximate solutions are insensible arrangements with the exact solution when \(\alpha = 2, \) and the solutions are continuously based on a fractional derivative. The graph in Fig. 1c represents the absolute errors of \(\vartheta \left( \xi \right)\) when \(\alpha = 2\).

Fig. 1
figure 1

Solution and graphical results of Example 1

Full size image

Example 2

Consider the following problem [8]:

$$ \gamma D^{\alpha } \vartheta \left( \xi \right) = 56\xi^{6} , \gamma = \left\{ {\begin{array}{*{20}c} {1, \xi \in \left( {0,\frac{1}{2}} \right), \alpha \in \left( {1,2} \right].} \\ {2, \xi \in \left( {\frac{1}{2},1} \right), } \\ \end{array} } \right. $$

subject to the boundary and interface conditions:

$$ \vartheta \left( 0 \right) = - 1, \vartheta \left( 1 \right) = \frac{769}{{512}}, \vartheta \left( {\frac{1}{2}^{ + } } \right) = \vartheta \left( {\frac{1}{2}^{ - } } \right) + 2,\vartheta ^{\prime}\left( {\frac{1}{2}^{ + } } \right) = \frac{1}{2} \vartheta ^{\prime}\left( {\frac{1}{2}^{ - } } \right). $$

As \( \alpha = 2\), the exact solution is.

$$ \vartheta \left( \xi \right) = \left\{ {\begin{array}{*{20}c} {\xi^{8} - 1 , \xi \in \left( {0,\frac{1}{2}} \right).} \\ {\frac{1}{2}\left( {\xi^{8} + \frac{1}{256}} \right), \xi \in \left( {\frac{1}{2},1} \right).} \\ \end{array} } \right. $$

After the initial conditions have been homogenized, choose

$$ \xi_{j} = \left\{ {\begin{array}{*{20}c} {\frac{j}{2N} , \xi \in \left( {0,\frac{1}{2}} \right),} \\ {\frac{1}{2} + \frac{j - 1}{{2\left( {N - 1} \right)}}, \xi \in \left( {\frac{1}{2},1} \right),} \\ \end{array} } \right.{\text{for}} j = 1,2, \ldots ,N. $$

Then we apply the RKHS method with \( N = 50\), Table 2 which describes the exact and approximate solutions of \( \vartheta \left( \xi \right) \) for \( \alpha = 2\) and approximate solutions for different values of \(\alpha\).

Table 2 Numerical results for \(\vartheta (\xi )\) in Example 2
Full size table

The graph in Fig. 2a represents the exact and approximate solution \(\vartheta \left( \xi \right)\) when \(\alpha = 2. \) In Fig. 2b, graphs of the approximate solutions of \(\vartheta \left( \xi \right)\) are plotted for different values of \(\alpha\). It is clear from Fig. 2b that the approximate solutions are insensible arrangements with the exact solution when \(\alpha = 2, \) and the solutions are continuously based on a fractional derivative. The graph in Fig. 2c represents the absolute errors of \(\vartheta \left( \xi \right)\) when \(\alpha = 2\).

Fig. 2
figure 2

Solution and graphical results of Example 2

Full size image

Example 3

Consider the following problem:

$$ \gamma D^{\alpha } \vartheta \left( \xi \right) = \left\{ {\begin{array}{*{20}c} {e^{\xi } , \xi \in \left( {0,\frac{1}{2}} \right) } \\ {sec^{2} \left( {\xi - \frac{1}{2}} \right)\tan \left( {\xi - \frac{1}{2}} \right), \xi \in \left( {\frac{1}{2},1} \right)} \\ \end{array} } \right., \gamma = \left\{ {\begin{array}{*{20}c} {1, \xi \in \left( {0,\frac{1}{2}} \right), \alpha \in \left( {1,2} \right].} \\ {2, \xi \in \left( {\frac{1}{2},1} \right), } \\ \end{array} } \right. $$

subject to the boundary and interface conditions:

$$ \vartheta \left( 0 \right) = 1, \vartheta \left( 1 \right) = e^{\frac{1}{2}} + \tan \left( \frac{1}{2} \right), \vartheta \left( {\frac{1}{2}^{ + } } \right) = \vartheta \left( {\frac{1}{2}^{ - } } \right),\vartheta ^{\prime}\left( {\frac{1}{2}^{ + } } \right) = e^{{ - \frac{1}{2}}} \vartheta ^{\prime}\left( {\frac{1}{2}^{ - } } \right). $$

As \( \alpha = 2\), the exact solution is \( \vartheta \left( \xi \right) = \left\{ {\begin{array}{*{20}l} {e^{\xi } ,} \hfill & {\xi \in \left( {0,\frac{1}{2}} \right).} \hfill \\ {e^{{\frac{1}{2}}} + \tan \left( {\xi - \frac{1}{2}} \right),~} \hfill & {~\xi \in \left( {\frac{1}{2},1} \right).} \hfill \\ \end{array} } \right. \)

After the initial conditions have been homogenized, choose

$$ \xi_{j} = \left\{ {\begin{array}{*{20}c} {\frac{j}{2N} , \xi \in \left( {0,\frac{1}{2}} \right),} \\ {\frac{1}{2} + \frac{j - 1}{{2\left( {N - 1} \right)}}, \xi \in \left( {\frac{1}{2},1} \right),} \\ \end{array} } \right.{\text{for}} j = 1,2, \ldots ,N. $$

Then we apply the RKHS method with \(N = 50\), Table 3 which describes the exact and approximate solutions of \( \vartheta \left( \xi \right) \) for \( \alpha = 2\) and approximate solutions for different values of \(\alpha\).

Table 3 Numerical results for \(\vartheta (\xi )\) in Example 3
Full size table

The graph in Fig. 3a represents the exact and approximate solution \(\vartheta \left( \xi \right)\) when \(\alpha = 2. \) In Fig. 3b, graphs of the approximate solutions of \(\vartheta \left( \xi \right)\) are plotted for different values of \(\alpha\). It is clear from Fig. 3b that the approximate solutions are insensible arrangements with the exact solution when \(\alpha = 2, \) and the solutions are continuously based on a fractional derivative. The graph in Fig. 3c represents the absolute errors of \(\vartheta \left( \xi \right)\) when \(\alpha = 2\).

Fig. 3
figure 3

Solution and graphical results of Example 3

Full size image

Example 4

Consider the following problem:

$$ \gamma D^{\alpha } \vartheta \left( \xi \right) = \left\{ {\begin{array}{*{20}l} {\sin \left( {\pi \xi } \right),} \hfill & {\xi \in \left( {0,\frac{1}{2}} \right)} \hfill \\ {\left( {\xi - \frac{1}{2}} \right),~} \hfill & {\xi \in \left( {\frac{1}{2},1} \right)} \hfill \\ \end{array} } \right.,~~~\gamma = \left\{ {\begin{array}{*{20}l} { - \pi ^{2} ,~~\xi \in \left( {0,\frac{1}{2}} \right),} \hfill & {\alpha \in \left( {1,2} \right].} \hfill \\ {6,} \hfill & {\xi \in \left( {\frac{1}{2},1} \right),~} \hfill \\ \end{array} } \right. $$

subject to the boundary and interface conditions:

$$ \vartheta \left( 0 \right) = 1, \vartheta \left( 1 \right) = \frac{9}{8}, \vartheta \left( {\frac{1}{2}^{ + } } \right) = \vartheta \left( {\frac{1}{2}^{ - } } \right),\vartheta ^{\prime}\left( {\frac{1}{2}^{ + } } \right) = \vartheta ^{\prime}\left( {\frac{1}{2}^{ - } } \right). $$

As \( \alpha = 2\), the exact solution is.

$$ \vartheta \left( \xi \right) = \left\{ {\begin{array}{*{20}l} {\sin \left( {\pi \xi } \right),} \hfill & {\xi \in \left( {0,\frac{1}{2}} \right).} \hfill \\ {\left( {\xi - \frac{1}{2}} \right)^{3} + 1 ,} \hfill & {\xi \in \left( {\frac{1}{2},1} \right).} \hfill \\ \end{array} } \right. $$

After the initial conditions have been homogenized, choose

$$ \xi _{j} = \left\{ {\begin{array}{*{20}l} {\frac{j}{{2N}},} \hfill & {\xi \in \left( {0,\frac{1}{2}} \right),} \hfill \\ {\frac{1}{2} + \frac{{j - 1}}{{2\left( {N - 1} \right)}},} \hfill & {\xi \in \left( {\frac{1}{2},1} \right),} \hfill \\ \end{array} } \right.{\text{for}}~j = 1,2,...,N. $$

Then we apply the RKHS method with \(N = 50\), Table 4 which describes the exact and approximate solutions of \( \vartheta \left( \xi \right) \) for \( \alpha = 2\) and approximate solutions for different values of \(\alpha\).

Table 4 Numerical results for \(\vartheta (\xi )\) in Example 4
Full size table

The graph in Fig. 4a represents the exact and approximate solution \(\vartheta \left( \xi \right)\) when \(\alpha = 2. \) In Fig. 4b, graphs of the approximate solutions of \(\vartheta \left( \xi \right)\) are plotted for different values of \(\alpha\). It is clear from Fig. 4b that the approximate solutions are insensible arrangements with the exact solution when \(\alpha = 2, \) and the solutions are continuously based on a fractional derivative. The graph in Fig. 4c represents the absolute errors of \(\vartheta \left( \xi \right)\) when \(\alpha = 2\).

Fig. 4
figure 4

Solution and graphical results of Example 4

Full size image

Example 5

Consider the following problem [8]:

$$ \rho \left( \xi \right)D^{\alpha } \vartheta \left( \xi \right) + \rho^{\prime}\left( \xi \right)\vartheta^{^{\prime}\left( \xi \right)} - \sigma \left( \xi \right)\vartheta \left( \xi \right) = {\mathcal{F}}\left( \xi \right), \xi \in \left( {0,\frac{1}{2}} \right) \cup \left( {\frac{1}{2},1} \right) \alpha \in \left( {1,2} \right]. $$

where:

$$ \rho \left( \xi \right) = \left\{ {\begin{array}{*{20}c} {3e^{{ - 10\xi^{4} \left( {\xi - \frac{1}{2}} \right)^{4} }} , \xi \in \left( {0,\frac{1}{2}} \right) } \\ {3 , \xi \in \left( {\frac{1}{2},1} \right)} \\ \end{array} } \right.,\sigma \left( \xi \right) = \left\{ {\begin{array}{*{20}c} {2 , \xi \in \left( {0,\frac{1}{2}} \right) . } \\ {1 , \xi \in \left( {\frac{1}{2},1} \right) . } \\ \end{array} } \right. $$

subject to the boundary and interface conditions:

$$ \vartheta \left( 0 \right) = 0, \vartheta \left( 1 \right) = 1.0156, \vartheta \left( {\frac{1}{2}^{ + } } \right) = \vartheta \left( {\frac{1}{2}^{ - } } \right),\vartheta ^{\prime}\left( {\frac{1}{2}^{ + } } \right) = \vartheta ^{\prime}\left( {\frac{1}{2}^{ - } } \right). $$

As \( \alpha = 2\) and \({\mathcal{F}}\left( \xi \right)\) is selected such that its exact solution is.

$$ \vartheta \left( \xi \right) = \left\{ {\begin{array}{*{20}l} {\sin \left( {\pi \xi } \right) ,} \hfill & {\xi \in \left( {0,\frac{1}{2}} \right).} \hfill \\ {2\left( {\xi - \frac{1}{2}} \right)^{7} + 1,} \hfill & {\xi \in \left( {\frac{1}{2},1} \right).} \hfill \\ \end{array} } \right. $$

After the initial conditions have been homogenized, choose

$$ \xi_{j} = \left\{ {\begin{array}{*{20}c} {\frac{j}{2N} , \xi \in \left( {0,\frac{1}{2}} \right),} \\ {\frac{1}{2} + \frac{j}{2N} , \xi \in \left( {\frac{1}{2},1} \right),} \\ \end{array} } \right.{\text{for}} j = 1,2, \ldots ,N. $$

Then we apply the RKHS method with \(N = 50\), Table 5 which describes the exact and approximate solutions of \( \vartheta \left( \xi \right) \) for \( \alpha = 2\) and approximate solutions for different values of \(\alpha\).

Table 5 Numerical results for \(\vartheta (\xi )\) in Example 5
Full size table

The graph in Fig. 5a represents the exact and approximate solution \(\vartheta \left( \xi \right)\) when \(\alpha = 2. \) In Fig. 5b, graphs of the approximate solutions of \(\vartheta \left( \xi \right)\) are plotted for different values of \(\alpha\). It is clear from Fig. 5b that the approximate solutions are insensible arrangements with the exact solution when \(\alpha = 2, \) and the solutions are continuously based on a fractional derivative. The graph in Fig. 5c represents the absolute errors of \(\vartheta \left( \xi \right)\) when \(\alpha = 2\).

Fig. 5
figure 5

Solution and graphical results of Example 5

Full size image

Conclusion

In this paper, a numerical method has been employed for solving 1-D interface problems of fractional order in the Caputo sense. The key to the solution procedure is the combination of the reproducing kernel functions and the shooting method. The main advantage of the method is its fast convergence to the solution. In practice, the utilization of the method is straightforward if some symbolic software such as Mathematica is used to implement the calculations. The results of examples illustrate the reliability and consistency of the method. Moreover, the solutions obtained are easily programmable approximants to the analytic solutions of the original problems with the accuracy required.