Prioritized Aggregation Operators for Complex Intuitionistic Fuzzy Sets Based on Aczel-Alsina T-norm and T-conorm and Their Applications in Decision-Making

Abstract

The Aczel-Alsina t-norms ware proposed by Aczel and Alsina in 1982, which are a very effective and dominant technique used in the construction of any kind of aggregation operators. Moreover, the Algebraic t-norms are a special case of the Aczel-Alsina t-norms because of the parameter $0<p<+\infty$. Additionally, a complex intuitionistic fuzzy (COIF) set is an essential and valuable part of the fuzzy set to handle vague and awkward situations in many real-life problems. Motivated by the above valuable and dominant ideas, the major contribution of this study is to propose the aggregation operators by involving the priority degree based on Aczel-Alsina t-norms for managing the COIF values, such as COIF Aczel-Alsina prioritized weighted averaging (COIFAAPWA), COIF Aczel-Alsina prioritized ordered weighted averaging (COIFAPOWA), COIF Aczel-Alsina prioritized weighted geometric (COIFAAPWG), and COIF Aczel-Alsina prioritized ordered weighted geometric (COIFAAPOWG) operators. The fundamental properties of these operators are also examined. Afterward, we develop a decision-making technique to process the multi-attribute decision-making (MADM) problem based on the COIF information and proposed operators. Lastly, we use some examples to show the supremacy and effectiveness of the developed approaches by checking the influence of the parameters and the comparison between proposed techniques with some existing techniques.

1 Introduction

Multi-attribute decision-making (MADM) is an important part of decision theory, which can give the best choice or ranking result for some alternatives under some attributes. At evaluating an attribute for alternatives, sometimes, it is difficult to express the evaluation value by a real number. In order to express this evaluation information without distortion, Zadeh [1] proposed the fuzzy set (FS), which is expressed by $\overline{\overline{{\mathbb{m}}_{\overline{\overline{\fancyscript{r}}}}}}:\widetilde{{\mathbb{Z}}_{U}}\to \left[\mathrm{0,1}\right]$, where the value of $\widetilde{{\mathbb{Z}}_{U}}\left(\widetilde{{\fancyscript{z}}_{\mathfrak{a}}}\right)\in \left[0, 1\right]$ is represented as a membership grade (MG). Various valuable applications have been described by scholars in mandelbrot sets [2] and decision-making methods [3, 4]. Furthermore, because the FS can only consider the MG, it cannot deal with the information from non-membership grade (NMG), to solve this problem, Atanassov [5] proposed intuitionistic FS (IFS), where two functions are defined in IFS, which are stated as: $\overline{\overline{{\mathbb{m}}_{\overline{\overline{\fancyscript{r}}}}}}:\widetilde{{\mathbb{Z}}_{U}}\to \left[\mathrm{0,1}\right]$, $\overline{\overline{{\mathbb{y}}_{\overline{\overline{{\Lambda }_{\Sigma }}}}}}:\widetilde{{\mathbb{Z}}_{U}}\to \left[\mathrm{0,1}\right]$, and $\widetilde{{\mathbb{Z}}_{U}}\left(\widetilde{{\fancyscript{z}}_{\mathfrak{a}}}\right)+\overline{\overline{{\mathbb{y}}_{\overline{\overline{{\Lambda }_{\Sigma }}}}}}\left(\widetilde{{\fancyscript{z}}_{\mathfrak{a}}}\right)\in \left[0, 1\right]$, $\overline{\overline{{\mathbb{m}}_{\overline{\overline{\fancyscript{r}}}}}}$ and $\overline{\overline{{\mathbb{y}}_{\overline{\overline{{\Lambda }_{\Sigma }}}}}}$ are represented as MG and NMG. Further, various valuable applications have been explored by scholars in distance measures [6], aggregation operators [7], COVID-19 problems [8], enhancement algorithms [9], support vector machines [10], dynamic perspective [11], and soft set [12] described based on IFSs.

The FSs and IFSs are the essential parts for describing fuzzy information, and they have been used in different fields such as game theory, artificial intelligence, neural networks, road signals, and machine learning. Although The FSs and IFSs are very valuable and dominant techniques, they also contained some limitations. Further, Ramot et al. [13] proposed the complex FS (CFS) which is described as $\overline{\overline{{\mathbb{m}}_{\overline{\overline{{\Lambda }_{\Sigma }}}}}}\left(\widetilde{{\fancyscript{z}}_{\mathfrak{a}}}\right)=\overline{\overline{{\mathbb{m}}_{\overline{\overline{\fancyscript{r}}}}}}\left(\widetilde{{\fancyscript{z}}_{\mathfrak{a}}}\right){e}^{i2\pi \left(\overline{\overline{{\mathbb{m}}_{\overline{\overline{\mathfrak{k}}}}}}\left(\widetilde{{\fancyscript{z}}_{\mathfrak{a}}}\right)\right)}$, $\overline{\overline{{\mathbb{m}}_{\overline{\overline{\fancyscript{r}}}}}},\overline{\overline{{\mathbb{m}}_{\overline{\overline{\mathfrak{k}}}}}}:\widetilde{{\mathbb{Z}}_{U}}\to \left[\mathrm{0,1}\right]$, and $\overline{\overline{{\mathbb{m}}_{\overline{\overline{\fancyscript{r}}}}}}\left(\widetilde{{\fancyscript{z}}_{\mathfrak{a}}}\right),\overline{\overline{{\mathbb{m}}_{\overline{\overline{\mathfrak{k}}}}}}\left(\widetilde{{\fancyscript{z}}_{\mathfrak{a}}}\right)\in \left[0, 1\right]$, $\overline{\overline{{\mathbb{m}}_{\overline{\overline{\fancyscript{r}}}}}}\left(\widetilde{{\fancyscript{z}}_{\mathfrak{a}}}\right),\overline{\overline{{\mathbb{m}}_{\overline{\overline{\mathfrak{k}}}}}}\left(\widetilde{{\fancyscript{z}}_{\mathfrak{a}}}\right)$ are represented as a complex-valued MG (CVMG). Further, various valuable applications have been developed by scholars in entropy measures [14], complex fuzzy N-soft sets [15], complex multi-fuzzy sets [16], and decision-making methods [17]. Furthermore, Alkouri and Salleh [18] proposed complex IFS (COIFS), which is the general of FSs, IFSs, and CFSs to manage various real-life dilemmas. COIFS contained two main functions, which are stated as $\overline{\overline{{\mathbb{m}}_{\overline{\overline{{\Lambda }_{\Sigma }}}}}}\left(\widetilde{{\fancyscript{z}}_{\mathfrak{a}}}\right)=\overline{\overline{{\mathbb{m}}_{\overline{\overline{\fancyscript{r}}}}}}\left(\widetilde{{\fancyscript{z}}_{\mathfrak{a}}}\right){e}^{i2\pi \left(\overline{\overline{{\mathbb{m}}_{\overline{\overline{\mathfrak{k}}}}}}\left(\widetilde{{\fancyscript{z}}_{\mathfrak{a}}}\right)\right)}$, $\overline{\overline{{\mathbb{m}}_{\overline{\overline{\fancyscript{r}}}}}},\overline{\overline{{\mathbb{m}}_{\overline{\overline{\mathfrak{k}}}}}}:\widetilde{{\mathbb{Z}}_{U}}\to \left[\mathrm{0,1}\right]$ and $\overline{\overline{{\mathbb{y}}_{\overline{\overline{{\Lambda }_{\Sigma }}}}}}\left(\widetilde{{\fancyscript{z}}_{\mathfrak{a}}}\right)=\overline{\overline{{\mathbb{y}}_{\overline{\overline{\fancyscript{r}}}}}}\left(\widetilde{{\fancyscript{z}}_{\mathfrak{a}}}\right){e}^{i2\pi \left(\overline{\overline{{\mathbb{y}}_{\overline{\overline{\mathfrak{k}}}}}}\left(\widetilde{{\fancyscript{z}}_{\mathfrak{a}}}\right)\right)}$, $\overline{\overline{{\mathbb{y}}_{\overline{\overline{\fancyscript{r}}}}}},\overline{\overline{{\mathbb{y}}_{\overline{\overline{\mathfrak{k}}}}}}:\widetilde{{\mathbb{Z}}_{U}}\to \left[\mathrm{0,1}\right]$, where the $\overline{\overline{{\mathbb{m}}_{\overline{\overline{\fancyscript{r}}}}}}\left(\widetilde{{\fancyscript{z}}_{\mathfrak{a}}}\right)+\overline{\overline{{\mathbb{y}}_{\overline{\overline{\fancyscript{r}}}}}}\left(\widetilde{{\fancyscript{z}}_{\mathfrak{a}}}\right),\overline{\overline{{\mathbb{m}}_{\overline{\overline{\mathfrak{k}}}}}}\left(\widetilde{{\fancyscript{z}}_{\mathfrak{a}}}\right)+\overline{\overline{{\mathbb{y}}_{\overline{\overline{\mathfrak{k}}}}}}\left(\widetilde{{\fancyscript{z}}_{\mathfrak{a}}}\right)\in \left[0, 1\right]$ are represented as a CVMG and complex-valued NMG (CVNMG). Noticed that the functions included in the COIFS are the modified version of FSs, IFSs, and CFSs. Various valuable applications have been developed by scholars, for instance, prioritized aggregation operators [19], decision-making [20, 21], and averaging/geometric aggregation operators [22, 23].

Different types of t-norms were extended by scholars and a lot of aggregation operators based on these all-existing norms are also developed. Among the different t-norms, the AA t-norm and t-conorm were proposed by Aczel and Alsina [24] in 1980, which are very modified and more general than the existing t-norms based on parameter $0<p<+\infty$. Furthermore, Pamucar et al. [25] proposed the ordinary priority approach and AA norms. However, all these norms were developed based on classical information, further, Senapati et al. [26] first developed the aggregation operators based on AA t-norms using hesitant FSs. Senapati et al. [27] again developed the aggregation operators based on AA t-norms for IFSs. Similarly, Yu and Xu [28] proposed the prioritized aggregation operators based on IFSs. Arora and Garg [29] developed the prioritized averaging/geometric aggregation operators for IFSs with soft sets and described their application in decision-making.

After a brief discussion, we noticed that the COIF information covered the pair of truth and falsity grades in the form of complex-valued information. Furthermore, the amplitude information and phase grade of the truth (falsity grade) indicated the extent of supporting (supporting against) and given additional information (in general we relate it with periodic function) of the term in a COIF value. The major difference is a phase term between COIF values and simple IFSs because the IFS copes with only one-dimensional data but the COIF information deals with two-dimensional data at a time which is more accurate and effective than the prevailing IFSs. In our many real-life scenarios, decision-makers have faced two-dimensional data in a lot of places, whereby including the second dimensional data, the complete data can be projected in one valued set and the issue of loss of data can be secured. Furthermore, to demonstrate the significance or importance of the phase or periodic term, we simplify it with the help of some suitable examples, for instance, a well-known university decided to install new software for processing the university's important data. For this, the president and the committee of the university meet with the supervisor of the company for looking at different types of software, where the supervisor of the company gives the following information concerning each software, (i) Distinct alternatives of software and (ii) distinct version of each software. The university members select the finest one and the latest one from all of them. Here, the complexity of two-dimensional data, namely, choosing the finest and latest software, this kind of problem cannot be evaluated in the presence of the simple or traditional IFSs. So, the finest and most valuable way to evaluate the above type of problem, we needed to use the COIF information, because it covered the truth and falsity of information in the form of the complex number, where the real part expressed the name, and the imaginary part represented the version of the software.

Moreover, the Aczel-Alsina (AA) t-norms are more general than the algebraic t-norms, because we can easily obtain the existing ones using the different parameter involved in the AA t-norms. Additionally, the COIFS is the generalization of the FSs, IFSs, and CFSs, at the same time, prioritized aggregation operators can consider the priority degree among the attributes. Therefore, kee** the dominancy and feasibility of the COIF set and taking the importance and reliability of the aggregation operators, prioritized information, and Aczel-Alsina t-norms, the major goal of this paper is to develop some novel aggregation operators based on the AA t-norm and t-conorm considering priority degree among the attributes with the decision information of COIFNs. The advantages of the proposed operators are listed below:

• (1) When $\overline{\overline{{\mathbb{m}}_{\overline{\overline{\mathfrak{k}}}}}}\left({\widetilde{{\fancyscript{z}}}_{\mathfrak{a}}}\right)=\overline{\overline{{\mathbb{y}}_{\overline{\overline{\mathfrak{k}}}}}}\left({\widetilde{{\fancyscript{z}}}_{\mathfrak{a}}}\right)=0$, we can obtain the Aczel-Alsina prioritized aggregation operators for IFSs (a special case of the proposed technique).

• (2) When $\overline{\overline{{\mathbb{y}}_{\overline{\overline{\mathfrak{k}}}}}}\left({\widetilde{{\fancyscript{z}}}_{\mathfrak{a}}}\right)=\overline{\overline{{\mathbb{y}}_{\overline{\overline{\fancyscript{r}}}}}}\left({\widetilde{{\fancyscript{z}}}_{\mathfrak{a}}}\right)=0$, we can obtain the Aczel-Alsina prioritized aggregation operators for CFSs (a special case of the proposed technique).

• (3) When $\overline{\overline{{\mathbb{y}}_{\overline{\overline{\mathfrak{k}}}}}}\left({\widetilde{{\fancyscript{z}}}_{\mathfrak{a}}}\right)=\overline{\overline{{\mathbb{m}}_{\overline{\overline{\mathfrak{k}}}}}}\left({\widetilde{{\fancyscript{z}}}_{\mathfrak{a}}}\right)=\overline{\overline{{\mathbb{y}}_{\overline{\overline{\fancyscript{r}}}}}}\left({\widetilde{{\fancyscript{z}}}_{\mathfrak{a}}}\right)=0$, we can obtain the Aczel-Alsina prioritized aggregation operators for FSs (a special case of the proposed technique).

• (4) Prioritized aggregation operators for FSs, IFSs, CFSs, and COIFSs are the special case of the proposed operators.

• (5) Aczel-Alsina aggregation operators for FSs, IFSs, CFSs, and COIFSs are the special case of the proposed operators.

• (6) Averaging aggregation operators for FSs, IFSs, CFSs, and COIFSs are a special case of the proposed operators.

• (7) Geometric aggregation operators for FSs, IFSs, CFSs, and COIFSs are a special case of the proposed operators.

Inspired by the above analysis, we concentrate to derive the following main contents which are shown as follows:

• (1) To develop some operational laws for COIFNs based on AA t-norm and t-conorm.

• (2) To develop the COIFAAPWA operator and COIFAAPOWA operator.

• (3) To develop the COIFAAPWG operator and COIFAAPOWG operator.

• (4) To discuss their valuable properties and some important results.

• (5) To develop a MADM method with the decision information of COIFNs.

• (6) To compare the developed operators with some existing operators for showing the flexibility of the proposed approach by some application examples.

The main construct of this article is shown as In Sect. 2, we address some basic concepts, called the COIFS and their algebraic and Aczel-Alsina operational laws. In Sect. 3, we develop the COIFAAPWA, COIFAPOWA, COIFAAPWG, and COIFAAPOWG, and explain their basic properties. We also analyze their special cases. In Sect. 4, we propose a MADM method with COIF information based on obtained operators, then we give some examples to show the decision steps and the superiority of the proposed approach. In Sect. 5, we compare the developed operators with some existing operators by illustrating examples and showing the flexibility of the derived approaches. Final and valuable remarks are listed in Sect. 6.

2 Preliminaries

In this section, we give some basic knowledge about COIFS and their algebraic and Aczel-Alsina operational laws, where the term $\widetilde{{\mathbb{Z}}_{U}}$ is used as a fixed set. The COIFS is the generalization of FSs, IFSs, and CFSs to process various real-life dilemmas. COIFS contained two main functions, which are stated as $\overline{\overline{{\mathbb{m}}_{\overline{\overline{{\Lambda }_{\Sigma }}}}}}\left({\widetilde{{\fancyscript{z}}}_{\mathfrak{a}}}\right)=\overline{\overline{{\mathbb{m}}_{\overline{\overline{\fancyscript{r}}}}}}\left({\widetilde{{\fancyscript{z}}}_{\mathfrak{a}}}\right){e}^{i2\pi \left(\overline{\overline{{\mathbb{m}}_{\overline{\overline{\mathfrak{k}}}}}}\left({\widetilde{{\fancyscript{z}}}_{\mathfrak{a}}}\right)\right)}$, $\overline{\overline{{\mathbb{m}}_{\overline{\overline{\fancyscript{r}}}}}},\overline{\overline{{\mathbb{m}}_{\overline{\overline{\mathfrak{k}}}}}}:\widetilde{{\mathbb{Z}}_{U}}\to \left[\mathrm{0,1}\right]$ and $\overline{\overline{{\mathbb{y}}_{\overline{\overline{{\Lambda }_{\Sigma }}}}}}\left({\widetilde{{\fancyscript{z}}}_{\mathfrak{a}}}\right)=\overline{\overline{{\mathbb{y}}_{\overline{\overline{\fancyscript{r}}}}}}\left({\widetilde{{\fancyscript{z}}}_{\mathfrak{a}}}\right){e}^{i2\pi \left(\overline{\overline{{\mathbb{y}}_{\overline{\overline{\mathfrak{k}}}}}}\left({\widetilde{{\fancyscript{z}}}_{\mathfrak{a}}}\right)\right)}$, $\overline{\overline{{\mathbb{y}}_{\overline{\overline{\fancyscript{r}}}}}},\overline{\overline{{\mathbb{y}}_{\overline{\overline{\mathfrak{k}}}}}}:\widetilde{{\mathbb{Z}}_{U}}\to \left[\mathrm{0,1}\right]$, where the $\overline{\overline{{\mathbb{m}}_{\overline{\overline{\fancyscript{r}}}}}}\left({\widetilde{{\fancyscript{z}}}_{\mathfrak{a}}}\right)+\overline{\overline{{\mathbb{y}}_{\overline{\overline{\fancyscript{r}}}}}}\left({\widetilde{{\fancyscript{z}}}_{\mathfrak{a}}}\right),\overline{\overline{{\mathbb{m}}_{\overline{\overline{\mathfrak{k}}}}}}\left({\widetilde{{\fancyscript{z}}}_{\mathfrak{a}}}\right)+\overline{\overline{{\mathbb{y}}_{\overline{\overline{\mathfrak{k}}}}}}\left({\widetilde{{\fancyscript{z}}}_{\mathfrak{a}}}\right)\in \left[0, 1\right]$ are represented as a CVMG and complex-valued NMG (CVNMG). Noticed that the functions included in the COIFS are the modified version of FSs, IFSs, and CFSs. The COIFS is defined below.

Definition 1

[18] The COIFS $\overline{\overline{{\Lambda }_{\Sigma }}}$ is described as

$$\overline{\overline{{\Lambda }_{\Sigma }}}=\left\{\left(\overline{\overline{{\mathbb{m}}_{\overline{\overline{{\Lambda }_{\Sigma }}}}}}\left({\widetilde{{\fancyscript{z}}}_{\mathfrak{a}}}\right),\overline{\overline{{\mathbb{y}}_{\overline{\overline{{\Lambda }_{\Sigma }}}}}}\left({\widetilde{{\fancyscript{z}}}_{\mathfrak{a}}}\right)\right):{\widetilde{{\fancyscript{z}}}_{\mathfrak{a}}}\in \widetilde{{\mathbb{Z}}_{U}}\right\}$$

(1)

the term $\overline{\overline{{\mathbb{m}}_{\overline{\overline{{\Lambda }_{\Sigma }}}}}}\left({\widetilde{{\fancyscript{z}}}_{\mathfrak{a}}}\right)=\overline{\overline{{\mathbb{m}}_{\overline{\overline{\fancyscript{r}}}}}}\left({\widetilde{{\fancyscript{z}}}_{\mathfrak{a}}}\right){e}^{i2\pi \left(\overline{\overline{{\mathbb{m}}_{\overline{\overline{\mathfrak{k}}}}}}\left({\widetilde{{\fancyscript{z}}}_{\mathfrak{a}}}\right)\right)}$ and the term $\overline{\overline{{\mathbb{y}}_{\overline{\overline{{\Lambda }_{\Sigma }}}}}}\left({\widetilde{{\fancyscript{z}}}_{\mathfrak{a}}}\right)=\overline{\overline{{\mathbb{y}}_{\overline{\overline{\fancyscript{r}}}}}}\left({\widetilde{{\fancyscript{z}}}_{\mathfrak{a}}}\right){e}^{i2\pi \left(\overline{\overline{{\mathbb{y}}_{\overline{\overline{\mathfrak{k}}}}}}\left({\widetilde{{\fancyscript{z}}}_{\mathfrak{a}}}\right)\right)}$ are used as supporting and supporting-against with a condition: $0\le \overline{\overline{{\mathbb{m}}_{\overline{\overline{\fancyscript{r}}}}}}\left({\widetilde{{\fancyscript{z}}}_{\mathfrak{a}}}\right)+\overline{\overline{{\mathbb{y}}_{\overline{\overline{\fancyscript{r}}}}}}\left({\widetilde{{\fancyscript{z}}}_{\mathfrak{a}}}\right)\le 1$ and $0\le \overline{\overline{{\mathbb{m}}_{\overline{\overline{\mathfrak{k}}}}}}\left({\widetilde{{\fancyscript{z}}}_{\mathfrak{a}}}\right)+\overline{\overline{{\mathbb{y}}_{\overline{\overline{\mathfrak{k}}}}}}\left({\widetilde{{\fancyscript{z}}}_{\mathfrak{a}}}\right)\le 1$, where $\overline{\overline{{\mathfrak{R}}_{\overline{\overline{{\Lambda }_{\Sigma }}}}}}\left({\widetilde{{\fancyscript{z}}}_{\mathfrak{a}}}\right)=\overline{\overline{{\mathfrak{R}}_{\overline{\overline{\fancyscript{r}}}}}}\left({\widetilde{{\fancyscript{z}}}_{\mathfrak{a}}}\right){e}^{i2\pi \left(\overline{\overline{{\mathfrak{R}}_{\overline{\overline{\mathfrak{k}}}}}}\left({\widetilde{{\fancyscript{z}}}_{\mathfrak{a}}}\right)\right)}=\left(1-\left(\overline{\overline{{\mathbb{m}}_{\overline{\overline{\fancyscript{r}}}}}}\left({\widetilde{{\fancyscript{z}}}_{\mathfrak{a}}}\right)+\overline{\overline{{\mathbb{y}}_{\overline{\overline{\fancyscript{r}}}}}}\left({\widetilde{{\fancyscript{z}}}_{\mathfrak{a}}}\right)\right)\right){e}^{i2\pi \left(1-\left(\overline{\overline{{\mathbb{m}}_{\overline{\overline{\mathfrak{k}}}}}}\left({\widetilde{{\fancyscript{z}}}_{\mathfrak{a}}}\right)+\overline{\overline{{\mathbb{y}}_{\overline{\overline{\mathfrak{k}}}}}}\left({\widetilde{{\fancyscript{z}}}_{\mathfrak{a}}}\right)\right)\right)}$ is used as a refusal grade. Finally, the COIF number (COIFN) is defined by: $\overline{\overline{{\Lambda }_{{\Sigma }_{j}}}}=\left(\overline{\overline{{\mathbb{m}}_{\overline{\overline{{\fancyscript{r}}_{j}}}}}}{e}^{i2\pi \left(\overline{\overline{{\mathbb{m}}_{\overline{\overline{{\mathfrak{k}}_{j}}}}}}\right)},\overline{\overline{{\mathbb{y}}_{\overline{\overline{{\fancyscript{r}}_{j}}}}}}{e}^{i2\pi \left(\overline{\overline{{\mathbb{y}}_{\overline{\overline{{\mathfrak{k}}_{j}}}}}}\right)}\right),j=\mathrm{1,2},\dots ,n$. Moreover, for develo** the any kind of aggregation operators, we need some valuable operational laws, therefore, here we discuss or revise the algebraic operational laws for COIFNs.

Definition 2

[18] there are two COIFNs $\overline{\overline{{\Lambda }_{{\Sigma }_{j}}}}=\left(\overline{\overline{{\mathbb{m}}_{\overline{\overline{{\fancyscript{r}}_{j}}}}}}{e}^{i2\pi \left(\overline{\overline{{\mathbb{m}}_{\overline{\overline{{\mathfrak{k}}_{j}}}}}}\right)},\overline{\overline{{\mathbb{y}}_{\overline{\overline{{\fancyscript{r}}_{j}}}}}}{e}^{i2\pi \left(\overline{\overline{{\mathbb{y}}_{\overline{\overline{{\mathfrak{k}}_{j}}}}}}\right)}\right),j=\mathrm{1,2}$, and $\overline{\overline{{\varpi }_{S}}}$ is a positive real number, then

$$\overline{\overline{{\Lambda }_{{\Sigma }_{1}}}}\oplus \overline{\overline{{\Lambda }_{{\Sigma }_{2}}}}=\left(\overline{\overline{{\mathbb{m}}_{\overline{\overline{{\fancyscript{r}}_{1}}}}}}+\overline{\overline{{\mathbb{m}}_{\overline{\overline{{\fancyscript{r}}_{2}}}}}}-\overline{\overline{{\mathbb{m}}_{\overline{\overline{{\fancyscript{r}}_{1}}}}}}\overline{\overline{{\mathbb{m}}_{\overline{\overline{{\fancyscript{r}}_{2}}}}}}{e}^{i2\pi \left(\overline{\overline{{\mathbb{m}}_{\overline{\overline{{\mathfrak{k}}_{1}}}}}}+\overline{\overline{{\mathbb{m}}_{\overline{\overline{{\mathfrak{k}}_{2}}}}}}-\overline{\overline{{\mathbb{m}}_{\overline{\overline{{\mathfrak{k}}_{1}}}}}}\overline{\overline{{\mathbb{m}}_{\overline{\overline{{\mathfrak{k}}_{2}}}}}}\right)},\left(\overline{\overline{{\mathbb{y}}_{\overline{\overline{{\fancyscript{r}}_{1}}}}}}\overline{\overline{{\mathbb{y}}_{\overline{\overline{{\fancyscript{r}}_{2}}}}}}\right){e}^{i2\pi \left(\overline{\overline{{\mathbb{y}}_{\overline{\overline{{\mathfrak{k}}_{1}}}}}}\overline{\overline{{\mathbb{y}}_{\overline{\overline{{\mathfrak{k}}_{2}}}}}}\right)}\right)$$

(2)

$$\overline{\overline{{\Lambda }_{{\Sigma }_{1}}}}\otimes \overline{\overline{{\Lambda }_{{\Sigma }_{2}}}}=\left(\left(\overline{\overline{{\mathbb{m}}_{\overline{\overline{{\fancyscript{r}}_{1}}}}}}\overline{\overline{{\mathbb{m}}_{\overline{\overline{{\fancyscript{r}}_{2}}}}}}\right){e}^{i2\pi \left(\overline{\overline{{\mathbb{m}}_{\overline{\overline{{\mathfrak{k}}_{1}}}}}}\overline{\overline{{\mathbb{m}}_{\overline{\overline{{\mathfrak{k}}_{2}}}}}}\right)},\overline{\overline{{\mathbb{y}}_{\overline{\overline{{\fancyscript{r}}_{1}}}}}}+\overline{\overline{{\mathbb{y}}_{\overline{\overline{{\fancyscript{r}}_{2}}}}}}-\overline{\overline{{\mathbb{y}}_{\overline{\overline{{\fancyscript{r}}_{1}}}}}}\overline{\overline{{\mathbb{y}}_{\overline{\overline{{\fancyscript{r}}_{2}}}}}}{e}^{i2\pi \left(\overline{\overline{{\mathbb{y}}_{\overline{\overline{{\mathfrak{k}}_{1}}}}}}+\overline{\overline{{\mathbb{y}}_{\overline{\overline{{\mathfrak{k}}_{2}}}}}}-\overline{\overline{{\mathbb{y}}_{\overline{\overline{{\mathfrak{k}}_{1}}}}}}\overline{\overline{{\mathbb{y}}_{\overline{\overline{{\mathfrak{k}}_{2}}}}}}\right)}\right)$$

(3)

$$\overline{\overline{{\varpi }_{S}}}\overline{\overline{{\Lambda }_{{\Sigma }_{1}}}}=\left(\left(1-{\left(1-\overline{\overline{{\mathbb{m}}_{\overline{\overline{{\fancyscript{r}}_{1}}}}}}\right)}^{\overline{\overline{{\varpi }_{S}}}}\right){e}^{i2\pi \left(1-{\left(1-\overline{\overline{{\mathbb{m}}_{\overline{\overline{{\mathfrak{k}}_{1}}}}}}\right)}^{\overline{\overline{{\varpi }_{S}}}}\right)},{\overline{\overline{{\mathbb{y}}_{\overline{\overline{{\fancyscript{r}}_{1}}}}}}}^{\overline{\overline{{\varpi }_{S}}}}{e}^{i2\pi \left({\overline{\overline{{\mathbb{y}}_{\overline{\overline{{\mathfrak{k}}_{1}}}}}}}^{\overline{\overline{{\varpi }_{S}}}}\right)}\right)$$

(4)

$${\overline{\overline{{\Lambda }_{{\Sigma }_{1}}}}}^{\overline{\overline{{\varpi }_{S}}}}=\left({\overline{\overline{{\mathbb{m}}_{\overline{\overline{{\fancyscript{r}}_{1}}}}}}}^{\overline{\overline{{\varpi }_{S}}}}{e}^{i2\pi \left({\overline{\overline{{\mathbb{m}}_{\overline{\overline{{\mathfrak{k}}_{1}}}}}}}^{\overline{\overline{{\varpi }_{S}}}}\right)},\left(1-{\left(1-\overline{\overline{{\mathbb{y}}_{\overline{\overline{{\fancyscript{r}}_{1}}}}}}\right)}^{\overline{\overline{{\varpi }_{S}}}}\right){e}^{i2\pi \left(1-{\left(1-\overline{\overline{{\mathbb{y}}_{\overline{\overline{{\mathfrak{k}}_{1}}}}}}\right)}^{\overline{\overline{{\varpi }_{S}}}}\right)}\right)$$

(5)

To further compare with the COIFNs, we need to define the score values and accuracy values, because they can help us to convert the COIFN into a real number, and in a real number, we can easily take a decision about which number is finest, and which one is not.

Definition 3

[18] the score and accuracy functions of COIFN $\overline{\overline{{\Lambda }_{{\Sigma }_{1}}}}=\left(\overline{\overline{{\mathbb{m}}_{\overline{\overline{{\fancyscript{r}}_{1}}}}}}{e}^{i2\pi \left(\overline{\overline{{\mathbb{m}}_{\overline{\overline{{\mathfrak{k}}_{1}}}}}}\right)},\overline{\overline{{\mathbb{y}}_{\overline{\overline{{\fancyscript{r}}_{1}}}}}}{e}^{i2\pi \left(\overline{\overline{{\mathbb{y}}_{\overline{\overline{{\mathfrak{k}}_{1}}}}}}\right)}\right),j=\mathrm{1,2}$, are defined as

$$\overline{\overline{{\mathcal{S}}_{SV}}}\left(\overline{\overline{{\Lambda }_{{\Sigma }_{1}}}}\right)=\frac{1}{2}\left(\overline{\overline{{\mathbb{m}}_{\overline{\overline{{\fancyscript{r}}_{1}}}}}}+\overline{\overline{{\mathbb{m}}_{\overline{\overline{{\mathfrak{k}}_{1}}}}}}-\overline{\overline{{\mathbb{y}}_{\overline{\overline{{\fancyscript{r}}_{1}}}}}}-\overline{\overline{{\mathbb{y}}_{\overline{\overline{{\mathfrak{k}}_{1}}}}}}\right),\overline{\overline{{\mathcal{S}}_{SV}}}\left(\overline{\overline{{\Lambda }_{{\Sigma }_{1}}}}\right)\in \left[-\mathrm{1,1}\right]$$

(6)

$$\overline{\overline{{\mathcal{H}}_{AV}}}\left(\overline{\overline{{\Lambda }_{{\Sigma }_{1}}}}\right)=\frac{1}{2}\left(\overline{\overline{{\mathbb{m}}_{\overline{\overline{{\fancyscript{r}}_{1}}}}}}+\overline{\overline{{\mathbb{m}}_{\overline{\overline{{\mathfrak{k}}_{1}}}}}}\_+\overline{\overline{{\mathbb{y}}_{\overline{\overline{{\fancyscript{r}}_{1}}}}}}+\overline{\overline{{\mathbb{y}}_{\overline{\overline{{\mathfrak{k}}_{1}}}}}}\right),\overline{\overline{{\mathcal{H}}_{AV}}}\left(\overline{\overline{{\Lambda }_{{\Sigma }_{1}}}}\right)\in \left[\mathrm{0,1}\right]$$

(7)

Then we have

• (1) If $\overline{\overline{{\mathcal{S}}_{SV}}}\left(\overline{\overline{{\Lambda }_{{\Sigma }_{1}}}}\right)>\overline{\overline{{\mathcal{S}}_{SV}}}\left(\overline{\overline{{\Lambda }_{{\Sigma }_{2}}}}\right)\Rightarrow \overline{\overline{{\Lambda }_{{\Sigma }_{1}}}}>\overline{\overline{{\Lambda }_{{\Sigma }_{2}}}}$.

• (2) If $\overline{\overline{{\mathcal{S}}_{SV}}}\left(\overline{\overline{{\Lambda }_{{\Sigma }_{1}}}}\right)<\overline{\overline{{\mathcal{S}}_{SV}}}\left(\overline{\overline{{\Lambda }_{{\Sigma }_{2}}}}\right)\Rightarrow \overline{\overline{{\Lambda }_{{\Sigma }_{1}}}}<\overline{\overline{{\Lambda }_{{\Sigma }_{2}}}}$.

• (3) If $\overline{\overline{{\mathcal{S}}_{SV}}}\left(\overline{\overline{{\Lambda }_{{\Sigma }_{1}}}}\right)=\overline{\overline{{\mathcal{S}}_{SV}}}\left(\overline{\overline{{\Lambda }_{{\Sigma }_{2}}}}\right)$, then

  • (i) If $\overline{\overline{{\mathcal{H}}_{AV}}}\left(\overline{\overline{{\Lambda }_{{\Sigma }_{1}}}}\right)>\overline{\overline{{\mathcal{H}}_{AV}}}\left(\overline{\overline{{\Lambda }_{{\Sigma }_{2}}}}\right)\Rightarrow \overline{\overline{{\Lambda }_{{\Sigma }_{1}}}}>\overline{\overline{{\Lambda }_{{\Sigma }_{2}}}}$.

  • (ii) If $\overline{\overline{{\mathcal{H}}_{AV}}}\left(\overline{\overline{{\Lambda }_{{\Sigma }_{1}}}}\right)<\overline{\overline{{\mathcal{H}}_{AV}}}\left(\overline{\overline{{\Lambda }_{{\Sigma }_{2}}}}\right)\Rightarrow \overline{\overline{{\Lambda }_{{\Sigma }_{1}}}}<\overline{\overline{{\Lambda }_{{\Sigma }_{2}}}}$.

  • (iii) If $\overline{\overline{{\mathcal{H}}_{AV}}}\left(\overline{\overline{{\Lambda }_{{\Sigma }_{1}}}}\right)=\overline{\overline{{\mathcal{H}}_{AV}}}\left(\overline{\overline{{\Lambda }_{{\Sigma }_{2}}}}\right)\Rightarrow \overline{\overline{{\Lambda }_{{\Sigma }_{1}}}}=\overline{\overline{{\Lambda }_{{\Sigma }_{2}}}}$.

It is also clear that the algebraic operational laws are very famous and helpful for accommodating or constructing any kind of operators. But we noticed that the Aczel-Alsina operational laws are the superior or general form of the algebraic operational laws because of parameter $\infty \ge \varpi \ge 0$, whereby using the value of $\varpi =1$, then we can easily derive the Eqs. (2, 3, 4, 5). Moreover, the Aczel-Alsina operational laws for COIFNs are defined below.

Definition 4

The Aczel-Alsina operational laws of two COIFNs $\overline{\overline{{\Lambda }_{{\Sigma }_{j}}}}=\left(\overline{\overline{{\mathbb{m}}_{\overline{\overline{{\fancyscript{r}}_{j}}}}}}{e}^{i2\pi \left(\overline{\overline{{\mathbb{m}}_{\overline{\overline{{\mathfrak{k}}_{j}}}}}}\right)},\overline{\overline{{\mathbb{y}}_{\overline{\overline{{\fancyscript{r}}_{j}}}}}}{e}^{i2\pi \left(\overline{\overline{{\mathbb{y}}_{\overline{\overline{{\mathfrak{k}}_{j}}}}}}\right)}\right),j=\mathrm{1,2}$, are defined as ($\overline{\overline{{\theta }_{S}}}$ is a positive real number)

$$\overline{\overline{{\Lambda }_{{\Sigma }_{1}}}}\oplus \overline{\overline{{\Lambda }_{{\Sigma }_{2}}}}=\left(\begin{array}{c}\left(1-{e}^{-{\left({\left(-\mathrm{LoG}\left(1-\overline{\overline{{\mathbb{m}}_{\overline{\overline{{\fancyscript{r}}_{1}}}}}}\right)\right)}^{\varpi }+{\left(-\mathrm{LoG}\left(1-\overline{\overline{{\mathbb{m}}_{\overline{\overline{{\fancyscript{r}}_{2}}}}}}\right)\right)}^{\varpi }\right)}^{\frac{1}{\varpi }}}\right){e}^{i2\pi \left(1-{e}^{-{\left({\left(-\mathrm{LoG}\left(1-\overline{\overline{{\mathbb{m}}_{\overline{\overline{{\fancyscript{r}}_{1}}}}}}\right)\right)}^{\varpi }+{\left(-\mathrm{LoG}\left(1-\overline{\overline{{\mathbb{m}}_{\overline{\overline{{\fancyscript{r}}_{2}}}}}}\right)\right)}^{\varpi }\right)}^{\frac{1}{\varpi }}}\right)},\\ \left({e}^{-{\left({\left(-\mathrm{LoG}\left(\overline{\overline{{\mathbb{y}}_{\overline{\overline{{\fancyscript{r}}_{1}}}}}}\right)\right)}^{\varpi }+{\left(-\mathrm{LoG}\left(\overline{\overline{{\mathbb{y}}_{\overline{\overline{{\fancyscript{r}}_{2}}}}}}\right)\right)}^{\varpi }\right)}^{\frac{1}{\varpi }}}\right){e}^{i2\pi \left({e}^{-{\left({\left(-\mathrm{LoG}\left(\overline{\overline{{\mathbb{y}}_{\overline{\overline{{\mathfrak{k}}_{1}}}}}}\right)\right)}^{\varpi }+{\left(-\mathrm{LoG}\left(\overline{\overline{{\mathbb{y}}_{\overline{\overline{{\mathfrak{k}}_{2}}}}}}\right)\right)}^{\varpi }\right)}^{\frac{1}{\varpi }}}\right)}\end{array}\right)$$

(8)

$$\overline{\overline{{\Lambda }_{{\Sigma }_{1}}}}\otimes \overline{\overline{{\Lambda }_{{\Sigma }_{2}}}}=\left(\begin{array}{c}\left({e}^{-{\left({\left(-\mathrm{LoG}\left(\overline{\overline{{\mathbb{m}}_{\overline{\overline{{\fancyscript{r}}_{1}}}}}}\right)\right)}^{\varpi }+{\left(-\mathrm{LoG}\left(\overline{\overline{{\mathbb{m}}_{\overline{\overline{{\fancyscript{r}}_{2}}}}}}\right)\right)}^{\varpi }\right)}^{\frac{1}{\varpi }}}\right){e}^{i2\pi \left({e}^{-{\left({\left(-\mathrm{LoG}\left(\overline{\overline{{\mathbb{m}}_{\overline{\overline{{\mathfrak{k}}_{1}}}}}}\right)\right)}^{\varpi }+{\left(-\mathrm{LoG}\left(\overline{\overline{{\mathbb{m}}_{\overline{\overline{{\mathfrak{k}}_{2}}}}}}\right)\right)}^{\varpi }\right)}^{\frac{1}{\varpi }}}\right)},\\ \left(1-{e}^{-{\left({\left(-\mathrm{LoG}\left(1-\overline{\overline{{\mathbb{y}}_{\overline{\overline{{\fancyscript{r}}_{1}}}}}}\right)\right)}^{\varpi }+{\left(-\mathrm{LoG}\left(1-\overline{\overline{{\mathbb{y}}_{\overline{\overline{{\fancyscript{r}}_{2}}}}}}\right)\right)}^{\varpi }\right)}^{\frac{1}{\varpi }}}\right){e}^{i2\pi \left(1-{e}^{-{\left({\left(-\mathrm{LoG}\left(1-\overline{\overline{{\mathbb{y}}_{\overline{\overline{{\fancyscript{r}}_{1}}}}}}\right)\right)}^{\varpi }+{\left(-\mathrm{LoG}\left(1-\overline{\overline{{\mathbb{y}}_{\overline{\overline{{\fancyscript{r}}_{2}}}}}}\right)\right)}^{\varpi }\right)}^{\frac{1}{\varpi }}}\right)}\end{array}\right)$$

(9)

$$\overline{\overline{{\theta }_{S}}}\overline{\overline{{\Lambda }_{{\Sigma }_{1}}}}=\left(\begin{array}{c}\left(1-{e}^{-{\left(\overline{\overline{{\theta }_{S}}}{\left(-\mathrm{LoG}\left(1-\overline{\overline{{\mathbb{m}}_{\overline{\overline{{\fancyscript{r}}_{1}}}}}}\right)\right)}^{\varpi }\right)}^{\frac{1}{\varpi }}}\right){e}^{i2\pi \left(1-{e}^{-{\left(\overline{\overline{{\theta }_{S}}}{\left(-\mathrm{LoG}\left(1-\overline{\overline{{\mathbb{m}}_{\overline{\overline{{\mathfrak{k}}_{1}}}}}}\right)\right)}^{\varpi }\right)}^{\frac{1}{\varpi }}}\right)},\\ \left({e}^{-{\left(\overline{\overline{{\theta }_{S}}}{\left(-\mathrm{LoG}\left(\overline{\overline{{\mathbb{y}}_{\overline{\overline{{\fancyscript{r}}_{1}}}}}}\right)\right)}^{\varpi }\right)}^{\frac{1}{\varpi }}}\right){e}^{i2\pi \left({e}^{-{\left(\overline{\overline{{\theta }_{S}}}{\left(-\mathrm{LoG}\left(\overline{\overline{{\mathbb{y}}_{\overline{\overline{{\mathfrak{k}}_{1}}}}}}\right)\right)}^{\varpi }\right)}^{\frac{1}{\varpi }}}\right)}\end{array}\right)$$

(10)

$${\overline{\overline{{\Lambda }_{{\Sigma }_{1}}}}}^{\overline{\overline{{\theta }_{S}}}}=\left(\begin{array}{c}\left({e}^{-{\left(\overline{\overline{{\theta }_{S}}}{\left(-\mathrm{LoG}\left(\overline{\overline{{\mathbb{m}}_{\overline{\overline{{\fancyscript{r}}_{1}}}}}}\right)\right)}^{\varpi }\right)}^{\frac{1}{\varpi }}}\right){e}^{i2\pi \left({e}^{-{\left(\overline{\overline{{\theta }_{S}}}{\left(-\mathrm{LoG}\left(\overline{\overline{{\mathbb{m}}_{\overline{\overline{{\mathfrak{k}}_{1}}}}}}\right)\right)}^{\varpi }\right)}^{\frac{1}{\varpi }}}\right)},\\ \left(1-{e}^{-{\left(\overline{\overline{{\theta }_{S}}}{\left(-\mathrm{LoG}\left(1-\overline{\overline{{\mathbb{y}}_{\overline{\overline{{\fancyscript{r}}_{1}}}}}}\right)\right)}^{\varpi }\right)}^{\frac{1}{\varpi }}}\right){e}^{i2\pi \left(1-{e}^{-{\left(\overline{\overline{{\theta }_{S}}}{\left(-\mathrm{LoG}\left(1-\overline{\overline{{\mathbb{y}}_{\overline{\overline{{\mathfrak{k}}_{1}}}}}}\right)\right)}^{\varpi }\right)}^{\frac{1}{\varpi }}}\right)}\end{array}\right)$$

(11)

Moreover, based on the Aczel-Alsina operational laws, we define the simple averaging and geometric aggregation operators for COIFNs, which are stated below.

Definition 5

The Aczel-Alsina Weighted Arithmetic operator for COIFNs (COIFAAWA) is defined by:

$${\text{COIFAAWA}}\left(\overline{\overline{{\Lambda }_{{\Sigma }_{1}}}},\overline{\overline{{\Lambda }_{{\Sigma }_{2}}}},\dots ,\overline{\overline{{\Lambda }_{{\Sigma }_{n}}}}\right)=\overline{\overline{{\mathbb{T}}_{1}}}\overline{\overline{{\Lambda }_{{\Sigma }_{1}}}}\oplus \overline{\overline{{\mathbb{T}}_{2}}}\overline{\overline{{\Lambda }_{{\Sigma }_{2}}}}\oplus \dots \oplus \overline{\overline{{\mathbb{T}}_{n}}}\overline{\overline{{\Lambda }_{{\Sigma }_{n}}}}={\oplus }_{j=1}^{n}\left(\overline{\overline{{\mathbb{T}}_{j}}}\overline{\overline{{\Lambda }_{{\Sigma }_{j}}}}\right) =\left(\begin{array}{c}\left(1-{e}^{-{\left(\sum_{j=1}^{n}\overline{\overline{{\mathbb{T}}_{j}}}{\left(-\mathrm{LoG}\left(1-\overline{\overline{{\mathbb{m}}_{\overline{\overline{{\fancyscript{r}}_{j}}}}}}\right)\right)}^{\varpi }\right)}^{\frac{1}{\varpi }}}\right){e}^{i2\pi \left(1-{e}^{-{\left(\sum_{j=1}^{n}\overline{\overline{{\mathbb{T}}_{j}}}{\left(-\mathrm{LoG}\left(1-\overline{\overline{{\mathbb{m}}_{\overline{\overline{{\mathfrak{k}}_{j}}}}}}\right)\right)}^{\varpi }\right)}^{\frac{1}{\varpi }}}\right)},\\ \left({e}^{-{\left(\sum_{j=1}^{n}\overline{\overline{{\mathbb{T}}_{j}}}{\left(-\mathrm{LoG}\left(\overline{\overline{{\mathbb{y}}_{\overline{\overline{{\fancyscript{r}}_{j}}}}}}\right)\right)}^{\varpi }\right)}^{\frac{1}{\varpi }}}\right){e}^{i2\pi \left({e}^{-{\left(\sum_{j=1}^{n}\overline{\overline{{\mathbb{T}}_{j}}}{\left(-\mathrm{LoG}\left(\overline{\overline{{\mathbb{y}}_{\overline{\overline{{\mathfrak{k}}_{j}}}}}}\right)\right)}^{\varpi }\right)}^{\frac{1}{\varpi }}}\right)}\end{array}\right)$$

(12)

Noticed that $\overline{\overline{\mathbb{T}}}={\left({\overline{\overline{\mathbb{T}}}}_{1},{\overline{\overline{\mathbb{T}}}}_{2},\dots ,{\overline{\overline{\mathbb{T}}}}_{n}\right)}^{T}$, with $\sum_{j=1}^{n}{\overline{\overline{\mathbb{T}}}}_{j}=1$, is a weight vector.

Definition 6

The Aczel-Alsina Weighted Geometric operator for COIFNs (COIFAAWG) operator is defined by:

$${\text{COIFAAWG}}\left(\overline{\overline{{\Lambda }_{{\Sigma }_{1}}}},\overline{\overline{{\Lambda }_{{\Sigma }_{2}}}},\dots ,\overline{\overline{{\Lambda }_{{\Sigma }_{n}}}}\right)={\overline{\overline{{\Lambda }_{{\Sigma }_{1}}}}}^{\overline{\overline{{\mathbb{T}}_{1}}}}\otimes {\overline{\overline{{\Lambda }_{{\Sigma }_{2}}}}}^{\overline{\overline{{\mathbb{T}}_{2}}}}\otimes \dots \otimes {\overline{\overline{{\Lambda }_{{\Sigma }_{n}}}}}^{\overline{\overline{{\mathbb{T}}_{n}}}}={\otimes }_{j=1}^{n}\left({\overline{\overline{{\Lambda }_{{\Sigma }_{j}}}}}^{\overline{\overline{{\mathbb{T}}_{j}}}}\right)=\left(\begin{array}{c}\left({e}^{-{\left(\sum_{j=1}^{n}{\left(-\mathrm{LoG}\left(\overline{\overline{{\mathbb{m}}_{\overline{\overline{{\fancyscript{r}}_{j}}}}}}\right)\right)}^{\varpi \overline{\overline{{\mathbb{T}}_{j}}}}\right)}^{\frac{1}{\varpi }}}\right){e}^{i2\pi \left({e}^{-{\left(\sum_{j=1}^{n}{\left(-\mathrm{LoG}\left(\overline{\overline{{\mathbb{m}}_{\overline{\overline{{\mathfrak{k}}_{j}}}}}}\right)\right)}^{\varpi \overline{\overline{{\mathbb{T}}_{j}}}}\right)}^{\frac{1}{\varpi }}}\right)},\\ \left(1-{e}^{-{\left(\sum_{j=1}^{n}{\left(-\mathrm{LoG}\left(1-\overline{\overline{{\mathbb{y}}_{\overline{\overline{{\fancyscript{r}}_{j}}}}}}\right)\right)}^{\varpi \overline{\overline{{\mathbb{T}}_{j}}}}\right)}^{\frac{1}{\varpi }}}\right){e}^{i2\pi \left(1-{e}^{-{\left(\sum_{j=1}^{n}{\left(-\mathrm{LoG}\left(1-\overline{\overline{{\mathbb{y}}_{\overline{\overline{{\mathfrak{k}}_{j}}}}}}\right)\right)}^{\varpi \overline{\overline{{\mathbb{T}}_{j}}}}\right)}^{\frac{1}{\varpi }}}\right)}\end{array}\right)$$

(13)

Noticed that $\overline{\overline{\mathbb{T}}}={\left({\overline{\overline{\mathbb{T}}}}_{1},{\overline{\overline{\mathbb{T}}}}_{2},\dots ,{\overline{\overline{\mathbb{T}}}}_{n}\right)}^{T}$, with $\sum_{j=1}^{n}{\overline{\overline{\mathbb{T}}}}_{j}=1$, is a weight vector.

3 Aczel-Alsina Prioritized Aggregation Operators for COIFSs

Explore the Aczel-Alsina prioritized aggregation operators for COIF information is a very challenging task because many scholars have developed the Aczel-Alsina, prioritized, and simple averaging and geometric aggregation operators for FSs, IFSs, CFSs, and COIFSs, but up to date, no one can obtain the Aczel-Alsina prioritized aggregation operators for COIF information. In this section, we develop the novel COIFAAPWA, COIFAAPOWA, COIFAAPWG, and COIFAAPOWG operators which are the combination of the three different structures such as the aggregation operators, prioritized aggregation operators, and Aczel-Alsina operational laws based on the COIF information. So, from the above information, it is clear that the simple averaging\geometric aggregation operators, prioritized averaging\geometric aggregation operators, and Aczel-Alsina averaging\geometric aggregation operators for FSs, IFSs, CFSs, and COIF sets are the special cases of the proposed operators. Furthermore, some feasible properties are also explored in this section under the COIFNs: $\overline{\overline{{\Lambda }_{{\Sigma }_{j}}}}=\left(\overline{\overline{{\mathbb{m}}_{\overline{\overline{{\fancyscript{r}}_{j}}}}}}{e}^{i2\pi \left(\overline{\overline{{\mathbb{m}}_{\overline{\overline{{\mathfrak{k}}_{j}}}}}}\right)},\overline{\overline{{\mathbb{y}}_{\overline{\overline{{\fancyscript{r}}_{j}}}}}}{e}^{i2\pi \left(\overline{\overline{{\mathbb{y}}_{\overline{\overline{{\mathfrak{k}}_{j}}}}}}\right)}\right),j=\mathrm{1,2},\dots ,n$.

Definition 7

The COIFAAPWA operator is defined by:

$${\text{COIFAAPWA}}\left(\overline{\overline{{\Lambda }_{{\Sigma }_{1}}}},\overline{\overline{{\Lambda }_{{\Sigma }_{2}}}},\dots ,\overline{\overline{{\Lambda }_{{\Sigma }_{n}}}}\right)=\left(\frac{\overline{\overline{{\mathbb{T}}_{1}}}}{\sum_{j=1}^{n}\overline{\overline{{\mathbb{T}}_{j}}}}\right)\overline{\overline{{\Lambda }_{{\Sigma }_{1}}}}\oplus \left(\frac{\overline{\overline{{\mathbb{T}}_{2}}}}{\sum_{j=1}^{n}\overline{\overline{{\mathbb{T}}_{j}}}}\right)\overline{\overline{{\Lambda }_{{\Sigma }_{2}}}}\oplus \dots \oplus \left(\frac{\overline{\overline{{\mathbb{T}}_{n}}}}{\sum_{j=1}^{n}\overline{\overline{{\mathbb{T}}_{j}}}}\right)\overline{\overline{{\Lambda }_{{\Sigma }_{n}}}}$$

(14)

Noticed that $\overline{\overline{{\mathbb{T}}_{j}}}=\sum_{k=1}^{j-1}\overline{\overline{{\mathcal{S}}_{SV}}}\left(\overline{\overline{{\Lambda }_{{\Sigma }_{k}}}}\right)$ and $\overline{\overline{{\mathbb{T}}_{1}}}=1$.

Theorem 1

The result of Eq. (14) is also a COIFN, and have.

$${\text{COIFAAPWA}}\left(\overline{\overline{{\Lambda }_{{\Sigma }_{1}}}},\overline{\overline{{\Lambda }_{{\Sigma }_{2}}}},\dots ,\overline{\overline{{\Lambda }_{{\Sigma }_{n}}}}\right)=\left(\begin{array}{c}\left(1-{e}^{-{\left(\sum_{j=1}^{n}\left(\frac{\overline{\overline{{\mathbb{T}}_{j}}}}{\sum_{j=1}^{n}\overline{\overline{{\mathbb{T}}_{j}}}}\right){\left(-\mathrm{LoG}\left(1-\overline{\overline{{\mathbb{m}}_{\overline{\overline{{\fancyscript{r}}_{j}}}}}}\right)\right)}^{\varpi }\right)}^{\frac{1}{\varpi }}}\right){e}^{i2\pi \left(1-{e}^{-{\left(\sum_{j=1}^{n}\overline{\overline{\left(\frac{\overline{\overline{{\mathbb{T}}_{j}}}}{\sum_{j=1}^{n}\overline{\overline{{\mathbb{T}}_{j}}}}\right)}}{\left(-\mathrm{LoG}\left(1-\overline{\overline{{\mathbb{m}}_{\overline{\overline{{\mathfrak{k}}_{j}}}}}}\right)\right)}^{\varpi }\right)}^{\frac{1}{\varpi }}}\right)},\\ \left({e}^{-{\left(\sum_{j=1}^{n}\left(\frac{\overline{\overline{{\mathbb{T}}_{j}}}}{\sum_{j=1}^{n}\overline{\overline{{\mathbb{T}}_{j}}}}\right){\left(-\mathrm{LoG}\left(\overline{\overline{{\mathbb{y}}_{\overline{\overline{{\fancyscript{r}}_{j}}}}}}\right)\right)}^{\varpi }\right)}^{\frac{1}{\varpi }}}\right){e}^{i2\pi \left({e}^{-{\left(\sum_{j=1}^{n}\left(\frac{\overline{\overline{{\mathbb{T}}_{j}}}}{\sum_{j=1}^{n}\overline{\overline{{\mathbb{T}}_{j}}}}\right){\left(-\mathrm{LoG}\left(\overline{\overline{{\mathbb{y}}_{\overline{\overline{{\mathfrak{k}}_{j}}}}}}\right)\right)}^{\varpi }\right)}^{\frac{1}{\varpi }}}\right)}\end{array}\right)$$

(15)

Additionally, from the Eq. (15), we can easily get the Aczel-Alsina (averaging/geometric) aggregation operators, prioritized (averaging/geometric) aggregation operators, and simple averaging/geometric aggregation operators for FSs, IFSs, CFSs, and COIFSs, because these all are the special cases of the presented operators. Furthermore, the relation among these operators is shown in Fig. 1.

Fig. 1

The relation between some existing operators and the proposed operators

Proof

To prove Eq. (15), we use the induction method.

• (1) when $n=2$, then

  $$\left(\frac{\overline{\overline{{\mathbb{T}}_{1}}}}{\sum_{j=1}^{n}\overline{\overline{{\mathbb{T}}_{j}}}}\right)\overline{\overline{{\Lambda }_{{\Sigma }_{1}}}}=\left(\begin{array}{c}\left(1-{e}^{-{\left(\left(\frac{\overline{\overline{{\mathbb{T}}_{1}}}}{\sum_{j=1}^{n}\overline{\overline{{\mathbb{T}}_{j}}}}\right){\left(-\mathrm{LoG}\left(1-\overline{\overline{{\mathbb{m}}_{\overline{\overline{{\fancyscript{r}}_{1}}}}}}\right)\right)}^{\varpi }\right)}^{\frac{1}{\varpi }}}\right){e}^{i2\pi \left(1-{e}^{-{\left(\left(\frac{\overline{\overline{{\mathbb{T}}_{1}}}}{\sum_{j=1}^{n}\overline{\overline{{\mathbb{T}}_{j}}}}\right){\left(-\mathrm{LoG}\left(1-\overline{\overline{{\mathbb{m}}_{\overline{\overline{{\mathfrak{k}}_{1}}}}}}\right)\right)}^{\varpi }\right)}^{\frac{1}{\varpi }}}\right)},\\ \left({e}^{-{\left(\left(\frac{\overline{\overline{{\mathbb{T}}_{1}}}}{\sum_{j=1}^{n}\overline{\overline{{\mathbb{T}}_{j}}}}\right){\left(-\mathrm{LoG}\left(\overline{\overline{{\mathbb{y}}_{\overline{\overline{{\fancyscript{r}}_{1}}}}}}\right)\right)}^{\varpi }\right)}^{\frac{1}{\varpi }}}\right){e}^{i2\pi \left({e}^{-{\left(\left(\frac{\overline{\overline{{\mathbb{T}}_{1}}}}{\sum_{j=1}^{n}\overline{\overline{{\mathbb{T}}_{j}}}}\right){\left(-\mathrm{LoG}\left(\overline{\overline{{\mathbb{y}}_{\overline{\overline{{\mathfrak{k}}_{1}}}}}}\right)\right)}^{\varpi }\right)}^{\frac{1}{\varpi }}}\right)}\end{array}\right)$$
  $$\left(\frac{\overline{\overline{{\mathbb{T}}_{2}}}}{\sum_{j=1}^{n}\overline{\overline{{\mathbb{T}}_{j}}}}\right)\overline{\overline{{\Lambda }_{{\Sigma }_{2}}}}=\left(\begin{array}{c}\left(1-{e}^{-{\left(\left(\frac{\overline{\overline{{\mathbb{T}}_{2}}}}{\sum_{j=1}^{n}\overline{\overline{{\mathbb{T}}_{j}}}}\right){\left(-\mathrm{LoG}\left(1-\overline{\overline{{\mathbb{m}}_{\overline{\overline{{\fancyscript{r}}_{2}}}}}}\right)\right)}^{\varpi }\right)}^{\frac{1}{\varpi }}}\right){e}^{i2\pi \left(1-{e}^{-{\left(\left(\frac{\overline{\overline{{\mathbb{T}}_{2}}}}{\sum_{j=1}^{n}\overline{\overline{{\mathbb{T}}_{j}}}}\right){\left(-\mathrm{LoG}\left(1-\overline{\overline{{\mathbb{m}}_{\overline{\overline{{\mathfrak{k}}_{2}}}}}}\right)\right)}^{\varpi }\right)}^{\frac{1}{\varpi }}}\right)},\\ \left({e}^{-{\left(\left(\frac{\overline{\overline{{\mathbb{T}}_{2}}}}{\sum_{j=1}^{n}\overline{\overline{{\mathbb{T}}_{j}}}}\right){\left(-\mathrm{LoG}\left(\overline{\overline{{\mathbb{y}}_{\overline{\overline{{\fancyscript{r}}_{2}}}}}}\right)\right)}^{\varpi }\right)}^{\frac{1}{\varpi }}}\right){e}^{i2\pi \left({e}^{-{\left(\left(\frac{\overline{\overline{{\mathbb{T}}_{2}}}}{\sum_{j=1}^{n}\overline{\overline{{\mathbb{T}}_{j}}}}\right){\left(-\mathrm{LoG}\left(\overline{\overline{{\mathbb{y}}_{\overline{\overline{{\mathfrak{k}}_{2}}}}}}\right)\right)}^{\varpi }\right)}^{\frac{1}{\varpi }}}\right)}\end{array}\right)$$

Thus, by combing the above two equations, we have

$${\text{COIFAAPWA}}\left(\overline{\overline{{\Lambda }_{{\Sigma }_{1}}}},\overline{\overline{{\Lambda }_{{\Sigma }_{2}}}}\right)=\left(\frac{\overline{\overline{{\mathbb{T}}_{1}}}}{\sum_{j=1}^{n}\overline{\overline{{\mathbb{T}}_{j}}}}\right)\overline{\overline{{\Lambda }_{{\Sigma }_{1}}}}\oplus \left(\frac{\overline{\overline{{\mathbb{T}}_{2}}}}{\sum_{j=1}^{n}\overline{\overline{{\mathbb{T}}_{j}}}}\right)\overline{\overline{{\Lambda }_{{\Sigma }_{2}}}}$$

$$=\left(\begin{array}{c}\left(1-{e}^{-{\left(\left(\frac{\overline{\overline{{\mathbb{T}}_{1}}}}{\sum_{j=1}^{n}\overline{\overline{{\mathbb{T}}_{j}}}}\right){\left(-\mathrm{LoG}\left(1-\overline{\overline{{\mathbb{m}}_{\overline{\overline{{\fancyscript{r}}_{1}}}}}}\right)\right)}^{\varpi }\right)}^{\frac{1}{\varpi }}}\right){e}^{i2\pi \left(1-{e}^{-{\left(\left(\frac{\overline{\overline{{\mathbb{T}}_{1}}}}{\sum_{j=1}^{n}\overline{\overline{{\mathbb{T}}_{j}}}}\right){\left(-\mathrm{LoG}\left(1-\overline{\overline{{\mathbb{m}}_{\overline{\overline{{\mathfrak{k}}_{1}}}}}}\right)\right)}^{\varpi }\right)}^{\frac{1}{\varpi }}}\right)},\\ \left({e}^{-{\left(\left(\frac{\overline{\overline{{\mathbb{T}}_{1}}}}{\sum_{j=1}^{n}\overline{\overline{{\mathbb{T}}_{j}}}}\right){\left(-\mathrm{LoG}\left(\overline{\overline{{\mathbb{y}}_{\overline{\overline{{\fancyscript{r}}_{1}}}}}}\right)\right)}^{\varpi }\right)}^{\frac{1}{\varpi }}}\right){e}^{i2\pi \left({e}^{-{\left(\left(\frac{\overline{\overline{{\mathbb{T}}_{1}}}}{\sum_{j=1}^{n}\overline{\overline{{\mathbb{T}}_{j}}}}\right){\left(-\mathrm{LoG}\left(\overline{\overline{{\mathbb{y}}_{\overline{\overline{{\mathfrak{k}}_{1}}}}}}\right)\right)}^{\varpi }\right)}^{\frac{1}{\varpi }}}\right)}\end{array}\right)\oplus \left(\begin{array}{c}\left(1-{e}^{-{\left(\left(\frac{\overline{\overline{{\mathbb{T}}_{2}}}}{\sum_{j=1}^{n}\overline{\overline{{\mathbb{T}}_{j}}}}\right){\left(-\mathrm{LoG}\left(1-\overline{\overline{{\mathbb{m}}_{\overline{\overline{{\fancyscript{r}}_{2}}}}}}\right)\right)}^{\varpi }\right)}^{\frac{1}{\varpi }}}\right){e}^{i2\pi \left(1-{e}^{-{\left(\left(\frac{\overline{\overline{{\mathbb{T}}_{2}}}}{\sum_{j=1}^{n}\overline{\overline{{\mathbb{T}}_{j}}}}\right){\left(-\mathrm{LoG}\left(1-\overline{\overline{{\mathbb{m}}_{\overline{\overline{{\mathfrak{k}}_{2}}}}}}\right)\right)}^{\varpi }\right)}^{\frac{1}{\varpi }}}\right)},\\ \left({e}^{-{\left(\left(\frac{\overline{\overline{{\mathbb{T}}_{2}}}}{\sum_{j=1}^{n}\overline{\overline{{\mathbb{T}}_{j}}}}\right){\left(-\mathrm{LoG}\left(\overline{\overline{{\mathbb{y}}_{\overline{\overline{{\fancyscript{r}}_{2}}}}}}\right)\right)}^{\varpi }\right)}^{\frac{1}{\varpi }}}\right){e}^{i2\pi \left({e}^{-{\left(\left(\frac{\overline{\overline{{\mathbb{T}}_{2}}}}{\sum_{j=1}^{n}\overline{\overline{{\mathbb{T}}_{j}}}}\right){\left(-\mathrm{LoG}\left(\overline{\overline{{\mathbb{y}}_{\overline{\overline{{\mathfrak{k}}_{2}}}}}}\right)\right)}^{\varpi }\right)}^{\frac{1}{\varpi }}}\right)}\end{array}\right)$$

$$=\left(\begin{array}{c}\left(1-{e}^{-{\left(\sum_{j=1}^{2}\left(\frac{\overline{\overline{{\mathbb{T}}_{j}}}}{\sum_{j=1}^{n}\overline{\overline{{\mathbb{T}}_{j}}}}\right){\left(-\mathrm{LoG}\left(1-\overline{\overline{{\mathbb{m}}_{\overline{\overline{{\fancyscript{r}}_{j}}}}}}\right)\right)}^{\varpi }\right)}^{\frac{1}{\varpi }}}\right){e}^{i2\pi \left(1-{e}^{-{\left(\sum_{j=1}^{2}\left(\frac{\overline{\overline{{\mathbb{T}}_{j}}}}{\sum_{j=1}^{n}\overline{\overline{{\mathbb{T}}_{j}}}}\right){\left(-\mathrm{LoG}\left(1-\overline{\overline{{\mathbb{m}}_{\overline{\overline{{\mathfrak{k}}_{j}}}}}}\right)\right)}^{\varpi }\right)}^{\frac{1}{\varpi }}}\right)},\\ \left({e}^{-{\left(\sum_{j=1}^{2}\left(\frac{\overline{\overline{{\mathbb{T}}_{j}}}}{\sum_{j=1}^{n}\overline{\overline{{\mathbb{T}}_{j}}}}\right){\left(-\mathrm{LoG}\left(\overline{\overline{{\mathbb{y}}_{\overline{\overline{{\fancyscript{r}}_{j}}}}}}\right)\right)}^{\varpi }\right)}^{\frac{1}{\varpi }}}\right){e}^{i2\pi \left({e}^{-{\left(\sum_{j=1}^{2}\left(\frac{\overline{\overline{{\mathbb{T}}_{j}}}}{\sum_{j=1}^{n}\overline{\overline{{\mathbb{T}}_{j}}}}\right){\left(-\mathrm{LoG}\left(\overline{\overline{{\mathbb{y}}_{\overline{\overline{{\mathfrak{k}}_{j}}}}}}\right)\right)}^{\varpi }\right)}^{\frac{1}{\varpi }}}\right)}\end{array}\right)$$

So, when n = 2, Eq. (15) is kept.

• (B) Suppose Eq. (15) is also kept for $n=k$, i.e.,

  $${\text{COIFAAPWA}}\left(\overline{\overline{{\Lambda }_{{\Sigma }_{1}}}},\overline{\overline{{\Lambda }_{{\Sigma }_{2}}}},\dots ,\overline{\overline{{\Lambda }_{{\Sigma }_{k}}}}\right)=\left(\begin{array}{c}\left(1-{e}^{-{\left(\sum_{j=1}^{k}\left(\frac{\overline{\overline{{\mathbb{T}}_{j}}}}{\sum_{j=1}^{n}\overline{\overline{{\mathbb{T}}_{j}}}}\right){\left(-\mathrm{LoG}\left(1-\overline{\overline{{\mathbb{m}}_{\overline{\overline{{\fancyscript{r}}_{j}}}}}}\right)\right)}^{\varpi }\right)}^{\frac{1}{\varpi }}}\right){e}^{i2\pi \left(1-{e}^{-{\left(\sum_{j=1}^{k}\left(\frac{\overline{\overline{{\mathbb{T}}_{j}}}}{\sum_{j=1}^{n}\overline{\overline{{\mathbb{T}}_{j}}}}\right){\left(-\mathrm{LoG}\left(1-\overline{\overline{{\mathbb{m}}_{\overline{\overline{{\mathfrak{k}}_{j}}}}}}\right)\right)}^{\varpi }\right)}^{\frac{1}{\varpi }}}\right)},\\ \left({e}^{-{\left(\sum_{j=1}^{k}\left(\frac{\overline{\overline{{\mathbb{T}}_{j}}}}{\sum_{j=1}^{n}\overline{\overline{{\mathbb{T}}_{j}}}}\right){\left(-\mathrm{LoG}\left(\overline{\overline{{\mathbb{y}}_{\overline{\overline{{\fancyscript{r}}_{j}}}}}}\right)\right)}^{\varpi }\right)}^{\frac{1}{\varpi }}}\right){e}^{i2\pi \left({e}^{-{\left(\sum_{j=1}^{k}\left(\frac{\overline{\overline{{\mathbb{T}}_{j}}}}{\sum_{j=1}^{n}\overline{\overline{{\mathbb{T}}_{j}}}}\right){\left(-\mathrm{LoG}\left(\overline{\overline{{\mathbb{y}}_{\overline{\overline{{\mathfrak{k}}_{j}}}}}}\right)\right)}^{\varpi }\right)}^{\frac{1}{\varpi }}}\right)}\end{array}\right)$$

Then when $n=k+1$, we have

$${\text{COIFAAPWA}}\left(\overline{\overline{{\Lambda }_{{\Sigma }_{1}}}},\overline{\overline{{\Lambda }_{{\Sigma }_{2}}}},\dots ,\overline{\overline{{\Lambda }_{{\Sigma }_{k+1}}}}\right)={\oplus }_{j=1}^{k+1}\left(\left(\frac{\overline{\overline{{\mathbb{T}}_{j}}}}{\sum_{j=1}^{n}\overline{\overline{{\mathbb{T}}_{j}}}}\right)\overline{\overline{{\Lambda }_{{\Sigma }_{j}}}}\right)={\oplus }_{j=1}^{k}\left(\left(\frac{\overline{\overline{{\mathbb{T}}_{j}}}}{\sum_{j=1}^{n}\overline{\overline{{\mathbb{T}}_{j}}}}\right)\overline{\overline{{\Lambda }_{{\Sigma }_{j}}}}\right)\oplus \left(\frac{\overline{\overline{{\mathbb{T}}_{k+1}}}}{\sum_{j=1}^{n}\overline{\overline{{\mathbb{T}}_{j}}}}\right)\overline{\overline{{\Lambda }_{{\Sigma }_{k+1}}}}$$

$$=\left(\begin{array}{c}\left(1-{e}^{-{\left(\sum_{j=1}^{k}\left(\frac{\overline{\overline{{\mathbb{T}}_{j}}}}{\sum_{j=1}^{n}\overline{\overline{{\mathbb{T}}_{j}}}}\right){\left(-\mathrm{LoG}\left(1-\overline{\overline{{\mathbb{m}}_{\overline{\overline{{\fancyscript{r}}_{j}}}}}}\right)\right)}^{\varpi }\right)}^{\frac{1}{\varpi }}}\right){e}^{i2\pi \left(1-{e}^{-{\left(\sum_{j=1}^{k}\left(\frac{\overline{\overline{{\mathbb{T}}_{j}}}}{\sum_{j=1}^{n}\overline{\overline{{\mathbb{T}}_{j}}}}\right){\left(-\mathrm{LoG}\left(1-\overline{\overline{{\mathbb{m}}_{\overline{\overline{{\mathfrak{k}}_{j}}}}}}\right)\right)}^{\varpi }\right)}^{\frac{1}{\varpi }}}\right)},\\ \left({e}^{-{\left(\sum_{j=1}^{k}\left(\frac{\overline{\overline{{\mathbb{T}}_{j}}}}{\sum_{j=1}^{n}\overline{\overline{{\mathbb{T}}_{j}}}}\right){\left(-\mathrm{LoG}\left(\overline{\overline{{\mathbb{y}}_{\overline{\overline{{\fancyscript{r}}_{j}}}}}}\right)\right)}^{\varpi }\right)}^{\frac{1}{\varpi }}}\right){e}^{i2\pi \left({e}^{-{\left(\sum_{j=1}^{k}\left(\frac{\overline{\overline{{\mathbb{T}}_{j}}}}{\sum_{j=1}^{n}\overline{\overline{{\mathbb{T}}_{j}}}}\right){\left(-\mathrm{LoG}\left(\overline{\overline{{\mathbb{y}}_{\overline{\overline{{\mathfrak{k}}_{j}}}}}}\right)\right)}^{\varpi }\right)}^{\frac{1}{\varpi }}}\right)}\end{array}\right)\oplus \left(\begin{array}{c}\left(1-{e}^{-{\left(\left(\frac{\overline{\overline{{\mathbb{T}}_{k+1}}}}{\sum_{j=1}^{n}\overline{\overline{{\mathbb{T}}_{j}}}}\right){\left(-\mathrm{LoG}\left(1-\overline{\overline{{\mathbb{m}}_{\overline{\overline{{\fancyscript{r}}_{k+1}}}}}}\right)\right)}^{\varpi }\right)}^{\frac{1}{\varpi }}}\right){e}^{i2\pi \left(1-{e}^{-{\left(\left(\frac{\overline{\overline{{\mathbb{T}}_{k+1}}}}{\sum_{j=1}^{n}\overline{\overline{{\mathbb{T}}_{j}}}}\right){\left(-\mathrm{LoG}\left(1-\overline{\overline{{\mathbb{m}}_{\overline{\overline{{\mathfrak{k}}_{k+1}}}}}}\right)\right)}^{\varpi }\right)}^{\frac{1}{\varpi }}}\right)},\\ \left({e}^{-{\left(\left(\frac{\overline{\overline{{\mathbb{T}}_{k+1}}}}{\sum_{j=1}^{n}\overline{\overline{{\mathbb{T}}_{j}}}}\right){\left(-\mathrm{LoG}\left(\overline{\overline{{\mathbb{y}}_{\overline{\overline{{\fancyscript{r}}_{k+1}}}}}}\right)\right)}^{\varpi }\right)}^{\frac{1}{\varpi }}}\right){e}^{i2\pi \left({e}^{-{\left(\left(\frac{\overline{\overline{{\mathbb{T}}_{k+1}}}}{\sum_{j=1}^{n}\overline{\overline{{\mathbb{T}}_{j}}}}\right){\left(-\mathrm{LoG}\left(\overline{\overline{{\mathbb{y}}_{\overline{\overline{{\mathfrak{k}}_{k+1}}}}}}\right)\right)}^{\varpi }\right)}^{\frac{1}{\varpi }}}\right)}\end{array}\right)$$

$$=\left(\begin{array}{c}\left(1-{e}^{-{\left(\sum_{j=1}^{k+1}\left(\frac{\overline{\overline{{\mathbb{T}}_{j}}}}{\sum_{j=1}^{n}\overline{\overline{{\mathbb{T}}_{j}}}}\right){\left(-\mathrm{LoG}\left(1-\overline{\overline{{\mathbb{m}}_{\overline{\overline{{\fancyscript{r}}_{j}}}}}}\right)\right)}^{\varpi }\right)}^{\frac{1}{\varpi }}}\right){e}^{i2\pi \left(1-{e}^{-{\left(\sum_{j=1}^{k+1}\left(\frac{\overline{\overline{{\mathbb{T}}_{j}}}}{\sum_{j=1}^{n}\overline{\overline{{\mathbb{T}}_{j}}}}\right){\left(-\mathrm{LoG}\left(1-\overline{\overline{{\mathbb{m}}_{\overline{\overline{{\mathfrak{k}}_{j}}}}}}\right)\right)}^{\varpi }\right)}^{\frac{1}{\varpi }}}\right)},\\ \left({e}^{-{\left(\sum_{j=1}^{k+1}\left(\frac{\overline{\overline{{\mathbb{T}}_{j}}}}{\sum_{j=1}^{n}\overline{\overline{{\mathbb{T}}_{j}}}}\right){\left(-\mathrm{LoG}\left(\overline{\overline{{\mathbb{y}}_{\overline{\overline{{\fancyscript{r}}_{j}}}}}}\right)\right)}^{\varpi }\right)}^{\frac{1}{\varpi }}}\right){e}^{i2\pi \left({e}^{-{\left(\sum_{j=1}^{k+1}\left(\frac{\overline{\overline{{\mathbb{T}}_{j}}}}{\sum_{j=1}^{n}\overline{\overline{{\mathbb{T}}_{j}}}}\right){\left(-\mathrm{LoG}\left(\overline{\overline{{\mathbb{y}}_{\overline{\overline{{\mathfrak{k}}_{j}}}}}}\right)\right)}^{\varpi }\right)}^{\frac{1}{\varpi }}}\right)}\end{array}\right)$$

i.e., when $n=k+1,$ Eq. (15) is also kept.

Finally, we can get Eq. (15) kept for all n.

Further, we verify the main properties of the COIFAAPWA operators, including idempotency, boundedness, and monotonicity.

Property 1

(idempotency) When $\overline{\overline{{\Lambda }_{{\Sigma }_{j}}}}=\overline{\overline{\Lambda }}$, then we get.

$${\text{COIFAAPWA}}\left(\overline{\overline{{\Lambda }_{{\Sigma }_{1}}}},\overline{\overline{{\Lambda }_{{\Sigma }_{2}}}},\dots ,\overline{\overline{{\Lambda }_{{\Sigma }_{n}}}}\right)=\overline{\overline{\Lambda }}$$

(16)

Proof

Because $\overline{\overline{{\Lambda }_{{\Sigma }_{j}}}}=\overline{\overline{\Lambda }}=\left(\overline{\overline{{\mathbb{m}}_{\overline{\overline{\fancyscript{r}}}}}}{e}^{i2\pi \left(\overline{\overline{{\mathbb{m}}_{\overline{\overline{\mathfrak{k}}}}}}\right)},\overline{\overline{{\mathbb{y}}_{\overline{\overline{\fancyscript{r}}}}}}{e}^{i2\pi \left(\overline{\overline{{\mathbb{y}}_{\overline{\overline{\mathfrak{k}}}}}}\right)}\right)$, we have.

$${\text{COIFAAPWA}}\left(\overline{\overline{{\Lambda }_{{\Sigma }_{1}}}},\overline{\overline{{\Lambda }_{{\Sigma }_{2}}}},\dots ,\overline{\overline{{\Lambda }_{{\Sigma }_{n}}}}\right)=\left(\begin{array}{c}\left(1-{e}^{-{\left(\sum_{j=1}^{n}\left(\frac{\overline{\overline{{\mathbb{T}}_{j}}}}{\sum_{j=1}^{n}\overline{\overline{{\mathbb{T}}_{j}}}}\right){\left(-\mathrm{LoG}\left(1-\overline{\overline{{\mathbb{m}}_{\overline{\overline{{\fancyscript{r}}_{j}}}}}}\right)\right)}^{\varpi }\right)}^{\frac{1}{\varpi }}}\right){e}^{i2\pi \left(1-{e}^{-{\left(\sum_{j=1}^{n}\left(\frac{\overline{\overline{{\mathbb{T}}_{j}}}}{\sum_{j=1}^{n}\overline{\overline{{\mathbb{T}}_{j}}}}\right){\left(-\mathrm{LoG}\left(1-\overline{\overline{{\mathbb{m}}_{\overline{\overline{{\mathfrak{k}}_{j}}}}}}\right)\right)}^{\varpi }\right)}^{\frac{1}{\varpi }}}\right)},\\ \left({e}^{-{\left(\sum_{j=1}^{n}\left(\frac{\overline{\overline{{\mathbb{T}}_{j}}}}{\sum_{j=1}^{n}\overline{\overline{{\mathbb{T}}_{j}}}}\right){\left(-\mathrm{LoG}\left(\overline{\overline{{\mathbb{y}}_{\overline{\overline{{\fancyscript{r}}_{j}}}}}}\right)\right)}^{\varpi }\right)}^{\frac{1}{\varpi }}}\right){e}^{i2\pi \left({e}^{-{\left(\sum_{j=1}^{n}\left(\frac{\overline{\overline{{\mathbb{T}}_{j}}}}{\sum_{j=1}^{n}\overline{\overline{{\mathbb{T}}_{j}}}}\right){\left(-\mathrm{LoG}\left(\overline{\overline{{\mathbb{y}}_{\overline{\overline{{\mathfrak{k}}_{j}}}}}}\right)\right)}^{\varpi }\right)}^{\frac{1}{\varpi }}}\right)}\end{array}\right)$$

$$=\left(\begin{array}{c}\left(1-{e}^{-{\left({\left(-\mathrm{LoG}\left(1-\overline{\overline{{\mathbb{m}}_{\overline{\overline{\fancyscript{r}}}}}}\right)\right)}^{\varpi }\right)}^{\frac{1}{\varpi }}}\right){e}^{i2\pi \left(1-{e}^{-{\left({\left(-\mathrm{LoG}\left(1-\overline{\overline{{\mathbb{m}}_{\overline{\overline{\mathfrak{k}}}}}}\right)\right)}^{\varpi }\right)}^{\frac{1}{\varpi }}}\right)},\\ \left({e}^{-{\left({\left(-\mathrm{LoG}\left(\overline{\overline{{\mathbb{y}}_{\overline{\overline{\fancyscript{r}}}}}}\right)\right)}^{\varpi }\right)}^{\frac{1}{\varpi }}}\right){e}^{i2\pi \left({e}^{-{\left({\left(-\mathrm{LoG}\left(\overline{\overline{{\mathbb{y}}_{\overline{\overline{\mathfrak{k}}}}}}\right)\right)}^{\varpi }\right)}^{\frac{1}{\varpi }}}\right)}\end{array}\right), where \left(\frac{\sum_{j=1}^{n}\overline{\overline{{\mathbb{T}}_{j}}}}{\sum_{j=1}^{n}\overline{\overline{{\mathbb{T}}_{j}}}}\right)=1$$

$$=\left(\begin{array}{c}\left(1-{e}^{\mathrm{LoG}\left(1-\overline{\overline{{\mathbb{m}}_{\overline{\overline{\fancyscript{r}}}}}}\right)}\right){e}^{i2\pi \left(1-{e}^{\mathrm{LoG}\left(1-\overline{\overline{{\mathbb{m}}_{\overline{\overline{\mathfrak{k}}}}}}\right)}\right)},\\ \left({e}^{\mathrm{LoG}\left(\overline{\overline{{\mathbb{y}}_{\overline{\overline{\fancyscript{r}}}}}}\right)}\right){e}^{i2\pi \left({e}^{\mathrm{LoG}\left(\overline{\overline{{\mathbb{y}}_{\overline{\overline{\mathfrak{k}}}}}}\right)}\right)}\end{array}\right)=\left(\overline{\overline{{\mathbb{m}}_{\overline{\overline{\fancyscript{r}}}}}}{e}^{i2\pi \left(\overline{\overline{{\mathbb{m}}_{\overline{\overline{\mathfrak{k}}}}}}\right)},\overline{\overline{{\mathbb{y}}_{\overline{\overline{\fancyscript{r}}}}}}{e}^{i2\pi \left(\overline{\overline{{\mathbb{y}}_{\overline{\overline{\mathfrak{k}}}}}}\right)}\right).$$

Property 2

(monotonicity): When $\overline{\overline{{\Lambda }_{{\Sigma }_{j}}}}\le {\overline{\overline{{\Lambda }_{{\Sigma }_{j}}}}}^{^{\prime}}=\left({\overline{\overline{{\mathbb{m}}_{\overline{\overline{{\fancyscript{r}}_{j}}}}}}}^{^{\prime}}{e}^{i2\pi \left({\overline{\overline{{\mathbb{m}}_{\overline{\overline{{\mathfrak{k}}_{j}}}}}}}^{^{\prime}}\right)},{\overline{\overline{{\mathbb{y}}_{\overline{\overline{{\fancyscript{r}}_{j}}}}}}}^{^{\prime}}{e}^{i2\pi \left({\overline{\overline{{\mathbb{y}}_{\overline{\overline{{\mathfrak{k}}_{j}}}}}}}^{^{\prime}}\right)}\right)$, then we get

$${\text{COIFAAPWA}}\left(\overline{\overline{{\Lambda }_{{\Sigma }_{1}}}},\overline{\overline{{\Lambda }_{{\Sigma }_{2}}}},\dots ,\overline{\overline{{\Lambda }_{{\Sigma }_{n}}}}\right)\le {\text{COIFAAPWA}}\left({\overline{\overline{{\Lambda }_{{\Sigma }_{1}}}}}^{^{\prime}},{\overline{\overline{{\Lambda }_{{\Sigma }_{2}}}}}^{^{\prime}},\dots ,{\overline{\overline{{\Lambda }_{{\Sigma }_{n}}}}}^{^{\prime}}\right)$$

(17)

Proof

Considering $\overline{\overline{{\Lambda }_{{\Sigma }_{j}}}}\le {\overline{\overline{{\Lambda }_{{\Sigma }_{j}}}}}^{^{\prime}}=\left({\overline{\overline{{\mathbb{m}}_{\overline{\overline{{\fancyscript{r}}_{j}}}}}}}^{^{\prime}}{e}^{i2\pi \left({\overline{\overline{{\mathbb{m}}_{\overline{\overline{{\mathfrak{k}}_{j}}}}}}}^{^{\prime}}\right)},{\overline{\overline{{\mathbb{y}}_{\overline{\overline{{\fancyscript{r}}_{j}}}}}}}^{^{\prime}}{e}^{i2\pi \left({\overline{\overline{{\mathbb{y}}_{\overline{\overline{{\mathfrak{k}}_{j}}}}}}}^{^{\prime}}\right)}\right)$, then $\overline{\overline{{\mathbb{m}}_{\overline{\overline{{\fancyscript{r}}_{j}}}}}}\le {\overline{\overline{{\mathbb{m}}_{\overline{\overline{{\fancyscript{r}}_{j}}}}}}}^{^{\prime}},\overline{\overline{{\mathbb{m}}_{\overline{\overline{{\mathfrak{k}}_{j}}}}}}\le {\overline{\overline{{\mathbb{m}}_{\overline{\overline{{\mathfrak{k}}_{j}}}}}}}^{^{\prime}}$ and $\overline{\overline{{\mathbb{y}}_{\overline{\overline{{\fancyscript{r}}_{j}}}}}}\ge {\overline{\overline{{\mathbb{y}}_{\overline{\overline{{\fancyscript{r}}_{j}}}}}}}^{^{\prime}},\overline{\overline{{\mathbb{y}}_{\overline{\overline{{\mathfrak{k}}_{j}}}}}}\ge {\overline{\overline{{\mathbb{y}}_{\overline{\overline{{\mathfrak{k}}_{j}}}}}}}^{^{\prime}}$, such as.

$$\overline{\overline{{\mathbb{m}}_{\overline{\overline{{\fancyscript{r}}_{j}}}}}}\le {\overline{\overline{{\mathbb{m}}_{\overline{\overline{{\fancyscript{r}}_{j}}}}}}}^{^{\prime}}\Rightarrow 1-\overline{\overline{{\mathbb{m}}_{\overline{\overline{{\fancyscript{r}}_{j}}}}}}\ge 1-{\overline{\overline{{\mathbb{m}}_{\overline{\overline{{\fancyscript{r}}_{j}}}}}}}^{^{\prime}}\Rightarrow {\left(-\mathrm{LoG}\left(1-\overline{\overline{{\mathbb{m}}_{\overline{\overline{{\fancyscript{r}}_{j}}}}}}\right)\right)}^{\varpi }\le {\left(-\mathrm{LoG}\left(1-{\overline{\overline{{\mathbb{m}}_{\overline{\overline{{\fancyscript{r}}_{j}}}}}}}^{^{\prime}}\right)\right)}^{\varpi }$$

$$\Rightarrow \sum_{j=1}^{n}\left(\frac{\overline{\overline{{\mathbb{T}}_{j}}}}{\sum_{j=1}^{n}\overline{\overline{{\mathbb{T}}_{j}}}}\right){\left(-\mathrm{LoG}\left(1-\overline{\overline{{\mathbb{m}}_{\overline{\overline{{\fancyscript{r}}_{j}}}}}}\right)\right)}^{\varpi }\le \sum_{j=1}^{n}\left(\frac{\overline{\overline{{\mathbb{T}}_{j}}}}{\sum_{j=1}^{n}\overline{\overline{{\mathbb{T}}_{j}}}}\right){\left(-\mathrm{LoG}\left(1-{\overline{\overline{{\mathbb{m}}_{\overline{\overline{{\fancyscript{r}}_{j}}}}}}}^{^{\prime}}\right)\right)}^{\varpi }$$

$$\Rightarrow -{\left(\sum_{j=1}^{n}\left(\frac{\overline{\overline{{\mathbb{T}}_{j}}}}{\sum_{j=1}^{n}\overline{\overline{{\mathbb{T}}_{j}}}}\right){\left(-\mathrm{LoG}\left(1-\overline{\overline{{\mathbb{m}}_{\overline{\overline{{\fancyscript{r}}_{j}}}}}}\right)\right)}^{\varpi }\right)}^{\frac{1}{\varpi }}\ge -{\left(\sum_{j=1}^{n}\left(\frac{\overline{\overline{{\mathbb{T}}_{j}}}}{\sum_{j=1}^{n}\overline{\overline{{\mathbb{T}}_{j}}}}\right){\left(-\mathrm{LoG}\left(1-{\overline{\overline{{\mathbb{m}}_{\overline{\overline{{\fancyscript{r}}_{j}}}}}}}^{^{\prime}}\right)\right)}^{\varpi }\right)}^{\frac{1}{\varpi }}$$

$$\Rightarrow {e}^{-{\left(\sum_{j=1}^{n}\left(\frac{\overline{\overline{{\mathbb{T}}_{j}}}}{\sum_{j=1}^{n}\overline{\overline{{\mathbb{T}}_{j}}}}\right){\left(-\mathrm{LoG}\left(1-\overline{\overline{{\mathbb{m}}_{\overline{\overline{{\fancyscript{r}}_{j}}}}}}\right)\right)}^{\varpi }\right)}^{\frac{1}{\varpi }}}\ge {e}^{-{\left(\sum_{j=1}^{n}\left(\frac{\overline{\overline{{\mathbb{T}}_{j}}}}{\sum_{j=1}^{n}\overline{\overline{{\mathbb{T}}_{j}}}}\right){\left(-\mathrm{LoG}\left(1-{\overline{\overline{{\mathbb{m}}_{\overline{\overline{{\fancyscript{r}}_{j}}}}}}}^{^{\prime}}\right)\right)}^{\varpi }\right)}^{\frac{1}{\varpi }}}$$

$$\Rightarrow 1-{e}^{-{\left(\sum_{j=1}^{n}\left(\frac{\overline{\overline{{\mathbb{T}}_{j}}}}{\sum_{j=1}^{n}\overline{\overline{{\mathbb{T}}_{j}}}}\right){\left(-\mathrm{LoG}\left(1-\overline{\overline{{\mathbb{m}}_{\overline{\overline{{\fancyscript{r}}_{j}}}}}}\right)\right)}^{\varpi }\right)}^{\frac{1}{\varpi }}}\le 1-{e}^{-{\left(\sum_{j=1}^{n}\left(\frac{\overline{\overline{{\mathbb{T}}_{j}}}}{\sum_{j=1}^{n}\overline{\overline{{\mathbb{T}}_{j}}}}\right){\left(-\mathrm{LoG}\left(1-{\overline{\overline{{\mathbb{m}}_{\overline{\overline{{\fancyscript{r}}_{j}}}}}}}^{^{\prime}}\right)\right)}^{\varpi }\right)}^{\frac{1}{\varpi }}}$$

Similarly, we get

$$1-{e}^{-{\left(\sum_{j=1}^{n}\left(\frac{\overline{\overline{{\mathbb{T}}_{j}}}}{\sum_{j=1}^{n}\overline{\overline{{\mathbb{T}}_{j}}}}\right){\left(-\mathrm{LoG}\left(1-\overline{\overline{{\mathbb{m}}_{\overline{\overline{{\mathfrak{k}}_{j}}}}}}\right)\right)}^{\varpi }\right)}^{\frac{1}{\varpi }}}\le 1-{e}^{-{\left(\sum_{j=1}^{n}\left(\frac{\overline{\overline{{\mathbb{T}}_{j}}}}{\sum_{j=1}^{n}\overline{\overline{{\mathbb{T}}_{j}}}}\right){\left(-\mathrm{LoG}\left(1-{\overline{\overline{{\mathbb{m}}_{\overline{\overline{{\mathfrak{k}}_{j}}}}}}}^{^{\prime}}\right)\right)}^{\varpi }\right)}^{\frac{1}{\varpi }}}$$

Further, we have

$$\overline{\overline{{\mathbb{y}}_{\overline{\overline{{\fancyscript{r}}_{j}}}}}}\ge {\overline{\overline{{\mathbb{y}}_{\overline{\overline{{\fancyscript{r}}_{j}}}}}}}^{^{\prime}}\Rightarrow {e}^{-{\left(\sum_{j=1}^{n}\left(\frac{\overline{\overline{{\mathbb{T}}_{j}}}}{\sum_{j=1}^{n}\overline{\overline{{\mathbb{T}}_{j}}}}\right){\left(-\mathrm{LoG}\left(\overline{\overline{{\mathbb{y}}_{\overline{\overline{{\fancyscript{r}}_{j}}}}}}\right)\right)}^{\varpi }\right)}^{\frac{1}{\varpi }}}\ge {e}^{-{\left(\sum_{j=1}^{n}\left(\frac{\overline{\overline{{\mathbb{T}}_{j}}}}{\sum_{j=1}^{n}\overline{\overline{{\mathbb{T}}_{j}}}}\right){\left(-\mathrm{LoG}\left({\overline{\overline{{\mathbb{y}}_{\overline{\overline{{\fancyscript{r}}_{j}}}}}}}^{^{\prime}}\right)\right)}^{\varpi }\right)}^{\frac{1}{\varpi }}}$$

Similarly, we get

$${e}^{-{\left(\sum_{j=1}^{n}\left(\frac{\overline{\overline{{\mathbb{T}}_{j}}}}{\sum_{j=1}^{n}\overline{\overline{{\mathbb{T}}_{j}}}}\right){\left(-\mathrm{LoG}\left(\overline{\overline{{\mathbb{y}}_{\overline{\overline{{\mathfrak{k}}_{j}}}}}}\right)\right)}^{\varpi }\right)}^{\frac{1}{\varpi }}}\ge {e}^{-{\left(\sum_{j=1}^{n}\left(\frac{\overline{\overline{{\mathbb{T}}_{j}}}}{\sum_{j=1}^{n}\overline{\overline{{\mathbb{T}}_{j}}}}\right){\left(-\mathrm{LoG}\left({\overline{\overline{{\mathbb{y}}_{\overline{\overline{{\mathfrak{k}}_{j}}}}}}}^{^{\prime}}\right)\right)}^{\varpi }\right)}^{\frac{1}{\varpi }}}$$

Then, by combining the above information, we can easily get

$${\text{COIFAAPWA}}\left(\overline{\overline{{\Lambda }_{{\Sigma }_{1}}}},\overline{\overline{{\Lambda }_{{\Sigma }_{2}}}},\dots ,\overline{\overline{{\Lambda }_{{\Sigma }_{n}}}}\right)\le {\text{COIFAAPWA}}\left({\overline{\overline{{\Lambda }_{{\Sigma }_{1}}}}}^{^{\prime}},{\overline{\overline{{\Lambda }_{{\Sigma }_{2}}}}}^{^{\prime}},\dots ,{\overline{\overline{{\Lambda }_{{\Sigma }_{n}}}}}^{^{\prime}}\right).$$

Property 3

(boundedness): When ${\overline{\overline{\Lambda }}}^{-}=\left(\underset{j}{\mathrm{min}}\overline{\overline{{\mathbb{m}}_{\overline{\overline{{\fancyscript{r}}_{j}}}}}}{e}^{i2\pi \left(\underset{j}{\mathrm{min}}\overline{\overline{{\mathbb{m}}_{\overline{\overline{{\mathfrak{k}}_{j}}}}}}\right)},\underset{j}{\mathrm{max}}\overline{\overline{{\mathbb{y}}_{\overline{\overline{{\fancyscript{r}}_{j}}}}}}{e}^{i2\pi \left(\underset{j}{\mathrm{max}}\overline{\overline{{\mathbb{y}}_{\overline{\overline{{\mathfrak{k}}_{j}}}}}}\right)}\right)$ and ${\overline{\overline{\Lambda }}}^{+}=\left(\underset{j}{\mathrm{max}}\overline{\overline{{\mathbb{m}}_{\overline{\overline{{\fancyscript{r}}_{j}}}}}}{e}^{i2\pi \left(\underset{j}{\mathrm{max}}\overline{\overline{{\mathbb{m}}_{\overline{\overline{{\mathfrak{k}}_{j}}}}}}\right)},\underset{j}{\mathrm{min}}\overline{\overline{{\mathbb{y}}_{\overline{\overline{{\fancyscript{r}}_{j}}}}}}{e}^{i2\pi \left(\underset{j}{\mathrm{min}}\overline{\overline{{\mathbb{y}}_{\overline{\overline{{\mathfrak{k}}_{j}}}}}}\right)}\right)$, then we get

$${\overline{\overline{\Lambda }}}^{-}\le {\text{COIFAAPWA}}\left(\overline{\overline{{\Lambda }_{{\Sigma }_{1}}}},\overline{\overline{{\Lambda }_{{\Sigma }_{2}}}},\dots ,\overline{\overline{{\Lambda }_{{\Sigma }_{n}}}}\right)\le {\overline{\overline{\Lambda }}}^{+}$$

(18)

Proof

Because ${\overline{\overline{\Lambda }}}^{-}=\left(\underset{j}{\mathrm{min}}\overline{\overline{{\mathbb{m}}_{\overline{\overline{{\fancyscript{r}}_{j}}}}}}{e}^{i2\pi \left(\underset{j}{\mathrm{min}}\overline{\overline{{\mathbb{m}}_{\overline{\overline{{\mathfrak{k}}_{j}}}}}}\right)},\underset{j}{\mathrm{max}}\overline{\overline{{\mathbb{y}}_{\overline{\overline{{\fancyscript{r}}_{j}}}}}}{e}^{i2\pi \left(\underset{j}{\mathrm{max}}\overline{\overline{{\mathbb{y}}_{\overline{\overline{{\mathfrak{k}}_{j}}}}}}\right)}\right)$ and ${\overline{\overline{\Lambda }}}^{+}=\left(\underset{j}{\mathrm{max}}\overline{\overline{{\mathbb{m}}_{\overline{\overline{{\fancyscript{r}}_{j}}}}}}{e}^{i2\pi \left(\underset{j}{\mathrm{max}}\overline{\overline{{\mathbb{m}}_{\overline{\overline{{\mathfrak{k}}_{j}}}}}}\right)},\underset{j}{\mathrm{min}}\overline{\overline{{\mathbb{y}}_{\overline{\overline{{\fancyscript{r}}_{j}}}}}}{e}^{i2\pi \left(\underset{j}{\mathrm{min}}\overline{\overline{{\mathbb{y}}_{\overline{\overline{{\mathfrak{k}}_{j}}}}}}\right)}\right)$, then.

$$1-{e}^{-{\left(\sum_{j=1}^{n}\left(\frac{\overline{\overline{{\mathbb{T}}_{j}}}}{\sum_{j=1}^{n}\overline{\overline{{\mathbb{T}}_{j}}}}\right){\left(-\mathrm{LoG}\left(1-{\overline{\overline{{\mathbb{m}}_{\overline{\overline{{\fancyscript{r}}_{j}}}}}}}^{-}\right)\right)}^{\varpi }\right)}^{\frac{1}{\varpi }}}\le 1-{e}^{-{\left(\sum_{j=1}^{n}\left(\frac{\overline{\overline{{\mathbb{T}}_{j}}}}{\sum_{j=1}^{n}\overline{\overline{{\mathbb{T}}_{j}}}}\right){\left(-\mathrm{LoG}\left(1-\overline{\overline{{\mathbb{m}}_{\overline{\overline{{\fancyscript{r}}_{j}}}}}}\right)\right)}^{\varpi }\right)}^{\frac{1}{\varpi }}}\le 1-{e}^{-{\left(\sum_{j=1}^{n}\left(\frac{\overline{\overline{{\mathbb{T}}_{j}}}}{\sum_{j=1}^{n}\overline{\overline{{\mathbb{T}}_{j}}}}\right){\left(-\mathrm{LoG}\left(1-{\overline{\overline{{\mathbb{m}}_{\overline{\overline{{\fancyscript{r}}_{j}}}}}}}^{+}\right)\right)}^{\varpi }\right)}^{\frac{1}{\varpi }}}$$

$$1-{e}^{-{\left(\sum_{j=1}^{n}\left(\frac{\overline{\overline{{\mathbb{T}}_{j}}}}{\sum_{j=1}^{n}\overline{\overline{{\mathbb{T}}_{j}}}}\right){\left(-\mathrm{LoG}\left(1-{\overline{\overline{{\mathbb{m}}_{\overline{\overline{{\mathfrak{k}}_{j}}}}}}}^{-}\right)\right)}^{\varpi }\right)}^{\frac{1}{\varpi }}}\le 1-{e}^{-{\left(\sum_{j=1}^{n}\left(\frac{\overline{\overline{{\mathbb{T}}_{j}}}}{\sum_{j=1}^{n}\overline{\overline{{\mathbb{T}}_{j}}}}\right){\left(-\mathrm{LoG}\left(1-\overline{\overline{{\mathbb{m}}_{\overline{\overline{{\mathfrak{k}}_{j}}}}}}\right)\right)}^{\varpi }\right)}^{\frac{1}{\varpi }}}\le 1-{e}^{-{\left(\sum_{j=1}^{n}\left(\frac{\overline{\overline{{\mathbb{T}}_{j}}}}{\sum_{j=1}^{n}\overline{\overline{{\mathbb{T}}_{j}}}}\right){\left(-\mathrm{LoG}\left(1-{\overline{\overline{{\mathbb{m}}_{\overline{\overline{{\mathfrak{k}}_{j}}}}}}}^{+}\right)\right)}^{\varpi }\right)}^{\frac{1}{\varpi }}}$$

$${e}^{-{\left(\sum_{j=1}^{n}\left(\frac{\overline{\overline{{\mathbb{T}}_{j}}}}{\sum_{j=1}^{n}\overline{\overline{{\mathbb{T}}_{j}}}}\right){\left(-\mathrm{LoG}\left({\overline{\overline{{\mathbb{m}}_{\overline{\overline{{\fancyscript{r}}_{j}}}}}}}^{-}\right)\right)}^{\varpi }\right)}^{\frac{1}{\varpi }}}\le {e}^{-{\left(\sum_{j=1}^{n}\left(\frac{\overline{\overline{{\mathbb{T}}_{j}}}}{\sum_{j=1}^{n}\overline{\overline{{\mathbb{T}}_{j}}}}\right){\left(-\mathrm{LoG}\left(\overline{\overline{{\mathbb{m}}_{\overline{\overline{{\fancyscript{r}}_{j}}}}}}\right)\right)}^{\varpi }\right)}^{\frac{1}{\varpi }}}\le {e}^{-{\left(\sum_{j=1}^{n}\left(\frac{\overline{\overline{{\mathbb{T}}_{j}}}}{\sum_{j=1}^{n}\overline{\overline{{\mathbb{T}}_{j}}}}\right){\left(-\mathrm{LoG}\left({\overline{\overline{{\mathbb{m}}_{\overline{\overline{{\fancyscript{r}}_{j}}}}}}}^{+}\right)\right)}^{\varpi }\right)}^{\frac{1}{\varpi }}}$$

$${e}^{-{\left(\sum_{j=1}^{n}\left(\frac{\overline{\overline{{\mathbb{T}}_{j}}}}{\sum_{j=1}^{n}\overline{\overline{{\mathbb{T}}_{j}}}}\right){\left(-\mathrm{LoG}\left({\overline{\overline{{\mathbb{m}}_{\overline{\overline{{\mathfrak{k}}_{j}}}}}}}^{-}\right)\right)}^{\varpi }\right)}^{\frac{1}{\varpi }}}\le {e}^{-{\left(\sum_{j=1}^{n}\left(\frac{\overline{\overline{{\mathbb{T}}_{j}}}}{\sum_{j=1}^{n}\overline{\overline{{\mathbb{T}}_{j}}}}\right){\left(-\mathrm{LoG}\left(\overline{\overline{{\mathbb{m}}_{\overline{\overline{{\mathfrak{k}}_{j}}}}}}\right)\right)}^{\varpi }\right)}^{\frac{1}{\varpi }}}\le {e}^{-{\left(\sum_{j=1}^{n}\left(\frac{\overline{\overline{{\mathbb{T}}_{j}}}}{\sum_{j=1}^{n}\overline{\overline{{\mathbb{T}}_{j}}}}\right){\left(-\mathrm{LoG}\left({\overline{\overline{{\mathbb{m}}_{\overline{\overline{{\mathfrak{k}}_{j}}}}}}}^{+}\right)\right)}^{\varpi }\right)}^{\frac{1}{\varpi }}}$$

Based on the above information, we can easily obtain

$${\overline{\overline{\Lambda }}}^{-}\le {\text{COIFAAPWA}}\left(\overline{\overline{{\Lambda }_{{\Sigma }_{1}}}},\overline{\overline{{\Lambda }_{{\Sigma }_{2}}}},\dots ,\overline{\overline{{\Lambda }_{{\Sigma }_{n}}}}\right)\le {\overline{\overline{\Lambda }}}^{+}.$$

Definition 8

The COIFAAPOWA operator is defined by:

$${\text{COIFAAPOWA}}\left(\overline{\overline{{\Lambda }_{{\Sigma }_{\blacksquare\left(1\right)}}}},\overline{\overline{{\Lambda }_{{\Sigma }_{\blacksquare\left(2\right)}}}},\dots ,\overline{\overline{{\Lambda }_{{\Sigma }_{\blacksquare\left(n\right)}}}}\right)=\left(\frac{\overline{\overline{{\mathbb{T}}_{1}}}}{\sum_{j=1}^{n}\overline{\overline{{\mathbb{T}}_{j}}}}\right)\overline{\overline{{\Lambda }_{{\Sigma }_{\blacksquare\left(1\right)}}}}\oplus \left(\frac{\overline{\overline{{\mathbb{T}}_{2}}}}{\sum_{j=1}^{n}\overline{\overline{{\mathbb{T}}_{j}}}}\right)\overline{\overline{{\Lambda }_{{\Sigma }_{\blacksquare\left(2\right)}}}}\oplus \dots \oplus \left(\frac{\overline{\overline{{\mathbb{T}}_{n}}}}{\sum_{j=1}^{n}\overline{\overline{{\mathbb{T}}_{j}}}}\right)\overline{\overline{{\Lambda }_{{\Sigma }_{\blacksquare\left(n\right)}}}}$$

(19)

Noticed that $\overline{\overline{{\mathbb{T}}_{j}}}=\sum_{k=1}^{j-1}\overline{\overline{{\mathcal{S}}_{SV}}}\left(\overline{\overline{{\Lambda }_{{\Sigma }_{k}}}}\right)$ and $\overline{\overline{{\mathbb{T}}_{1}}}=1$ and $\blacksquare\left(j-1\right)\le \blacksquare\left(j\right)$.

Theorem 2

Equation (19) is also a COIFN, and has.

$${\text{COIFAAPOWA}}\left(\overline{\overline{{\Lambda }_{{\Sigma }_{1}}}},\overline{\overline{{\Lambda }_{{\Sigma }_{2}}}},\dots ,\overline{\overline{{\Lambda }_{{\Sigma }_{n}}}}\right)=\left(\begin{array}{c}\left(1-{e}^{-{\left(\sum_{j=1}^{n}\left(\frac{\overline{\overline{{\mathbb{T}}_{j}}}}{\sum_{j=1}^{n}\overline{\overline{{\mathbb{T}}_{j}}}}\right){\left(-\mathrm{LoG}\left(1-\overline{\overline{{\mathbb{m}}_{\overline{\overline{{\fancyscript{r}}_{\blacksquare\left(j\right)}}}}}}\right)\right)}^{\varpi }\right)}^{\frac{1}{\varpi }}}\right){e}^{i2\pi \left(1-{e}^{-{\left(\sum_{j=1}^{n}\overline{\overline{\left(\frac{\overline{\overline{{\mathbb{T}}_{j}}}}{\sum_{j=1}^{n}\overline{\overline{{\mathbb{T}}_{j}}}}\right)}}{\left(-\mathrm{LoG}\left(1-\overline{\overline{{\mathbb{m}}_{\overline{\overline{{\mathfrak{k}}_{\blacksquare\left(j\right)}}}}}}\right)\right)}^{\varpi }\right)}^{\frac{1}{\varpi }}}\right)},\\ \left({e}^{-{\left(\sum_{j=1}^{n}\left(\frac{\overline{\overline{{\mathbb{T}}_{j}}}}{\sum_{j=1}^{n}\overline{\overline{{\mathbb{T}}_{j}}}}\right){\left(-\mathrm{LoG}\left(\overline{\overline{{\mathbb{y}}_{\overline{\overline{{\fancyscript{r}}_{\blacksquare\left(j\right)}}}}}}\right)\right)}^{\varpi }\right)}^{\frac{1}{\varpi }}}\right){e}^{i2\pi \left({e}^{-{\left(\sum_{j=1}^{n}\left(\frac{\overline{\overline{{\mathbb{T}}_{j}}}}{\sum_{j=1}^{n}\overline{\overline{{\mathbb{T}}_{j}}}}\right){\left(-\mathrm{LoG}\left(\overline{\overline{{\mathbb{y}}_{\overline{\overline{{\mathfrak{k}}_{\blacksquare\left(j\right)}}}}}}\right)\right)}^{\varpi }\right)}^{\frac{1}{\varpi }}}\right)}\end{array}\right)$$

(20)

Additionally, from Eq. (20), we can easily get the Aczel-Alsina (averaging/geometric) aggregation operators, prioritized (averaging/geometric) aggregation operators, and simple averaging/geometric aggregation operators for FSs, IFSs, CFSs, and COIFSs, because these all are the special cases of the presented operators.

The proof is omitted.

Further, the main properties of the COIFAAPOWA operators include idempotency, monotonicity, and boundedness.

Property 4

(idempotency): When $\overline{\overline{{\Lambda }_{{\Sigma }_{j}}}}=\overline{\overline{\Lambda }}$, then we get.

$${\text{COIFAAPOWA}}\left(\overline{\overline{{\Lambda }_{{\Sigma }_{1}}}},\overline{\overline{{\Lambda }_{{\Sigma }_{2}}}},\dots ,\overline{\overline{{\Lambda }_{{\Sigma }_{n}}}}\right)=\overline{\overline{\Lambda }}$$

(21)

Property 5

(monotonicity): When $\overline{\overline{{\Lambda }_{{\Sigma }_{j}}}}\le {\overline{\overline{{\Lambda }_{{\Sigma }_{j}}}}}^{^{\prime}}$, then we get.

$${\text{COIFAAPOWA}}\left(\overline{\overline{{\Lambda }_{{\Sigma }_{1}}}},\overline{\overline{{\Lambda }_{{\Sigma }_{2}}}},\dots ,\overline{\overline{{\Lambda }_{{\Sigma }_{n}}}}\right)\le {\text{COIFAAPOWA}}\left({\overline{\overline{{\Lambda }_{{\Sigma }_{1}}}}}^{^{\prime}},{\overline{\overline{{\Lambda }_{{\Sigma }_{2}}}}}^{^{\prime}},\dots ,{\overline{\overline{{\Lambda }_{{\Sigma }_{n}}}}}^{^{\prime}}\right)$$

(22)

Property 6

(boundedness): Let ${\overline{\overline{\Lambda }}}^{-}=\left(\underset{j}{\mathrm{min}}\overline{\overline{{\mathbb{m}}_{\overline{\overline{{\fancyscript{r}}_{j}}}}}}{e}^{i2\pi \left(\underset{j}{\mathrm{min}}\overline{\overline{{\mathbb{m}}_{\overline{\overline{{\mathfrak{k}}_{j}}}}}}\right)},\underset{j}{\mathrm{max}}\overline{\overline{{\mathbb{y}}_{\overline{\overline{{\fancyscript{r}}_{j}}}}}}{e}^{i2\pi \left(\underset{j}{\mathrm{max}}\overline{\overline{{\mathbb{y}}_{\overline{\overline{{\mathfrak{k}}_{j}}}}}}\right)}\right)$ and ${\overline{\overline{\Lambda }}}^{+}=\left(\underset{j}{\mathrm{max}}\overline{\overline{{\mathbb{m}}_{\overline{\overline{{\fancyscript{r}}_{j}}}}}}{e}^{i2\pi \left(\underset{j}{\mathrm{max}}\overline{\overline{{\mathbb{m}}_{\overline{\overline{{\mathfrak{k}}_{j}}}}}}\right)},\underset{j}{\mathrm{min}}\overline{\overline{{\mathbb{y}}_{\overline{\overline{{\fancyscript{r}}_{j}}}}}}{e}^{i2\pi \left(\underset{j}{\mathrm{min}}\overline{\overline{{\mathbb{y}}_{\overline{\overline{{\mathfrak{k}}_{j}}}}}}\right)}\right)$, then we get.

$${\overline{\overline{\Lambda }}}^{-}\le {\text{COIFAAPOWA}}\left(\overline{\overline{{\Lambda }_{{\Sigma }_{1}}}},\overline{\overline{{\Lambda }_{{\Sigma }_{2}}}},\dots ,\overline{\overline{{\Lambda }_{{\Sigma }_{n}}}}\right)\le {\overline{\overline{\Lambda }}}^{+}$$

(23)

Definition 9

The COIFAAPWG operator is defined by:

$${\text{COIFAAPWG}}\left(\overline{\overline{{\Lambda }_{{\Sigma }_{1}}}},\overline{\overline{{\Lambda }_{{\Sigma }_{2}}}},\dots ,\overline{\overline{{\Lambda }_{{\Sigma }_{n}}}}\right)={\overline{\overline{{\Lambda }_{{\Sigma }_{1}}}}}^{\left(\frac{\overline{\overline{{\mathbb{T}}_{1}}}}{\sum_{j=1}^{n}\overline{\overline{{\mathbb{T}}_{j}}}}\right)}\otimes {\overline{\overline{{\Lambda }_{{\Sigma }_{2}}}}}^{\left(\frac{\overline{\overline{{\mathbb{T}}_{2}}}}{\sum_{j=1}^{n}\overline{\overline{{\mathbb{T}}_{j}}}}\right)}\otimes \dots \otimes {\overline{\overline{{\Lambda }_{{\Sigma }_{n}}}}}^{\left(\frac{\overline{\overline{{\mathbb{T}}_{n}}}}{\sum_{j=1}^{n}\overline{\overline{{\mathbb{T}}_{j}}}}\right)}$$

(24)

Noticed that $\overline{\overline{{\mathbb{T}}_{j}}}=\sum_{k=1}^{j-1}\overline{\overline{{\mathcal{S}}_{SV}}}\left(\overline{\overline{{\Lambda }_{{\Sigma }_{k}}}}\right)$ and $\overline{\overline{{\mathbb{T}}_{1}}}=1$.

Theorem 3

The result of Eq. (24) is again a COIFN, and have

$${\text{COIFAAPWG}}\left(\overline{\overline{{\Lambda }_{{\Sigma }_{1}}}},\overline{\overline{{\Lambda }_{{\Sigma }_{2}}}},\dots ,\overline{\overline{{\Lambda }_{{\Sigma }_{n}}}}\right)=\left(\begin{array}{c}\left({e}^{-{\left(\sum_{j=1}^{n}\left(\frac{\overline{\overline{{\mathbb{T}}_{j}}}}{\sum_{j=1}^{n}\overline{\overline{{\mathbb{T}}_{j}}}}\right){\left(-\mathrm{LoG}\left(\overline{\overline{{\mathbb{m}}_{\overline{\overline{{\fancyscript{r}}_{j}}}}}}\right)\right)}^{\varpi }\right)}^{\frac{1}{\varpi }}}\right){e}^{i2\pi \left({e}^{-{\left(\sum_{j=1}^{n}\left(\frac{\overline{\overline{{\mathbb{T}}_{j}}}}{\sum_{j=1}^{n}\overline{\overline{{\mathbb{T}}_{j}}}}\right){\left(-\mathrm{LoG}\left(\overline{\overline{{\mathbb{m}}_{\overline{\overline{{\mathfrak{k}}_{j}}}}}}\right)\right)}^{\varpi }\right)}^{\frac{1}{\varpi }}}\right)},\\ \left(1-{e}^{-{\left(\sum_{j=1}^{n}\left(\frac{\overline{\overline{{\mathbb{T}}_{j}}}}{\sum_{j=1}^{n}\overline{\overline{{\mathbb{T}}_{j}}}}\right){\left(-\mathrm{LoG}\left(1-\overline{\overline{{\mathbb{y}}_{\overline{\overline{{\fancyscript{r}}_{j}}}}}}\right)\right)}^{\varpi }\right)}^{\frac{1}{\varpi }}}\right){e}^{i2\pi \left(1-{e}^{-{\left(\sum_{j=1}^{n}\overline{\overline{\left(\frac{\overline{\overline{{\mathbb{T}}_{j}}}}{\sum_{j=1}^{n}\overline{\overline{{\mathbb{T}}_{j}}}}\right)}}{\left(-\mathrm{LoG}\left(1-\overline{\overline{{\mathbb{y}}_{\overline{\overline{{\mathfrak{k}}_{j}}}}}}\right)\right)}^{\varpi }\right)}^{\frac{1}{\varpi }}}\right)}\end{array}\right)$$

(25)

Additionally, from Eq. (25), we can easily get the Aczel-Alsina (averaging/geometric) aggregation operators, prioritized (averaging/geometric) aggregation operators, and simple averaging/geometric aggregation operators for FSs, IFSs, CFSs, and COIFSs, because these all are the special cases of the presented operators.

Property 7

(idempotency): When $\overline{\overline{{\Lambda }_{{\Sigma }_{j}}}}=\overline{\overline{\Lambda }}$, then we get.

$${\text{COIFAAPWG}}\left(\overline{\overline{{\Lambda }_{{\Sigma }_{1}}}},\overline{\overline{{\Lambda }_{{\Sigma }_{2}}}},\dots ,\overline{\overline{{\Lambda }_{{\Sigma }_{n}}}}\right)=\overline{\overline{\Lambda }}$$

(26)

Property 8

(monotonicity): When $\overline{\overline{{\Lambda }_{{\Sigma }_{j}}}}\le {\overline{\overline{{\Lambda }_{{\Sigma }_{j}}}}}^{^{\prime}}=\left({\overline{\overline{{\mathbb{m}}_{\overline{\overline{{\fancyscript{r}}_{j}}}}}}}^{^{\prime}}{e}^{i2\pi \left({\overline{\overline{{\mathbb{m}}_{\overline{\overline{{\mathfrak{k}}_{j}}}}}}}^{^{\prime}}\right)},{\overline{\overline{{\mathbb{y}}_{\overline{\overline{{\fancyscript{r}}_{j}}}}}}}^{^{\prime}}{e}^{i2\pi \left({\overline{\overline{{\mathbb{y}}_{\overline{\overline{{\mathfrak{k}}_{j}}}}}}}^{^{\prime}}\right)}\right)$, then we get.

$${\text{COIFAAPWG}}\left(\overline{\overline{{\Lambda }_{{\Sigma }_{1}}}},\overline{\overline{{\Lambda }_{{\Sigma }_{2}}}},\dots ,\overline{\overline{{\Lambda }_{{\Sigma }_{n}}}}\right)\le {\text{COIFAAPWG}}\left({\overline{\overline{{\Lambda }_{{\Sigma }_{1}}}}}^{^{\prime}},{\overline{\overline{{\Lambda }_{{\Sigma }_{2}}}}}^{^{\prime}},\dots ,{\overline{\overline{{\Lambda }_{{\Sigma }_{n}}}}}^{^{\prime}}\right)$$

(27)

Property 9

(boundedness): When ${\overline{\overline{\Lambda }}}^{-}=\left(\underset{j}{\mathrm{min}}\overline{\overline{{\mathbb{m}}_{\overline{\overline{{\fancyscript{r}}_{j}}}}}}{e}^{i2\pi \left(\underset{j}{\mathrm{min}}\overline{\overline{{\mathbb{m}}_{\overline{\overline{{\mathfrak{k}}_{j}}}}}}\right)},\underset{j}{\mathrm{max}}\overline{\overline{{\mathbb{y}}_{\overline{\overline{{\fancyscript{r}}_{j}}}}}}{e}^{i2\pi \left(\underset{j}{\mathrm{max}}\overline{\overline{{\mathbb{y}}_{\overline{\overline{{\mathfrak{k}}_{j}}}}}}\right)}\right)$ and ${\overline{\overline{\Lambda }}}^{+}=\left(\underset{j}{\mathrm{max}}\overline{\overline{{\mathbb{m}}_{\overline{\overline{{\fancyscript{r}}_{j}}}}}}{e}^{i2\pi \left(\underset{j}{\mathrm{max}}\overline{\overline{{\mathbb{m}}_{\overline{\overline{{\mathfrak{k}}_{j}}}}}}\right)},\underset{j}{\mathrm{min}}\overline{\overline{{\mathbb{y}}_{\overline{\overline{{\fancyscript{r}}_{j}}}}}}{e}^{i2\pi \left(\underset{j}{\mathrm{min}}\overline{\overline{{\mathbb{y}}_{\overline{\overline{{\mathfrak{k}}_{j}}}}}}\right)}\right)$, then we get

$${\overline{\overline{\Lambda }}}^{-}\le COIFAAPWG\left(\overline{\overline{{\Lambda }_{{\Sigma }_{1}}}},\overline{\overline{{\Lambda }_{{\Sigma }_{2}}}},\dots ,\overline{\overline{{\Lambda }_{{\Sigma }_{n}}}}\right)\le {\overline{\overline{\Lambda }}}^{+}$$

(28)

Definition 10

The COIFAAPOWG operator is defined by:

$${\text{COIFAAPOWG}}\left(\overline{\overline{{\Lambda }_{{\Sigma }_{\blacksquare\left(1\right)}}}},\overline{\overline{{\Lambda }_{{\Sigma }_{\blacksquare\left(2\right)}}}},\dots ,\overline{\overline{{\Lambda }_{{\Sigma }_{\blacksquare\left(n\right)}}}}\right)={\overline{\overline{{\Lambda }_{{\Sigma }_{\blacksquare\left(1\right)}}}}}^{\left(\frac{\overline{\overline{{\mathbb{T}}_{1}}}}{\sum_{j=1}^{n}\overline{\overline{{\mathbb{T}}_{j}}}}\right)}\otimes {\overline{\overline{{\Lambda }_{{\Sigma }_{\blacksquare\left(2\right)}}}}}^{\left(\frac{\overline{\overline{{\mathbb{T}}_{2}}}}{\sum_{j=1}^{n}\overline{\overline{{\mathbb{T}}_{j}}}}\right)}\otimes \dots \otimes {\overline{\overline{{\Lambda }_{{\Sigma }_{\blacksquare\left(n\right)}}}}}^{\left(\frac{\overline{\overline{{\mathbb{T}}_{n}}}}{\sum_{j=1}^{n}\overline{\overline{{\mathbb{T}}_{j}}}}\right)}$$

(29)

Noticed that $\overline{\overline{{\mathbb{T}}_{j}}}=\sum_{k=1}^{j-1}\overline{\overline{{\mathcal{S}}_{SV}}}\left(\overline{\overline{{\Lambda }_{{\Sigma }_{k}}}}\right)$ and $\overline{\overline{{\mathbb{T}}_{1}}}=1$ and $\blacksquare\left(j-1\right)\le \blacksquare\left(j\right)$.

Theorem 4

The result of Eq. (29) is again a COIFN, and we have

$${\text{COIFAAPOWG}}\left(\overline{\overline{{\Lambda }_{{\Sigma }_{1}}}},\overline{\overline{{\Lambda }_{{\Sigma }_{2}}}},\dots ,\overline{\overline{{\Lambda }_{{\Sigma }_{n}}}}\right)=\left(\begin{array}{c}\left({e}^{-{\left(\sum_{j=1}^{n}\left(\frac{\overline{\overline{{\mathbb{T}}_{j}}}}{\sum_{j=1}^{n}\overline{\overline{{\mathbb{T}}_{j}}}}\right){\left(-\mathrm{LoG}\left(\overline{\overline{{\mathbb{m}}_{\overline{\overline{{\fancyscript{r}}_{\blacksquare\left(j\right)}}}}}}\right)\right)}^{\varpi }\right)}^{\frac{1}{\varpi }}}\right){e}^{i2\pi \left({e}^{-{\left(\sum_{j=1}^{n}\left(\frac{\overline{\overline{{\mathbb{T}}_{j}}}}{\sum_{j=1}^{n}\overline{\overline{{\mathbb{T}}_{j}}}}\right){\left(-\mathrm{LoG}\left(\overline{\overline{{\mathbb{m}}_{\overline{\overline{{\mathfrak{k}}_{\blacksquare\left(j\right)}}}}}}\right)\right)}^{\varpi }\right)}^{\frac{1}{\varpi }}}\right)},\\ \left(1-{e}^{-{\left(\sum_{j=1}^{n}\left(\frac{\overline{\overline{{\mathbb{T}}_{j}}}}{\sum_{j=1}^{n}\overline{\overline{{\mathbb{T}}_{j}}}}\right){\left(-\mathrm{LoG}\left(1-\overline{\overline{{\mathbb{y}}_{\overline{\overline{{\fancyscript{r}}_{\blacksquare\left(j\right)}}}}}}\right)\right)}^{\varpi }\right)}^{\frac{1}{\varpi }}}\right){e}^{i2\pi \left(1-{e}^{-{\left(\sum_{j=1}^{n}\overline{\overline{\left(\frac{\overline{\overline{{\mathbb{T}}_{j}}}}{\sum_{j=1}^{n}\overline{\overline{{\mathbb{T}}_{j}}}}\right)}}{\left(-\mathrm{LoG}\left(1-\overline{\overline{{\mathbb{y}}_{\overline{\overline{{\mathfrak{k}}_{\blacksquare\left(j\right)}}}}}}\right)\right)}^{\varpi }\right)}^{\frac{1}{\varpi }}}\right)}\end{array}\right)$$

(30)

Additionally, from Eq. (30), we can easily get the Aczel-Alsina (averaging/geometric) aggregation operators, prioritized (averaging/geometric) aggregation operators, and simple averaging/geometric aggregation operators for FSs, IFSs, CFSs, and COIFSs, because these all are the special cases of the presented operators.

Property 10

When $\overline{\overline{{\Lambda }_{{\Sigma }_{j}}}}=\overline{\overline{\Lambda }}$, then we get

$${\text{COIFAAPOWG}}\left(\overline{\overline{{\Lambda }_{{\Sigma }_{1}}}},\overline{\overline{{\Lambda }_{{\Sigma }_{2}}}},\dots ,\overline{\overline{{\Lambda }_{{\Sigma }_{n}}}}\right)=\overline{\overline{\Lambda }}$$

(31)

Property 11

When $\overline{\overline{{\Lambda }_{{\Sigma }_{j}}}}\le {\overline{\overline{{\Lambda }_{{\Sigma }_{j}}}}}^{^{\prime}}=\left({\overline{\overline{{\mathbb{m}}_{\overline{\overline{{\fancyscript{r}}_{j}}}}}}}^{^{\prime}}{e}^{i2\pi \left({\overline{\overline{{\mathbb{m}}_{\overline{\overline{{\mathfrak{k}}_{j}}}}}}}^{^{\prime}}\right)},{\overline{\overline{{\mathbb{y}}_{\overline{\overline{{\fancyscript{r}}_{j}}}}}}}^{^{\prime}}{e}^{i2\pi \left({\overline{\overline{{\mathbb{y}}_{\overline{\overline{{\mathfrak{k}}_{j}}}}}}}^{^{\prime}}\right)}\right)$, then we get

$${\text{COIFAAPOWG}}\left(\overline{\overline{{\Lambda }_{{\Sigma }_{1}}}},\overline{\overline{{\Lambda }_{{\Sigma }_{2}}}},\dots ,\overline{\overline{{\Lambda }_{{\Sigma }_{n}}}}\right)\le {\text{COIFAAPOWG}}\left({\overline{\overline{{\Lambda }_{{\Sigma }_{1}}}}}^{^{\prime}},{\overline{\overline{{\Lambda }_{{\Sigma }_{2}}}}}^{^{\prime}},\dots ,{\overline{\overline{{\Lambda }_{{\Sigma }_{n}}}}}^{^{\prime}}\right)$$

(32)

Property 12

When ${\overline{\overline{\Lambda }}}^{-}=\left(\underset{j}{\mathrm{min}}\overline{\overline{{\mathbb{m}}_{\overline{\overline{{\fancyscript{r}}_{j}}}}}}{e}^{i2\pi \left(\underset{j}{\mathrm{min}}\overline{\overline{{\mathbb{m}}_{\overline{\overline{{\mathfrak{k}}_{j}}}}}}\right)},\underset{j}{\mathrm{max}}\overline{\overline{{\mathbb{y}}_{\overline{\overline{{\fancyscript{r}}_{j}}}}}}{e}^{i2\pi \left(\underset{j}{\mathrm{max}}\overline{\overline{{\mathbb{y}}_{\overline{\overline{{\mathfrak{k}}_{j}}}}}}\right)}\right)$ and ${\overline{\overline{\Lambda }}}^{+}=\left(\underset{j}{\mathrm{max}}\overline{\overline{{\mathbb{m}}_{\overline{\overline{{\fancyscript{r}}_{j}}}}}}{e}^{i2\pi \left(\underset{j}{\mathrm{max}}\overline{\overline{{\mathbb{m}}_{\overline{\overline{{\mathfrak{k}}_{j}}}}}}\right)},\underset{j}{\mathrm{min}}\overline{\overline{{\mathbb{y}}_{\overline{\overline{{\fancyscript{r}}_{j}}}}}}{e}^{i2\pi \left(\underset{j}{\mathrm{min}}\overline{\overline{{\mathbb{y}}_{\overline{\overline{{\mathfrak{k}}_{j}}}}}}\right)}\right)$, then we get

$${\overline{\overline{\Lambda }}}^{-}\le {\text{COIFAAPOWG}}\left(\overline{\overline{{\Lambda }_{{\Sigma }_{1}}}},\overline{\overline{{\Lambda }_{{\Sigma }_{2}}}},\dots ,\overline{\overline{{\Lambda }_{{\Sigma }_{n}}}}\right)\le {\overline{\overline{\Lambda }}}^{+}$$

(33)

The qualitative comparisons of the proposed work with some existing methods based on Theorems 1–4 and properties 1–12 are shown in Table 1.

Table 1 Qualitative comparison of the proposed work with some existing methods

From Table 1, we can easily get that the proposed techniques are very superior and reliable, because every structure has a lot of limitations, but only the derived technique has very complete and perfect, therefore, in the following, we use these operators to propose the MADM method.

4 Application

Decision-making procedures, clustering analysis, pattern recognition, and artificial intelligence are some valuable and dominant applications in fuzzy set theory. The MADM technique is an important section of the decision-making procedure. For selecting the finest optimal from the family of preferences, the MADM technique is a very suitable and reliable procedure to get the best one. In this part, we propose a MADM method based on developed operators for COIF information.

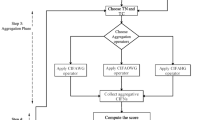
Suppose the set of alternatives is $\overline{\overline{{\Lambda }_{\Sigma }}}=\left\{\overline{\overline{{\Lambda }_{{\Sigma }_{1}}}},\overline{\overline{{\Lambda }_{{\Sigma }_{2}}}},\dots ,\overline{\overline{{\Lambda }_{{\Sigma }_{m}}}}\right\}$ which are evaluated by the finite attributes $\overline{\overline{{\Lambda }_{\Sigma }^{^{\prime}}}}=\left\{\overline{\overline{{\Lambda }_{{\Sigma }_{1}}^{^{\prime}}}},\overline{\overline{{\Lambda }_{{\Sigma }_{2}}^{^{\prime}}}},\dots ,\overline{\overline{{\Lambda }_{{\Sigma }_{n}}^{^{\prime}}}}\right\}$ under the consideration of priority information $\overline{\overline{{\mathbb{T}}_{j}}}=\sum_{k=1}^{j-1}\overline{\overline{{\mathcal{S}}_{SV}}}\left(\overline{\overline{{\Lambda }_{{\Sigma }_{k}}}}\right)$ and $\overline{\overline{{\mathbb{T}}_{1}}}=1$, and the evaluation information for alternative $\overline{\overline{{\Lambda }_{{\Sigma }_{j}}}}$ under the attribute $\overline{\overline{{\Lambda }_{{\Sigma }_{k}}^{^{\prime}}}}$ is expressed by a COIFN $\overline{\overline{{\Lambda }_{{\Sigma }_{jk}}}}=\left(\overline{\overline{{\mathbb{m}}_{\overline{\overline{{\fancyscript{r}}_{jk}}}}}}{e}^{i2\pi \left(\overline{\overline{{\mathbb{m}}_{\overline{\overline{{\mathfrak{k}}_{jk}}}}}}\right)},\overline{\overline{{\mathbb{y}}_{\overline{\overline{{\fancyscript{r}}_{jk}}}}}}{e}^{i2\pi \left(\overline{\overline{{\mathbb{y}}_{\overline{\overline{{\mathfrak{k}}_{jk}}}}}}\right)}\right),j=\mathrm{1,2},\dots ,m,k=\mathrm{1,2},\dots ,n$, then we can give the decision-making method as follows (the graphical abstract of this section is shown in Fig. 2).

Fig. 2

Graphical abstract of this Section

4.1 The Decision Procedure

The decision steps are shown as.

Step 1::

Organized a decision matrix for a MADM problem based on COIFNs, which is expressed by

$$N=\left\{\begin{array}{cc}\left(\overline{\overline{{\mathbb{m}}_{\overline{\overline{{\fancyscript{r}}_{jk}}}}}}{e}^{i2\pi \left(\overline{\overline{{\mathbb{m}}_{\overline{\overline{{\mathfrak{k}}_{jk}}}}}}\right)},\overline{\overline{{\mathbb{y}}_{\overline{\overline{{\fancyscript{r}}_{jk}}}}}}{e}^{i2\pi \left(\overline{\overline{{\mathbb{y}}_{\overline{\overline{{\mathfrak{k}}_{jk}}}}}}\right)}\right)& for\, benefit\\ \left(\overline{\overline{{\mathbb{y}}_{\overline{\overline{{\fancyscript{r}}_{jk}}}}}}{e}^{i2\pi \left(\overline{\overline{{\mathbb{y}}_{\overline{\overline{{\mathfrak{k}}_{jk}}}}}}\right)},\overline{\overline{{\mathbb{m}}_{\overline{\overline{{\fancyscript{r}}_{jk}}}}}}{e}^{i2\pi \left(\overline{\overline{{\mathbb{m}}_{\overline{\overline{{\mathfrak{k}}_{jk}}}}}}\right)}\right)& for \,cost\end{array}\right.$$

Step 2::

Aggregate all attribute values which are given in the decision matrix by the COIFAAPWA operator or COIFAAPWG operator.

Step 3::

get the score or accuracy values of the aggregated information based on Eq. (6) and Eq. (7).

Step 4::

Obtain the ranking order based on the obtained score or accuracy values.

4.2 Practical Example

4.2.1 Problem Statement

A well-known enterprise wants to invest its money in some businesses, for this, the owner of the company found the following businesses which are represented as a family of alternatives, such as:$\overline{\overline{{\Lambda }_{{C}_{j}}}},j=1,\mathrm{2,3},\mathrm{4,5}$, where the complete information is as follows: $\overline{\overline{{\Lambda }_{{C}_{1}}}}$: Laptop business; $\overline{\overline{{\Lambda }_{{C}_{2}}}}:$ Mobile business; $\overline{\overline{{\Lambda }_{{C}_{3}}}}:$ Software; $\overline{\overline{{\Lambda }_{{C}_{4}}}}:$ Book shops; and$\overline{\overline{{\Lambda }_{{C}_{5}}}}$: Car business, where for each alternative the owner of the company provided two types of information such as the name and version of each item. For these all alternatives, they are evaluated by attributes represented by different features, which are described by.

$\overline{\overline{{\boldsymbol{\Lambda }}_{{{\varvec{C}}}_{1}}^{\boldsymbol{^{\prime}}}}}$: Comfortability.

$\overline{\overline{{\boldsymbol{\Lambda }}_{{{\varvec{C}}}_{2}}^{\boldsymbol{^{\prime}}}}}$: Chance of succession.

$\overline{\overline{{\boldsymbol{\Lambda }}_{{{\varvec{C}}}_{3}}^{\boldsymbol{^{\prime}}}}}$: Price level.

$\overline{\overline{{\boldsymbol{\Lambda }}_{{{\varvec{C}}}_{4}}^{\boldsymbol{^{\prime}}}}}$: Other dues.

To handle the above problem, we give the below procedure.

4.2.2 The Decision Procedure for this Example

Based on the developed operators, we give the decision steps as follows:

Step 1::

We obtain a matrix by COIFNs which are shown in Table 2.

Table 2 Decision matrix (COIF numbers)

Because all information is the benefit type, the information in the decision matrix is not needed to be normalized.

Step 2::

Aggregate all attribute values which are given in the decision matrix by the COIFAAPWA operator and COIFAAPWG operator, shown in Table 3. The mathematical calculation for one grade is stated below, the other values are obtained in the same way. We know that the value of $\overline{\overline{{\mathbb{T}}_{1}}}=1$ (according to Definition 7), then to find the values of others, we use the idea of $\overline{\overline{{\mathbb{T}}_{j}}}=\sum_{k=1}^{j-1}\overline{\overline{{\mathcal{S}}_{SV}}}\left(\overline{\overline{{\Lambda }_{{\Sigma }_{k}}}}\right)$, such that

Table 3 The aggregated values for $\varpi =2$

$$\overline{\overline{{\mathbb{T}}_{2}}}=\sum_{k=1}^{2-1}\overline{\overline{{\mathcal{S}}_{SV}}}\left(\overline{\overline{{\Lambda }_{{\Sigma }_{k}}}}\right)=\sum_{k=1}^{1}\overline{\overline{{\mathcal{S}}_{SV}}}\left(\overline{\overline{{\Lambda }_{{\Sigma }_{k}}}}\right)=\overline{\overline{{\mathcal{S}}_{SV}}}\left(\overline{\overline{{\Lambda }_{{\Sigma }_{1}}}}\right)=\frac{1}{2}\left(0.6+0.5-0.2-0.3\right)=0.3$$

$$\overline{\overline{{\mathbb{T}}_{3}}}=\sum_{k=1}^{3-1}\overline{\overline{{\mathcal{S}}_{SV}}}\left(\overline{\overline{{\Lambda }_{{\Sigma }_{k}}}}\right)=\sum_{k=1}^{2}\overline{\overline{{\mathcal{S}}_{SV}}}\left(\overline{\overline{{\Lambda }_{{\Sigma }_{k}}}}\right)=\overline{\overline{{\mathcal{S}}_{SV}}}\left(\overline{\overline{{\Lambda }_{{\Sigma }_{1}}}}\right)+\overline{\overline{{\mathcal{S}}_{SV}}}\left(\overline{\overline{{\Lambda }_{{\Sigma }_{2}}}}\right)=0.6$$

$$\overline{\overline{{\mathbb{T}}_{4}}}=\sum_{k=1}^{4-1}\overline{\overline{{\mathcal{S}}_{SV}}}\left(\overline{\overline{{\Lambda }_{{\Sigma }_{k}}}}\right)=\sum_{k=1}^{3}\overline{\overline{{\mathcal{S}}_{SV}}}\left(\overline{\overline{{\Lambda }_{{\Sigma }_{k}}}}\right)=\overline{\overline{{\mathcal{S}}_{SV}}}\left(\overline{\overline{{\Lambda }_{{\Sigma }_{1}}}}\right)+\overline{\overline{{\mathcal{S}}_{SV}}}\left(\overline{\overline{{\Lambda }_{{\Sigma }_{2}}}}\right)+\overline{\overline{{\mathcal{S}}_{SV}}}\left(\overline{\overline{{\Lambda }_{{\Sigma }_{3}}}}\right)=0.9$$

Then we get the values of ${\text{COIFAAPWA}}\left(\overline{\overline{{\Lambda }_{{\Sigma }_{1}}}},\overline{\overline{{\Lambda }_{{\Sigma }_{2}}}},\overline{\overline{{\Lambda }_{{\Sigma }_{3}}}},\overline{\overline{{\Lambda }_{{\Sigma }_{4}}}}\right)$, such that where $\sum_{j=1}^{n}\overline{\overline{{\mathbb{T}}_{j}}}=2.8$, then we have

$$\left(1-{e}^{-{\left(\sum_{j=1}^{4}\left(\frac{\overline{\overline{{\mathbb{T}}_{j}}}}{\sum_{j=1}^{n}\overline{\overline{{\mathbb{T}}_{j}}}}\right){\left(-\mathrm{LoG}\left(1-\overline{\overline{{\mathbb{m}}_{\overline{\overline{{\fancyscript{r}}_{j}}}}}}\right)\right)}^{\varpi }\right)}^{\frac{1}{\varpi }}}\right)$$

$$=\left(1-{e}^{-{\left(\begin{array}{c}\left(\left(\frac{\overline{\overline{{\mathbb{T}}_{1}}}}{\sum_{j=1}^{4}\overline{\overline{{\mathbb{T}}_{j}}}}\right){\left(-\mathrm{LoG}\left(1-\overline{\overline{{\mathbb{m}}_{\overline{\overline{{\fancyscript{r}}_{1}}}}}}\right)\right)}^{\varpi }\right)+\left(\left(\frac{\overline{\overline{{\mathbb{T}}_{2}}}}{\sum_{j=1}^{4}\overline{\overline{{\mathbb{T}}_{j}}}}\right){\left(-\mathrm{LoG}\left(1-\overline{\overline{{\mathbb{m}}_{\overline{\overline{{\fancyscript{r}}_{2}}}}}}\right)\right)}^{\varpi }\right)+\\ \left(\left(\frac{\overline{\overline{{\mathbb{T}}_{3}}}}{\sum_{j=1}^{4}\overline{\overline{{\mathbb{T}}_{j}}}}\right){\left(-\mathrm{LoG}\left(1-\overline{\overline{{\mathbb{m}}_{\overline{\overline{{\fancyscript{r}}_{3}}}}}}\right)\right)}^{\varpi }\right)+\left(\left(\frac{\overline{\overline{{\mathbb{T}}_{4}}}}{\sum_{j=1}^{4}\overline{\overline{{\mathbb{T}}_{j}}}}\right){\left(-\mathrm{LoG}\left(1-\overline{\overline{{\mathbb{m}}_{\overline{\overline{{\fancyscript{r}}_{4}}}}}}\right)\right)}^{\varpi }\right)\end{array}\right)}^{\frac{1}{\varpi }}}\right)$$

$$=\left(1-{e}^{-{\left(\left(\left(\frac{1}{2.8}\right){\left(-\mathrm{LoG}\left(1-0.6\right)\right)}^{2}\right)+\left(\left(\frac{0.3}{2.8}\right){\left(-\mathrm{LoG}\left(1-0.61\right)\right)}^{2}\right)+\left(\left(\frac{0.6}{2.8}\right){\left(-\mathrm{LoG}\left(1-0.62\right)\right)}^{2}\right)+\left(\left(\frac{0.9}{2.9}\right){\left(-\mathrm{LoG}\left(1-0.63\right)\right)}^{2}\right)\right)}^\frac{1}{2}}\right)$$

$$=0.3396$$

$$\left(1-{e}^{-{\left(\sum_{j=1}^{4}\overline{\overline{\left(\frac{\overline{\overline{{\mathbb{T}}_{j}}}}{\sum_{j=1}^{n}\overline{\overline{{\mathbb{T}}_{j}}}}\right)}}{\left(-\mathrm{LoG}\left(1-\overline{\overline{{\mathbb{m}}_{\overline{\overline{{\mathfrak{k}}_{j}}}}}}\right)\right)}^{\varpi }\right)}^{\frac{1}{\varpi }}}\right)=0.2699$$

Similarly, we get the falsity of the information, such as:

$$\left({e}^{-{\left(\sum_{j=1}^{4}\left(\frac{\overline{\overline{{\mathbb{T}}_{j}}}}{\sum_{j=1}^{n}\overline{\overline{{\mathbb{T}}_{j}}}}\right){\left(-\mathrm{LoG}\left(\overline{\overline{{\mathbb{y}}_{\overline{\overline{{\fancyscript{r}}_{j}}}}}}\right)\right)}^{\varpi }\right)}^{\frac{1}{\varpi }}}\right)$$

$$=\left({e}^{-{\left(\begin{array}{c}\left(\left(\frac{\overline{\overline{{\mathbb{T}}_{1}}}}{\sum_{j=1}^{4}\overline{\overline{{\mathbb{T}}_{j}}}}\right){\left(-\mathrm{LoG}\left(\overline{\overline{{\mathbb{y}}_{\overline{\overline{{\fancyscript{r}}_{1}}}}}}\right)\right)}^{\varpi }\right)+\left(\left(\frac{\overline{\overline{{\mathbb{T}}_{2}}}}{\sum_{j=1}^{4}\overline{\overline{{\mathbb{T}}_{j}}}}\right){\left(-\mathrm{LoG}\left(\overline{\overline{{\mathbb{y}}_{\overline{\overline{{\fancyscript{r}}_{2}}}}}}\right)\right)}^{\varpi }\right)+\\ \left(\left(\frac{\overline{\overline{{\mathbb{T}}_{3}}}}{\sum_{j=1}^{4}\overline{\overline{{\mathbb{T}}_{j}}}}\right){\left(-\mathrm{LoG}\left(\overline{\overline{{\mathbb{y}}_{\overline{\overline{{\fancyscript{r}}_{3}}}}}}\right)\right)}^{\varpi }\right)+\left(\left(\frac{\overline{\overline{{\mathbb{T}}_{4}}}}{\sum_{j=1}^{4}\overline{\overline{{\mathbb{T}}_{j}}}}\right){\left(-\mathrm{LoG}\left(\overline{\overline{{\mathbb{y}}_{\overline{\overline{{\fancyscript{r}}_{4}}}}}}\right)\right)}^{\varpi }\right)\end{array}\right)}^{\frac{1}{\varpi }}}\right)$$

$$=\left({e}^{-{\left(\left(\left(\frac{1}{2.8}\right){\left(-\mathrm{LoG}\left(0.2\right)\right)}^{2}\right)+\left(\left(\frac{0.3}{2.8}\right){\left(-\mathrm{LoG}\left(0.21\right)\right)}^{2}\right)+\left(\left(\frac{0.6}{2.8}\right){\left(-\mathrm{LoG}\left(0.22\right)\right)}^{2}\right)+\left(\left(\frac{0.9}{2.9}\right){\left(-\mathrm{LoG}\left(0.23\right)\right)}^{2}\right)\right)}^\frac{1}{2}}\right)$$

$$=0.5123$$

$$\left({e}^{-{\left(\sum_{j=1}^{4}\left(\frac{\overline{\overline{{\mathbb{T}}_{j}}}}{\sum_{j=1}^{n}\overline{\overline{{\mathbb{T}}_{j}}}}\right){\left(-\mathrm{LoG}\left(\overline{\overline{{\mathbb{y}}_{\overline{\overline{{\mathfrak{k}}_{j}}}}}}\right)\right)}^{\varpi }\right)}^{\frac{1}{\varpi }}}\right)=0.6051$$

Therefore, the final value is $\left(\left(\mathrm{0.3396,0.2699}\right),\left(\mathrm{0.5123,0.6051}\right)\right)$, which is given in Table 3.

Step 3::

Get the score or accuracy values of the aggregated information by Eq. (6) and Eq. (7), see Table 4.

Table 4 The score values for the aggregated results

Step 4::

Obtain the ranking order based on the obtained score values, see Table 5.

Table 5 Contained ranking order

From Table 5, we can see that two operators can get the same best choice, i.e.,$\overline{\overline{{\Lambda }_{{{\varvec{C}}}_{3}}}}$, of course, the ranking results are the almost same.

Moreover, to show the advantages of the proposed operators, we use the information in Table 2 by excluding their imaginary part, then the final information is given in Table 6.

Table 6 The intuitionistic fuzzy information produced from Table 2

Further, we aggregate all attribute values which are given in Table 6 by the COIFAAPWA operator and COIFAAPWG operator, and get the aggregated results (see Table 7).

Table 7 The aggregated values based on Table 6 for $\varpi =2$

Then we get the score values of the aggregated information by Eq. (6), see Table 8.

Table 8 Availability of the score values from Table 7

Moreover, we get the ranking results based on Table 8, see Table 9.

Table 9 The ranking results are based on Table 8

From Table 9, we can obtain the same ranking results, and the best choice is $\overline{\overline{{\Lambda }_{{{\varvec{C}}}_{3}}}}$.

Furthermore, we can check the stability of the developed operators by different values of parameter $\varpi$.

4.2.3 Stability or Influence of Parameter $\boldsymbol{\varpi }$

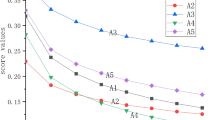
Based on the different values of the parameter, we can aggregate the decision information described in Table 1 by the COIFAAPWA and COIFAAPWG operators, and then check the ranking results which are shown in Table 10.

Table 10 The ranking results for the different values of parameter ψ

From Table 10, we can obtain the same ranking results, and the best decision is $\overline{\overline{{\Lambda }_{{{\varvec{C}}}_{3}}}}$.

Further, we can also get the ranking results based on the information in Table 6 by the COIFAAPWA and COIFAAPWG operators, which are shown in Table 11.

Table 11 The ranking results for the different values of the parameter ψ based on the information in Table 6

From Table 11, we can obtain the same ranking results, and the best decision is $\overline{\overline{{\Lambda }_{{{\varvec{C}}}_{3}}}}$.

5 Comparative Analysis

Here, we compare the developed operators with some existing operators based on the information given in Table 2 and Table 6. To do this work, we use the following existing operators: Senapati et al. [27] proposed aggregation operators based on AA t-norms for IFSs. Yu and Xu [28] proposed the prioritized aggregation operators based on IFSs. Arora and Garg [29] proposed the prioritized averaging/geometric aggregation operators for IFSs with soft sets. Garg and Rani [21] developed aggregation operators based on COIF information. Then, we use the information in Table 2, the comparative analysis is described in Table 12.

Table 12 The comparative analysis is based on the information in Table 2

From Table 12, three existing operators in [27,28,29] cannot process this decision problem because they can only deal with the decision information in IFSs. The operators proposed by Garg and Rani [21] and in this paper can obtain the same best choice, further, the operators proposed by Garg and Rani [21] can get the same ranking result as the COIFAAPWA operator, and are a little different from COIFAAPWG operator.

Further, we use the decision information in Table 6 and the same existing operators in Table 12 to solve this decision problem and get the results in Table 13.

Table 13 The comparative analysis based on the information in Table 6

From Table 13, all operators except in [29] can obtain the same best choice, only the operators in [21] cannot solve this problem because they can only process the information in IFSs with soft sets. Further, all operators except in [29] and [28] can obtain the same ranking result $\overline{\overline{{\Lambda }_{{{\varvec{C}}}_{3}}}}>\overline{\overline{{\Lambda }_{{{\varvec{C}}}_{1}}}}>\overline{\overline{{\Lambda }_{{{\varvec{C}}}_{4}}}}>\overline{\overline{{\Lambda }_{{{\varvec{C}}}_{5}}}}>\overline{\overline{{\Lambda }_{{{\varvec{C}}}_{2}}}}$, only the operators in [28] produce a slightly different result from the others.

Therefore, the proposed operators are very feasible to cope with vague information and complicated decision-making problems.

6 Conclusion

The major contributions of this work are listed below:

• (1) We developed some operational laws for COIFNs based on AA t-norm and t-conorm.

• (2) We proposed the COIFAAPWA, COIFAPOWA, COIFAAPWG, and COIFAAPOWG, and explained their basic properties.

• (3) We analyzed some special cases of the proposed AA-prioritized aggregation operators.

• (4) We developed a MADM process for COIF information based on obtained operators.

• (5) We compared some existing operators with the proposed operators to show the flexibility of the derived approaches.

Where the Aczel-Alsina, prioritized, and simple averaging/geometric aggregation operators based on FSs, IFSs, CFSs, and COIFSs are the special cases of the proposed works.

6.1 Limitations

Although the Aczel-Alsina prioritized aggregation operators based on the COIFSs are a very powerful and dominant technique for processing awkward and unreliable information in genuine-life problems, in some cases, the proposed information has been not working effectively, especially, when we talked about the triplet such as truth grade, abstinence grade, and falsity grade by complex values, therefore, for solving the above problems, we requires to propose these operators based on complex picture fuzzy sets, complex spherical fuzzy sets, and complex T-spherical fuzzy sets.

6.2 Future Directions

In the future, we will explore some new ideas by extending the proposed operators to complex linguistic FSs [30], the TOPSIS method [31], linear Diophantine sets [32, 33], an extension of N-soft sets [3, 34, 35], Aczel-Alsina aggregation operators [36], similarity measures [37,38,39], and complex spherical FSs [40].