Dynamic modeling of curved fish bone active camber morphing concept using shallow shell theory and negative-stiffness artificial springs

Abstract

Existing models for the morphing concept of fish bone active camber (FishBAC) rely on several simplifying assumptions, hindering the accurate evaluation of its static and dynamic response. This study proposes a general framework according to which the theory of shallow shells and the Rayleigh–Ritz method are combined with artificial springs to present a basis for the dynamic evaluation of FishBAC, focusing on the free-vibration behavior as a first step for such objectives. A comprehensive code, which considers any desired boundary conditions, is written in Wolfram Mathematica to obtain the frequency parameter. After establishing the validity of the formulation through a set of comparisons with other articles and methods, a few FishBACs based on NACA 4412 are examined. Partitioning the structure and using the dimensions of these sections as the input yield accurate results compared to the finite element findings in COMSOL Multiphysics in an eigenfrequency analysis. The findings also show the notable error of neglecting the existence of curvature in the mean camber line of the trailing edges of airfoils or the span of wings based on FishBAC.

Appendix

Different terms of Eq. 12 are delineated in what follows. The matrix ${\mathbf{C}}_{mnij,k}$ is comprised of two types of stiffness: (1) inherent stiffness of the element, and (2) the stiffness imposed by artificial springs. In its general form, ${\mathbf{C}}_{mnij,k}$ is described as

$${\mathbf{C}}_{mnij,k} = \left[ {\begin{array}{*{20}c} {{\mathbf{K}}_{k}^{UU} + {\mathbf{K}}_{k}^{{UU,{\text{spring}}}} } & {{\mathbf{K}}_{k}^{UV} } & {{\mathbf{K}}_{k}^{UW} } \\ {{\mathbf{K}}_{k}^{{UV}^{\text{T}}} } & {{\mathbf{K}}_{k}^{VV} + {\mathbf{K}}_{k}^{{VV,{\text{spring}}}} } & {{\mathbf{K}}_{k}^{VW} } \\ {{\mathbf{K}}_{k}^{{UW}^{\text{T}}} } & {{\mathbf{K}}_{k}^{{VW}^{\text{T}}} } & {{\mathbf{K}}_{k}^{WW} + {\mathbf{K}}_{k}^{{WW,{\text{spring}}}} } \\ \end{array} } \right]$$

(13)

where the letter $\text{T}$ represents the transpose, and other terms are expressed as

$${\mathbf{K}}_{k}^{UU} = \frac{{12a_{k} b_{k} D_{k} }}{{h_{k}^{2} }}\left[ {\frac{{\left( {1 - \nu_{1} } \right)}}{{2b_{k}^{2} }}{\mathbf{E}}_{mn}^{{\left( {0,0} \right)}} {\mathbf{F}}_{ij}^{{\left( {1,1} \right)}} + \frac{1}{{a_{k}^{2} }}{\mathbf{E}}_{mn}^{{\left( {1,1} \right)}} {\mathbf{F}}_{ij}^{{\left( {0,0} \right)}} } \right]$$

(14a)

$${\mathbf{K}}_{k}^{UV} = \frac{{6D_{k} }}{{h_{k}^{2} }}\left[ {2\nu_{k} {\mathbf{E}}_{mn}^{{\left( {1,0} \right)}} {\mathbf{F}}_{ij}^{{\left( {0,1} \right)}} + \left( {1 - \nu_{k} } \right){\mathbf{E}}_{mn}^{{\left( {0,1} \right)}} {\mathbf{F}}_{ij}^{{\left( {1,0} \right)}} } \right]$$

(14b)

$${\mathbf{K}}_{k}^{UW} = \frac{{12b_{k} D_{k} \left( {R_{x} + R_{y} \nu_{k} } \right)}}{{h_{k}^{2} R_{x} R_{y} }}\left( {{\mathbf{E}}_{mn}^{{\left( {1,0} \right)}} {\mathbf{F}}_{ij}^{{\left( {0,0} \right)}} } \right)$$

(14c)

$${\mathbf{K}}_{k}^{VV} = \frac{{12a_{k} b_{k} D_{k} }}{{h_{k}^{2} }}\left[ {\frac{{\left( {1 - \nu_{1} } \right)}}{{2a_{k}^{2} }}{\mathbf{E}}_{mn}^{{\left( {1,1} \right)}} {\mathbf{F}}_{ij}^{{\left( {0,0} \right)}} + \frac{1}{{b_{k}^{2} }}{\mathbf{E}}_{mn}^{{\left( {0,0} \right)}} {\mathbf{F}}_{ij}^{{\left( {1,1} \right)}} } \right]$$

(14d)

$${\mathbf{K}}_{k}^{VW} = \frac{{12a_{k} D_{k} \left( {R_{x} + R_{y} \nu_{k} } \right)}}{{h_{k}^{2} R_{x} R_{y} }}\left( {{\mathbf{E}}_{mn}^{{\left( {0,0} \right)}} {\mathbf{F}}_{ij}^{{\left( {1,0} \right)}} } \right)$$

(14e)

$$\begin{aligned} {\mathbf{K}}_{k}^{WW} & = \frac{{12a_{k} b_{k} D_{k} \left( {R_{x}^{2} + R_{y}^{2} + 2R_{x} R_{y} \nu_{k} } \right)}}{{h_{k}^{2} R_{x}^{2} R_{y}^{2} }}\left( {{\mathbf{E}}_{mn}^{{\left( {0,0} \right)}} {\mathbf{F}}_{ij}^{{\left( {0,0} \right)}} } \right) \\ & \quad + \frac{{D_{k} }}{{a_{k}^{3} b_{k}^{3} }}\left[ {a_{k}^{4} {\mathbf{E}}_{mn}^{{\left( {0,0} \right)}} {\mathbf{F}}_{ij}^{{\left( {2,2} \right)}} + 2a_{k}^{2} b_{k}^{2} \left( {1 - \nu_{k} } \right){\mathbf{E}}_{mn}^{{\left( {1,1} \right)}} {\mathbf{F}}_{ij}^{{\left( {1,1} \right)}} + a_{k}^{2} b_{k}^{2} \nu_{k} \left( {{\mathbf{E}}_{mn}^{{\left( {0,2} \right)}} {\mathbf{F}}_{ij}^{{\left( {2,0} \right)}} + {\mathbf{E}}_{mn}^{{\left( {2,0} \right)}} {\mathbf{F}}_{ij}^{{\left( {0,2} \right)}} } \right) + b_{k}^{4} {\mathbf{E}}_{mn}^{{\left( {2,2} \right)}} {\mathbf{F}}_{ij}^{{\left( {0,0} \right)}} } \right] \\ \end{aligned}$$

(14f)

$$\begin{aligned} {\mathbf{K}}_{k}^{{UU,{\text{spring}}}} & = K_{T}^{{{\text{Side}}1}} a_{k} \left( {{\mathbf{E}}_{mn}^{{\left( {0,0} \right)}} \psi_{i} \left( 0 \right)\psi_{j} \left( 0 \right)} \right) + K_{T}^{{{\text{Side}}2}} b_{k} \left( {\phi_{m} \left( 1 \right)\phi_{n} \left( 1 \right){\mathbf{F}}_{ij}^{{\left( {0,0} \right)}} } \right) \\ & \quad + K_{T}^{{{\text{Side}}3}} a_{k} \left( {{\mathbf{E}}_{mn}^{{\left( {0,0} \right)}} \psi_{i} \left( 1 \right)\psi_{j} \left( 1 \right)} \right) + K_{T}^{{{\text{Side}}4}} b_{k} \left( {\phi_{m} \left( 0 \right)\phi_{n} \left( 0 \right){\mathbf{F}}_{ij}^{{\left( {0,0} \right)}} } \right) \\ \end{aligned}$$

(14g)

$${\mathbf{K}}_{k}^{{VV,{\text{spring}}}} = {\mathbf{K}}_{k}^{{UU,{\text{spring}}}}$$

(14i)

$$\begin{aligned} {\mathbf{K}}_{k}^{{WW,{\text{spring}}}} & = K_{T}^{{{\text{Side}}1}} a_{k} \left( {{\mathbf{E}}_{mn}^{{\left( {0,0} \right)}} \psi_{i} \left( 0 \right)\psi_{j} \left( 0 \right)} \right) + K_{T}^{{{\text{Side}}2}} b_{k} \left( {\phi_{m} \left( 1 \right)\phi_{n} \left( 1 \right){\mathbf{F}}_{ij}^{{\left( {0,0} \right)}} } \right) \\ & \quad + K_{T}^{{{\text{Side}}3}} a_{k} \left( {{\mathbf{E}}_{mn}^{{\left( {0,0} \right)}} \psi_{i} \left( 1 \right)\psi_{j} \left( 1 \right)} \right) + K_{T}^{{{\text{Side}}4}} b_{k} \left( {\phi_{m} \left( 0 \right)\phi_{n} \left( 0 \right){\mathbf{F}}_{ij}^{{\left( {0,0} \right)}} } \right) \\ & \quad + K_{T}^{{{\text{Side}}1}} \frac{{a_{k} }}{{b_{k}^{2} }}\left( {{\mathbf{E}}_{mn}^{{\left( {0,0} \right)}} \psi_{i} \left( 0 \right)\psi_{j} \left( 0 \right)} \right) + K_{T}^{{{\text{Side}}2}} \frac{{b_{k} }}{{a_{k}^{2} }}\left( {\phi_{m} \left( 1 \right)\phi_{n} \left( 1 \right){\mathbf{F}}_{ij}^{{\left( {0,0} \right)}} } \right) \\ & \quad + K_{T}^{{{\text{Side}}3}} \frac{{a_{k} }}{{b_{k}^{2} }}\left( {{\mathbf{E}}_{mn}^{{\left( {0,0} \right)}} \psi_{i} \left( 1 \right)\psi_{j} \left( 1 \right)} \right) + K_{T}^{{{\text{Side}}4}} \frac{{b_{k} }}{{a_{k}^{2} }}\left( {\phi_{m} \left( 0 \right)\phi_{n} \left( 0 \right){\mathbf{F}}_{ij}^{{\left( {0,0} \right)}} } \right) \\ \end{aligned}$$

(14h)

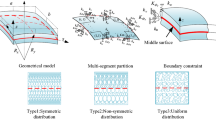
where Side1–4 are the numbers associated with the sides of each partition in Fig. 2b, and the recurring terms ${\mathbf{E}}_{mn}^{{\left( {r,s} \right)}}$ and ${\mathbf{F}}_{ij}^{{\left( {r,s} \right)}}$ are described as

$${\mathbf{E}}_{mn}^{{\left( {r,s} \right)}} = \mathop \int \limits_{0}^{1} \left( {\frac{{{\text{d}}^{r} \phi_{m} }}{{{\text{d}}\zeta^{r} }}} \right)\left( {\frac{{{\text{d}}^{s} \phi_{n} }}{{{\text{d}}\zeta^{s} }}} \right){\text{d}}\zeta$$

(15a)

$${\mathbf{F}}_{ij}^{{\left( {r,s} \right)}} = \mathop \int \limits_{0}^{1} \left( {\frac{{{\text{d}}^{r} \phi_{i} }}{{{\text{d}}\eta^{r} }}} \right)\left( {\frac{{{\text{d}}^{s} \phi_{j} }}{{{\text{d}}\eta^{s} }}} \right){\text{d}}\eta$$

(15b)

Also, ${\mathbf{B}}_{mnij,k}$ is written as

$${\mathbf{B}}_{mnij,k} = \left[ {\begin{array}{*{20}c} {{\mathbf{M}}_{k}^{UU} } & 0 & 0 \\ 0 & {{\mathbf{M}}_{k}^{VV} } & 0 \\ 0 & 0 & {{\mathbf{M}}_{k}^{WW} } \\ \end{array} } \right]$$

(16)

where the matrices ${\mathbf{M}}_{k}^{UU}$, ${\mathbf{M}}_{k}^{VV}$ and ${\mathbf{M}}_{k}^{WW}$ are equally defined as

$${\mathbf{M}}_{k}^{UU} = {\mathbf{M}}_{k}^{VV} = {\mathbf{M}}_{k}^{WW} = a_{k} b_{k} h_{k} \rho_{k} {\mathbf{E}}_{mn}^{{\left( {0,0} \right)}} {\mathbf{F}}_{ij}^{{\left( {0,0} \right)}}$$

(17)

For the developed formulation in this article where the partition $k$ is attached to the partition $l$, the definition of the coupling matrix ${\mathbf{D}}_{mnij,kl}$ (initiating from the common side between the two partitions) is written as

$${\mathbf{D}}_{mnij,kl} = \left[ {\begin{array}{*{20}c} {{\mathbf{D}}_{k,l}^{UU} } & 0 & 0 \\ 0 & {{\mathbf{D}}_{k,l}^{VV} } & 0 \\ 0 & 0 & {{\mathbf{D}}_{k,l}^{WW} } \\ \end{array} } \right]$$

(18)

where

$${\mathbf{D}}_{k,l}^{UU} = {\mathbf{D}}_{k,l}^{VV} = - K_{T}^{{{\text{Side}}2}} b_{k} \phi_{m} \left( 1 \right)\phi_{n} \left( 0 \right){\mathbf{F}}_{ij}^{{\left( {0,0} \right)}}$$

(19a)

$${\mathbf{D}}_{k,l}^{WW} = - K_{T}^{{{\text{Side}}2}} b_{k} \phi_{m} \left( 1 \right)\phi_{n} \left( 0 \right){\mathbf{F}}_{ij}^{{\left( {0,0} \right)}} - K_{R}^{{{\text{Side}}2}} b_{k} \frac{{\phi^{\prime}_{m} \left( 1 \right)\phi^{\prime}_{n} \left( 0 \right)}}{{a_{k} a_{l} }}{\mathbf{F}}_{ij}^{{\left( {0,0} \right)}}$$

(19b)

If, according to Fig. 2a, the partition $k$ is connected to the partition $p$, then one can write

$${\mathbf{D}}_{k,p}^{UU} = {\mathbf{D}}_{k,p}^{VV} = - K_{T}^{{{\text{Side}}3}} a_{k} {\mathbf{E}}_{mn}^{{\left( {0,0} \right)}} \psi_{i} \left( 1 \right)\phi_{j} \left( 0 \right)$$

(20a)

$${\mathbf{D}}_{k,p}^{WW} = - K_{T}^{{{\text{Side}}3}} a_{k} {\mathbf{E}}_{mn}^{{\left( {0,0} \right)}} \psi_{i} \left( 1 \right)\phi_{j} \left( 0 \right) - K_{R}^{{{\text{Side}}3}} a_{k} {\mathbf{E}}_{mn}^{{\left( {0,0} \right)}} \frac{{\psi ^{\prime}_{m} \left( 1 \right)\psi ^{\prime}_{n} \left( 0 \right)}}{{b_{k} b_{l} }}$$

(20b)