Robust Model Structure Recovery for Ultra-High-Dimensional Varying-Coefficient Models

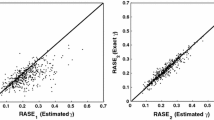
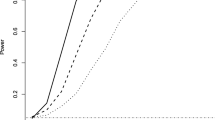
Abstract

As an important extension of the varying-coefficient model, the partially linear varying-coefficient model has been widely studied in the literature. It is vital that how to simultaneously eliminate the redundant covariates and separate the varying and nonzero constant coefficients for varying-coefficient models. In this paper, we consider the penalized composite quantile regression to explore the model structure of ultra-high-dimensional varying-coefficient models. Under some regularity conditions, we study the convergence rate and asymptotic normality of the oracle estimator and prove that, with probability approaching one, the oracle estimator is a local solution of the nonconvex penalized composite quantile regression. Simulation studies indicate that the novel method as well as the oracle method performs in both low dimension and high dimension cases. An environmental data application is also analyzed by utilizing the proposed procedure.

Appendix

Let C denote a generic constant that might assume different values at different places. To facilitate the proof, we define

$$\begin{aligned}{} & {} \varPi =({\textbf{B}}(U_1,{\textbf{x}}^{v}_{1}), \ldots , {\textbf{B}}(U_n,{\textbf{x}}^{v}_{n}))^{\top },~~H=({\textbf{B}}(U_1), \ldots , {\textbf{B}}(U_n))^{\top },\\{} & {} W=\text{ diag }(w_1,\ldots ,w_n),~~{\textbf{w}}=(w_1,\ldots ,w_n)^{\top },\\{} & {} \varPi _W^2=\varPi ^{\top }W\varPi ,~~\widehat{{\textbf{B}}}(U_i,{\textbf{x}}^{v}_{i})=\varPi _W^{-1}{\textbf{B}}(U_i,{\textbf{x}}^{v}_{i}),\\{} & {} P=\varPi (\varPi ^\top W\varPi )^{-1}\varPi ^{\top }W,~~{\textbf{X}}^{c*}=(I-P){\textbf{X}}^c,~~A=\text{ diag }(\sigma _1,\ldots ,\sigma _n),\\{} & {} \varLambda _n^*=\frac{1}{n}{\textbf{X}}^{c*\top }A{\textbf{X}}^{c*}=\frac{1}{n}\sum _{i=1}^n{ \sigma _i {\textbf{x}}^{c*}_i {\textbf{x}}^{c*\top }_i },\\{} & {} S_n^*=\frac{1}{n}{\textbf{X}}^{c*\top }W{\textbf{X}}^{c*}=\frac{1}{n}\sum _{i=1}^n{ w_i {\textbf{x}}^{c*}_i {\textbf{x}}^{c*\top }_i },\\{} & {} \varvec{\gamma }_{0v}=(\varvec{\gamma }_{0j}^\top ,j\in S_v)^\top ,~\varvec{\alpha }_{0}^{v}(u)=(\alpha _{0j}(u),j\in S_v)^{\top },\\{} & {} r_{ni}={\textbf{B}}(U_i,{\textbf{x}}^{v}_{i})^\top \varvec{\gamma }_{0v}-{\textbf{x}}^{v\top }_{i}\varvec{\alpha }_{0}^{v}(U_i), \tilde{{\textbf{x}}}^{c}_i=n^{-1/2}{\textbf{x}}^{c*}_i,\\{} & {} {\textbf{b}}=(b_{\tau _1},\ldots ,b_{\tau _K})^\top , ~~{\textbf{b}}_0=(b_{0\tau _1},\ldots ,b_{0\tau _K})^\top , ~~\varvec{\omega }=\sqrt{n}({\textbf{b}}-{\textbf{b}}_0),\\{} & {} \varvec{\theta }_1=\sqrt{n}(\varvec{\beta }_c-\varvec{\beta }_{0c}), ~~ \varvec{\theta }_2=\varPi _W(\varvec{\gamma }_v-\varvec{\gamma }_{0v})+\varPi _W^{-1}\varPi ^\top W{\textbf{X}}^c(\varvec{\beta }_c-\varvec{\beta }_{0c}). \end{aligned}$$

We first give some technical lemmas which will be frequently used in the subsequent proof.

Lemma 8.1

Under conditions (C1)–(C6), the following properties hold:

• (a) $\sup _{i}|r_{ni}|=O_p(\sqrt{p_{n2}}m_n^{-r})$,

• (b) The eigenvalues of $\frac{m_n}{n}\varPi ^{\top }\varPi$ and $\frac{m_n}{n}H^{\top }H$ are bounded in probability,

• (c) $\max _{i}\Vert \widehat{{\textbf{B}}}(U_i,{\textbf{x}}^{v}_{i})\Vert =O_p(\sqrt{p_{n2}m_n/n})$,

• (d) $\sum _{i=1}^n{ w_i\tilde{{\textbf{x}}}^{c}_i\widehat{{\textbf{B}}}(U_i,{\textbf{x}}^{v}_{i})^{\top } }=0$.

Proof

(a) Note that ${\textbf{B}}(U_i,{\textbf{x}}_{i})=\left( X_{i1}{\textbf{B}}(U_i)^{\top },\ldots ,X_{ip_n}{\textbf{B}}(U_i)^{\top } \right) ^{\top }$, based on the result (2.3) and condition (C4), we have

$$\begin{aligned} \sup _{i}|r_{ni}|^2= & {} \sup _{i}|{\textbf{B}}(U_i,{\textbf{x}}^{v}_{i})^\top \varvec{\gamma }_{0v}-{\textbf{x}}^{v\top }_{i}\varvec{\alpha }_{0}^{v}(U_i)|^2\\\le & {} \sup _{i}\lambda _{\max }({\textbf{x}}^{v}_{i}{\textbf{x}}^{v\top }_{i})\sum _{j\in S_v} ({\textbf{B}}(U_i)^{\top }\varvec{\gamma }_{0j}-\alpha _{0j}(U_i))^2 \\\rightarrow & {} \sup _{i}\lambda _{\max }(E[{\textbf{x}}^{v}_{i}{\textbf{x}}^{v\top }_{i}|U_i])\sum _{j\in S_v} ({\textbf{B}}(U_i)^{\top }\varvec{\gamma }_{0j}-\alpha _{0j}(U_i))^2 \\\le & {} \sup _{i}\lambda _{\max }(E[{\textbf{x}}^{v}_{i}{\textbf{x}}^{v\top }_{i}|U_i])\sum _{j\in S_v}{ \sup _{i}({\textbf{B}}(U_i)^{\top }\varvec{\gamma }_{0j}-\alpha _{0j}(U_i))^2 }\\= & {} O_p(p_{n2}m_n^{-2r}), \end{aligned}$$

which implies the result of (a).

(b) This conclusion can be directly obtained from lemma A.4 of [18], so we omit its proof here.

(c) It is obvious that $\Vert \varPi _W^{-1}\Vert =O_p(\sqrt{m_n/n})$ by result (b) and condition (C3). Moreover, from the definition of ${\textbf{B}}(U_i,{\textbf{x}}^{v}_{i})$, we can verify $\Vert {\textbf{B}}(U_i,{\textbf{x}}^{v}_{i})\Vert =O_p(\sqrt{p_{n2}})$ by noting that $E(B_j^2(U))=m_n^{-1}$, $j=1,\ldots ,m_n$. Then, we have

$$\begin{aligned} \Vert \widehat{{\textbf{B}}}(U_i,{\textbf{x}}^{v}_{i})\Vert= & {} \Vert \varPi _W^{-1}{\textbf{B}}(U_i,{\textbf{x}}^{v}_{i})\Vert \le \Vert \varPi _W^{-1}\Vert \Vert \widehat{{\textbf{B}}}(U_i,{\textbf{x}}^{v}_{i})\Vert \\= & {} O_p(\sqrt{m_n/n}\sqrt{p_{n2}})=O_p(\sqrt{p_{n2}m_n/n}). \end{aligned}$$

(d) As $W\varPi -P^{\top }W\varPi =W\varPi -W\varPi (\varPi ^{\top }W\varPi )^{-1}\varPi ^{\top }W\varPi =W\varPi -W\varPi =0$, then

$$\begin{aligned} \sum _{i=1}^n{ w_i\tilde{{\textbf{x}}}^{c}_i\widehat{{\textbf{B}}}(U_i,{\textbf{x}}^{v}_{i})^{\top } }= & {} n^{-1/2}{\textbf{X}}^{c*\top }W\varPi \varPi _W^{-1}=n^{-1/2}{\textbf{X}}^{c\top }(I-P^\top )W\varPi \varPi _W^{-1} \\= & {} n^{-1/2}{\textbf{X}}^{c\top }(W\varPi -P^{\top }W\varPi )\varPi _W^{-1}=0. \end{aligned}$$

$\square$

Lemma 8.2

Under conditions (C1)–(C7), we have

• (a) The eigenvalues of ${\textbf{X}}^{c*\top }{\textbf{X}}^{c*}/n$ are bounded in probability,

• (b) $S_n^*=S_n+o_p(1)$ and $\varLambda _n^*=\varLambda _n+o_p(1)$.

Proof

(a) Note that

$$\begin{aligned} \lambda _{\max }({\textbf{X}}^{c*\top }{\textbf{X}}^{c*}/n)=\lambda _{\max }(n^{-1}{\textbf{X}}^{c\top }(I-P)^{\top }(I-P){\textbf{X}}^{c})\le \lambda _{\max }(n^{-1}{\textbf{X}}^{c\top }{\textbf{X}}^{c}). \end{aligned}$$

Thus, (a) is derived by condition (C4) and the fact that $I-P$ is a projection matrix.

(b) Recall that ${\textbf{X}}^c=\varvec{\varPhi }^*+\varvec{\varDelta }_n$, then $n^{-1/2}{\textbf{X}}^{c*}=n^{-1/2}(I-P){\textbf{X}}^{c}=n^{-1/2}\varvec{\varDelta }_n+n^{-1/2}(\varvec{\varPhi }^*-P{\textbf{X}}^{c})$. For $l=1,\ldots ,p_{n1}$, let $\varvec{\gamma }_l^* \in R^{m_n}$ be defined as the following weighted least-squares problem, that is $\varvec{\gamma }_l^*=\arg \min _{\varvec{\gamma }}\sum _{i=1}^n{ w_i (X_{il}-{\textbf{B}}(U_i,{\textbf{x}}^{v}_{i})^{\top }\varvec{\gamma }_l)^2 }$. Further define $\hat{\phi }_l(U_i,{\textbf{x}}^{v}_{i})={\textbf{B}}(U_i,{\textbf{x}}^{v}_{i})^{\top }\varvec{\gamma }_l^*$, we can obtain that the (i, l)th element of $P{\textbf{X}}^{c}$ is $\hat{\phi }_l(U_i,{\textbf{x}}^{v}_{i})$ actually. Taking into account of conditions (C1), (C2) and (C4), it follows from Theorem 1 of [33] that $(\phi _l^*(U_i, {\textbf{x}}^v_i)-\hat{\phi }_l(U_i,{\textbf{x}}^v_i))^2=O_p\left( p_{n2}n^{-2r/(2r+1)} \right)$. Therefore,

$$\begin{aligned} n^{-1}\Vert \varvec{\varPhi }^*-P{\textbf{X}}^{c}\Vert ^2= & {} n^{-1}\lambda _{\max }\{ (\varvec{\varPhi }^*-P{\textbf{X}}^{c})^{\top }(\varvec{\varPhi }^*-P{\textbf{X}}^{c}) \} \\\le & {} n^{-1}\text{ trace }\{(\varvec{\varPhi }^*-P{\textbf{X}}^{c})^{\top }(\varvec{\varPhi }^*-P{\textbf{X}}^{c}) \}\\= & {} n^{-1}\sum _{i=1}^n{ \sum _{l=1}^{p_{n1}} { (\phi _l^*(U_i, {\textbf{x}}^v_i)-\hat{\phi }_l(U_i, {\textbf{x}}^v_i))^2 }}\\= & {} O_p\left( p_{n1}p_{n2}n^{-2r/(2r+1)} \right) =o_p(1), \end{aligned}$$

where the last equality holds due to condition (C7).

Consequently, we have $n^{-1/2}{\textbf{X}}^{c*}=n^{-1/2}\varvec{\varDelta }_n+o_p(1)$ and

$$\begin{aligned} S_n^*= & {} (n^{-1/2}{\textbf{X}}^{c*\top })W(n^{-1/2}{\textbf{X}}^{c*})\\= & {} n^{-1}\varvec{\varDelta }_n^{\top }W\varvec{\varDelta }_n + n^{-1/2}\varvec{\varDelta }_n^{\top }W o_P(1)+o_P(1)=S_n+o_p(1), \end{aligned}$$

where the last equality holds because $n^{-1/2}\varvec{\varDelta }_n^{\top }W=O_p(1)$ from conditions (C4) and (C5). Similarly, we can prove $\varLambda _n^*=\varLambda _n+o_p(1)$. $\square$

Note that

$$\begin{aligned}{} & {} \frac{1}{n}\sum _{k=1}^K { \sum _{i=1}^n { \rho _{\tau _k}\left( Y_i-b_{\tau _k}-{\textbf{x}}^{c\top }_{i}\varvec{\beta }_c-{\textbf{B}}(U_i,{\textbf{x}}^v_{i})^{\top } \varvec{\gamma }_v \right) }}\\{} & {} \quad =\frac{1}{n}\sum _{k=1}^K { \sum _{i=1}^n { \rho _{\tau _k}\left( \varepsilon _{ik}-\varvec{\nu }_k^{\top }\varvec{\omega }-\tilde{{\textbf{x}}}^{c\top }_{i}\varvec{\theta }_1-\widehat{{\textbf{B}}}(U_i,{\textbf{x}}^{v}_{i})^{\top } \varvec{\theta }_2-r_{ni} \right) }}, \end{aligned}$$

where $\varvec{\nu }_k=e_k/\sqrt{n}$, $e_k=(0,\ldots ,0,1,0,\ldots ,0)^{\top } \in R^K$ is a unit vector with the kth element being 1. Define

$$\begin{aligned} (\widehat{\varvec{\omega }},\widehat{\varvec{\theta }}_1,\widehat{\varvec{\theta }}_2)=\arg \min _{(\varvec{\omega },\varvec{\theta }_1,\varvec{\theta }_2)}\frac{1}{n}\sum _{k=1}^K { \sum _{i=1}^n { \rho _{\tau _k}\left( \varepsilon _{ik}-\varvec{\nu }_k^{\top }\varvec{\omega }-\tilde{{\textbf{x}}}^{c\top }_{i}\varvec{\theta }_1-\widehat{{\textbf{B}}}(U_i,{\textbf{x}}^{v}_{i})^{\top } \varvec{\theta }_2-r_{ni} \right) }}. \end{aligned}$$

Lemma 8.3

Let $\widetilde{\varvec{\theta }}_1=\sqrt{n}({\textbf{X}}^{c*\top }W{\textbf{X}}^{c*})^{-1}{\textbf{X}}^{c*\top }{\textbf{w}}$. Under conditions (C1)–(C7), we have (a) $\Vert \widetilde{\varvec{\theta }}_1\Vert =O_p(\sqrt{p_{n1}})$; (b) $\Vert \widehat{\varvec{\theta }}_1-\widetilde{\varvec{\theta }}_1\Vert =o_p(1)$.

Proof

(a) From the proof of Lemma 8.2 (b), we have $n^{-1/2}{\textbf{X}}^{c*}=n^{-1/2}\varvec{\varDelta }_n+o_P(1)$ and $n^{-1}{\textbf{X}}^{c*\top }W{\textbf{X}}^{c*}=S_n+o_p(1)$. Then, $\widetilde{\varvec{\theta }}_1=S_n^{*-1}(n^{-1/2}{\textbf{X}}^{c*\top }{\textbf{w}})=S_n^{*-1}(( n^{-1/2}\varvec{\varDelta }_n+o_p(1))^{\top }{\textbf{w}})$, which implies $\Vert \widetilde{\varvec{\theta }}_1\Vert =O_P(\sqrt{p_{n1}})$ by conditions (C3) and (C5).

(b) Define

$$\begin{aligned} R_i(\varvec{\omega },\varvec{\theta }_1,\widetilde{\varvec{\theta }}_1,\varvec{\theta }_2)= & {} \sum _{k=1}^K{ \rho _{\tau _k}\left( \varepsilon _{ik}-\nu _k^{\top }\varvec{\omega }-\tilde{{\textbf{x}}}^{c\top }_{i}\varvec{\theta }_1-\widehat{{\textbf{B}}}(U_i,{\textbf{x}}^{v}_{i})^{\top } \varvec{\theta }_2-r_{ni} \right) }\\{} & {} -\sum _{k=1}^K{ \rho _{\tau _k}\left( \varepsilon _{ik}-\nu _k^{\top }\varvec{\omega }-\tilde{{\textbf{x}}}^{c\top }_{i}\widetilde{\varvec{\theta }}_1-\widehat{{\textbf{B}}}(U_i,{\textbf{x}}^{v}_{i})^{\top } \varvec{\theta }_2-r_{ni} \right) . } \end{aligned}$$

Let $d_n=p_{n1}+p_{n2}m_n$, by the results of Lemmas 8.1$-$8.3 in [42] and Lemma 8.1 (d) that ${\textbf{X}}^{c*}$ is orthogonality to $W\varPi$, we have, for any finite positive constant M,

$$\begin{aligned}{} & {} \sup _{\begin{array}{c} \Vert \varvec{\theta }_1-\widetilde{\varvec{\theta }}_1\Vert \le M \\ \Vert \varvec{\theta }_2\Vert \le C\sqrt{d_n} \end{array} } \left| \sum _{i=1}^n \left\{ R_i(\varvec{\omega },\varvec{\theta }_1,\widetilde{\varvec{\theta }}_1,\varvec{\theta }_2)- E(R_i(\varvec{\omega },\varvec{\theta }_1,\widetilde{\varvec{\theta }}_1,\varvec{\theta }_2))\right. \right. \\{} & {} \left. \left. + (\varvec{\theta }_1-\widetilde{\varvec{\theta }}_1)^{\top }\tilde{{\textbf{x}}}^{c}_{i}\sum _{k=1}^K{ \psi _{\tau _k}(\varepsilon _{ik}) } \right\} \right| =o_p(1), \\{} & {} \sup _{\begin{array}{c} \Vert \varvec{\theta }_1-\widetilde{\varvec{\theta }}_1\Vert \le M \\ \Vert \varvec{\theta }_2\Vert \le C\sqrt{d_n} \end{array} } \left| \sum _{i=1}^n{ E(R_i(\varvec{\omega },\varvec{\theta }_1,\widetilde{\varvec{\theta }}_1,\varvec{\theta }_2)) } - \frac{1}{2}(\varvec{\theta }_1^{\top }S_n\varvec{\theta }_1-\widetilde{\varvec{\theta }}_1^{\top }S_n\widetilde{\varvec{\theta }}_1)\right| =o_p(1), \end{aligned}$$

where $E(R_i(\varvec{\omega },\varvec{\theta }_1,\widetilde{\varvec{\theta }}_1,\varvec{\theta }_2))$ denotes the condition expectation $E(R_i(\varvec{\omega },\varvec{\theta }_1,\widetilde{\varvec{\theta }}_1,\varvec{\theta }_2)\mid {\textbf{x}}_i, U_i)$. Applying the triangle inequality to above two expressions yields

$$\begin{aligned}{} & {} \sup _{\begin{array}{c} \Vert \varvec{\theta }_1-\widetilde{\varvec{\theta }}_1\Vert \le M \\ \Vert \varvec{\theta }_2\Vert \le C\sqrt{d_n} \end{array} } \Bigg | \sum _{i=1}^n{ \left\{ R_i(\varvec{\omega },\varvec{\theta }_1,\widetilde{\varvec{\theta }}_1,\varvec{\theta }_2) + (\varvec{\theta }_1-\widetilde{\varvec{\theta }}_1)^{\top }\tilde{{\textbf{x}}}^{c}_{i}\sum _{k=1}^K{ \psi _{\tau _k}(\varepsilon _{ik}) } \right\} } \\{} & {} ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~- \frac{1}{2}(\varvec{\theta }_1^{\top }S_n\varvec{\theta }_1-\widetilde{\varvec{\theta }}_1^{\top }S_n\widetilde{\varvec{\theta }}_1)\Bigg |=o_p(1). \end{aligned}$$

In addition, based on previous arguments in the proof of (a), we have

$$\begin{aligned} \sum _{i=1}^n\left[ (\varvec{\theta }_1-\widetilde{\varvec{\theta }}_1)^{\top }\tilde{{\textbf{x}}}^{c}_{i}\sum _{k=1}^K{ \psi _{\tau _k}(\varepsilon _{ik}) }\right]= & {} (\varvec{\theta }_1-\widetilde{\varvec{\theta }}_1)^{\top }{\textbf{X}}^{c*\top }(W+o_P(1))/\sqrt{n}\\= & {} (\varvec{\theta }_1-\widetilde{\varvec{\theta }}_1)^{\top }S_n\widetilde{\varvec{\theta }}_1, \end{aligned}$$

which means

$$\begin{aligned}{} & {} \sum _{i=1}^n\left[ (\varvec{\theta }_1-\widetilde{\varvec{\theta }}_1)^{\top }\tilde{{\textbf{x}}}^{c}_{i}\sum _{k=1}^K{ \psi _{\tau _k}(\varepsilon _{ik}) }\right] - \frac{1}{2}(\varvec{\theta }_1^{\top }S_n\varvec{\theta }_1-\widetilde{\varvec{\theta }}_1^{\top }S_n\widetilde{\varvec{\theta }}_1)\\= & {} (\varvec{\theta }_1-\widetilde{\varvec{\theta }}_1)^{\top }S_n\widetilde{\varvec{\theta }}_1 - \frac{1}{2}(\varvec{\theta }_1^{\top }S_n\varvec{\theta }_1-\widetilde{\varvec{\theta }}_1^{\top }S_n\widetilde{\varvec{\theta }}_1)\\= & {} -\frac{1}{2}(\varvec{\theta }_1-\widetilde{\varvec{\theta }}_1)^{\top }S_n(\varvec{\theta }_1-\widetilde{\varvec{\theta }}_1). \end{aligned}$$

Therefore, it follows that

$$\begin{aligned} \sup _{\begin{array}{c} \Vert \varvec{\theta }_1-\widetilde{\varvec{\theta }}_1\Vert \le M \\ \Vert \varvec{\theta }_2\Vert \le C\sqrt{d_n} \end{array} } \left| \sum _{i=1}^n{ R_i(\varvec{\omega },\varvec{\theta }_1,\widetilde{\varvec{\theta }}_1,\varvec{\theta }_2) } -\frac{1}{2}(\varvec{\theta }_1-\widetilde{\varvec{\theta }}_1)^{\top }S_n(\varvec{\theta }_1-\widetilde{\varvec{\theta }}_1) \right| =o_p(1). \end{aligned}$$

On the other hand, condition (C5) indicates $\frac{1}{2}(\varvec{\theta }_1-\widetilde{\varvec{\theta }}_1)^{\top }S_n(\varvec{\theta }_1-\widetilde{\varvec{\theta }}_1)>CM^2$ for any $\Vert \varvec{\theta }_1-\widetilde{\varvec{\theta }}_1\Vert >M$ and some finite constant $C>0$. This means

$$\begin{aligned} \lim _{n \rightarrow \infty } P \left\{ \inf _{\begin{array}{c} \Vert \varvec{\theta }_1-\widetilde{\varvec{\theta }}_1\Vert \le M \\ \Vert \varvec{\theta }_2\Vert \le C\sqrt{d_n} \end{array}} \sum _{i=1}^n{ R_i(\varvec{\omega },\varvec{\theta }_1,\widetilde{\varvec{\theta }}_1,\varvec{\theta }_2) }>0 \right\} =1. \end{aligned}$$

(8.1)

By the definition of $\widehat{\varvec{\theta }}_1$ and the convexity of function $\rho _{\tau _k}(\cdot )$, $k=1,\ldots ,K$, (8.1) implies that $P(\Vert \varvec{\theta }_1-\widetilde{\varvec{\theta }}_1\Vert >M)\rightarrow 0$ for any finite $M>0$ as $n\rightarrow \infty$, that is $\Vert \varvec{\theta }_1-\widetilde{\varvec{\theta }}_1\Vert =o_p(1)$. This completes the proof. $\square$

Proof of Theorem 3.4

• (i) This proof is directly followed by the results (a) and (b) of Lemma 8.3.

• (ii) We keep using the notations in Lemma 8.3 and further introduce some definitions. Let $a_n$ be a sequence of positive numbers and $\varvec{\vartheta }=(\varvec{\omega }^{\top },\varvec{\theta }_1^{\top },\varvec{\theta }_2^{\top })^{\top }$. Define

  $$\begin{aligned} Q_i(\varvec{\vartheta },a_n)= & {} \sum _{k=1}^K{ \rho _{\tau _k}\left( \varepsilon _{ik}-a_n\varvec{\nu }_k^T\varvec{\omega }-a_n\tilde{{\textbf{x}}}^{c\top }_{i}\varvec{\theta }_1-a_n\widehat{{\textbf{B}}}(U_i,{\textbf{x}}^v_{i})^{\top } \varvec{\theta }_2-r_{ni} \right) }, \\ D_i(\varvec{\vartheta },a_n)= & {} Q_i(\varvec{\vartheta },a_n)-Q_i(\varvec{\vartheta },0)-E(Q_i(\varvec{\vartheta },a_n)-Q_i(\varvec{\vartheta },0))\\ {}{} & {} +a_n \sum _{k=1}^K{(\varvec{\nu }_k^T\varvec{\omega }+\tilde{{\textbf{x}}}^{c\top }_{i}\varvec{\theta }_1+\widehat{{\textbf{B}}}(U_i,{\textbf{x}}^v_{i})^{\top } \varvec{\theta }_2) \psi _{\tau _k}( \varepsilon _{ik}) }. \end{aligned}$$

Observing that $\rho _{\tau }(u)=|u|/2+(\tau -1/2)u$, then

$$\begin{aligned}{} & {} Q_i(\varvec{\vartheta },a_n)-Q_i(\varvec{\vartheta },0)\\= & {} \sum _{k=1}^K{ \frac{1}{2}\left\{ |\varepsilon _{ik}-a_n\varvec{\nu }_k^T\varvec{\omega }-a_n\tilde{{\textbf{x}}}^{c\top }_{i}\varvec{\theta }_1-a_n\widehat{{\textbf{B}}}(U_i,{\textbf{x}}^v_{i})^{\top } \varvec{\theta }_2-r_{ni}|-|\varepsilon _{ik}-r_{ni}| \right\} }\\{} & {} + a_n \sum _{k=1}^K{ (\tau _k-1/2)} \left\{ \varvec{\nu }_k^T\varvec{\omega }+ \tilde{{\textbf{x}}}^{c\top }_{i}\varvec{\theta }_1 + \widehat{{\textbf{B}}}(U_i,{\textbf{x}}^v_{i})^{\top } \varvec{\theta }_2\right\} . \end{aligned}$$

Let

$$\begin{aligned} Q_i^*(\varvec{\vartheta },a_n)=\sum _{k=1}^K{ \frac{1}{2}\left\{ |\varepsilon _{ik}-a_n\varvec{\nu }_k^T\varvec{\omega }-a_n\tilde{{\textbf{x}}}^{c\top }_{i}\varvec{\theta }_1-a_n\widehat{{\textbf{B}}}(U_i,{\textbf{x}}^v_{i})^{\top } \varvec{\theta }_2-r_{ni}|-|\varepsilon _{ik}-r_{ni}| \right\} }, \end{aligned}$$

and $D_i(\varvec{\vartheta },a_n)$ can be rewritten as

$$\begin{aligned} D_i(\varvec{\vartheta },a_n)= & {} Q_i^*(\varvec{\vartheta },a_n)-E(Q_i^*(\varvec{\vartheta },a_n))+a_n \sum _{k=1}^K{\psi _{\tau _k}( \varepsilon _{ik}) }\left\{ \varvec{\nu }_k^T\varvec{\omega }\right. \\{} & {} \left. + \tilde{{\textbf{x}}}^{c\top }_{i}\varvec{\theta }_1 + \widehat{{\textbf{B}}}(U_i,{\textbf{x}}^v_{i})^{\top } \varvec{\theta }_2 \right\} . \end{aligned}$$

We first prove that for any given $\varpi >0$, there exists a constant $L>0$ satisfying

$$\begin{aligned} P\left\{ \inf _{\Vert \varvec{\vartheta }\Vert <L} d_n^{-1} \sum _{i=1}^n{ \left( Q_i(\varvec{\vartheta },\sqrt{d_n})-Q_i(\varvec{\vartheta },0)\right) \ge 0} \right\} \ge 1-\varpi . \end{aligned}$$

(8.2)

Since

$$\begin{aligned}{} & {} d_n^{-1} \sum _{i=1}^n{ \left( Q_i(\varvec{\vartheta },\sqrt{d_n})-Q_i(\varvec{\vartheta },0) \right) } \\{} & {} =d_n^{-1}\sum _{i=1}^n{D_i(\varvec{\vartheta },\sqrt{d_n})}+d_n^{-1}\sum _{i=1}^n{ E(Q_i(\varvec{\vartheta },\sqrt{d_n})-Q_i(\varvec{\vartheta },0))} \\{} & {} ~~- d_n^{-1/2}\sum _{k=1}^K{(\varvec{\nu }_k^T\varvec{\omega }+\tilde{{\textbf{x}}}^{c\top }_{i}\varvec{\theta }_1+\widehat{{\textbf{B}}}(U_i,{\textbf{x}}^v_{i})^{\top } \varvec{\theta }_2) \psi _{\tau _k}( \varepsilon _{ik}) }\\{} & {} \triangleq \var** _1+\var** _2+\var** _3. \end{aligned}$$

Following the similar arguments in the proof of Lemma B.1 in [32], we can verify

$$\begin{aligned} \sup _{\Vert \varvec{\vartheta }\Vert <L}\left| \sum _{i=1}^n{D_i(\varvec{\vartheta },\sqrt{d_n})} \right| =o_p(d_n) \end{aligned}$$

under conditions $p_{n2}^3/m_n^{2(r-1)}\rightarrow 0$ and $p_{n1}/(m_np_{n2})\rightarrow 0$. Thus $\var** _1=o_p(1)$.

Let $s_{ni}=\varvec{\nu }_k^T\varvec{\omega }+\tilde{{\textbf{x}}}^{c\top }_{i}\varvec{\theta }_1+\widehat{{\textbf{B}}}(U_i,{\textbf{x}}^v_{i})^{\top } \varvec{\theta }_2$, applying the Knight’s identity to $\var** _2$ yields

$$\begin{aligned} \var** _2= & {} d_n^{-1}\sum _{i=1}^n{ E\left\{ \sum _{k=1}^K{ \int _{r_{ni}}^{\sqrt{d_n}s_{ni}+r_{ni}}[I(\varepsilon _{ik}<t)-I(\varepsilon _{ik}<0)]dt } \mid ({\textbf{x}}_i,U_i) \right\} }\\= & {} d_n^{-1}\sum _{i=1}^n{ \sum _{k=1}^K{ \int _{r_{ni}}^{\sqrt{d_n}s_{ni}+r_{ni}}f_i(b_{0\tau _k})t(1+o(1))dt }} \\= & {} d_n^{-1}\sum _{i=1}^n{ \left\{ \sum _{k=1}^K{f_i(b_{0\tau _k})} \left[ \frac{1}{2}d_ns_{ni}^2+\sqrt{d_n}s_{ni}r_{ni}\right] \right\} (1+o(1)) } \\= & {} C(1+o(1))\varvec{\omega }^{\top } \left\{ \sum _{i=1}^n{ \sum _{k=1}^K{f_i(b_{0\tau _k})}\varvec{\nu }_k\varvec{\nu }_k^{\top } }\right\} \varvec{\omega }\\{} & {} \quad + C(1+o(1))\varvec{\theta }_1^{\top } \left\{ \frac{1}{n}\sum _{i=1}^n{ w_i {\textbf{x}}^{c*}_{i}{\textbf{x}}^{c*\top }_{i}} \right\} \varvec{\theta }_1 \\{} & {} \quad +C(1+o(1))\varvec{\theta }_2^{\top } \left\{ \frac{1}{n}\sum _{i=1}^n{ w_i \widehat{{\textbf{B}}}(U_i,{\textbf{x}}^v_{i})\widehat{{\textbf{B}}}(U_i,{\textbf{x}}^v_{i})^{\top } } \right\} \varvec{\theta }_2 +C(1+o(1))\times \\{} & {} \left\{ \varvec{\omega }^{\top } \left[ \sum _{i=1}^n{ \sum _{k=1}^K{f_i(b_{0\tau _k})}\varvec{\nu }_k\tilde{{\textbf{x}}}^{c\top }_{i} }\right] \varvec{\theta }_1 + \varvec{\omega }^{\top } \left[ \sum _{i=1}^n{ \sum _{k=1}^K{f_i(b_{0\tau _k})}\varvec{\nu }_k\widehat{{\textbf{B}}}(U_i,{\textbf{x}}^v_{i})^{\top } }\right] \varvec{\theta }_2\right\} \\{} & {} \quad +d_n^{-1/2}(1+o(1))\sum _{i=1}^n{ \sum _{k=1}^K{ f_i(b_{0\tau _k}) }r_{ni} (\varvec{\nu }_k^{\top }\varvec{\omega }+\tilde{{\textbf{x}}}^{c\top }_{i}\varvec{\theta }_1+\widehat{{\textbf{B}}}(U_i,{\textbf{x}}^v_{i})^{\top } \varvec{\theta }_2) } \\\triangleq & {} \var** _{21}+\var** _{22}+\var** _{23}+\var** _{24}+\var** _{25}, \end{aligned}$$

where the fourth equality holds by Lemma 8.1 (d) that $\sum _{i=1}^n{ w_i\tilde{{\textbf{x}}}^{c}_i\widehat{{\textbf{B}}}(U_i,{\textbf{x}}^{v}_{i})^{\top } }=0$. Based on conditions (C3) and (C7), Lemma 8.1 (c), Lemma 8.2 as well as the constraint $\Vert \varvec{\vartheta }\Vert <L$, we can obtain that $\var** _{21}=O_p(\Vert \varvec{\omega }\Vert ^2)$, $\var** _{22}=O_p(\Vert \varvec{\theta }_1\Vert ^2)$, $\var** _{23}=O_p(\Vert \varvec{\theta }_2\Vert ^2)$ and $\var** _{24}=O_p(1)$.

For the term $\var** _{25}$, as $\Vert {\textbf{r}}_n\Vert =O_p(\sqrt{np_{n2}}m_n^{-r})$ by Lemma 8.1 (a), where ${\textbf{r}}_n=(r_{n1},\ldots ,r_{nn})^{\top }$. Obviously, $d_n^{-1/2}\sum _{i=1}^n{ \sum _{k=1}^K{ f_i(b_{0\tau _k}) }r_{ni} \varvec{\nu }_k^{\top }\varvec{\omega }}=O_p(\Vert \varvec{\omega }\Vert )$. Moreover, it follows from conditions (C3) and (C4), Lemma 8.2 (a) and the Cauchy–Schwarz inequality that

$$\begin{aligned}{} & {} d_n^{-1/2}\sum _{i=1}^n{ \sum _{k=1}^K{f_i(b_{0\tau _k})} r_{ni} \tilde{{\textbf{x}}}^{c\top }_{i}\varvec{\theta }_1 }= d_n^{-1/2}\sum _{i=1}^n{ w_ir_{ni} \tilde{{\textbf{x}}}^{c\top }_{i}\varvec{\theta }_1 }=(nd_n)^{-1/2}\varvec{\theta }_1^{\top }{\textbf{X}}^{c*\top }W{\textbf{r}}_n\\\le & {} d_n^{-1/2}\Vert n^{-1/2}{\textbf{X}}^{c*}\varvec{\theta }_1\Vert \Vert W{\textbf{r}}_n\Vert =O_p(d_n^{-1/2}\sqrt{np_{n2}}m_n^{-r})\Vert \varvec{\theta }_1\Vert =O_p(\Vert \varvec{\theta }_1\Vert ), \end{aligned}$$

where the last equality holds by the condition $p_{n1}/(m_np_{n2})\rightarrow 0$ in condition (C7). Similarly,

$$\begin{aligned}{} & {} d_n^{-1/2}\sum _{i=1}^n{ \sum _{k=1}^K{f_i(b_{0\tau _k})} r_{ni} \widehat{{\textbf{B}}}(U_i,{\textbf{x}}^v_{i})^{\top } \varvec{\theta }_2 } \\= & {} d_n^{-1/2}\sum _{i=1}^n{ w_ir_{ni} \widehat{{\textbf{B}}}(U_i,{\textbf{x}}^v_{i})^{\top } \varvec{\theta }_2 }=d_n^{-1/2}\varvec{\theta }_2^{\top }\varPi _W^{-1}\varPi ^{\top }W{\textbf{r}}_n\\\le & {} d_n^{-1/2}\Vert \varvec{\theta }_2^{\top }\varPi _W^{-1}\varPi ^{\top }W^{1/2}\Vert \Vert W^{1/2}{\textbf{r}}_n\Vert =O_p(d_n^{-1/2}\sqrt{np_{n2}}m_n^{-r})\Vert \varvec{\theta }_2\Vert =O_p(\Vert \varvec{\theta }_2\Vert ). \end{aligned}$$

Hence, $\var** _2=O_p(\Vert \varvec{\vartheta }\Vert )$.

In the next, we consider $\var** _3$. Obviously, $E(\var** _3)=0$ holds. Meanwhile, condition (C3) implies that $\varvec{\omega }^{\top } \sum _{i=1}^n{ \sum _{k=1}^K{\varvec{\nu }_k\varvec{\nu }_k^{\top }}\psi _{\tau _k}^2( \varepsilon _{ik}) } \varvec{\omega }=O_p(\Vert \varvec{\omega }\Vert ^2)$ and there exists a constant $C>0$ such that

$$\begin{aligned} \varvec{\theta }_2^{\top } \sum _{i=1}^n{\widehat{{\textbf{B}}}(U_i,{\textbf{x}}^v_{i})\widehat{{\textbf{B}}}(U_i,{\textbf{x}}^v_{i})^{\top } } \varvec{\theta }_2 \le C\varvec{\theta }_2^{\top } \sum _{i=1}^n{ w_i\widehat{{\textbf{B}}}(U_i,{\textbf{x}}^v_{i})\widehat{{\textbf{B}}}(U_i,{\textbf{x}}^v_{i})^{\top } }\varvec{\theta }_2=O_p(\Vert \varvec{\theta }_2\Vert ^2). \end{aligned}$$

By the definition of $\tilde{{\textbf{x}}}^{c}_{i}$ and Lemma 8.2 (a), we have

$$\begin{aligned} E(\var** _3^2)\le C E\left\{ \Vert \varvec{\omega }\Vert ^2+\varvec{\theta }_1^{\top }(n^{-1}{\textbf{X}}^{c*}{\textbf{X}}^{c*\top })\varvec{\theta }_1+ \Vert \varvec{\theta }_2\Vert ^2\right\} =O( \Vert \varvec{\vartheta }\Vert ^2), \end{aligned}$$

which means $\var** _3=O_p(d_n^{-1/2} \Vert \varvec{\vartheta }\Vert )$.

Therefore, (8.2) holds as the quadratic term dominate for sufficiently large L. Further by the convexity, we have $\Vert \hat{\varvec{\vartheta }}\Vert =O_p(\sqrt{d_n})$ and then $\Vert \varPi _W(\widehat{\varvec{\gamma }}_v-\varvec{\gamma }_{0v})\Vert =O_p(\sqrt{d_n})$ from the definition of $\hat{\varvec{\vartheta }}$. Consequently, it follows from Lemma 8.1 (a) and conditions (C3) and (C4) that

$$\begin{aligned}{} & {} \frac{1}{n}\sum _{i=1}^n\sum _{j\in S_v} \Vert \hat{\alpha }_j(U_i)-\alpha _{0j}(U_i)\Vert ^2\\= & {} \frac{1}{n}\sum _{i=1}^n { w_i\left( {\textbf{B}}(U_i,{\textbf{x}}^{v}_{i})^{\top }(\widehat{\varvec{\gamma }}_v-\varvec{\gamma }_{0v}) -r_{ni} \right) ^2 } \\\le & {} \frac{2}{n}(\widehat{\varvec{\gamma }}_v-\varvec{\gamma }_{0v})^{\top }\varPi _W^2(\widehat{\varvec{\gamma }}_v-\varvec{\gamma }_{0v})+ O_p\left( \frac{2}{n} n p_{n2}m_n^{-2r} \right) \\= & {} O_p(d_n/n+p_{n2}m_n^{-2r})=O_p\left( \frac{p_{n2}m_n}{n}+\frac{p_{n1}}{n}+\frac{p_{n2}}{m_n^{2r}} \right) . \end{aligned}$$

This completes the proof. $\Box$

Proof of Theorem 3.5

We first demonstrate $A_n\varSigma _n^{-1/2}\widetilde{\varvec{\theta }}_1~\mathop \rightarrow \limits ^D~ N({\varvec{0}},G)$. In fact, by the definition of $\widetilde{\varvec{\theta }}_1$ and the proof of Lemma 8.2 (b), we have

$$\begin{aligned} A_n\varSigma _n^{-1/2}\widetilde{\varvec{\theta }}_1= & {} A_n\varSigma _n^{-1/2} S_n^{-1} (n^{-1/2}\varvec{\varDelta }_n^{\top }{\textbf{w}})(1+o_p(1))\\{} & {} \quad +A_n\varSigma _n^{-1/2} S_n^{-1} (n^{-1/2}(\varvec{\varPhi }^*-P{\textbf{X}}^c)^{\top }{\textbf{w}})(1+o_p(1))\\= & {} A_n\varSigma _n^{-1/2} S_n^{-1} (n^{-1/2}\varvec{\varDelta }_n^{\top }{\textbf{w}})(1+o_p(1))+o_p(1). \end{aligned}$$

Rewrite $A_n\varSigma _n^{-1/2} S_n^{-1} (n^{-1/2}\varvec{\varDelta }_n^{\top }{\textbf{w}})=\sum _{i=1}^n{ H_{ni} }$, where $H_{ni}=n^{-1/2}A_n\varSigma _n^{-1/2} S_n^{-1}\varvec{\delta }_{i}w_i$. Then, $E(H_{ni})={\varvec{0}}$ and

$$\begin{aligned} \sum _{i=1}^n{ E(H_{ni}H_{ni}^{\top }) }= A_n\varSigma _n^{-1/2} S_n^{-1} \varLambda _n S_n^{-1} \varSigma _n^{-1/2}A_n^{\top }= A_n\varSigma _n^{-1/2}\varSigma _n \varSigma _n^{-1/2}A_n^{\top } \rightarrow G. \end{aligned}$$

Moreover, based on conditions (C3), (C4) and (C6), we can verify that for any $\kappa >0$,

$$\begin{aligned}{} & {} \sum _{i=1}^n{ E\left\{ \Vert H_{ni}\Vert ^2I(\Vert H_{ni}\Vert >\kappa ) \right\} } \le \kappa ^{-2}\sum _{i=1}^n{ E(\Vert H_{ni}\Vert ^4) } \\\le & {} (n\kappa )^{-2}\sum _{i=1}^n{ E(w_i^4)\left\{ \varvec{\delta }_{i}^{\top } S_n^{-1}\varSigma _n^{-1/2}A_n^{\top }A_n \varSigma _n^{-1/2} S_n^{-1}\varvec{\delta }_{i} \right\} ^2 } \\\le & {} C(n\kappa )^{-2}\sum _{i=1}^n{ E(\Vert \varvec{\delta }_{i}\Vert ^4) }=O_p(p_{n1}^2/n)=o_p(1), \end{aligned}$$

where the last inequality holds because $\lambda _{\max }(A_n^TA_n)=\lambda _{\max }(A_nA_n^T)$ and G is positive definite, the last equality due to $p_{n1}^2/n\rightarrow 0$ in condition (C7). Thus, the Lindeberg–Feller condition holds for $\{H_{ni}\}$ and $A_n\varSigma _n^{-1/2}\widetilde{\varvec{\theta }}_1~\mathop \rightarrow \limits ^D~ N(\varvec{0},G)$ is proved. Note that $\widetilde{\varvec{\theta }}_1=\widehat{\varvec{\theta }}_1+o_P(1)$ from lemma 8.3 (b) and $\widehat{\varvec{\theta }}_1=\sqrt{n}(\widehat{\varvec{\beta }}_c -\varvec{\beta }_{0c})$, the proof of Theorem 4.3 is followed. $\Box$

Lemma 8.4

Under conditions (C1)–(C8), we have

$$\begin{aligned}{} & {} \Pr \left( \max _{j\in {\widetilde{S}}_z}|g^1_j(\widehat{{\textbf{b}}}^o, \widehat{\varvec{\beta }}^o, \widehat{\varvec{\gamma }}^o)|\ge n\lambda _1\right) \rightarrow 0, \\{} & {} \Pr \left( \max _{j\notin S_v}\Vert {\textbf{g}}^2_j(\widehat{{\textbf{b}}}^o, \widehat{\varvec{\beta }}^o, \widehat{\varvec{\gamma }}^o)\Vert \ge n\sqrt{m_n}\lambda _2\right) \rightarrow 0. \end{aligned}$$

Proof

Let $\xi _{ik}({\hat{b}}_{\tau _k}^o,\widehat{\varvec{\beta }}^{1o},\widehat{\varvec{\gamma }}^{2o})={\hat{b}}_{\tau _k}^o-b_{0\tau _k}+{\textbf{x}}_{i}^{1\top }(\widehat{\varvec{\beta }}^{1o}-\varvec{\beta }_{0}^{1}) +{\textbf{z}}_{i}^{2\top }(\widehat{\varvec{\gamma }}^{2o}-\varvec{\gamma }_{0}^{2})$, then we have

$$\begin{aligned} -g^1_j= & {} \sum _{k=1}^K \sum _{i=1}^n \psi _{\tau _k}\left( Y_i-{\hat{b}}_{\tau _k}^o-{\textbf{x}}_{i}^{1\top }\widehat{\varvec{\beta }}^{1o}-{\textbf{z}}_{i}^{2\top }\widehat{\varvec{\gamma }}^{2o}\right) X_{ij}\\= & {} \sum _{k=1}^K \sum _{i=1}^n X_{ij} [\tau _k-I( Y_i-{\hat{b}}_{\tau _k}^o-{\textbf{x}}_{i}^{1\top }\widehat{\varvec{\beta }}^{1o}-{\textbf{z}}_{i}^{2\top }\widehat{\varvec{\gamma }}^{2o}<0)]\\= & {} \sum _{k=1}^K \sum _{i=1}^n X_{ij} [\tau _k-I(\varepsilon _i< b_{0\tau _k})] \\{} & {} \quad +\sum _{k=1}^K \sum _{i=1}^n X_{ij} [I(\varepsilon _i< b_{0\tau _k})-I( \varepsilon _i<b_{0\tau _k}+\xi _{ik}({\hat{b}}_{\tau _k}^o,\widehat{\varvec{\beta }}^{1o},\widehat{\varvec{\gamma }}^{2o})+R(U_i))]\\\triangleq & {} T_{nj}+\sum _{k=1}^K\sum _{i=1}^n[D_{n1j}^{k}({\hat{b}}_{\tau _k}^o, \widehat{\varvec{\beta }}^{1o}, \widehat{\varvec{\gamma }}^{2o})+D_{n2j}^{k}({\hat{b}}_{\tau _k}^o, \widehat{\varvec{\beta }}^{1o}, \widehat{\varvec{\gamma }}^{2o})], \end{aligned}$$

where $R(u)=\sum _{j\in S_v}X_{ij}(\eta _{0j}(u)-\widetilde{{\textbf{B}}}(u)^{\top }\varvec{\gamma }_{0j})$, $T_{nj}=\sum _{k=1}^K\sum _{i=1}^n X_{ij} [\tau _k-I(\varepsilon _i< b_{0\tau _k})]$,

$$\begin{aligned} D_{n1j}^{k}(b_{\tau _k}, \varvec{\beta }^{1}, \varvec{\gamma }^{2})=\sum _{i=1}^n X_{ij}[F_i(b_{0\tau _k})-F_i(b_{0\tau _k}+\xi _{ik}(b_{\tau _k}, \varvec{\beta }^{1}, \varvec{\gamma }^{2})+R(U_i))]\nonumber \\ \end{aligned}$$

(8.3)

and

$$\begin{aligned} D_{n2j}^{k}(b_{\tau _k}, \varvec{\beta }^{1}, \varvec{\gamma }^{2})=D_{n3j}^{k}(b_{\tau _k}, \varvec{\beta }^{1}, \varvec{\gamma }^{2})-D_{n1j}^{k}(b_{\tau _k}, \varvec{\beta }^{1}, \varvec{\gamma }^{2}) \end{aligned}$$

(8.4)

with

$$\begin{aligned}{} & {} D_{n3j}^{k}(b_{\tau _k}, \varvec{\beta }^{1}, \varvec{\gamma }^{2})\nonumber \\ {}{} & {} \quad =\sum _{i=1}^nX_{ij} [I(\varepsilon _i< b_{0\tau _k})-I( \varepsilon _i<b_{0\tau _k}+\xi _{ik}(b_{\tau _k}, \varvec{\beta }^{1}, \varvec{\gamma }^{2})+R(U_i))]. \end{aligned}$$

(8.5)

Note that $ET_{nj}=0$ and

$$\begin{aligned} E[(\tau _k-I(\varepsilon _i< b_{0\tau _k}))^2|X_{ij}]= & {} E[\tau _k^2-2\tau _kI(\varepsilon _i< b_{0\tau _k})+I(\varepsilon _i< b_{0\tau _k})|X_{ij}]\\= & {} (1-\tau _k)\tau _k\le \frac{1}{4}, \end{aligned}$$

then using condition (C4),

$$\begin{aligned} ET_{nj}^2\le & {} K\sum _{k=1}^K\sum _{i=1}^nE\{X_{ij}^2E[(\tau _k-I(\varepsilon _i< b_{0\tau _k}))^2|X_{ij}]\}\\\le & {} \frac{1}{4}nK^2. \end{aligned}$$

By Bernstein’s inequality and condition (C8),

$$\begin{aligned} \Pr \left( \max _{j\in {\widetilde{S}}_z}|T_{nj}|>\frac{n\lambda _1}{3}\right)\le & {} p_n\exp \left( -\frac{n^2\lambda _1^2/9}{2(nK^2/4+Cn\lambda _1/3)}\right) \\= & {} \exp \left\{ \log {p_n}(1-Cn\lambda _1^2/\log {p_n})\right\} \rightarrow 0. \end{aligned}$$

Using Lemma 8.5, we have

$$\begin{aligned} \Pr \left( \max _{j\in {\widetilde{S}}_z}\left| \sum _{k=1}^K\sum _{i=1}^nD_{n1j}^{k}({\hat{b}}_{\tau _k}^o, \widehat{\varvec{\beta }}^{1o}, \widehat{\varvec{\gamma }}^{2o})\right| >\frac{n\lambda _1}{3}\right) \rightarrow 0 \end{aligned}$$

and

$$\begin{aligned} \Pr \left( \max _{j\in {\widetilde{S}}_z}\left| \sum _{k=1}^K\sum _{i=1}^nD_{n2j}^{k}({\hat{b}}_{\tau _k}^o, \widehat{\varvec{\beta }}^{1o}, \widehat{\varvec{\gamma }}^{2o})\right| >\frac{n\lambda _1}{3}\right) \rightarrow 0. \end{aligned}$$

Hence, $\Pr \left( \max _{j\in {\widetilde{S}}_z}|g^1_j(\widehat{{\textbf{b}}}^o, \widehat{\varvec{\beta }}^o, \widehat{\varvec{\gamma }}^o)|\ge n\lambda _1\right) \rightarrow 0$.

Similarly, we can also prove that $\Pr \left( \max _{j\notin S_v}\Vert {\textbf{g}}^2_j(\widehat{{\textbf{b}}}^o, \widehat{\varvec{\beta }}^o, \widehat{\varvec{\gamma }}^o)\Vert \ge n\sqrt{m_n}\lambda _2\right) \rightarrow 0.$ $\square$

Lemma 8.5

Let $k_n=\sqrt{q_{n}}(\sqrt{ m_n/n}+m_n^{-r})$. For any finite positive constant C, define

$$\begin{aligned} {\mathcal {B}}(b_{0\tau _k},\varvec{\beta }_{0}^{1},\varvec{\gamma }_{0}^{2})=\left\{ (b_{\tau _k},\varvec{\beta }^{1},\varvec{\gamma }^{2}): |b_{\tau _k}-b_{0\tau _k}|+\Vert \varvec{\beta }^{1}-\varvec{\beta }_{0}^{1}\Vert +\Vert \varvec{\gamma }^{2}-\varvec{\gamma }_{0}^{2}\Vert \le C k_n\right\} , \end{aligned}$$

under conditions (C1)–(C8), we have

$$\begin{aligned}{} & {} \Pr \left( \max _{j\in {\widetilde{S}}_z}\sup _{(b_{\tau _k},\varvec{\beta }^{1},\varvec{\gamma }^{2})\in {\mathcal {B}}(b_{0\tau _k},\varvec{\beta }_{0}^{1},\varvec{\gamma }_{0}^{2})}|D^k_{n1j}(b_{\tau _k},\varvec{\beta }^{1},\varvec{\gamma }^{2})|\ge n\lambda _1/3\right) \rightarrow 0, \\{} & {} \Pr \left( \max _{j\in {\widetilde{S}}_z}\sup _{(b_{\tau _k},\varvec{\beta }^{1},\varvec{\gamma }^{2})\in {\mathcal {B}}(b_{0\tau _k},\varvec{\beta }_{0}^{1},\varvec{\gamma }_{0}^{2})}|D^k_{n2j}(b_{\tau _k},\varvec{\beta }^{1},\varvec{\gamma }^{2})|\ge n\lambda _1/3\right) \rightarrow 0, \end{aligned}$$

where $D^k_{n1j}$ and $D^k_{n2j}$ are defined in (8.3) and (8.4).

Proof

. For any $(b_{\tau _k},\varvec{\beta }^{1},\varvec{\gamma }^{2})\in {\mathcal {B}}(b_{0\tau _k},\varvec{\beta }_{0}^{1},\varvec{\gamma }_{0}^{2})$, it follows from conditions (C3), (C4) and (C8) that

$$\begin{aligned}{} & {} E|D^k_{n1j}(b_{\tau _k},\varvec{\beta }^{1},\varvec{\gamma }^{2})|\\\le & {} \sum _{i=1}^n E[X_{ij}f_i(b_{0\tau _k})(1+o(1)) (|b_{\tau _k}-b_{0\tau _k}|+\Vert {\textbf{x}}_{i}^{1}\Vert \Vert \varvec{\beta }^{1}-\varvec{\beta }_{0}^{1}\Vert \\{} & {} \quad +\Vert {\textbf{z}}_i^{2}\Vert \varvec{\gamma }^{2}-\varvec{\gamma }_{0}^{2}\Vert +|R(U_i)|)]\\= & {} nO(1)\left( \sqrt{q_{n}}k_n+\sqrt{p_{n2}m_n}k_n+\sqrt{p_{n2}}m_n^{-r}\right) \\= & {} nO(1)\left( q_nm_n/\sqrt{n}+q_{n}m_n^{-r+1/2}\right) \\= & {} o(n\lambda _1). \end{aligned}$$

Using conditions (C3) and (C4),

$$\begin{aligned}{} & {} E(D^k_{n3j})^2\\= & {} \sum _{i=1}^nE\{X_{ij}^2 E[(I(\varepsilon _i< b_{0\tau _k})-I( \varepsilon _i<b_{0\tau _k}+\xi _{ik}(b_{\tau _k}, \varvec{\beta }^{1}, \varvec{\gamma }^{2})+R(U_i)))^2|{\textbf{x}}_i,U_i]\\= & {} f(b_{0\tau _k})(1+o(1))\sum _{i=1}^nE[X_{ij}^2|\xi _{ik}(b_{\tau _k}, \varvec{\beta }^{1}, \varvec{\gamma }^{2})+R(U_i))|]\\\le & {} f(b_{0\tau _k})(1+o(1))\sum _{i=1}^nE[X_{ij}^2(|b_{\tau _k}-b_{0\tau _k}|+\Vert {\textbf{x}}_{i}^{1}\Vert \Vert \varvec{\beta }^{1}-\varvec{\beta }_{0}^{1}\Vert \\{} & {} \quad +\Vert {\textbf{z}}_i^{2}\Vert \varvec{\gamma }^{2}-\varvec{\gamma }_{0}^{2}\Vert +|R(U_i)|)]\\= & {} nO(1)\left( q_nm_n/\sqrt{n}+q_{n}m_n^{-r+1/2}\right) . \end{aligned}$$

Since $E(D^k_{n2j})^2=E(D^k_{n3j})^2+E(D^k_{n1j})^2-2E(D^k_{n3j}D^k_{n1j})=E(D^k_{n3j})^2-E(D^k_{n1j})^2$, by condition (C8), we have

$$\begin{aligned}{} & {} \Pr \left( \max _{j\in {\widetilde{S}}_z}\sup _{(b_{\tau _k},\varvec{\beta }_c,\varvec{\gamma }_v)\in {\mathcal {B}}(b_{0\tau _k},\varvec{\beta }_{0c},\varvec{\gamma }_{0v})}|D^k_{n2j}(b_{\tau _k},\varvec{\beta }_c,\varvec{\gamma }_v)|\ge n\lambda _1/3\right) \\\le & {} CKp_n\exp \left\{ -\frac{n^2\lambda _1^2/9}{2\left( n\left( q_nm_n/\sqrt{n}+q_{n}m_n^{-r+1/2}\right) +Cn\lambda _1/3\right) }\right\} \\= & {} CKp_n\exp \left\{ -\frac{n\lambda _1/9}{2\left( \left( q_nm_n/\sqrt{n}+q_{n}m_n^{-r+1/2}\right) /\lambda _1+C/3\right) }\right\} \\\rightarrow & {} 0. \end{aligned}$$

$\square$

Proof of Theorem 4.3

We only need to show that $(\widehat{{\textbf{b}}}^o, \widehat{\varvec{\beta }}^o, \widehat{\varvec{\gamma }}^o)$ satisfies Equations (4.1)–(4.5) of Lemma 4.2. By the definition of $(\widehat{{\textbf{b}}}^o, \widehat{\varvec{\beta }}^o, \widehat{\varvec{\gamma }}^o)$, it is easy to know that (4.1) holds. Note that

$$\begin{aligned} \min _{j\notin {\widetilde{S}}_z}|\hat{\beta }^o_j|\ge \min _{j\notin {\widetilde{S}}_z}|\beta _{0j}|-\max _{j\notin {\widetilde{S}}_z}|\hat{\beta }^o_j-\beta _{0j}| \end{aligned}$$

and

$$\begin{aligned} \min _{j\in S_v}\Vert \widehat{\varvec{\gamma }}_{j}^o\Vert \ge \min _{j\in S_v}\Vert \varvec{\gamma }_{0j}\Vert -\max _{j\in S_v}\Vert \widehat{\varvec{\gamma }}_{j}^o-\varvec{\gamma }_{0j}\Vert . \end{aligned}$$

Hence, (4.2) and (4.3) hold based on Theorem 4.1 and conditions (C8)–(C9). (4.4) and (4.5) can be obtained by Lemma 8.4. $\Box$