Abstract
We consider three classes of functions defined using the class \({\mathcal {P}}\) of all analytic functions \(p(z)=1+cz+\cdots \) on the open unit disk having positive real part and study several radius problems for these classes. The first class consists of all normalized analytic functions f with \(f/g\in {\mathcal {P}}\) and \(g/(zp)\in {\mathcal {P}}\) for some normalized analytic function g and \(p\in {\mathcal {P}}\). The second class is defined by replacing the condition \(f/g\in {\mathcal {P}}\) by \(|(f/g)-1|<1\) while the other class consists of normalized analytic functions f with \(f/(zp)\in {\mathcal {P}}\) for some \(p\in {\mathcal {P}}\). We have determined radii so that the functions in these classes to belong to various subclasses of starlike functions. These subclasses includes the classes of starlike functions of order \(\alpha \), parabolic starlike functions, as well as the classes of starlike functions associated with lemniscate of Bernoulli, reverse lemniscate, sine function, a rational function, cardioid, lune, nephroid and modified sigmoid function.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Let \({\mathbb {D}}\) denote the open unit disc in \({\mathbb {C}}\). Let \({\mathcal {A}}:=\{f: f \text { is analytic on } {\mathbb {D}}, f(0)= 0, \text { and } f'(0)=1\} \). Let \({\mathcal {S}}:=\{f\in {\mathcal {A}}: f \text { is univalent on } {\mathbb {D}}\}\). An analytic function f is subordinate to another analytic function g, written \(f\prec g\), if \(f(z)=g(w(z))\) for some analytic function \(w:{\mathbb {D}}\rightarrow {\mathbb {D}}\) that fixes the origin. If \(g \in {\mathcal {S}}\), then \(f\prec g\) if and only if the functions f and g takes the origin to the same point as well as the range of f is a subset of the range of g: \(f({\mathbb {D}})\subseteq g({\mathbb {D}})\). Several well known subclasses of starlike and convex functions were characterized by subordination of \(zf'(z)/f(z)\) or \(1+(zf''(z)/f'(z)\) to some function in \({\mathcal {P}}\). Using a function \(\varphi \), univalent in unit disc \({\mathbb {D}}\) with \({\text {Re}} \varphi (z)>0\), starlike with respect to \(\varphi (0)=1\), symmetric about the real axis and \(\varphi '(0)>0\), Ma and Minda [22] gave a unified treatment for several subclasses of starlike and convex functions by studying the classes \({\mathcal {S}}^*(\varphi )=\{f \in {\mathcal {A}}: zf'(z)/f(z)\prec \varphi (z)\}\) and \({\mathcal {K}}(\varphi )=\{f \in {\mathcal {A}}: 1+zf''(z)/f'(z)\prec \varphi (z)\}\). Convolution theorems for these two classes in a more general setting was previously studied by Shanmugham [35] with the stronger assumption that \(\varphi \) is convex. Several authors considered these classes for various choices of the function \(\varphi \). For \(-1< B<A \le 1\), let \(\varphi \) be the bilinear transform that maps the unit disc \({\mathbb {D}}\) onto the disc whose diametric end points are \((1+A)/(1+B)\) and \((1-A)/(1-B)\); if we impose \(\varphi (0)=1\), then this map** is given by \(\varphi (z)=(1+Az)/(1+Bz)\). For this function \(\varphi \), the classes \({\mathcal {S}}^*(\varphi )\) and \({\mathcal {K}}(\varphi )\) reduce respectively to the classes \({\mathcal {S}}^*[A, B]\) and \({\mathcal {K}}[A, B]\) of Janowski starlike and convex functions. Other well-known choices for \(\varphi (z)\) include \(\sqrt{1+z}, \ e^z, \ 1+\sin z, \ z+\sqrt{1+z^2}\). Readers may refer to [11, 39] for brief survey of these classes.
The class \({\mathcal {P}}\) of analytic functions \(p(z)=1+cz+\cdots \) on \({\mathbb {D}}\) having positive real part is known as the class of Carathéodory functions or the class of functions with positive real part. For \(0\le \alpha <1\), let \({\mathcal {P}}(\alpha ):=\{p \in {\mathcal {P}} : {\text {Re}} p(z)>\alpha \}\). For any two subclasses \({\mathcal {F}}\) and \({\mathcal {G}}\) of \({\mathcal {A}}\), the \({\mathcal {G}}-\)radius for the class \({\mathcal {F}}\), denoted by \(R_{{\mathcal {G}}}({\mathcal {F}})\), is the largest number \(R_{{\mathcal {G}}}\in (0, 1)\) such that \(r^{-1}f(rz)\in {\mathcal {G}}\), for all \(f\in {\mathcal {F}}\) and for \(0<r<R_{{\mathcal {G}}}\). Among the several studies available on radius problems, a major focus has been on ratio between two classes of functions, where one of them belong to some particular subclasses of \({\mathcal {A}}\) and can be seen in [23,24,25, 30, 31]. Let \(\varPhi \) be a function defined on \({\mathbb {D}}\). For \(\varPhi (z)=1, 1/(1+z), 1/(1-z)^2, 1/(1-z^2), 1+(z/2)\), various authors have considered radius problems for classes of functions f satisfying the following conditions: (i) \({\text {Re}}f(z)/g(z)> 0 \) and \({\text {Re}} g(z)/(z\varPhi (z))> 0\), (ii) \(\left| (f(z)/g(z))-1\right| < 1\) and \({\text {Re}} g(z)/(z\varPhi (z)) > 0\), (iii) \({\text {Re}} f(z)/(z\varPhi (z)) > 0\). See [2, 7, 14, 15, 33]. Also, in 2019, Lecko and Sim [20] considered two functions \(\varPhi (z)= 1/(1-z)^2, 1/(1-z^2)\) where \(z\varPhi (z)\) are starlike functions with integer coefficients and studied on \({\text {Re}} f(z)/(z\varPhi (z)) > 0\). Similar studies can be seen in [16,17,18].
Motivated by the aforestated works, we define three classes of functions by making use of the class \({\mathcal {P}}\) as follows:
and
We determine radii for functions in the classes \({\mathcal {G}}_1, {\mathcal {G}}_2, {\mathcal {G}}_3\) to belong to several subclasses of \({\mathcal {A}}\) like starlike functions of order \(\alpha \), starlike functions associated with lemniscate of Bernoulli, reverse lemniscate, sine function, exponential function, cardioid, lune, nephroid, a particular rational function, modified sigmoid function and parabolic starlike functions. The disc that contains the image of unit disc \({\mathbb {D}}\) under the map** \(zf'(z)/f(z)\) aids in determining the radius of various classes and we discuss this map** in the following section.
2 Map** of \(zf'(z)/f(z)\) for \({\mathcal {G}}_1\), \({\mathcal {G}}_2\), \({\mathcal {G}}_3\)
In this section, we show that the classes \({\mathcal {G}}_1, {\mathcal {G}}_2, {\mathcal {G}}_3\) are non-empty and contain non-univalent functions. We also determine the disk containing the image of the disc \({\mathbb {D}}\) under the function \(zf'/f\) when f belongs to each of the classes. We shall use the function \(p_0:{\mathbb {D}}\rightarrow {\mathbb {C}}\) defined by
This function \(p_0\) belongs to \({\mathcal {P}}\) and maps the unit disc \({\mathbb {D}}\) onto the right half-plane. For functions \(p \in {\mathcal {P}}(\alpha )\), we shall use the following inequality [34, Lemma 2]:
2.1 The class \({\mathcal {G}}_1\)
Define the functions \(f_1, g_1:{\mathbb {D}}\longrightarrow {\mathbb {C}}\) by
The functions \(f_1\) and \(g_1\) satisfy \(f_1/g_1 \in {\mathcal {P}}\) and \(g_1/zp_0 \in {\mathcal {P}}\) where \(p_0\in {\mathcal {P}}\) is given in (4). Thus the function \(f_1\in {\mathcal {G}}_1\) and the class \({\mathcal {G}}_1\) is non-empty. It is an extremal function for the class \({\mathcal {G}}_1\). From the coefficients of Taylor series expansion of functions \(f_1\) given by
it is evident that the functions \(f_1 \) is not univalent. Hence, the class \({\mathcal {G}}_1\) contains non-univalent functions. As
the function \(f_1'\) vanishes at \(z=-\rho =-(\sqrt{10}-3)\). From Theorem 1, it is apparent that the radii of univalence of the class \({\mathcal {G}}_1\) is \(\sqrt{10}-3\) and it coincides with its radius of starlikeness.
If the function \(f\in {\mathcal {G}}_1\), then there exists an element \(g \in {\mathcal {A}}\) and \(p\in {\mathcal {P}}\) such that
Let \(p_1, \ p_2\) be two functions defined on unit disc \({\mathbb {D}}\) by
From (7) and (8), we have \(f(z)=zp_1(z)p_2(z)p(z)\). Then a calculation shows that
Since \(p_1, \ p_2, \ p \in {\mathcal {P}}\), it follows from (5) and (9) that
2.2 The class \({\mathcal {G}}_2\)
The functions \(f_2\) and \(g_2\) are defined on the unit disc \({\mathbb {D}}\) as follows:
The functions \(f_2\) and \(g_2\) satisfy \(f_2/g_2 \in {\mathcal {P}}\) and \(g_2/(zp_0) \in {\mathcal {P}}(1/2)\) where \(p_0\in {\mathcal {P}}\) is given in (4). Thus the function \(f_2\in {\mathcal {G}}_2\) and the class \({\mathcal {G}}_2\) is non empty. It is an extremal function for the class \({\mathcal {G}}_2\). Note that the Taylor series expansion of
and it is clear that the function \(f_2\) is not univalent function, as it does not satisfy de Brange’s theorem. Thus the class \({\mathcal {G}}_2\) contains non-univalent functions. Since
the function \(f_2'\) vanishes at \(z=-\zeta =- 1/ 5\) and it follows that the radius of univalence of the class of functions \({\mathcal {G}}_2\) is 1/5 by the Theorem 1. It also coincides with radius of starlikeness.
If the function \(f \in {\mathcal {G}}_2\), then there exists a normalized analytic function g and \(p\in {\mathcal {P}}\) such that
Let \(h_1\) and \(h_2\) be two functions, \(h_1, h_2:{\mathbb {D}}\longrightarrow {\mathbb {C}}\) defined as
Using (12) and (13), we have \(f(z)=zh_1(z)h_2(z)p(z)\), it can be shown that
As \(h_1, p \in {\mathcal {P}}\) and \(h_2 \in {\mathcal {P}}(1/2)\), it follows from (5) and (14) that
It would be interesting to find the boundary of the set \( \cup _{f\in {\mathcal {G}}_2}\{zf'(z)/f(z): |z|\le r\}\). This would help in finding sharp radii to some of the problems where we have got only a lower bound.
2.3 The class \({\mathcal {G}}_3\)
The function \(g_1\), defined by (6), belongs to the class \({\mathcal {G}}_3\) and therefore the class \({\mathcal {G}}_3\) is non-empty. It is an extremal function for the class \({\mathcal {G}}_3\). From the coefficients of Taylor series expansion of functions \(g_1\) given by
it is evident that the function \(g_1 \) is not univalent. Hence, the class \({\mathcal {G}}_3\) contains non-univalent functions. As
the function \(g_1'\) vanishes at \(z=-\eta =-(\sqrt{5}-2)\). From Theorem 1, it is apparent that the radii of univalence of the class \({\mathcal {G}}_3\) coincide with their radii of starlikeness. We now discuss the map** \(zf'(z)/f(z)\) when the function \(f \in {\mathcal {G}}_3\). Let \(p\in {\mathcal {P}}\) and \(p_1\) be a function defined on unit disc \({\mathbb {D}}\) such that
It is clear from (16) that \(f(z)=zp_1(z)p(z)\). Then it follows that
Applying (5) in (17), we obtain
Using the equations (10), (15), (18), we investigate several radius problems associated with functions in the classes \({\mathcal {G}}_1\), \({\mathcal {G}}_2\) and \({\mathcal {G}}_3\) in the next section.
3 Radius of starlikeness
In this section, we determine the radii of the classes \({\mathcal {G}}_1, \ {\mathcal {G}}_2, \ {\mathcal {G}}_3\) to belong to various Ma-Minda starlike classes of functions. For \(0\le \alpha \le 1\), the class \({\mathcal {S}}^*(\alpha )={\mathcal {S}}^*[1-2\alpha , -1]=\{f\in {\mathcal {A}}: {\text {Re}} zf'(z)/f(z)>\alpha \}\) is the class of starlike functions of order \(\alpha \). These classes were studied extensively in [6, 11,12,13].
Theorem 1
The following sharp results hold for the class \({\mathcal {S}}^{*}(\alpha )\):
-
(i)
\(R_{{\mathcal {S}}^{*}(\alpha )}({\mathcal {G}}_1)= (1-\alpha )/ \left( 3+\sqrt{10-2\alpha +\alpha ^2}\right) \).
-
(ii)
\(R_{{\mathcal {S}}^{*}(\alpha )}({\mathcal {G}}_2)= 2(1-\alpha )/ \left( 5+\sqrt{25-4\alpha +\alpha ^2}\right) \).
-
(iii)
\(R_{{\mathcal {S}}^{*}(\alpha )}({\mathcal {G}}_3)= (1-\alpha )/ \left( 2+\sqrt{5-2\alpha +\alpha ^2}\right) \).
Proof
-
(i)
The function defined by \(m(r)=(1-6r-r^2)(1-r^2)^{-1}, \ 0\le r<1\) is a decreasing function. Let \(\rho =R_{{\mathcal {S}}^{*}(\alpha )}({\mathcal {G}}_1)\) be the root of the equation \(m(r)=\alpha \). From (10), it follows that
$$\begin{aligned} {\text {Re}}\frac{zf'(z)}{f(z)}\ge \frac{1-6r-r^2}{1-r^2}=m(r)\ge m(\rho )=\alpha . \end{aligned}$$This shows that \(R_{{\mathcal {S}}^{*}(\alpha )}({\mathcal {G}}_1)\) is at least \(\rho \). At \(z=-R_{{\mathcal {S}}^{*}(\alpha )}({\mathcal {G}}_1)=-\rho \), the function \(f_1\) defined in (6) satisfies
$$\begin{aligned} {\text {Re}}\frac{zf_1'(z)}{f_1(z)}=\frac{1-6\rho -\rho ^2}{1-\rho ^2}=\alpha . \end{aligned}$$Thus the radius is sharp.
-
(ii)
The function \(n(r):[0,1)\longrightarrow {\mathbb {R}}\) defined by \(n(r)=(1-5r)(1-r^2)^{-1}\) is a decreasing function. Let \(\rho =R_{{\mathcal {S}}^{*}(\alpha )}({\mathcal {G}}_2)\) be the root of the equation \(n(r)=\alpha \). Let \(f\in {\mathcal {G}}_2\) and let \(h_1, p \in {\mathcal {P}}\) and \(h_2 \in {\mathcal {P}}(1/2)\) be the functions defined in Sect. 2.2. For \(h\in {\mathcal {P}}\), by [4, Lemma 2.3], we have
$$\begin{aligned} {\text {Re}}\frac{zh'(z)}{h(z)}\ge - \frac{2r}{1-r^2},\quad |z|\le r. \end{aligned}$$(19)For \(k\in {\mathcal {P}}(1/2)\), by [4, Lemma 2.4], we have
$$\begin{aligned} {\text {Re}}\frac{zk'(z)}{k(z)}\ge - \frac{r}{1+r},\quad |z|\le r. \end{aligned}$$(20)Using (19) and (20) in (14), it follows that
$$\begin{aligned} {\text {Re}}\frac{zf'(z)}{f(z)}\ge 1-\frac{4r}{1-r^2}-\frac{r}{1+r}=\frac{1-5r}{1-r^2}=n(r)\ge n(\rho )=\alpha . \end{aligned}$$This shows that \(R_{{\mathcal {S}}^{*}(\alpha )}({\mathcal {G}}_2)\) is at least \(\rho \). At \(z=-R_{{\mathcal {S}}^{*}(\alpha )}({\mathcal {G}}_1)=-\rho \), the function \(f_2\) defined in (11) satisfies
$$\begin{aligned} {\text {Re}}\frac{zf_2'(z)}{f_2(z)}=\frac{1-5\rho }{1-\rho ^2}=\alpha . \end{aligned}$$Thus the radius is sharp.
-
(iii)
The function defined by \(s(r)=(1-4r-r^2)(1-r^2)^{-1}, \ 0\le r<1\) is a decreasing function. Let \(\rho = R_{{\mathcal {S}}^{*}(\alpha )}({\mathcal {G}}_3)\) be the root of the equation \(s(r)=\alpha \). From (18), it follows that
$$\begin{aligned} {\text {Re}}\frac{zf'(z)}{f(z)}\ge \frac{1-4r-r^2}{1-r^2}=s(r)\ge s(\rho )=\alpha . \end{aligned}$$This shows that \(R_{{\mathcal {S}}^{*}(\alpha )}({\mathcal {G}}_3)\) is at least \(\rho \). For the function \(g_1\) defined in (6), at \(z=-R_{{\mathcal {S}}^{*}(\alpha )}({\mathcal {G}}_2)=-\rho \),
$$\begin{aligned} {\text {Re}}\frac{zg_1'(z)}{g_1(z)}=\frac{1-4\rho -\rho ^2}{1-\rho ^2}=\alpha . \end{aligned}$$Thus the radius is sharp.
\(\square \)
The class \({\mathcal {S}}_{L}^{*}={\mathcal {S}}^{*}(\sqrt{1+z})\) and it represents the collection of functions in the class \({\mathcal {A}}\) whose \(zf'(z)/f(z)\) lies in the region bounded by the lemniscate of Bernoulli \(|w^2-1|=1\). Various studies on \({\mathcal {S}}_{L}^{*}\) can be seen in [3, 28, 38]. Ali et al. [1, Lemma 2.2] had proved, for \(2\sqrt{2}/3<a<\sqrt{2}\), that
Using this lemma, we obtain radii results for the classes \({\mathcal {G}}_1, \ {\mathcal {G}}_2, \ {\mathcal {G}}_3\) to be in the class \({\mathcal {S}}_{L}^{*}\) in the following theorem.
Theorem 2
The following results for the class \({\mathcal {S}}_{L}^{*}\) are sharp.
-
(i)
\(R_{{\mathcal {S}}_{L}^{*}}({\mathcal {G}}_1)= (3-2\sqrt{2})/ (\sqrt{2}-1)\left( 3+\sqrt{12-2\sqrt{2}}\right) \approx 0.0687\).
-
(ii)
\(R_{{\mathcal {S}}_{L}^{*}}({\mathcal {G}}_2)= 2(\sqrt{2}-1)/ \left( 5+\sqrt{33-4\sqrt{2}}\right) \approx 0.0809\).
-
(iii)
\(R_{{\mathcal {S}}_{L}^{*}}({\mathcal {G}}_3)= (3-2\sqrt{2})/ (\sqrt{2}-1)\left( 2+\sqrt{7-2\sqrt{2}}\right) \approx 0.1025\).
Proof
-
(i)
The function defined by \(m(r)=6r(1-r^2)^{-1}+1, \ 0\le r<1\) is an increasing function. Let \(\rho =R_{{\mathcal {S}}_{L}^{*}}({\mathcal {G}}_1)\) be the root of the equation \(m(r)=\sqrt{2}\). For \(0<r\le R_{{\mathcal {S}}_{L}^{*}}({\mathcal {G}}_1)\), we have \(m(r)\le \sqrt{2}\). That is,
$$\begin{aligned} \frac{6r}{1-r^2}+1\le \sqrt{2}=m(\rho ). \end{aligned}$$For the class \({\mathcal {G}}_1\), the centre of the disc is 1, therefore, by (21), the disc obtained in (10) is contained in the region bounded by lemniscate. For the function \(f_1\) defined in (6), at \(z=R_{{\mathcal {S}}_{L}^{*}}({\mathcal {G}}_1)=\rho \),
$$\begin{aligned} \left| \left( \frac{zf'(z)}{f(z)}\right) ^2-1\right| =\left| \left( \frac{1+6\rho -\rho ^2}{1-\rho ^2}\right) ^2-1\right| =1. \end{aligned}$$ -
(ii)
The function \(n(r):[0, 1)\longrightarrow {\mathbb {R}}\) defined by \(n(r)=(5r+r^2)(1-r^2)^{-1}+1\) is an increasing function. Let \(\rho =R_{{\mathcal {S}}_{L}^{*}}({\mathcal {G}}_2)\) be the root of the equation \(n(r)=\sqrt{2}\). For \(0<r\le R_{{\mathcal {S}}_{L}^{*}}({\mathcal {G}}_2)\), we have \(n(r)\le \sqrt{2}\). That is,
$$\begin{aligned} \frac{5r+r^2}{1-r^2}+1\le \sqrt{2}=n(\rho ). \end{aligned}$$For the class \({\mathcal {G}}_2\), the centre of the disc is 1, therefore, by (21), the disc obtained in (15) is contained in the region bounded by lemniscate. For the function \(f_2\) defined in (11), at \(z=R_{{\mathcal {S}}_{L}^{*}}({\mathcal {G}}_2)=\rho \),
$$\begin{aligned} \left| \left( \frac{zf'(z)}{f(z)}\right) ^2-1\right| =\left| \left( \frac{1+5\rho }{1-\rho ^2}\right) ^2-1\right| =1. \end{aligned}$$ -
(iii)
The function defined by \(s(r)=4r(1-r^2)^{-1}+1, \ 0\le r<1\) is an increasing function. Let \(\rho = R_{{\mathcal {S}}_{L}^{*}}({\mathcal {G}}_3)\) be the root of the equation \(s(r)=\sqrt{2}\). For \(0<r\le R_{{\mathcal {S}}_{L}^{*}}({\mathcal {G}}_3)\), we have \(s(r)\le \sqrt{2}\). That is,
$$\begin{aligned} \frac{4r}{1-r^2}+1\le \sqrt{2}=s(\rho ). \end{aligned}$$For the class \({\mathcal {G}}_3\), the centre of the disc is 1, therefore, by (21), the disc obtained in (18) is contained in the region bounded by lemniscate. For the function \(g_1\) defined in (6), at \(z=R_{{\mathcal {S}}_{L}^{*}}({\mathcal {G}}_3)=\rho \),
$$\begin{aligned} \left| \left( \frac{zf'(z)}{f(z)}\right) ^2-1\right| =\left| \left( \frac{1+4\rho -\rho ^2}{1-\rho ^2}\right) ^2-1\right| =\left| (\sqrt{2})^2-1\right| =1. \end{aligned}$$
\(\square \)
Let \(\varphi _{PAR}(z):=1+\left( 2/\pi ^2\left( \log (1+\sqrt{z})/(1-\sqrt{z}) \right) ^2 \right) \). Since \(\varphi _{PAR}({\mathbb {D}})=\{w:{\text {Re}}w>|w-1|\}\) is a parabolic region, the functions in the class \({\mathcal {S}}_{p}:={\mathcal {S}}^{*}(\varphi _{PAR})\) are known as parabolic starlike functions. These functions are studied by authors in [9, 21, 32]. Shanmugam and Ravichandran [36, pp.321] had proved, for \(1/2< a<3/2\), that
The following theorem gives the radius of parabolic starlikeness of the three classes \({\mathcal {G}}_1\), \({\mathcal {G}}_2\) and \({\mathcal {G}}_3\).
Theorem 3
The following results hold for the class \({\mathcal {S}}_{p}\):
-
(i)
\(R_{{\mathcal {S}}_{p}}({\mathcal {G}}_1)= \sqrt{37}-6 \approx 0.0827\).
-
(ii)
\(R_{{\mathcal {S}}_{p}}({\mathcal {G}}_2)\ge (2\sqrt{7}-5)/ 3 \approx 0.0972\).
-
(iii)
\(R_{{\mathcal {S}}_{p}}({\mathcal {G}}_3)= \sqrt{17}-4 \approx 0.1231\).
Proof
-
(i)
The function defined by \(m(r)=(1-6r-r^2)(1-r^2)^{-1}, \ 0\le r<1\) is a decreasing function. Let \(\rho =R_{{\mathcal {S}}_{p}}({\mathcal {G}}_1)\) be the root of the equation \(m(r)=1/2\). For \(0<r\le R_{{\mathcal {S}}_{p}}({\mathcal {G}}_1)\), we have \(m(r)\ge 1/2\). That is,
$$\begin{aligned} \frac{6r}{1-r^2}\le \frac{1}{2}=m(\rho ). \end{aligned}$$For the class \({\mathcal {G}}_1\), the centre of the disc is 1, therefore, by (22), the disc obtained in (10) is contained in the region bounded by parabola. For the function \(f_1\) defined in (6), at \(z=R_{{\mathcal {S}}_{p}}({\mathcal {G}}_1)=\rho \),
$$\begin{aligned} {\text {Re}}\frac{zf_1'(z)}{f_1(z)}=\frac{1+6\rho -\rho ^2}{1-\rho ^2}=\frac{1}{2}=\left| \frac{zf_1'(z)}{f_1(z)}-1\right| . \end{aligned}$$ -
(ii)
The function \(n(r):[0, 1)\longrightarrow {\mathbb {R}}\) defined by \(n(r)=(1-5r-2r^2)(1-r^2)^{-1}+1\) is a decreasing function. Let \(\rho =R_{{\mathcal {S}}_{p}}({\mathcal {G}}_2)\) be the root of the equation \(n(r)=1/2\). For \(0<r\le R_{{\mathcal {S}}_{p}}({\mathcal {G}}_2)\), we have \(n(r)\ge 1/2\). That is,
$$\begin{aligned} \frac{r(r+5)}{1-r^2}\le \frac{1}{2}=n(\rho ). \end{aligned}$$For the class \({\mathcal {G}}_2\), the centre of the disc is 1, therefore, by (22), the disc obtained in (15) is contained in the region bounded by parabola. This shows that \(R_{{\mathcal {S}}_{p}}({\mathcal {G}}_2)\) is at least \(\rho \).
-
(iii)
The function defined by \(s(r)=1-(4r(1-r^2)^{-1}), \ 0\le r<1\) is a decreasing function. Let \(\rho = R_{{\mathcal {S}}_{p}}({\mathcal {G}}_3)\) be the root of the equation \(s(r)=1/2\). For \(0<r\le R_{{\mathcal {S}}_{p}}({\mathcal {G}}_3)\), we have \(s(r)\ge 1/2\). That is,
$$\begin{aligned} \frac{4r}{1-r^2}\le \frac{1}{2}=s(\rho ). \end{aligned}$$For the class \({\mathcal {G}}_3\), the centre of the disc is 1, therefore, by (22), the disc obtained in (18) is contained in the region bounded by parabola. For the function \(g_1\) defined in (6), at \(z=-R_{{\mathcal {S}}_{p}}({\mathcal {G}}_3)=-\rho \),
$$\begin{aligned} {\text {Re}}\frac{zg_1'(z)}{g_1(z)}=\frac{1-4\rho -\rho ^2}{1-\rho ^2}=\frac{1}{2}=\left| \frac{zg_1'(z)}{g_1(z)}-1\right| . \end{aligned}$$
\(\square \)
In 2015, Mendiratta et al. [27] introduced the class of starlike functions associated with the exponential function as \({\mathcal {S}}_{e}^{*}={\mathcal {S}}^{*}(e^z)\) and it satisfies the condition \(\left| \log zf'(z)/f(z)\right| <1\). They had also proved, for \(e^{-1}\le a\le (e+e^{-1})/2\), that
Theorem 4
The following results hold for the class \({\mathcal {S}}_{e}^{*}\):
-
(i)
\(R_{{\mathcal {S}}_{e}^{*}}({\mathcal {G}}_1)= (e-1)/\left( 3e+\sqrt{10e^{2}-2e+1 }\right) \approx 0.1042\).
-
(ii)
\(R_{{\mathcal {S}}_{e}^{*}}({\mathcal {G}}_2)\ge 2(e^2+e-2)/(2+e)\left( 5e+\sqrt{8+4e+29e^{2} }\right) \approx 0.1213\).
-
(iii)
\(R_{{\mathcal {S}}_{e}^{*}}({\mathcal {G}}_3)= 2(e-1)^2/(e+1)\left( 4e+\sqrt{4-8e+20e^{2}}\right) \approx 0.1543\).
Proof
-
(i)
The function defined by \(m(r)=(1-6r-r^2)(1-r^2)^{-1}, \ 0\le r<1\) is a decreasing function. Let \(\rho =R_{{\mathcal {S}}_{e}^{*}}({\mathcal {G}}_1)\) be the root of the equation \(m(r)=1/e\). For \(0<r\le R_{{\mathcal {S}}_{e}^{*}}({\mathcal {G}}_1)\), we have \(m(r)\ge 1/e\). That is,
$$\begin{aligned} \frac{6r}{1-r^2}\le 1- \frac{1}{e}. \end{aligned}$$For the class \({\mathcal {G}}_1\), the centre of the disc is 1, therefore, by (23), the disc obtained in (10) is contained in the region bounded by exponential function. For the function \(f_1\) defined in (6), at \(z=R_{{\mathcal {S}}_{e}^{*}}({\mathcal {G}}_1)=\rho \),
$$\begin{aligned} \left| \log \frac{zf_1'(z)}{f_1(z)}\right| =\left| \log \frac{1+6\rho -\rho ^2}{1-\rho ^2}\right| =1. \end{aligned}$$ -
(ii)
The function \(n(r):[0, 1)\longrightarrow {\mathbb {R}}\) defined by \(n(r)=(1-5r-2r^2)(1-r^2)^{-1}+1\) is a decreasing function. Let \(\rho =R_{{\mathcal {S}}_{e}^{*}}({\mathcal {G}}_2)\) be the root of the equation \(n(r)=1/e\). For \(0<r\le R_{{\mathcal {S}}_{e}^{*}}({\mathcal {G}}_2)\), we have \(n(r)\ge 1/e\). That is,
$$\begin{aligned} \frac{r(r+5)}{1-r^2}\le 1-\frac{1}{e}. \end{aligned}$$For the class \({\mathcal {G}}_2\), the centre of the disc is 1, therefore, by (23), the disc obtained in (15) is contained in the region bounded by the exponential function. This shows that \(R_{{\mathcal {S}}_{e}^{*}}({\mathcal {G}}_2)\) is at least \(\rho \).
-
(iii)
The function defined by \(s(r)=1-(4r(1-r^2)^{-1}), \ 0\le r<1\) is a decreasing function. Let \(\rho =R_{{\mathcal {S}}_{e}^{*}}({\mathcal {G}}_3)\) be the root of the equation \(s(r)=1/e\). For \(0<r\le R_{{\mathcal {S}}_{e}^{*}}({\mathcal {G}}_3)\), we have \(s(r)\ge 1/e\). That is,
$$\begin{aligned} \frac{4r}{1-r^2}\le \frac{e-1}{e}. \end{aligned}$$For the class \({\mathcal {G}}_3\), the centre of the disc is 1, therefore, by (23), the disc obtained in (18) is contained in the region bounded by the exponential function. For the function \(g_1\) defined in (6), at \(z=R_{{\mathcal {S}}_{e}^{*}}({\mathcal {G}}_3)=\rho \),
$$\begin{aligned} \left| \log \frac{zg_1'(z)}{g_1(z)}\right| =\left| \log \frac{1+4\rho -\rho ^2}{1-\rho ^2}\right| =1. \end{aligned}$$
\(\square \)
Theorem 5 provides radii results for starlike functions associated with a cardioid. Sharma et al. [37] studied various properties of the class \({\mathcal {S}}_{c}^{*}={\mathcal {S}}^{*}(1+(4/3)z+(2/3)z^2)\). Geometrically, if a function \(f\in {\mathcal {S}}_{c}^{*}\) then \(zf'(z)/f(z)\) lies in the region bounded by the cardioid
They had also proved, for \(1/3 < a \le 5/3\), that
Theorem 5
The following results hold for the class \({\mathcal {S}}_{c}^{*}\):
-
(i)
\(R_{{\mathcal {S}}_{c}^{*}}({\mathcal {G}}_1)= (\sqrt{85}-9)/2 \approx 0.1097\).
-
(ii)
\(R_{{\mathcal {S}}_{c}^{*}}({\mathcal {G}}_2)\ge (\sqrt{265}-15)/10 \approx 0.1279\).
-
(iii)
\(R_{{\mathcal {S}}_{c}^{*}}({\mathcal {G}}_3)= \sqrt{10}-3 \approx 0.1623\).
Proof
-
(i)
The function defined by \(m(r)=(1-6r-r^2)(1-r^2)^{-1}, \ 0\le r<1\) is a decreasing function. Let \(\rho =R_{{\mathcal {S}}_{c}^{*}}({\mathcal {G}}_1)\) be the root of the equation \(m(r)=1/3\). For \(0<r\le R_{{\mathcal {S}}_{c}^{*}}({\mathcal {G}}_1)\), we have \(m(r)\ge 1/3\). That is,
$$\begin{aligned} \frac{6r}{1-r^2}\le 1- \frac{1}{3}. \end{aligned}$$For the class \({\mathcal {G}}_1\), the centre of the disc is 1, therefore, by (24), the disc obtained in (10) is contained in the region bounded by the cardioid. For the function \(f_1\) defined in (6), at \(z=R_{{\mathcal {S}}_{c}^{*}}({\mathcal {G}}_1)=\rho \),
$$\begin{aligned} \left| \frac{zf_1'(z)}{f_1(z)}\right| =\left| \frac{1+6\rho -\rho ^2}{1-\rho ^2}\right| =\frac{1}{3}=\varOmega _{c}(-1). \end{aligned}$$ -
(ii)
The function \(n(r):[0, 1)\longrightarrow {\mathbb {R}}\) defined by \(n(r)=(1-5r-2r^2)(1-r^2)^{-1}+1\) is a decreasing function. Let \(\rho =R_{{\mathcal {S}}_{c}^{*}}({\mathcal {G}}_2)\) be the root of the equation \(n(r)=1/3\). For \(0<r\le R_{{\mathcal {S}}_{c}^{*}}({\mathcal {G}}_2)\), we have \(n(r)\ge 1/3\). That is,
$$\begin{aligned} \frac{r(r+5)}{1-r^2}\le 1-\frac{1}{3}. \end{aligned}$$For the class \({\mathcal {G}}_2\), the centre of the disc is 1, therefore, by (24), the disc obtained in (15) is contained in the region bounded by the cardioid. This shows that \(R_{{\mathcal {S}}_{c}^{*}}({\mathcal {G}}_2)\) is at least \(\rho \).
-
(iii)
The function defined by \(s(r)=1-(4r(1-r^2)^{-1}), \ 0\le r<1\) is a decreasing function. Let \(\rho =R_{{\mathcal {S}}_{c}^{*}}({\mathcal {G}}_3)\) be the root of the equation \(s(r)=1/3\). For \(0<r\le R_{{\mathcal {S}}_{c}^{*}}({\mathcal {G}}_3)\), we have \(s(r)\ge 1/3\). That is,
$$\begin{aligned} \frac{4r}{1-r^2}\le \frac{2}{3}. \end{aligned}$$For the class \({\mathcal {G}}_3\), the centre of the disc is 1, therefore, by (24), the disc obtained in (18) is contained in the region bounded by the cardioid. For the function \(g_1\) defined in (6), at \(z=R_{{\mathcal {S}}_{c}^{*}}({\mathcal {G}}_3)=\rho \),
$$\begin{aligned} \left| \frac{zf_1'(z)}{f_1(z)}\right| =\left| \frac{1+4\rho -\rho ^2}{1-\rho ^2}\right| =\frac{1}{3}=\varOmega _{c}(-1). \end{aligned}$$
\(\square \)
In 2019, Cho et al. [5] considered the class of starlike functions associated with sine function where the class \({\mathcal {S}}_{sin}^{*}\) is defined as \({\mathcal {S}}_{sin}^{*}=\{f\in {\mathcal {A}}: zf'(z)/f(z)\prec 1+ \sin z:=q_0(z)\}\) for \(z \in {\mathbb {D}}\). For \(\left| a-1\right| \le \sin 1\), they had established the following inclusion:
Here \(\varOmega _{s}:=q_{0}({\mathbb {D}})\) is the image of the unit disk \({\mathbb {D}}\) under the map**s \(q_{0}(z)=1+\sin z\).
Theorem 6
The following results are sharp for the class \({\mathcal {S}}_{sin}^{*}\).
-
(i)
\(R_{{\mathcal {S}}_{sin}^{*}}({\mathcal {G}}_1)= \sin 1 /\left( 3+\sqrt{9+ \sin ^2 1 }\right) \approx 0.1375\).
-
(ii)
\(R_{{\mathcal {S}}_{sin}^{*}}({\mathcal {G}}_2)= 2\sin 1 /\left( 5+\sqrt{25+ 4\sin 1+4\sin ^2 1 }\right) \approx 0.1589\).
-
(iii)
\(R_{{\mathcal {S}}_{sin}^{*}}({\mathcal {G}}_3)= \sin 1 /\left( 2+\sqrt{4+ \sin ^2 1 }\right) \approx 0.2018\).
Proof
-
(i)
The function defined by \(m(r)=(1-6r-r^2)(1-r^2)^{-1}, \ 0\le r<1\) is a decreasing function. Let \(\rho =R_{{\mathcal {S}}_{sin}^{*}}({\mathcal {G}}_1)\) be the root of the equation \(m(r)=1-\sin 1\).For \(0<r\le R_{{\mathcal {S}}_{sin}^{*}}({\mathcal {G}}_1)\), we have \(m(r)\ge 1-\sin 1\). That is,
$$\begin{aligned}\frac{6r}{1-r^2}\le \sin 1.\end{aligned}$$For the class \({\mathcal {G}}_1\), the centre of the disc is 1, therefore, by (25), the disc obtained in (10) is contained in the region \(\varOmega _{s}\) bounded by the sine function. For the function \(f_1\) defined in (6), at \(z=-R_{{\mathcal {S}}_{sin}^{*}}({\mathcal {G}}_1)=-\rho \),
$$\begin{aligned} \left| \frac{zf_1'(z)}{f_1(z)}\right| =\left| \frac{1-6\rho -\rho ^2}{1-\rho ^2}\right| =1+\sin 1=q_0(1). \end{aligned}$$ -
(ii)
The function \(n(r):[0, 1)\longrightarrow {\mathbb {R}}\) defined by \(n(r)=(1-5r-2r^2)(1-r^2)^{-1}+1\) is a decreasing function. Let \(\rho =R_{{\mathcal {S}}_{sin}^{*}}({\mathcal {G}}_2)\) be the root of the equation \(n(r)=1-\sin 1\). For \(0<r\le R_{{\mathcal {S}}_{sin}^{*}}({\mathcal {G}}_2)\), we have \(n(r)\ge 1-\sin 1\). That is,
$$\begin{aligned} \frac{r(r+5)}{1-r^2}\le \sin 1.\end{aligned}$$For the class \({\mathcal {G}}_2\), the centre of the disc is 1, therefore, by (25), the disc obtained in (15) is contained in the region bounded by the sine function. For the function \(f_2\) defined in (11), at \(z=R_{{\mathcal {S}}_{sin}^{*}}({\mathcal {G}}_1)=\rho \),
$$\begin{aligned} \left| \frac{zf_2'(z)}{f_2(z)}\right| =\left| \frac{1+5\rho }{1-\rho ^2}\right| =1+\sin 1=q_0(1). \end{aligned}$$ -
(iii)
The function defined by \(s(r)=1-(4r(1-r^2)^{-1}), \ 0\le r<1\) is a decreasing function. Let \(\rho =R_{{\mathcal {S}}_{sin}^{*}}({\mathcal {G}}_3)\) be the root of the equation \(s(r)=1-\sin 1\). For \(0<r\le R_{{\mathcal {S}}_{sin}^{*}}({\mathcal {G}}_3)\), we have \(s(r)\ge 1-\sin 1\). That is,
$$\begin{aligned} \frac{4r}{1-r^2}\le \sin 1.\end{aligned}$$For the class \({\mathcal {G}}_3\), the centre of the disc is 1, therefore, by (25), the disc obtained in (18) is contained in the region bounded by the sine function. For the function \(g_1\) defined in (6), at \(z=-R_{{\mathcal {S}}_{sin}^{*}}({\mathcal {G}}_3)=-\rho \),
$$\begin{aligned} \left| \frac{zf_1'(z)}{f_1(z)}\right| =\left| \frac{1-4\rho -\rho ^2}{1-\rho ^2}\right| =1+\sin 1=q_0(1). \end{aligned}$$
\(\square \)
In 2015, Raina and Sokół[29] introduced the class  . They showed that a function
. They showed that a function  if and only if \(zf'(z)/f(z)\) belongs to a lune shaped region \({\mathcal {L}}:=\{w \in {\mathbb {C}}: \left| w^{2}-1\right| < 2 |w|\}\). Gandhi and Ravichandran [8, Lemma 2.1] proved that
if and only if \(zf'(z)/f(z)\) belongs to a lune shaped region \({\mathcal {L}}:=\{w \in {\mathbb {C}}: \left| w^{2}-1\right| < 2 |w|\}\). Gandhi and Ravichandran [8, Lemma 2.1] proved that
Theorem 7
The following results hold for the class  :
:
-
(i)
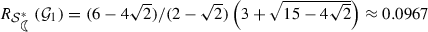 .
. -
(ii)
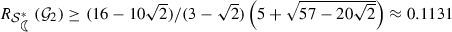 .
. -
(iii)
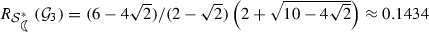 .
.
Proof
-
(i)
The function defined by \(m(r)=(1-6r-r^2)(1-r^2)^{-1}, \ 0\le r<1\) is a decreasing function. Let
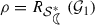 be the root of the equation \(m(r)=\sqrt{2}-1\). For
be the root of the equation \(m(r)=\sqrt{2}-1\). For 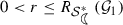 , we have \(m(r)\ge \sqrt{2}-1\). That is, $$\begin{aligned} \frac{6r}{1-r^2}\le 2-\sqrt{2}. \end{aligned}$$
, we have \(m(r)\ge \sqrt{2}-1\). That is, $$\begin{aligned} \frac{6r}{1-r^2}\le 2-\sqrt{2}. \end{aligned}$$For the class \({\mathcal {G}}_1\), the centre of the disc is 1, therefore, by (26), the disc obtained in (10) is contained in the region bounded by the intersection of disks \(\left\{ w:|w - 1| < \sqrt{2}\right\} \) and \(\left\{ w:|w + 1| < \sqrt{2}\right\} \). For the function \(f_1\) defined in (6), at
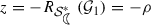 , $$\begin{aligned} \left| \left( \frac{zf_1'(z)}{f_1(z)}\right) ^2-1\right| =\left| \left( \frac{1-6\rho -\rho ^2}{1-\rho ^2}\right) ^2-1\right| =2\left| \frac{1-6\rho -\rho ^2}{1-\rho ^2}\right| . \end{aligned}$$
, $$\begin{aligned} \left| \left( \frac{zf_1'(z)}{f_1(z)}\right) ^2-1\right| =\left| \left( \frac{1-6\rho -\rho ^2}{1-\rho ^2}\right) ^2-1\right| =2\left| \frac{1-6\rho -\rho ^2}{1-\rho ^2}\right| . \end{aligned}$$ -
(ii)
The function \(n(r):[0, 1)\longrightarrow {\mathbb {R}}\) defined by \(n(r)=(1-5r-2r^2)(1-r^2)^{-1}+1\) is a decreasing function. Let
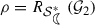 be the root of the equation \(n(r)=\sqrt{2}-1\). For
be the root of the equation \(n(r)=\sqrt{2}-1\). For 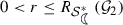 , we have \(n(r)\ge \sqrt{2}-1\). That is, $$\begin{aligned} \frac{r(r+5)}{1-r^2}\le 2-\sqrt{2}. \end{aligned}$$
, we have \(n(r)\ge \sqrt{2}-1\). That is, $$\begin{aligned} \frac{r(r+5)}{1-r^2}\le 2-\sqrt{2}. \end{aligned}$$For the class \({\mathcal {G}}_2\), the centre of the disc is 1, therefore, by (26), the disc obtained in (15) is contained in the region bounded by the lune. This shows that
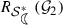 is at least \(\rho \).
is at least \(\rho \). -
(iii)
The function \(s(r):[0, 1)\longrightarrow {\mathbb {R}}\) defined by \(s(r)=1-(4r(1-r^2)^{-1})\) is a decreasing function. Let
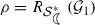 be the root of the equation \(s(r)=\sqrt{2}-1\). For
be the root of the equation \(s(r)=\sqrt{2}-1\). For 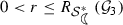 , we have \(s(r)\ge \sqrt{2}-1\). That is, $$\begin{aligned} \frac{4r}{1-r^2}\le 2-\sqrt{2}. \end{aligned}$$
, we have \(s(r)\ge \sqrt{2}-1\). That is, $$\begin{aligned} \frac{4r}{1-r^2}\le 2-\sqrt{2}. \end{aligned}$$For the class \({\mathcal {G}}_3\), the centre of the disc is 1, therefore, by (26), the disc obtained in (18) is contained in the region bounded by the lune. For the function \(g_1\) defined in (6), at
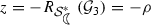 , $$\begin{aligned} \left| \left( \frac{zg_1'(z)}{g_1(z)}\right) ^2-1\right| =\left| \left( \frac{1-4\rho -\rho ^2}{1-\rho ^2}\right) ^2-1\right| =2\left| \frac{1-4\rho -\rho ^2}{1-\rho ^2}\right| . \end{aligned}$$
, $$\begin{aligned} \left| \left( \frac{zg_1'(z)}{g_1(z)}\right) ^2-1\right| =\left| \left( \frac{1-4\rho -\rho ^2}{1-\rho ^2}\right) ^2-1\right| =2\left| \frac{1-4\rho -\rho ^2}{1-\rho ^2}\right| . \end{aligned}$$
\(\square \)
In the next theorem, we provide radii for starlike functions associated with a rational function. Kumar and Ravichandran [19] introduced the class of starlike functions associated with a rational function
where \(k=\sqrt{2}+1\), defined by \({\mathcal {S}}_{R}^{*}={\mathcal {S}}^{*}(\psi (z))\). For \(2(\sqrt{2}-1) < a \le \sqrt{2}\), they had proved that
Theorem 8
The following results hold for the class \({\mathcal {S}}_{R}^{*}\):
-
(i)
\(R_{{\mathcal {S}}_{R}^{*}}({\mathcal {G}}_1)= (3-2\sqrt{2})/\left( 3+\sqrt{26-12\sqrt{2}}\right) \approx 0.0285\).
-
(ii)
\(R_{{\mathcal {S}}_{R}^{*}}({\mathcal {G}}_2)\ge (20-14\sqrt{2})/(2-\sqrt{2})\left( 5+\sqrt{105-56\sqrt{2}}\right) \approx 0.0340\).
-
(iii)
\(R_{{\mathcal {S}}_{R}^{*}}({\mathcal {G}}_3)= (3-2\sqrt{2})/\left( 2+\sqrt{21-12\sqrt{2}}\right) \approx 0.0428\).
Proof
-
(i)
The function defined by \(m(r)=(1-6r-r^2)(1-r^2)^{-1}, \ 0\le r<1\) is a decreasing function. Let \(\rho =R_{{\mathcal {S}}_{R}^{*}}({\mathcal {G}}_1)\) be the root of the equation \(m(r)=2(\sqrt{2}-1)\). For \(0<r\le R_{{\mathcal {S}}_{R}^{*}}({\mathcal {G}}_1)\), we have \(m(r)\ge 2(\sqrt{2}-1)\). That is,
$$\begin{aligned} \frac{6r}{1-r^2}\le 1-2(\sqrt{2}-1). \end{aligned}$$For the class \({\mathcal {G}}_1\), the centre of the disc is 1, therefore, by (27), the disc obtained in (10) is contained in the region bounded by the rational function. For the function \(f_1\) defined in (6), at \(z=-R_{{\mathcal {S}}_{R}^{*}}({\mathcal {G}}_1)=-\rho \),
$$\begin{aligned} \left| \frac{zf_1'(z)}{f_1(z)}\right| =\left| \frac{1-6\rho -\rho ^2}{1-\rho ^2}\right| =2(\sqrt{2}-1)=\psi (1). \end{aligned}$$ -
(ii)
The function \(n(r):[0, 1)\longrightarrow {\mathbb {R}}\) defined by \(n(r)=(1-5r-2r^2)(1-r^2)^{-1}+1\) is a decreasing function. Let \(\rho =R_{{\mathcal {S}}_{R}^{*}}({\mathcal {G}}_2)\) be the root of the equation \(n(r)=2(\sqrt{2}-1)\). The function defined by
$$\begin{aligned} n(r)=\frac{1-5r-2r^2}{1-r^2}+1 \end{aligned}$$is a decreasing function. For \(0<r\le R_{{\mathcal {S}}_{R}^{*}}({\mathcal {G}}_2)\), we have \(n(r)\ge 2(\sqrt{2}-1)\). That is,
$$\begin{aligned} \frac{r(r+5)}{1-r^2}\le 3-2\sqrt{2}. \end{aligned}$$For the class \({\mathcal {G}}_2\), the centre of the disc is 1, therefore, by (27), the disc obtained in (15) is contained in the region bounded by the rational function. This shows that \(R_{{\mathcal {S}}_{R}^{*}}({\mathcal {G}}_2)\) is at least \(\rho \).
-
(iii)
The function defined by \(s(r)=1-(4r(1-r^2)^{-1}), \ 0\le r<1\) is a decreasing function. Let \(\rho =R_{{\mathcal {S}}_{R}^{*}}({\mathcal {G}}_3)\) be the root of the equation \(s(r)=2(\sqrt{2}-1)\). For \(0<r\le R_{{\mathcal {S}}_{R}^{*}}({\mathcal {G}}_3)\), we have \(s(r)\ge 2(\sqrt{2}-1)\). That is,
$$\begin{aligned} \frac{4r}{1-r^2}\le 2-\sqrt{2}. \end{aligned}$$For the class \({\mathcal {G}}_3\), the centre of the disc is 1, therefore, by (27), the disc obtained in (18) is contained in the region bounded by the rational function. For the function \(g_1\) defined in (6), at \(z=-R_{{\mathcal {S}}_{R}^{*}}({\mathcal {G}}_3)=-\rho \),
$$\begin{aligned} \left| \frac{zg_1'(z)}{g_1(z)}\right| =\left| \frac{1-4\rho -\rho ^2}{1-\rho ^2}\right| =2(\sqrt{2}-1)=\psi (1). \end{aligned}$$
\(\square \)
Mendiratta et al. [26] studied the subclass of starlike function associated with left half of shifted lemniscate of Bernoulli, given by \(\left| (w-\sqrt{2})^{2}-1\right| < 1\). The class \({\mathcal {S}}_{RL}^{*}\) is defined as
For \(\sqrt{2}/3 \le a < \sqrt{2}\), they had proved the following inclusion:
where
Using this result, we obtain \({\mathcal {S}}_{RL}^{*}\)-radii of the classes \({\mathcal {G}}_1, \ {\mathcal {G}}_2, \ {\mathcal {G}}_3\) in the following theorem.
Theorem 9
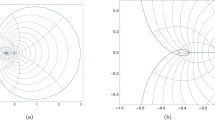
Let \(\eta =\sqrt{2(\sqrt{2}-1)}-2(\sqrt{2}-1)\). Then the following sharp results hold for the class \({\mathcal {S}}_{RL}^{*}\).
-
(i)
\(R_{{\mathcal {S}}_{RL}^{*}}({\mathcal {G}}_1)\) is the smallest positive root \((\approx 0.0475)\) in (0, 1) of the equation \((36+2\eta )r^2-\eta r^2-\eta =0\).
-
(ii)
\(R_{{\mathcal {S}}_{RL}^{*}}({\mathcal {G}}_2)\) is the smallest positive root \((\approx 0.0567)\) in (0, 1) of the equation \((1-\eta )r^4+10r^3+(25-2\eta ) r^2-\eta =0\).
-
(iii)
\(R_{{\mathcal {S}}_{RL}^{*}}({\mathcal {G}}_3)\) is the smallest positive root \((\approx 0.0711)\) in (0, 1) of the equation \(\eta r^4-(16+2\eta )r^2+\eta =0\).
Proof
-
(i)
The function defined by \(m(r)=(6r(1-r^2)^{-1})+1, \ 0\le r<1\) is an increasing function. Let \(\rho =R_{{\mathcal {S}}_{RL}^{*}}({\mathcal {G}}_3)\) be the root of the equation \(m(r)=1+\sqrt{\eta }\). For \(0<r\le R_{{\mathcal {S}}_{RL}^{*}}({\mathcal {G}}_1)\), we have \(m(r)\le \sqrt{2}\). That is,
$$\begin{aligned} \left( \frac{6r}{1-r^2}\right) ^2 \le \eta =(m(\rho )-1)^2. \end{aligned}$$For the class \({\mathcal {G}}_1\), the centre of the disc is 1, therefore, by (28), the disc obtained in (10) is contained in the region bounded by the reverse lemniscate. This shows that \(R_{{\mathcal {S}}_{RL}^{*}}({\mathcal {G}}_1)\) is at least \(\rho \). For the function \(f_1\) defined in (6), the radius is sharp.
-
(ii)
The function defined by \(n(r)=(5r+r^2)(1-r^2)^{-1}+1, \ 0\le r<1\) is an increasing function. Let \(R_{{\mathcal {S}}_{RL}^{*}}({\mathcal {G}}_2)\) be the root of the equation \(n(r)=1+\sqrt{\eta }\). For \(0<r\le R_{{\mathcal {S}}_{RL}^{*}}({\mathcal {G}}_2)\), we have \(n(r)\le \sqrt{2}\). That is,
$$\begin{aligned} \left( \frac{5r+r^2}{1-r^2}\right) ^2\le \eta =(n(\rho )-1)^2. \end{aligned}$$For the class \({\mathcal {G}}_2\), the centre of the disc is 1, therefore, by (28), the disc obtained in (15) is contained in the region bounded by reverse lemniscate. This shows that \(R_{{\mathcal {S}}_{RL}^{*}}({\mathcal {G}}_2)\) is at least \(\rho \). The obtained radius is sharp for the function \(f_2\) defined in (11).
-
(iii)
The function defined by \(s(r)=4r(1-r^2)^{-1}+1, \ 0\le r<1\) is an increasing function. Let \(R_{{\mathcal {S}}_{RL}^{*}}({\mathcal {G}}_3)\) be the root of the equation \(s(r)=1+\sqrt{\eta }\). For \(0<r\le R_{{\mathcal {S}}_{RL}^{*}}({\mathcal {G}}_3)\), we have \(s(r)\le \sqrt{2}\). That is,
$$\begin{aligned} \left( \frac{4r}{1-r^2}\right) ^2 \le \eta =(s(\rho )-1)^2. \end{aligned}$$For the class \({\mathcal {G}}_3\), the centre of the disc is 1, therefore, by (28), the disc obtained in (18) is contained in the region bounded by reverse lemniscate. This shows that \(R_{{\mathcal {S}}_{RL}^{*}}({\mathcal {G}}_3)\) is at least \(\rho \). The obtained radius is sharp for the function \(g_1\) defined in (6).
The sharpness of the results can be seen by looking at the graphs. \(\square \)
In 2020, Wani and Swaminathan [40, Lemma 2.2] introduced the class \({\mathcal {S}}_{Ne}^{*}={\mathcal {S}}^{*}(1+z-(z^3/3))\) that maps the open unit disc \({\mathbb {D}}\) onto the interior of a two cusped kidney shaped curve \(\varOmega _{Ne}:=\{u+iv: ((u-1)^2+v^2-4/9)^3-4v^2/3<0\}\). For \(1/3 < a \le 1\), they had proved that
Our next theorem determines the \({\mathcal {S}}_{Ne}^{*}\)-radii results for the classes \({\mathcal {G}}_1\), \({\mathcal {G}}_2\) and \({\mathcal {G}}_3\).
Theorem 10
The following sharp results hold for the class \({\mathcal {S}}_{Ne}^{*}\).
-
(i)
\(R_{{\mathcal {S}}_{Ne}^{*}}({\mathcal {G}}_1)= (\sqrt{85}-9)/2 \approx 0.1097\).
-
(ii)
\(R_{{\mathcal {S}}_{Ne}^{*}}({\mathcal {G}}_2)=(\sqrt{265}-15)/10 \approx 0.1278\).
-
(iii)
\(R_{{\mathcal {S}}_{Ne}^{*}}({\mathcal {G}}_3)=\sqrt{10}-3\approx 0.1622\).
Proof
-
(i)
The function defined by \(m(r)=(1-6r-r^2)(1-r^2)^{-1}, \ 0\le r<1\) is a decreasing function. Let \(\rho = R_{{\mathcal {S}}_{Ne}^{*}}({\mathcal {G}}_1)\) be the root of the equation \(m(r)=1/3\). For \(0<r\le R_{{\mathcal {S}}_{Ne}^{*}}({\mathcal {G}}_1)\), we have \(m(r)\ge 1/3\). That is,
$$\begin{aligned} \frac{6r}{1-r^2}\le 1-\frac{1}{3}. \end{aligned}$$For the class \({\mathcal {G}}_1\), the centre of the disc is 1, therefore, by (29), the disc obtained in (10) is contained in the region bounded by the nephroid. For the function \(f_1\) defined in (6), at \(z=R_{{\mathcal {S}}_{Ne}^{*}}({\mathcal {G}}_1)=\rho \),
$$\begin{aligned} \left| \frac{zf_1'(z)}{f_1(z)}\right| =\left| \frac{1+6\rho -\rho ^2}{1-\rho ^2}\right| =\frac{1}{3}\in \partial \varOmega _{Ne} \end{aligned}$$where \(\partial \varOmega _{Ne}\) denotes the boundary of nephroid domain.
-
(ii)
The function \(n(r):[0, 1)\longrightarrow {\mathbb {R}}\) defined by \(n(r)=(1-5r-2r^2)(1-r^2)^{-1}+1\) is a decreasing function. Let \(\rho =R_{{\mathcal {S}}_{Ne}^{*}}({\mathcal {G}}_2)\) be the root of the equation \(n(r)=1/3\). For \(0<r\le R_{{\mathcal {S}}_{Ne}^{*}}({\mathcal {G}}_2)\), we have \(n(r)\ge 1/3\). That is,
$$\begin{aligned} \frac{r(r+5)}{1-r^2}\le \frac{2}{3}. \end{aligned}$$For the class \({\mathcal {G}}_2\), the centre of the disc is 1, therefore, by (29), the disc obtained in (15) is contained in the region bounded by the nephroid. For the function \(f_2\) defined in (11), at \(z=R_{{\mathcal {S}}_{Ne}^{*}}({\mathcal {G}}_2)=\rho \),
$$\begin{aligned} \left| \frac{zf_2'(z)}{f_2(z)}\right| =\left| \frac{1+5\rho }{1-\rho ^2}\right| =\frac{5}{3}\in \partial \varOmega _{Ne}. \end{aligned}$$ -
(iii)
The function defined by \(s(r)=1-(4r(1-r^2)^{-1}), \ 0\le r<1\) is a decreasing function. Let \(\rho =R_{{\mathcal {S}}_{Ne}^{*}}({\mathcal {G}}_3)\) be the root of the equation \(s(r)=1/3\). For \(0<r\le R_{{\mathcal {S}}_{Ne}^{*}}({\mathcal {G}}_3)\), we have \(s(r)\ge 1/3\). That is,
$$\begin{aligned} \frac{4r}{1-r^2}\le \frac{2}{3}. \end{aligned}$$For the class \({\mathcal {G}}_3\), the centre of the disc is 1, therefore, by (29), the disc obtained in (18) is contained in the region bounded by the nephroid. For the function \(g_1\) defined in (6), at \(z=R_{{\mathcal {S}}_{Ne}^{*}}({\mathcal {G}}_3)=\rho \),
$$\begin{aligned} \left| \frac{zg_1'(z)}{g_1(z)}\right| =\left| \frac{1+4\rho -\rho ^2}{1-\rho ^2}\right| =\frac{1}{3}\in \partial \varOmega _{Ne}. \end{aligned}$$
\(\square \)
In 2020, Goel and Kumar [10] introduced the class \({\mathcal {S}}_{SG}^{*}\) that maps the open unit disc \({\mathbb {D}}\) onto a domain \(\varDelta _{SG}:=\{w\in {\mathbb {C}}:|\log ( w/(2-w))|<1\}\) and \({\mathcal {S}}_{SG}^{*}={\mathcal {S}}^{*}(2/(1+e^{-z}))\). For \(2/(1+e)<a<2e/(1+e)\), they had proved the following inclusion:
provided \(r_{SG}=((e-1)/(e+1))-|a-1|\). Theorem 11 provides \({\mathcal {S}}_{SG}^{*}\)-radii of the classes \({\mathcal {G}}_1, \ {\mathcal {G}}_2, \ {\mathcal {G}}_3\).
Theorem 11
The following sharp results hold for the class \({\mathcal {S}}_{SG}^{*}\).
-
(i)
\(R_{{\mathcal {S}}_{SG}^{*}}({\mathcal {G}}_1)= 2(e-1)/\left( (6+6e)+\sqrt{40+64e+40e^2}\right) \approx 0.0766\).
-
(ii)
\(R_{{\mathcal {S}}_{SG}^{*}}({\mathcal {G}}_2)=2(e-1)/\left( (5+5e)+\sqrt{25+42e+33e^2}\right) \approx 0.0901\).
-
(iii)
\(R_{{\mathcal {S}}_{SG}^{*}}({\mathcal {G}}_3)=2(e-1)/\left( (4+4e)+\sqrt{20+24e+20e^2}\right) \approx 0.1140\).
Proof
-
(i)
The function defined by \(m(r)=(1-6r-r^2)(1-r^2)^{-1}, \ 0\le r<1\) is a decreasing function. Let \(\rho =R_{{\mathcal {S}}_{SG}^{*}}({\mathcal {G}}_1)\) be the root of the equation \(m(r)=2/(1+e)\). For \(0<r\le R_{{\mathcal {S}}_{SG}^{*}}({\mathcal {G}}_1)\), we have \(m(r)\ge 2/(1+e)\). That is,
$$\begin{aligned} \frac{6r}{1-r^2}\le \frac{e-1}{e+1}. \end{aligned}$$For the class \({\mathcal {G}}_1\), the centre of the disc is 1, therefore, by (30), the disc obtained in (10) is contained in the region bounded by the modified sigmoid. For the function \(f_1\) defined in (6), at \(z=R_{{\mathcal {S}}_{SG}^{*}}({\mathcal {G}}_1)=\rho \),
$$\begin{aligned} \left| \log \frac{zf_1'(z)/f_1(z)}{2-(zf_1'(z)/f_1(z))}\right| =\left| \log \frac{(1+6\rho -\rho ^2)/(1-\rho ^2)}{2-((1+6\rho -\rho ^2)/(1-\rho ^2))}\right| =1. \end{aligned}$$ -
(ii)
The function \(n(r):[0, 1)\longrightarrow {\mathbb {R}}\) defined by \(n(r)=(1-5r-2r^2)(1-r^2)^{-1}+1\) is a decreasing function. Let \(\rho =R_{{\mathcal {S}}_{SG}^{*}}({\mathcal {G}}_2)\) be the root of the equation \(n(r)=2/(1+e)\). For \(0<r\le R_{{\mathcal {S}}_{SG}^{*}}({\mathcal {G}}_2)\), we have \(n(r)\ge 2/1+e\). That is,
$$\begin{aligned}\frac{r(r+5)}{1-r^2}\le \frac{e-1}{e+1}.\end{aligned}$$For the class \({\mathcal {G}}_2\), the centre of the disc is 1, therefore, by (30), the disc obtained in (15) is contained in the region bounded by the modified sigmoid. For the function \(f_2\) defined in (11), at \(z=R_{{\mathcal {S}}_{SG}^{*}}({\mathcal {G}}_2)=\rho \),
$$\begin{aligned} \left| \log \frac{zf_2'(z)/f_2(z)}{2-(zf_2'(z)/f_2(z))}\right| =\left| \log \frac{(1+5\rho )/(1-\rho ^2)}{2-((1+5\rho )/(1-\rho ^2))}\right| =1. \end{aligned}$$ -
(iii)
The function defined by \(s(r)=1-(4r(1-r^2)^{-1}), \ 0\le r<1\) is a decreasing function. Let \(\rho =R_{{\mathcal {S}}_{SG}^{*}}({\mathcal {G}}_3)\) be the root of the equation \(s(r)=2/(1+e)\). For \(0<r\le R_{{\mathcal {S}}_{SG}^{*}}({\mathcal {G}}_3)\), we have \(s(r)\ge 2/(1+e)\). That is,
$$\begin{aligned}\frac{4r}{1-r^2}\le \frac{e-1}{e+1}.\end{aligned}$$For the class \({\mathcal {G}}_3\), the centre of the disc is 1, therefore, by (30), the disc obtained in (18) is contained in the region bounded by the modified sigmoid. For the function \(g_1\) defined in (6), at \(z=R_{{\mathcal {S}}_{SG}^{*}}({\mathcal {G}}_3)=\rho \),
$$\begin{aligned} \left| \log \frac{zg_1'(z)/g_1(z)}{2-(zg_1'(z)/g_1(z))}\right| =\left| \log \frac{(1+4\rho -\rho ^2)/(1-\rho ^2)}{2-((1+4\rho -\rho ^2)/(1-\rho ^2))}\right| =1. \end{aligned}$$
\(\square \)
Though we have no proof, we believe that the sharp radii for the class \({\mathcal {G}}_2\) are the following:
-
1.
\(R_{{\mathcal {S}}_{p}}({\mathcal {G}}_2)= 5-2\sqrt{6} \approx 0.1010\).
-
(i)
\(R_{{\mathcal {S}}_{e}^{*}}({\mathcal {G}}_2)= 2(e^2+e+2)/(2+e)\left( 5e+\sqrt{-8+4e+29e^{2} }\right) \approx 0.1276\).
-
(ii)
\(R_{{\mathcal {S}}_{c}^{*}}({\mathcal {G}}_2)= (15-\sqrt{217})/2 \approx 0.1345\).
-
(iii)
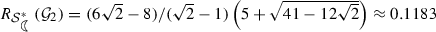 .
. -
(iv)
\(R_{{\mathcal {S}}_{R}^{*}}({\mathcal {G}}_2)= (10\sqrt{2}-14)/(\sqrt{2}-1)\left( 5+\sqrt{81-40\sqrt{2}}\right) \approx 0.0345\).
Our estimate for these radii are respectively 0.0972, 0.1213, 0.1279, 0.1131, 0.0340 and are very much close to the above mentioned values.
Availability of data and material
Not applicable. The manuscript has no associated data.
References
Ali, R.M., Jain, N.K., Ravichandran, V.: Radii of starlikeness associated with the lemniscate of Bernoulli and the left-half plane. Appl. Math. Comput. 218(11), 6557–6565 (2012)
Ali, R.M., Jain, N.K., Ravichandran, V.: On the radius constants for classes of analytic functions. Bull. Malays. Math. Sci. Soc. 36(1), 23–38 (2013)
Aouf, M.K., Dziok, J., Sokół, J.: On a subclass of strongly starlike functions. Appl. Math. Lett. 24(1), 27–32 (2011)
Causey, W.M., Merkes, E.P.: Radii of starlikeness of certain classes of analytic functions. J. Math. Anal. Appl. 31, 579–586 (1970)
Cho, N.E., Kumar, V., Kumar, S.S., Ravichandran, V.: Radius problems for starlike functions associated with the sine function. Bull. Iran. Math. Soc. 45(1), 213–232 (2019)
Duren, P.L.: Univalent Functions, GTM, vol. 259. Springer-Verlag, New York (1983)
El-Faqeer A.S.A., Mohd M.H., Ravichandran V., Supramaniam S.: Radius of starlikeness of functions defined by ratios of analytic functions, Appl. Math. E-Notes, to appear
Gandhi, S., Ravichandran, V.: Starlike functions associated with a lune. Asian-Eur. J. Math. 10(4), 1750064 (2017)
Gangadharan, A., Ravichandran, V., Shanmugam, T.N.: Radii of convexity and strong starlikeness for some classes of analytic functions. J. Math. Anal. Appl. 211(1), 301–313 (1997)
Goel, P., Kumar, S.: Sivaprasad: Certain class of starlike functions associated with modified sigmoid function. Bull. Malays. Math. Sci. Soc. 43(1), 957–991 (2020)
Goodman, A.W.: Univalent Functions, vol. II. Mariner, Tampa, FL (1983)
Janowski, W.: Extremal problems for a family of functions with positive real part and for some related families. Ann. Polon. Math. 23, 159–177 (1970/71)
Janowski, W.: Some extremal problems for certain families of analytic functions. I. Ann. Polon. Math. 28, 297–326 (1973)
Kanaga, R., Ravichandran, V.: Starlikeness for certain close-to-star functions. Hacet. J. Math. Stat. 50(2), 414–432 (2021)
Khatter, K., Lee, S.K., Ravichandran, V.: Radius of starlikeness for classes of analytic functions. Bull. Malays. Math. Sci. Soc. 43(6), 4469–4493 (2020)
Kowalczyk, B., Lecko, A.: Radius problem in classes of polynomial close-to-convex functions I. Bull. Soc. Sci. Lett. Łódź Sér. Rech. Déform. 63(1), 65–77 (2013)
Kowalczyk, B., Lecko, A.: Radius problem in classes of polynomial close-to-convex functions II. Partial solutions. Bull. Soc. Sci. Lett. Łódź Sér. Rech. Déform. 63(2), 23–34 (2013)
Kowalczyk, B., Lecko, A., Śmiarowska, B.: On some coefficient inequality in the subclass of close-to-convex functions. Bull. Soc. Sci. Lett. Łódź Sér. Rech. Déform. 67(1), 79–90 (2017)
Kumar, S., Ravichandran, V.: A subclass of starlike functions associated with a rational function. Southeast Asian Bull. Math. 40(2), 199–212 (2016)
Lecko, A., Sim, Y.J.: Coefficient problems in the subclasses of close-to-star functions. Results Math. 74(3), 104 (2019)
Ma, W.C., Minda, D.: Uniformly convex functions. Ann. Polon. Math. 57(2), 165–175 (1992)
Ma, W.C., Minda, D.: A unified treatment of some special classes of univalent functions, Proceedings of the Conference on Complex Analysis (Tian**), 1992, Conf. Proc. Lecture Notes Anal., I, Int. Press, Cambridge, MA, pp. 157–169 (1994)
MacGregor, T.H.: The radius of convexity for starlike functions of order \(\frac{1}{2}\). Proc. Am. Math. Soc. 14, 71–76 (1963)
MacGregor, T.H.: The radius of univalence of certain analytic functions. Proc. Am. Math. Soc. 14, 514–520 (1963)
MacGregor, T.H.: A class of univalent functions. Proc. Am. Math. Soc. 15, 311–317 (1964)
Mendiratta, R., Nagpal, S., Ravichandran, V.: A subclass of starlike functions associated with left-half of the lemniscate of Bernoulli. Internat. J. Math. 25(9), 1450090 (2014)
Mendiratta, R., Nagpal, S., Ravichandran, V.: On a subclass of strongly starlike functions associated with exponential function. Bull. Malays. Math. Sci. Soc. 38(1), 365–386 (2015)
Paprocki, E., Sokół, J.: The extremal problems in some subclass of strongly starlike functions. Zeszyty Nauk. Politech. Rzeszowskiej Mat. 20, 89–94 (1996)
Raina, R.K., Sokół, J.: Some properties related to a certain class of starlike functions. C. R. Math. Acad. Sci. Paris 353(11), 973–978 (2015)
Ratti, J.S.: The radius of convexity of certain analytic functions. Indian J. Pure Appl. Math. 1(1), 30–36 (1970)
Ratti, J.S.: The radius of univalence of certain analytic functions. Math. Z. 107, 241–248 (1968)
Ravichandran, V., Rønning, F., Shanmugam, T.N.: Radius of convexity and radius of starlikeness for some classes of analytic functions. Complex Variables Theory Appl. 33(1–4), 265–280 (1997)
Sebastian, A., Ravichandran, V.: Radius of starlikeness of certain analytic functions. Math. Slovaca 71(1), 83–104 (2021)
Shah, G.M.: On the univalence of some analytic functions. Pacific J. Math. 43, 239–250 (1972)
Shanmugam, T.N.: Convolution and differential subordination. Internat. J. Math. Math. Sci. 12(2), 333–340 (1989)
Shanmugam, T.N., Ravichandran, V.: Certain properties of uniformly convex functions, Computational methods and function theory 1994 (Penang), Ser. Approx. Decompos., vol. 5, World Sci. Publ., River Edge, NJ, pp. 319–324 (1995)
Sharma, K., Jain, N.K., Ravichandran, V.: Starlike functions associated with a cardioid. Afr. Mat. 27(5–6), 923–939 (2016)
Sokół, J., Stankiewicz, J.: Radius of convexity of some subclasses of strongly starlike functions. Zeszyty Nauk. Politech. Rzeszowskiej Mat. 19, 101–105 (1996)
Srivastava, H.M., Owa, S. (eds.): Current Topics in Analytic Function Theory. World Scientific Publishing Co., Inc, River Edge, NJ (1992)
Wani, L.A., Swaminathan, A.: Starlike and convex functions associated with a nephroid domain. Bull. Malays. Math. Sci. Soc. 44(1), 79–104 (2021)
Acknowledgements
The authors are thankful to the referee for his/her comments.
Funding
Asha Sebastian is supported by an institute fellowship from NIT Tiruchirappalli.
Author information
Authors and Affiliations
Contributions
All authors jointly worked on the results and they read and approved the final manuscript.
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Additional information
Dedicated to Prof. Dato’ Indera Rosihan M. Ali.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Lecko, A., Ravichandran, V. & Sebastian, A. Starlikeness of certain non-univalent functions. Anal.Math.Phys. 11, 163 (2021). https://doi.org/10.1007/s13324-021-00600-6
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1007/s13324-021-00600-6



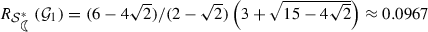 .
.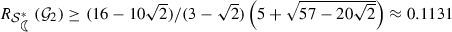 .
.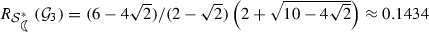 .
.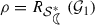 be the root of the equation
be the root of the equation 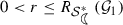 , we have
, we have 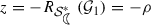 ,
, 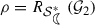 be the root of the equation
be the root of the equation 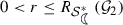 , we have
, we have 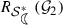 is at least
is at least 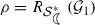 be the root of the equation
be the root of the equation 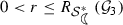 , we have
, we have 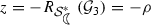 ,
, 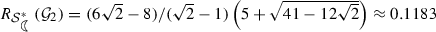 .
.