Younger children and mothers’ labour supply in rural India: Evidence from fertility stop** behaviour

“I myself would like one son.

And I don’t want many children.

But it isn’t a question of what I want.

Until I have a son, I won’t stop having children.”

--(Clark, 2000)

Abstract

This paper estimates the causal effect of having young children aged 0–5 years on mothers’ labour force participation in rural India. To address the potential endogeneity in the fertility decision, I exploit Indian families’ preference for having sons. I leverage exogenous variation in the gender of older children aged 6 + years as an instrumental variable for having younger children aged 0–5 years in the family. IV estimates show that the mothers’ participation is significantly reduced by 9.9% due to the presence of young children aged 0–5 years in the household, with the negative effect mostly driven by mothers belonging to the highest income quartile; mothers with high education; and mothers residing in nuclear families. The findings highlight the need for investment in high-skilled jobs and formal childcare facilities to encourage mothers’ labour supply. Using the testable implications for the generalizability of LATE discussed in Angrist (The Economic Journal, 114: C52 C83, 2004), I show that the estimated causal effect is homogenous across compliers, always takers, and never takers and thus, generalizable to the whole population of interest.

Introduction

Studies estimating the effect of fertility on mothers’ labour force participation look at the effect of having an additional child on mothers’ labour supply without taking into account the age of the child (see, e.g. Rosenzweig and Wolpin (1980), Angrist and Evans (1998), Fontaine (2017), Lundborg et al. (2017)). However, there are differential effects on the participation decision of the mother depending on the age of the children. A preschool-aged child, for example, requires more care and attention from the mother compared to an older child and consequently poses more responsibility onto mothers. Also, a mother’s physical presence is deemed necessary in the early years of childhood, thus, making it difficult for mothers with young children to work. In this paper, I fill this gap by estimating the causal effect of having preschool children aged 0–5 years on mothers’ labour force participation. I use the latest wave of the India Human Development Survey (IHDS) conducted in 2011–2012 from the rural areas of India where almost 70 percent of the female population lives (Census, 2011).

The main challenge involved in the estimation of the causal effect is that fertility decisions and mothers’ labour supply are jointly and simultaneously determined. Mothers who decide to have (more) children are not a random subgroup of the population. For instance, women who are more family-oriented and thus, have lower labour market attachment or earnings potential, might choose to have more children. On the other hand, women who are more career-oriented and have higher labour market attachment may decide to delay motherhood and have fewer children (Fahle & McGarry 2017; Jensen 2012; Miller et al., 2022).¹

To deal with this problem of endogeneity in fertility decisions, I use the instrumental variable strategy.² I exploit the preference of Indian parents to have at least one son in the family, as an exogenous source of variation in the presence of younger children. Parents without any male child aged 6 + years are more likely to have continued childbearing and thus, are more likely to have younger children aged 0–5 years as compared to parents who already have a male child. And since the gender of children is virtually randomly assigned, a dummy variable indicating whether parents already have a boy child or not aged 6 + years—conditional on the number of children—serves as an instrument (exogenous shock) for further childbearing.³

This paper makes several other methodological contributions to the literature. It is widely recognized that women are overrepresented in unpaid family work, especially in rural areas, where they spend much more time on-farm activities than outside work resulting in underreporting of women’s work arising from measurement limitations. In this paper, I use a more comprehensive measure of women's work to accurately capture their labour force participation. Thanks to the richness of the IHDS data at hand, I analyze the overall participation of women including both paid work as well as unpaid family work at family farms and family businesses. In the survey data I use, respondents are probed to specify each household member’s contribution to each family business, farming activity as well as any other activities earning an income or a wage. This helps in overcoming the challenges of underestimating women’s participation in the labour force (Donahoe, 1999).⁴

Next, using recent developments in the literature of instrumental variable analysis, I show that my estimates are externally valid and generalize to the whole population of interest.⁵

Finally, in this paper, I characterize the subpopulation of mothers who are more likely to withdraw from the labour market in response to having preschool children between 0 and 5 years of age. It is essential from a policy perspective to be able to identify mothers with the highest effects of fertility on their labour supply so that targeted policy measures can be taken to improve their labour force participation.

This is also the first study to estimate the causal effect of fertility on mothers’ labour supply in the Indian context.⁶ The existing evidence globally on the effect of fertility on mothers’ labour supply has been mixed across countries suggesting that the relation between fertility and mothers’ labour force participation is very demographic and context-specific, thus, requiring greater attention in the Indian context.⁷

The results of this paper also have important policy implications. This paper finds that mothers’ labour force participation reduces significantly by 9.9% due to the presence of preschool children aged 0–5 years in the household. Using the heterogeneity analysis, I show that the negative effect of the presence of younger children in the family is driven by mothers with higher education, residing in nuclear families, and belonging to families from the highest income quartile. The results highlight the need for investment in the quality infrastructure of formal childcare and daycare facilities, including direct provision of public preschool and daycare nurseries, to encourage mothers residing in nuclear families as well as mothers who stay out of labour force due to unavailability of good childcare facilities to raise their labour supply.

Concurrently, policies introducing high-skilled and white-collar job opportunities with good remunerations are needed to incentivize educated mothers to join the labour market. Due to the unavailability of skilled jobs in rural India and because of lower returns to the existing labour market, educated mothers and mothers from high-income families prefer to stay at home and invest their time in their children. With higher earnings and availability of good quality formal childcare facilities, mothers shall be able to substitute their decreased time investment with better and more productive formal childcare alternatives and compensate for the negative effect of reduced time investment on children’s development (Nicoletti et al. 2020; Agostinelli & Sorrenti 2018). Additionally, publicly funded information campaigns that encourage and value women as workers and project childcare as a shared responsibility in the home, are likely to remove some of the guilt that women often experience when they leave children behind to go out to work (Das & Žumbytė, 2017).

The remainder of the paper is organized as follows. Section “Literature review” reviews some relevant literature. Sections “Data” and “Empirical Model: Female Labour Supply” describe the data and methodology used in this study. Section “Instrument relevance and validity” discusses the relevance and validity of the instrument. Section “Estimation results” presents the main results of the paper and finally, section seven concludes.

Literature review

There is a vast literature on the determinants of female labour force participation in India that points towards both demand and supply-side factors in play. On the supply side, factors such as education, social group, expected wages, marital status, presence of children in the household, and income level of the family are crucial determinants of female labour force participation (FLFP). On the demand side, labour market conditions like the availability of jobs, infrastructure, and changes in the sectoral structure—e.g., declining share of agriculture and manufacturing which employ more women—have been found to affect female participation. This paper looks at one of the determinants of female labour supply decision, namely fertility. Because of the biologically dictated burden of childbearing and childrearing on the mothers, motherhood is an important determinant of mothers’ labour supply decision.

Globally, there is extensive literature attempting to explain the causal effect of fertility on the female labour supply. The pieces of evidence have been mixed with some studies finding a very strong negative effect of fertility (see, e.g. Rosenzweig and Wolpin (1980), Angrist and Evans (1998), Fontaine (2017), Lundborg et al. (2017), etc.); while some conclude no significant effect of fertility on female labour supply (see, e.g. Lee (2002), Fleisher and Rhodes (1979), etc.). Another study by Trako (2016) on a develo** country in the Balkans finds that fertility raises the labour force participation of both parents. Agüero and Marks (2011) use infertility as an instrument and investigate the causal relationship between children and female labour force participation in 26 develo** countries. Their sample does not include India. They find no effect of fertility on the likelihood and intensity to work. Aaronson et al. (2021) analyzed data from 103 countries between 1787 and 2015 and find a negative relationship between fertility and mothers’ labour supply for countries at a later stage of economic development. They find no causal effect for countries at a lower level of income, including the USA and Western European countries prior to World War II. These mixed pieces of evidence suggest that the relationship between fertility and mothers’ labour supply is complex in nature and is very culture and demographic-specific, thus, requiring greater attention for the Indian case, where this causal relationship is not yet explored.

There are several challenges in the estimation of the uni-directional effect of fertility on labour supply. First, the two phenomena may be explained by common factors such as education. The education level of mothers may influence both, their career opportunities and their childbearing behaviour. Second, there is the problem of reverse causality as both fertility and labour supply decisions are jointly determined. For example, a woman might decide not to work if there is a child to be taken care of in the house or she may decide to work to contribute to the family’s income and thus, material investment in children’s welfare. On the other hand, an ambitious woman wishing to work may decide to delay motherhood (or have fewer children), or alternatively, a woman with lesser labour market attachment might self-select into motherhood and have more children (Fahle & McGarry 2017; Jensen 2012; Miller et al., 2022). Because of this endogeneity problem, simple OLS would generally provide biased estimates (Killingsworth & Heckman, 1986).

Many papers use the instrumental variable and difference-in-differences estimation to tackle this problem of endogeneity. In the literature, the following two empirical strategies have been commonly used to handle this endogeneity problem by exploiting an exogenous source of variation in the number of children through the instrumental variable technique. The first strategy proposed by Rosenzweig and Wolpin (1980) exploits the natural occurrence of multiple first births as an exogenous source of variation in the number of children to estimate the effect of fertility on parents’ labour supply. The second strategy, first introduced by Angrist and Evans (1998), exploits the preference for mixed sex-composition of the children of American parents. They proposed that parents of same-sex siblings are more likely to have an additional child and thus, use this as an instrument for having a third child among women with at least two children.

Preference for sons in India

India is characterized by a high prevalence of son preference. Prior research has identified some important social, religious and economic reasons that may potentially contribute to the presence of son preference, such as the financial and labour contributions of sons to the family, their perpetuation of the family name, dowry practice, the entitlement of sons to perform certain religious ceremonies, and sons being the source of old-age support (Arnold et al., 1998, 2002; Mutharayappa et al., 1997; Vlassoff 1990).

In contrast, daughters may represent a substantial economic burden in places where their parents provide a dowry. The bridal dowry practice also often entails the loss or mortgage of family land at the time of a daughter’s marriage. Marriages in India are exogamous for women, who leave their natal family village to marry into families in villages much further away to avoid marrying a possible relative. Sons, on the other hand, are expected to care for parents and natal family members in their old age by remaining with the natal family and working on the family land. Thus, Indian families express a strong preference for having at least one son, and often two, among their children (Mutharayappa et al., 1997).

To have at least one son in the family, parents often engage in son-preferring Differential Fertility Stop** Behaviour (DSB) wherein they continue having children until their desired number of sons is achieved. In fact, some studies have found that couples with more sons are more likely to use contraception than couples with more daughters (Clark, 2000). Another set of literature on the fertility behaviour of families finds that the birth of a daughter with no older brothers increases the intended fertility of parents as they intend to have more children until they get a son (Jayachandran & Pande, 2017).

Kugler and Kumar (2017) in their paper exploit this preference for having sons to study quantity-quality tradeoff of children. They use the gender of the first child as an instrument for family size as parents tend to have more children if the firstborn is a girl. Deriving motivation from this extensive literature on son preference and differential fertility-stop** behaviour of Indian parents, in this paper, I exploit the prevalence of son preference in Indian society as an exogenous source of variation in the presence of young children aged 0–5 years. I leverage exogenous variation in the gender of older children aged 6 + years as an instrumental variable for having younger children aged 0–5 years in the family. The idea is that parents who do not already have a male child aged are more likely to continue having children. Thus, not having a male child aged 6 + years is associated with a higher likelihood of having younger children aged 0–5 years in the family.

Data

I use data from the latest wave of the India Human Development Survey (IHDS) conducted in 2011–2012. IHDS is a nationally representative, multi-topic survey of 41,554 households in 1503 villages and 971 urban neighbourhoods in 33 states across India. Data are publicly available through ICPSR (Interuniversity Consortium for Political and Social Research). The first round of interviews was completed in 2004–2005 and the second round of IHDS re-interviewed 83% of the households in 2011–2012 (N = 42,152). The survey contains a wide range of information on individual demographics and socio-economic characteristics like fertility, education, employment, health, income, and consumption level of the household. The employment data is very detailed and the women are asked about work status, the number of hours per day, and the number of days spent by a woman in the year preceding the survey in all types of economic activities (own farm work, non-farm business, regular salaried/wage work in farm and non-farm set-up). As discussed in the introduction, this helps in overcoming the challenges of underestimating women’s participation in the labour force, which is a major concern in the develo** world.

IHDS classifies persons working greater than 240 h in the preceding year as employed according to the Usual Principal Subsidiary approach. This is in line with National Sample Survey Organization (NSSO) employment surveys that take into account subsidiary work status (worked greater than 30 days) to calculate employment rates. The Usual Principal Subsidiary approach of measuring unemployment looks at both the principal activity and subsidiary activity status of the worker. According to this, all individuals who are either unemployed or outside the labour force but have worked for a minor period of not less than 30 days during the reference year are classified as subsidiary-status workers. It takes the value 1, when a woman worked > 240 h in the last year and takes 0, otherwise.

I limit the analysis to mothers in rural India, aged between 15 and 49 years old with at least one child aged 6 + years and no children aged 18 + years. Women without any children older than 5 years at the time of the survey are excluded from the sample because the identification strategy exploits the gender of children aged 6 + years in the family as the instrument for having younger children aged 0–5 years. Mothers with children older than 18 years at the time of the survey are also excluded from the sample because of the following two reasons. Firstly, for these women, it is highly likely that their elder children start working or move out of the household which may affect the participation decision of mothers through channels other than through the presence of younger children. Secondly, these women are less likely to have very young children aged 0–5, which is the variable of interest. In my data, only 17% of mothers with children over 18 years have young children aged 0–5 years, whereas this number is 39% for mothers without children over 18 years.

I also carry out some data consistency checks and eliminated mothers for whom (i) the number of children in the household did not match the reported number of children ever born; (ii) the number of children alive did not match the reported number; and, (iii) the numbers of sons and daughters in the household did not match the reported number. The final sample consists of 7553 observations of rural mothers aged 15–49 years, having at least one child aged 6 + years and no children older than 18 years.

Descriptive statistics

Demographic and labour force participation descriptive statistics for the mothers are reported in Table 1. The table includes variables such as mothers’ age, education, household size, religion, and caste, among others. Descriptive statistics of the data indicate that the labour force participation rate in rural India for mothers aged 15–49 with at least one child above 6 years and no child above 18 years is only 56% (Table 1). The mean age for the sample of mothers is 32.5 years and the mean education is just above primary education. With respect to the family composition, mothers in my sample have on average 2.67 children, and 38% of them have at least one child aged 0–5 years. The average household size is 3.3 and almost 40% and 28% of women reside with their mothers-in-law and fathers-in-law, respectively. The average household asset index is 14 on a scale of 0–33.⁸

Table 1 Descriptive statistics

There is a strong correlation between the presence of young children and mothers’ labour supply decision as shown in Table 2. The labour force participation rate for mothers with no children aged 0–5 years is 60.6%, whereas it is only 50% among mothers with younger children. The difference in the participation rate for mothers with and without preschool-aged children is statistically significant at the 1% level.

Table 2 The participation rate among mothers with and without younger children aged 0–5 years

The data also indicates that fertility is not randomly assigned among women and there may be potential self-selection involved into childbearing and fertility. The total fertility of mothers decreases with higher education, as shown in panel A of Table 3. Uneducated women have average fertility of 3, whereas, among women with tertiary education, the average fertility is 1.95. Also, lesser-educated women have on average a higher number of younger children aged 0–5 years.

Table 3 Evidence for potential self-selection into childbearing

Indian society is characterized as a highly patriarchal society and co-residence of women with parents-in-law is ubiquitous, especially in rural India where most families are involved in family farming activities. There is evidence from the past literature that mothers-in-law in the household could affect the fertility decision of women through various channels such as providing childcare support and imposing their own preference for the number of grandchildren and their gender on their daughter-in-law. Panel A of Table 3 shows a strong association between the presence of a mother-in-law in the household and fertility. About 61% of women residing with mothers-in-law have younger children, while only 49% of women without mothers-in-law residing in the same house have younger children aged 0–5 years. Further, women residing with their mothers-in-law have on an average higher number of younger children aged 0–5 years and on average work less as compared to women not residing with their mothers-in-law.

Also, mothers in households belonging to higher quintiles of per capita household income (excluding woman’s own income) tend to have a lesser number of children on average as compared to mothers belonging to lower quintiles of per capita household income (Table 3, panel B).

Empirical model: female labour supply

First, I estimate the regression of the presence of children aged 0–5 years on mothers’ labour supply using the following ordinary least squares (OLS) model:

$${Work}_{i} = {\upbeta }_{0}+{\upbeta }_{1} {\text{kid}0\_5}_{i}+\upgamma {\text{X}}_{i}+ {\mu }_{i}$$

‘Work_i’ is a binary variable for mothers’ participation as defined by the Usual Principal Subsidiary Status. It takes the value 1, when a woman worked > 240 h in the last year and takes 0, otherwise.⁹ Variable ‘kid0_5_i’ is the independent variable of interest and captures the presence of preschool children aged 0–5 years. It takes the value 1 if the mother has a young child aged 0–5 years and 0 otherwise. X_i is the vector of individual and household level covariates and state-fixed effects and µ_i is the error term. Coefficient ${\upbeta }_{1}$ captures the correlation between the presence of preschool children and mothers’ participation.

Next, to estimate the causal effect of having young children aged up to 5 years on mothers’ labour supply decision, I estimate the following two-stage least square (2SLS) model.

First stage equation:

$$kid0\_5_{i} = \alpha + \beta {\text{noson}}6{\text{plus}}_{i} + \gamma {\text{X}}_{i} + \omega_{i}$$

Structural equation:

$$Work_{i} = \delta + \theta kid0\_5_{i} + \emptyset {\text{X}}_{i} + \varepsilon_{i}$$

Variable $^{\prime}kid0\_5^{\prime}$ captures the presence of children aged 0–5 years. Since this variable is endogenous to the mothers’ participation, I instrument it with $^{\prime}noson6plus^{\prime}$ which indicates that the mother doesn’t have a son aged 6 + already. This instrument is drawn from the literature indicating that Indian parents are “son preferring” and desire at least one boy child in the family. In this context, mothers without a boy child are more likely to have another child. Variable ‘noson6plus’ is a binary variable indicating whether the mother already has a boy child aged 6 or above. It takes the value 1, if the mother doesn’t have a son aged 6 + and 0, otherwise. is the first-stage estimate and captures the effect of not having a son aged 6 + on the probability of having a younger child aged 0–5 years.

${X}_{i}$ is a vector of the following control variables and is drawn from the literature on determinants of female labour force participation in the Indian context. We control for

• a) ‘Nkid6plus’ capturing the total number of children aged 6 + years. As having a younger child aged 0–5 years mechanically also depends on the number of children a woman already has. I also tried with the quadratic terms of Nkid6plus and the dummies for each number, to capture the non-linearity. But they turn out to be insignificant and increase the standard error of the estimates. As a robustness check, I also used mothers’ age-fixed effects instead of using Nkid6plus to proxy the number of children aged 6 + years.

• b) Social status and wealth of the household proxied by (i) Income per capita of the household excluding woman’s own earnings; (ii) assets index and its square; and (iii) highest education of the male in the household. The asset index is calculated based on the number of durable consumer goods and housing-related assets possessed by the household and ranges from 0 to 33. These assets include items such as television, fridge, telephone, motorcycle, washing machine, etc.

• c) Other individual-level characteristics of the mothers like age and age squared; education; marital status.

• d) Social groups like Caste and Religion to capture the direct impacts of culturally or religiously determined restrictions on women, which are expected to be strongest among Muslim and high-caste Hindu households (Klasen & Pieters, 2015).

• e) Variables for household composition: i) binary variable indicating the presence of daughter aged 6 + (nodaught6plus); ii) whether mother-in-law resides in the household (MIL_in_HH); iii) whether father-in-law resides in the household (FIL_in_HH); iv) joint family or not (jointfamily)- defined as co-living of two or more ever-married women together; v) family size excluding woman’s own children.

• f) Share of unemployed married women in the household, excluding the surveyed woman. This captures the effect of social norms in the family. Families with a higher share of unemployed married women (other than the woman of interest) are expected to have stricter social norms restricting the woman from working (share_nonWK_married). This is calculated as the ratio of the ‘number of non-working married women in the household excluding the reference woman’ and the ‘total number of married women in the household excluding this woman’. However, women living in nuclear families do not have any other married women in the household, and in such cases, this variable takes the value 0 and I am controlling for the joint family to capture these women.

  and

• g) Dummy variable for states to control for state-fixed effects.

Instrument relevance and validity

Instrument relevance: the first stage

Estimation using the instrumental variable requires that the instrument is relevant. In my application, this would mean that not having a son aged 6 or above is strongly correlated with the presence of young children aged 0–5. I regress the endogenous variable, kid0_5, on the instrument, noson6plus, controlling for various covariates discussed above. The results indicate that not having a male child increases the probability of having younger children by 32.4% (Table 4, column 1), statistically significant at the 1% level. The first stage F-statistics is 509.9. The full results of first-stage regression are reported in Table 12 of the appendix.

Table 4 Validation analysis for son preference in India

I also carry out various sub-sample analyses to confirm a strong son preference. The results are reported in Table 4. For the sub-sample of mothers with one child aged 6 + years, not having a boy child increases the probability of having an additional child aged 0–5 years by 7.9% (column 2). Among mothers with two children aged 6 + years, mothers with mixed-sex and two daughters are 7% and 39.5% more likely to have another child aged 0–5 years, respectively, as compared to mothers with two sons (column 3). For the sample of mothers with at least two children aged 6 + , mothers with mixed-sex children and all daughters are 3.8% and 40% more likely to have another child aged 0–5 years as compared to mothers with all sons (column 6). The estimates are significant at the 1% level. Corroborating with the fact that Indian parents exhibit strong son-preferring behaviour, parents with all daughters go on to have more children in the hope of having at least one male child in the family. Parents with a mixed-sex composition of children are more likely to have younger children aged 0–5 years as compared to parents with all sons (columns 4 and 7) but less likely compared to parents with all daughters (columns 5 and 8). The results highlight that preference for sons is significantly stronger as compared to the preference for the mixed-sex composition of children or daughters, upholding the relevance of the instrument.

Instrument validity

In addition to the instrument being relevant, it should also be as good as random. Even though the presence of a boy child aged 6 + years conditional on the number of children aged 6 + years is plausibly randomly assigned, there exist some concerns. One concern is the presence of sex-selective abortions. In this case, the instrument is no longer randomly assigned and the estimates are biased. In the context of India, this is an important concern as India is a highly son-preferring society with the sex ratio of children less than 7 years biased towards males. According to the Census (2011), there are only 943 females per 1000 males in India. The overall child sex ratio (aged 0–6 years) has fallen drastically from 962 girls per 1,000 boys in 1981 to 945, 927, and 918 girls per 1,000 boys in the three successive Censuses of 1991, 2001, and 2011, respectively (Jejeebhoy et al., 2015).

The conditional sex ratio for second-order births with firstborn girls declined from 906 per 1000 boys (99% CI is 798–1013) in 1990 to 836 (733–939) in 2005; an annual decline of 0.52%. However, the sex ratio for firstborns and second-order births with firstborn boys did not change between 1990 and 2005, staying near the natural range of 950–975 girls per 1000 boys (Jha et al., 2011). This gender imbalance is usually attributed to the widespread practice of sex-selective abortions and neglect of girl children in the early years of life.¹⁰ In the literature, there are consistent estimates of about 2% sex-selective abortions out of total annual pregnancies (Rosenblum, 2014).

Anukriti (2018) examines an Indian program called Devi Rupak that seeks to lower fertility, improve the sex ratio and resolve the fertility-sex ratio trade-off. The program provides financial incentives to parents that have either one child (INR 500 for a girl, INR 200 for a boy) or two daughters and no sons (INR 200). She finds that son preference in India is so strong that the sex ratio at birth worsened as high son preference families are unwilling to forgo a son despite substantially higher benefits for a daughter.

Using United States census data for Indian, Korean, and Chinese parents, Almond and Edlund (2008) find that the sex ratio of the oldest child is biologically normal, but that of subsequent children is heavily male-biased, especially when there was no previous son. The sex ratio of the second child was 1.17 (854 girls per 1000 boys) if the first child was a girl and at third parity, it was reported as 1.51 (662 girls per 1000 boys) if the first two children were girls. Selective abortion of girls, especially at higher parity and without any previous son, has increased substantially in India. Most of India’s population now live in states where selective abortion of girls is common.

Previous studies have also documented that the extent of the practice of sex-selective abortion varies significantly across different religions. Muslims, who comprise 14% of India’s population, show no significant increase in male-biased sex ratios in the post-ultrasound period. This is attributed to the greater abhorrence of abortions among Muslims (Bhalotra et al., 2018). Using Canadian census data, Almond et al. (2009) find that Hindu and Sikh immigrants exhibit male-biased sex ratios while Muslim and Christian immigrants from South Asia instead have larger family sizes. The strong condemnation against infanticide expressed in Christianity and Islam carries over into significantly lower degrees of prenatal sex selection among members of these religious groups (Almond et al., 2009). While immigrants of Christian or Muslim religion preferred sons as evidenced by continued fertility following only daughters, there is little evidence of sex selection (Almond & Edlund, 2008).

One way to check whether the instrument is as good as random is via balancing check, i.e. to examine whether mothers differ in demographic characteristics by the instrument, controlling for the total number of children aged 6 + years (as the presence of younger children aged 0–5 years mechanically depends on the number of children women already has) and state-fixed effects. Table 5 reports the difference in means in the demographic characteristics of mothers with and without a son aged 6 + years, controlling for the state-fixed effects and the number of children aged 6 + years. I find no statistically significant difference in the demographic characteristics like mothers’ own education, highest education level of males in the family, presence of father-in-law and share of non-working women in the household between mothers with and without a son aged 6 + years. However, there is a significant difference in terms of the demographics like assets, per capita household income (excluding mothers’ own income), women’s age (by approx. 0.80 years or 9.6 months), presence of mother-in-law in the household. Also, mothers with a son aged 6 + years are significantly more likely to belong to the general/upper caste and less likely to be Muslim.

Table 5 Statistical test for balance

These significant differences hint towards the possibility of the prevalence of sex-selective abortions in favour of sons in certain subpopulations. In order to address this potential issue of sex-selective abortions, firstly, I add control for variables like caste, religion, woman’s age, income, assets, and presence of mother-in-law in all my empirical specifications to account for the differences in observables across mothers with and without a son aged 6 + years.¹¹

Secondly, I carry out a separate analysis on Muslim mothers who are less likely to engage in sex-selective abortions due to a greater abhorrence of abortion (Almond et al., 2009; Almond & Edlund 2008).

Thirdly, I carry out analysis on the sample of mothers with at-most two children aged 6 + years, as sex-selective abortions are mostly prevalent at higher birth orders. I report the sex ratio at first and second-order births for this sample in panel A of Table 16. It can be seen that the male–female sex ratio is 1.09 and 1.11 at first and second birth orders, respectively, which is close to the natural rate of 1.03 to 1.07, making sex-selective abortions a minor concern in this sample. I also present the results of the balancing test for this sample of mothers (mothers with at most two children aged 6 + years and no child over 18 years) in panel B of Table 16. The results indicate that the differences between mothers with and without a son aged 6 + years in this sample, after controlling for state-fixed effects and the number of children aged 6 + , disappear for most of the variables, except for a few demographics like per-capita income excluding women’s own income, household assets, women’s age, and Muslims.

Next, the exclusion restriction requires that the presence of a son aged 6 + years should not have a direct effect on mothers’ labour force participation other than through its impact on fertility. A possible threat to the validity of this assumption is the potential differential involvement of mothers in the care of pre-existing sons and daughters aged 6 + years. This would imply that mothers respond differently in the presence or absence of male children aged 6 + years. For example, by increasing their labour supply for improving financial investment in sons or reducing labour supply to invest more time in sons and thus, threatening the validity of exclusion restriction.

To check if there are differences in the labour supply of mothers with and without a son aged 6 + , I compare the labour supply of mothers who have most likely completed their fertility and have the same number of older children aged 6 + years but different sex compositions, i.e. comparing mothers with and without a son aged 6 + years conditional on the number of children aged 6 + years. The analysis is described in detail in Sect. "Robustness Checks".

Monotonicity

Identification of the LATE with instrumental variables also requires the “monotonicity” assumption, stating that there shall be no defiers in the population (Imbens & Angrist, 1994). In my application, this boils down to assuming that not having a son aged 6 + can only make mothers more likely to have an additional younger child. That is to say, there are no mothers with a preference for daughters. Given the ubiquity of son preference in the Indian context, the assumption about the absence of defiers seems plausible.

However, recent literature has proved that IVs are still valid under a weaker condition than monotonicity (de Chaisemartin, 2017). IV estimation can tolerate the presence of some defiers. In this paper, I also comment on how many defiers can be tolerated in this analysis for the LATE to hold for compliers. The results can be found in the appendix- Sect. "Tolerating defiance".

Estimation results

Main results

This section presents the main results of the effect of having younger children aged 0–5 years on mothers’ labour supply. I use the binary variable ‘noson6plus’, indicating that the mother does not already have a boy child aged 6 + years, as an instrument for the presence of young children. Table 6 reports the main result from OLS and second-stage regression.

Table 6 Results from the main specification

The OLS estimates (Table 6, column 1) provide the average treatment effect (ATE) of the presence of young children on mothers’ participation. The results indicate that after controlling for other covariates, mothers with preschool children aged 0–5 are on average 6% less likely to work. This is statistically significant at the 1% level. As discussed above, the OLS estimation does not take into account the problem of endogeneity between fertility and mothers’ labour force participation. Thus, the estimates are biased and provide a mere correlation between fertility and mothers’ labour supply.

Under the assumptions discussed above, IV estimates solve the problem of endogeneity and provide the local average treatment effect (LATE) for the compliers. Using the IV estimation, I find that the effect of the presence of younger children aged 0–5 years reduces the participation of the mothers by 9.9% which is statistically significant at 5%. The first stage is highly significant with an F-stat of 509. Column (2) shows that not having a son aged 6 + is associated with a 32.4% more likelihood of the presence of younger children aged 0–5 years.¹²

Table 12 in the appendix also reports the effects of other covariates on fertility. The results are consistent with the existing literature on female labour force participation. The effect of social norms within a family, depicted by the share of non-working married women in the family, on female labour force participation is negative and highly significant. Living in joint families helps women to work more. Women’s age and education also have expected effects. Corroborating with the existing literature, women’s participation first increases and then decreases with the age of women. Less-educated women are less likely to work than women with no education, but high-educated women with tertiary education are more likely to work indicating a U-shaped relationship between education and female labour force participation.

With respect to the social groups, I find that lower-caste women from SC, ST and OBC are more likely to work as compared to upper-caste women. The impact of religion appears to be stronger with Muslim women less likely to work by around 13.5% and Christian women are 10.4% more likely to work compared to upper-caste Hindu women.

Consistent with the literature, the income effect seems to strongly affect female participation. Women’s decision to work is negatively related to the income of the household excluding woman’s own earnings and the assets of the household. The presence of an adult male with higher levels of education discourages women to work in the labour market.

Robustness checks

To test the robustness of estimates to various specifications of the control function, I also run models including various interactions of the variable ‘noson6plus’ with other variables like religion, number of children aged 6 + (Nkid6plus), presence of daughter aged 6 + (daught6plus), etc. as instruments and the results are more or less consistent with the IV estimate of the effect of preschool children aged 0–5 years on mothers’ participation around − 9% (Table 13 and 14). I also introduced non-linear terms for the number of children aged 6 + years (Nkid6plus), which turn out to be insignificant. I also use mothers’ age-fixed effects in place of Nkid6plus to proxy the number of children aged 6 + and the estimate of the causal effect of fertility on mothers’ labour force participation is 11.2%.

Next, I carry out the estimation with a limited set of control variables—the number of children aged 6 + , presence of daughter, woman’s age, age square, education, marital status, caste, religion, assets, assets square, highest male education in the household and state-fixed effects. I eliminate controls of household composition as these are likely to be endogenous to the mother’s participation. The IV estimate remains stable at − 9.2%. The estimates are also robust to the clustering of standard errors at the district level (Primary Sampling Unit (PSU)).¹³ Further, I also introduce the age of the eldest child (among children aged 6 +) as an additional control to control for any effect of childcare given by the elder sibling to the younger sibling and the estimate is robust to this inclusion.

As a robustness check, I also carry out the analysis on the sample including the women with children aged 18 + years. The number of observations rises to 14,570. In this case, the presence of younger children reduces mothers’ participation by 9.4%, significant at the 5% level. The results are reported in Table 15 in the appendix.

As described in the paper before, in order to take into account the issue of the prevalence of sex-selective abortions in India, I run the sub-sample analysis on women with at most 2 children of 6 + years, as according to the literature, sex-selective abortion is evident at higher parities in India. The results are stable and indicate that the presence of younger children reduces the participation of mothers by 10.3% and this effect is significant at the 5% level (Table 16, panel C).

Next, I also carry out the analysis on a sub-sample of Muslim women as they are less likely to engage in selective abortions due to religious reasons. The results indicate that the presence of younger children reduces the participation of mothers by 20%, but the estimate is not significant, likely due to a lower number of data points (Table 17).

To check the robustness of estimates to the concern about the potential differential involvement of mothers in the care of pre-existing sons and daughters aged 6 + years, that threatens the validity of exclusion restriction, I execute various sub-sample analyses and compare the labour supply of mothers who have most likely completed their fertility and have the same number of older children aged 6 + years but different sex compositions, i.e. comparing mothers with and without a son aged 6 + years conditional on the number of children aged 6 + years. Firstly, I restrict the sample to mothers aged 45 + years, as these mothers are most likely to have completed their fertility 5 years back and are less likely to have children aged 0–5 years. Secondly, I further restrict these women aged 45 + years to those who report to be either infertile or sterilized when the survey was conducted (as these mothers have also most likely completed their fertility and are not going to have any more children in the future). Finally, since IHDS is a longitudinal survey with two rounds of the survey conducted so far in 2005 and 2011, I restrict the sample to mothers present in both the above described samples and who are aged 45 + years with at least one child aged 6 + years in 2011 and who reported to be infertile or sterilized in 2005. This sample contains 569 women.

In each of the three samples described above, I find that the first stage is absent, i.e. not having a son aged 6 + years does not make mothers any more likely to have another child aged 0–5 years. Then, I compare the labour supply of mothers with and without a son aged 6 + years, conditional on the total number of children aged 6 + years and other controls. I also carry out this analysis separately by splitting the sample by the number of children aged 6 + years (i.e. mothers with 1, 2, 3, 4 and 5 + number of children aged 6 + years). This comparison would tell if mothers with and without a son aged 6 + years behave differently in terms of labour supply. I do not find any significant difference in the labour supply for mothers with and without a son in all the above samples, thus, holding the validity of exclusion restriction. The first stage and reduced form results are reported in Table 21.

Finally, I also investigate the possibility that the treatment is correlated with unobservables by using the test recently developed by Oster (2019). Firstly, I compute bounds for the first-stage and reduced-form estimates in two polar cases. In the first case, there are no unobservables and the empirical model is correctly specified and in the second case, the selection on unobservables is as high as the selection on observables (called Beta). If zero can be excluded from the bounding set, accounting for unobservables does not change the direction of our estimates and the estimates are robust to omitted variable bias. Secondly, I estimate the degree of selection on unobservable that would be required to drive the ITT estimates to 0 (called Delta, $\widetilde{\delta }$). For instance, in our case, one of the omitted unobservable variables could be sex-selective abortions. The results of this analysis are reported in Table 18. Reassuringly, the estimate and the bound have the same sign for both the first stage and the reduced form. The results indicate that assuming that the selection on unobservables is as high as the selection on observables, the first stage as well as reduced form coefficients are stable and robust to omitted variable bias, conditional on state fixed effects and the number of children aged 6 + years. I also find that the selection on unobservables should be at least 2.327 times of selection on observables (i.e. $\widetilde{\delta }=2.327$) to drive the first stage estimate to zero. And for reduced form estimate, $\widetilde{\delta }=-17.106$. These results from Oster tests lower the concern regarding the presence of sex-selective abortions and raise the confidence in the IV estimates’ stability.

Table 7 Number of children aged 0–5 years

Average causal response

Table 7 reports the number of children aged 0–5 (Nkid0_5) among the sample of mothers aged 15–49 years with at least one child aged 6 + and no child aged 18 + years. Until now we looked at the weighted average of the causal effect of the presence of children aged 0–5 years on mothers’ participation decision. But this effect also captures the cumulative effect of having more than one child aged 0–5 years. In this section, I describe the weighting function that tells us how the compliers are distributed over the range of Nkid0_5, i.e. the relative size of the group of compliers with Nkid0_5 = 1, Nkid0_5 = 2, and so on.

Firstly, I carry out the analysis of the effect of the number of children aged 0–5 years (Nkid0_5) on mothers’ participation rate by instrumenting Nkid0_5 with noson6plus. The results are reported in Table 19 in the appendix. The first stage is significant and indicates that not having a son aged 6 + years increases Nkid0_5 by 0.502, significant at the 1% level. The IV estimate suggests that an increase in Nkid0_5 reduces participation by 6.42%, significant at the 5% level.

Table 8 Counting compliers

Next, I estimate the average causal response (ACR) weighting function. ACR weighting function can be consistently estimated by comparing the CDF of the endogenous variable (i.e. Nkid0_5) with the instrument (noson6plus) switched off and on. The weighted function is normalized by the first stage (Angrist & Pischke, 2008).

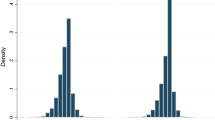
Figure 1 plots the CDF of the number of children aged 0–5 years (probability that the number of children aged 0–5 is less than or equal to the value of Nkid0_5 on the X-axis) for mothers with and without a son aged 6 + years. The difference between the CDF normalized by the first stage gives the weights of each value of Nkid0_5 in the 2SLS estimation. The CDF differences decline with the number of children aged 0–5 and become almost 0 at Nkid0_5 equals 3 and 4. Mothers with a son aged 6 + years are 40% more likely to not have a child aged 0–5 years. Whereas, mothers without a son aged 6 + are almost 19% more likely to have a child aged 0–5 years and 3–4% more likely to have 2 children aged 0–5 years. Thus, the 2SLS estimate in this paper is mostly capturing the effect for mothers with 1 and 2 children aged 0–5 years on mothers’ labour supply.

Fig. 1

Average causal response weighting function. Note The figure plots the CDF of the number of children aged 0–5 years (Nkid0_5) with the instrument switched off and on, i.e. for noson6plus = 0 and noson6plus = 1. The difference in the CDF depicts the weights for the range of Nkid0_5

More on compliant population

Instrumental Variable estimates capture only the local average treatment effect (LATE) only for a subpopulation called compliers.¹⁴ Compliers are the subgroup of the population who change their behaviour because of the change in the instrument. In this study, compliers are the mothers who go on to have an additional child if they do not have a son aged 6 + but would not choose to have another child if they already have a boy aged 6 + years. In this section, following Angrist and Pischke (2008) and Angrist & Fernández-Val (2013), I say as much as possible about the compliers for the instrument ‘noson6plus’ used in this paper.

First, I comment on the size of the complier group and the proportion of compliers in treated and untreated populations. The ingredients for this analysis are reported in Table 8. I find that the proportion of compliers in the population, as given by the first stage, is 32.4%. Among the treated population, i.e. mothers with a preschool-aged child, compliers comprise 19%. These are the mothers who went on to have another child because they did not already have a son aged 6 + years. Compliers, among the untreated population, comprise 41%. These are the mothers who did not have an additional child because they already had a son aged 6 + years.

Whilst the share of compliers in the treated and untreated population are large, they are well below 1. As a result, in order to assess the generalizability of my results to the entire population of interest, I look at the characteristics of compliers and check whether compliers are comparable to the general population. Table 9 reports the compliers’ characteristics ratios for mothers’ religion, education, caste, household composition, and income/wealth level. A significant ratio greater than indicates that compliers are more likely to have that characteristic as compared to the general population. If compliers are similar to the general population, the case for extrapolation of causal effects to the whole population of interest is stronger. The results suggest that the compliers are positively selected and their population is significantly very different from the general population. For instance, compliers are more likely to be Hindu and less likely to be Muslims and Christians. They are also more likely to be educated, belong to a higher caste, have more assets, have more than 2 children aged 6 + , have a mother-in-law in the household, and have at least one daughter in the HH, as compared to the general population.

Table 9 Complier characterization

As discussed in Angrist (2004) and Black et al. (2017), the LATE parameter would also generalize to the whole population if complying behaviour was ignorable,¹⁵ that is, if there is no selection into the treatment (having an additional child) and effect of having children aged 0–5 years on mothers’ labour force participation is homogenous across compliers, always-takers and never-takers. And, similarly, not having children aged 0–5 years produce the same effect on mothers’ participation across the whole population.

Mathematically, LATE would generalize if:

$${\text{E}}\left[ {Y_{i} \left( 1 \right)\left| {\text{C}} \right.} \right] = {\text{ E}}\left[ {Y_{i} \left( 1 \right)\left| {{\text{AT}}} \right.} \right] = {\text{ E}}\left[ {Y_{i} \left( 1 \right)\left| {{\text{NT}}} \right.} \right]$$

$${\text{E}}\left[ {Y_{i} \left( 0 \right)\left| {\text{C}} \right.} \right] = {\text{ E}}\left[ {Y_{i} \left( 0 \right)\left| {{\text{AT}}} \right.} \right] = {\text{ E}}\left[ {Y_{i} \left( 0 \right)\left| {{\text{NT}}} \right.} \right]$$

Two testable implications of ‘no selection bias’ in the LATE framework, are the following:

$${\text{E}}\left[ {Y_{i} \left( 1 \right)\left| {D_{i} = 1,{ }Z_{i} = 0} \right.} \right] = {\text{E}}\left[ {Y_{i} \left( 1 \right)\left| {D_{i} = 1,{ }Z_{i} = 1} \right.} \right]$$

$${\text{E}}\left[ {Y_{i} \left( 0 \right)\left| {D_{i} = 0,{ }Z_{i} = 1} \right.} \right] = {\text{E}}\left[ {Y_{i} \left( 0 \right)\left| {D_{i} = 0,{ }Z_{i} = 0} \right.} \right]$$

i.e. among treated, the treatment effect is not different for always-takers and compliers and among untreated, the treatment effect is not different for never-takers and compliers.

So, I compare E(Y|AT and C) vis-à-vis E(Y|AT) and E(Y|NT) vis-à-vis E(Y|NT and C) and find that they are not significantly different. The results are reported in Table 10. I do not find any evidence of differentiating effect of having a young child on mothers’ participation between treated compliers and always-takers (column 1) and between non-treated compliers and never-takers (column 2), which is suggestive evidence of the fact that the LATE estimate for compliers could be generalized to always takers and never takers.

Table 10 Generalizability of LATE estimate

In summary, the results suggest that even if the compliers are significantly different from the general population in terms of their observable characteristics, the IV estimate is externally valid for the general population, suggesting that the returns of having a younger child on mothers’ participation must be homogenous across different sub-populations.

Fathers’ labour supply

In this section, I examine the effect of the presence of preschool children aged 0–5 years on fathers’ labour supply. I analyze the sample of husbands of women aged 15–49 years with at least one child aged 6 + and no child above 18 years. I use not having a son aged 6 + years (noson6plus) as an instrument for the presence of children aged 0–5 years (kid0_5), conditioning on the number of children aged 6 + years the parents already have. The results are reported in Table 20 in the appendix. As expected the fathers’ labour participation is unaffected by the presence of children aged 0–5 years. Since 95% of the fathers in the sample are working, I also carry out an analysis on the hours worked in the last year by the fathers. IV estimates again are insignificant and the presence of younger children aged 0–5 years does not affect the labour supply of the fathers. These results are suggestive of the fact that fertility is an important contributor to the gender gap in the labour market. This is also reassuring that the instrument is not capturing any spurious effects.

Heterogeneity in the effect of fertility on labour supply

In this section, I examine whether the effect of fertility on mothers’ labour-force participation may be sensitive to or driven by certain sub-populations in the sample. It is helpful from a policy perspective to identify the sub-population of mothers with the highest response to fertility on their labour force participation. Table 11 reports the IV estimates for the heterogeneity analysis.

Table 11 Heterogeneity analysis

Firstly, I carry out the heterogeneity analysis of the effect of fertility on mothers’ labour supply by mothers’ education level. For this analysis, the sample is divided into two groups based on the median education level: below or completed primary level (≤ 5th standard) and above primary level (> 5th standard, comprise of secondary, higher secondary, and tertiary education). The results indicate that the effect of fertility on mothers’ labour supply is negative and statistically significant for women with higher education, but insignificant for women with below-median education levels. This seems reasonable as women’s preference and demand for white-collar and high-skilled jobs grow stronger as their education increases, and because these types of formal sector jobs are very scarce in rural India their labour supply responds to fertility more as they have difficulty finding matching skilled jobs. Moreover, cultural norms restrict the number of jobs that are considered acceptable for women, making it harder for mothers to find suitable jobs.

Also, these educated women possibly belong to economically well-off families, and consequently have a lesser need to work. While, less educated mothers, on the other hand, who possibly belong to economically backward families, engage in paid work to support the family.

Secondly, I explore whether the effect of fertility on mothers’ labour-force participation is likely to vary with the income of the family excluding women’s own income. For this, the sample is divided into quartiles. The IV estimates show that the negative effect of fertility on mothers’ labour supply remains insignificant for mothers belonging to the bottom three quartiles. It is however highly negative and significant for mothers belonging to the highest income quartile. For these mothers, the presence of a young child 0–5 years, reduces labour supply by 22.8%, statistically significant at the 5% level. This seems reasonable as mothers belonging to affluent families have a lesser need to work compared to mothers belonging to lower-income families, to support their families financially. They still bear the primary responsibility for raising children and managing the home. Also, there is evidence that children benefit from being raised by mothers themselves, as mothers simply know better about their children, and thus, women who can afford to be at home are willing to raise their children by themselves and invest their time towards the children’s care, education, and development, instead of working for better reasons.

The incentive to work, if any, is worsened by cultural setbacks, unavailability of formal sector jobs in rural India, the absence of child-care facilities at work, inflexible working conditions, gender biases in hiring and promotions, gender wage differentials, and lack of female-friendly offices.

Thirdly, I carry out the estimation by splitting the sample along the line of the husband’s education (below and above primary education). I find that wives of educated husbands are significantly affected by the presence of younger children, whereas, there is no significant effect on wives of lowly educated husbands. This is likely due to the income effect as described before.

Fourthly, I also carry out the heterogeneity analysis by residence in a joint family. The results, reported in Table 11, indicate that fertility negatively affects the labour supply of mothers living in nuclear families. For mothers living in nuclear families, the presence of young children reduces mothers’ labour supply by 12.9%, which is statistically significant at the 10% level. While the effect is insignificant for mothers residing in joint families. Residing in extended families can help mothers with the sharing of childcare responsibilities and is a major source of informal childcare in India.

Lastly, I check for heterogeneity by religion. Hindu women significantly lower their participation due to the presence of younger children. For other religions, the magnitude of the estimate is even higher than the magnitude for Hindus but the effect is imprecisely estimated and statistically insignificant, most likely due to fewer observations.

The maximum negative effect of fertility on mothers’ labour supply seems to be driven mostly by the highly educated cohort of mothers; mothers belonging to high-income families and with educated husbands and mothers residing in nuclear families. These results are suggestive of the fact that women’s labour supply is driven by necessity rather than opportunities. Mothers tend to stay out of the labour market until they have a compelling need to work to financially support the family. And lack of opportunities from the demand side like unavailability of suitable and respectable jobs as well as from the supply side such as disproportionate responsibilities associated with childbearing and raising children, and socioeconomic and cultural barriers, makes it harder for mothers to work outside the home.

Concluding remarks

This paper is the first to estimate the causal effect of the presence of preschool-aged children between 0 and 5 years on mothers’ labour force participation. Using Indian Human Development Survey from rural India conducted in 2011–2012, I show that the presence of young children aged 0–5 years reduces the mothers’ labour supply significantly by 9.9% points. Next, this paper sheds light on women who are most affected by the presence of younger children. Using heterogeneity analysis, I show that the negative effect is largely driven by mothers with higher education, mothers from families belonging to the highest income quartile, and mothers residing in nuclear families. This suggests that the labour supply of mothers with younger children in India is necessity-driven rather than opportunity-driven as educated and wealthier women are more likely to withdraw from the labour market because of both lower opportunities and lower returns to the labour market in rural India as well as the lower financial necessity to work.

The findings of this paper might have important implications in terms of public policy. There is a selective withdrawal by educated mothers from the labour market resulting in the underutilization of the nation's human resources. For educated and wealthier women, the unavailability of well-paying and skilled jobs and lower returns to their education in the labour market in rural India results in a higher cost of participation and thus, higher withdrawal from the labour market. Policies introducing high-skilled and white-collar job opportunities with good remunerations are needed to incentivize mothers in rural India to work outside the home. These mothers prefer to stay at home and manage domestic tasks, such as schooling children and investing time in their development as they understand that their support for children is better for their development than what they could buy as a replacement with the money from work. With higher earnings, these mothers shall be able to substitute their decreased time investment with better and more productive alternatives and compensate for the negative effect of reduced time investment on children’s development (Nicoletti et al., 2020; Agostinelli & Sorrenti 2018).

In addition to higher pay, the availability of quality alternative sources of childcare is equally crucial. In India, the lack of good formal childcare further discourages mothers to work. Investment in the quality and quantity of formal childcare facilities, schools, and daycare facilities, including direct provision of public preschool and day-care nurseries, is required as a substitute for informal childcare facilities to help mothers residing in nuclear families and incentivize mothers who are out of labour force to invest their time on childcare and development.

Appendices

Appendix

See (Tables 12, 13, 14, 15, 16, 17, 18, 19, 20, and 21).

Table 12 Main specification (sample—mothers aged <  = 49 years with at least one child aged 6 + years and no child above 18 years)

Table 13 Model robustness—first stage results

Table 14 Model robustness—second stage results

Table 15 Results including mothers with children aged 18 + years in the analysis: Robustness check

Table 16 Robustness check to account for sex-selective abortions: Sample of mothers with at most 2 children aged 6 + years and no child above 18 years

Table 17 Second stage results: Muslim mothers with at least one child aged 6 + years and no child above 18 years. Robustness check to account for sex-selective abortions

Table 18 Oster test: checking robustness of estimates to omitted variable bias

Table 19 Effect of the number of children aged 0–5 years on mothers’ participation decision

Table 20 Fathers’ labor supply

Table 21 Check for exclusion restriction- potential differential involvement of mothers in the care of sons and daughters

Tolerating defiance

An assumption about monotonicity or absence of defiers is required for the IV estimate to identify the LATE for the compliers. Otherwise, IV estimate is the weighted difference between the effect of the treatment among compliers and defiers. However, recent literature, including de Chaisemartin (2017) shows that the 2SLS still estimates a LATE if the monotonicity condition is replaced by a weaker condition, which allows the presence of some defiers. Although, given the ubiquity of son preference in the Indian context, the assumption about monotonicity seems veristic. However, in this paper, following de Chaisemartin (2017), I comment on the number of defiers that can be tolerated and the LATE for defiers, for the IV estimate to identify the LATE for compliers.

• 1. Ratio of compliers to defiers should be at least2.079 to identify the LATE for a subset of compliers called surviving-compliers. That is, for each defier in the population (mothers who are girl-preferring), there should be at least two compliers (mothers who are son-preferring). This seems reasonable in the Indian context given the prevalence of the son preference.

• 2. The absolute difference between LATE for compliers and defiers should be less than or equal to 5.165% for LATE to be identified which is almost 52% of the Wald estimate. So, the LATE for defiers must lie in the range of 4.73% and 15.16%.