Dispersal distances and cultural effects in the spread of the Neolithic along the northern Mediterranean coast

Abstract

We estimate a spread rate of 7.5–10.6 km/year for the Neolithic expansion along the northern shore of the western Mediterranean. Comparing to theory and numerical simulations of demic-cultural waves of advance, we find that the length of coastal jumps was $240\le \Delta \le 427$ km. We also derive what we believe are the first analytical equations for spread rates of waves of advance along a coast, and they agree with the simulation results. We show that the importance of cultural diffusion in this Neolithic spread was less than 21%, so demic diffusion was responsible for at least 79% of the observed spread rate. We argue that these results suggest that the spread took place using boats, and also a limited interaction between the incoming farmers and the autochthonous hunter-gatherers.

Introduction

When the Neolithic spread across Europe, population densities rose quickly to unprecedented levels (Shennan and Edinborough 2007; García Puchol et al. 2018; Porcic et al. 2021) and many aspects of social organization were transformed (Bocquet-Appel and Bar-Yosef 2008). The Neolithic spread in Europe along two main routes, one inland across the Balkans and central Europe and the other one along the northern Mediterranean coast (Shennan 2018). For the inland route, quantitative analyses of the radiocarbon dates have been performed since 50 years ago, with the consistent result that the spread rate was about 1 km/year on average (Ammerman and Cavalli-Sforza 1971, 1984; Pinhasi et al. 2005) and varied regionally (Ammerman and Cavalli-Sforza 1971, 1984; Bocquet-Appel et al. 2012; Henderson et al. 2014; Fort 2015; Porcic et al. 2020; Davison et al. 2006). For the coastal route, on the other hand, the Neolithic spread has been also studied since more than 40 years ago (Guilaine 1976; Arnaud 1982). A careful dismissal of the radiocarbon dates affected by the old wood effect and other uncertainties led to realize, 20 years ago, that an extremely rapid spread took place (Zilhao 2001, 2011) and long jumps (sometimes called “leapfrog dispersal”) were proposed to explain such a fast spread and its discontinuous distribution (Zilhao 1993). However, at the time, there were not enough data to estimate the corresponding spread rate quantitatively. It was possible to solve this problem more recently, by using the earliest Neolithic date for each coastal region along the Western Mediterranean (Isern et al. 2017). In this way, a spread rate of 8.7 km/year was estimated, and it was argued using numerical simulations that such a fast rate implies very long “jumps” (i.e., dispersal movements) of at least about 350 km per generation. However, some key issues were not tackled by Isern et al. (2017). In our opinion, the two most interesting unanswered questions are the following. What minimum and maximum distances moved per generation (by the pioneering farmers) are consistent with the archeological data? What percentages of demic and cultural diffusion are possible for this Neolithic spread? The present paper deals with both questions.

Several authors have previously modeled the spread of the Neolithic in the western Mediterranean. Bergin used numerical simulations to explore more complex mechanisms than those that can be captured by analytical equations for the spread rate (Bergin 2016). For example, he analyzed the effects of a population threshold (above which some farmers leave their current location) and a land-quality threshold (such that farmers choose the highest-quality destination available within a given distance, provided that its land quality for farming is above this threshold). These thresholds and many other parameters used in those simulations are difficult to estimate from ethnographic and archeological data but, by varying their values and computing the linear correlation coefficient between observed and modeled arrival times of the Neolithic, Bergin concluded that long jumps along the coast are necessary to successfully reproduce the arrival times implied by the archeological data. He also analyzed the roles of topographic slope, dispersal along rivers, and climatic factors (Bergin 2016). A similar approach was applied by Bernabeu and co-workers (Bernabeu et al. 2015), who tested several possible starting points for the Neolithic dispersal in Iberia and found higher correlations for starting points in the East (Bernabeu et al. 2015; Pardo-Gordó et al. 2015). They also found that the most reliable databases lead to the highest correlations, which led them to stress that the quality of samples needs to be considered (Bernabeu et al. 2015; Pardo-Gordó et al. 2017). Moreover, they modeled the pattern of pottery substyles in East Iberia throughout the Early Neolithic by using a network approach and suggested that the observed changes could be due to the special role played by some specific nodes that would have facilitated or limited the information flow over the entire network (Bernabeu et al. 2017). Recently, de Vareilles et al. have quantified some drops in crop diversity during the spread of the Neolithic in the western Mediterranean and suggested that they are more likely due to founder effects than to climatic and environmental variations (Vareilles et al. 2020). Very recently, Leppard has attempted to understand the rapid neolithisation of the western Mediterranean in terms of the social organization of early Neolithic communities (Leppard 2021).

Guilaine has stressed that the pottery decoration made with the impressed groove technique was a first flow of neolithisation along the coast, whereas the Cardial arrived later and also to inland regions (Guilaine 2018). He and his co-workers have recently highlighted the crucial importance of some early Neolithic dates in the French Languedoc and argued that it is illusory to estimate the rate of propagation of the Neolithic wave of advance in the western Mediterranean because “the rhythm of diffusion varied considerably from one point to another in this area” (Manen et al. 2019). Such a variation is perfectly possible, although it does not rule out the viability to estimate an average spread rate (as done by Isern et al. 2017 and in the present paper). There is some controversy on this issue and several related ones (Ammerman 2021; Manen et al. 2021). For our purposes here, it is enough to mention that a model with an average spread rate on the one hand (Isern et al. 2017) and a model with a variable spread rate (arrhythmic model) on the other (Manen et al. 2019) are perfectly compatible; i.e., both of them can be valid for the same case study (the arrhythmic model being obviously more detailed). However, a quantitative formulation of the arrhythmic model requires to estimate the spread rate (in km/year) at different regions and this does not seem viable for the western Mediterranean at present, due to the wide error bars of the earliest regional dates compared to the overall temporal variation (see Fig. 3 in Isern et al. 2017 or Fig. 3 in the present paper). In spite of this difficulty, the arrhythmic model is of major interest not only qualitatively but also quantitatively, because estimating the spread rate (in km/year) at successive regions along the front propagation direction is possible in other case studies, e.g., the Neolithic slowdown in northern Europe (Isern and Fort 2012; Isern et al. 2012).

Materials and methods

Database

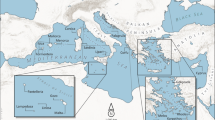
We have gathered a database of 215 early Neolithic dates in the western Mediterranean using previously published databases and publications (Bernabeu et al. 2015; Manen et al. 2019; Alday and Soto 2018; Edo and Antolín 2016; Bergadà et al. 2018; Binder et al. 2017; Drake et al. 2016; Fyfe et al. 2019; García-Puchol et al. 2018, 2017; Ibáñez-Estévez et al. 2017; Martínez-Grau et al. 2020, 2021; Martins et al. 2015; Oms et al. 2018; Perrin et al. 2018; Perrin and Manen 2021; Zilhao 2021). Details of each database/publication and the selection procedure followed for each one are included in Supp. Info., Sec. S1. We have calibrated all dates at https://c14.arch.ox.ac.uk/oxcal/OxCal.html (OxCal 4.4) with 95.4% probability (curve IntCal20). This has resulted in a list of dates for each of 9 geographic regions (first column of Table 1). Our database contains the complete list of dates for each region (Supp. Info. excel file). Finally, we have selected the oldest reliable date for each region, which is also reported in Table 1. The corresponding sites are shown in the map in Fig. 1. Besides updating the database by Isern et al. (2017), we have included three additional regions, namely 1 southwestern Italy, 2 central western Italy, and 4 Languedoc/Roussillon (see Fig. 1). Due to the inclusion of the first two of these regions, the coastal distance covered is about 3200 km (in contrast to 2500 km in Ref. (Isern et al. 2017).

Table 1 Oldest Neolithic date in 9 regions (obtained by selecting the earliest realiable site for each region from the database included as a Supp. Info. excel file). A map with the location of the corresponding sites (last column) is included in Fig. 1

Fig. 1

Map with the location of the oldest reliable Neolithic site for each of 9 regions (obtained from the database included as a Supp. Info. excel file). The list of regions, sites and dates is included in Table 1

Simulations

Spatial numerical simulations have been widely applied to many archeological topics, including human dispersals (Barceló and Castillo 2016). We consider two populations (farmers and hunter-gatherers). Initially, there are hunter-gatherers at their saturation density in all cells of the simulation grid. In the approach by Isern et al. (2017), the initial population of farmers was assumed to be located at a single coastal cell, namely that containing the oldest site in their database. Here, we consider that the initial population is located at a set of contiguous coastal cells because this seems more realistic, due to the fact that the Neolithic had already spread to eastern regions before it reached those in our database. However, we have checked that this difference in the distribution of initial farmers does not have any effect on the results. In contrast to Isern et al. (2017), here we consider a rectangular grid, in which this is simpler to simulate than a real geography and has the crucial advantage of making it possible to find analytical results that are very useful to check the simulations (such analytical results are given in the“Theory” section below). The simulation grid is composed of 100 x 100 square cells with side $d=$ 50 km, which is the characteristic distance dispersed per generation inland by pre-industrial populations according to ethnographic data (Fort et al. 2007). Moreover, previous work on inland expansions has shown that a dispersal distance of $d=$ 50 km per generation leads, if combined with realistic values for the other parameters (see below), to spread rates similar to the observed one for the European Neolithic (about 1 km/year) (Fort et al. 2007).

Each generation has duration $T=32$ years according to ethnographic data (Fort et al. 2004a) and corresponds to a cycle of the following three processes:

• (i) Reproduction. In our model, we consider two populations, namely farmers (F) and hunter-gatherers (HG). Both farmers and hunter-gatherers reproduce logistically. A logistic curve has been observed in many different biological systems (Murray 1993), including human populations (Lotka 1956). In fact, using a non-logistic function for HGs would not change the results because in this paper we will derive new equations for coastal spread (Eqs. (1)–(2) below) according to which the reproduction function of HGs has no effect on the spread rate (this also happens for inland spread (Fort 2012)). Ethnographic data have been previously used to estimate the initial growth rate $a$ (or, equivalently, the net fecundity ${R}_{0}={e}^{aT}$ (Fort et al. 2007)) of each population as ${R}_{0}^{F}=2.45$ (Isern et al. 2008) and ${R}_{0}^{HG}=1.81$ (Fort et al. 2004b) and their carrying capacities as ${p}_{ \mathrm{max}}^{ F}$ =1.28 farmers/km² and ${p}_{ \mathrm{max}}^{ HG}$ =0.064 hunter-gatherers/km² (Currat and Excoffier 2005). Therefore, no potential variation in these parameters is taken into account. In fact, all results below are independent of the values of ${R}_{0}^{HG}$, ${p}_{ \mathrm{max}}^{ F}$, and ${p}_{ \mathrm{max}}^{ HG}$ because none of these three parameters affects any spread rate (Eqs. (1)-(3) below).

• (ii) Cultural transmission. Theoretical work based on cultural transmission theory (Cavalli-Sforza and Feldman 1981) has shown (see Eq. (44) in (Fort 2011) that if the cultural transmission is vertical (interbreeding between farmers and hunter-gatherers), then the density (per unit area) of famers ${p}_{F}$ (for each generation and cell) is increased by $\eta \frac{{p}_{F}+{p}_{HG} }{{p}_{F} {p}_{HG}}$, and the density of hunter-gatherers ${p}_{HG}$ is reduced by the same amount, where $\eta >0$ is the intensity of cultural transmission. For horizontal transmission (acculturation of hunter-gatherers, i.e., conversion into farmers), the corresponding equation is a little more complicated but this difference does not affect the spread rate (Fort 2012), so the same results will hold (with the intensity $\eta$ of vertical transmission replaced by the intensity $C$ of horizontal transmission (Fort 2012)). Therefore, it is not necessary to consider such a more complicated approach more explicitly for our purposes. The maximum value of $\eta$ is $\eta$ = 1 but that of $C$ is $C$ → ∞, so for notational simplicity here we will use $\eta$ with possible values up to $\eta \to \infty$.

• (iii) Dispersal. For each cell and generation, a fraction ${p}_{e}$ (which is called the persistence in demography) of each population does not move. We use the value ${p}_{e}=0.38$, which has been estimated from ethnographic observations of pre-industrial populations (Fort et al. 2007). For inland cells, for simplicity, we assume that all individuals who move do so to one of the nearest four cells with the same probability. Thus, a fraction $(1-{p}_{e})/4$ of individuals jump a distance of $d=50$ km to each of the four nearest cells. It is possible to consider inland jumps of several distances (Fort 2012), but we expect that our conclusions would not change because we are interested in the spread rate of the Neolithic front along the coast and this is driven essentially by the coastal jumps, which are necessarily longer for the spread to be sufficiently fast to agree with the archeological data (Isern et al. 2017; Fort et al. 2012) (this will be also shown below).

First model: forward and backward dispersal

For clarity, let the left side of our rectangular simulation grid correspond to the coast. Individuals on this side ($x=0$ in Fig. 2a) cannot jump to the left, because the sea cannot be inhabited. Thus, for cells on the left side of our grid (coast), a fraction $(1-{p}_{e})/3$ of individuals jump each generation to the cell located at a distance $d=50$ km to the right (inland) and the rest of individuals who travel do so along the coast (Fig. 2a). We consider first the case in which $(1-{p}_{e})/3$ of individuals move up a longer distance, which we call $\Delta >50$ km, and $(1-{p}_{e})/3$ of individuals move down the same distance $\Delta$, all of them along the coast (Fig. 2a). In this way, coastal dispersal is isotropic. Some previous models have applied more complicated dispersal mechanisms which include not only long-distance movements along the coast (with distance $\Delta$) but also short-distance coastal movements (with distance $d=50$ km) (Isern et al. 2017; Fort et al. 2012). However, it is well known from ecological theories of biological invasions that the spread rate is determined by the long-distance movements (Clark 1998; Fort 2007), and this also holds for human populations (Fort and Pareta 2020), so including short-distance jumps would complicate the model unnecessarily (especially the equations in the “Theory” section).

Fig. 2

Potential movements of individuals along the y and x axes. The coast is the vertical thin line ($x=0$). The Neolithic wave of advance spreads upwards. Simulations are run on a square grid of nodes separated a distance $d$ and located on the coast ($x=0$) and to the right of it ($x>0$). Some of these nodes are shown as black circles. (a) The “forward and backward dispersal” model allows jumps from an arbitrary coastal node ($y$) upwards ($y+\Delta$), downwards ($y-\Delta$), and inland (to the right, $x=d$). (b) The “forward dispersal only” model allows jumps inland (to the right) and along the coast in the direction of the Neolithic spread (upwards) but not against it (downwards). For both models, inland jumps to the four nearest nodes are possible (as shown in the lower right part of each panel) but with a smaller length $d$ than that of jumps along the coast ($\Delta$)

Second model: forward dispersal only

Instead of the isotropic model above, an extremely non-isotropic model was introduced by Isern et al. (2017), where it was assumed that all individuals that jump along the coast do so “forward,” i.e., in the direction of the Neolithic spread (i.e., westwards in the case of the west Mediterranean). That model is useful as a first step, but is based on a very strong assumption. Indeed, there is not reason a priori to exclude that some individuals may jump backwards along the coast. In fact, as far as we know, the only ethnographic data available for human dispersal in range expansions refer to the colonization of the USA in the nineteenth century, and they show indeed that a substantial part of the population dispersed in directions different from that on the front propagation (and even in the opposite one) (Fort and Pujol 2007). For this reason, we have considered the case (introduced in the previous paragraph) in which jum** “backward” and “forward” along the coast are equally likely (Fig. 2a) and we will compare it to the case in which all individuals that jump along the coast do so “forward” (Fig. 2b). In our simulations, therefore, in the “forward and backward” case (previous paragraph), the probabilities of jum** forward ${p}_{f}$ and backward ${p}_{b}$ a distance $\Delta$ are the same, namely ${p}_{f}={p}_{b}=(1-{p}_{e})/3$, and equal to the probability of jum** inland ${p}_{i}=(1-{p}_{e})/3$ (see Fig. 2a). On the other hand, in the “forward” case, we have ${p}_{f}=(1-{p}_{e})/2$, ${p}_{b}=0$ and ${p}_{i}=(1-{p}_{e})/2$ (see Fig. 2b). Clearly, between these two extreme cases, there are many others such that jum** forward is more likely than backward (${p}_{f}>{p}_{b}$) but it is not necessary to consider all of them, because obviously they will yield results necessarily intermediate between those of the two extreme cases considered.

It is possible to simulate, instead of coastal jumps of a single distance, jumps with a probability for each dispersal distance along the coast (Isern et al. 2017). However, this does not lead to multiple points of coastal entry of the Neolithic (Fig. 2 in Isern et al. 2017), which contradicts the archeological data known at present (Fig. 1 in Isern et al. 2017). For this reason, we will consider a single distance $\Delta$ for dispersal along the coast. This will also make the analytical approach (see “Theory” section) substantially simpler.

Each cycle of the 3 steps above corresponds to one generation, i.e., 32 years according to ethnographic data (Fort et al. 2004a). The simulations have been performed by writing FORTRAN programs (available at the author’s webpage http://copernic.udg.edu/QuimFort/fort.htm) that implement the three steps above. At the end of each cycle or generation, we find the front position by linear interpolation between the coastal points where the population density of farmers is closest to 10% of ${p}_{ \mathrm{max}}^{ F}$, i.e., just below and above 10% of ${p}_{ \mathrm{max}}^{ F}$ (but changing this percentage would not change the results). A plot of the front position versus time for the last few generations shows that they are linearly related (Pearson correlation coefficient $r>$ 0.9) and we find the spread rate from this linear regression.

Theory

In this section, we summarize some new analytical approximations (which are derived in detail in the Appendix) for Neolithic spread rates along a coast:

• (A) For the “forward and backward” case introduced in the previous section, the spread rate is given approximately by Eq. (10), i.e.,

  $$s=\begin{array}{c}\\ \mathrm{min}\\ \lambda >0\end{array}\frac{ln\left[{R}_{0}^{F}\left(1+\eta \right)\left(\frac{{2p}_{e}+1}{3}+\frac{2}{3}(1-{p}_{e})\mathrm{cosh}(\lambda\Delta )\right)\right]}{\lambda T}.$$

  (1)

• (B) For the “forward” case introduced in the previous section, the spread rate is given approximately by Eq. (12), i.e.,

  $$s=\begin{array}{c}\\ \mathrm{min}\\ \lambda >0\end{array}\frac{ln\left[{R}_{0}^{F}\left(1+\eta \right)\left(\frac{{p}_{e}+1}{2}+\frac{1-{p}_{e}}{2}{e}^{\lambda\Delta }\right)\right]}{\lambda T}.$$

  (2)

Both equations are derived in the Appendix. In the next section, we will show that they are rather accurate and very useful to compute coastal spread rates and check the simulation results. As far as the author knows, these are the first equations for spread rates along a coast. They can be also of interest in Ecology to study biological invasions (with $\eta =0$ if there is no interbreeding).

Results

Observed spread rate

Table 1 gives the earliest reliable Neolithic radiocarbon date for each region in western Mediterranean Europe, calibrated with 95.4% confidence level (CL) using OxCal (https://c14.arch.ox.ac.uk/). We show these intervals as error bars in Fig. 3. We plot dates versus their distances and not the other way around because the calibrated radiocarbon dates are subject to errors, whereas distances along the coast are more certain in principle (Mather 1946). Distances are measured along the coast (using https://www.sea-seek.com) from the point on the western coast of Italy that is closest to the easternmost site in Table 1 (Favella della Corte, site 1 in Fig. 1 and error bar 1 in Fig. 3) to the point on the coast that is closer to the site in Table 1 considered. The regression of the means of the error bars in Fig. 3 yields a mean spread rate (inverse of the slope) of 9.1 km/year (Fig. 3). The Pearson correlation coefficient is rather high ($r=0.84$), which indicates that the approximation of a uniform spread rate is statistically valid, and the slope is significantly different from zero (P < 0.005) which implies that a chronological gradient exists. However, although this approach is useful as a first approximation, it does not take the magnitudes of the error bars into account. We expect intuitively that their effect may be important, because if we choose for the date of each region a value on its error bar at random (instead of the mean), the slope of the fitted line can be rather different for different choices. This is due to the fact that, in our specific case study, the error bars (Fig. 3) are similar in magnitude (about 250 years for regions 3–4) to the overall variation in dates (about 400 years). In turn, the reason for this is the fastness of this Neolithic expansion. Let us mention that, in contrast, for the spread of the Neolithic across inland Europe, the overall range of dates is much larger, about 4000 years (Fort et al. 2012); i.e., the Neolithic spread substantially more slowly (Pinhasi et al. 2005; Fort et al. 2012), so we expect intuitively a smaller effect of the error bars in that case study (but not in ours). Clearly, we need a way to confirm (or modify) the estimation above for the spread rate by taking into account the uncertainties in the calibrated radiocarbon dates (error bars in Fig. 3).

Fig. 3

95.4% confidence level error bars of the earliest Neolithic calibrated radiocarbon dates (obtained using https://c14.arch.ox.ac.uk/) in several regions in the western Mediterranean, namely 1 Southwestern Italy, 2 Central western Italy, 3 Northwestern Italy/Southeastern France, 4 Languedoc/Roussillon, 5 Catalonia, 6 Valencia, 7 Andalusia, 8 southern Portugal (Algarve), and 9 central Portugal. The horizontal axis gives the coastal distance (estimated using https://www.sea-seek.com/) between the point on the coast that is closest to the considered site and that which is closest to the easternmost one (Favella della Corte, site 1 in Fig. 1 and error bar 1 here). The straight line is the linear fit to the means of the error bars. It is useful as a first approximation but we have used a more precise approach (based on bootstrap resampling) to estimate the spread rate and its error

There are several ways to take the error bars into account. A widely used approach assigns a weight to each y-value (date in our case) equal to the inverse of its error (Bevington 1969; Press et al. 1997). However, in our opinion, this approach is not useful for our purposes. An easy way to see this is to note that, if all data had the same error bar, obviously all weights would be the same; i.e., such an approach would not take into account any effect of the error bars. But even if all error bars were the same, they would surely have an effect on the uncertainty of the slope. Therefore, we need a different approach.

A very reasonable approach to take the role of the error bars into account is to carry out a resampling procedure, i.e., to take a value at random (or using some probability distribution) from each error bar, perform a linear regression, repeat this procedure many times, and compute averages and/or ranges (Gangal et al. 2014; Souza et al. 2020). This is the approach that we have used, by performing a bootstrap resampling as follows. From the OxCal distribution (i.e., that obtained by calibrating at https://c14.arch.ox.ac.uk/) for each of the 9 sites (Table 1), we drew n samples or dates. This was not done at random, but requiring that the probability of drawing a specific date for a given site is equal to the probability of that date in the calibrated distribution obtained from the uncalibrated date of that site in Table 1. We computed the linear regression using the first date drawn for each of the 9 sites, the linear regression using the second dates for the 9 sites, etc. By increasing the total number of regressions n, we observed that the range for the slope quickly converged and remained essentially the same for n > 20 regressions. Thus, there is no need to increase the value of n further, and in this paper, we shall use the range obtained in this way, namely 7.5–10.6 km/year (80% CL, n = 25), for the observed spread rate of the Neolithic in the western Mediterranean.

It is worth to note the early arrival of the Neolithic to the French Languedoc, i.e., the fact that the Neolithic in the Languedoc/Rousillon region (error bar 4 in Fig. 3) is older than those in central Italy and eastern France (error bars 2–3) and substantially older (even without overlap) than those in Eastern Iberia (error bars 5–6). Admittedly, future fieldwork could lead to older error bars in some regions and/or to a narrower error bar for region 4, perhaps in the younger part of that in Fig. 3. However, this is a speculative idea (i.e., it may perfectly turn out to be wrong), so we will not develop it further. In any case, we think that the methodology introduced in this paper (and specially the new Eqs. (1)–(2), which are the first ones for coastal spread) will remain useful to re-analyze this case study when more data are available (as well as to study other coastal spread rates).

Minimum and maximum distances of travel along the coast

We have run the simulations described in the “Simulations” section without cultural transmission ($\eta =0$) for several values of the coastal dispersal length per generation $\Delta$. For the first model introduced in the “Simulations” section, i.e., “forward and backward dispersal” (Fig. 2a), the simulation results are shown in Fig. 4a as a full line. We also include the analytical results for the same model, given by Eq. (1) (again for $\eta =0$), as circles in Fig. 4a. We see that Eq. (1) is a very good approximation (with errors below 5%) to the simulations (full line). Thus, Eq. (1) provides a very useful check of the simulations. The accuracy of Eq. (1) was unexpected by the author, given an approximation that is necessary to derive it (Appendix). For each value of $\Delta$, the full line in Fig. 4a gives the minimum possible spread rate (i.e., that obtained for $\eta =0$). For the same value of $\Delta$, the rates with cultural transmission ($\eta >0$) can be obtained using the same simulation approach (or, alternatively, using Eq. (1)), but we show in turn that this is in fact unnecessary (for our purposes). Indeed, such rates will correspond to a vertical line (from the point of the full line in Fig. 4a that corresponds to the value of $\Delta$ considered) upwards (because it is well known that the spread rate increases with the intensity of cultural transmission (Fort 2012, 2011)). However, the maximum spread rate can be found very easily (without need of simulations) because it is given by the remarkably simple equation (Fort 2012)

Fig. 4

Coastal Neolithic spread rate as a function of the coastal dispersal distance per generation for two models, namely (a) “forward and backward” jumps (isotropic coastal dispersal), and (b) only “forward” jumps (extremely anisotropic coastal dispersal). The horizontal lines give the maximum and minimum spread rates obtained from the archeological data (i.e., 10.6 and 7.5 km/year). The full line is the minimum speed (no cultural diffusion, $\eta =0$), obtained from the simulations, and the dashed line is the maximum speed ($\eta \to \infty$), obtained from Eq. (3). The circles correspond to the minimum speed ($\eta =0$), obtained from Eq. (1) in panel (a) and Eq. (2) in panel (b). According to the model, only the area between the full and dashed lines (hatched in panel (a)) is possible. According to the archaeological data, only the area between the two horizontal lines is possible. From panel (a) we obtain Δmin=240 km, Δ*=339 km and Δ_max=427 km. From panel (b) we obtain again Δ_min=240 km and Δ*=339 km but Δ_max=343 km

$${s}_{\mathrm{max}}=\frac{\Delta }{T}.$$

(3)

This is simply the dispersal length divided by the generation time, a very intuitive result because obviously a population front cannot travel faster than the individuals of the population. We show the maximum spread rate (3) in Fig. 4a as a dashed line. Thus, only the spread rates between the full and dashed lines in Fig. 4a (hatched area) are possible according to the “forward and backward” model. But archeological data imply that the spread rate must be in the range 7.5–10.6 km/year (see the “Observed spread rate” section above). We show these minimum and maximum observed values as two horizontal lines in Fig. 4a. Only spread rates between these two horizontal lines are possible according to the radiocarbon data. Hence, combining the simulation and archeological bounds, we see that the minimum value of $\Delta$ is that corresponding to the lower left arrow in Fig. 4a (Δ_min=240 km) and the maximum value of $\Delta$ is that corresponding to the right arrow in Fig. 4a (Δ_max=427 km). We conclude that in the “forward and backward” model, the range of possible coastal jump lengths is 240–427 km per generation.

Next, we have followed the same approach but using the second model introduced in the “Simulations” section, i.e., the “forward dispersal only” (Fig. 2b) simulation program to obtain the full line in Fig. 4b and Eq. (2) to obtain the circles in Fig. 4b. From this figure, we conclude that the range of possible coastal jump lengths is 240–343 km per generation. It is worth to note that the lower bound (240 km) is the same as for the “forward and backward” model because, as mentioned below Eq. (3), the maximum possible speed (dashed line in Fig. 4a–b) does not depend on the detailed dispersal mechanism (it is simply the maximum dispersal distance moved in the front propagation direction per generation, Eq. (3)). We also note that the full and dashed lines in Fig. 4b are very close to each other (the difference between both lines diminishes gradually from 8% for $\Delta =50$ km to 1% for $\Delta =550$ km). This is due to the fact that dispersal is extremely anisotropic in this case (along the coast there are only jumps forward), so the spread rate (full line in Fig. 4b) is almost equal to the maximum possible one (Eq. (3), dashed line in Fig. 4b) and the small differences between them are due to the short jumps of 50 km inland from the coast¹. The differences between the “forward and backward” and the “only forward” models (i.e., between the full lines in Fig. 4a–b) are between 15 and 20%.

Recall that between the “forward and backward” and the “forward” cases, there are many others, in which the dispersal is gradually biased from the isotropic case (“forward and backward,” Figs. 2a and 4a) towards the extremely anisotropic one (only “forward” jumps, Figs. 2b and 4b). It is very interesting that these two extreme cases (Fig. 4a–b) do not yield so different results after all, in the sense that the ranges of coastal jump lengths are similar, namely 240–427 km (Fig. 4a) and 240–343 km (Fig. 4b) per generation. It is also worth to note that the overall range ($240\le \Delta \le 427$ km) that follows from the two ranges above is simply that for the isotropic case (Fig. 4a). The reason is that for a given jump distance, non-isotropic dispersal (Fig. 4b and any intermediate case between Fig. 4a–b) will obviously lead to faster speeds (see Fig. 2) compared with isotropic dispersal (Fig. 4a), so that shorter jumps will be needed to attain the observed speed.

We can summarize the results with the statement that coastal jumps had lengths in the range $240\le \Delta \le 427$ km per generation. A previous approach considering only an extremely anisotropic case (with a slightly more complicated dispersal mechanism, i.e., involving also short coastal jumps) and a different database estimated the approximate range $350\le \Delta \le 450$ km (Isern et al. 2017). Here we have obtained $240\le \Delta \le 427$ km. One reason for this difference is that the data in Isern et al. (2017) excluding northern Africa (which is clearly an outlier) imply a spread rate of 10.0 km/yr, which for extremely anisotropic dispersal (Fig. 4b in the present paper) implies that Δ > 300 km (in contrast, the same approach leads to Δ < 300 km for the average spread rate obtained in this paper, namely 9.1 km/yr). Another difference with Isern et al. (2017) is that here we have performed a careful estimation of the range of the spread rate (in the “Observed spread rate” section) and obtained 7.5–10.6 km/year, using a new database that includes 3 additional regions, as well as updated information for the other regions (Fig. 3, Table 1 and Supp. Info. database). We have also considered isotropic dispersal (Figs. 2a and 4a), which was not done by Isern et al. (2017). However, the work by Isern et al. (2017) was a very useful first step and it derived the range $350\le \Delta \le 450$ km, which is quite similar to that derived in the present paper ($240\le \Delta \le 427$ km) in spite of the methodology and database differences summarized above. We have found that the characteristic length of coastal jumps (at least $\Delta =240$ km) was surely much larger than the dispersal distance ($d=50$ km) that is necessary for inland jumps (Fort et al. 2007) to explain the much slower Neolithic spread rate in inland Europe (about 1 km/year (Ammerman and Cavalli-Sforza 1971; Pinhasi et al. 2005)). This confirms the need of long jumps to explain the Neolithic spread along the western Mediterranean.

For clarity, it is worth to add a brief methodological remark. We have only needed the minimum and maximum spread rates (for each value of the coastal dispersal distance $\Delta$). For this reason, although we have considered two populations (farmers and hunter-gatherers), for our purposes, it has been enough to run the simulations without cultural transmission between both populations $\eta$ = 0 (or, equivalently, with only farmers) because this yields the minimum spread rate (Fort 2012) (for a given value of the coastal dispersal distance $\Delta$) and on the other hand, the maximum spread rate (i.e., for sufficiently strong cultural transmission) is simply $\Delta /T$, i.e., Eq. (3) (Fort 2012) (so simulations are not necessary to find the maximum spread rate).

Minimum and maximum percentages of cultural diffusion

Finally, we can address the following important point, which has not been tackled previously. In contrast to inland spread, we have no ethnographic data on intergenerational dispersal distances along a coast for pre-industrial farmers. So in principle, it might seem that it is not possible to estimate the relative importance of demic and cultural diffusion (in contrast, such an estimation has been done previously for inland Neolithic spread by using ethnographic dispersal distances (Fort 2012)). However, since the radiocarbon dates lead to bounds on the dispersal distances (namely $240\le \Delta \le 427$ km per generation, as shown above), it makes sense to ask the following question. Is it possible to find also quantitative bounds on the relative importance of demic and cultural diffusion in the spread of the Neolithic along the western Mediterranean coast? The percentage of cultural diffusion is given by (Fort 2012)

$$\frac{s-{s}_{\eta =0}}{s}\cdot 100,$$

(4)

where $s$ is the spread rate predicted by the demic-cultural model (which should fall within the observed range, if the model and parameter values are realistic). ${s}_{\eta =0}$ is the corresponding rate without cultural diffusion ($\eta =0$), i.e., for the purely demic case. Similarly, the percentage of demic diffusion is

$$\frac{{s}_{\eta =0}}{s} \cdot 100,$$

(5)

and the percentages given by Eqs. (4) and (5) add up to 100%.

Figure 5 shows the maximum percentage of cultural diffusion as a function of the coastal jump length $\Delta$ for both the “forward and backward” and the only “forward” jump models. We have obtained Fig. 5 as follows. As explained in the previous section, for each value of $\Delta$, Fig. 4a (“forward and backward” model) gives the minimum and maximum spread rates according to the simulations, which correspond respectively to the full line ($\eta =0$, no cultural diffusion) and the dashed line ($\eta \to \infty$, very strong cultural diffusion; in this limit Eq. (4) saturates at a finite value because the speed also saturates its maximum given by ${s}_{\mathrm{max}}=\frac{\Delta }{T}$, Eq. (3) (Fort 2012)). Thus, for each value of $\Delta$, the maximum cultural effect is given by Eq. (4) with ${s}_{\eta =0}$ given by the full line in Fig. 4a (simulations with $\eta =0$) and $s$ given by the dashed line in Fig. 4a (${s}_{\mathrm{max}}=\frac{\Delta }{T}$, Eq. (3)) because according to Eq. (4), the maximum value ${s}_{\mathrm{max}}$ for the spread rate $s$ will correspond to the maximum cultural effect, i.e.,

Fig. 5

Maximum percentage of cultural diffusion as a function of the coastal dispersal distance per generation for two models, namely “forward and backward” jumps (isotropic coastal dispersal), and only “forward” jumps (extremely anisotropic coastal dispersal). Other models with intermediate dispersal anisotropy will give percentages between those implied by both models. The hatched rectangle ($\Delta <240$ km or spread rate below 7.5 km/year) is inconsistent with the archeological data. The hatched area (Δ < Δ_min=240 km) is inconsistent with archaeological data (Figs. 4a–b). This figure shows that the effect of cultural diffusion was below 21% and, therefore, that of demic diffusion was above 79%

$$\frac{{s}_{\mathrm{max}}-{s}_{\eta =0}}{{s}_{\mathrm{max}}}\cdot 100.$$

(6)

We have applied this approach to plot the “forward and backward” model in Fig. 5 for $240<\Delta <339\mathrm{ km}.$ This lower value (${\Delta }_{\mathrm{min}}=$ 240 km) is the minimum jump length consistent with the radiocarbon data, as obtained from Fig. 4a. For this reason, the hatched area in Fig. 5 is inconsistent with the data. On the other hand, the former upper value (${\Delta }^{*}=$ 339 km in Figs. 4a and 5) comes from the fact that for $\Delta >{\Delta }^{*}=339\mathrm{ km}$, the dashed line in Fig. 4a is faster than 10.6 km/year (dashed-dotted horizontal line) because 339 km/32 year = 10.6 km/year. For Δ > Δ* = 339km, the dashed line in Fig. 4a is thus inconsistent with the observed range (7.5–10.6 km/year). Hence, for $\Delta >{\Delta }^{*}=339$ km, the maximum cultural effect in Fig. 5 is given by Eq. (4) with $s=10.6$ km/year (upper horizontal line in Fig. 4a) instead of Eq. (3) (dashed line in Fig. 4a). For ${\Delta }_{\mathrm{max}}=427$ $\mathrm{km}$, the purely demic speed (full line in Fig. 4a) is ${s}_{\eta =0}=10.6$ km/year, i.e., the maximum value according to the archeological data, so cultural transmission is not possible (because it would lead to a faster speed) and this is why the cultural effect is 0% in Fig. 5 for $\Delta =427$ km and the “forward and backward” model. The upper curve in Fig. 5 implies that the maximum cultural effect is 21% for the “forward and backward” model (and this value can be attained for ${\Delta }_{\mathrm{min}}=240$ km).

The curve for the “forward only” model in Fig. 5 has been obtained in the same way. The value ${\Delta }^{*}=339$ km is the same as for the previous “forward and backward” model because, as explained above, it is the intersection of the dashed line and the dashed-dotted horizontal line, which are the same in Fig. 4a and b (i.e., ${\Delta }^{*}$ is the solution to the equation  $\frac{{\Delta }^{*}}{32 \mathrm{year}}=$10.6 km/year). Similarly, the value ${\Delta }_{\mathrm{min}}=$ 240 km is also the same in Fig. 4a and b, because it is the intersection of the dashed line and the dotted horizontal line (i.e., $\frac{{\Delta }_{\mathrm{min}}}{32\mathrm{year}}=$ 7.5 km/year). However, ${\Delta }_{\mathrm{max}}$ is different. Its value is ${\Delta }_{\mathrm{max}}$=343 km for the “forward only” model (Figs. 4b and 5) because for this model and $\Delta >343$ km the spread rate (Fig. 4b) is faster than the range implied by the archeological data (7.5–10.6 km/year). The percentage of cultural diffusion is smaller for the “forward only” case than for the “forward and backward” one because for a given distance, in the “forward only” case, all of the population that moves by sea travel in the direction of the spread, which obviously implies a faster demic spread rate ${s}_{\eta =0}$ (full lines in Fig. 4a–b) but the maximum demic-cultural rate is the same (${s}_{\mathrm{max}}=\frac{\Delta }{T}$, Eq. (3)), so Eq. (6) yields a lower value for the maximum cultural effect. The curve of the cultural effect always decreases so, again, the maximum cultural effect can be attained for ${\Delta }_{\mathrm{min}}=240$ km. It is very interesting that this maximum cultural effect for the “forward only” model is below 2%, i.e., about ten times less than for the “forward and backward” model. Such an important (ten-fold) difference between non-isotropic (“forward only”) and isotropic (“forward and backward”) dispersal is a new result, because no previous comparison of the cultural effect under both types of dispersal had been reported (neither for the western Mediterranean nor for any other Neolithic waves of advance).

The former paragraphs and Fig. 5 correspond to the maximum cultural effect for each value of $\Delta$. What is the minimum cultural effect? It is 0% in all cases (i.e., the maximum demic effect is 100%). The reason is very clear intuitively. We can always find a value of the coastal jump length $\Delta$ that agrees with the observed spread rate, without any need of cultural diffusion (this value of $\Delta$ can be found from Fig. 4a–b by drawing a horizontal line at the desired spread rate, and finding out the value of $\Delta$ for which this horizontal line crosses the full line, i.e., the spread rate for $\eta =0$).

Figure 5 leads to the new conclusion that, according to the “forward and backward” jump model, the cultural effect was between 0 and 21%, and according to the “forward” model it was between 0 and 2%. Thus, interestingly, we can derive a maximum for the importance of cultural diffusion (21%) in spite of the fact that we cannot derive a maximum for the importance of demic diffusion (due to lack of data on dispersal distances $\Delta$ per generation for pre-industrial coastal populations of farmers). The possibility to find a maximum for the importance of cultural diffusion (range 0–21%), and therefore a minimum for that of demic diffusion (range 79–100%), is due to the fact that, for a given value of the dispersal length $\Delta$, the demic-cultural spread rate $s$ in Eq. (4) cannot increase indefinitely for increasing values of the intensity $\eta$ of cultural diffusion because the spread rate is inherently limited by the values of the dispersal length $\Delta$ and generation time $T$ (see Eq. (3) and the interpretation below it), and this leads to the maximum for the cultural effect given by Eq. (6) for the value of $\Delta$ considered.

Conclusions

In this work, we have estimated the spread rate of the Neolithic along the northern shore of the western Mediterranean as 7.5–10.6 km/year by carefully taking into account the implications of the errors in the radiocarbon dates, which are substantial if compared to the duration of this spread (Fig. 3). This rate is much faster than the average one for the Neolithic in inland Europe (about 1 km/year). So far, only one other so fast Neolithic spread rate is known, namely that of the Neolithic expansion in Austronesia (Fort 2003). Interestingly, it also took place in a maritime context. In contrast, inland Neolithic expansions are consistently slower, e.g. the Neolithic spread across inland Europe (Pinhasi et al. 2005), the Khoi-khoi expansion of herders in southern Africa (Jerardino et al. 2014), the Bantu expansion in eastern Africa (Isern and Fort 2019) the spread of domesticated rice in eastern and southeastern Asia (Cobo et al. 2019) and the Neolithic spread in Scandinavia (Fort et al. 2018).

We have also used numerical simulations, based on quantitative models of demic-cultural waves of advance, to constrain the possible values of the dispersal length per generation of early farmers in the western Mediterranean. We have assumed a dispersal mechanism with longer distances along the coast than inland. This is necessary to explain the fast observed coastal rate (without contradicting the characteristic inland dispersal distance $d\approx 50$ km implied by both ethnographic data and the slower inland spread rate). We have found that the length of coastal jumps was $240\le \Delta \le 427$ km, and that this range is valid for all intermediate cases between isotropic (Fig. 2a) and extremely anisotropic (Fig. 2b) coastal dispersal. The intuitive reasons behind the existence of this range of possible values of $\Delta$ are that, as seen in Fig. 4a, jumps shorter than Δ_min=240 km lead to a Neolithic spread slower than 7.5 km/year (even if cultural diffusion is very intense, dashed line or $\eta \to \infty$) and jumps longer than Δ_max=427 km lead to a Neolithic spread faster than 10.6 km/year (even in the absence of cultural diffusion, full line or $\eta =0$).

In our opinion, the very fast rate (7.5–10.6 km/year) and the long distances per generation involved ($240\le \Delta \le 427\mathrm{ km}$) in this coastal spread suggest that travel took place using boats. This would explain why the Neolithic in western Europe spread so rapidly (or equivalently, with so long dispersal distances $\Delta$) along the coast, but not inland. Indeed, since humans can walk at a speed of about 5 km per hour, the characteristic distance of inland dispersal per generation estimated from ethnography, i.e. $d=50$ km (Fort et al. 2007) is attainable by foot in a single day (with a 10-h walk) but the long distances of coastal dispersal derived in this paper ($240\le \Delta \le 427\mathrm{ km}$) are definitely too long to be traveled by foot in a single day. From this perspective, it is reasonable to think that the fastest spread of the Neolithic along the coast than inland was due to the fact that boats provided the means of transportation that made it possible to cover such long distances in only 1 or 2 days, and thus to easily visit and keep in contact with the families of pioneering farmers. Indeed, reconstructions of the boats presumably used by ancient Polynesian farmers can attain speeds of about 19 km/h (Finney 1977, 1967), so 240 km could possibly be traveled in about 13 h. Moreover, from an ethnographic perspective, the distances of coastal dispersal derived in this paper ($240\le \Delta \le 427$ $\mathrm{km}$ per generation) are not surprising at all for human populations used to sea travel. As a first example, displacements of young people from Fiji and Samoa to get married in Tonga (which implies more than 700 km per generation) are known to take place since more than 300 years ago (Kaeppler 1978). As a second example, in the nineteenth century, some people living in the island of Nukuria had moved 30 years before from Mimigo (about 1100 km away), and there were also migrations from the Gilberts to the Solomons (1900 km), from the Gilbert Islands to Buka (2200 km), etc. (Parkinson 1986). These are examples for specific individuals (not histograms for complete populations) of distances moved per generation (which are the kind of distances useful to model range expansions (Fort et al. 2004a)). But even without referring to a time interval of one generation, it is also noteworthy that sea distances well above 50 km were easily covered by several pre-industrial populations, for example more than 240 km to transport obsidian in near Oceania at least 20,000 years ago (Hunt and Lipo 2017), more than 400 km for the same reason and in the same region by Lapita communities 3,000 years ago (Hunt and Lipo 2017), 150 km for some of the Kula ring travels at the beginning of the twentieth century (Malinkowski 1922) or the routine travels of 650–975 km by Caribbean peoples with paddling canoes at the time of European conquest (Shearn 2020).

The relative importance of cultural and demic diffusion in the Neolithic spread in the western Mediterranean had not been analyzed previously. This case study is more difficult than all previous ones (inland expansions) due to the absence of histograms for the dispersal distance $\Delta$ from ethnographic data of preindustrial populations. In spite of this, we have shown that it is possible to constrain the cultural effect. It turns out to be less than 21% (Fig. 5), so demic diffusion was responsible for at least 79% of the observed spread rate. The upper bound of 21% for cultural diffusion in the western Mediterranean is smaller than those known for inland Neolithic expansions, namely 30% for Europe² (Fort 2012), 42% for Scandinavia³ (Fort et al. 2018), 47% and 37% for the southern and eastern Bantu spreads in eastern Africa⁴ (Isern and Fort 2019), 68% for the Khoi-khoi spread in southern Africa⁵ (Jerardino et al. 2014), and 42% for the spread of rice-based farming in eastern and southeastern Asia⁶ (Cobo et al. 2019). It should be stressed that these are upper bounds; so for example in the western Mediterranean, the cultural effect could be up to 21% but as low as 0% according to the archeological data available at present. The data available therefore suggest that Neolithic populations spread faster by sea, with longer dispersal distances and little cultural diffusion (incorporation of hunter-gatherers). Thus, the interactions between farmers and hunter-gatherers were clearly limited in the spread of the Neolithic along the western Mediterranean.

We have derived new equations for the spread rate of a demic-cultural wave of advance along a coast (Eqs. (1)–(2), derived in the Appendix). These equations are not exact but, rather surprisingly, they turn out to be a very good approximation (compare the circles to the full lines in Fig. 4a–b). They can be very useful, on one hand, to check the results of numerical simulations, and on the other hand to obtain spread rates only in only some seconds (whereas running the simulation program can take 5–10 min).

It would be of interest to find histograms of dispersal distances per generation for pre-industrial coastal populations of farmers, if possible, and compare to the distances inferred in the present work from the archeological data. Such distances have been reported for pre-industrial farming inland populations (see Ammerman and Cavalli-Sforza 1984 and the tables in Fort 2020, Sec. S1) but not, to the best of our knowledge, for coastal ones.

Appendix. Analytical approximations for coastal spread rates

Fort et al. (2007) reported an equation for the spread rate of an invasion front in the simple case of an inland expansion in which all individuals move the same distance in each of the four directions to the nearest square cells of a grid (see Eqs. (16)–(17) in Fort et al. 2007). Here we use the same method for coastal expansions. For clarity, we will perform each derivation first for a single population (farmers), and then generalize it to two interacting populations (farmers and hunter-gatherers).

In the notation used below, the coast is the line with $x=0$ (i.e., the $y$ axis) and separates the sea $\left(x<0\right)$ from the land $\left(x>0\right)$. When referring to the cell $\left(x,y\right)$, we mean the cell with central point $\left(x,y\right)$. Thus, we are dealing with a rectangular grid of nodes separated a distance $d$ both in the vertical and horizontal directions, and each node is the central point of a square cell with side $d$.

For reproduction functions that can be linearized (i.e., that are proportional to the population density if the latter is small enough), it is well known that replacing the reproduction function by its linear approximation leads to simpler equations that make it possible to find out the front speed (see Sec. 3.1 in Fort and Méndez 2002). As mentioned above (“Simulations” section, (i) Reproduction), we consider logistic reproduction and farmers have initial growth rate ${a}_{F}$, net fecundity ${R}_{0}^{F}={e}^{{a}_{F}T}$ and carrying capacity ${p}_{ \mathrm{max}}^{ F}$, where $T$ is one generation. The logistic dynamics can be easily linearized by considering low values of the population density of farmers ${p}_{F}(t)$, i.e., (Murray 1993; Isern et al. 2008), ${p}_{F}\left(t+T\right)=\frac{{R}_{0}^{F} {p}_{F}\left(t\right){ p}_{ \mathrm{max}}^{ F} }{{p}_{ \mathrm{max} }^{ F} + {p}_{F}\left(t\right) ({R}_{0}^{F}-1)}\approx {R}_{0}^{F} {p}_{F}\left(t\right)$, so it will suffice to use this simple reproduction function (which is valid for ${p}_{F}\ll { p}_{ \mathrm{max}}^{ F}$) in our calculations below.

• (A) “Forward and backward” case. Combining the definition of this case (see the “Simulations” section, (iii) Dispersal) with the explanation in the previous paragraph, it is obvious that for ${p}_{F}\ll { p}_{ \mathrm{max}}^{ F}$, the population density of farmers at time $t+T$ and the coastal cell $\left(0,y\right)$ is related to those at time $t$ and the neighboring nodes as

$${p}_{F}\left(0,y,t+T\right)={R}_{0}^{F}\left[{p}_{e} {p}_{F}\left(0,y,t\right)+\frac{1-{p}_{e}}{3}\left({p}_{F}\left(0+d,y,t\right)+{p}_{F}\left(0,y-\Delta ,t\right)+{p}_{F}\left(0,y+\Delta ,t\right)\right)\right],$$

(7)

where, as explained in the “Simulations” section $d=50$ km is the inland-travel distance and $\Delta$ is the sea-travel distance (Fig. 2a). The first term inside the brackets corresponds to the fraction ${p}_{e}$ of the population that does not move from the coastal cell $\left(x,y\right)$ considered, the second term to the fraction that jumps from the nearest inland cell, and the two last terms to the fractions that jump from two coastal cells (Fig. 2a). ${R}_{0}^{F}$ corresponds to net reproduction, i.e., births minus deaths (in the linear approximation, i.e., for ${p}_{F}\ll { p}_{ \mathrm{max}}^{ F}$, which is enough for our purposes, as explained in the previous paragraph).

In order to find the spread rate for equations of the type of Eq. (7) analytically, previous work dealing with inland range expansions (Fort et al. 2007; Fort and Méndez 1999) has successfully applied the following reasoning. An inland front with isotropic dispersal in homogeneous space will not be a straight line in general. For example, if the population is initially in a single node, the front will be circular. Therefore, in general, the local speed at each node of the grid has a different direction (radial in this example). But obviously for sufficiently large times, the front curvature will be negligible (at scales much larger than that of individual dispersal movements), so the local speeds will be approximately parallel in a sufficiently small region. For example, if we consider a node $({x}_{0},y)$ with the same $x$ coordinate as that of the inland node $({x}_{0},{y}_{0})$ occupied by the initial population, the local speeds of the inland front near node $({x}_{0},y)$ will be approximately parallel to the $y$ axis and, therefore, the local population density $p$ will approximately depend on $y$ but not on $x$. Note that for inland expansions, this approximation can be as precise as we wish simply by considering a sufficiently large time after the start of the front propagation. We shall now see that this is not the case for coastal expansions, and for this reason it will be necessary to introduce an assumption in order to determine the spread rate of coastal expansions.

In this paper, we deal with coastal expansions. We assume (as in the “Simulations” section) that the initial population is located at a set of contiguous cells on the coast ($x=0$). Admittedly, some dependence of $p$ on $x$ will exist, even for large times after the initial of the front propagation (because we have checked with simulations that the front is faster along the coast than inland). However, we may again assume that the dependence of $p$ only on $y$ is a valid approximation near the coast (an unexpected result is that this approximation is in fact rather accurate, as discussed below and seen in Fig. 4a–b). As mentioned above, we choose the $y$ axis ($x=0$) parallel to the coast and the $x$ axis orthogonal to it. Let us focus on the coast ($x=0$). Although this is not strictly necessary, for clarity, let us assume that the Neolithic population, with density ${p}_{F}$, is located initially at the lower part of the coast (e.g., $y<{y}_{0}$), where ${p}_{F}={ p}_{ \mathrm{max}}^{ F}$, whereas in the upper part ($y>{y}_{0}$) there are initially no Neolithic individuals (${p}_{F}=0$). In other words, the Neolithic population has initially the shape of a step. Some Neolithic individuals will move to values of $y>{y}_{0}$ and reproduce, some time later their children will again disperse and reproduce, etc. This simple dynamics may be called the propagation of an invasion front (which is also called wave of advance). Obviously, the initial step will modify its shape but it is intuitively clear that the Neolithic population density ${p}_{F}$ will always decrease upwards (with ${p}_{F}\to { p}_{ \mathrm{max}}^{ F}$ for $y\to -\infty$ and ${p}_{F}\to 0$ for $y\to \infty$). We assume as usual (Fort and Méndez 2002) (and the simulations verify this) that after an initial transient, the speed $s$ and the shape of the front will become constant. Consider an observer initially at location ${y}_{i}$ that moves (already from $t=0$) with speed $s$ (where $s$ is the front speed after the initial transient). Such an observer obviously has position $y={y}_{i}+st$. Therefore, for this observer, the value of $z=y-st={y}_{i}$ is constant, where we have defined the new coordinate $z=y-st$. Similarly, due to the fact that this observer moves with the front, any point of the front profile (e.g., the point with ${p}_{F}={ p}_{ \mathrm{max}}^{ F}/2)$ will obviously have a constant value of $z$ (after the initial transient). Thus, for such an observer, the population density along the coast ${p}_{F}\left(x=0,y,t\right)$ depends only on $z$ (but not on $y$ and $t$ separately). For this reason, as usual (Fort and Méndez 2002), we look for a solution to Eq. (7) that depends only on $z$ (this is usually called a constant-shape solution). Unfortunately, it seems that the solution of Eq. (7) $p(z)$ for all values of $z$ cannot be found analytically, so we look as usual (Fort and Méndez 2002) for a solution with the form $p={p}_{0}\mathrm{exp}[-\lambda z]$, with $\lambda >0$. This solution can be valid for $z\to \infty$ (i.e., $y\to \infty$) but not for $z\to -\infty$ (i.e., $y\to \infty$) because it does not satisfy the condition, explained above, that ${p}_{F}\to { p}_{ \mathrm{max}}^{ F}$ for $y\to -\infty$. Using this function $p={p}_{0}\mathrm{exp}[-\lambda z]$ into Eq. (7), we see that $p={p}_{0}\mathrm{exp}[-\lambda z]$ is indeed a solution to this equation, provided that

$${e}^{-\lambda (y-st-sT)}={R}_{0}\left[{p}_{e}{ e}^{-\lambda (y-st)}+\frac{1-{p}_{e}}{3}\left(1+{ e}^{\lambda\Delta }+{ e}^{-\lambda\Delta }\right){ e}^{-\lambda (y-st)}\right],$$

and using the definition $\mathrm{cosh}\left(\lambda\Delta \right)=\frac{{e}^{\lambda\Delta }+{e}^{-\lambda\Delta }}{2}$, we easily arrive at

$${e}^{\lambda sT}={R}_{0}\left[ \frac{{2p}_{e}+1}{3}+\frac{2}{3}(1-{p}_{e})\mathrm{cosh}(\lambda\Delta )\right],$$

(8)

Finally, we apply that for equations with a growth rate that can be linearized (i.e., with a growth rate that is proportional to the population density for low values of the latter, which is the case for logistic growth), it is well known that the front speed (spread rate) is given by the minimum possible one (Saarloos 2003). Thus, the coastal spread rate for the “forward and backward” case is given by

$$s\approx \begin{array}{c}\\ \mathrm{min}\\ \lambda >0\end{array}\frac{ln\left[{R}_{0}\left(\frac{{2p}_{e}+1}{3}+\frac{2}{3}(1-{p}_{e})\mathrm{cosh}(\lambda\Delta )\right)\right]}{\lambda T}.$$

(9)

Apparently, it is not possible to simplify further this equation for the spread rate $s$, but we can easily plot the fraction in Eq. (9) as a function of $\lambda$ for given values of the parameters (${R}_{0}, {p}_{e},\Delta$, and $T$) and find out the minimum visually or numerically (we have done this visually using the mathematica software, but many other programs are equally useful and, in fact, a graphics program or even a scientific calculator is enough to find out the minimum for given parameter values).

This procedure leads to the spread rates shown as circles in Fig. 4a, which are very similar to those obtained from the numerical simulations described in the “Simulations” section (full line in Fig. 4a). Therefore, although for coastal expansions (in contrast to inland expansions) the result (9) of this method is not exact (because $p$ is not strictly independent of $x$, see (i) above Eq. (8)), Eq. (9) is rather accurate according to Fig. 4a (the differences between the speeds from Eq. (9) and the simulations are below 5%).

If the spread of farmers takes place in the presence of autochthonous hunter-gatherers distributed all over the landscape, then ${R}_{0}^{F}={e}^{{a}_{F}T}$ must be replaced by ${R}_{0}^{F}\left(1+\eta \right)$ in the linearized equation (in our case Eq. (7)), where $\eta$ is the intensity of cultural transmission (see Eqs. (49)–(51) in Fort 2011 or Eqs. (14)–(17) in Fort 2012). Clearly, the same change must be made in Eqs. (8)–(9), so the spread rate of farmers is in this more general case given by Eq. (1), namely

$$s\approx \begin{array}{c}\\ \mathrm{min}\\ \lambda >0\end{array}\frac{ln\left[{R}_{0}^{F}\left(1+\eta \right)\left(\frac{{2p}_{e}+1}{3}+\frac{2}{3}(1-{p}_{e})\mathrm{cosh}(\lambda\Delta )\right)\right]}{\lambda T}.$$

(10)

• (B) “Forward” case. It has been also introduced in the “Simulations” section, (iii) Dispersal. Let again the wave of advance travel upwards (i.e., towards increasing values of $y$) along the coast ($x=0$). Then in the "forward" case (Fig. 2b), Eq. (7) is obviously replaced by

  $${p}_{F}\left(0,y,t+T\right)={R}_{0}^{F}\left[{p}_{e} {p}_{F}\left(0,y,t\right)+\frac{1-{p}_{e}}{2}\left({p}_{F}\left(0+d,y,t\right)+{p}_{F}\left(0,y-\Delta ,t\right)\right)\right],$$

  (11)

  where the first term inside the brackets corresponds to the fraction ${p}_{e}$ of the population that does not move from the coastal cell $\left(0,y\right)$ considered, the second term to the fraction that jumps from the nearest inland cell, and the last term to the fraction that jumps upwards from a coastal cell (Fig. 2b). Following the same steps as above, we find that Eq. (10) is replaced by a simpler equation, namely Eq. (2), i.e.

$$s\approx \begin{array}{c}\\ \mathrm{min}\\ \lambda >0\end{array}\frac{ln\left[{R}_{0}^{F}\left(1+\eta \right)\left(\frac{{p}_{e}+1}{2}+\frac{1-{p}_{e}}{2}{e}^{\lambda\Delta }\right)\right]}{\lambda T}.$$

(12)

As for case (A) above, we stress that for coastal expansions the result (12) is not exact but it is very accurate because its results for $\eta$=0 (circles in Fig. 4b) are very similar to those of numerical simulations (full line in Fig. 4b, also for $\eta =0$).