Intraspecific variation promotes coexistence under competition for essential resources

Abstract

Intraspecific variation may be key to coexistence in diverse communities, with some even suggesting it is necessary for large numbers of competitors to coexist. However, theory provides little support for this argument, instead finding that intraspecific variation generally makes it more difficult for species to coexist. Here we present a model of competition where two species compete for two essential resources and individuals within populations vary in their ability to take up different resources. We found a range of cases where intraspecific variation expands the range of conditions under which coexistence can occur, which provides a mechanism that allows the ecologically neutral evolutionary stable strategy (ESS) to become ecologically stable. We demonstrate that this result relies on nonlinearity in the function that describes how traits map onto ecological function. A sigmoid map** function is necessary in order to model essential resources because it allows for variation in an unbounded trait while maintaining biologically realistic boundaries on uptake rates, and differs from other kinds of nonlinearity, which only unidirectionally increase or decrease ecological function. The sigmoid function’s nonlinearity spreads individuals unevenly along the growth function, which allows positive growth contributions from some individuals to compensate for growth loses from others, akin to source-sink dynamics, leading to coexistence. In this way, intraspecific trait variation is able to amplify niche differences, thereby strengthening coexistence. We discuss empirical systems beyond competition for essential resources in which piecewise functions (i.e., thresholds) are important.

Appendices

Appendix 1. Invasion analyses

To determine the effect of ITV on coexistence, analytically solve the invasion growth rate in a community without ITV (Klausmeier et al. 2007; Fox and Vasseur 2008). We then compare this to an invasion analysis of the model with intraspecific variation in one or both competitors in order to inform our understanding of the importance of ITV for coexistence. The invasion growth rate is proportional to Eq. 4, but where R₁ and R₂ represent the equilibrium resource densities in a community with a single (resident) consumer. Since all other parameters in the model are symmetric or equal (d₁ = d₂ = 0.1; y₁₁ = y₂₂ = 0.5; y₂₁ = y₁₂ = 1), the results would be symmetric for scenarios in which N₂ is the invader. We proceed with N₁ as the invader and N₂ as the resident.

The resident equilibrium resource densities ${R}_{11}$ and ${R}_{21}$ depend upon which resource is most limiting for the resident’s growth (see Fox and Vasseur 2008) such that:

$$\left\{{R}_{11},{R}_{21}\right\}=\left\{{S}_{1}+\frac{{d}_{1}+{S}_{2}({u}_{2}-1){y}_{22}}{{y}_{12}-{u}_{2}{y}_{12}},\frac{{d}_{1}}{{y}_{22}\left(1-{u}_{2}\right)}\right\}$$

(14)

when R₁ is the limiting resource and

$$\left\{{R}_{11},{R}_{21}\right\}=\left\{\frac{{d}_{1}}{{y}_{12}{u}_{2}},\frac{{S}_{1}{u}_{2}{y}_{12}-{S}_{2}{u}_{2}{y}_{22}-{d}_{1}}{{u}_{2}{y}_{22}}\right\}$$

(15)

when R₂ is the limiting resource. The point where resource limitation switches from R₁ to R₂, as a function of u, can be determined as:

$${u}_{c1}={d}_{1}\left(-2+\frac{{S}_{1}{y}_{11}+{S}_{2}{y}_{21}}{{d}_{1}}+\sqrt{4+\frac{{\left(-{S}_{1}{y}_{11}+{S}_{2}{y}_{21}\right)}^{2}}{2\left(-{S}_{1}{y}_{11}+{S}_{2}{y}_{21}\right)}}\right)$$

(16)

There is an additional condition that defines the persistence boundary for the resident consumer. When R₁ and R₂ cannot meet or exceed the inflow concentrations of the resources S₁ and S₂, the consumer cannot persist (N₂ = 0) and therefore ${R}_{11}={S}_{1}$ and/or ${R}_{21}={S}_{2}$.

Using this set of conditions, we calculate the invasion growth rate of consumer (with ITV) into a resident community (without ITV) as:

$${I}_{inv}={\omega }_{inv}{y}_{1inv}{\overline{u} }_{inv}{R}_{1}+\left(1-{\omega }_{inv}\right){y}_{2inv}\stackrel{-}{\left(1-{u}_{inv}\right)}{R}_{2}-{d}_{inv}$$

(17)

In cases where both the invading and resident consumer have ITV, Eq. 17 still represents the invasion growth rate. However, R₁ and R₂ will deviate from the analytical values determined in Eqs. 14 and 15 to reflect the effects of ITV. To analyze these cases, we utilize numerical simulation of the resident dynamics to determine the R₁ and R₂ at equilibrium. We use Eq. 17 to calculate the maximum invasion growth rate for any amount of ITV δ (see Figs. 5 and 7 for details on how much variation is necessary to produce various outcomes).

A different approach is needed to calculate the equilibrium resource values when the resident in allopatry has intraspecific variation. For simplicity, we assume that the resident has a constant amount of variation, δ = 1. To do this, we use the same categorical growth partitioning scheme to calculate the growth of the resident population as we do with the invader,

$${g}_{res}={\omega }_{res}{y}_{1res}{\overline{u} }_{res}{R}_{1}+\left(1-{\omega }_{res}\right){y}_{2res}\stackrel{-}{\left(1-{u}_{res}\right)}{R}_{2}$$

(18)

which is then substituted into the following system of equations:

$$\frac{d{R}_{i}}{dt}=D\left({S}_{res}-{R}_{res}\right)-\frac{{N}_{res}{g}_{res}}{{y}_{i res}}$$

(19)

$$\frac{d{N}_{res}}{dt}={N}_{res}\left({g}_{res}-{d}_{res}\right)$$

(20)

where i = {1,2}. This system of equations can then be numerically solved for R₁ and R₂ at equilibrium. Invasion analyses can then proceed as described in the main text by substituting these solutions into Eq. 17.

Appendix 2. Resident variation

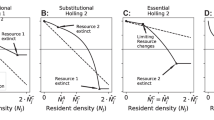
Previous work linking ITV to coexistence has found that the benefits of ITV are typically constrained to cases where there are strict assumptions about the form of ITV itself. For example, Barabás and D’Andrea (2016) found that two species with the same mean trait value (on a single trait axis) could coexist if one had large ITV relative to the other. Here the generalist (large ITV) is successful outside the area of trait overlap while the specialist (small ITV) is dominant within this area. When the mean trait values differ among species, adding ITV in equal amounts to both competitors does not promote coexistence (Hart et al. 2016) but instead increases the niche overlap of species, leading to more intense interspecific competition and a weakening of the stabilizing mechanism. In contrast, we found that, in the case of essential resource competition, equal amounts of ITV in one or both competitors are capable to generating coexistence outside of the range of conditions under which coexistence is possible without ITV.

This is demonstrated in Fig. 5, where in the absence of ITV, the invader has a negative invasion growth rate and both consumers are entirely limited by R₂. Increasing ITV in the invader leads to coexistence even when only a small fraction of individuals are limited by R₁, because the contribution of those individuals to the population growth rate is outsized (Fig. 5b). Similarly, when the resident competitor has ITV, coexistence occurs because a large enough fraction of the resident population shifts to limitation by R₁ (Fig. 5c). Even when only a small fraction of the population exists inside of the coexistence region, it can grow quickly enough to result in positive total population growth rates (Fig. 5d).

The range of conditions that support coexistence expands more evenly along both axes if both the resident and the invader have fixed variation (Fig. 5c). Fixed variation in both populations does not have any conditions under which the invader displaces the resident (Fig. 5c), which can occur when the invader’s variation is optimized for maximum invasion growth rate (Fig. 5d).

Appendix 3. Sufficient amounts of intraspecific variation

Throughout the main text, we discuss competition outcomes with intraspecific variation. Here, we describe how much variation is necessary for these outcomes to occur. Relatively modest amounts of variation (δ < 1) can result in positive invasion growth rates and coexistence where it would otherwise not be possible (Fig. 6), particularly when the resident’s preferences for R₁ and R₂ are close to symmetrical (i.e., u₂ =  ~ 0.5). Larger amounts of variation are necessary to produce positive invasion growth rates when the resident’s resource preferences become strongly skewed in either direction (Fig. 6), which roughly corresponds to the regions where intraspecific variation leads to displacement of the resident by the invader rather than coexistence (see Fig. 2b in the main text).

In some cases, when variation increases beyond a certain point (i.e., becomes “too large”), it is no longer beneficial for invasion. We demonstrate this by calculating invasion growth rates for a range of δ from 0 to 10 for three fixed u₁, u₂ combinations just outside of the coexistence boundary (Fig. 7). If variation spreads the trait distribution in such a way that a large proportion of the population has an uptake ratio that skews heavily toward being limited by the same resource as its competitor, the proportion that is limited by the opposite resource is unable to compensate for the high degree of niche overlap experienced by the rest of the population (Fig. 7). As a result, overall population growth rates will be negative.

Since ITV’s effect on coexistence is the product of nonlinearity in the uptake function u(ϕ) (Eq. 4), it is useful to consider how different values of δ change the distribution of uptake rates. As ITV increases, the distribution of uptake rates in the population becomes increasingly bimodal (Fig. 8), consistent with the conclusion that continuous change in the trait ϕ mapped onto the sigmoid uptake function u(ϕ) results in individuals being spread unevenly across the uptake rate parameter space. The steepness of the nonlinearity in the function depends on the sha** parameter h (Eq. 4), which we assume is equal to 1 throughout our analyses. Larger amounts of ITV would be necessary for individuals to shift their limiting resource for values of h < 1. However, our results remain qualitatively the same.

Appendix 4. Other trait distributions

Although we assume a uniform distribution for our analyses to aid in mathematical tractability, our results are robust to other trait distributions. For example, if trait variation takes the form of a normal distribution such that ω is calculated as

$${\omega }_{j}=\left\{\begin{array}{c}1 \qquad\qquad\qquad\qquad {\mathrm{if}} \, \, {\phi }_{c}<\mu -3\sigma \\ \frac{\Phi \left({\phi }_{c}\right)-\Phi \left(-\mathrm{Tan}\frac{\pi }{2-\pi \left(\mu -3\sigma \right)}\right)}{\Phi \left(-\mathrm{Tan}\frac{\pi }{2-\pi \left(\mu +3\sigma \right)}\right)-\Phi \left(-\mathrm{Tan}\frac{\pi }{2-\pi \left(\mu -3\sigma \right)}\right)} \, {\mathrm{if}} \, \, \mu -3\sigma <{\phi }_{c}<\mu -3\sigma \\ 0 \qquad\qquad\qquad\qquad {\mathrm{if}} \, \, {\phi }_{c}>\mu +3\sigma \end{array}\right.$$

(21)

where Φ is the cumulative distribution function of a normal distribution with a mean μ and a standard deviation σ, and ϕ_c is the colimiting trait value, we show that variation in uptake rates still allows for positive invasion growth rates outside of the region where they are possible without variation (Fig. 9).

Appendix 5. Competition between asterionella formosa and cyclotella meneghiniana

We show that ITV in uptake rates can alter zero-net growth isoclines and consumption vectors such that coexistence is possible under resource conditions that would otherwise lead to competitive exclusion (Fig. 3 in the main text). Tilman (1977) performed competition experiments with the diatoms Asterionella formosa and Cyclotella meneghiniana under various resource conditions. Tilman (1982) further shows that the competitive outcomes of these experiments generally agree with the graphical predictions based on zero-net growth isoclines and consumption vectors parameterized for these species. However, two data points that fall within the graphical region where C. meneghiniana should win resulted in coexistence in the experiments. Using yield and death rate parameters from Tilman (1977) and R^* values from Tilman (1982) (Table 1), we calculated uptake rates of each resource for each species using

$${u}_{ij}=\frac{{d}_{j}}{{R}_{ij}^{*} {y}_{ij}}$$

(22)

where i,j = {1,2}. We then used resource supply values (S₁, S₂) extracted from Tilman (1982) using ImageJ (Schneider et al. 2012) to numerically solve our model for the outcomes of competition with and without ITV in the uptake rates of A. formosa. Without ITV, the outcomes are as predicted by the graphical model (Fig. 10). Intraspecific trait variation in the uptake rates of A. formosa alters the outcomes of competition at three data points, including the two that do not align with the prediction in the original data set (Fig. 10).✓

Table 1 Parameter values from Tilman (1977, 1982) used to numerically solve our model for competitive outcomes between A. formosa and C. meneghiniana with and without ITV in the uptake rates of A. formosa

Appendix 6. Other functional forms

In the main text, we consider what a trait map** function that would allow ITV to promote coexistence might look like. The sigmoid trait map** function (Eq. 4) used in our model is the critical component that allows ITV to contribute to stabilizing mechanisms and, thereby, promote competition. In this appendix, we consider other functional forms of trait map**.

Here we consider four alternatives (Table 2) to the trait map** function used in the main text (Eq. 4). We consider a sigmoid function that differs in detail from the sigmoid function used in the main text but produces a qualitatively similar function form. Importantly, it retains the two key features of (Eq. 4)—nonlinearity and piecewise shifts. We also consider linear, saturating, and exponentially increasing functions. The latter retain the feature of nonlinearity, though with only one kind of concavity, while the former has neither. As noted in the main text, sigmoid functions also provide a way of naturally constraining uptake preference to the plausible range (0,1) while still allowing the trait to be unbound in the range (− ∞, ∞). None of the other functions presented in this appendix has this feature and must have additional constraints added to trait space in order to maintain the plausible range for uptake preference.

We used each functional to calculate the total population growth rate across different trait range midpoints u_mid and at four different levels of variation δ (Fig. 11). The two sigmoid functions produced qualitatively identical results, demonstrating that the details of the function are not as important as retaining the features of nonlinearity and piecewise shifts (Fig. 11a and b). In particular, adding a relatively small amount of variation when either sigmoid function is used expands the range of u_mid at which the invasion growth rate is positive. However, relatively large amounts of variation reduce the total growth rate across all u_mid values, indicating that too much variation is detrimental to coexistence (see Appendix 3. Sufficient amounts of intraspecific variation). When a linear function is used to map traits onto uptake preference, adding variation does not change the range of u_mid across which the invasion growth rate is positive (Fig. 11c). The saturating and exponentially increasing functions (Fig. 11d and e, respectively) both decrease the range of u_mid values over which growth rates are positive.

Table 2 Summary of functional forms of the trait map** function considered in Appendix 6: Other functional forms