2D PIV/PTV–3D uRANS RSM Investigation on the Combined Effect of Iron Filings Filtering Techniques in a Backward Facing Step Flow

Abstract

The presence of suspended particles in liquid fluids is one of the main reasons for hydraulic system failure. Metallic impurities in particular increase the presence of toxic substances in wastewater; therefore, it is vital to study and address the behaviour of such particles in water flows. The current literature lacks studiees approaching the combined effect of different filtering techniques in backward-facing step (BFS) flows. This work aims to analyse the behaviour of iron filings within a BFS system, making use of a combined experimental 2D PIV/PTV–3D uRANS computational approach. Experiments and computations are performed at a Reynolds number $\mathrm{{Re}}_{H} = 3684.63$. Computational measurements are performed in several planes whereas the experimental campaign is focused on the dynamics of the particles through the streamwise middle plane. A half plane reattachment length of $X_{\rm{r}} = 11.73h$ is measured for an inlet flow turbulence intensity of about 1%. The trajectories of the iron filings under the influence of an external magnetic field are examined. A comparison with their paths under the influence of no attractive forces elucidates that the presence of an external magnetic field alters their elliptical trajectories. Moreover, a more forward magnet placement reveals greater trajectory disruptions.

Introduction

The behaviour of turbulent flows has been historically the subject of many studies concerning both natural and industrial engineering environments. For years, several efforts have been made by fluid dynamicists to measure and describe, in a global manner and with sufficiently high spatial and temporal resolution, the inherent complex three-dimensional flow structures that comprise almost any turbulent-flow field.¹ It was not until the invention of photography and introduction of the first commercial camera that the image capture process of flow visualization gained new dimensions.² Photographic recording techniques allowed the ability to record the observed flow patterns and complex unsteady flow structures.^2,3 The subsequent discovery of the well-known three-dimensional coherent structures that make up these turbulent flows promoted numerous research studies on the quantitative modeling of turbulent fluid flows. Along with the advances in imaging technologies, the latest improvements achieved in computer, laser and data acquisition technologies allowed the scientific community to go even further within these optical fluid techniques.¹

As a consequence, two large families of non-intrusive flow field investigation methods emerged: (1) the region-based methods or Eulerian methods, which rely on performing simultaneous measurements of the velocity field of an entire small region or interrogation window, and (2) the feature-based methods, for which single point velocity measurements are obtained by tracking the fluid flow particles individually. Particle Image Velocimetry (PIV) and Particle Tracking Velocimetry (PTV) stand as the most representative techniques among the former and latter flow field investigation methods, respectively. The general idea behind the PIV technique is to quantify the local flow motion by searching the box displacement that maximizes the cross-correlation product of box pixel light or colour intensities between two consecutive frames. In contrast, the PTV technique consists in detecting the presence of individual particles or even more complex shapes (corners, faces, etc.) and tracking them through consecutive frames, following a classical Lagrangian approach. It provides the trajectory of an object and its position along successive frames, which can be then mapped into a grid to obtain a dense velocity field.⁴ Both planar and volumetric PIV and PTV techniques have been proven suitable for obtaining velocity fields and analysing the spatial organization and temporal evolution of turbulent structures.^5,6 The potential of the combined use of these techniques in separated flows was demonstrated by Agarwal et al.,⁷ who employed time-resolved tomographic particle tracking methods to characterize the evolution of intermittent quasi-streamwise vortices (QSVs) developed between the Kelvin-Helmholtz vortices in a turbulent shear layer.

Separation and reattachment of turbulent flows can be widely observed in many industrial applications, e.g., in diffusers, combustion chambers, channels with sudden expansion, heat transfer systems and even aerodynamic flows around airfoils and buildings, among others.⁸ Turbulent flow separation and subsequent reattachment inherently imply the presence of dynamic recirculations where some of these turbulent structures arise. Among the flow geometries used for the studies of separated flows, the most frequently selected is the backward-facing step (BFS) because of its simplicity. BFS flows are important because flow separation drastically increases the momentum, heat and mass transfer downstream of the step.⁹ In such geometries the flow experiences an adverse pressure gradient that causes the boundary layer to separate from the solid surface. The flow subsequently reattaches downstream forming the so-called recirculation bubble. BFS flows exhibit complex flow mechanisms such as separation, formation, development and evaluation of turbulent eddies and the interaction between these vortices and the side wall.¹⁰ In particular, coherent vortex structures (CVS, Fig. 1) have been discovered to play an important role in the investigation of such flows.⁶ According to Scharnowski et al.,³⁰ correction that was later on revisited and alternatively incorporated to the transport equation of the specific dissipation rate $\omega$ as a modification of the $\omega$-destruction term by Eisfeld and Rumsey.¹⁷

Although the BFS flows present a fairly simple geometry and a predictable separation edge, the formed separated/reattaching shear layer intrinsically generates a complex multi-scale vortical flow structure that entails the shedding of vortices as large in size as the step height.³¹ As a consequence of its low-frequency unsteadiness, this shear layer undergoes a non-periodic, roughly two-dimensional, vertical motion that causes the impact point of the reattachment to shift upstream and downstream over a range of as much as two step heights.³² This reattaching im**ement point defines the so-called reattachment length, which is known to be the most important spatial scale for characterizing flow separation and subsequent reattachment.³² Based on Armaly et al.,³³ the BFS flows maintain a bidimensional behaviour downstream from the step in test benches featuring high aspect ratios (AR$\sim$10), regardless of the simulated Reynolds number. Moreover, the open literature reports several studies emphasizing the differences in the reattachment lengths of 2D and 3D time-averaged flows with spanwise dimensions of the order of the step height. Lim et al.³⁴ performed experiments on a backward-facing step flow of air through a rectangular duct with an aspect ratio (AR) of 3.3 and expansion ratio (ER) of 2 at a Reynolds number of 10,000. They found smaller reattachment lengths for the reported 3D cases than for the 2D ones. Velocities were measured with Laser-Doppler Velocimetry (LDV) and hot wire anemometry. Nie et al.³⁵ performed LDV measurements on air flowing over a BFS with an aspect ratio of 2 over a range of Reynolds numbers between 100–8000 with a especial focus on reversed flow regions. Piirto et al.⁸ performed PIV measurements on water flowing in a square duct with an expansion ratio ER of 1.25 and an AR of 4.7 for Reynolds numbers in a range between 12,000 and 55,000. Both studies confirmed that the reattachment lengths are smaller for 3D flows than for similar 2D flow configurations.

Fig. 1

Coherent vortex structures (CVS) in an instantaneous Backward-Facing Step flow: visualization (upper), simplified two-dimensional representation: FSR = free shear region; CR = corner region; RR = redevelo** region; R = mean reattachment point (lower simplified representation). Adapted from Ref. 36, under the terms of the Creative Commons CC BY 4.0 license.

Moreover, considerable efforts have been reported in the open literature with the aim of mitigating the effects of separated flows by means of: (1) active flow control via feedback mechanisms with optimization and (2) passive flow control methodologies, such as the ones investigated by Fidanis et al.³⁷ However, the inherent change in hydraulic diameter that these BFS geometries present does not always imply detrimental effects, making them appropriate to behave as suspended particle retention systems. The most conventional technique for particle collection is sedimentation, for which fluid velocity is reduced as a result of an increase in the pipeline’s hydraulic diameter until the falling and deposition of particles due to gravity forces.^38,39 Another common retention technique is to use a membrane as a filter to prevent particle circulation without affecting the fluid flow.⁴⁰

According to industry experts, the presence of suspended particles in fluids is one of the main causes of hydraulic system failure, this contamination being responsible for around 80% of the hydraulic machinery breakdowns (including pipes and hoses, fittings, pumps and valves).^41,42 These particles can have a great variety of sizes and natures; for this reason, it is imperative to apply the most affordable and efficient retention technique for each individual application. The in-depth study of the characteristics that influence the retention of particles and their understanding can lead to greater cleanliness of working fluids in critical environments as well as to an improvement in the efficiency of the facilities. Nowadays, particle separation technologies concerning hydraulic circuits of automotive and household appliances sectors (e.g. automobile painting, filtration of water from hot water pipes, refrigerators or washing machines to name a few) are closely linked to the know-how and knowledge gained by the companies develo** these products over the years. The generation of open access expertise on sizing the equipment necessary to retain and remove particles depending on its nature, size and distribution will allow designers to avoid prototy** and lengthy trial and error phases and will help them identify the most efficient designs in shorter time frames.

If the particles are made up of materials with ferromagnetic properties, a magnetic field can also be included within the test bench system, enhancing the influence of the gravity force.⁴⁰ This field can exert a force capable of manipulating the behaviour of these particles in a non-intrusive manner. Oberteuffer⁴³ defined the principle of operation of any magnetic separation device as the interaction between magnetic forces and competing gravitational, hydrodynamic and interparticle forces within the magnetic separator. A review of physical principles, devices and applications of this separation technique is also included in this report. A manipulation of suspended magnetic particles by an external magnetic field can be encountered in a wide variety of applications including magnetohydrodynamic pum** in microchannels, fluid mixing, stabilizing or agitating a magnetic particles containing fluid or supporting bioreactions in microchannels, among others.^44,45 Moreover, several studies have addressed the influence of external magnetic fields to efficiently control the dynamics of diverse flows by means of optical flow techniques.^46,47,48 Among others, by conducting a magneto-aerodynamics research, **aodong et al.⁴⁶ evidenced that under the influence of a magnetic field a strengthened vortex flow of air and a convection flow of the N2-air mixture could be observed by means of PIV techniques. By similar optical techniques, Takeuchi et al.⁴⁷ measured a reduction of the turbulence levels of an internal air flow under the influence of magnets located externally to the fluid domain. The lift-off and blowout properties of a methane/air co-flow diffusion flame were showed to improve under the influence of magnetic gradients by Gilard et al.⁴⁸ Besides, previous publications have also dealt with magnetically induced flows seeded with magnetic tracer particles.^49,50 Tan et al.⁴⁹ traced the trajectories of micro-swimmers affected by an external magnetic field using $\mu$PIV techniques whereas Lee and Choi⁵⁰ investigated the magnetic particle movement of a ferrofluid in a two-phase liquid-gas flow under an external magnetic field.

Current literature covers many independent studies dealing with backward-facing step flows, with separation methods of particles of different nature, with how fluid flows are themselves influenced by the presence of magnetic forces or with the behaviour of flows of ferromagnetic fluids or even fluids seeded with tracer particles of magnetic nature in many different scenarios (with and without the influence of a magnetic field). However, studies addressing the combined effect of different retention systems on impurities of a magnetic nature in BFS flows and analysing the dynamics of said impurities through non-intrusive optical systems are still deficient. Besides, and regarding magnetic separators within hydraulic circuits of automotive and household appliances sectors, many developments and patents have been granted in the last decades. However, the available open literature on this subject is limited to date, and considerable extensive and critical reviews on this topic need to be further developed. As a consequence, the present report presents a qualitative examination of the behaviour of magnetic particles within a BFS retention system. The dynamics of such particles under the influence of an external magnetic field are compared to the general trend of the same when no extra forces but for the gravity are accounted for. To perform reliable motion estimations, a coupled 2D PIV/PTV–3D CFD simulation approach has been selected. The general purpose of this approach is, in first instance, to correctly assess and evaluate the present BFS flow topology and, afterwards, to evaluate the dynamics of the magnetic filings as they pass through the streamwise middle plane.

As the present case of study presents an AR value of 7.5, a computational multi-plane inspection has been carried out with the aim of inspecting the complex 3D flow topology expected. Considering the complexity and three-dimensionality of the fluid case under consideration, the development of a high-fidelity 3D measurement technique to aid in better characterizing and resolving all fluid scales and particle motions seems both natural and necessary. However, and as stated by Chandramouli et al.,⁵¹ even state-of-the-art techniques capable of reproducing 3D flow fields such as tomographic PIV (Tomo-PIV⁵²) or 3D Lagrangian PTV techniques such as Shake-the-Box⁵³ still have limitations in their spatial-temporal extent that make them unable to capture spatially well-resolved observations. Furthermore, Wang et al.⁵⁴ presented a more extended compilation of the methods and efforts devoted to achieving high-resolution 3D flow measurements, from which it can be inferred that these kind of measurements still depend heavily on the provision of more precise hardware (e.g. to increase the number of photographic devices able to properly capture and process higher particle image densities or to employ high-speed cameras with higher image capturing rates) and they are much more cost-prohibitive in most industrial projects than planar PIV/PTV data acquisition. Consequently, huge progress has been made in recent years towards accurately interpolate and reconstruct 3D full-scale observations from 2D and 3D sparse partial datasets.^{51,55,56,57,58,59} Although out of the scope of the present work, the authors anticipate that future steps will be taken towards the development of a high-resolution 3D flow inference and reconstruction technique from sparse 2D measurements with the purpose of being able to integrate it with relative ease, both technically and economically, in the development of future industrial projects. The experimental 2D inspection is therefore also motivated by these aspects.

This work is organized as follows. The experimental facility and flow setup are presented in Sect. “Experimental Facility”. The strategies for grid generation along with the computational setup, mathematical modeling and numerical approach are discussed in Sect. Computational Approach. Section Results and Discussion examines the computational results of the case study, which include predictions for mean velocity profiles, turbulent kinetic energy and Reynolds stresses for different streamwise sections together with an estimation of the reattachment length of the BFS under specific flow conditions. Section Results and Discussion also covers a qualitative description of the dynamics of the magnetic filings and the influence of the BFS flow structures on them. Finally, some conclusions are drawn in Sect. Conclusions.

Experimental Facility

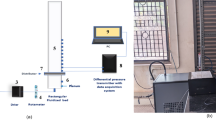
The experimental investigation was conducted using an in-house developed BFS test rig. Figure 2a depicts a schematic of the single-phase flow system employed. A vertical retention tank is mounted in which the flow coming from the pump is discharged. A conical section at the exit allows for a smooth transition between the upstream flow and the immediately subsequent optical fluid domain. The presence of a controller and a needle valve upstream of the retention tank enabled controling the working regime of the pump. The regulation of the flow through the installation was made by properly tuning a shut off ball valve located downstream of the fluid domain of interest. To feed the water flow with the particles under consideration, iron filings were manually injected into the vertical retention tank, thus achieving the final two-phase flow. The mixture of water and suspended magnetic particles passed through the rectangular channel and spilled into the accumulation tank. Mainly due to their size, it was intended that the seeded magnetic particles were not recirculated through the pump.

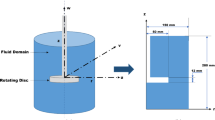
The channel geometry (Fig. 2b) is based on the fluid domain reported by Teso et al.,⁴⁰ who conducted numerical investigations on the dynamics of a single-phase water flow. Transparent methacrylate was chosen as manufacturing material as it permits optical access for both lightning system and cameras. As for the inlet and outlet regions, 150-mm methacrylate pipes with a hydraulic diameter of 16 mm were designed and embedded to each side of the rectangular channel. Both the inlet and outlet sections integrated female connections with captive nut and fitting to allow for external methacrylate pipe connections. The inside dimension of the channel was $60\times 60\times 400$ mm. As a result, the height of the duct before the sudden expansion can be said to be half of the inlet tube diameter, h = 8 mm, and after the sudden expansion H = 30 mm. The step height was then S = 22 mm, and the expansion ratio was $\mathrm{{ER}} = (S + h)/h = H/h = 3.75$. Moreover, for the three-dimensional predictions, the width of the channel was W = 60 mm, setting thus the aspect ratio W/h value to 7.5. For the definition of the characteristic length, different options are used in the literature concerning the definition of the Reynolds number.⁶⁰ The water mean flow rate through the inlet section was 0.03 L/s, which corresponds to an averaged mass flow velocity $U_{m1}$ = 0.149 m/s and to a Reynolds number based on the step height $\mathrm{{Re}}_{H}$ = $\rho$ $U_{m1}$S/$\mu$ = 3684.63.

Fig. 2

Experimental high frame rate LED–PIV setup. (a) Experimental in-house mounted BFS test rig. (b) Detailed drawing of the flow domain. (c) Schematic of the analysed BFS flow, where a descriptive sketch of the LED-based light sheet illumination system is displayed in a zoomed-in view. The streamwise, wall-normal and spanwise and directions are denoted by x, y and z, respectively.

A random composition of iron oxides was used as the base component of the inspected magnetic particles. The magnetic properties of this material lead to a magnetization of the particles when they are directly exposed to the magnetic field but, because of its lack of magnetic memory, the impurities become demagnetized as soon as the field is removed. The size of the examined particles ranges between 400 $\mu$m and 1.2 mm, since it is the most frequently encountered size range of this particular magnetic material among the industrial and domestic applications addressed. A consistent concentration of 100 g/15 L of suspended impurities in water was ensured for each experiment, which led to a non-uniform number of particles dropped. The magnet utilized in the experiments is a N40 magnetization-grade permanent magnet composed of neodymium. It is an axially magnetized cuboid-shaped magnet with dimensions of $46\times 30\times 10$ mm and the poles located on its large rectangular faces. Such a magnet was selected as it is representative of the largest magnet size that can be accommodated for the given applications. The nominal magnetic intensity of the field ranges between 12,600 and 12,900 Gauss.

A 2D PIV/PTV system was used to visualize the instantaneous velocity fields and the trajectories of the magnetic particles at the measurement plane (Fig. 2c). The lightning source consisted of an ultra-bright high-powered Light Emitting Diode (LED) Pulsing System (LPS) head emitting in a wavelength of 532 nm with 7 mJ maximum power per pulse. This has been proven to be a suitable device for planar and volume-resolving particle-based velocimetry techniques.⁶¹ The LED light was bundled into a light sheet by means of a fibre optic illumination system. The entry side of the fibre bundle is round (10 mm diameter) while the exit fibres at the opposite end are arranged along a straight line of approximately 38 mm height and 0.5 mm thickness. A light sheet can then be formed by projecting this line into the area under investigation using a short focal length cylindrical lens ($f = 25 mm$). The LED system was mounted onto a translation positioning system that allowed controling the projection of the light sheet to the region of interest. Hence, the measurement plane for the particle tracking analysis was located coincident with the geometric half of the investigated channel in the transversal direction, illuminating roughly 20 mm length in the longitudinal direction.

The particle images illuminated by the LED source were captured by an IDS UI-3370SE industrial camera with a $2048\times 2048$ pixels high-sensibility CMOS-Global Shutter square sensor. A Computar F 2.8 C-Mount Lens up to 6 MPx with a focal length of 35 mm was also used. The camera was mounted perpendicular to the channel onto a double translational guide positioning system that allowed the recording device to be exactly placed in both the longitudinal and traversal directions. Synchronization of the laser shootings and the camera exposures are controlled by an ILA 5150 GmbH v2 Synchronizer along with SigMa software. The overall repetition rate used to acquire the velocity field snapshots was 79 Hz and approximately 250 time-resolved snapshots were captured for each case. The data processing was carried out by an in-house MATLAB-based code developed within the Green Energy investigation group of the University of the Basque Country as an extension of the two-dimensional particle tracking velocimetry (2D-PTV) Part2Track open source code.⁶²

Computational Approach

Computational Domain and Grid Generation

Due to the complex three-dimensional flow structures expected, it was decided not to model the geometry as being symmetrical about the x–y plane. To model the wall-bounded flow conditions, a fluid domain similar to that reported in the previous section was chosen (Fig. 3a). The target mass flow rate was set constant at the inlet whereas the flow turbulent quantities (turbulent viscosity ratio of 10 and a turbulent intensity of 1%.) were specified by means of a Dirichlet condition at both the inlet and outlet boundaries. In line with the experiment, the BFS flow discharged into a quiescent atmosphere, and so a Dirichlet boundary condition at the outlet boundary was imposed whereby the pressure was assigned a value of zero (incompressible flows only care about relative pressure differences). The pressure was given a zero-gradient Neumann boundary condition at all other boundaries. At the walls, an adiabatic viscous no-slip condition was imposed by which the velocity in the vicinities of the solid boundaries approaches zero. Since the velocity is equal to zero, a blended wall function was employed which ensures that both turbulent and laminar kinetic energies are also reduced to zero at the walls.

Fig. 3

Computational fluid domain. (a) Boundary conditions. (b) 3D surface mesh and detail of a cutaway view of the inner grid (c).

The BFS geometry was meshed using a fully structured multiblocked approach with the resultant mesh stretched along the wall normal direction and designed for full boundary-layer resolution. A $y^+ < 1$ condition was ensured across all of the solid surfaces inspected. The grid resolution in the axial direction was such that the aspect ratio of all the cells around the computational mesh was within acceptable limits (maximum value around AR = 20). The mesh refinement was achieved through a uniform scaling of mesh nodes in the z direction, whereas different mesh laws were employed for the block edges coincident with the x and y directions. The selected mesh featured a total of 240 mesh nodes around the circumference of each cylindrical surface. One hundred seventy nodes were distributed across the axial length of both the inlet and outlet cylindrical ducts, where a stretching along the wall parallel direction was set such that the elements in the vicinities of the inlet and outlet interfaces present AR values near 1. Similarly, 400 nodes were imposed for the axial length of the core rectangular duct, with a similar longitudinal stretching seeking AR$\sim$1 values near the front and rear solid walls. As for the vertical y direction, a total of 60 nodes were imposed by means of a bi-geometric mesh law with a growth ratio of 1.3 for all edges. A close-up of the surface mesh of the model alongside some computational grid details is shown in Fig. 3b and c. Hence, the optimum density of the grid was determined by selecting the mesh for which a further increase in element density led to negligible differences in results. The final mesh element count was 15.1 million.

Governing Equations

Reynolds Stress Transport (RST) models, also known as second-moment closure models, directly calculate the components of the Reynolds stress tensor by solving their governing transport equations.

RST models approximate the stress tensor as:

$$\begin{aligned} {{\textbf {T}}_\mathrm{{RANS}}} = -\rho {\textbf {R}} + \frac{2}{3}tr{\textbf {(R)}}{} {\textbf {I}} \end{aligned}$$

(1)

R is the Reynolds stress tensor defined as:

$$\begin{aligned} {\textbf {R}} = \begin{pmatrix} \overline{{u'u'}} &{} \overline{{u'v'}} &{} \overline{{u'w'}}\\ \overline{{v'u'}} &{} \overline{{v'v'}} &{} \overline{{v'w'}}\\ \overline{{w'u'}} &{} \overline{{w'v'}} &{} \overline{{w'w'}}\\ \end{pmatrix} \end{aligned}$$

(2)

RST models have the potential to predict complex flows more accurately than eddy viscosity models because the transport equations for the Reynolds stresses naturally account for the effects of turbulence anisotropy, streamline curvature, swirl rotation and high strain rates. Seven equations must be solved (as opposed to the two equations of a $k-\epsilon$ or a $k-\omega$ model): six equations for the Reynolds stresses (symmetric tensor) and one equation for the isotropic turbulent dissipation $\epsilon$.

The generic transport equations for the Reynolds stress tensor R and the isotropic turbulent dissipation $\epsilon$ are:

$$\begin{aligned} \frac{\partial }{\partial t}(\rho {\textbf {R}}) + {\nabla }\cdot (\rho {\textbf {R}} \overline{{\textbf {u}}})= & {} {\nabla }\cdot {\textbf {D}} + {\textbf {P}} + {\textbf {G}} - \frac{2}{3}{} {\textbf {I}}{\gamma _{M}} \\ &+ \underline{\phi } -\rho \underline{\epsilon } + {{\textbf {S}}_{\textbf {R}}} \end{aligned}$$

(3)

$$ \begin{aligned} \frac{\partial }{{\partial t}}(\rho \epsilon ) + \nabla \cdot (\rho \epsilon \overline{{\mathbf{u}}} ) = & \nabla \cdot \left[ {\left( {\mu + \frac{{\mu _{t} }}{{\sigma _{\epsilon } }}} \right)\nabla \epsilon } \right] + \frac{1}{{T_{e} }}C_{{\epsilon 1}} P_{\epsilon } \\ & - C_{{\epsilon 2}} f_{2} \rho \left( {\frac{\epsilon }{{T_{e} }} - \frac{{\epsilon _{0} }}{{T_{0} }}} \right) + S_{\epsilon } \\ \end{aligned} $$

(4)

$$\begin{aligned} k = \frac{1}{2}tr{{\textbf {(R)}}}, \quad T_{e}= & {} \frac{k}{\epsilon }, \quad T_{0} = \mathrm{{max}}\left({\frac{k_0}{\epsilon _0},{C_t}\sqrt{\frac{\nu }{\epsilon _0}}}\right) \end{aligned}$$

(5)

$$\begin{aligned} {\sigma _e} = 1.3, \quad {C_{\epsilon 1}}= & {} 1.44, \quad {C_{\epsilon 2}} = 1.92, \quad {f_2} = 1 \end{aligned}$$

(6)

In the preceding equations, tr(R) refers the trace of the Reynolds stress tensor, I denotes the identity tensor, $\overline{{\textbf {u}}}$ denotes the Reynolds averaged mean velocity, D denotes the Reynolds Stress Diffusion, P denotes the Turbulent Production, G denotes the Buoyancy Production, $\gamma _{M}$ denotes the Dilatation Dissipation, $\underline{\phi }$ denotes the pressure strain tensor, $\underline{\epsilon }$ denotes the turbulent dissipation rate tensor, $\mu$ denotes the dynamic viscosity, $\mu _{t}$ denotes the turbulent viscosity, $\sigma _{\epsilon }$, ${C_{\epsilon 1}}$ and ${C_{\epsilon 2}}$ are model coefficients, ${P_{\epsilon 1}}$ denotes the turbulent dissipation production term, $f_2$ denotes a model dependent dam** function, $T_{e}$ denotes the large-eddy time scale, $\epsilon _{0}$ denotes the ambient turbulent dissipation value, $T_{0}$ denotes a specific time scale based on $k_{0}$, $\epsilon _{0}$ and a model coefficient $C_{t}$ and ${{\textbf {S}}_{\textbf {R}}}$ and ${{\textbf {S}}_\epsilon }$ denote the user-specified source terms.

To model the pressure-strain term, a low Reynolds number variant of the Quadratic Pressure-Strain model implemented in Simcenter STAR-CCM+ is selected, i.e. the Elliptic Blending RST model of Manceau and Hanjalić,⁶³ revised a posteriori by Lardeau and Manceau.⁶⁴ This model contains specific treatments for all-$y^+$ meshes, whereas the simple Quadratic Pressure-Strain model can only be used with a high-$y^+$ wall treatment (that is, using wall functions) without resolving the viscous-affected near-wall region. Moreover, this model is based on a in homogeneous near-wall formulation of the quasi-linear quadratic pressure strain term. The blending function is used to blend the viscous sub-layer with the log-layer formulation of the pressure-strain term. This approach requires the solution of an elliptic equation for the blending parameter $\alpha$.

The pressure-strain model of Manceau and Hanjalić is based on a blending of near-wall and quadratic pressure strain models for the pressure-strain and dissipation:

$$\begin{aligned} \underline{\phi } - \underline{\epsilon } = (1-{\alpha }^3) (\underline{\phi }^w-\underline{\epsilon }^w) + {\alpha }^3(\underline{\phi }^h-\underline{\epsilon }^h) \end{aligned}$$

(7)

• In the outer region, the quasi-linear version of the Sarkar, Speziale and Gatski model²⁰ is used:

  $$ \begin{aligned} \underline{\phi } ^{h} = & - \left[ {C_{1} \rho \epsilon + C_{{1s}} {\text{tr}}({\mathbf{P}} + {\mathbf{G}})} \right]{\mathbf{A}}\\ & + \left( {C_{3} - C_{{3s}} \sqrt {{\mathbf{A}}:{\mathbf{A}}} } \right)\rho k{\mathbf{S}} \\ & + C_{4} \rho k\left( {{\mathbf{S}} \cdot {\mathbf{A}} + {\mathbf{A}} \cdot {\mathbf{S}} - \frac{2}{3}{\mathbf{A}}:{\mathbf{SI}}} \right)\\ & + C_{4} \rho k\left( {{\mathbf{W}} \cdot {\mathbf{A}} + {\mathbf{A}} \cdot {\mathbf{W}}^{T} } \right) \\ \end{aligned} $$

  (8)

• In the near-wall layer:

  $$\begin{aligned} \underline{{\phi }}^w = -5\rho \frac{\epsilon }{k} \left[{{\textbf {R}}\cdot {\textbf {N}} + {\textbf {N}}\cdot {\textbf {R}} - \frac{1}{2}{} {\textbf {R:N}}({\textbf {N+I}})} \right] \end{aligned}$$

  (9)

• For the dissipation rate, the formulations for the near-wall layer and the outer region are:

  $$\begin{aligned} \begin{aligned} \underline{{\epsilon }}^w = {\textbf {R}}\frac{\epsilon }{k}, \quad \quad \underline{{\epsilon }}^h = \frac{2}{3}{\epsilon }{} {\textbf {I}} \end{aligned} \end{aligned}$$

  (10)

• The blending parameter $\alpha$ is the solution of the elliptic equation:

  $$\begin{aligned} {\alpha } - {L}^2{\nabla }^2{\alpha } = 1 \end{aligned}$$

  (11)

• where:

  $$ \begin{aligned} {\mathbf{P}} = & - \rho \left( {{\mathbf{R}} \cdot \nabla \overline{{\mathbf{u}}} ^{T} + \nabla \overline{{\mathbf{u}}} \cdot {\mathbf{R}}^{T} } \right) \\ = & - \rho \left( {{\mathbf{R}} \cdot \nabla \overline{{\mathbf{u}}} ^{T} + \overline{{\nabla {\mathbf{u}}}} \cdot {\mathbf{R}}} \right) \\ \end{aligned} $$

  (12)
  $$\begin{aligned} {\textbf {G}}= & {} 0, \quad {\textbf {N}} = {\textbf {n}}\times {\textbf {n}} = \frac{{\nabla }\alpha }{\sqrt{{\nabla }\alpha \cdot {\nabla }\alpha }}\end{aligned}$$

  (13)
  $$ \begin{gathered} {\mathbf{A}} = \frac{{\mathbf{R}}}{k} - \frac{2}{3}{\mathbf{I}},\quad {\mathbf{S}} = \frac{1}{2}\left( {\nabla \overline{{\mathbf{u}}} + \nabla \overline{{\mathbf{u}}} ^{T} } \right), \hfill \\ {\mathbf{W}} = \frac{1}{2}\left( {\nabla \overline{{\mathbf{u}}} - \nabla \overline{{\mathbf{u}}} ^{T} } \right) \hfill \\ \end{gathered} $$

  (14)
  $$ \begin{gathered} \mu _{t} = \rho C_{\mu } kT,\quad T = \max \left( {\frac{k}{\epsilon },C_{t} \sqrt {\frac{\nu }{\epsilon }} } \right), \hfill \\ L = C_{l} \max \left( {\frac{{k^{{\frac{3}{2}}} }}{\epsilon },C_{\eta } \frac{{\nu ^{{\frac{3}{4}}} }}{{\epsilon ^{{\frac{1}{4}}} }}} \right) \hfill \\ \end{gathered} $$

  (15)

• An additional source term is also added to the transport equation for $\epsilon$, in order to reproduce the correct near-wall behaviour of the dissipation rate:

  $$\begin{aligned} E = {A_1}\nu ({\textbf {R:N}})\frac{k}{\epsilon }(1-\alpha ^3)[{\nabla }(\Vert {\textbf {S:n}}\Vert {\textbf {n}})]^2 \end{aligned}$$

  (16)

• with the following model coefficients:

  $$ \begin{gathered} A_{1} = 0.115,\quad C_{1} = 1.7,\quad C_{{1s}} = 0.9, \hfill \\ C_{3} = 0.8,\quad C_{{3s}} = 0.65,\quad C_{4} = 0.625, \hfill \\ C_{5} = 0.2,\quad C_{l} = 0.133,\quad C_{t} = 6,\quad C_{\eta } = 80, \hfill \\ \end{gathered} $$

  (17)

Computational Method

Numerical simulations were performed using the finite volume commercial CFD software Simcenter STAR-CCM+ version 15.06.008-R8 double precision. The incompressible unsteady flow field was computed using an unsteady Reynolds-Averaged Navier-Stokes (uRANS) approach with an implicit second-order discretization scheme for the temporal terms. A segregated pressure-based solver with the SIMPLE algorithm was selected for the pressure-velocity coupling, along with the use of the AMG Linear Solver for both continuity and momentum equations. The flow-field gradients were computed with a Hybrid Gauss-Least Squares (LSQ) method and a second-order upwind scheme was used for the convective terms. The dynamic viscosity was assumed to be constant. The converge criterion was based on a simple calculation of the convective time of a particle inside the fluid domain. Consequently, the simulation was run for a physical time of 5 s and a reduction of at least three orders of magnitude was achieved for every solved equation.

Results and Discussion

The results presented within this work can be broadly split into two sections: (1) a discussion on the flow topology addressed by the outlined numerical approaches and (2) an exposition of the combined effect of the key BFS flow mechanisms and of an external magnetic field on the behaviour of some iron filings. Section Computational Results discusses the salient flow mechanisms of a confined 3D BFS flow, where the most relevant features of the time-averaged vortices that appear downstream of the step and of the reattachment curve are identified. Lastly, Sect. Experimental Results describes and qualitatively compares the behaviour of some iron filings with and without the influence of an external magnetic field for two different magnet configurations.

Computational Results

Figure 4 shows the 2D fields measured in the spanwise z = 0 half plane. The streamwise velocity field is presented in first instance along with the steady-state streamline pattern of the recirculation region. Results show an expected shape of the reattachment curve in which the large vortex spans down several step heights downstream of the expansion section to the dimensionless length of x$\sim$11.5 ($\sim$25 cm behind the step) and presents a clearly visible split shape. A small vortex can be seen in the bottom left corner of any of the shown contours (x$\sim$0 and y$\sim$ − 1h, coincident with CR, Fig. 1) just downstream of the step. This secondary backflow small vortex presents a counter-clockwise rotation direction, opposite to the main one, which gives rise to the formation of a stagnant zone in this spatial region as a consequence of a relatively low rotational velocity.⁶⁵ Moreover, Fig. 4 evidences that the time-averaged streamlines follow parallel directions in the first half of the separated shear layer (nearly until x$\sim$5h, just above the free shear region, FSR, Fig 1) while they begin to curl and fold downwards, closer to the wall, as the shear layer evolves into its second half.^31,36 Thus, and according to Dejoan et al.,⁶⁶ a shear-layer instability and a shedding-type instability are involved in the promotion of the reattachment effect, corresponding the former to the rolling process of the shear layer and the latter to the interaction between the shear layer and the bottom wall.

Fig. 4

Time-averaged velocity field for z = 0 plane: contours of (a) streamwise velocity u, (b) wall-normal velocity v, (c) $u_{\rm{RMS}}$, (d) $v_{\rm{RMS}}$ and (e) Reynolds stress $\overline{{u'v'}}$, along with steady streamline pattern.

Although a thorough examination of the instantaneous spatial and temporal evolution of the CVS is out of the scope of this research, it is worth pointing that the growth and subsequent development of the spanwise coherent vortex structures that arise in the recirculation zone are known to be governed and explained by the Kelvin-Helmholtz instability.^31,36 The time-averaged evolution of these CVSs gives rise to the streamline pattern shown in Figs. 4 and 5a and, consequently, it explains the two main vortical structures encountered in the develo** and shedding stages, respectively (Fig. 1).

Figure 5b shows the steady-state streamline pattern in an y$\sim$0.3 plane along with the streamwise wall shear stress contour over the y = 0 bottom plane. For simplicity, only negative values of the wall shear stress contour have been represented. A leftwards shift of the core of the main vortical structure of the develo** region (Fig. 1) can be clearly seen, which leads to a weak flow asymmetry and evidences the clear 3D nature of the flow as a consequence of a moderate AR value. A more exhaustive inspection reveals a great influence of the lateral walls in the BFS flow topology. The streamlines are curved in the spanwise direction once the flow approaches the end of the recirculation zone and a noticeable backflow takes place near the lateral walls. This implies both a strong convergence of the streamlines and the appearance of the higher absolute values of the wall shear stresses in the vicinities of these regions (z$\sim$h and z$\sim$ − h, Fig. 5b). Some of these streamlines are deflected afterwards in the spanwise direction towards the z = 0 half plane and subsequently divided, creating: (1) a strong backflow that forms the main vortical structure of the recirculation zone (negative values of the wall shear stresses contour, between x/h$\sim$1 and x/h$\sim$2.5) and (2) a mild forward flow (null values of the wall shear stresses contour between x/h$\sim$2.5 and x/h$\sim$4.5) that forms an “S” shape in the vertical direction for the flow to accommodate to the direction and velocity of the streamlines near the shear layer (Figs. 4 and 5a, y/h$\sim$0). Furthermore, and opposite to a planar mixing layer, the free shear layer of a BFS flow experiences an adverse pressure gradient that compels it to curve and forces it to be finite. Hence, the strong interaction between the shear layer and the recirculation region gives rise to the formation of a mild reverse flow near the point where the mean dividing streamline approaches the BFS bottom wall (end of the reattachment zone, Figs. 4 and 5a). This backflow entails the vortical structure located in the shedding zone (x$\sim$10h) and leads to the tailoring of additional three-dimensional coherent structures in the latter half of the shear layer.³¹ Moreover, according to Eisfeld and Rumsey,¹⁷ the length-scale correction included in the employed RSM turbulence model suppresses the back-bending of the streamlines near the reattachment point, providing a much more smoother shape at this point (x$\sim$11.5h).

Fig. 5

Time-averaged streamwise velocity contour for z = 0 plane (a) and time-averaged wall shear stress contour for y = 0 plane (b). Steady streamline pattern of image (b) corresponds to y = 0.3 plane.

At z = 0 middle plane, the reattachment locus is defined by either the point where the mean dividing streamline approaches the y = 0 plane or the location where the velocity profile near the wall changes from positive to negative and the wall-shear stress value becomes zero.⁴⁰ However, according to Biswas et al.,⁶⁰ the measured reattachment lengths at the mid-plane do not match the predictions of the two-dimensional simulations. This comes as a consequence of the impact of the inherent three-dimensional effects on the flow topology of the mid-plane of the channel. Indeed, several studies^8,9,35,65 reported that due to the 3D nature of the flow, the reattachment point is actually not a point but a curve on the bottom plane of the BFS geometry. Furthermore, Piirto et al.,⁸ among others, reported 0.5–1.5h smaller half plane reattachment distances for 3D cases than for the corresponding 2D flow cases.

Consequently, whereas the reattachment length of the half plane can be extracted from measurements in the middle plane itself, the real shape of the reattachment curve should be obtained from measurements taken from a different perspective (const. y coordinate plane, y = 0, Fig. 5b). Figure 5b provides a way of checking the consistency of the aforementioned statements. Here, the length and shape of the reattachment curve can be observed through the y$\sim$0.3 plane streamline pattern representation. The results show good agreement with the topologies of the reattachment curves reported by Bogatko et al. and Zajec et al.,^9,65 where the maximum length of the recirculation zone was encountered in the vicinities of the central section. Moreover, and similarly to what Fig. 5b showcases, this length of the recirculation zone was shown to decrease when the distance from the side walls is reduced.^9,65 Again, the results reveal a rightwards shift of the core of the reattachment vortical structure (x$\sim$ 10.5h) as a consequence of the BFS flow three-dimensionality. In addition, the core region of the recirculation locus presents a slight diagonal line shape, which implies that the maximum length of the recirculation zone is not located at the exact centre of the BFS geometry (z = 0 plane), but mildly shifted leftwards. Additionally, and in concordance with several previous studies, the reattachment length is known to be longer for transitional flow regimes when compared to their homologous turbulent regimes,^35,36 which somehow justifies a bigger obtained reattachment length, $X_{\rm{r}}=11.73h$, compared to the $X_{\rm{r}}=7.82h$ result reproted by Teso et al.⁴⁰ The size of the separated zone has been demostrated to depend not only on the step height but also on the degree of turbulence of the upstream flow.⁹ In fact, a decrease in the length of the separation region as a result of an increase in the degree of turbulence of the upstream flow has been proven.⁹ Hence, it is worth noting that the exhibited results correspond to a turbulence intensity of the inlet flow of about 1%.

Nevertheless, a more accurate and detailed analysis of the results extracted from numerical computations requires the inspection of the profiles of some measured quantities at various line segments. Eight line segments have been designated for this purpose, all of them contained in the z = 0 plane, with their positions indicated in the figures below. For the ease of comparison, all the profiles have been appropriately normalized with the reference velocity, $U_\mathrm{{ref}}$, and scaled accordingly. Streamwise velocity measurements are shown in Fig. 6. The data show that near the wall, an early reattachment takes place, evidencing the appearance of a vortical structure near the $x/H=6$ line segment. Profiles of $x/H=2$ and $x/H=4$ present negative streamwise velocity values as they are examined slightly away from the wall, which are reversed for the $x/H=6$ profile (line segment located just after the core of the develo** vortex region). Far away from the wall, and near the centre line of the BSF geometry, high velocity values and step gradients can be observed which match with the principle of the shear layer development. From 3 step heights on, the step gradients decay as the shear layer evolves in its second half and the flow streamlines start to bend downwards closer to the wall. Also evident from the measurements is the influence of the reattachment region on the flow upstream of it. $x/H=10$ line segment profile evidences the appearance of a backflow near the wall due to negative streamwise velocity values, which is the prelude of the shedding vortex region (contours in Fig. 6). This vortex is even more noticeable in the profile of $x/H=11$ segment. Moreover, it is not until downstream of the half plane reattachment point ($x/H=12$) that the measured velocity profiles show more constant values and a constant step gradient. This shows that the reattachment point is located somewhere between $x/H=11$ and $x/H=12$ line segments, as stated in the previous subsection.

Fig. 6

Streamwise mean velocity profiles for eight different line segments in z = 0 plane.

The profiles of the turbulent kinetic energy for the same eight segments behind the step are presented in Fig. 7. As stated by Bogatko et al.⁶⁵ the largest values of TKE are located in the region of the mixing shear layer whereas their minimum values can be generally encountered in the region of the secondary vortex. A well-known flow turbulization effect similar to that found in any separate flow occurs, as the presence of a step and a sudden expansion lead to the formation of additional vortices. Consequently, the turbulent kinetic energy experiences a sudden increase soon after the step, towards the centre of the BFS geometry, the largest values of TKE becoming the ones located in the vicinities of the central section. Hence, the higher values of the TKE profiles correspond with the principle of the shear layer development (see profiles of $x/H=2$, $x/H=4$ and $x/H=6$, near the centre line). Additionally, a relatively constant increase can be inferred from the profiles until the $x/H=10$ line segment is reached. Values of normalized TKE are relatively high up to $x/H=10$, a point after which the maximum values of kinetic energy start to decay and the profiles start to flatten. These results show quite good qualitative agreement with the data reported by Arya et al.⁶⁷

Fig. 7

Turbulent kinetic energy profiles for eight different line segments in z = 0 plane.

Figure 8 shows the profiles of the the measured shear stresses for the same eight segments behind the step. Information about the six second-order statistics that comprise the Reynolds stress tensor is provided. The behaviour of the three principal shear stresses ($\overline{{u'u'}}$, $\overline{{v'v'}}$ and $\overline{{w'w'}}$) resembles the performance of the TKE profiles. The largest values of these second-order correlations are located in the region of the mixing shear layer and, at the same time, they experience an abrupt increase just downstream of the step where the velocity differences are maximum. Moreover, they experience a steady increment throughout several step heights up to the $x/H=10$ line segment. After this point, the maximum values approach lower limit values and the profiles show a more flattened appearance. All these features bring these results into harmony with the outcomes published by Seegmiller et al.,⁶⁸ who also attributed these characteristics to a common demeanour of a free shear layer. Notably, the values of the principal shear stresses are low in the central region right after the step as initially this represents a low-turbulence region (parallel streamlines in a shear layer yet to develop). The same overall behaviour can be reported for the $\overline{{u'v'}}$ shear stress component as it exhibits the same general features but it is opposite in sign. As reported by Le et al.⁶⁹ the fluctuations in the transitional case are significantly more intense when compared to a fully turbulent BFS flow. This has also been observed in other transitional flows entailing free shear layers.⁷⁰ A maximum non-dimensional shear stress of $\overline{{u'u'}} = 0.0528$ has been obtained.

As the present case cannot be considered as a 2D BFS flow case, velocity fluctuations in all three different directions behave as chaotic fluctuations that are not random nor independent. As a consequence, neither of the values of the second moments of the velocity components containing the spanwise direction are equal to zero. However, note that the additional shear stresses induced as a result of the velocity fluctuations associated to this spanwise direction are one and two orders of magnitude lower compared to the $\overline{{u'v'}}$ and $\overline{{u'u'}}$, $\overline{{v'v'}}$ and $\overline{{w'w'}}$ velocity fluctuations, respectively (values of $\overline{{u'w'}}$ and $\overline{{v'w'}}$ are of the order of $10^{-4}$). In the present investigation the maximum normalized second moment of different fluctuations is $\overline{{u'v'}} = -0.0138$.

Fig. 8

Profiles of the six components of the Reynolds shear stress tensor for eight different line segments in z = 0 plane.

Experimental Results

For the present case study, it was assumed that the particle dispersion was sufficiently high and particle size sufficiently small that particle-particle interactions could be neglected and that the influence of the particles themselves on the development of the fluid flow field was marginal. The hydrodynamic transport problem is therefore decoupled from the particle transport problem, but not vice versa. Under these hypotheses, the physical mechanisms that address the behaviour of the magnetic filings are the influence of external surface and volume forces (gravity, magnetic field) along with diffusion and convection transport processes. Moreover, the impact of the former transport process has been considered negligible because of its low relative influence on the forced convective flow under review.

Teso et al.⁴⁰ conducted a numerical investigation on the reattachment length of a slightly different BFS geometry, based on analysing the variations of the average streamwise velocity near the walls. Four longitudinal lines of the same length as the channel were employed to report the velocity variations all along the centre line of the external planes of the box whereas several streamwise and spanwise planes were also measured to assess their velocity profiles. The results extracted from the conducted high-fidelity LES WALE turbulent approach revealed a reattachment length $X_{\rm{r}}=7.82h$ of about 0.18 m for $U_\mathrm{{ref}}= 1 m/s$ and $\mathrm{{Re}}_{h}$ $\sim$ 25,800 (based on $U_\mathrm{{ref}}$) flow conditions. As neither the same exact BFS geometry nor similar flow conditions were employed for the caption of the particle images, the reported reattachment length by Teso et al.⁴⁰ could not be considered as a limitation of the extension of the main CV flow structures. However, and based on previous test campaigns, the reattachment length of the conducted CFD simulation was selected as a limitation of the experimental study in the streamwise direction. Hence, to assess the performance of the metallic filings up to and before the reattachment point, the employed optical instrumentation was tuned according to past experiences. Thus, various sets of snapshots were taken, with and without the influence of an external magnetic field, capturing from $X_{\rm{r}}=1 \mathrm{{cm}}$ to $X_{\rm{r}}=16 \mathrm{{cm}}$ in the streamwise direction.

Fig. 9

Time-resolved image sequence acquired at 79 Hz of the elliptical trajectory of a magnetic particle within the Coherent Vortex Structures (CVS) of a BFS flow.

Figure 9 depicts the time evolution of some iron filings in default of an external magnetic field over a sequence of 12 time steps. By careful inspection, an aggregation of particles can be intuited at around $X_{\rm{r}}=4$–6 cm, a region which is coincident with the first point of the middle plane (z = 0) where the streamwise velocity cancels out and is reversed afterwards (see velocity profiles before and after $x/H=6$, Fig. 6). Note that the mentioned particle cluster around this position can be observed from the beginning of the image sequence (image 1, Fig. 9). This is explained by the fact that the moment of capturing the sequence of images represented in Fig. 9 is posterior to the beginning of the conducted experiment. In addition, it can be inferred that the particle trajectories exhibit an elliptical shape, which is fully consistent with the topology of the large-scale vortex structures reported in the previous subsection. The exact shape of some of these elliptical trajectories can be better intuited in Fig. 10a. For simplicity and visual clarity, only the behaviour of the particles that were tracked along a sequence of 50 time steps has been represented. Although few particle locations were found by the code in the 50 time steps investigated, a sequence of said length was considered to accurately represent the general behaviour of the filings for this particular configuration. The data of the remaining points of each of the plotted trajectories could not be assigned particle tracks or be filtered out due to insufficient information.

The results reported in Fig. 10a show that the vast majority of the iron filings precipitated within the first $X_{\rm{r}}=12\,{\rm{cm}}$ of the channel’s bottom face. The filtered particles should presumably start to rotate, depending on their size, mass and orientation, around the cores of the different large-scale vortical flow features until being deposited. However, particles that are deposited within the first $X_{\rm{r}}=12 \mathrm{{cm}}$ tend to precipitate notwithstanding the flow directionality shown in the previous subsection (Sect. 4.1), descending vertically without being driven by the convective recirculation generated in that region. Furthermore, particles that moved backwards across the bottom face of the BFS geometry were also detected, arguably because of the influence of the backflow generated by the central vortical structure (Fig. 10a, lower horizontal leftwards trajectories, between $X_{\rm{r}}$ = 7 and 11 cm). A nearly similar behaviour can be reported for some filings that did not precipitate within the first $X_{\rm{r}}=12 \mathrm{{cm}}$ but they did it before reaching a longitudinal distance of $X_{\rm{r}}=16 \, \mathrm{{cm}}$, except for the rearward movements. This suggests that the flow momentum was not sufficient for the generated vortical structures to be capable themselves of entraining all the iron filings under consideration. This last scenario has not been represented in Fig. 10a because of of redundancy. The remaining untrapped particles were driven by the main flow by means of convective transport processes and buoyancy effects (Fig. 10a, upper nearly horizontal rightwards trajectory).

Fig. 10

The x-y planar view of different particle tracks for the (a) no magnet case, (b) magnet placed at $X_{\rm{r}} = 10$ cm case and (c) magnet placed at $X_{\rm{r}} = 2~$ cm case. Time-resolved sequences of 50 time steps each. The streamlines of the different magnetic particles are coloured by their instantaneous velocity, measured in m/s (Color figure online).

To assess and investigate the effect of a magnetic field on the particle trajectories, the magnet reported in Sect. 2 was installed outside the BFS geometry by sticking it together with the outer bottom face of the water domain. Two different configurations of the magnet were evaluated, positioning the magnet in the middle of the recirculation region ($X_{\rm{r}}=10 \mathrm{{cm}}$) and in the vicinities of the step ($X_{\rm{r}}=2~\mathrm{{cm}}$).

When the magnet was placed within the separated flow region, subtle differences arise concerning particle trends (Fig. 11). Filings that were inherently going to be deposited roughly within the first $X_{\rm{r}}=7 \mathrm{{cm}}$ (mainly due to the gravity force and, to a much lesser extent, to the vortical flow nature of this region) did not see their elliptical trajectories altered. On the contrary, particles that by proximity were also subjected to the effect of the external magnetic field experimented a change in their trajectories, redirecting their paths towards the magnet and accelerating their deposition.

Fig. 11

Time-resolved image sequence acquired at 79 Hz of the trajectories of magnetic iron filings within the Coherent Vortex Structures (CVS) of a BFS flow, in the presence of a magnet located at $X_{\rm{r}} = 10\;$ cm.

These effects can be better understood by looking at Fig. 10b, where the paths of the particles that were tracked along a sequence of 50 time steps have been represented. Again, such a sequence length was considered to faithfully reflect almost all possible scenarios concerning the behaviour of the particles for this particular configuration. The missed data points could not be assigned particle tracks or got filtered out due to insufficient information. For this particular case, filings moving backwards across the bottom face of the BFS geometry were not detected. However, the few particles that precipitated roughly within the range of $X_{\rm{r}}$ = 7–9 cm were subjected to an extension of their trajectories once deposited, being dragged onwards and horizontally across the bottom face of the fluid domain until being accumulated together with the particles attracted by the effect of the magnet (Fig. 10b, light blue trajectories ending nearly at $X_{\rm{r}}$ = 8–9 cm). Both latter effects are undoubtedly a consequence of the strong influence of the external magnetic field in this particular region. Nevertheless, and despite the presence of the magnet, not all the particles that travelled along with the bulk flow were attracted by the magnetic force, resulting again in some untrapped particles, presumably due to a stronger contribution of the convective forces on their dynamics (Fig. 10b, upper nearly horizontal rightwards trajectories).

A forward movement of the magnet towards the step ($X_{\rm{r}}=2~\mathrm{{cm}}$) clearly evidences a totally different trend regarding magnetic filing motions (Fig. 12). A considerably higher number of particles saw their theoretical presumed trajectories disrupted, being polarized and accelerating their deposition towards the magnet position by a sudden directional change. A great number of particles were hence trapped within the first $X_{\rm{r}}$ = 2–4 cm of the channel geometry. Even though the position of the magnet matched the reported placement of the secondary vortex anchored to the corner region of the step (x $\sim$ 0 and y$\sim$ −1h in Figs. 4 and 5a), not a single magnetic filing was detected describing any of the streamlines that shaped this curled flow feature. This effect may arguably be due to the stronger contribution of the attractive forces against convective effects.

Fig. 12

Time-resolved image sequence acquired at 79 Hz of the trajectories of magnetic iron filings within the Coherent Vortex Structures (CVS) of a BFS flow in the presence of a magnet located at $X_{\rm{r}}$ = 2 cm.

The exact shape of some of these trajectories can be seen in Fig. 10c. As before, a sequence of 50 time steps was considered to faithfully represent almost all possible scenarios for this particular configuration, whereas the incomplete trajectories came as a consequence of missed data points that could not be assigned particle tracks or got filtered out due to insufficient information. Here, the particle tracks of the magnetically attracted filings are represented, along with the tracks of some other particles that were not directly captured by the effect of the magnet and were either transported or transported and lately deposited by means of the inertia of the bulk flow. Hence, the results show again some untrapped particles, presumably due to a stronger contribution of the convective forces compared to the gravitational effects on their dynamics (Fig. 10c, upper nearly horizontal rightwards trajectories). Furthermore, a considerable number of filings that were apparently going to be retained within the recirculation region can be seen to precipitate in shorter distances from the step as a matter of being not only influenced by the downward gravity force but also subjected to a gentle effect of the external magnetic field (Fig. 10c, trajectories ending nearly between $X_{\rm{r}}$ = 5,5 – 7,5 cm). The elliptical shape of these trajectories seemed to remain unaffected though. Thus, for this particular case, two main regions of agglomeration of particles can be intuited: (1) the vicinities of the magnet placement ($X_{\rm{r}}\sim 2~\mathrm{{cm}}$) and (2) a more forward region, with $X_{\rm{r}}$ = 5,5 – 7,5 cm. However, filings moving forwards or backwards across the bottom face of the BFS geometry between the agglomeration regions were not detected. The former effect is undoubtedly a consequence of the strong influence of the external magnetic field in this particular region, whereas the latter is explained by the weak enough influence of the attractive magnetic force, unable to drag the particles along the bottom face of the fluid domain, allowing them to clump together.

In any of the reported cases the filtering capacity of a larger magnet was studied as a consequence of the spatial limitations previously mentioned in Sect. 2. However, the question arises at this point as to whether the replacement of the employed magnet with a similar size and more powerful magnetic device could lead, in any of the presented situations, to a better control of or even to an increase in the number of retained particles. Moreover, no quantitative study has been carried out based on numerically quantifying the capacities of the different filtering systems exposed with the purpose of comparing them from an efficiency point of view, as the present investigation was more aimed at qualitatively verifying the combined effect of the retention systems employed on the dynamics of the studied particles, evaluating the differences found in the various inspected configurations and also validating the functionality of the inspection method used. Therefore, these questions remain to be elucidated in further investigations.

Conclusion

The presence of suspended particles in liquid fluids is one of the main reasons of hydraulic system failure. Impurities of magnetic nature, in particular, are known to increase the presence of toxic substances in wastewater and cause serious detrimental consequences to the environment. Studies addressing the behaviour of such particles in water flows are necessary in view of develo** and improving new and existing filtration processes. The current open literature as yet lacks studies approaching the combined effect of different filtering techniques in Backward-Facing Step (BFS) flows. Hence, in this study, research addressing the combined effect of a three-dimensional BFS flow and a magnetic field, both acting as retention systems on impurities of a magnetic nature, is presented. Furthermore, the dynamics of the aforementioned impurities have been evaluated through a non-intrusive optical system. Hence, a combined 2D PIV/PTV–3D uRANS CFD simulation approach has been employed to analyse and illustrate the behaviour of some magnetic particles in the sine of a confined BFS flow system. Experiments and computations were performed at a Reynolds number $\mathrm{{Re}}_{H} = 3684.63$, based on the step height h and the inlet streamwise mean velocity $U_\mathrm{{ref}}$. The computational measurements were performed in several planes from two different perspectives to correctly assess and evaluate the complex three-dimensional flow topology. The experimental campaign was focused on assessing the dynamics of the magnetic filings during its passage through the streamwise middle plane. The computational transitional behaviour of the fluid phase is predicted using the Reynolds stress model.

Computations shed light on several relevant features of a 3D BFS flow behaviour, i.e. the shape of time-averaged vortices downstream of the step, the shape of the reattachment curve and the streamwise velocity, turbulent kinetic energy and Reynolds shear stresses fluctuations at eight different line segments along the middle spanwise z = 0 plane along the separation region. Steady-state streamline patterns over two different planes are obtained to explain and justify the flow topology. The present results revealed a slight asymmetry of the flow, motivated by an AR value of 7.5 and the resultant three-dimensional effects. The recirculation locus presents a mild diagonal line shape in its core region, shifting thereby the maximum length of the recirculation zone lightly leftwards and proving it to increase with the distance from the side walls. A half plane reattachment length of $X_{\rm{r}}=11.73h$ against the $X_{\rm{r}}=7.82h$ result reported by Teso et al.⁴⁰ was found for a turbulence intensity of the inlet flow of about 1%.

The streamwise velocity, turbulence kinetic energy and Reynolds shear stress profiles showed quite good qualitative agreement with the data reported in the open literature. High velocity values and step gradients near the centre line of the BSF geometry were observed, which match with the principle of the shear layer development. After three step heights on, the step gradients decay as the shear layer evolves in its second half. $x/H=10$, $x/H=11$ and $x/H=12$ line segment profiles evidenced the appearance of a backflow in the shedding region that reinforced the reattachment length abovementioned. Similarly, the shapes of the TKE profiles were very similar to the three principal shear stresses ($\overline{{u'u'}}$, $\overline{{v'v'}}$ and $\overline{{w'w'}}$), featuring the largest values in the region of the mixing shear layer by an abrupt increase just downstream of the step. Moreover, a steady increment throughout several step heights up to the $x/H=10$ line segment was shown, after which maximum values approached lower upper bounds and the profiles show a more flattened appearance. A maximum non-dimensional shear stress of $\overline{{u'u'}} = 0.0528$ was found, whereas the maximum normalized second moment of different velocity fluctuations was $\overline{{u'v'}} = - 0.0138$. Furthermore, shear stresses concerning velocity fluctuations associated to this spanwise direction were found to be one and two orders of magnitude lower compared to the $\overline{{u'v'}}$ and $\overline{{u'u'}}$, $\overline{{v'v'}}$ and $\overline{{w'w'}}$ velocity fluctuations, respectively.

The trajectories of water-suspended iron filings under the influence of an external magnetic field were compared to their paths when no extra forces except gravity were considered. For the no magnet case, it was suggested that, under the studied conditions, insufficient flow momentum was generated for the vortical structures to be able to entrain the majority of the iron filings. Thus, the captured particles described elliptical trajectories notwithstanding the flow directionality, descending vertically without being dragged by the convective flow. For the two cases for which the iron filings were subjected to the influence of an external magnetic field, the shape of these trajectories was altered, the deposition distances of the particles being modified and enhancing the deposition effect. In addition, it has been shown that a more forward placement of the magnet results in a more pronounced alteration of the trajectories of the filings as they shorten their settling distance, evidencing that the latter can be controlled in a greater number of cases. There is no room for the study of the retaining capacity of a larger magnet as a result of the spatial limitations mentioned in previous sections. Apart from that, a suitable numerical quantification and evaluation of the filtering capacities of the exposed systems from the point of view of efficiency, for both the already exposed case studies and those that would imply a possible replacement of the current magnet by a more powerful magnetic device, need further investigation.