Automated Exploration of Envelopes and Offsets with Networking of Technologies

Abstract

We explore envelopes and offsets of plane curves using automated methods, based on the usage of Computer Algebra Systems and Dynamical Geometry Systems. Work is performed using both parametric presentations and implicit equations. Implicitization involves well-known algorithms from the theory of Gröbner bases. In particular, irreducibility of the involved polynomials, whence irreducibility of the obtained curves is checked using the latest developments of the software tool GeoGebra Discovery. We conclude with comments on the 4C’s of twenty-first century Education, applied to mathematics and show how networking between technologies provides a suitable environment to apply and develop a 5th C, namely curiosity.

1 Introduction

The conference series Applications of Computer Algebra (ACA), has been held yearly for 26 years, has a recurring working group on educational aspects of computer algebra. Our paper is a contribution to this track of the ACA conference. We would like to demonstrate our experiences on a graphically challenging topic: the visualization of envelopes and offsets, but at the same time we explain several difficulties that are partly technical, mathematical and communication related. Our report includes several aspects that arose during our experiments: challenges in formalization, difficulties in expressing formulas and visualizing them in software systems, heavy computations, and communication issues between humans and machines. As a result, our paper is a mixture of concepts of mathematical, technical and educational ideas, but it reflects how scientific work in an educational context is usual in today’s applications.

1.1 Preliminary Remarks

Automated methods for the study of plane algebraic curves is a live domain of exploration and of new developments. In this paper, we collect several ideas and concepts in an explanatory but summarized form, by highlighting multiple aspects of our work. In particular:

• We focus on benchmarking several pieces of software, and at the same time, we try to introduce new technical approaches since the traditional methods do not suffice.

• We emphasize several aspects of using various applications, but, at the same time we try to figure out how the different definitions can be compared and which one fits our project the most.

Meanwhile, sometimes we need to face technical issues, including fixing errors or submitting bug reports to the developers of computer algebra and dynamic geometry tools. In some cases this kind of work is somewhat eclectic, but our report faithfully communicates (or, at least, it tries to) how usage of bleeding edge technology and achieving new mathematical knowledge are performed.

We think this kind of work remains (at least, still for a while) an experimental process, and as such, a “jump in the dark”. Even so, we still believe that the final results show that such a confusing interplay of various concepts and tools may indeed have a crystallized meaning after the end of day.

1.2 Envelopes and Offsets

Envelopes of parameterized families of plane curves, of space curves, of surfaces, are an important topic both because of the mathematics involved and because of their applications (e.g. the determination of safety zones around sprinklers, robotic plants, Luna Park attractions, etc. [10]). Despite their important applications, they disappeared from the curriculum decades ago, even if, among other famous mathematicians, Fields medalist René Thom strongly disagreed with that [22]. He claimed that a drawback of this domain is the small number of its theorems, and the need to study numerous special cases [22]. If at that time, envelopes did not receive enough attention, things have changed since then, as a quick websearch can show. Moreover, there exist numerous non-equivalent definitions of envelopes; see [4,5,6, 16].

We list here the 4 widely known definitions, the names of the 3 first cases are those of Kock [16]. Consider a parameterized family ${\mathscr {F}}$ of plane curves ${\mathscr {C}}_k$, dependent on a real parameter k.

Definition 1

A plane curve ${\mathscr {E}}$ is called an envelope of the family ${\mathscr {F}}$ if the following properties hold:

• Every curve ${\mathscr {C}}_k$ in ${\mathscr {F}}$ is tangent to ${\mathscr {E}}$;

• To every point M on ${\mathscr {E}}$ is associated a value k(M) of the parameter k, such that the curve ${\mathscr {C}}_{k(M)}$ is tangent to ${\mathscr {E}}$ at the point M;

• The function k(M) is non-constant on every arc of ${\mathscr {E}}$.

This is Bruce and Giblin’s Definition 5.12 [6]; Kock [16] calls it impredicative. A simple example of the construction of an envelope with this definition is given in [11]. The work is performed according to the following steps:

• (i) A parametric family of lines is given and explored with a Computer Algebra System.

• (ii) Analyzing the simultaneous plot of numerous lines, the existence and the nature of an envelope is conjectured.

• (iii) Using the algebraic features of the CAS, the conjectured is proven.

Such a process is hardly applicable in general, whence the name impredicative.

Definition 2

A plane curve ${\mathscr {E}}$ is called an envelope of the family ${\mathscr {F}}$ if it is the set of limits of intersection points of infinitesimally closed pairs of curves ${\mathscr {C}}_k$.

This is Bruce and Giblin’s Definition 5.8 [6]. Kock [16] calls it synthetic. It is illustrated in [11].

Definition 3

The envelope is the boundary of the region filled by the curves ${\mathscr {C}}_k$.

This is Bruce and Giblin’s Definition 5.16 [6]. A study of such an envelope is to be found in [10], namely looking for a boundary for a safety zone around a mobile device (a robot, or a Luna Park construction) shown in [13]:

Definition 4

Let a parameterized family of plane curves ${\mathscr {C}}_t$ be given by the equation $F(x,y,t)=0$. If an envelope exists, it is given by the solution of the system of equations

$$\begin{aligned} {\left\{ \begin{array}{ll} F(x,y,t)=0, \\ \frac{\partial F}{\partial t} F(x,y,t)=0. \end{array}\right. } \end{aligned}$$

It is easily shown that Definition 2 implies Definition 4. Note that this is the only definition given by Berger [2]. With this definition, we see the envelope as the projection over the (x, y)-plane of the points, in the (x, y, t) 3-dimensional space, belonging to the surface with equation $F(x,y)=0$ and having tangent plane parallel to the t-axis (or being singular points of the projection map and, thus, not having a tangent plane, properly speaking).

Offsets can be defined as envelopes, as follows:

Definition 5

Let d be a positive real number. The offset at distance d of a given curve ${\mathscr {C}}$ is the envelope of circles of radius d centered on ${\mathscr {C}}$.

We rephrase this definition, using the formulation in [18]:

Definition 6

Let ${\mathscr {C}}$ be a given plane curve, called the generator. Offset curves, also called parallel curves, are the locus of points trace by the unit normal vector of ${\mathscr {C}}$ multiplied by a signed distance d.

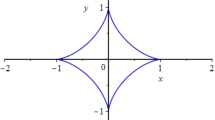
As the number d denotes a signed distance, the definition enables to distinguish two different components, one which will be called exterior and one which be called interior. Note also that the definition of a unit normal vector involves the computation of a square root, therefore an offset will be generally more complicated than the generator curve. This is illustrated in Fig. 1, showing the offset at distance 1 of the parabola whose equation is $y^2=x$. The external offset is smooth, but the internal has cusps and a double point. These issues are studied in [18].

Fig. 1

Offset at distance 1 of a parabola

Cusps and double points are not the only specific issues of offsets. When the progenitor has tangent discontinuities, the exterior offset ($d>0$) is discontinuous and the interior ($d<0$) has a self-intersection; see [18]. Other important issues, related to curvature, are discussed there. Other examples have been explored, such as offsets of an astroid (a curve with 4 cusps) in [9], and of a regular trifolium [14], a curve with a triple point. Offsets of Cassini ovals have been explored in [15]; these ovals are important in various scientific domains, such as electrostatics and depollution of soils (delineation of the zone of influence of wells).

1.3 The Usage of Technology

The usage of technology makes the study of envelopes a live domain of study and may attract students to exploration and discovery (e.g., see [11,12,13]). A Dynamic Geometry System (DGS) provides an environment for automated exploration and discovery. In particular, GeoGebra¹ and its companion package GeoGebra Discovery² have commands for the automated determination of an envelope under certain conditions for the construction and commands for the determination of geometric loci [3, 17]. We saw in the previous subsection that offsets are studied either as envelopes or as loci, whence the importance to have these two kinds of commands available. They exist in different versions, depending on the way the generator ${\mathscr {C}}$ and the offset have been defined: either by a purely geometric construction or using a slider bar to make the value of the parameter vary.

Nevertheless, the commands may not work in certain situations. It may be then useful to transfer the data (the equations) to a Computer Algebra System, which analytic solutions will be computed with. The output may be afterwards transferred back to the DGS. GeoGebra contains already a CAS, namely Giac, which enables a vast amount of computations. Making this networking between DGS and CAS more automated is a current topic of Research and Development (R &D), in particular within new developments of GeoGebra Discovery.

In a polynomial setting, the solve command of the CAS uses algorithms from the theory of Gröbner bases [1, 8, 19]. In various situations, it is possible to transform the given data into a polynomial form. Then the CAS provides a parametric presentation of the envelope (which can be described as the disjoint union of several components). These equations are copied into the DGS for the final graphical presentation (e.g. using the Curve command of GeoGebra).

Both DGS and CAS enable to construct animations, but with important differences. With the CAS, the animation has to be programmed, then executed. The possibility for the user to intervene directly on the animation is quite limited. A central feature of a DGS is dragging, i.e. moving a point directly on the plot using the mouse. The animation can be totally interactive. Both technologies led to the following remark: It is well known that, when a curve is given by a parametrization, this parametrization is not unique. Now, when the curve is given by a trigonometric parametrization, this presentation can be transformed into a rational one, using well-known trigonometric identities for sine and cosine, as in [9, 14]. The animations with a rational presentation and with a trigonometric presentation behave in very different ways, and their observation is an enriching activity.

In this paper:

• 1. We show how this networking of technologies is used.

• 2. We analyze the differences between the animations provided by the CAS and the interactive exploration enabled by the DGS, and how to have profit of these differences.

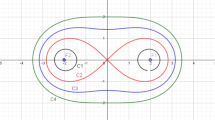
• 3. We analyze the possible contradiction between the first intuition and the actual output, in particular with regards to the issue of safety zones evoked above. In Fig. 2 we show a family of circles centered on an astroid. The envelope of the family is different from the hull enclosing all the circles in the family.

The present paper is an additional contribution to the exploration of envelopes and offsets of classical curves, following [13] for offsets of a deltoid and [10] for an astroid. We provide more elements of comparison between different definitions of envelopes and offsets and proceed further, obtaining an algebraic description of the studied offsets, which was missing in previous work. We obtain a polynomial presentation and study the irreducibility of the polynomials. Finally, we discuss briefly some educational aspects of this kind of study, in particular communication between humans and machines, especially in a period of general distance learning because of the Covid-19 pandemic.

2 Offsets of an Astroid

An astroid is a plane curve given by the following parametrization:

$$\begin{aligned} {\left\{ \begin{array}{ll} x=\cos ^3 t, \\ y=\sin ^3 t, \end{array}\right. } \qquad t \in [0,2\pi ]. \end{aligned}$$

(1)

It can be easily shown that the astroid is a rational algebraic curve, namely a sextic, given by the polynomial equation

$$\begin{aligned} (x^2+y^2-1)^3+27x^2y^2=0. \end{aligned}$$

(2)

We prefer generally to plot the curve using the parametric presentation, as the implicit plot may be inaccurate in a neighborhood of singular points [23].

2.1 Envelopes of Families of Circles Centered on the Astroid: With the Analytic Definition

We work here according to Definition 4. If $d>0$, the offset at distance d can be viewed as the envelope of the circles ${\mathscr {C}}_t$ whose equation is

$$\begin{aligned} (x-\cos ^3 t)^2+(y-\sin ^3 t)^2-d^2=0. \end{aligned}$$

(3)

Denote by $F_t$ the polynomial on the left-hand side of this equation. According to Definition 4, the eventual envelope is defined by the system of equations

$$\begin{aligned} {\left\{ \begin{array}{ll} (x-\cos ^3 t)^2+(y-\sin ^3 t)^2-d^2=0, \\ 6(x - \cos ^3 t)\; \cos ^2 t \sin t - 6(y - \sin ^3 t) \; \sin ^2 t \cos t =0. \end{array}\right. } \end{aligned}$$

(4)

The solutions are given as follows, determining immediately two components:

$$\begin{aligned} {\left\{ \begin{array}{ll} x= \cos ^3 t + \sqrt{d^2 \sin ^2 t}, \\ y=\frac{1}{\sin t} \; (\cos ^4 t + \cos t \; \sqrt{d^2 \sin ^2 t} + 1 - 2 \cos ^2 t), \end{array}\right. } \end{aligned}$$

(5)

and

$$\begin{aligned} {\left\{ \begin{array}{ll} x= \cos ^3 t - \sqrt{d^2 \sin ^2 t}, \\ y=\frac{1}{\sin t} \; (\cos ^4 t - \cos t \; \sqrt{d^2 \sin ^2 t} + 1 - 2 \cos ^2 t). \end{array}\right. } \end{aligned}$$

(6)

Fig. 2

Examples of offsets as envelopes

Figure 2 shows the astroid and the offsets at distance d for various values of d, computed as envelopes. The general computation has been performed with Maple, using the following code:

The simplify command has been used for the sake of having a simpler formulas display. The option discont = [usefdiscont] has been used in order not to have superfluous segments in the plot. Note the range for the variable t in the plot commands: it does not include 0 and $2 \pi$ in order for Maple not to connect the beginning and the end of two curves inappropriately.

2.2 Locus of the Endpoints of Normal Vectors

We use here the trigonometric parametrization ((1)). At a non-singular point $M(\cos ^3 t, \sin ^3 t)$ of the astroid, a tangent vector is $\overset{\rightarrow }{V}=(-\cos ^2t \sin t, \sin ^2 t \cos t)$ and a normal vector is $\overset{\rightarrow }{V}=(\sin ^2 t \cos t,\cos ^2t \sin t, 3 \sin ^2 t \cos t)$ (we divided by a factor 3). Thus, a unit normal vector $\overset{\rightarrow }{n}$ is given by:

$$\begin{aligned} \overset{\rightarrow }{n}\ = \frac{1}{\sqrt{\sin ^2 u \cos ^2 u}} \left( \sin ^2 u \cos u, cos^2 u \sin u \right) . \end{aligned}$$

(7)

The endpoint of the normal vector for the offset at signed distance d is thus:

$$\begin{aligned} B=\left( \cos ^3 u + \frac{d \sin ^2 u \cos u}{\sqrt{\sin ^2 u \cos ^2 u}}, \sin ^3 u + \frac{d \cos ^2 u \sin u}{\sqrt{\sin ^2 u \cos ^2 u}} \right) . \end{aligned}$$

(8)

A screen snapshot of a GeoGebra applet showing the geometric locus of points B is displayed in Fig. 3. The Locus(Point, Slider) command has been used, therefore the plot is based on numerical data, not on explicit equations.

Fig. 3

The geometric locus of endpoints of normal vectors at distance d

Exploration with strong zooming out reveals that for $d<1.48$, the locus has self intersections (actually, the obtained locus is the union of 4 curved triangles) and for $d>1.5$ the locus is smooth (it is the union of 4 arcs); see Fig. 4. The determination of the limiting value of d requests an analytic presentation of the locus, which cannot be provided by the software, at this stage of development. Other ways for strong zooming are given on  [24].

Fig. 4

Exploration of self-intersection of the locus

Remark 1

If the curve is given by an implicit equation, normal vectors are obtained using the gradient of the polynomial, but an analytic description of the endpoints B is not easy to obtain. After all, the equation of the curve is implicit.

2.3 Envelopes of Families of Circles Centered on the Astroid: Boundary Curve

We work now according to Definition 3. Figure 6 shows screen snapshots from a GeoGebra session,³ for 2 different values of the offset distance. As mentioned in Sect. 1, offsets can describe safety zones around machines and/or robots. we will see here that the boundary zones have different shapes according to the required safety distance from the machine. Note that the obtained curves, such as in Fig. 5, and the boundary curves that we determine in the present subsection, look quite complicated; in practice, the engineers would choose to build barriers with a more simple form, such as circles, enclosing the boundary curve determined by the computations. The authors saw that in various entertainment parks; see Fig. 5. Things may be more complicated for safety zones around moving robots in an industrial plant.

Fig. 5

A circular safety fence

The astroid has been plotted using the Curve command with the trigonometric presentation 1. Then the envelope has been plotted, copying the formulas obtained with Maple as in the previous subsection, into GeoGebra command line. A point A is attached to the astroid and a circle centered at A with radius d is plotted. Moving the point A along the astroid with Trace On for the circle yields the figure on display. No need to point out that the boundary curve of the region filled by the circles is different from the envelope determined in the previous subsection.

Fig. 6

Exploration of the boundary curve of the zone filled by the given circles

In this session, the offset distance d is entered as a parameter, whence the need of a slider bar and the possibility of an interactive exploration. Similar animation can be built with Maple, using the animate command, but the DGS provides here a possibility of direct intervention on the display, dragging the point A with the mouse. For the reader’s sake, we give here the Maple code (the values of a and b vary according to the given value for d, and must be assigned a value before running the commands):

The question is now how to determine, if possible, an analytic description of the boundary curve. The interactive exploration provides an intuition that for $d=1/10$, this curve should be the union of arcs of the envelope from Sect. 2.1 and arcs of circles centered at the cusps of the astroid. For $d=2$, this is not true, since in this case the envelope is not part of the boundary anymore (Fig. 6).

In [13], we studied offsets of a deltoid, here we perform similar work based on an astroid. Once again, new constructions of interesting plane curves appear.

The features and activities that we describe here show how to implement and develop the 4 C’s of Education in the twenty-first century [7]: Critical thinking, Creativity, Communication and Collaboration. If the first two C’s are human characteristics, the exploration that we propose requires the two last C’s both for humans and for machines and expands also the man-and-machine C’s. Strong zooming is a must in order to have an accurate conjecture of what happens, in particular regarding singular points.

2.4 The Implicit Curve Approach

Definition 4 allows us to use a mechanical approach to study the offsets of an astroid. In some former works of ours we gave a detailed description how the implicit algebraic equation of a curve can be usually obtained, and which algebraic means can be followed to extend the study to obtain its offset. In particular, in [13,14,15] we studied offsets of an ellipse and a deltoid, the trifolium curve, and the Cassini ovals. Among other methods, the implicit algebraic form of the input curve played an important role in determining the offset curve. We used an effective algorithm to eliminate all variables but x and y in the polynomial ideal that is constructed from the polynomials of Definition 4. To obtain the result, the algorithm used the theory of Gröbner bases [8]. The algorithm we used was implemented in the Giac computer algebra system, and it was called every time when the input curve was changed in GeoGebra’s user interface.

Different inputs lead to different levels of computational difficulties. Here we refer the reader to a recent benchmark https://tinyurl.com/GD-artplotter-83 that reports on the speed for computing the offset curve for different algebraic inputs. In this paper we collect some particular data from this benchmark, performed in September 2021, by running GeoGebra Discovery version 2021Sep03 on a typical PC (we used an Intel(R) Core(TM) i7-4770 CPU @ 3.40GHz with Ubuntu 18.04 installed), see Table 1. (In the table FPS stands for “frame per seconds”, that is, a single computation takes the reciprocal of this number.)

Table 1 Speed of computation for various offsets

The results suggest the conjecture that in most cases the higher the input degree, the higher the output degree as well. Also, the higher the input degree, the slower the operation—in most cases. We expected therefore some slowdown for the astroid that has input degree 6.

On the other hand, the output degree is sometimes higher than we expect. For example, the case for the input cissoid

$$\begin{aligned} 2 \; x^{3} + 2 \; x \; y^{2} - 3 \; x^{2} + y^{2} = 0 \end{aligned}$$

results in the output 1-offset

$$\begin{aligned}{} & {} 4 \; x^{12} + 4 \; x^{2} \; y^{10} + 20 \; x^{4} \; y^{8} + 40 \; x^{6} \; y^{6} + 40 \; x^{8} \; y^{4} + 20x^{10} \; y^{2} + 4 \; x^{11} + 4 \; x \; y^{10} + 20 \; x^{3} \; y^{8}\\{} & {} \qquad + 40x^{5} \; y^{6} + 40 \; x^{7} \; y^{4} + 20 \; x^{9} \; y^{2} - 71 \; x^{10} - 3 \; y^{10} + 13 \; x^{2} \; y^{8} - 14x^{4} \; y^{6} - 150 \; x^{6} \; y^{4} - 191 \; x^{8} \; y^{2} - 8 \; x^{9} + 24 \; x \; y^{8} - 192 \; x^{3} \; y^{6}\\{} & {} \qquad - 464x^{5} \; y^{4} - 256 \; x^{7} \; y^{2} + 433 \; x^{8} - 23 \; y^{8} - 180x^{2} \; y^{6} + 334 \; x^{4} \; y^{4} + 924 \; x^{6} \; y^{2} - 280 \; x^{7} + 152 \; x \; y^{6}\\{} & {} \qquad + 728x^{3} \; y^{4} + 296 \; x^{5} \; y^{2} - 895 \; x^{6} - 31 \; y^{6} - 589 \; x^{2} \; y^{4} - 1645 \; x^{4} \; y^{2} + 956x^{5} - 100 \; x \; y^{4} + 408 \; x^{3} \; y^{2} + 639 \; x^{4} + 207 \; y^{4} + 926 \; x^{2} \; y^{2}\\{} & {} \qquad - 1072x^{3} - 480\; x \; y^{2} + 15 \; x^{2} - 25 \; y^{2} + 400 \; x - 125=0, \end{aligned}$$

but this polynomial is a product of two other polynomials, namely $x^{2} + y^{2} - 1$ and

$$\begin{aligned}{} & {} 4 \; x^{10} + 4 \; x^{9} + 16 \; x^{8} \; y^{2} - 67 \; x^{8} + 16 \; x^{7} \; y^{2} - 4 x^{7} + 24 \; x^{6} \; y^{4} - 108 \; x^{6} \; y^{2} + 366 \; x^{6} + 24 \; x^{5} \; y^{4}\\{} & {} \qquad - 236x^{5} \; y^{2} - 284 \; x^{5} + 16 \; x^{4} \; y^{6} - 18 \; x^{4} \; y^{4} + 450 \; x^{4} \; y^{2} - 529x^{4} + 16 \; x^{3} \; y^{6} - 204 \; x^{3} \; y^{4} + 344 \; x^{3} \; y^{2}\\{} & {} \qquad + 672x^{3} + 4 \; x^{2} \; y^{8} + 20 \; x^{2} \; y^{6} - 134 \; x^{2} \; y^{4} - 666x^{2} \; y^{2} + 110 \; x^{2} + 4 \; x \; y^{8} + 28 \; x \; y^{6} + 180 \; x \; y^{4}\\{} & {} \qquad + 80 \; xy^{2} - 400 \; x - 3 \; y^{8} - 26 \; y^{6} - 57 \; y^{4} + 150 \; y^{2} + 125. \end{aligned}$$

From a geometrical point of view, the first factor seems unnecessary, because it supports the input only for its point (0, 0), otherwise this circle is fully contained in the region that is described by the other factor (see Fig. 7).

Fig. 7

An example of unexpected parts of the algebraic output

We reported in [14] that GeoGebra Discovery supports a direct way to obtain the output offset curve in a user-friendly way. This feature has been recently incorporated into the mainstream version of GeoGebra since May 2021 (version 5.0.641.0). That is, by considering Definition 5, the user needs to

• 1. Enter the input algebraic formula to define the curve ${\mathscr {C}}$,

• 2. Set up a segment for the distance d,

• 3. Attach an arbitrary point P on ${\mathscr {C}}$,

• 4. Create a circle c with center P and radius d,

• 5. And issue the command Envelope (c, P)

to get the offset computed and plotted in GeoGebra. This simple “5-steps-recipe” works very stably for a large amount of input curves in the case if their degree is not more than 4.

Unfortunately, the astroid case gives no output—GeoGebra times out and neither an implicit formula, nor an output curve is shown. But luckily, we can exploit a technical error in GeoGebra, namely, that a slow computation is not always fully aborted, but still continued in the background inside the Giac engine. So, after several minutes of seemingly idle time Giac prints the result as a debug message in the console window, and surprisingly, by just copying-and-pasting this formula into GeoGebra’s Input Bar we actually obtain the correct output!

We omit the full output—it is of degree 52 and it begins with the term

$$\begin{aligned} 17592186044416\;x^{52}+\ldots \end{aligned}$$

It was calculated in 6 minutes on a normal PC. When plotting the output formula in GeoGebra we get a figure like Fig. 8, here we chose $d=1/2$.

Fig. 8

A graph of the obtained degree 52 implicit curve, plotted in GeoGebra

Clearly, this figure is somewhat unexpected. In fact, the inaccurate parts are consequences of the numerical errors introduced by the plotting algorithm in GeoGebra. To avoid them, we need to factor the 52 degree polynomial first. We obtain several factors, namely:

• 1. Four factors of the form

  $$\begin{aligned} ((x\pm 1)^2+y^2-(1/2)^2)^3\text { and }(x^2+(y\pm 1)^2-(1/2)^2)^3, \end{aligned}$$

  after multiplication we get a total of degree 24,

• 2. Two factors of the form

  $$\begin{aligned}{} & {} 4x^6 + 12x^4 y^2 - 13x^4 - 36x^3 y + 12x^2 y^4 + 82x^2 y^2 \\{} & {} \qquad + 32x^2 - 36x y^3 - 64x y + 4y^6 - 13y^4 + 32y^2 \end{aligned}$$

  and

  $$\begin{aligned} 4x^6 + 12x^4 y^2 - 13x^4 + 36x^3 y + 12x^2 y^4 + 82x^2 y^2 + 32x^2 + 36x y^3 + 64x y + 4y^6 - 13y^4 + 32y^2, \end{aligned}$$

  after multiplication we get a total of degree 12,

• 3. Two factors of the form

  $$\begin{aligned} F_{1,2}(x,y)=(16x^4+32x^2y^2+16y^4-8x^2-8y^2\pm 128xy+81)^2, \end{aligned}$$

  after multiplication we get a total of degree 16.

The first two sets of factors are shown in Fig. 9. Clearly, the first factors correspond to four circles that are positioned in points $(\pm 1,0)$ and $(0,\pm 1)$, with radius $d=1/2$. From the geometrical perspective these circles describe only limit situations, so, in some sense, they may be omitted. On the other hand, the second factors indeed have a geometrical meaning (cf. Fig. 2b).

Fig. 9

Visualization of the obtained factors, plotted in GeoGebra

Seemingly the third factors do not have any real points, but this statement is not true: there are some isolated points that are the solutions of the equations $F_1=0$ and $F_2=0$, respectively. For $F_1(x,y)=0$ we get $(x,y)=(3/(2\sqrt{2}),3/(2\sqrt{2}))$ and $(-3/(2\sqrt{2}),-3/(2\sqrt{2}))$, and for $F_2(x,y)=0$ we get $(x,y)=(3/(2\sqrt{2}),-3/(2\sqrt{2}))$ and $(-3/(2\sqrt{2}),3/(2\sqrt{2}))$. Since these are isolated points (all outside of the unit square), no geometrical meaning of them can be identified.

In fact, solving the equations $F_1=0$ and $F_2=0$ is not trivial. Here we used GeoGebra Discovery’s experimental command Real Quantifier Elimination to project the solution set on each axis. Its parameter is of form $\exists y\ (F_1=0)$ if we are interested in the possible values for x. (See [21] for a survey on real quantifier elimination and its application.)

We summarize that the symbolic computation of the output via elimination of the implicit algebraic input seems to be too heavy for today’s technological means. That is, computing the offset curve of an astroid, or, in more general, of a degree 6 curve, seems to remain a challenging problem.

3 The 5 C’s of Twenty-First Century Learning

We cannot finish this paper without a short discussion on the current atmosphere of learning and teaching. This is a general issue, and its influence on mathematical developments and mathematics education is important. The Covid-19 pandemic has reinforced the need for distance-learning, creating special needs and special features of mathematics education. Already in the previous years appeared a classification of the so-called 4 C’s of twenty-first century education, namely Collaboration, Communication, Critical thinking and Creativity [7, 20, 25]. Generally speaking, these 4 C’s were always viewed as human characteristics. In our work, we developed other points of view on at least some of them. Critical thinking and creativity are definitely human, but we showed that besides collaboration and communication between humans, we need to consider and analyze them between man-and-machine and between technologies.

Figure 10 summarizes our discussion;

Fig. 10

The visual analysis of the 4Cs of learning

Collaboration and communication are especially important; they made the huge difference between the Titanic and Noah’s Ark: according to what has been told, we may think that in Noah’s Ark, all the passengers knew that they are “on the same boat”, i.e., they share the same experience and face the same danger, whence the need for solidarity. On the Titanic, it seems that solidarity was (collaboration and communication) was not always there. Whence the consequences. we may mention that it happens that a user installs on his/her computer two programs which “fight” against the other, provoking damages to the work,sometimes making the computer crash. In our work, we showed how we made two kinds of software collaborate, meanwhile making the data transfer by hand. We wish that in the near future, this collaboration will be more automated.

We emphasized the efficiency of networking between technologies. We were mostly interested in CAS and DGS, but websurfing is also there. In many cases, the curves which are obtained may be identified, even by a newcomer, as there exist numerous websites presenting catalogues of classical curves, either algebraic or not. If more than one presentation exists, the websites give them, implicit equation, parametrization, and often also a polar presentation. When quartics need to be identified, a complete catalogue exists. A partial catalog of sextics is also available. For the rest, we should add a 5th C to the above list: Curiosity. This 5th characteristic is of the utmost importance to discover new objects, new properties.