Introduction

The high-velocity air fuel (HVAF) process, which has been developed on the basis of the high-velocity oxygen fuel (HVOF) process, is a potential candidate to realize both low-oxygen and low-porosity coatings. Activated combustion-high-velocity air fuel (AC-HVAF) system is equipped with a ceramic catalyst disk that is heated above the auto-ignition temperature of the gas mixture after initial ignition. As a result of the ceramic catalytic disk activating the fuel molecules, this is referred to as activated combustion, which leads to stable combustion at a relatively low temperature.

Since the combustion temperature of the air–fuel mixture is about 1000 K lower than the temperature of the oxygen fuel mixture, the HVAF process is particularly suitable for spraying spray materials that are susceptible to oxidation or degradation at high temperatures (Ref 1). Therefore, it is suitable for fabricating MCrAlY coatings, where M represents the metals nickel, cobalt or their combination. A relatively small change in the oxide content and microstructure of the MCrAlY coating can affect the functionality of the coating for oxidation protection or as an adhesion layer (Ref 2).

In recent years, simulation has been proven to be a powerful method for the analysis of thermal spray processes. Computational fluid dynamics (CFD) simulations were performed to investigate the gas dynamics and in-flight behavior of particles in the HVOF process. Gu et al. (Ref 3) developed a CFD model to study the steady-state, turbulent, and compressible combustion flow of a HVOF process and also analyzed the effects of fuel-oxygen ratio and total gas flow rate on the gas phase. Li et al. (Ref 4) analyzed the gas dynamics, in-flight particle behavior, and various parameters in a Diamond Jet HVOF gun by calculating the particle temperature and velocity. Jadidi et al. (Ref 5) used a three-dimensional model to simulate particle velocity, temperature, and trajectories in the suspension HVOF spraying process and also reported the radial distribution of particles at different stand-off distances. Wang et al. developed a two-dimensional numerical model using a non-premixed combustion model to model combustion in an HVOF process and were able to clearly observe the mixing region, ignition, burning, and acceleration regions (Ref 6). Various combustion models, such as the eddy dissipation concept and the eddy dissipation model, were studied by Emami et al. in modeling a hydrogen-fueled dual-stage HVOF system for their effect on the temperature and velocity field in the system (Ref 7). Numerical simulation is widely used to model the HVOF spraying process and determine the in-flight behavior of the particles. However, modeling of the AC-HVAF process is still in its early stages. Numerical modeling of the low temperature HVAF process was implemented using a combustion model based on a non-premixed probability density function model (Ref 8). Hou et al. analyzed the flow using two-dimensional CFD simulation assuming a single-stage reaction combustion model (Ref 9). Katanoda et al. reported a numerical study of HVAF process without considering the combustion chamber (Ref 10). Recently, Jiang et al. modeled the HVAF process by considering the small holes on the catalytic ceramic as gas inlets to simulate the flight process of Fe-based amorphous alloy particles (Ref 11). A comprehensive AC-HVAF simulation was studied by Liu et al. considering the ceramic sheet and radial inlets on the flow field (Ref 12). Gao et al. performed two-dimensional CFD simulations without considering the mixing chamber. The effects of different fuel types and process parameters on the performance of AC-HVAF were studied (Ref 13), and different air–fuel ratios and nozzle geometries were investigated in recent studies (Ref 14).

However, due to model simplifications, the existing models so far represent only the subprocesses and therefore are not able to explain in detail the correlations between the different phenomena of the entire process, e.g., the mixing process of the air–fuel mixture in the mixing chamber is rarely investigated and the distribution of the compressed air in the spray gun system is also not considered in the simulation models studied to date. Hence, this study aims to propose a complete simulation model of the spray gun system that also includes the distribution of compressed air and the integration of the mixing chamber. The objective of the work is to gain a comprehensive understanding of the AC-HVAF process and to develop a tool to study the influence of process parameters on particle in-flight properties.

Computational Method

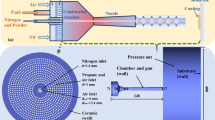
Computational fluid dynamic simulations of AK-07 AC-HVAF thermal spray gun (Kermetico, Inc., Benicia, USA) were conducted using Ansys Fluent 2021 R2 (ANSYS, Inc., Canonsburg, USA). The thermal spray gun is equipped with combustion chamber #3 with an internal diameter of 70 mm, a de Laval nozzle with extended throat section with total length of 225 mm, critical diameter of 14 mm and expansion diameter of 17.2 mm, powder injector and air distributor for chamber #3. As it is shown in Fig. 1(a), the fuel and compressed air are injected into the mixing chamber separately. Moreover, due to its effect to the combustion and flow behavior throughout the system, the mixing process of the gases in the mixing chamber is considered in the simulation model. This section describes the flow dynamic model, combustion model, and discrete phase model used to model the AC-HVAF process.

Fig. 1
figure 1

Schematic diagram of HVAF spray process (a) and detailed description of boundary conditions of flow domain (b)

Full size image

Simulation Domain

The simulation model covers all components of the spray gun such as mixing chamber, combustion chamber, nozzle and the burner housing and also the free jet region. The simulation domain of the AC-HVAF process is shown in Fig. 1b. The fact that the compressed air is not being injected directly into the mixing chamber and flows through the burner housing to provide additional cooling to the entire spray gun is also included in the geometric model in order to be able to study its influence on the entire process. Due to the symmetrical design of the HVAF spray gun, a half simulation model can be used. The boundaries of the domain consist of gas inlets with Tair = 300 K as pressure inlet and Tpropane = 313.15 K as mass flow inlet, outlet with pressure pamb = 101,325 Pa and backflow total temperature Tout = 300 K. The wall temperature of the mixing chamber, the combustion chamber and the nozzle are assumed to be constant at 300 K. The ceramic catalyst disk is assumed to be adiabatic. In the simulation model, it is assumed that combustion takes place only in the combustion chamber. The substrate is not included in the simulation model since the purpose of this study is to investigate the flow field and particle behavior in the free jet region.

The investigated process parameters are summarized in Table 1. The propane mass flow rates I, II, and III listed were determined at propane pressures of 551,581, 448,159, and 655,002 Pa, respectively. The nitrogen flow rate was given by the HVAF thermal spray equipment manufacturer, and it corresponds to the value of 40 indicated on the rotameter. Three gas mixtures with different air–fuel ratios (AFR) were investigated. I, II, and III represent a mixture with AFR = 13.781, a mixture with AFR = 18.392, and a mixture with AFR = 11.379, respectively. The air–fuel equivalence ratio λ is defined by the ratio between AFR and stoichiometric AFR. The stoichiometric AFR for propane-air mixture (λ = 1) is at 15.667. Thus, for the given mixtures I, II, and III, λ is 0.879 for a nearly stoichiometry mixture, 1.17 for a lean mixture, and 0.726 for a rich mixture. These scenarios were investigated to gain a comprehensive understanding of the influence of process parameters in various operating conditions on flow characteristics in terms of temperature and velocity field.

Table 1 Process parameters of the HVAF process and material properties of CoNiCrAlY
Full size table

CoNiCrAlY particles are injected axially using nitrogen as the carrier gas into the combustion chamber. Since it is well known that the oxygen content in the coatings generally increases with decreasing particle size, both coarse powder fraction of − 63 + 11 µm (Amdry 9954) and fine powder fraction of − 38 + 5.5 µm (Amdry 9951) were studied to determine the influence of the gas flow on the particle in-flight properties. The particle size distribution and SEM images of different powder fractions of CoNiCrAlY are demonstrated in Fig. 2. The coarse and fine powders have a median diameter d50 of 28.5 µm and 17.4 µm, respectively. It can be seen from the SEM images that both powders have a spherical shape with satellites. The used material properties of CoNiCrAlY are listed in Table 1. The specific heat capacity was obtained via differential scanning calorimetry measurements using SETSYS Evolution (SETARAM Inc., Caluire, France) up to 1,273.15 K and extrapolated to 1653 K.

Fig. 2
figure 2

Particle size distribution and SEM images of coarse (− 63 + 11 µm) and fine (− 38 + 5.5 µm) CoNiCrAlY (a) and specific heat of CoNiCrAlY over temperature (b)

Full size image

Flow Dynamic Model

The AC-HVAF process is a combination of a complex physical and chemical process which involves turbulent flow, combustion, heat transfer, and compressible gas flow. The gas flow is described by the governing equations such as mass conservation, momentum conservation, energy transport, species transport, turbulent kinetic energy and turbulent dissipation rate. The realizable k-ε turbulent model is implemented to characterize the turbulent motion of the gas flow. The k-ε model contains a formulation for the turbulent viscosity and a transport equation for the dissipation rate which has been derived from an exact equation for the transport of the mean-square vorticity fluctuation (Ref 15). Therefore, it can more accurately predict the spreading rate of both planar and round jets and has been extensively validated for free flows including jets and mixing layers, boundary layer flows and separated flows (Ref 15, 16). The modeled transport equations for turbulent kinetic energy \(\mathrm{k}\) and turbulent kinetic energy dissipation rate \(\upepsilon \) are given in Eq 1 and 2:

$$\frac{\partial \rho k}{\partial t}+\nabla \cdot \left(\rho k\overrightarrow{v}\right)=\nabla \cdot \left({\rho D}_{k}\nabla k\right)+{G}_{k}+{G}_{b}-\rho \epsilon -{Y}_{M}+{S}_{k}$$
(1)
$$\frac{\partial \rho \epsilon }{\partial t}+\nabla \cdot \left(\rho \epsilon \overrightarrow{v}\right)=\nabla \cdot \left(\rho {D}_{\epsilon }\nabla \epsilon \right)+\rho {C}_{1}{S}_{\epsilon }-\rho {C}_{2}\frac{{\epsilon }^{2}}{k+\sqrt{\nu \epsilon }}+{C}_{1\epsilon }\frac{\epsilon }{k}{C}_{3\epsilon }{G}_{b}+{S}_{\epsilon }$$
(2)

Combustion Model

In the combustion chamber, a gas mixture of air and fuel, in this case propane, is first ignited, then the ceramic catalyst disk is heated to above the auto-ignition temperature of the gas mixture, which allows a constantly ignited combustion process. The combustion reaction of the gas mixture is modeled by the eddy dissipation model (EDM), which tracks each chemical species by its own transport equation. In the EDM, the chemical reaction is assumed to be fast and the overall rate of reaction is controlled by turbulence mixing (Ref 17). Combustion proceeds whenever turbulence is present \(\left(\mathrm{k}/\upepsilon >0\right)\), and an ignition source is not required to initiate combustion. This assumption is validated by previous observations of the HVOF spraying process (Ref 18) and has been proven to be suitable for modeling flames with fast reaction kinetics. Furthermore, this model has also been shown to be feasible in related studies in HVOF spraying by Li et al. (Ref 19) in modeling combustion of propylene and Kamnis et al. (Ref 20) in modeling combustion of kerosene. According to the earlier reported simulation results (Ref 11), the concentration of other intermediate products in the full flow field is extremely low, except for CO. As a result, the reaction between propane and oxygen can be simplified by the two-step method (Ref 21). The chemical reactions are represented by two global reactions according to Eq 3 and 4:

$${C}_{3}{H}_{8}+3.5 \cdot {O}_{2}\to 3 \cdot CO+4 \cdot {H}_{2}O$$
(3)
$$CO+0.5 \cdot {O}_{2}\to C{O}_{2}$$
(4)

Discrete Phase Model

To simulate the interaction between the gas stream and the particles, a discrete phase model with a two-way coupling method is applied to account for the interaction between the gas stream and the powders. The drag force is the major force acting on the particles and can be described as follows:

$${m}_{p}\frac{d{v}_{p}}{dt}=\frac{1}{2}{C}_{d}{A}_{p}{\rho }_{g}\left({v}_{p}-{v}_{g}\right)\left|{v}_{p}-{v}_{g}\right|$$
(5)

Based on the SEM images in Fig. 2a, the particles are assumed to be spherical. The relationship between the drag coefficient \({\mathrm{C}}_{\mathrm{d}}\) and \(\mathrm{Re}\) is calculated using the approach of spherical drag law by Morsi and Alexander in (Ref 22). The convective heat transfer between the gas mixture and the particles is written as follows:

$${m}_{p}{c}_{p}\frac{d{T}_{p}}{dt}=h{A}_{p}\left({T}_{g}-{T}_{p}\right)$$
(6)

The heat transfer coefficient h is evaluated using the correlation of Ranz and Marshall (Ref 23). In this study, the phase change of the particle state from solidus to liquidus is not considered.

Results and Discussion

In this section, the simulation results of the AC-HVAF process are presented, taking into account the mixing process, the gas flow and the flight behavior of the particles. Three different conditions for the ratio of air to fuel in the mixture and the flight behavior of two different powder fractions are evaluated and analyzed.

Grid Independence Study

Due to the complexity of the model and coupled system of equations, the numerical computation of such flow problems depends on the selected numerical mesh. Three-dimensional simulations are very sensitive to grid resolution. Velocity and temperature are two important variables in the thermal spray process, therefore, it is important to ensure that these two variables are independent of the grid resolution used. Three grids with 4,437,440, 11,351,374, and 17,541,164 cells were examined as reference, fine, and finer grids, respectively. The grid refinements were mainly carried out in the combustion chamber, nozzle and free jet region to accurately calculate the velocity and temperature field. In the conventional meshing method, the computational mesh initially consisted mainly of tetrahedral cells due to the complex geometry of the simulation model. In order to reduce the number of cells, the tetrahedral cells were then converted into polyhedral cells. Finally, the computational mesh consists mainly of polyhedral and hexahedral cells.

The results show similar gas velocities along the flow field. In all simulation results, shock diamonds are observed at the exit of the nozzle. Compared to the gas velocity, the results show that the gas temperature is more sensitive to the grid density. The differences in flow behavior of the carrier gas along the centerline of the combustion chamber are shown in Fig. 3. This is important to observe as the particles are injected axially. It can be seen that the reference grids display a significant difference from the fine and finer grids. The flow behavior calculated with fine grids agrees well with that calculated with finer grids. Therefore, the fine grid with 11,351,374 cells is used in this work as it provides sufficient simulation accuracy considering the computational cost.

Fig. 3
figure 3

Flow field of the carrier gas in the combustion chamber in different grid resolutions

Full size image

Mixing of Air and Propane

Figure 4 shows the mixing process of propane and air in the mixing chamber in mixture I. Compressed air flows out of the inlet and is distributed radially into the mixing chamber. Propane is injected axially through the propane inlet and then mixed with the compressed air before the gas mixture flows over the ceramic disk into the combustion chamber. The mass fraction of propane after mixing was approximately 6-8% and the rest of the mixture consists of O2 and N2. The simulation showed that the mass fraction of propane at the outlet of the mixing chamber is highly uniform before it flows through the ceramic catalyst disk into the combustion chamber.

Fig. 4
figure 4

Mixing process of propane and air

Full size image

The mass average of propane mass fraction at the outlet of the mixing chamber and at the outlet of the nozzle is shown in Table 2. The mass fraction of propane at the nozzle exit indicates that the combustion of propane in both mixture I and mixture II is complete. In contrast, the propane from mixture III was still traceable at the nozzle exit.

Table 2 Mass fraction of propane before and after combustion
Full size table

Gas Flow

Figure 5 shows the simulated contours of temperature and velocity flow field of different process parameters in the steady state. pA denotes the pressure of the compressed air at the inlet, VN—the nitrogen flow rate, and ds—the stand-off distance. At the nozzle exit, it can be seen that the temperature decreases, while at the same time, the velocity increases before the shock diamonds occur, which were also captured in the simulation. In this region, the jet is accelerated to more than 1,400 m/s, indicating a supersonic state with \(\mathrm{Ma} > 2\). The shock diamonds at the exit of the nozzle occur due to the periodic under-expansion and over-expansion of the gas. The wave pattern dissipates after approximately 160 mm due to turbulent shear. Subsequently, the velocity and temperature of the gas flow decrease rapidly.

Fig. 5
figure 5

Calculated contours of temperature and velocity from the combustion chamber to the substrate

Full size image

As can be seen in Fig. 6, mixture I and III reach a maximum temperature of just over 1,700 K, while mixture II has a maximum temperature of about 1,600 K. It can be observed that the temperature of mixture II along the centerline is 100 K lower than the temperature of mixture I and II. The maximum velocity differs only slightly between the different mixtures, with mixture II reaching a maximum velocity of slightly over 1,450 m/s. The jet from mixture I and III is accelerated to just under 1,550 m/s. Since the melting temperature of CoNiCrAlY is relatively high, mixture II might not be able to melt or partially melt the powders. Considering the propane consumption and the simulated velocity and temperature of the gas flow, the process parameter with mixture I is used for further investigations.

Fig. 6
figure 6

Comparison of simulated temperature and velocity of gas flow of different mixtures along the centerline

Full size image

The calculated contours of the pressure field and Mach number of mixture I along the centerline are shown in Fig. 7. The indicated pressure is relative to the pressure of the ambient atmosphere. As mentioned in previous section, the extended nozzle throat section is also considered in the simulation. From Fig. 7, it can be seen that the pressure decreases in two stages. In the convergent region of the nozzle, the pressure drops sharply. In the extended nozzle throat region, the pressure decreases slowly before continuing to decrease in the divergent region of the nozzle. In the atmospheric environment, the pressure of the gas stream experiences a fluctuation, the amplitude of which decreases and then remains at the normal atmospheric pressure level. As for the Mach number, the gas flow reaches Ma = 1 at the exit of the nozzle throat section before it continues to increase to Ma > 2. The same phenomenon in the free jet region regarding the fluctuation and dissipation is also observed in the simulated Mach number contour.

Fig. 7
figure 7

Calculated contour of the pressure field and Mach number along the centerline

Full size image

Effect of Particle Size on In-Flight Behavior

In this study, only N2 is used as the carrier gas for transporting the powder. In order to predict the coating properties, it is important to investigate the flight behavior of the particles during the spraying process. Figure 8 shows the simulated axial velocity and temperature of particles of different sizes. Coarse and fine powders are defined by blue and gray lines, respectively. The median particle diameter d50 is described by the solid line, and the diameters d10 and d90 are described by the dashed line. The indices c and f stand for coarse and fine. It can be seen that the particle size has a significant effect on the particle in-flight properties such as temperature and velocity. The fine particles have a higher velocity and are more heated than the coarse particles. As the melting temperature of CoNiCrAlY is relatively high (more than 1,600 K), the coarse particles might not be sufficiently heated, which could lead to a porous coating with significant splat boundaries due to their low ductility (Ref 24). In contrast, the fine particles were heated to the partially molten state and accelerated to a higher velocity region. Since the finer particles were heated to the melting temperature, it is noted that the phase change from solid to liquid state should be included in future studies. In doing so, the correlation between the melting rate and the heat transfer between the gas mixture and the particle need to be considered. Moreover, the correlation between the melting rate and the conductive heat transfer within a particle should be considered in order to accurately predict the particle properties.

Fig. 8
figure 8

Comparison of simulated particle in-flight properties of different sizes in a gas flow from mixture I (AFR = 13.781)

Full size image

Conclusion

In this article, a novel approach to model the AC-HVAF process with pressure inlet boundary conditions and integration of the mixing chamber is presented. The distribution of compressed air in the spray gun is also considered in the simulation model. In-flight properties of powder of different sizes were successfully simulated. The following results were observed:

  • The mixing process can be observed clearly and the mass fraction of propane at the exit of the mixing chamber is considerably uniform

  • The temperature of the coarse powder fraction might be too low for sufficient plastic deformation

  • The fine powder is more suitable for the AC-HVAF process than the coarse powder due to its higher velocity and sufficient heating

As a next step, we can build on this work by validating the simulation results with particle diagnostic system such as DPV-2000 (Tecnar, Montreal, Canada) and SprayWatch 4S (Oseir Ltd., Tampere, Finland). In addition, the simulation model could be extended to consider the phase change of the particles from solid to liquid state. In order to increase the accuracy in predicting the particle in-flight properties, the influence of the powder feed rate on the temperature distribution in the combustion chamber will also be investigated in future work. As a further extension, heat transfer between the burner housing and the compressed air, which is also used for cooling, could provide a better understanding of the entire spray gun system. The model can be used in future work for a parameter study for a coating of CoNiCrAlY with low oxidation and low porosity. Finally, the studied parameters can be applied and their significance for the coating properties can be further investigated.