Introduction

Powder metallurgy is a commonly used method for manufacturing of cutting tool inserts. Cemented carbide powder makes up the important part of the process, and there is a need to investigate how the initial powder properties influence the behavior at later stages of compaction. Predicting the compaction behavior based on measurements is certainly beneficial as investigating a powder by a full process of pressing and sintering can be both a time consuming and costly avenue of approach.

It goes without saying that modeling is also a very important issue when it comes to predicting the compaction behavior. In particular, this concerns macro- and micromechanical modeling. In the first case (macromechanical modeling), macroscopic constitutive models are at issue where powder compaction to high density is treated phenomenologically assuming a porous solid and using, for example, a Gurson model (Ref 1), a CamClay model (Ref 2) or a Drucker–Prager CAP model (Ref 3, 4). When analysing cemented carbide powder materials, most often the Drucker–Prager CAP model (Ref 4) is used. The application of this model to numerical analysis of different kinds of cutting inserts (and in particular concerning the issue of determination of constitutive quantities) has been discussed extensively in, for example, (Ref 5) and (Ref 6). When it comes to a micromechanical approach, either analytical (Ref 7) or numerical methods, such as the discrete element method (DEM) (Ref 8,9,10), are of interest. In (Ref 9) and (Ref 10), DEM simulations are compared with experiments and it is concluded that the numerical results are accurate up to material densities being approximately 50- 60 % of a fully compacted insert, which evidently is not sufficient for simulation of the entire manufacturing process. It should be noted that research has been conducted in order to include the effect from neighboring contacts into micromechanical modeling of powder compaction, (Ref 11) and (Ref 12), to extend the validity of DEM modeling.

At mechanical modeling of compaction of (hard metal) powder materials, strength parameters are of obvious importance. In particular, the granule strength and the green body strength are at issue here. The granule strength is a necessary ingredient when including the fracture behavior in a DEM-analysis, while the green body strength is (for one thing) an important quantity for validation of macromechanical modeling attempts. As in particular experimental determination of the granule strength can be a cumbersome task, it would be interesting to see whether there exists a relevant correlation between these two strength parameters that would simplify such experimental efforts. Accordingly, this is the matter of interest in the present investigation.

Powder materials as well as their resulting pressed green bodies are subjected to testing in order to characterize their properties, and in particular in this work, granule strength and green body strength. Five different tungsten carbide powder materials are produced in a standard production machine, with varying amount of pressing agent (PEG) and different hardness. The two strength properties are of direct importance during production but also as input to the above discussed macro- and micromechanical modeling attempts (as already indicated above). The testing includes powder characterization (granule strength) and green body bending properties (strength). The results are evaluated statistically using the Design of Experiment (DOE) software Modde 12 (Ref 13) in order to determine the correlation between measurements. The described approach resembles the one used in a parallel and recently published investigation concerning the relationship between pressing energy and green strength (Ref 14).

Material and Methods

Material

The cemented carbide powder that is used in this study has been presented previously in (Ref 14) and here only the most important details are discussed. The powder consists of approximately 88 wt.% tungsten carbide (WC), 10 wt.% cobalt (Co), 2 wt.% pressing agent (average value polyethylene glycol, PEG), and 0.5 wt.% alloys. The amount of PEG is, however, varied in the investigation as specified below. (The amount of the other materials are kept constant.) The particle sizes of the raw materials are approximately 1 μm. The spray drying process creates spherical particles with a diameter of approximately 100 μm, which make up the powder. Cobalt (Co) is used as the bonding material. The carbide powder also contains some alloys, for instance chromium carbide which is used to deaccelerate grain growth during sintering. In order to achieve a variation of the properties of the cemented carbide after compaction, the PEG amount is varied according to Table 1. (Note that the PEG molar mass is also varied.) It should be mentioned that during sintering, not investigated here, the pressing agent (PEG) is decomposed, leaving only the cemented carbide in the finished insert.

Table 1 Powder labels, amount [wt.%] of PEG, hardness of PEG (qualitative) and molar mass of PEG (qualitative)
Full size table

Measurements

Two types of measurements are carried through currently. GFP-measurements (“Granularfestigkeits-Prüfsystem”) are performed on single granules to determine the granule strength, while three-point bend (3PB) experiments are used to determine the green strength. GFP is a granule strength measurement system manufactured by Etewe (Ref 15) as described in detail. The material mixtures for the tungsten carbide powder used in both experiments are the same, with, as mentioned above, the PEG amount being varied according to Table 1. (Note that the PEG molar mass is also varied.)

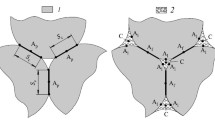
The strength of the granules is determined by the GFP-machine by pressing down a single particle while recording the force and displacement curve until it breaks. In Figure 1, it is shown how spread out particles are seen optically in the GFP.

Fig. 1
figure 1

Spread out particles as seen optically in the GFP. Here, the < 63 µm fraction with an average diameter of 51.86 µm is shown

Full size image

For the measurement, powder is spread out evenly on a flat plate. The machine recognizes single particles optically, as seen in Fig. 1. From every powder, 500 granules are measured. As the granules are not sorted out in any way, the measurement includes some granules that are already broken or otherwise faulty, or have significantly different constitutive behavior due to, for example, PEG-concentration. In order to have only intact and unbroken granules considered, as well as granules with not too deviating constitutive behavior, the data are corrected by setting a minimum and maximum break pressure as well as strain limits according to

$$0.{\text{1 MPa }} < F_{est} < { 2}.{\text{5 MPa}}; \, 0.0{1 } < \varepsilon < \, 0.0{8}$$
(1)

Measurements that do not fulfill these limits are disregarded. Note that the break pressure is defined in Equation (2), and ε is the global engineering strain in the z-direction (see Fig. 1) at granule rupture. All powders are run twice to find the measurement uncertainty, and the data are collected and analysed using the commercial software MATLAB (Ref 16).

The recorded properties of interest are the maximum force before rupture, strain prior to rupture, granule size (measured optically), and relative humidity in the surrounding air. The break pressure, or granule strength, is a measurement on the stress acting in the granule just prior to fracture. It is defined according to

$$F_{est} = \, 16F_{B} /\left( {\pi \left( {d_{x} + d_{y} } \right)^{2} } \right)$$
(2)

In (2), FB is the maximum force and dx and dy are measured granule diameters in the x- and y-directions, respectively (see Fig. 1).

For testing of the green strength, green body cuboid pieces with measurements 6.025 mm x 6.245 mm x 25 mm are pressed in a standard production machine. The cuboids are pressed with a maximal pressing force of 14.6 kN to 15.0 kN. The test specimens are subject to a 3PB testing with a standard load cell, as shown in Fig. 2, where the green body is placed on two support pins and centered with respect to the loading pin. The loading pin then moves in a vertical direction until the body cracks. The test is repeated 3 times for every type of powder. In order to minimize the effect from humidity, the tests have been performed randomized during two after each other following days.

Fig. 2
figure 2

Test setup for the three-point bending test. Picture taken after test ending

Full size image

From the test, the stress as a function of the flexural strain is recorded. The fracture stress σB is calculated based on standard engineering beam theory assuming elastic material behavior, according to

$$\sigma_{B} = \, {{3F_{B} l} \mathord{\left/ {\vphantom {{3F_{B} l} {\left( {2BH^{2} } \right)}}} \right. \kern-\nulldelimiterspace} {\left( {2BH^{2} } \right)}}$$
(3)

In (3), FB is the applied bending force at fracture and l = 20 mm is the length between the support pins.

Results and Discussion

In this section, the experimental results pertinent to the granule strength and green strength measurements are presented separately. After that, results related to the correlation between these properties are presented. In the latter case, as mentioned above, the Design of Experiment (DOE) software Modde 12 (Ref 13) is used.

Granule Strength Results

The GFP results for the granule strength, or break pressure, are shown in Fig. 3. These results will then be used for the correlation analysis. Analysing the experimental outcome in some detail it is noted that the molar mass of the PEG is the factor that affects the strength the most. A high value on the molar mass increases the strength. There is a clear distinction of the powders, as powders with a hard type of PEG generally can take up more load. Additionally, the granule size has some effect as larger granules tend to break at lower pressures. These trends can also be seen in Fig. 3.

Fig. 3
figure 3

Scatter plot of the GFP-measured break pressure (granule strength) calculated for all granules, as a function of the granule diameter. The plot shows significant differences between powders. Note that M 2.0 (ref) is the same material as M 2.0 but manufactured at a different site in order to ensure generality of the results

Full size image

Figure 4 shows how the relative humidity affects the granule strength. The results in the figure are pertinent to one powder, S 1.5, measured on four different occasions, and it shows a weak trend toward higher humidity resulting in weaker granules. More importantly though, the effects from the PEG and the granule size are obviously much larger.

Fig. 4
figure 4

Scatter plot of GFP-measured break pressure (granule strength) as function of the relative humidity. The figure shows results for one powder, S 1.5, with properties according to Table 1

Full size image

In the context of granule strength measurements, a comment regarding the validity of Eq 2 seems appropriate. Obviously, this is a global measure on the granule strength remembering that σB is the average stress in the granule at failure. A more detailed analysis of this feature would have to be based on the local contact stresses given by contact mechanics analyses for elastic materials (Ref 17) or elastoplastic materials (Ref 18). Such an analysis would require detailed knowledge about the constitutive characteristics of the granule. In the present case though, correlation between properties is at issue, and not highly accurate values on σB, and for this purpose, average values from Eq (2) are sufficient.

Green Strength Results

The green strength is as mentioned above determined by a three-point bending test, where the maximal force prior fracture is recorded. The green strength (fracture stress) is then determined from Eq (3). Figure 5 shows the results of the bending tests, where the fracture stress is plotted against the strain prior to fracture. Note that the strain, as well as the fracture stress in Eq (3), is determined according to standard engineering beam theory.

Fig. 5
figure 5

Results of the three-point bending test measurements. The markers correspond to each test’s breaking point and show a clear difference for the different PEG types where harder PEG correlates to higher stress prior rupture. Note that M 2.0 (ref) is the same material as M 2.0 but manufactured at a different site in order to ensure generality of the results

Full size image

The test results show large differences for the different PEG types. It can be seen that the powder H 2.5 endures significantly higher loads compared to the other powders. It can also be seen that the harder the PEG type in the powder is, the higher the fracture stress becomes.

It should be mentioned that also in the green strength analysis, simplifications are made concerning the evaluation. As mentioned above, standard engineering beam theory is used to determine fracture stress and strain which consequently limits the analysis to elastic material behavior. From inspection of the bending test outcome, it can be concluded, however, that this is a satisfactory assumption as very little nonlinearities are found. Furthermore, as mentioned above in relation to the granule strength results: Only correlation of the properties is at issue.

Correlation Results

Correlation between the two properties is tested using so-called multiple linear regression (MLR) remembering that in this case, two response variables are at issue. The analysis is as previously mentioned performed using the Design of Experiment (DOE) software Modde 12 (Ref 13). Correlation is presently determined based on the coefficient of determination R2. R2 takes on values between 0 and 1 where 1 indicates perfect correlation between the quantities at issue.

The results from the analysis are depicted as a scatter plot in Fig. 6. Clearly the results are very well fitted to a linear curve (as also indicated in Fig. 6). The R2 coefficient for a linear fit takes on the value 0.9662 indicating almost perfect correlation.

Fig. 6
figure 6

Scatter plot of fracture stress for a green body and the break pressure (granule strength) for the granules

Full size image

In order to get some insight into the physics behind the present results, micrographs were taken of the cracks in the green body at three-point bend testing. A representative picture of the crack propagation is shown in Fig. 7 where it is obvious that the crack has propagated in both a trans- and intergranular path. No further studies of this matter was performed here, but it should be noted in passing that the fracture behavior of granule materials has been investigated using DEM and delamination modeling in, for example, (Ref 10) and (Ref 19, 20). The present results are indeed valuable for such types of analyses.

Fig. 7
figure 7

Crack propagation in a green body following a three-point bending test

Full size image

Conclusions

Correlation between the powder material properties granule strength and green strength was investigated experimentally and numerically using a Design of Experiment (DOE) software. The investigation was pertinent to cemented carbide powder materials. In order to achieve a variation of the properties of the cemented carbide after compaction, the PEG (pressing agent) amount and PEG molar mass was varied.

It is found that the correlation between the two quantities is extremely good with the R2 coefficient for a linear fit taking on the value 0.9662. From a physical point of view, good correlation is perhaps not surprising as intergranular crack propagation (during a three-point bending test) is much harder to achieve than intergranular crack propagation. What is surprising though is that the correlation is essentially perfect indicating that crack propagation features are completely determined by the strength of the granules.

From a practical point of view, the results suggest that it is possible to get information about one of the properties for a similar set of materials by experimentally determine the other one. This is a valuable finding not previously presented in the literature. The results are applicable for powder materials granulated with a pressing agent and being spray dried with PEG to roughly the same size.