Abstract
We analyze the general equilibrium effects of countercyclical unemployment benefit policies. Our heterogenous-agent model features costly job search with imperfect insurance of unemployment risk and individual savings. Our model predicts: (1) the additional unemployment under a countercyclical policy relative to that under an acyclical policy to be a superlinear function of the aggregate shock?s size, (2) a higher unemployment rate sensitivity to UI policy changes when individual savings are relatively low. Our estimates of the effects of UI policy changes are based on transition dynamics following a large, unanticipated increase in the unemployment rate.



Similar content being viewed by others
Notes
The CARES Act of 2020, for instance, added $600 per week to the pre-existing level of UI benefits (the maximum pre-existing benefits varied from $200 per week to $600 per week across states) and extended the duration of benefits, initially to a maximum of 39 weeks, and later extending this to 53 weeks (the pre-existing duration for most states was 26 weeks). Similarly, UI benefits following the Great Recession were extended by 99 weeks from the usual 26 weeks.
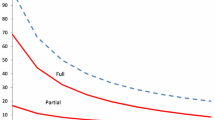
This intuition holds over a short, finite period following the aggregate shock. The excess unemployment rate approaches zero as \(t\rightarrow \infty \) when the equilibria under both policies revert back to the same steady-state.
[11] analyzes implications of UI policy over the business cycle in a model featuring individual savings but do not consider the disincentives to job search from higher UI payments since the model does not feature costly job search.
Instead of modeling the dependence of UI payments on recent earnings through accumulated savings, an alternate choice would be to make UI payments depend explicitly on the agent’s past year’s labor income. The latter modeling choice would require us to introduce cross-sectional heterogeneity in wages in order to capture differences among high and low income agents in their incentives to search for a job. Because heterogeneous wages would significantly deviate from standard general equilibrium models in the UI literature, we leave its analysis for future research.
For instance, Ganong et al. [26] report that UI benefits in Nevada reach their maximum for individuals with weekly income above $902. This is close to the mean income of $886 per week in that state. Both of these are values for 2019.
In our model, the cost of being unemployed is inversely related to the agent’s savings k because a higher capital stock provides: (i) a higher capital rental income and (ii) a larger buffer to weather an unemployment spell for a longer period of time.
References
Krueger, A.B., Meyer, B.D.: Labor supply effects of social insurance. Working Paper 9014, National Bureau of Economic Research (2002)
Chetty, R.: Moral hazard versus liquidity and optimal unemployment insurance. J. Polit. Econ. 116(2), 173–234 (2008)
Hansen, G.D., Imrohoroglu, A.: The role of unemployment insurance in an economy with liquidity constraints and moral hazard. J. Polit. Econ. 100(1), 118–142 (1992)
Wang, C., Williamson, S.D.: Moral hazard, optimal unemployment insurance, and experience rating. J. Monet. Econ. 49(7), 1337–1371 (2002)
Achdou, Y., Han, J., Lasry, J.-M., Lions, P.-L., Moll, B.: Income and wealth distribution in macroeconomics: a continuous-time approach. Rev. Econ. Stud. 89(1), 45–86 (2022)
Mian, A.R., Straub, L., Sufi, A.: The saving glut of the rich. Working Paper 26941, National Bureau of Economic Research (2021)
Jung, P., Kuester, K.: Optimal labor-market policy in recessions. Am. Econ. J. Macroecon. 7(2), 124–156 (2015)
Landais, C., Michaillat, P., Saez, E.: A macroeconomic approach to optimal unemployment insurance: theory. Am. Econ. J. Econ. Pol. 10(2), 152–181 (2018)
Mitman, K., Rabinovich, S.: Do unemployment benefit extensions explain the emergence of jobless recoveries? Technical report, CEPR (2019)
Pei, Y., **e, Z.: A quantitative theory of time-consistent unemployment insurance. J. Monet. Econ. 117, 848–870 (2021)
Krusell, P., Mukoyama, T., Sahin, A.: Labor-market matching with precautionary savings and aggregate fluctuations. Rev. Econ. Stud. 77(4), 1477–1507 (2010)
Bayraktar, E., Mitra, I., Zhang, J.: A quantitative comparison of unemployment benefit extension and level increase. Working Paper 10211, ssrn (2023)
Shavell, S., Weiss, L.: The optimal payment of unemployment insurance benefits over time. J. Polit. Econ. 87(6), 1347–62 (1979)
Hopenhayn, H., Nicolini, J.P.: Optimal unemployment insurance. J. Polit. Econ. 105(2), 412–38 (1997)
Shimer, R., Werning, I.: Liquidity and insurance for the unemployed. Am. Econ. Rev. 98(5), 1922–42 (2008)
Lentz, R., Tranaes, T.: Job search and savings: wealth effects and duration dependence. J. Law Econ. 23, 467–89 (2005)
Kroft, K., Notowidigdo, M.J.: Should unemployment insurance vary with the unemployment rate? Theory and evidence. Rev. Econ. Stud. 83(3), 1092–1124 (2016)
Nakajima, M.: A quantitative analysis of unemployment benefit extensions. J. Monet. Econ. 59(7), 686–702 (2012)
Chetty, R.: Consumption commitments, unemployment durations, and local risk aversion. Working Paper 10211, National Bureau of Economic Research (2003)
Card, D., Chetty, R., Weber, A.: Cash-on-hand and competing models of intertemporal behavior: new evidence from the labor market. Quart. J. Econ. 122(4), 1511–60 (2007)
Kroft, K., Notowidigdo, M.J.: Should unemployment insurance vary with the unemployment rate? Theory and evidence. Rev. Econ. Stud. 83 (2016)
Krueger, A.B., Mueller, A.I.: Job search and unemployment insurance: New evidence from time use data. J. Public Econ. 94(3), 298–307 (2010)
DellaVigna, S., Heining, J., Schmieder, J.F., Trenkle, S.: Evidence on job search models from a survey of unemployed workers in germany. Working Paper 27037, National Bureau of Economic Research (2020)
Marinescu, I., Skandalis, D.: Unemployment insurance and job search behavior. Quart. J. Econ. 136(2), 887–931 (2021)
Achdou, Y., Buera, F.J., Lasry, J.-M., Lions, P.-L., Moll, B.: Partial differential equation models in macroeconomics. Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences 372(2028), 20130397 (2014). https://doi.org/10.1098/rsta.2013.0397 , https://royalsocietypublishing.org/doi/pdf/10.1098/rsta.2013.0397
Ganong, P., Noel, P., Vavra, J.: Us unemployment insurance replacement rates during the pandemic. J. Public Econ. 191 (2020)
Chodorow-Reich, G., Coglianese, J., Karabarbounis, L.: The macro effects of unemployment benefit extensions: a measurement error approach. Q. J. Econ. 134(1), 227–279 (2019)
Farooq, A., Kugler, A.D., Muratori, U.: Do unemployment insurance benefits improve match and employer quality? evidence from recent u.s. recessions. Working Paper 27574, National Bureau of Economic Research (July 2020). https://doi.org/10.3386/w27574. http://www.nber.org/papers/w27574
Acknowledgements
We thank Toni Braun, Simon Fuchs, Mark Jensen, Zoe **e, and Yu Xu and seminar participants at the University of Michigan and the Federal Reserve Bank of Atlanta for useful comments and suggestions. E. Bayraktar is supported in part by the National Science Foundation under grant DMS-2106556 and in part by the Susan M. Smith Professorship. J. Zhang is supported by the National Natural Science Foundation of China under Grant No.12201113. The views expressed here are ours and not necessarily those of the Federal Reserve Bank of Atlanta, the Federal Reserve System or the National Science Foundation.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Financial interests
The authors have no competing interests to declare that are relevant to the content of this article.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Algorithm
Algorithm
1.1 Algorithm for stationary equilibrium
In the precrisis period \(t<0\), the UI payments are a a piece-wise linear function of k, \(y_1^{\star }(k) = \min \left( a + b (k-{\underline{k}}, {\bar{y}}) \right) \), which increases linearly with slope b for individuals with \(k \le k_H = {\underline{k}}+\frac{{\bar{y}}-a}{b}\). Given these parameters \(a, b, {\bar{y}}\), we consider a stationary equilibrium which can be summarized by a coupled HJB-KF equation system. For \(k \in [{\underline{k}}, \infty )\),
where \(c^{\star }_1, s^{\star }\) are such that the right hand side of (A1) attains maximum, \(c^{\star }_2\) is such that the right hand side of (A2) attains maximum, more specifically,
and \(r^{\star }, w^{\star }, \theta ^{\star }\) satisfy market clearing conditions
with \(K^{\star } = \int _{{\underline{k}}}^{\infty } k(g_1(k)+ g_2(k)) dk\) and \(L^{\star } = \int _{{\underline{k}}}^{\infty } g_2(k) dk\).
Notice that \(w^{\star } = w(r^{\star }) = (1-\alpha ) (\frac{r^{\star }}{\alpha })^{\alpha /(\alpha -1)}\) while \(\theta ^{\star }\) depends on both the interest rate and the distribution functions.
Our computational approach is adopted from [5] (hereafter referred to as “AHLLM”). In AHLLM, individuals make decisions solely on consumption and their employment state is determined by an exogenous two-state continuous-time Markov chain. Consequently, the employment rate in the stationary equilibrium is a constant \(L= \frac{\lambda _{1, 2}}{\lambda _{1, 2}+\lambda _{2, 1}}\) where \(\lambda _{1,2}(\lambda _{2,1})\) is the constant intensity rate of transition from the unemployment(employment) state to the employment(unemployment) state. For a each given interest rate r, the total capital of demand \(K_d(r) = L(\frac{r}{\alpha })^{1/(\alpha -1)}\) can be computed directly and a total capital of supply \(K_s(r) = \int _{{\underline{k}}}^{\infty } k(g^r_1(k)+ g^r_2(k)) dk \) can be obtained by solving a system of HJB-KF equations. Here, \(g^r_1\) and \( g^r_2\) are solutions of KF equations whose coefficients depend on the solution of the HJB equation given the interest rate r and the corresponding \(w= w(r)\).
In AHLLM, a fixed-point algorithm is employed to find the interest rate r such that \(K_s(r) = K_d(r)\), indicating a stationary equilibrium. In each iteration of the fixed point algorithm, AHLLM uses a variate of finite difference method, "upwind-scheme", to solve HJB equations. The solution of HJB equations are then used to generate coefficients in KF equations, whose solution is obtained by solving a linear equation system. The value of r will be adjusted after each iteration based on whether there is an excess demand or an excess supply of total capital.
In our case, we aim to find a pair \((r^{\star }, \theta ^{\star })\) such that not only does \(K_s(r^{\star }) = K_d(r^{\star })\) hold but also (A7) holds. We decompose this task into a two-layer fixed-point algorithm. The algorithmic details are outlined in Algorithm 1, where, in the second loop of the fixed point algorithm, we obtain L and \(\theta \) such that (A7) holds for each \(r^{(n)}\) in the first loop. In the first loop, we iterate over \(r^{(n)}\) until \(K_s(r^{\star }) = K_d(r^{\star })\) holds.
Remark 2
In the algorithm, all value functions \(v_i^{\star }\) and density functions \(g^{\star }_i\) are represented by \(2\times I\) matrices, where I is the number of mesh points on interval \([{\underline{k}}, {\bar{k}}]\) for a large \({{\bar{k}}}\). The \(\Vert \cdot \Vert \) norm is \(\Vert \cdot \Vert _{\sup }\) on \(2\times I\) matrices.
Remark 3
For fixed \(r^{(n)}, \theta ^{(n)}\), the solution of (A2,A1) is obtained using "upwind-scheme", as in AHLLM. For detailed information, please refer to the Online appendix of AHLLM.
1.2 Algorithm for time dependent equilibrium
Although we have infinite horizon in our problem, we do not start from the steady state due to the unanticipated shock at time \(t = 0\). Moreover, with a time-dependent UI payments \(y_{1t}\), the equilibrium solution for our model is in form of transition dynamics. As in AHLLM, for the convenience of numerical computation, we assign a large time T as the terminal time and assume that with this long enough time T, the economy has converged to the same steady state as in the precrisis period. We use the time-dependent equilibrium of this finite horizon problem to approximate the transition dynamics of the original infinite horizon problem, which can be summarized by a coupled HJB-KF equation system. For \(k \in [{\underline{k}}, \infty ), t\in [0, T]\),
and \(r_t, w_t, y_{1t}, \theta _t\) satisfy
with given employment rate \(L^{\star }\) in steady state, \(K_t = \int _{{\underline{k}}}^{\infty } k(g_1(k,t)+ g_2(k,t)) dk\) and \(L_t = \int _{{\underline{k}}}^{\infty } g_2(k,t) dk\).
The terminal conditions are given by \(v_2(k,T) = v_2^{\star }(k), v_1(k, T) = v_1^{\star }(k)\) where \(v_2^{\star }(k), v_1^{\star }(k)\) are the solutions of the stationary equilibrium (A1,A2,A3,A4). The initial distributions \(g_1(k, 0), g_2(k,0) \) are given by (7) and \(g_2(\cdot , 0) = g_1^{\star }(\cdot , 0)+ g_2^{\star }(\cdot , 0) - g_1(\cdot , 0)\). This indicates a uniform job loss for all k and guarantees a drop of employment rate from \(L^{\star }\) to an exogenous constant \(L_0\).
With the above initial and terminal conditions, Algorithm 2 outlines the procedure for solving (A8,A9, A10, A11). In each iteration the value functions \(v_i(\cdot , t)\) is derived backward in time given the terminal condition and the density function \(g_i(\cdot , t)\) is derived forward in time given the initial condition. A detailed description is also available in the Online appendix of AHLLM. Paths of \((K_t, L_t, \theta _t)\) are updated simultaneously in each iteration based on the density functions \(g_i(\cdot , t)\). The algorithm converges to the equilibrium when the maximum change in paths of \((K_t, L_t, \theta _t)\) between two consecutive iterations is sufficiently small.
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Bayraktar, E., Mitra, I. & Zhang, J. Countercyclical unemployment benefits: a general equilibrium analysis of transition dynamics. Math Finan Econ (2024). https://doi.org/10.1007/s11579-023-00351-x
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s11579-023-00351-x