Temperature effects on adsorption and capillarity water retention mechanisms in constrained unsaturated soils

Abstract

This paper focuses on the impact of elevated temperatures on the adsorptive and capillarity water retention mechanisms of unsaturated soils under constrained (constant volume) conditions. This topic is critical for simulating the thermo-hydraulic behavior of soils in hydrogeological or geotechnical applications, including climate change effects on near surface soils, energy piles or soil borehole thermal energy storage systems in unsaturated soil layers, and buffers for geological nuclear waste repositories. A nonisothermal soil water retention curve (SWRC) that separately considers the temperature-dependency of the key parameters governing adsorptive and capillarity water retention mechanisms and soil physical parameters (e.g., surface tension, contact angle, adsorption capacity, cation exchange capacity, mean cavitation suction, air entry value and equilibrium film thickness) was developed to provide insights into the impact of temperature on water retention over the full suction range. The nonisothermal SWRC was validated using experimental data on high plasticity clays, with a good prediction of temperature effects on adsorption and capillarity water retention mechanisms in constrained unsaturated soils.

1 Introduction

The soil water retention curve (SWRC) is a fundamental constitutive relationship governing water storage in unsaturated soils that is used in quantifying water distribution and flow [16, 46]. The SWRC is also critical for interpreting the mechanical behavior of unsaturated soils, such as shear strength [18, 47], deformation [35, 48, 67], and effective stress [47, 114]. The SWRC reflects the equilibrium condition between the volumetric water content (or degree of saturation) and suction. Suction is composed of osmotic suction and matric suction components. Osmotic suction arises in the presence of chemical concentration gradients [84, 85], while matric suction describes the soil water potential with respect to pure water relative to ambient pore air pressure in the absence of a salt solution [16, 46]. The matric suction can be quantified by two physical mechanisms: (1) capillarity associated with the presence of a curved air-water meniscus between soil particles, and (2) adsorption associated with water retention on or within soil particles due exchangeable cation hydration, mineral surface hydration, or crystal interlayer surface hydration [46, 113]. The adsorption and capillarity mechanisms control the amounts of water storage in the hydration, pendular, funicular, and capillary regimes of the SWRC when moving from high to low matric suction values [12].

Because the SWRC governs the interactions between soil particles, pore air, and pore water, there are a number of variables that affect the SWRC, including those related to particle mineralogy variables (e.g., cation exchange capacity, specific surface area, etc.), soil structure variables (e.g., void ratio, pore size distribution, etc.), and environmental variables (e.g., temperature, humidity, etc.) and pore fluid characteristics (e.g., pH, salinity, etc.) [3, 11, 19, 20, 36, 37, 39, 43, 65, 84, 89, 115]. Multiple parameterized SWRC models have been proposed to represent the evolution of the SWRC over the full suction range, while temperature effects have seldom been considered from a mechanistic perspective.

Given the emergence of hydrologic problems associated with nonisothermal near-surface water flow in soils associated with climate change and geotechnical problems that involve nonisothermal analysis (such as thermally active geotechnical structures combined with geothermal heating/cooling systems, and radioactive waste geological disposal repositories), there is an urgent need to investigate the SWRC under elevated temperatures. Several researchers have performed experimental tests to examine changes in the shape of the SWRC at high temperatures and generally revealed a downward shift of the SWRC, resulting in a decrease in volumetric water content under constant suction [22, 25, 57, 63, 89, 91, 95, 99, 100]. This phenomenon is typically explained by temperature-induced changes in soil and water physicochemical parameters (e.g., surface tension, contact angle, clay fabric, pore water chemistry, etc.) [4, 15, 69, 72, 99]. Several temperature-dependent variations have been incorporated into the existing SWRC models originally developed for isothermal conditions [6, 25, 33, 41, 63, 70, 76, 78, 80, 86, 118]. For instance, Grant and Salehzadeh [25] explored temperature effects on the water-air interfacial tension, contact angle, and the enthalpy of immersion per unit area. They proposed an equation describing the matric suction between the elevated and reference temperatures. A similar approach was adopted in other studies [2, 4, 78]. Some researchers have extended the water retention regimes-based SWRC model into nonisothermal conditions. For example, Vahedifard et al. [87] analyzed the temperature effects on adsorption and capillarity water retention mechanisms separately and found that temperature effects on the SWRC of sands, silts, and clay can be significant, particularly for fine-grained soils subjected to high temperatures (e.g., > 60 °C). Recently, McCartney [60] proposed a conceptual model based on the Lu [46] SWRC model considering temperature effects on surface tension, wetting fluid-solid contact angle, cavitation suction, maximum adsorption capacity, and maximum suction to characterize the coupled thermo-hydraulic properties of MX80 bentonite in engineered barrier systems. The conceptual model indicated that water retention may increase or decrease with temperature in different water retention regimes due to the temperature dependency of these different parameters. However, the specific relationships between the aforementioned parameters and temperature, as well as their underlying mechanisms, were not fully explored.

Understanding temperature effects on the SWRC across the full matric suction range is particularly important for compacted sodium bentonite used as a buffer material in high-level radioactive waste (HLW) disposal repositories [14, 54,55,56, 64, 77, 107, 116, 119]. This is especially the case as the temperatures in buffer systems in repositories may reach values up to 200 °C, much higher than that in other hydrologic systems or geotechnical applications [26, 52, 53, 117]. Lu and McCartney [51, 52] conducted tank-scale tests on compacted MX80 bentonite and measured temperature-dependent transient SWRCs at different locations under coupled heat transfer and water imbibition processes with a central temperature of 200 °C simulating high thermal gradients in the repository. Sanchez [73], Lloret and Villar [44] proposed an empirical equation for the SWRC of compacted FEBEX bentonite. With the experimental SWRCs of compacted MX80 bentonite determined under controlled temperatures, Jacinto et al. [33] modified the SWRC model of van Genuchten [88] by considering the temperature effects on porosity, air entry suction, slope coefficient of the linear part of the retention curve, as well as the saturated water content. Wan et al. [99] investigated the temperature effects on the SWRC of compacted GMZ01 bentonite at temperatures ranging from 20 to 80 °C and reported that the influence of temperature on the water retention capacity significantly depends on suction. However, the concept of residual water content (or residual suction) may be an artifact of the way that the SWRC has been measured in the past (e.g., liquid outflow using a pressure plate) and that if vapor equilibrium had been used, they might have been able to reach a maximum suction. Modifying the SWRC of Lu [46] provides a more fundamental approach to considering the different ways that temperature may affect water retention over the full range of suction.

In this study, a new nonisothermal SWRC that separately considers the temperature-dependency of the key parameters governing different water retention mechanisms and soil physical parameters was developed to provide insights into the impact of temperature on water retention over the full suction range. The new nonisothermal SWRC model will be useful for simulating coupled heat transfer and water flow processes in hydrogeologic and geotechnical applications involving elevated temperatures.

2 Background

Among the isothermal SWRC models, three widely used SWRC models are those of Brooks and Corey [8], van Genuchten [88], and Fredlund and **ng [17]. These SWRC models have parameters that describe the shape of the SWRC in the capillary regime established from experimental studies (i.e., a parameter describing the air entry suction and a parameter describing the pore size distribution) but do not clearly distinguish between the different water retention mechanisms beyond a parameter governing the residual degree of saturation. Building on the model of Revil and Lu [66], Lu [46] proposed a generalized SWRC that more explicitly considers the adsorption and capillarity water retention mechanisms by introducing four new matric suction-related parameters (i.e., adsorption capacity, adsorption strength, mean cavitation, and maximum suction), as described by the following set of equations:

$$\theta (\psi )={\theta }_{{\text{a}}}(\psi )+{\theta }_{{\text{c}}}(\psi )$$

(1)

$${\theta }_{{\text{a}}}(\psi )={\theta }_{{\text{a}},{\text{max}}}\left\{1-{\left[{\text{exp}}\left(\frac{\psi -{\psi }_{{\text{max}}}}{\psi }\right)\right]}^{{M}_{{\text{L}}}}\right\}$$

(2)

$${\theta }_{{\text{c}}}(\psi )=\frac{1}{2}\left[1-{\text{erf}}\left(\sqrt{2}\frac{\psi -{\psi }_{{\text{c}}}}{{\psi }_{{\text{c}}}}\right)\right]\left[{\theta }_{{\text{s}}}-{\theta }_{{\text{a}}}(\psi )\right]{\left[1+{\left(\alpha \psi \right)}^{{N}_{{\text{L}}}}\right]}^{1/{N}_{{\text{L}}}-1}$$

(3)

where ψ is the matric suction (kPa), ψ_max is the maximum matric suction (kPa) which corresponding to the endpoint of the SWRC when the water content is zero, ψ_c is the mean cavitation suction (kPa) that is associated with the physical-phase transition point between the adsorption and capillarity mechanisms, θ(ψ) is the (volumetric) water content (m³/m³) corresponds to the suction ψ, θ_a(ψ) and θ_c(ψ) represent the water content (m³/m³) corresponds to the adsorption and capillarity mechanism respectively, θ_s is saturated water content (m³/m³) equal to porosity of the soil, θ_a,max is the adsorption capacity (m³/m³) which corresponds to the maximum water content contributed by the adsorption mechanism, M_L is the adsorption strength (dimensionless) that controls the changing rate of adsorption near the maximum matric suction and is only controlled by mineral type and quantity and bears little relation to pore-size distribution, N_L is capillary pore-size distribution parameter (dimensionless) that controls the curve slope in the capillary regime, α is the reciprocal of the air entry suction (1/kPa) which is associated with the inflection point of the SWRC at high water content range, and erf() is the error function. An essential feature of Eq. (2) is that the parameter M_L does not control the total amount of the adsorbed water, which is governed by the adsorption capacity θ_a,max. Cavitation is the process of forming vapor bubbles inside or on the boundary of a liquid body under tension. This phase transition phenomenon generally occurs in water when the liquid water pressure falls below the saturated vapor pressure, in which case the intermolecular water pressure essentially reaches the tensile strength of liquid water [7, 58]. Although the parameter ψ_c in Eq. (3) has a clear physical meaning, the method to determine this parameter is not well established, meaning that the value of ψ_c is essentially used as a fitting parameter in practice. While the SWRC model of Lu [46] was developed for isothermal conditions, the fact that it explicitly considers the adsorption and capillarity water retention mechanisms facilities the incorporation of temperature effects into the individual parameters. Similar to Lu [46], the term “suction” in follow context refers specifically to matric suction, excluding osmotic effects.

3 Nonisothermal SWRC model

The proposed nonisothermal SWRC model is developed based the individual ways that temperature may affect the adsorption and capillarity water retention mechanisms. In a water-saturated soil, there are three types of pore water, including bound water, capillary water that can be drained, and trapped water that is not bound or drainable. Among them, the sum of the bound water plus the trapped water is attributed to the adsorption force [66]. Without loss of generality of the water retention mechanism, this study mainly focuses on the high plasticity clayey soils used in nuclear waste repository buffer systems (e.g., Boom clay, bentonite, etc.), which show significant adsorption compared to granular soils and retain water over a wide range of suction. Although bentonite is composed of various minerals, the main constituent is montmorillonite (above 75–95%), which controls the soil water retention characteristics and other performance features of buffer systems [44, 91, 92, 99]. The influence of other minor mineral components in bentonite (i.e., quartz, plagioclase, calcite, etc.) is not in the scope of this paper. It is useful to first review the effects of temperature on each of the key parameters in the SWRC of Lu [46] focusing on a mono-dispersed bentonite with particle-scale characteristics represented by those of montmorillonite. This assumption is necessary to effectively up-scale from the particle scale to the soil macrostructure scale in evaluating temperature effects. Although the SWRC can be expressed as a relation between suction and gravimetric water content [99, 112], the SWRC form of Lu [46] and some other works [60, 66, 71, 87], i.e., suction vs. volumetric water content or degree of saturation is used in this study. This approach simplifies issues in converting between gravimetric and volumetric water contents due to the greater density of adsorbed pore water.

3.1 Temperature effects on adsorption

Adsorption occurs at high suctions or low water contents, where cation hydration, crystal layer surface hydration, and particle surface hydration take place [38, 61]. Cation hydration operates in the maximum matric suction range as its origin is the Coulomb electric force at the atomic scale. Although an approximately constant value of the maximum matric suction (e.g., ~ 1.0 GPa) was assumed in some previous studies on the SWRC [17, 46, 99], it should be noted that this parameter is intrinsically related to the endpoint of the SWRC when the soil is dry, while the value could be temperature dependent. Lu and Khorshidi [49] proposed a relationship for the maximum suction based on the Brunauer-Emmett-Teller (BET) model [9], given as follows:

$${u}_{{\text{max}}}=\frac{RT}{3{000v}_{w}}c$$

(4)

$$c={\text{exp}}\left(\frac{{E}_{1}-{E}_{L}}{RT}\right)$$

(5)

where u_max is the maximum suction (kPa), v_w is the molar volume of water (0.000018 m³/mol), R is the universal gas constant (8.31432 J/mol/K), T is the absolute temperature in Kelvin, c is the BET equilibrium constant of the soil (dimensionless) that related to the enthalpy of sorption for the first molecular layer of water (Fig. 1), E₁ is the heat of adsorption for the first layer, E_L is the heat of adsorption for the second and higher layers and is equal to the heat of liquefaction. The difference between the two energy parameters (E₁-E_L) in the exponent is the energy needed to transfer from adsorbed gas to liquid. Since the (E₁-E_L) is independent of temperature, the temperature-dependence of parameter c can be determined by Eq. (5). Here, the maximum suction u_max can be regarded as maximum matric suction ψ_max as the gravitational and osmotic contributions are assumed to be negligible. An example of the temperature dependence of ψ_max for temperatures between 273 to 473 K is shown in Fig. 1.

Fig. 1

Example of the temperature dependence of maximum matric suction and BET equilibrium constant of MX80 bentonite

For suctions below ψ_max, the van der Waals force is primarily responsible for inner-layer surface hydration, and particle surface hydration gradually plays a significant role as the Coulomb force diminishes rapidly as hydration water increases beyond a few layers of water molecules. The total amount of the adsorption water, controlled by both Coulomb and van der Waals forces, corresponds to the adsorption capacity near the lower bound suction of the adsorption [66, 83]. As previous definitions for the adsorption capacity have issues when applied to compacted soils [66], a new equation for the adsorption capacity is proposed:

$${\theta }_{{\text{a}},{\text{max}}}={(1-\theta }_{s})\left(\frac{CEC}{{\overline{\xi }}_{s}}+{b}_{w}\right)$$

(6)

where θ_a,max is the adsorption capacity (m³/m³), CEC is the cation exchange capacity (meq/g), b_w is a temperature-dependent model parameter associated with the amount of water trapped in the pore space during desorption that denotes the excess mass of water per gram of dry soil, on the order of 0.10 g/g [66], and ${\overline{\xi }}_{s}$ is a model parameter reflecting the slope of the sorption curve that can be calculated as follows:

$${\overline{\xi }}_{s}=\frac{c-1}{c}\frac{{CEC}_{{\text{r}}}}{{v}_{m,{\text{r}}}}$$

(7)

where v_m represents the gravimetric water content when the first monolayer is fully saturated, CEC_r and v_m,r are the values of CEC and v_m at a reference temperature of 293 K. For clay minerals with high CEC, the value of ${\overline{\xi }}_{s}$ is calculated to be 2.80 (with the same units as the CEC) [66]. In the second bracket in Eq. (6), the first term primarily is associated with the soil mineralogy, while the second term is associated with the pore structure and pore size distribution.

The temperature dependence of the CEC has been observed in the literature and has been used to explain the temperature effect on the swelling potential of expansive soils, as the CEC is related to the thickness of the double diffuse layer (DDL) [82, 109, 120]. For lower temperature ranges between 293 and 373 K, a small increase in the CEC has been observed by some researchers [24, 97]. An increasing trend of swelling pressure with temperature rises from 293 to 363 K has been reported on sodium bentonite, while the changing rate decreases with increasing temperature [1, 5, 108]. Furthermore, after a threshold, the swelling potential may have a decreasing trend. In fact, the decrease in CEC with increasing temperature under high-temperature conditions (e.g., above 373 K) has been widely confirmed and can be interpreted from the point that the capacity of a soil particle holding exchangeable cations depends on the size of the double diffuse layer and the dipolar water that is attracted to that layer [62, 74, 120]. One hypothesis is that when extremely high temperatures are applied to a soil, the DDL thickness is diminished because the heat removes the dipolar water from the DDL and carries with it exchangeable cations [24].

Thus, the reduction of the thickness of the DDL with temperature corresponds to a reduction in the CEC of soil. The temperature dependence of CEC can be expressed as follows:

$$CEC={\frac{1}{2}CEC}_{{\text{max}}}\left[{\text{cos}}\left(A\pi \frac{BT-{T}_{1}}{{T}_{2}-{T}_{1}}\right)+1\right]$$

(8)

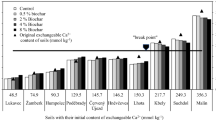
where CEC_max is the maximum value of CEC, T₁ is the temperature corresponding to the CEC_max typically occurs around 373 K (100 °C), T₂ is the temperature corresponding to CEC_min, which typically occurs around 1273 K (1000 °C), A and B are parameters which are typically close to unity. A fitting of Eq. (8) to data for different soils under various temperatures is shown in Fig. 2. Thus, the temperature dependence of adsorption capacity can be estimated by the change of CEC under various temperatures. Through the analysis above, an example of the temperature dependence of adsorption capacity (b_w is assumed as constant here) and CEC for MX80 bentonite with a dry density of 1.6 Mg/m³ are shown in Fig. 3.

Fig. 2

Relationship between CEC and temperature: a Buckshot clay; b Kütahya bentonite

Fig. 3

Example of the temperature dependence of adsorption capacity and cation exchange capacity of MX80 bentonite with a dry density of 1.6 Mg/m³

3.2 Temperature effects on capillarity

The temperature effects on capillarity water retention mechanisms have been well studied in the literature, with temperature affecting the interfacial surface tension, fluid-solid contact angle, and enthalpy of immersion [25, 78, 87]. The study in this work follows a similar approach to these studies but involves a new way to determine the mean cavitation suction and its temperature dependence. Matric suction arising from the capillarity water retention mechanism can be described by the Young-Laplace equation [110]:

$$\psi =\frac{2\sigma {\text{cos}}\beta }{r}$$

(9)

where σ is the water-air interfacial tension (N/m), r is the pore size (the average radius of the water-air interface, in meters), β is the contact angle of the water-air interface with the solid (in radians). The term cos β is alternately known as the “wetting coefficient” [25].

The partial derivative of ψ with respect to temperature can be expressed as [4, 87]:

$$\frac{\partial \psi }{\partial T}=\frac{\psi }{\sigma }\frac{\partial \sigma }{\partial T}+\frac{\psi }{\sigma {\text{cos}}\beta }\frac{\partial ({\text{cos}}\beta )}{\partial T}$$

(10)

The temperature effect on water-air interfacial tension can be described by [27]:

$$\sigma ={A}_{1}+{B}_{1}\cdot T$$

(11)

where T is the absolute temperature in Kelvin, A₁ and B₁ are fitting parameters, suggested by Haar et al. [60] through regression analysis as 0.11766 N/m and − 0.0001535 N/m/K, respectively.

Grant and Salehzadeh [25] demonstrated that incorporating a temperature-dependent contact angle allows the temperature derivative of the wetting coefficient, cos β, to be expressed in terms of independently measurable physical-chemical quantities as follows:

$$\frac{d{\text{cos}}\beta }{dT}=\frac{1}{\sigma }\left(\frac{\sigma {\text{cos}}\beta +\Delta h}{T}-{\text{cos}}\beta \frac{d\sigma }{dT}\right)$$

(12)

where ∆h is the enthalpy of immersion per unit area (J/m²). The temperature dependence of enthalpy can be expressed as follows [87, 101]:

$$\Delta h={\Delta h}_{{\text{r}}}{\left(\frac{1-{T}_{{\text{r}}}}{1-T}\right)}^{0.38}$$

(13)

where T_r is the reference temperature (K), Δh_r is the enthalpy of immersion per unit area at T_r, and − 0.516 J/m² is adopted for high plasticity clay in this work.

The solution of Eq. (12) enables the calculation of the wetting coefficient, cos β, as a function of temperature. By substituting Eq. (11) into Eq. (12), a general form can be obtained as follows:

$$\left({A}_{1}\cdot T+{B}_{1}\cdot{T}^{2}\right)\frac{d{\text{cos}}\beta }{dT}-{A}_{1}\cdot {\text{cos}}\beta =\Delta h$$

(14)

Solving Eq. (14) for cosβ yields the temperature-dependent form of the contact angle, given as follows:

$${\text{cos}}\beta = \frac{{C}_{1}\cdot T-\Delta h}{{A}_{1}+{B}_{1}\cdot T}$$

(15)

where C is a constant (J/m²/K) that can be determined as follows [25]:

$${C}_{1}= \frac{{\Delta h}_{{\text{r}}}+{A}_{1}{({\text{cos}}\beta )}_{{\text{r}}}+{B}_{1}{({\text{cos}}\beta )}_{{\text{r}}}\cdot{T}_{{\text{r}}}}{{T}_{{\text{r}}}}$$

(16)

where (cosβ)_r is the wetting coefficient at reference temperature with a value close to 1.0. A value of − 0.00151 for parameter C₁ was calculated and utilized for high plasticity clays in this work. Using the definitions of ∆h and C₁, Eq. (10) can be rewritten as follows:

$$\psi = \left(\chi +T\right)\frac{\partial \psi }{\partial T}$$

(17)

where χ is the temperature correction factor (K), determined as follows:

$$\chi = -\frac{\Delta h}{{C}_{1}}$$

(18)

By separation of variables and integration, Eq. (17) leads to the following closed-form expression for the nonisothermal matric suction in the capillary regime, as follows [25, 87]:

$$\psi ={\psi }_{{\text{r}}}\left(\frac{\chi +T}{{\chi }_{{\text{r}}}+{T}_{{\text{r}}}}\right)$$

(19)

where ψ_r is the matric suction at a reference temperature (kPa).

Another important parameter related to capillarity in Eq. (3) is the mean cavitation suction represented by ψ_c. The mean cavitation suction is a threshold value between the capillarity and adsorption water retention mechanisms, and should be temperature-dependent. For soil under a matric suction near the mean cavitation suction, most of the pore water is assumed to be in the form of continuous films on the soil particle surfaces or liquid menisci lenses between particles. When wetting from this suction value, the soil particle surfaces become coated by thick water films and capillarity plays a dominant role. When drying from this suction value, the free water tends to cavitate and turns to vapor, and liquid water remains only in the form of adsorptive films bound onto or within the soil particles. A challenge is that Lu [46] did not provide guidance on how to determine this important parameter.

The mean cavitation suction is assumed to be related to the maximum adsorption water content because it also represents the boundary between the adsorption and capillarity water retention mechanisms. The gravimetric water content w (g/g) due to adsorption can be calculated using the specific surface area SSA (m²/g), and the equilibrium film thickness H (m) as follows [83, 114]:

$$w= {\rho }_{w,{\text{ave}}}\cdot SSA\cdot H$$

(20)

where ρ_w,ave is the average density of water film (g/m³). The gravimetric water content can be converted to volumetric water content, as follows:

$$\theta =\frac{w\cdot {\rho }_{{\text{d}}}}{{\rho }_{w,{\text{ave}}}}={\rho }_{{\text{d}}}\cdot SSA\cdot H$$

(21)

where ρ_d is the dry density of the soil (g/m³). Considering van der Waals forces as the governing component of adsorption on the soil particle surface, H can be expressed as a function of matric suction [32, 50]:

$$H= {\left(\frac{{A}_{H}}{6\pi \psi }\right)}^{1/3}$$

(22)

where A_H is the Hamaker constant that can be calculated by the Lifshitz theory [42] using the interaction of static dielectric constant in a medium [31, 79], as follows:

$${A}_{H}=\frac{3}{4} {k}_{{\text{B}}}T{\left(\frac{{\varepsilon }_{s}-{\varepsilon }_{w}}{{\varepsilon }_{s}{+\varepsilon }_{w}}\right)}^{2}+\frac{3{h}_{P}{v}_{e}}{16\sqrt{2}}\frac{{\left({RI}_{s}^{2}-{RI}_{w}^{2}\right)}^{2}}{{\left({RI}_{s}^{2}+{RI}_{w}^{2}\right)}^{3/2}}$$

(23)

where k_B is the Boltzmann constant (1.3806505 × 10^–23 J/K), h_P is the Planck constant (6.626068 × 10^–34 Js), v_e is the main electronic adsorption frequency in ultraviolet light, ε_s is the dielectric constant of soil particle, ε_w is the dielectric constant of water (Fig. 4), RI_s is the refractive index of soil particle, RI_w is the refractive index of water. The effects of temperature on the dielectric properties of major soil constituents have been previously characterized. The impact of changing temperature on the dielectric constant of soil solids and air is negligible [102, 103]. Based on the work by Fernández et al. [13], Marshall [59] proposed an equation to describe the dielectric constant of water ε_w for water density ranging from 0.25 to 1.1 Mg/m³ and temperature ranging from 238 to 1196 K, as follows:

$${\text{lg }}\left( {\varepsilon_{w} { }{-}1} \right){ } = { }0.7017 + \frac{642.0}{T}{ }{-}{ }\frac{{1.167 \times 10^{5} }}{{T^{2} }} + \frac{{9.190 \times 10^{6} }}{{T^{3} }}{ } + \left( {1.667 - \frac{11.41}{T}{ }{-}{ }\frac{{3.526 \times 10^{4} }}{{T^{2} }}} \right){\text{lg }}\rho_{w}$$

(24)

where ρ_w is the density of water (Fig. 4). Although the refractive index varies with soil mineralogy and wavelength, the value of refractive index for most minerals is around 1.55, except for hematite and goethite, respectively [23]. For a given wavelength, the temperature dependence on the refractive index of water is mainly due to the change in water density. Note that the decrease in water refractive index from 273 to 373 K (with various wavelengths) is only about 1.2% [34, 75]. Thus, in this study, constant values of 1.55 and 1.33 were selected for the refractive index of soil and water in Eq. (16) for simplicity.

Fig. 4

Relationship between water dielectric constant, water density and temperature

Since the intermolecular adsorptive forces elevate the water pressure locally, rendering adsorbed water less likely to cavitate than capillary water, the occurrence of cavitation can potentially be used to distinguish between the adsorption and capillarity water retention mechanisms and clarify the transitional behavior in soil water retention [58]. Moreover, a mean value of cavitation suction can be adopted for probabilistic analysis of the cavitation process, as cavitation is believed to be a rapid yet smooth process over a range of suctions that can be well described by a probability distribution function such as the normal distribution [29, 46]. Thus, by combining Eqs. (21) and (22) and replacing the matric suction ψ in Eq. (22) with the mean cavitation suction ψ_c and the volumetric water content θ in Eq. (21) with θ_a,max, the mean cavitation suction ψ_c can be determined:

$${\psi }_{c}= \frac{{A}_{H}}{6\pi }{\left(\frac{{\theta }_{{\text{a}},{\text{max}}}}{{\rho }_{{\text{d}}}\cdot SSA}\right)}^{-3}$$

(25)

In Eq. (25), the value of ρ_d is assumed to be constant for the soil under constrained conditions. The SSA may vary with the temperature, but the change is expected to be small, especially for the temperature ranges representative of hydrological and geotechnical applications. Thus, a constant value of SSA is selected for simplifying fitting work in this study. The temperature effect on the θ_a,max has been analyzed above (Fig. 2), while the temperature dependence of the ψ_c and A_H for MX80 bentonite with 1.6 Mg/m³ in dry density is shown in Fig. 5. Curves in the figure show an increasing trend of ψ_c with increasing temperature, indicating that the suction range controlled by the adsorption mechanism becomes smaller. In other words, higher suction is required to follow the drying-path SWRC under elevated temperatures to reach the adsorption mechanism. Due to the negative correlation between temperature and maximum suction (Fig. 1), the positive correlations between temperature and adsorption capacity (Fig. 3) and the positive correlation between temperature and mean cavitation suction (Fig. 5), the shape of the SWRC at low degrees of saturation becomes flatter with increasing temperature.

Fig. 5

Example of the temperature dependence of mean cavitation suction and Hamaker constant of MX80 bentonite with dry density of 1.6 Mg/m³

Experimental evidence reveals that the air entry suction ψ_aev decreases as temperature increases [10, 99]. Meanwhile, for suctions higher than ψ_aev, the SWRCs at different temperatures are almost parallel, suggesting that parameter n of the SWRCs are not significantly affected by temperature. Therefore, the SWRC model of Lu [46] can be extended to a new one that can takes into account temperature effects by only introducing the temperature influence on the ψ_aev. The relationship between the air entry suction and temperature can be described as follows:

$${\psi }_{{\text{aev}}}={\text{exp}}\left[\eta \left(\frac{{T}_{{\text{r}}}}{T}-1\right)\right]{\psi }_{{\text{aev}},{\text{r}}}$$

(26)

where ψ_aev,r is the air entry suction (kPa) at the reference temperature T_r, and η is a soil texture-related coefficient. The relationship between the air entry suction and temperature for Boom clay and GMZ01 bentonite is shown in Fig. 6. The magnitude of ψ_aev depends on the soil mineralogy and particle size distribution. For example, the value for GMZ01 bentonite (Fig. 6b) is greater than the value for Boom clay (Fig. 6a) at the same dry density.

Fig. 6

Relationship between air entry suction and temperature: a Boom clay; b GMZ01 bentonite

In summary, the new nonisothermal SWRC based on the SWRC model of Lu [46] is defined using a set of three equations:

$$\theta (\psi , T)={\theta }_{{\text{a}}}(\psi , T)+{\theta }_{{\text{c}}}(\psi , T)$$

(27)

$${\theta }_{{\text{a}}}={\theta }_{{\text{a}},{\text{max}}}\left(T\right)\left\{1-{\left[{\text{exp}}\left(\frac{\psi -{\psi }_{{\text{max}}}\left(T\right)}{\psi }\right)\right]}^{M}\right\}$$

(28)

$${\theta }_{{\text{c}}}=\frac{{\theta }_{{\text{s}}}-{\theta }_{{\text{a}}}}{2}\left\{1-{\text{erf}}\left[\sqrt{2}\frac{\psi }{{\psi }_{{\text{c}}}\left(T\right)}\left(\frac{\chi \left(T\right)+T}{{\chi }_{{\text{r}}}+{T}_{{\text{r}}}}\right)-\sqrt{2}\right]\right\}\cdot {\left\{1+{\left[\alpha \psi \left(\frac{\chi \left(T\right)+T}{{\chi }_{{\text{r}}}+{T}_{{\text{r}}}}\right)\right]}^{N}\right\}}^{1/N-1}$$

(29)

In these equations, the temperature-dependent values of θ_a,max, ψ_max (u_max), ψ_c and χ are defined using Eqs. (6), (4), (25), and (18). When incorporating the effects of temperature on the suction at elevated temperature in the capillary regime from Eq. (19), the r subscript is dropped from the suction at the reference temperature as the temperature-dependency arises from the parameters listed in the previous sentence. The temperature-dependency for α can be considered by the inverse of the ψ_aev defined by Eq. (26). The value of θ_s is assumed to be constant for constrained unsaturated soil. M is assumed to only be related to the clay mineralogy and is not considered to be temperature-dependent, while N is related to the pore size distribution and is also assumed to not be temperature-dependent for simplicity. A causal diagram for the parameters of the nonisothermal SWRC is depicted in Fig. 7. An example of the nonisothermal SWRC model for adsorption and capillarity regimes for MX80 bentonite with 1.45 Mg/m³ in dry density is shown in Fig. 8 for temperatures of 293 and 333 K.

Fig. 7

Causal diagram of the parameters of the nonisothermal SWRC (nonisothermal parameters marked in red and isothermal parameters in blue)

Fig. 8

Schematic diagram of nonisothermal SWRC considering the effects of temperature on the adsorption and capillarity water retention mechanisms

4 Model validation

To validate the performance of the new proposed nonisothermal SWRC, a comparison with the tested and fitted SWRCs for four types of high plasticity clays (without loss of generality) in literature is conducted. All the soils cited here are in relation to the buffer material used in geological nuclear waste repositories, where the nonisothermal condition is particularly prominent. Among them, Boom clay is a natural potential host clay for a repository, while the FEBEX, MX80, and GMZ01 are three types of commonly used sodium bentonites compacted into buffers. All the SWRC datasets are cited or calculated by the raw measurements of suction vs. gravimetric water content in the reference. Besides, the dry density of the specimen for different clays varies from 1.4 to 1.7 Mg/m³, covering commonly used ranges in the buffers for nuclear waste repositories. The fundamental physical properties of the four high plasticity clays considered in the validation are listed in Table 1, which include parameters given in the literature [69, 89, 92, 98] or back-calculated in this work.

Table 1 Physical properties of high plasticity clays considered in the validation

The nonisothermal SWRC model fitted to the data for Boom clay at room temperature and predicted for elevated temperatures are presented in Fig. 9a. The fitting for room temperature data was performed using least-square regression, and the coefficient of determination (R²) used for evaluating the quality of fit and the root mean square error (RMSE) used for evaluation of the difference between the measured data and predicted values are listed in Tables 2 and 4 (see Appendix). The temperatures shown in Fig. 9 and Tables 2 and 4 are shown in °C to be consistent with the literature, but are converted to K for use in the SWRC model. The new SWRC model shows a good fit to the room temperature data with R² greater than 0.99 and good prediction with RMSE less than 0.03. Similar comparisons of fitted SWRCs for room temperature and predicted SWRCs for elevated temperature with experimental data for FEBEX, MX80 and GMZ01 bentonites are shown in Figs. 9b, c and d, respectively. Although the temperature-dependency of the SWRC may not appear significant in these figures due to the logarithmic scale for suction, the temperature can still have a significant effect that should be considered in coupled heat transfer and water flow analyses. Note that bentonite typically contains large amounts of montmorillonite, which has a higher CEC and SSA than other constitutent minerals (e.g., kaolinite, illite, quartz, etc.). The variation in suction with saturation changes for bentonites is higher, with a much higher air entry value (lower α) than Boom clay and other clayey, silty, and sandy soils. Thus, compared with Fig. 9a, a flatter evolution in Figs. 9b, c and d is witnessed for the curves under the high suction range, especially in the adsorption. The fitting of room temperature and prediction of elevated temperature curves in Figs. 9b, c and d demonstrated that the proposed SWRC model agrees well with the experimental SWRC data of different bentonites with different dry densities under various temperatures, with R² greater than 0.92 and RMSE less than 0.06. The difference between SWRCs at different temperatures in Fig. 9 is noticeable. To quantitatively evaluate the temperature effects, the fitting values and the relative error between the highest (80 °C) and lowest (~ 22 °C) temperature for three specific suctions (113000, 38000, and 4200 kPa) which are commonly selected by vapor equilibrium technique in literature [54, 96, 99] are listed in Table 3. The relative error is defined as follows:

$$\delta =\frac{{S}_{{T}_{2}}-{S}_{{T}_{1}}}{{S}_{{T}_{1}}}$$

(30)

where δ is the relative error, T₁ and T₂ are the lowest and highest temperature, respectively, and S_T is the degree of saturation at temperature T. Although the values of ψ_max in Table 2 were treated as a fitting parameter for these soils as it is difficult to determine experimentally, the values show good agreement with previous modeling works and assumptions [46, 119].

Fig. 9

SWRC calibration for high plasticity clays: a Boom clay; b Compacted FEBEX bentonite; c Compacted MX80 bentonite; d Compacted GMZ01 bentonite

Table 2 Nonisothermal SWRC model parameters for the high plasticity clays tested under different temperatures

Table 3 Quantitative comparison of relative differences between degrees of saturation at highest and lowest temperatures in Fig. 9

A comparison between the fitted CEC and SSA at the reference temperature and values measured in the literature [30, 40, 81, 89, 90, 93, 98, 104, 106, 111, 121] is shown in Figs. 10a and b, respectively. Results in Fig. 10a demonstrated that the fitted CEC is consistent with the tested data, as the fitted and tested values follow the 1: 1 line with R² of 0.97. Meanwhile, although the fitted and tested SSA values are correlated R² of 0.76, it is interesting to note that the fitted SSA is overpredicted, meaning that the fitted SSA is usually greater than the measured SSA (Fig. 10b). In fact, the SSA value used in this study is for predicting the ψ_c (Eq. (25)), which controls the SWRC shap at the transition between the adsorption and capillarity water retention mechanisms. If a lower value of SSA is used, a stepped curve is observed. Thus, for smooth and coherent SWRC, a higher value of SSA than measured in the literature is adopted here. Besides, the SSA measurement is method dependent, and the measured value might vary with batches of samples.

Fig. 10

Comparison of CEC and SSA from fitting analysis and measured in literature. Honty [30]; Kumpulainen and Kiviranta[40]; Tessier et al. [81]; Villar et al. [90]; Villar et al. [93]; Villar [96]; Wu et al. [104]; Ye et al. [106]; Yukselen and Kaya [111]; Červinka and Kolomá [121]

Experimental tests have highlighted the variability in pore size within clayey soil, with pores smaller than a certain threshold believed to be difficult to further compress [44]. Such micro pores are commonly assumed to be saturated in order to simplify modeling efforts [21], despite the fact that the pore size distribution can be influenced by various factors including mineral composition, saturation level, among others. Although various methods exist for differentiating between micro and macro pores, a threshold value of pore size in the pore size distribution functions is commonly used [45, 77]. Specifically, a threshold of 150 nm is widely applied for high plasticity clay [44, 105]. Using the same threshold value on the mercury intrusion porosimetry (MIP) data of the four high plasticity clays [28, 45, 69, 94], the relationship between the “ratio of micropores to total pores (e_m/e)” and the “ratio of adsorption capacity to saturated water content (θ_a,max /θ_s)”, is depicted in Fig. 11. The MIP tests were conducted on the four clays with similar densities (1.4–1.7 Mg/m³) under similar suction ranges (4–43 MPa). The results in Fig. 11 show a strong linear correlation between the two parameters, indicating the feasibility of estimating the adsorption capacity θ_a,max from pore size data.

Fig. 11

Relationship between micropore content and adsorption capacity

Another evaluation of the new SWRC can be conducted regarding the temperature dependency of the model parameter α in Eq. (29). Note that the value of α adapted for fitting SWRCs increases with increasing temperature (Table 2), as α is typically assumed equal to the inverse of air entry suction (Eq. (26)). A summary of the calculated air entry suction (ψ_aev = 1/α) for the four clays is shown in Fig. 12. Results in the figure show that the air entry suction decreases with increasing temperature, while the decreasing rate is soil-texture dependence. The fitted air entry suction for GMZ01 bentonite is consistent with the value measured in the literature [99]. Generally, a decrease in the air entry suction with increasing dry density is observed.

Fig. 12

Summary of the temperature dependence of the air entry suction (inverse of α)

5 Conclusions

This paper presents a general soil water retention curve that accounts for the effects of temperature on both adsorption and capillarity water retention mechanisms in unsaturated soils under confined conditions. For the adsorption water retention mechanism, a negative correlation between maximum matric suction and temperature was analyzed through BET theory. Additionally, a new non-monotonic CEC-temperature equation was proposed for characterizing the temperature effect on adsorption capacity. For the capillarity water retention mechanism, the mean cavitation suction, related to the transition between capillarity to adsorption water retention mechanisms, was studied along with the widely known temperature-sensitive parameters such as surface tension, contact angle, and air entry suction. A relationship between the mean cavitation suction and basic soil physical parameters such as the SSA and dry density was developed. The mean cavitation suction, which pertains to the curve continuity around the physical-phase transition point between the adsorption and capillarity water retention mechanisms, shows a positive correlation with elevated temperature. The proposed nonisothermal SWRC model was validated using data from the literature for high plasticity clays having different dry densities, including natural clay and compacted bentonites. Model predictions with high R² indicate that the proposed model can simulate the tested data well under different temperatures by considering temperature effects on adsorption and capillarity water retention mechanisms. The new nonisothermal SWRC model will be useful for simulating coupled heat transfer and water flow processes in hydrogeologic and geotechnical applications involving elevated temperatures.

Appendix

See Table 4

Table 4 Supplementary model parameters for Table 2