Introduction

The properties change in a certain direction from one material to another in functionally graded materials (FGMs),, e.g. from ceramic to metal, depending on the variation function. FGMs are often proposed as materials to decrease residual thermal stresses in material compositions. Since plates are widely used components in many fields such as fusion power generation, aerospace, and chemical industries, functionally graded (FG) plates are developed for optimal solutions. The main objective is to achieve continuous gradation of material properties in one direction according to the working conditions of the composite plate. In this way, an abrupt stress change at the interface is avoided. Although this is theoretically reasonable, the hardness of the production arises from the continuous change of material properties.

Due to the lack of manufacturing techniques, layered composites are usually proposed to the industry to meet the requirements of FGMs. One way is to change the volume ratio of inclusions in the composite layers. The variation obtained, called the step function, is an approximation of continuous material gradation from one side of the material to the other. The desired functional gradation can be represented in the material by choosing a sufficient number of layers. The selection of the number of layers and the gradation function for the material properties are decisive for the design. Appropriate gradation reduces stress changes and stress concentrations caused by changes in material properties and geometric discontinuities, respectively [1,2,3]. Naebe and Shirvanimoghaddam [4] have described in detail the FGM’s fabrication techniques, applications, and advantages. As the use of FGM has increased in many fields such as defense, structure, and chemistry, the studies on this topic have also deepened. Theoretical, numerical, and experimental studies on FGM for proper method, fabrication and application are still a current need. The analysis of thermal stresses that may occur in this type of structural elements is very important when they are exposed to the effects of temperature either suddenly or over time, depending on their intended use [5,6,7].

The planar equations of thermoelasticity are presented and solved using numerical methods to analyze the thermal behavior of cylindrical pressure vessels [8]. The concentration of thermal stresses around oriented defects near the interface of welded two different materials was presented in a study modeling the interaction in one direction [9]. Statistical methods and a developed approach were used to determine the bending of FG plates under thermal loading [10].

In a comprehensive review study of thermal barrier coatings (TBCs) used in many specialized structural fields, the authors noted that the use of TBCs allows adaptation to elevated temperatures and, in particular, reduces the cost of the cooling process and thermal efficiency due to insulation capacity. They also discussed the methods of coatings and their advantages [11]. Dai et al. [12] analyzed the thermal effect on a hollow cylindrical structural element functionally graded for different conditions, considering the change in material properties with temperature changes, and presented the numerical solutions of the governing equations. An ring-shaped, functionally graded plate is analyzed for thermal loading along its thickness using three-dimensional elasticity by Yang et al. [13]. The exponential change in thermal conductivity in the functionally graded coating was solved [14]. Especially in ceramic-based functionally graded thermal barrier coating (TBC), cracking is vulnerable to occur in interfaces of substrate and coating due to stress jump that may occur with the different surface energies, thermal expansion coefficient [15, 16] or in the ceramic substrate due to the high residual stresses under the thermal loading [17]. A comparison between layered and functionally graded coatings for structural elements was presented to analyze crack initiation and propagation [18]. For the stress distribution in functionally graded coatings, a solution is proposed that was derived considering the bending of plates, without the solution having been verified [19].

The behavior of FGMs was studied for thermal loading in a recent study for stress intensity factor using some techniques and finite element program [20]. Nojumi and Wang [21] proposed a finite element type to analyze FGMs for the state of fracture under thermomechanical loading. Iqbal et al. [22] utilized a finite element model for the thermomechanical behavior of FGMs with the material gradation of power series. Martinez-Paneda and Gallego [23] analyzed crack formation in FGMs using ABAQUS user subroutine.

The buckling of underwater pipes made of functionally graded materials that transport fluids at high temperatures was analyzed by Wang and Soares [24] by comparing an analytically developed solution with results from the literature. Farrokh et. al [25] analyzed the buckling of FG plates for the influence of temperature changes, considering the optimal material distribution. The buckling of cylindrical shells made of FGM is studied analytically for thermal impact by Zang et al.[26]. The effects of the sudden cooling process on FGMs composed of five Al2O3 layers with different ZrO2 content was investigated using numerical methods, and a comparative graph of the heat flux was obtained [27]. Buckling of FGM was investigated by size-dependent exact theory [28]. Safari et al. [29] analyzed thick hollow cylinders made of FGM for for thermal shocks.

There are some more general studies analyzing the thermal stress of FGMs. Dhital et al. [30] developed custom subroutines in Abaqus that define the material properties gradation in the elements to perform thermal stress analysis of FGMs. They emphasized the importance of the incompatible graded finite element with six nodes (QM6) with the advantage of accuracy rate and computation time. Shahzamanian et al. [31] examined the thermal effect on rotating FG disks with variations along the radial direction using numerical and analytical methods.

Gari et al. [32] investigated the thermal stresses caused by the high operating temperatures of functionally graded tubular fuel cells using a numerical model. Gautam and Chaturvedi [33] performed an optimization for thermal stress behavior of functionally graded material in engineering applications by creating a code on MATLAB. Moreover, the study emphasized the crucial effect of volume fraction when a sufficient number of sub-layer are applied but it could not be verified certainly for heterogenous or nonthermal conductive materials. The material composition in FGM plates was optimized to minimize the thermal stress using a hybrid genetic algorithm by Ding and Wu [34].

The propagation of a crack was studied for FGMs, which have the mechanical and thermal properties exponentially change [35]. Power functions are utilized for a thick hollow cylinder to express the change in material properties in the radial direction, and a solution for thermal stresses was obtained under steady-state conditions [36]. The flexure of a laminated plate with a functionally graded core was studied under thermal and mechanical effects [37]. An analytical and numerical study of the behavior of brake disks in the automotive industry made of different materials used as were carried out under temperature distribution [38] and another analytical study investigated thermal residual stress distributions for FGMs [39]. Some recent studies have focused on determining and reducing the stress concentrations associated with FGMs [40,41,42]. Bi-directional gradation of material properties [43] and bi-direcitonal thermal effect [44] have been presented in the recent literature.

In this study, analytical formulas for functionally graded and layered composite plates with variable elastic modulus and thermal expansion coefficient are derived using the strain suppression method in elasticity [45] to obtain practical and accurate expressions for thermal stresses. To validate the solutions, photoelastic experiments were conducted to determine the distribution of thermal stress in a laminated plate having the change in elastic and thermal coefficients. To illustrate the stress concentration, a cavity was modeled in these experiments. An earlier article [5] deals exclusively with the gradation of the thermal expansion coefficient in functionally graded plates. Although the experimental model used in this study is analogous to that in [5], the issues in creating the model with different materials that have different elastic moduli and critical temperature values are discussed here. A finite element model is validated by the results from experimental and analytical models. The effect of the change in the thermal expansion coefficient was studied before [5]. The simulatenous change in the elastic modulus is discussed for stress concentration using the developed experimental models. The optimum layer number in a laminated plate, which has a similar stress distribution with a continuous gradation of material properties, is also discussed. The ratio of elastic moduli affects the stress concentration at the tip of the cavity perpendicular to the interface in a two-layer composite plate and an empirical formula is proposed.

The Derivation of Analytical Formulas

The thermal stress formulas are derived here for FG plates with a continuous change in elastic modulus and thermal expansion coefficient, and for laminated composites with n layers having different constant values of these material constants. The behavior is assumed to be linear-elastic and mainly approximated as bending based on the strain suppression method for the transversely isotropic material.

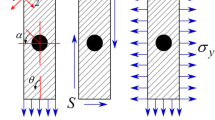
The model is considered as a free plate of thickness h under a temperature change varying along the thickness (Fig. 1). The dimension L is large enough that the solution satisfies the statically equivalent boundary conditions according to Saint Venant’s principle. Two material parameters change along the thickness with some functions of only z, the elastic modulus (E), and the thermal expansion coefficient (α).

Fig. 1
figure 1

The FG plate with a graded modulus of elasticity E(z), graded coefficient of thermal expansion α(z), and thickness h for a temperature change, expressed as T(z)

Full size image

Under a temperature change defined as a function T(z), the free thermal expansion at a point can be stated in two directions as follows:

$$\varepsilon_{x} = \varepsilon_{y} = \alpha (z)T(z)$$
(1)

Considering the linear-elastic behavior, these expansions are suppressed by the stress components expressed as below:

$$\sigma_{x}^{s} = \sigma_{y}^{s} = - \frac{\alpha (z)T(z)E(z)}{{1 - \nu }}$$
(2)

where s and \({\varvec{\nu}}\) indicates the suppression terms and the Poisson’s ratio, respectively. These components cause tractions at the boundaries of the plate. Since the plate is free of external forces, an equivalent opposite force of N and a couple of M caused by the traction must be superimposed to determine the state of stress of the problem. These are calculated from the following integrals along both x and y directions:

$$N = \int\limits_{ - h/2}^{h/2} {\frac{\alpha (z)T(z)E(z)}{{1 - \nu }}} dz, \, M{ = }\int\limits_{ - h/2}^{h/2} {\frac{\alpha (z)T(z)E(z)}{{1 - \nu }}} zdz$$
(3)

Dividing these by the corresponding equivalent rigidities, one can obtain the stress far enough from the edges for each traction. The axial rigidity for a section with unit thickness is expressed in equation (4) to calculate the strain component due to the normal force.

$$\int\limits_{ - h/2}^{h/2} {E(z)dz}$$
(4)

The effect of the couple results from the asymmetry of the temperature function. Considering Euler–Bernoulli Theory of bending, the equation of equivalence with the curvature is expressed as below:

$$\int\limits_{ - h/2}^{h/2} {\frac{{Ez^{2} }}{\rho }dz} = M$$
(5)

where ρ is the radius of curvature about the corresponding axis. Substituting the expression for M given in equation (3) into equation (5), the strain term can be obtained for the couple. Consequently, there are two mechanical strain components resulting from the temperature change. The normal strains caused by the normal force and bending moment are given in equation (6), respectively.

$$C_{1} = \frac{{\int\limits_{ - h/2}^{h/2} {\frac{\alpha (z)T(z)E(z)}{{1 - \nu }}} dz}}{{\int\limits_{ - h/2}^{h/2} {E(z)dz} }},\;C_{2} = \frac{{\int\limits_{ - h/2}^{h/2} {\frac{\alpha (z)T(z)E(z)}{{1 - \nu }}z} dz}}{{\int\limits_{ - h/2}^{h/2} {E(z)z^{2} dz} }}$$
(6)

When these effects are superposed on the free thermal strain given in equation (1), the resulting strain for the plate free of external forces is obtained. From this, the expression for thermal stress at a point on the plate due to a change in temperature with variable coefficients for elastic modulus and thermal expansion is written as follows:

$$\sigma_{x} = \sigma_{y} = E(z)\left[ {\frac{ - \alpha (z)T(z)}{{\left( {1 - \nu } \right)}} + C_{1} + C_{2} z} \right]$$
(7)

This expression is obtained for a continuous variation in E(z) and α(z). The functions of change in the thermal expansion coefficient and temperature change are combined using the thermal expansion definition as follows:

$$\varepsilon (z) = \alpha (z)T(z)$$
(8)

If the material is laminated composite and the temperature is constant for each layer, E and ε are also constants for each layer. Then, the constants C1 and C2 can be calculated for an n-layered laminated composite plate from the above equations in the following form:

$$C_{1} = \frac{{\int\limits_{0}^{{h_{1} }} {\varepsilon_{1} E_{1} dz + \int\limits_{{h_{1} }}^{{h_{2} }} {\varepsilon_{2} E_{2} dz + } ... + \int\limits_{{h_{n - 1} }}^{{h_{n} }} {\varepsilon_{n} E_{n} dz} } }}{{(1 - \nu )\left[ {\int\limits_{0}^{{h_{1} }} {E_{1} dz + \int\limits_{{h_{1} }}^{{h_{2} }} {E_{2} dz + } ... + \int\limits_{{h_{n - 1} }}^{{h_{n} }} {E_{n} dz} } } \right]}}$$
(9)
$$C_{2} = \frac{{\int\limits_{0}^{{h_{1} }} {\varepsilon_{1} E_{1} zdz + \int\limits_{{h_{1} }}^{{h_{2} }} {\varepsilon_{2} E_{2} zdz + } ... + \int\limits_{{h_{n - 1} }}^{{h_{n} }} {\varepsilon_{n} E_{n} zdz} } }}{{(1 - \nu )\left[ {\int\limits_{0}^{{h_{1} }} {E_{1} z^{2} dz + \int\limits_{{h_{1} }}^{{h_{2} }} {E_{2} z^{2} dz + } ... + \int\limits_{{h_{n - 1} }}^{{h_{n} }} {E_{n} z^{2} dz} } } \right]}}$$
(10)

where h1, h2,…, hn are the layers’ heights from bottom to top. Since the layered composites have material discontinuities at the interfaces, equation (7) can be used in the form given in equation (11):

$$\begin{aligned} \sigma_{x} = \sigma_{y} = &\; E_{i} \left[ { - \frac{{\varepsilon_{Ti} }}{{\left( {1 - \nu } \right)}} + C_{1} + C_{2} z} \right] \\& \text{ for } h_{i - 1} \le z \le h_{i} \text{ and } i = 1, \, 2, \, ... \, , \, n \end{aligned}$$
(11)

where \({E}_{i}\) and \({\varepsilon }_{Ti}\) are the elastic modulus and thermal strain for the ith layer, and \({h}_{0}=-h/2\).

Experimental Work

An experimental analysis is presented in this section to validate the analytical solution. This involves two photothermoelastic laminated composite models with two and four layers having different elastic moduli and thermal expansion coefficients. They are assumed to be loaded by partly temperature change. Since the change in thermal expansion can be leaded by a change in the thermal properties and/or temperature (equation 8), the difference in the thermal expansion coefficient is modeled by the mechanical modeling of the strain-freezing method of photoelasticity. For this purpose, one part of the model was obtained from a cylindrical rod in which the strains are fixed due to an axial compressive load, while the other part initially has no strains or residual stresses [5].

Determination of the Materials for the Experimental Model

Some available materials were studied for their characteristic properties in the experiment based on strain-freezing method. One of these properties is the critical temperature at which the material behaves linear-elastic, and the second is modulus of elasticity at this temperature. For determination of the critical temperature values of the specimens from different Araldite plates manufactured under different conditions, single/dual cantilever beam tests with a temperature rise of 2 °C/min were performed with 15 μm amplitude, and 1 Hz frequency using the Dynamic Mechanical Analyzer (DMA) Q800, TA Instruments (Graphics obtained are shown in the figures given in Appendix). Because the critical temperature is mostly around 155 °C, the elastic moduli of the samples were determined by film tension test at this temperature in DMA (Table 1).

Table 1 The properties of intended materials determined by DMA
Full size table

When comparing the differences between the elastic moduli, the materials labeled E11 and E13 were selected as reasonable choices for two-layer plate model. The output curves of the single cantilever and film tension tests in DMA are shown in the appendix. The four-layer plate is based on the two-layer plate. The main part is chosen as E11 with the same thickness. The overall thickness of the plate was not changed, but the coating of the main part was graded so that a three-layer caoted with the decreasing elastic modulus was used instead of single-layer E13. The material labels used in four-layer plate model are E11, E12, E12, and E1.

To determine the temperature-dependent behavior of the thermal expansion coefficient of the selected materials for two-layer plate, the DMA tests were performed for each material using the controlled force method with a constant force of 0.0001 N. The temperature was increased with a temperature ramp of 2 °C/min up to 180 °C. The measured values of strains are plotted for the temperature change. The obtained graphs are shown in the appendix. As can be seen from these graphs, the coefficients of thermal expansion change abruptly around the glass transition temperature. The coefficients are constant values for both materials since the strain curves are nearly linear at higher temperatures. The coefficients of thermal expansion at 155 °C were determined to be 0.000155 and 0.000195, respectively. In Table 2, the mechanical, thermal and optical properties for E11 and E13 at 155 °C are given.

Table 2 Mechanical and optical properties of the materials of experimental models at 155 °C
Full size table

Preparation of the Model

To obtain the layer of the models, in which thermal expansion is modeled as mechanical strain, a cylindrical specimen of E11 was subjected to an axial load of P = 1367 N. It was then heated at a rate of 5 °C/hour to its viscoelastic temperature of 155 °C. After it was cooled to room temperature with the same regime, the frozen strain was determined to be \({\varepsilon }_{1}=\left(\alpha T\right)=0.009\). Then the first layer of the model was obtained from this cylinder by a sensitive cutting process in the milling machine. This process is shown in Fig. 2. A similar procedure for prepering the model can be found in detail in an earlier article [5].

Fig. 2
figure 2

Some steps of the preparation of the model: The axial loading is applied to a cylindrical Araldite to obtain the mechanical model of the thermal strain in the axisymmetric cross-section of the first layer of the model. The first layer is sliced using a precise cutting machine with cooling lubricant. The layers are bonded to each other applying an epoxy-based adhesive to interfaces. A cavity is drilled with lubricant in the first layer of the model to represent a defect

Full size image

The second layer for the two-layer plate was made of E13, which has the same cross-sectional geometry as the first part. It exhibits neither initial strain nor residual stress. In the four-layer plate, the layers apart from E11 were also in the same condition as E13 in the two-layer plate.

An epoxy-based adhesive was used to bond these parts. The hardener was added in a specific ratio to avoid the effects of a rapid reaction. In addition, the adhesive was applied very thinly, homogeneously, and evenly to the surfaces of the parts so that there was no intermediate phase (Fig. 2). The model was then subjected to 0.15 MPa constant compressive stress for 24 h to avoid air bubbles and achieve perfect bonding. The model was then polymerized at 45 °C for 24 h. In the final stage of model fabrication, a cavity was drilled to model a defect. This cavity is located in the layer where the mechanical strain was fixed. A cooling lubricant was used during drilling to avoid residual stresses (Fig. 2).

The model (Fig. 3) was then heated to 155 °C to activate the strain frozen in the first layer. Since the reactivating strain is \({\varepsilon }_{1}=\left(\alpha T\right)=-0.009\), the cooling of the first layer of the composite is modeled and a new thermal stress distribution was obtained in the model at this temperature for this case.

Fig. 3
figure 3

Isochromatic fringe patterns on the slice taken from the model. The general view of cylindrical composite plate models and the dimensions of the models are also shown. \({\varepsilon }_{1}=\left(\alpha T\right)=-0.009\) and \({\varepsilon }_{2}=0\)

Full size image

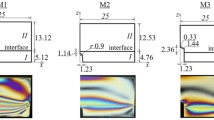
After kee** the temperature of the model at 155 °C for 3–4 h, the new thermal stress distribution in the entire of each model was frozen by slowly cooling it to room temperature. The distribution can be considered due to a constant temperature decreases for the entrie plate having two layers with different elastic moduli and thermal expansion coefficients. For the four-layer plate model, the effect of the gradation in the coating can be observed in the stress distribution. To obtain results for the temperature rise in the same magnitude, the measured stress values must be multiplied by -1. A 2-mm-thick slice enclosing the top of the cavity was cut out of models by a precision cutting machine (Fig. 3). The distribution of the isochromatic fringe patterns on the slices are shown in Fig. 3.

The Thermal Stress Values

To determine the stress values, the formula in the method of photoelasticity is used which gives the difference between in-plane principal stresses, σ1 and σ2 (equation 12).

$$\left| {\left. {\sigma_{1} - \sigma_{2} } \right|} \right. = f_{\sigma } \frac{m}{t}$$
(12)

Here, m is the fringe order measured by the Berek compensator mounted on Leica DM4500P polarizing microscope, t is the thickness measured by precise micrometers at the relevant location through which the light passes, and fσ is the optical coefficient of the material. Using equation (12), the stress curves for two- and four-layer plates were plotted in Fig. 4 across the thickness at the center, from the top of cavity. The dimensions are slightly different for two- and four-layer plates. This situation results from the cutting and producting of the models. In Fig. 4, the thicknesses for both and the layers of the four-layer plate are shown by dahsed lines. The circumferential component at the edge of the cavity in two-layer composite is also plotted in Fig. 4. To compare the results with those from analytical solution, the stress distributions along the thickness were also given in Fig. 4, where the fringe patterns are mostly unaffected by the edges and the cavity.

Fig. 4
figure 4

Thermal stress distributions on the models were determined by optical measurements. There are thermal stress variations on the models accross the thickness from the top of the cavity, the stress curve around the cavity for two-layer plate, and in the region where the effects of the edges do not occur (units are in MPa)

Full size image

A Proposal for a Continuous Material Gradation in the Experimental Models

The first experimental model is a two-layer composite material, so the material properties change abruptly at the interface. If this absolute change is proposed in an FGM with a linear change from bottom to top, the spatially varying material functions can be expressed as follows:

$$E(z) = 1.08031z + 30.18$$
(13)
$$\varepsilon (z) = - 0.000495z + 0.0045$$
(14)

Here, the thermal expansion ε is defined in equation (8). Substituting equations (13) and (14) into equations (9) and (10), \({C}_{1}\) and \({C}_{2}\) are calculated. Then the distribution of thermal stress is obtained using equation (11).

The continuous gradation of the material can be approximated with layers having constant material properties. To obtain the optimal number of layers, layered composites with n layers, values of n taken as 2, 4, and 8 with the gradations given in equations (13) and (14) were considered. In these composites, each layer has the same height and the values of the material constants are calculated at the center of the layer using equations (13) and (14). The integration constants of \({C}_{1}\) and \({C}_{2}\) are calculated for these plates using equations (9) and (10) are used. For the experimental model, there are two layers with different heights. Equations (9) and (10) are also applied to the experimental model with different values for \({h}_{1}\) and \({h}_{2}\) (see Fig. 3). Table 3 lists the integral coefficients for the different cases. All these cases represent different gradations of the same materials for a plate with the same geometry. The gradation equations for these cases are given in equations (13) and (14), except for the case called “experimental model”. For this case, the constants \(E\) and \({\varepsilon }_{f}\) are from the experiment listed in Table 2. The dimensions of the layers in the case of “2 layers with unequal height” are the same as those in the experimental model. For cases other than the “experimental model”, the material constants are calculated using gradation equations (equations 13 and 14) at the center of each layer. The cases “experimental model” and “2 layers with unequal height” are used to observe the effects of the height of the layers. The case labeled “continuous gradation” represents the functionally graded plate for the gradation equations, while the other cases correspond to the laminated plates. In Table 3, the values of the coefficients approach those obtained for continuous gradation as n increases.

Table 3 The calculated values of C1 and C2 for different cases
Full size table

The analytical solutions of equations (6) through (11) are applied to obtain the stress distribution for the plates listed in Table 3. The variations of the stress distributions for these cases with \({\varepsilon }_{1}=0.009\) and \({\varepsilon }_{2}=0\) are shown in Fig. 5.

Fig. 5
figure 5

Thermal stress distributions for laminated composite plates with two layers with the heights as in the experiment, with two, four, and eight layers with equal heights, and the functionally graded plate with continuous gradation are shown here. The changes in material properties are determined according to the gradation equations given in equations (13) and (14) at the center of each layer in laminated composites except for the model “exp_2layers”. This model has the same properties as the experimental model while the material properties of the case “2 layers with unequal height” are changed according to the gradation equations. (a) The data obtained by the analytical formulas of equations (6) to (11). (b) The data obtained by the numerical analysis of the model. The continuous gradation for each case is solved with analytical formulas and gradation equations for the plate

Full size image

The second experimental model can be assumed to be a plate coated with a layered composite material. This coating is used instead of “layer 2” in the first model. If the change in the elastic moduli of the layers is considered as a continuous gradation of the elastic modulus for this coating, it can be expressed as follows:

$$E(z) = - 0.61288z^{2} + 10.04139z - 0.94955$$
(15)

where the coordinate variable is used as in Fig. 3. For the continuous gradation of the elastic modulus given in equation (15), the thermal stress distribution can be obtained using equations (6)-(11) for the thermal expansion \({\varepsilon }_{1}=\left(\alpha T\right)=-0.009\) created in “layer 1”. The constants are calculated as in equation (16) for this case.

$${C}_{1}=0.00693, {C}_{2}=-0.00099$$
(16)

The stress distributions for the FGM coated model with \({\varepsilon }_{1}=0.009\) and \({\varepsilon }_{2}=0\) is shown in Fig. 5.

Numerical Analysis

The stress concentration in an FG plate depends on many variables. The analytical solution and the experimental models derived here are used to validate the proposed numerical model, which is used to analyze the effects of the elastic modulus and thermal expansion coefficient on the thermal stress distribution and stress concentration as a relatively fast and cost-effective method. To compare numerical and experimental analyzes in a meaningful way, the finite element model is preferred as half of the unit thickness cross-section shown in Fig. 3. This cross-section is defined in ABAQUS with the axisymmetric condition at the inner boundary. The mesh element is CAX4R ( A 4-node bilinear axisymmetric quadrilateral, reduced integration, hourglass control type element) in the element library of the program Fig. 6. The approximate global size of the mesh is 0.2. Mesh refinement was performed around the cavity. As an example of the view of the finite element model, Fig. 7 shows the meshed geometry of the two-layer experimental model and the distribution of the model, where S11 stands for \({\sigma }_{xx}\).

Fig. 6
figure 6

Finite element mesh model and S11 component of stress distribution for the case “2-layer experimental model”

Full size image
Fig. 7
figure 7

Comparisons of thermal stress distributions for the experimental models (a) along path I in 2-layer and 4-layer plates, (b) along path II in 2-layer and 4-layer plates, (c) along path III, (d) along the circumference of the half of the cavity starting from the bottom (see Fig. 3). All distances are measured in mm. Paths are shown in Fig. 4

Full size image

The models given in Table 3 were analyzed numerically, and the stress distribution along a path unaffected by the singularities of the boundaries and the cavity was compared with the values obtained from analytical solution. This comparison for the curves resulting from the finite element models is also made with those of the analytical solution of continuous gradation for the same plate (Fig. 5). The curves for all cases other than continuous gradation are obtained from the finite element results in this figure.

Results and Discussion

For functionally graded and laminated plates, the analytical results, the measurements from the experiments, and the finite element results are compared for the stress distributions. Using the analytical solution, some linear functions for the variations of these values were applied to the plates mentioned here. This gives a general idea about the thermal stress field when the material properties are changed. Additionally, the analytical analysis gives good results for both types of plates without defects, as the results agree well with those of the experiment and the numerical model. As a result of this verificaion, a possible defect was also modeled as a cavity in both the experiment and numerical models to see the thermal stress concentration. These models provide quite good stress values and the numerical model was used to study the effects of elastic modulus on stress concentration. The effect of laminated coating on the stress concentration is revealed by the four-layer experimental model.

The curve of \({\sigma }_{x}\) obtained from the experiment is compared with those in different regions of the other models in Fig. 7. Figure 7a compares \({\sigma }_{x}\) for the experimental and numerical analysis along the path I, starting from the tip of the cavity whose coordinate is z = 3.02 mm. Figure 7b shows the validation for the results of all methods in the corresponding region of the model. In this figure, the analytical solution gives some larger values for the stress in the first layer where the cavity was modeled in the experimental and numerical models. The maximum difference between the analytical and numerical solutions is about 42% in the first layer, while it becomes smaller in the second layer. The experimental results are mostly close to those from numerical models. They provide a sufficient approximation for understanding the stress concentration. The four-layer plate model, considered as a plate coated by three layers, results in a 13% lower stress concentration at the tip of the cavity than the two-layer plate model. Figure 7c and d show the comparison of \({\sigma }_{x}\) values from experimental and numerical analysis along path III, and along the circumference of the cavity, where s denotes the circumferential distance. They agree well.

The distributions of \({\sigma }_{x}\) from the finite element model are shown in Fig. 5 for the cases of laminated plates solved with the presented analytical solution (see Table 3). In this figure, the obtained results are compared with the stress distribution for the plate, which has a continuous gradation of the elastic modulus and the thermal expansion coefficient as linear functions according to equations (13) and (14). The stress values in the lower and upper regions deviate significantly from the continuous gradation, although they converge as the number of layers increases. When comparing the graphs in Fig. 5, the finite element results show larger differences than the analytical results according to the continuous gradation. This could be due to the effect of the cavity in the numerical model.

The distribution of \({\sigma }_{x}\) for the functionally graded plate with continuous gradation is very similar to the characteristic distribution of simple bending. From this point of view, a neutral axis passes through the point z = 12.12 mm in the problem considered here, for which the changes in the elastic modulus and the coefficient of thermal expansion are linear. So, most of the plate is under compression.

To calculate the stress concentration factor (KC) at the cavity tip, the stress at this point was divided by the stress at the same level of the unaffected stress distribution (Fig. 4). This value is determined as 2.16 using the values -0.302 from the two-layer experiment and -0.140 from the analytical result at the same location when no cavity is present.

A similar calculation was performed for the finite element models. Table 4 lists the values of KC calculated from the finite element results for all cases. The value of 2.58 obtained here for the two-layer experimental model is slightly larger than the value of 2.16 obtained from the measured values in the experiment. The difference is 16.3% according to the experimental result.

Table 4 KC values calculated for all cases acquired from the finite element models
Full size table

In Table 4, there are some compressive stress values for the experimental and 4-layered models, while the stress at the cavity tip is tensile for the 2- and 8-layered models. These are the results for the thermal expansion corresponding to the value of \({\varepsilon }_{f}=\alpha T(z)\). This situation can be explained as follows: Due to the interaction of the different materials of the layers, compressive stresses generally appear at the tip of the cavity whose dimensions are the same for all models. However, in the case of 2 layers with the same height, the interface is far from the tip and the negative effect disappears. In the case of 8 layers with the same height, the cavity tip is located in the second layer, which is the middle layer between two layers with different positive thermal expansion values.

Table 4 shows that the value of KC decreases when the number of layers in the plate is increased. This shows that the total thermal expansion can be distributed over the plate, changing the elastic and thermal properties with a sufficient number of layers. Thus, the material properties can be manipulated to avoid high stress concentrations.

The numerical model was used to study the effects of elastic modulus on thermal stress concentration in the experimental model. For a constant difference in thermal expansion between two layers, the value of elastic modulus for the second layer is changed as listed in Table 5. Some of the σx curves obtained from the finite element analysis of the laminated plates are shown in Fig. 8. When the material had an equal elastic modulus of 20.36 MPa for both layers, the difference in thermal expansion in this analysis resulted in a stress of -0.2198 MPa at the cavity tip. The smaller the ratio of the moduli of the two layers, the larger the change in peak stress. The stress distributions of these models along path I, starting from the tip of the cavity are shown in Fig. 9. Here, the stress value at the tip of the cavity increases for the cases from 1 to 10 in Table 5, respectively.

Table 5 The circumferential stress at the tip of the cavity in the model with the same geometry as “experimental model” for different values of elastic modulus of the second layer (CN: case number, LN: layer number)
Full size table
Fig. 8
figure 8

Distributions of the stress component \({\sigma }_{xx}\) on the finite element models with 4 and 8 layers

Full size image
Fig. 9
figure 9

The thermal stress distribution along path I as the ratio of the elastic moduli of layers is changed according to the first model in Table 5 for the experimental model. (a) The change in stress distribution is shown according to the ratio of elastic moduli of layers. The stress at the tip of the cavity becomes larger as the ratio of elastic moduli in Table 5 is set from 1 to 9. (b) The stress variation coefficient with respect to the ratio of elastic moduli of layers is shown. This coefficient is calculated according to the value determined for the plate with the same material for two layers. Points are obtained using the data in Table 5. A curve of a rational function with a solid line was fitted to these data

Full size image

The same analysis was carried out for a second model of a composite plate whose first layer has a modulus of elasticity of 40 MPa. The data for this analysis are also given in Table 5. To calculate the stress variation coefficient (SVC), the problem of a plate with a thermal expansion difference of 0.009 but a single elastic modulus of 40 MPa was solved. This has the same geometry as the “two-layer experimental model”. The stress at the the cavity tip was found to be -0.4318 MPa for this case.

Figure 9 shows SVC at the the cavity tip as a function of the ratio of the elastic moduli of the two layers in the composite plates listed in Table 5. A rational curve was fitted by using the MATLAB application of Curve Fitting Toolbox 3.5.8. The fitted curve has the form of a rational function given in equation (15).

$$SVC = \frac{1.394}{{\left( {{\raise0.7ex\hbox{${E_{1} }$} \!\mathord{\left/ {\vphantom {{E_{1} } {E_{2} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${E_{2} }$}}} \right) + 0.4069}}$$
(17)

This expression can be used to predict the stress variation for a value of the ratio of the elastic modulus compared to the value in case two layers have the same elastic modulus.

Conclusions

A plate member may be exposed to a high temperature gradient and some abrasive chemicals simultaneously in a structure such as a reactor. The design of such a component is optimized by a functional gradation in the intended direction. The determination of the thermal stress distribution is crucial, since some defects may appear in the material causing stress concentrations. Functionally graded plates are generally manufactured as layered composite plates to achieve the change in material properties. The most general approach to this lamination is to use layers of equal height. To understand the effect of the layer number to achieve a sufficient reduction in stress concentration, some models are presented here. These models are used to determine the optimal number of layers in a laminated composite plate that has a similar stress distribution with a continuous gradation and to understand the effect of the ratio of elastic moduli of the layers on the stress concentration. The following conclusions are presented for this work:

  • An analytical formula is proposed for thermal stress distribution in FGMs or laminated composite plates without defects. It is concluded that laminated composites have some stress discontinuities at the interfaces that affect the stress concentration. In Fig. 5a, the analytical results show that the stress field of the laminated plate approaches that of the plate with continuous gradation when the number of layers is increased. The more layers used, the lower the stress values at the critical points. The 8-layer composite gives reasonable results in functional gradation. The constants in the analytical formula C1 and C2 of the layered plates approach those of the functionally graded plate. Considering the results for “two-layer experimental model” and “2 layers with unequal height”, the choice of elastic modulus and thermal expansion coefficient in the form of some linear variations leads to discontinuities with lower values of change. The continuous gradation proposed here for the material constants leads to a continuous stress distribution with two signs. There is a zero-stress point, similar to simple bending. The experimental model, in which the first layer is coated by a three-layer coating, shows that the stress concentration decreases. If the coating has a continuous gradation, the stress varies differently than that of two-layer composite.

  • The analytical solution is supported by two experimental models of a laminated composite plate, which are also used to identify the stress concentration around a possible defect. The experimental models are the mechanical modeling of thermal expansion by the strain-freezing method of photothermoelasticity. The two-layer model is a plate consisting of two layers with different elastic moduli and thermal expansion coefficients, while the four-layer model is considered as the plate coated by a three-layer composite material.For two-layer model the temperature changes in the layers are 67.5⁰C and 7.5⁰C, respectively, to satisfy \({\varepsilon }_{1}\), considering the coefficients of thermal expansion of the materials in Table 2.

  • A finite element model is developed to analyze laminated composite plates under statical thermal loading. A similar case is obtained from the finite element models with the same properties. The stress distributions for the laminated composites approach those for the plate with the material constants of continuous gradation. The stress concentration factor (KC) also decreases when the variations are some linear functions. It is only 1.25 when the plate consists of 8 layers with the corresponding material constants (Table 4). Thus, the number of layers increases by 4 times and the value of KC at the tip of the cavity decreases by \(\frac{2.30}{1.25}=1.84\) times. From these values, it can be deduced that the value of KC asymptotically approaches 1 as the number of layers increases. Since a 25% increase in the stress value can be tolerated with the safety coefficients in the design, the 8-layer composite can be preferred to continuous gradation for similar thermal behavior.

  • In addition, the effect of the ratio of elastic moduli on stress concentration in a two-layer laminated composite is presented. The use of soft material as a layer in the plate reduces the stress concentration near a defect. From the numerical analysis, the results of which are presented in Table 5, it is concluded that the larger elastic modulus for the second layer leads to a larger coefficient of stress variation at the tip of the cavity. This means that an optimal value of the elastic modulus for the layers must be determined to avoid high thermal stress concentrations. Smaller values of the elastic modulus lead to a larger decrease in stress concentration. Equation (11) is a useful tool for predicting the decrease in stress concentration in the presented model for different ratios of elastic moduli.

The experimental and numerical models provides thermal stresses for laminated composite plates, where the mechanical and thermal properties change. Future work can be maintained by develo** these models for continuous gradation under both thermal and mechanical effects to optimize material gradation for functionality. Bidirectional functionally graded plates can also be considered for thermal stress analysis in a future work. The empirical formula derived here can be accepted as a result that serves this objective. In particular, the stress concentration can be determined in these models. For the particular case of the two-layer experimental model here, the stress concentration at the tip of the spherical cavity with a distance of 2.60 mm from the interface is about 2.16. This result also shows how defects lead to unexpected failure of the material due to the thermal expansion of a composite plate. This high concentration can be reduced by functionally gradation of the material properties with a sufficient number of layers and/or FGM coating.