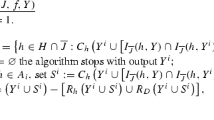The lattice of envy-free many-to-many matchings with contracts

Abstract

We study envy-free allocations in a many-to-many matching model with contracts in which agents on one side of the market (doctors) are endowed with substitutable choice functions and agents on the other side of the market (hospitals) are endowed with responsive preferences. Envy-freeness is a weakening of stability that allows blocking contracts involving a hospital with a vacant position and a doctor that does not envy any of the doctors that the hospital currently employs. We show that the set of envy-free allocations has a lattice structure. Furthermore, we define a Tarski operator on this lattice and use it to model a vacancy chain dynamic process by which, starting from any envy-free allocation, a stable one is reached.

Appendix

Proof of Proposition 1

Let $Y, Y' \in {\mathcal {E}}.$

(i) To see that $\lambda ^{Y,Y'} \in {\mathcal {E}},$ we proceed in three steps.

Step 1: $\varvec{\lambda ^{Y,Y'} \in {\mathcal {A}}}.$ Let $x,x'\in \lambda ^{Y,Y'}$ with $x\ne x'$ and let $d \in D.$ By definition of $\lambda ^{Y,Y'}$ and property (i) of $C_d$ we have $x_H \ne x'_H.$ It remains to see that $\vert \lambda ^{Y,Y'}_h \vert \le q_h$ for each $h\in H$. Assume there is $h\in H$ such that $\vert \lambda ^{Y,Y'}_h \vert >q_{h}$. Since Y and $Y'$ are allocations, we have that $\vert Y_{h} \vert \le q_{h}$ and $\vert Y_{h}' \vert \le q_{h}$. Therefore, there are $x,x'\in X$ such that $x\in \lambda ^{Y,Y'}_h{\setminus } Y_{h}'$ and $x'\in \lambda ^{Y,Y'}_h{\setminus } Y_{h}$. Moreover, as $\lambda ^{Y,Y'}_h\subseteq Y_h\cup Y'_{h}$ by definition of $\lambda ^{Y,Y'}_h$ and $x\in \lambda ^{Y,Y'}_h{\setminus } Y_{h}'$, it follows that $x \in Y_h {\setminus } Y_h'.$ Similarly, $x'\in Y'_h{\setminus } Y_{h}$. Hence, $x\ne x'.$ Let $d=x_D$ and $d'=x'_D.$ Since $x\in \lambda ^{Y,Y'}_d=C_d(Y \cup Y')$ and $x \notin Y'_h$, by substitutability,

$$\begin{aligned} x\in C_{d}(Y' \cup \{x\}). \end{aligned}$$

(1)

If $x \succ _h x',$ then (1) implies that doctor d has justified envy towards doctor $d'$ at $Y',$ contradicting that $Y' \in {\mathcal {E}}.$ Thus,

$$\begin{aligned} x'\succ _{h}x. \end{aligned}$$

(2)

Since $x'\in \lambda ^{Y,Y'}_{d'}=C_d(Y \cup Y')$ and $x' \notin Y_h$, by substitutability,

$$\begin{aligned} x'\in C_{d'}(Y \cup \{x'\}). \end{aligned}$$

(3)

Now, (2) and (3) imply that doctor $d'$ has justified envy towards doctor d at Y,  contradicting that $Y \in {\mathcal {E}}.$ Therefore, $\vert \lambda ^{Y,Y'}_h \vert \le q_{h}.$ We conclude that $\lambda ^{Y,Y'} \in {\mathcal {A}}.$

Step 2: $\varvec{\lambda ^{Y,Y'} \in {\mathcal {I}}}.$ Let $d\in D.$ By definition of $\lambda ^{Y,Y'}$ and path independence of $C_d,$

$$\begin{aligned} C_{d}\left( \lambda ^{Y,Y'} \right) =C_{d}\left( C_{d}(Y\cup Y')\right) =C_{d}(Y\cup Y')=\lambda ^{Y,Y'}_d. \end{aligned}$$

(4)

Now, take any $h\in H$ and any $x\in \lambda ^{Y,Y'}_h$. By definition of $\lambda ^{Y,Y'}$, $x\in Y \cup Y'$. Hence, $x\in Y$ or $x\in Y'$. Since both Y and $Y'$ are individually rational allocations, $x\succ _{h}\emptyset .$ Then, by responsiveness, $C_{h}\left( \lambda ^{Y,Y'} \right) =\lambda ^{Y,Y'}_h.$ This fact together with (4) proves that $\lambda ^{Y,Y'} \in {\mathcal {I}}.$

Step 3: $\varvec{\lambda ^{Y,Y'} \in {\mathcal {E}}}.$ Assume this is not the case. Then, there is a doctor $d'\in D$ that has justified envy towards a doctor $d \in D$ (possibly $d=d'$) at $\lambda ^{Y,Y'}.$ This implies that there are $x\in \lambda ^{Y,Y'}_d$ and $x'\in X_{d'}{\setminus } \lambda ^{Y,Y'}$ such that $x'_H =x_H=h,$

$$\begin{aligned} x' \succ _{h} x\text { and }x' \in C_{d'}(\lambda ^{Y,Y'} \cup \{x'\}). \end{aligned}$$

(5)

By definition of $\lambda ^{Y,Y'}$, $x'\in C_{d'}\left( C_{d'}\left( Y\cup Y^{\prime }\right) \cup \{x'\}\right)$ and, by path independence,

$$\begin{aligned} x'\in C_{d'}\left( Y\cup Y^{\prime }\cup \{x'\}\right) . \end{aligned}$$

(6)

Notice that $x' \notin Y \cup Y'.$ Otherwise, (6) implies $x' \in \lambda ^{Y,Y'},$ contradicting our hypothesis. Since $x\in \lambda ^{Y,Y'}\subseteq Y\cup Y'$, assume w.l.o.g. that $x\in Y.$ By (6) and the substitutability of $C_{d'}$,

$$\begin{aligned} x'\in C_{d'}(Y\cup \{x'\}). \end{aligned}$$

(7)

By (5), $x' \succ _{h} x.$ Therefore, by (7), doctor $d'$ has justified envy towards doctor d at Y. This contradicts that $Y \in {\mathcal {E}}.$ We conclude that $\lambda ^{Y,Y'} \in {\mathcal {E}}.$

(ii) To see that $\lambda ^{Y,Y'}$ is the join of Y and $Y'$ under the partial order $\succeq _D$, we proceed as follows. By Proposition 1 (i), $\lambda ^{Y,Y'} \in {\mathcal {E}}.$ First, we prove that $\lambda ^{Y,Y'}$ is an upper bound of Y and $Y'$ for the doctors. By definition of $\lambda ^{Y,Y'}$ and path independence,

$$\begin{aligned} C_{d}(\lambda ^{Y,Y'} \cup Y)= C_{d}(C_{d}(Y \cup Y') \cup Y)= C_{d}(Y\cup Y' \cup Y)= C_{d}(Y \cup Y')=\lambda ^{Y,Y'}_d \end{aligned}$$

for each $d\in D$. This implies that $\lambda ^{Y,Y'}\succeq _D Y.$ Similarly, $\lambda ^{Y,Y'}\succeq _D Y'.$ Second, we prove that $\lambda ^{Y,Y'}$ is the join of Y and $Y'$ for the doctors. Let ${\overline{Y}} \in {\mathcal {E}}$ such that ${\overline{Y}}\succeq _D Y$ and ${\overline{Y}}\succeq _D Y'.$ That is,

$$\begin{aligned} {\overline{Y}}_d=C_{d}({\overline{Y}} \cup Y) \text { and } {\overline{Y}}_d=C_{d}({\overline{Y}} \cup Y') \end{aligned}$$

(8)

for each $d\in D.$ We need to show that ${\overline{Y}} \succeq _D \lambda ^{Y,Y'}$, that is ${\overline{Y}}_d=C_{d}({\overline{Y}} \cup \lambda ^{Y,Y'})$ for each $d\in D$. Using repeatedly path independence, (8), and the definition of $\lambda ^{Y,Y'}$,

$$\begin{aligned} {\overline{Y}}_d= & {} C_{d}({\overline{Y}} \cup Y)=C_{d}(C_{d}({\overline{Y}} \cup Y') \cup Y)=C_{d}({\overline{Y}} \cup Y' \cup Y)\\= & {} C_{d}({\overline{Y}} \cup C_{d}( Y' \cup Y))=C_{d}({\overline{Y}} \cup \lambda ^{Y,Y'}) \end{aligned}$$

for each $d\in D.$ Thus, ${\overline{Y}} \succeq _D \lambda ^{Y,Y'}$. Therefore, $\lambda ^{Y,Y'}$ is the join for Y and $Y'$. $\square$

Proof of Theorem 1

First, by Proposition 1 (ii), the set of envy-free allocations ${\mathcal {E}}$ forms a join-semilattice under the partial order $\succeq _D$.¹³ Second, the empty allocation $Y^{\emptyset }$ in which all hospitals have their positions unfilled (that is by definition an envy-free allocation) is the minimum element of ${\mathcal {E}}$ under the partial order $\succeq _D$. To see this, let $Y\in {\mathcal {E}}$. Since $Y_d=C_d(Y \cup Y^{\emptyset })$ for each $d\in D$, it follows that $Y=Y \vee Y^{\emptyset }$. Thus, $Y \succeq _D Y^{\emptyset }$ for each $Y \in {\mathcal {E}}.$ Finally, given that the set of envy-free allocations is finite and is a join-semilattice with a minimum element, it follows that the set of envy-free allocations forms a lattice under the partial order $\succeq _D$ (see Stanley, 2011, for more details). $\square$

Proof of Theorem 2

Let $Y \in {\mathcal {E}}.$

• (i) In order to see that ${\mathcal {T}}^Y \in {\mathcal {E}},$ we proceed in three steps.

  Step 1: $\varvec{{\mathcal {T}}^Y \in {\mathcal {A}}}$. We need to show that

  $$\begin{aligned} \text { for any distinct }x,x' \in {\mathcal {T}}^Y,~x_D \ne x'_D \text { or }x_H \ne x'_H, \end{aligned}$$

  (9)

  and

  $$\begin{aligned} \vert {\mathcal {T}}^Y_h \vert \le q_h\text { for each }h\in H. \end{aligned}$$

  (10)

  Pick two distinct $x,x'\in {\mathcal {T}}^Y$, if $x_D \ne x'_D$ we are done, so assume $x_D=x'_D=d$. Since $x,x' \in C_d \left( Y\cup {\mathcal {B}}_d^Y \right) ,$ by definition of $C_d$, $x_H\ne x'_H.$ This proves (9). To see (10), assume otherwise. Then, there is $h\in H$ such that $\vert {\mathcal {T}}^Y_h \vert > q_h.$ Since $Y \in {\mathcal {A}}$, we have that $\vert Y_h \vert \le q_h.$ Hence, there is $x\in {\mathcal {T}}^Y_h {\setminus } Y_h$. Let $d=x_D.$ Then $x \in {\mathcal {T}}^Y_d$ and, as ${\mathcal {T}}^Y_d=C_d \left( Y\cup {\mathcal {B}}_d^Y \right) \subseteq Y\cup {\mathcal {B}}_d^Y,$ $x \in {\mathcal {B}}_d^Y$ because $x\notin Y.$ Hence, x is a blocking contract for Y, i.e.,

  $$\begin{aligned} x \in C_d \left( Y\cup \lbrace x \rbrace \right) \text { and } x \in C_h \left( Y\cup \lbrace x \rbrace \right) \end{aligned}$$

  (11)

  Now, we claim $\vert Y_{h} \vert < q_{h}.$ Assume otherwise that $\vert Y_{h} \vert = q_{h}$. Since x is a blocking contract for Y,  there is $x' \in Y$ with $x_H=x'_H=h$ such that $\left( Y_h {\setminus } \{x'\}\right) \cup \{x\} \succ _h Y_h,$ and, by responsiveness, this happens if and only if

  $$\begin{aligned} x\succ _h x'. \end{aligned}$$

  (12)

  Thus, by (11) and (12) d has justified envy towards doctor $x'_D$ at Y. This contradicts that $Y \in {\mathcal {E}}$. Then, $\vert Y_{h} \vert < q_{h},$ proving our claim. Furthermore, since $\vert Y_{h} \vert < q_{h}$ and we assume that $\vert {\mathcal {T}}^Y_h \vert > q_h$, there is ${\widetilde{x}} \in X$ such that ${\widetilde{x}}\ne x$ and ${\widetilde{x}}\in {\mathcal {T}}^Y_h {\setminus } Y_h.$ Let $d'={\widetilde{x}}_D.$ Then ${\widetilde{x}} \in {\mathcal {T}}^Y_{d'}$ and, as ${\mathcal {T}}^Y_{d'}=C_{d'} \left( Y\cup {\mathcal {B}}_{d'}^Y \right) \subseteq Y\cup {\mathcal {B}}_{d'}^Y,$ ${\widetilde{x}} \in {\mathcal {B}}_{d'}^Y$ because ${\widetilde{x}}\notin Y.$ Remember that $x \in {\mathcal {B}}_d^Y$, thus $x\succ _h y$ for each blocking contract y for Y such that $h=y_H$. In particular, $x\succ _h {\widetilde{x}}.$ Then, ${\widetilde{x}} \notin {\mathcal {B}}_{\star }^Y,$ contradicting that ${\widetilde{x}}\in {\mathcal {B}}^Y_{d'}.$ Therefore, (10) holds. We conclude that ${\mathcal {T}}^Y \in {\mathcal {A}}.$

  Step 2: $\varvec{{\mathcal {T}}^Y \in {\mathcal {I}}}$. Assume otherwise, then there is $x\in {\mathcal {T}}^Y$ such that $x\notin C_d({\mathcal {T}}^Y)$ or $x\notin C_h({\mathcal {T}}^Y)$ where $d=x_D$ and $h=x_H$. By definition of ${\mathcal {T}}^Y$ and path independence, ${\mathcal {T}}^Y_{d}=C_d \left( Y \cup {\mathcal {B}}^Y_{d}\right) =C_d \left( C_d \left( Y \cup {\mathcal {B}}^Y_{d}\right) \right) =C_d({\mathcal {T}}^Y).$ Hence, $x\in {\mathcal {T}}^Y_d$ implies $x \in C_d({\mathcal {T}}^Y)$ and, by our contradiction hypothesis, $x\notin C_h({\mathcal {T}}^Y).$ Since $C_h({\mathcal {T}}^Y) \subseteq {\mathcal {T}}^Y_h \subseteq {\mathcal {T}}^Y$, by consistency of $C_h$ it follows that $C_h({\mathcal {T}}^Y_h)=C_h({\mathcal {T}}^Y).$ Hence, $x\notin C_h({\mathcal {T}}^Y_h).$ As $\vert {\mathcal {T}}^Y_h {\setminus } \{x\} \vert < q_h,$ by Remark (1), $x\notin C_h({\mathcal {T}}^Y_h)=C_h(\left( {\mathcal {T}}^Y_h{\setminus } \{x\}\right) \cup \{x\})$ is equivalent to

  $$\begin{aligned} \emptyset \succ _h x. \end{aligned}$$

  (13)

  The fact that $Y \in {\mathcal {I}}$ and (13) imply that $x\notin Y.$ Moreover, as ${\mathcal {T}}^Y_d= C_d\left( Y \cup {\mathcal {B}}^Y_{d}\right) \subseteq Y \cup {\mathcal {B}}^Y_{d},$ $x \in {\mathcal {T}}^Y_d$ implies $x\in {\mathcal {B}}^Y_{d}$ and, therefore, x is a blocking contract for Y. Thus, $x\in C_h (Y\cup \{x\}).$ Notice that, by consistency of $C_h,$ we have $C_h (Y\cup \{x\})=C_h (Y_h\cup \{x\}),$ so $x\in C_h (Y_h \cup \{x\}).$ There are two cases to consider. If $\vert Y_h \vert = q_h,$ by Remark 1, there is a contract $y\in Y$ such that $x\succ _h y$. As $Y \in {\mathcal {I}}$ we have $y\succ _h \emptyset$ and, by transitivity, $x\succ _h \emptyset .$ If $\vert Y_h \vert < q_h$, by Remark 1, we also obtain $x\succ _h \emptyset .$ In either case, we contradict (13). We conclude that ${\mathcal {T}}^Y \in {\mathcal {I}}.$

  Step 3: $\varvec{{\mathcal {T}}^Y \in {\mathcal {E}}}$. Assume otherwise. Then, there are $x \in {\mathcal {T}}^Y$ and $x' \in X {\setminus } {\mathcal {T}}^Y$ with $x_D=d,$ $x'_D=d',$ and $x_H=x'_H=h$ such that $x'\succ _h x$ and $x' \in C_{d'}({\mathcal {T}}^Y \cup \{x'\}).$ By definition of ${\mathcal {T}}$ and path independence, $C_{d'}({\mathcal {T}}^Y \cup \{x'\})= C_{d'}(C_{d'}(Y \cup {\mathcal {B}}_{d'}^Y) \cup \{x'\})= C_{d'}(Y \cup {\mathcal {B}}_{d'}^Y \cup \{x'\}).$ Therefore,

  $$\begin{aligned} x' \in C_{d'}(Y \cup {\mathcal {B}}_{d'}^Y \cup \{x'\}). \end{aligned}$$

  (14)

  If $x' \in Y,$ then $x' \in C_{d'}(Y \cup {\mathcal {B}}_{d'}^Y)={\mathcal {T}}^Y_{d'}.$ This contradicts that $x' \in X \setminus {\mathcal {T}}^Y.$ Hence,

  $$\begin{aligned} x' \in X \setminus Y. \end{aligned}$$

  (15)

  Furthermore, (14) and substitutability imply

  $$\begin{aligned} x' \in C_{d'}(Y \cup \{x'\}). \end{aligned}$$

  (16)

  As ${\mathcal {T}}^Y_{d}=C_{d}(Y \cup {\mathcal {B}}^Y_{d})\subseteq Y \cup {\mathcal {B}}^Y_{d}$ and $x \in {\mathcal {T}}^Y_{d},$ we have $x \in Y \cup {\mathcal {B}}^Y_{d}.$ There are two cases to consider:

  ${\varvec{1}}.$:

  $\varvec{x \in Y}.$ Then, (15) and (16) together with the facts that $x_D=d,$ $x'_D=d',$ $x_H=x'_H=h,$ and $x'\succ _h x$ imply that $d'$ has justified envy towards d at Y,  contradicting that $Y \in {\mathcal {E}}.$

  ${\varvec{2}}.$:

  $\varvec{x \in {\mathcal {B}}^Y_d}.$ Then, $x \in {\mathcal {B}}^Y_\star .$ This implies that x is a blocking contract for Y and, as $Y \in {\mathcal {E}},$ $\vert Y_h \vert < q_h.$ As ${\mathcal {T}}^Y \in {\mathcal {I}}$ and $x \in {\mathcal {T}}^Y,$ $x\succ _h \emptyset .$ Moreover, as $x' \succ _h x$ by this step’s hypothesis, it follows that $x' \succ _h \emptyset .$ This last fact together with (16) and $\vert Y_h \vert < q_h$ imply that $x' \in {\mathcal {B}}^Y.$ Then, $x' \succ _h x$ contradicts that $x \in {\mathcal {B}}^Y_\star .$

  In either case, we reach a contradiction. We conclude that ${\mathcal {T}}^Y \in {\mathcal {E}}.$

• (ii) Let $d \in D.$ By definition of ${\mathcal {T}}$ and path independence,

  $$\begin{aligned} C_d({\mathcal {T}}^Y_d \cup Y)=C_d(C_d(Y \cup {\mathcal {B}}^Y_d)\cup Y)=C_d(Y \cup {\mathcal {B}}^Y_d\cup Y)=C_d(Y \cup {\mathcal {B}}^Y_d)={\mathcal {T}}_d^Y. \end{aligned}$$

  Thus, $C_d({\mathcal {T}}^Y_d \cup Y)={\mathcal {T}}^Y_d.$ As d is arbitrary, ${\mathcal {T}}^Y \succeq _D Y.$

• (iii) ($\Longrightarrow$) Assume $Y \in {\mathcal {E}} {\setminus } {\mathcal {S}}.$ Thus, ${\mathcal {B}}^Y_\star \ne \emptyset .$ Therefore, there is $d \in D$ such that ${\mathcal {B}}^Y_d \ne \emptyset .$ This implies that ${\mathcal {T}}^Y_d=C_d(Y \cup {\mathcal {B}}^Y_d)\ne Y_d.$ Hence, ${\mathcal {T}}^Y \ne Y.$

  ($\Longleftarrow$) Assume $Y \in {\mathcal {S}}.$ Thus, ${\mathcal {B}}^Y=\emptyset .$ Therefore, ${\mathcal {B}}^Y_d=\emptyset$ for each $d \in D.$ Then, by definition of ${\mathcal {T}},$ ${\mathcal {T}}^Y_d=Y_d$ for each $d \in D.$ Hence, ${\mathcal {T}}^Y=Y.$

$\square$

To prove Theorem 3, we first prove the following lemma.

Lemma 1

If Y and $Y'$ are two doctor envy-free allocations such that $Y \succeq _D Y'$, then ${\mathcal {T}}^{Y} \succeq _D {\mathcal {T}}^{Y'}$.

Proof

Let $Y,Y'\in {\mathcal {E}}$ be such that $Y \succeq _D Y'$ and assume that ${\mathcal {T}}^{Y} \succeq _D {\mathcal {T}}^{Y'}$ does not hold. This implies the existence of $d\in D$ such that

$$\begin{aligned} {\mathcal {T}}_d^Y\ne C_d \left( {\mathcal {T}}^{Y} \cup {\mathcal {T}}^{Y'}\right) . \end{aligned}$$

(17)

Using the definition of ${\mathcal {T}}^{Y}$ and path independence,

$$\begin{aligned} C_d \left( {\mathcal {T}}^{Y} \cup {\mathcal {T}}^{Y'}\right)= & {} C_{d} \left( C_d\left( Y \cup {\mathcal {B}}^Y_d \right) \cup C_d\left( Y' \cup {\mathcal {B}}^{Y'}_d \right) \right) \\= & {} C_{d} \left( Y \cup {\mathcal {B}}^Y_d \cup C_d\left( Y' \cup {\mathcal {B}}^{Y'}_d \right) \right) = C_{d} \left( Y \cup {\mathcal {B}}^Y_d \cup Y' \cup {\mathcal {B}}^{Y'}_d \right) \nonumber \\= & {} C_{d} \left( Y \cup Y' \cup {\mathcal {B}}^Y_d\cup {\mathcal {B}}^{Y'}_d \right) .\nonumber \end{aligned}$$

(18)

Using again path independence, it follows that

$$\begin{aligned} C_{d} \left( Y \cup Y' \cup {\mathcal {B}}^Y_d\cup {\mathcal {B}}^{Y'}_d \right) =C_{d} \left( C_d\left( Y \cup Y'\right) \cup {\mathcal {B}}^Y_d\cup {\mathcal {B}}^{Y'}_d \right) \end{aligned}$$

(19)

as by hypothesis $C_d\left( Y \cup Y'\right) =Y$, using (18) and (19) we get

$$\begin{aligned} C_d \left( {\mathcal {T}}^{Y} \cup {\mathcal {T}}^{Y'}\right) =C_{d} \left( Y\cup {\mathcal {B}}^Y_d\cup {\mathcal {B}}^{Y'}_d \right) . \end{aligned}$$

(20)

Now, using the definition of ${\mathcal {T}}$ and (20), (17) becomes

$$\begin{aligned} C_d\left( Y\cup {\mathcal {B}}^Y_d \right) \ne C_{d} \left( Y\cup {\mathcal {B}}^Y_d\cup {\mathcal {B}}^{Y'}_d \right) . \end{aligned}$$

(21)

By (21), there is a contract $x\in X$ such that

$$\begin{aligned} x\in C_d\left( Y\cup {\mathcal {B}}^Y_d\cup {\mathcal {B}}^{Y'}_d \right) \end{aligned}$$

(22)

and

$$\begin{aligned} x\in {\mathcal {B}}^{Y'}_d\setminus \left( Y\cup {\mathcal {B}}^Y_d \right) . \end{aligned}$$

(23)

Now, by (22), (23), and substitutability,

$$\begin{aligned} x \in C_{d}\left( Y \cup \left\{ x\right\} \right) . \end{aligned}$$

(24)

Since $Y'\in {\mathcal {E}}$ and $Y'$ has a blocking contract x,  $\vert Y'_h \vert < q_h$ with $h=x_H$. There are two cases to consider:

${\varvec{1}}$.:

$\varvec{ \vert Y_h \vert =q_h}.$ Let $x'\in Y_h {\setminus } Y'_h$ and let $d'=x'_D$. Notice that, as $Y \succeq _D Y'$, $x'\in Y =C_{d'}\left( Y \cup Y'\right) .$ This, together with $x'\in Y_h {\setminus } Y'_h$ implies, by substitutability, that

$$\begin{aligned} x'\in C_{d'}\left( Y' \cup \left\{ x'\right\} \right) . \end{aligned}$$

(25)

Therefore, $x'$ is a blocking contract for $Y'$ and thus $x'\in {\mathcal {B}}^{Y'}.$ By (23), $x \notin Y.$ This fact together with $x' \in Y$ imply $x' \ne x.$ Furthermore, by (23),

$$\begin{aligned} x \succ _h x'. \end{aligned}$$

(26)

Since $x' \in Y,$ $x \notin Y,$ (24), and (26), it follows that d has justified envy towards $d'$ at Y, contradicting that $Y\in {\mathcal {E}}.$

${\varvec{2}}$.:

$\varvec{ \vert Y_h \vert <q_h}.$ By (24), $x \in C_d(Y \cup \{x\})$. Since x is a blocking contract for $Y'$, $x \succ _h \emptyset .$ Since, $x \notin {\mathcal {B}}^Y_d$ by (23), it follows that there is $x' \in {\mathcal {B}}^Y$ such that $x' \succ _h x.$ Let $d'=x'_D.$ Then,

$$\begin{aligned} x' \in C_{d'}(Y \cup \{x'\}). \end{aligned}$$

(27)

By consistency, $C_{d'}(Y\cup \{x'\})=C_{d'}(Y_{d'}\cup \{x'\}).$ As $Y \succeq _D Y',$ $Y_{d'}=C_{d'}(Y\cup Y').$ Therefore, using also path independence,

$$\begin{aligned} C_{d'}(Y\cup \{x'\})=C_{d'}(C_{d'}(Y\cup Y')\cup \{x'\})=C_{d'}(Y\cup Y' \cup \{x'\}). \end{aligned}$$

Then, $x' \in C_{d'}(Y\cup \{x'\})$ implies $x' \in C_{d'}(Y\cup Y'\cup \{x'\})$ and in turn, by substitutability,

$$\begin{aligned} x' \in C_{d'}(Y' \cup \{x'\}). \end{aligned}$$

(28)

As $\vert Y_h' \vert <q_h,$ by (28) we have that $x' \in {\mathcal {B}}^{Y'}.$ Moreover, as $x' \succ _h x$ we have $x \notin {\mathcal {B}}^{Y'}_{\star },$ contradicting (23).

As in each case we reach a contradiction, we conclude that ${\mathcal {T}}^Y \succeq _D {\mathcal {T}}^{Y'}.$ $\square$

Proof of Theorem 3

We need to see that operator ${\mathcal {T}}$ verifies the hypothesis of Tarski’s Theorem. First, notice that the envy-free lattice is finite and therefore complete. Second, by Theorem 2 (i), ${\mathcal {T}}$ is from the envy-free lattice to itself. Finally, ${\mathcal {T}}$ is isotone by Lemma 1. Then, by Tarski’s Theorem, the set of fixed points of ${\mathcal {T}}$ is non-empty and forms a lattice under $\succeq _D$. Moreover, by Theorem 2 (iii), the set of fixed points of operator ${\mathcal {T}}$ is the set of stable allocations. $\square$

The following two lemmata are needed to prove Theorem 4.

Lemma 2

Let Y be an allocation. Then, $\sum _{h\in H} \vert Y_h \vert =\sum _{d\in D} \vert Y_d \vert .$

Proof

Let Y be an allocation. Recall that $Y_d$ is the subset of contracts in Y that name doctor d and, similarly, $Y_h$ is the subset of contracts in Y that name hospital h. Therefore, $\sum _{h\in H} \vert Y_h \vert = \vert Y \vert =\sum _{d\in D} \vert Y_d \vert .$ $\square$

Lemma 3

Let Y be an envy-free allocation and $Y'$ be a stable allocation. Then, $Y\vee Y'$ is a stable allocation.

Proof

Let Y be an envy-free allocation and $Y'$ be a stable allocation. By, Proposition 1 (i), $Y\vee Y' \in {\mathcal {E}}$. Assume that $Y\vee Y' \notin {\mathcal {S}}.$ Thus, there is a blocking contract x for $Y\vee Y'$. Let ${h}={x}_H$ and $d={x}_D.$ Then, ${x}\in C_{{d}}(Y\vee Y' \cup \{{x}\})$, ${x}\in C_{{h}}(Y\vee Y' \cup \{{x}\}),$ and

$$\begin{aligned} \vert (Y\vee Y')_{{h}} \vert <q_{{h}}. \end{aligned}$$

(29)

By definition of $Y\vee Y'$ and path independence, $C_{{d}}(Y\vee Y' \cup \{{x}\})=C_{{d}}(C_d(Y\cup Y') \cup \{{x}\})= C_{{d}}(Y \cup Y' \cup \{{x}\}).$ Thus, $x\in C_{{d}}(Y \cup Y' \cup \{{x}\}).$ Furthermore, by substitutability,

$$\begin{aligned} {x}\in C_{{d}}(Y' \cup \{{x}\}). \end{aligned}$$

(30)

Since x is a blocking contract for $Y\vee Y'$, Remark 1 and (29) imply ${x}\succ _{{h}} \emptyset$. This last fact together with the stability of allocation $Y'$ and (30) imply that

$$\begin{aligned} \vert Y'_{{h}} \vert =q_{h}. \end{aligned}$$

(31)

(Otherwise, x is a blocking contract for $Y'$ which is a contradiction). Next, we claim that there is ${\widetilde{h}} \in H$ such that

$$\begin{aligned} \vert (Y\vee Y')_{{\widetilde{h}}} \vert > \vert Y'_{{\widetilde{h}}} \vert . \end{aligned}$$

(32)

Assume that (32) does not hold. Then, $\vert (Y\vee Y')_{h} \vert \le \vert Y'_{h} \vert$ for each $h\in H$. Notice that, by (29) and (31), for ${h}\in H$ we have $\vert (Y\vee Y')_{{h}} \vert < \vert Y'_{{h}} \vert .$ This implies that $\sum _{h\in H} \vert (Y\vee Y')_{h} \vert <\sum _{h\in H} \vert Y'_{h} \vert .$ Thus, by Lemma 2,

$$\begin{aligned} \sum _{d\in D} \vert (Y\vee Y')_{d} \vert <\sum _{d\in D} \vert Y'_{d} \vert . \end{aligned}$$

(33)

Furthermore, since $Y' \subseteq Y \cup Y'$ we have, by LAD and the fact that $Y'\in {\mathcal {I}}$, $\vert Y'_d \vert = \vert C_d(Y') \vert \le \vert C_d(Y \cup Y') \vert$. This implies that, by definition of $Y\vee Y'$, $\sum _{d\in D} \vert Y'_{d} \vert \le \sum _{d\in D} \vert (Y\vee Y')_{d} \vert .$ This contradicts (33), implying that (32) holds and the claim is proven. Thus, there is ${\widetilde{h}} \in H$ such that $\vert (Y\vee Y')_{{\widetilde{h}}} \vert > \vert Y'_{{\widetilde{h}}} \vert .$ Then, there is a contract ${\widetilde{x}}\in (Y\vee Y') {\setminus } Y'$ such that ${\widetilde{x}}_H={\widetilde{h}}.$ Let ${\widetilde{d}}={\widetilde{x}}_D.$ Since $Y\vee Y'\in {\mathcal {I}},$ $Y\vee Y'=C_{{\widetilde{d}}}(Y\vee Y')=C_{{\widetilde{d}}}(Y\vee Y' \cup \{{\widetilde{x}}\}).$ Therefore, ${\widetilde{x}}\in Y\vee Y'$ implies ${\widetilde{x}}\in C_{{\widetilde{d}}}(Y\vee Y' \cup \{{\widetilde{x}}\}).$ Furthermore, by definition of $Y\vee Y'$ and path independence, ${\widetilde{x}}\in C_{{\widetilde{d}}}(Y \cup Y' \cup \{{\widetilde{x}}\})$ and, by substitutability,

$$\begin{aligned} {\widetilde{x}}\in C_{{\widetilde{d}}}(Y' \cup \{{\widetilde{x}}\}). \end{aligned}$$

(34)

Given that $Y\vee Y'$ is an allocation, by (32) we have that $\vert Y'_{{\widetilde{h}}} \vert < \vert (Y\vee Y')_{{\widetilde{h}}} \vert \le q_{{\widetilde{h}}}$. Thus, $\vert Y'_{{\widetilde{h}}} \vert < q_{{\widetilde{h}}}$, ${\widetilde{x}} \notin Y'$, and ${\widetilde{x}}\succ _{{\widetilde{h}}} \emptyset$ imply, by Remark 1, that

$$\begin{aligned} {\widetilde{x}}\in C_{{\widetilde{h}}}(Y' \cup \{{\widetilde{x}}\}). \end{aligned}$$

(35)

Then, (34) and (35) imply that ${\widetilde{x}}$ is a blocking contract for $Y'$, contradicting the stability of allocation $Y'$. Therefore, $Y\vee Y'$ is a stable allocation. $\square$

Proof of Theorem 4

Let $Y \in {\mathcal {E}}.$ By Lemma 3, $Y \vee Y^{H}$ is a stable allocation. By Lemma 1 and Theorem 2 (iii), $Y \vee Y^{H} \succeq _{D} Y$ implies that $Y \vee Y^{H} \succeq _ D {\mathcal {F}}^Y$. Moreover, given that ${\mathcal {T}}$ is a weakly Pareto improving operator by Theorem 2 (ii), ${\mathcal {F}}^Y \succeq _D Y$. Since $Y^{H}$ is the doctors’ pessimal stable allocation, ${\mathcal {F}}^Y \succeq _D Y^{H}.$ As ${\mathcal {F}}^Y \succeq _D Y$ and ${\mathcal {F}}^Y \succeq _D Y^{H},$ by definition of join, ${\mathcal {F}}^Y \succeq _D Y \vee Y^{H}$. Thus, by antisymmetry, ${\mathcal {F}}^Y = Y \vee Y^{H}.$ $\square$

Proof of Proposition 2

Let $Y \in {\mathcal {E}}$ and $d \in D.$ By LAD and individual rationality of Y,  we have that $\vert {\mathcal {T}}^Y_{d} \vert = \vert C_d(Y \cup {\mathcal {B}}^Y_{d}) \vert \ge \vert C_d(Y) \vert = \vert Y_d \vert .$ Iterating we obtain that $\vert {\mathcal {F}}^Y_d \vert \ge \vert Y_d \vert .$ By definition, ${\mathcal {F}}^Y$ is a fixed point of our Tarski operator. Thus, ${\mathcal {F}}^Y$ is stable by Theorem 2 (iii). Then, by the Rural Hospitals Theorem $\vert {\mathcal {F}}^Y_d \vert = \vert Y'_d \vert$ for each $Y' \in {\mathcal {S}}$ and each $d \in D.$ Therefore, $\vert Y_d \vert \le \vert {\mathcal {F}}^Y_d \vert = \vert Y'_d \vert$ for each $Y' \in {\mathcal {S}}$ and each $d \in D.$ $\square$