1 Introduction

Modeling energy commodity prices is a challenging task. Frequent shocks in the supply–demand balance observed in real markets (Křehlík and Baruník 2017) have resulted in very erratic price dynamics, especially in energy markets such as those for natural gas and electricity (Naeem et al. 2020). In these markets, one can observe alternating periods of stable prices and periods of turbulent prices in which a strong mean-reversion component forces prices to fall after a jump or spike has occurred (Geman and Roncoroni 2006; Fernandes et al. 2021). As a result, empirical distributions of log-returns are characterized by high values of volatility as well as nonzero skewness and fat tails with high values of kurtosis (Weron 2013; Liu and Serletis 2023). Although price time series are typically nonstationary, log-returns show better behavior (Voit 2005; Bücher and Segers 2018), and it is very important that a given model captures the first four central moments of the empirical distribution of log-returns (Geman 2005). Indeed, in addition to standard deviation, the model must be able to reproduce skewness and kurtosis well, the former for the properties of upward and downward movements, the latter for extreme events that may be particularly relevant in commodity markets(Carter et al. 2017).

The literature on this topic has grown exponentially in recent years. Two main directions have been followed by the research. In the first direction, mean-reverting jump diffusion processes have been employed to explain the jump behavior of commodity prices observed in real markets (Cartea and Figuera 2005; Mason and Wilmot 2014; Borovkova and Schmeck 2017; Kegnenlezom et al. 2019; Mari and Mari 2021). In the second direction, regime-switching processes (Hamilton 1989) have been proposed with the aim of distinguishing stable from turbulent motion of the observed prices. Regime-switching models have been widely used to describe the price dynamics of electricity (Huisman and Mahieu 2003; Mari 2006; Eichler and Türk 2013; Paraschiv et al. 2015; Mehrdoust and Noorani 2021) and the price dynamics of other energy commodities such as natural gas (Leonhardt et al. 2017; Scarcioffolo and Etienne 2021) and crude oil (Zhu et al. 2017; Serletis and Xu 2019; Ruble and Powell 2021; Scarcioffolo and Etienne 2021). By introducing different mean-reversion rates and volatilities depending on the state of the system, regime-switching models allow us to combine stable and turbulent dynamics in a single model. For these reasons, they can be considered good candidates for describing the complex price dynamics observed in commodity markets. The main disadvantage is that, because of the large number of parameters involved, great care must be taken in calibrating these models to market data.

Based on these considerations, we propose a new approach to simply and accurately model the dynamics of electricity and natural gas prices observed in real markets. Our methodology is based on machine learning (ML) techniques, specifically smoothing and clustering algorithms for market prices data analysis, and deep learning (DL) methods for studying the dynamics of observed prices. ML is a promising field of investigation in finance (Rundo et al. 2019) and time series analysis (Xu et al. 2020), allowing us to build simple models to describe complex dynamics.

In the spirit of Occam’s razor, which advocates the principle of parsimony in explaining experimental data, the main purposes of our study are twofold: (1) to build the simplest model capable of incorporating the main stylized facts of electricity and natural gas market price behavior, including dynamic correlation; (2) to define an appropriate model calibration procedure on market data to satisfactorily reproduce the first four moments of empirical log-return distributions.

The empirical analysis was conducted on the Italian energy market, specifically on the time series of electricity and natural gas prices provided by GME (Gestore dei Mercati Energetici SpA). Our dataset consists of daily frequency time series from 1 June 2017 to 31 May 2022. This is a very particular period when energy prices were affected by the consequences of a pandemic emergency, the beginning of a new economic recovery, and the turbulence caused by the first months of the war in Ukraine. It is certainly a good test for the proposed methodology.

The starting point of our study is the observation that the empirical distributions of electricity log-returns show, on close analysis, a Gaussian component in which a very large fraction of the observed log-returns can be included (Mari and Mari 2021). Log-returns not belonging to the Gaussian component of the dynamics can be then identified with price jumps. As will be shown in Sect. 3, these aspects also characterize the empirical distribution of log-returns of electricity and natural gas observed in the Italian market. Dividing log-returns into Gaussian and jump log-returns can be used to build and calibrate appropriate models of price dynamics.

For each energy commodity, namely natural gas and electricity, we propose a regime-switching model in which two regimes are used to describe the basic dynamics with the aim of capturing the stable upward and downward movements; two other regimes are used to describe the turbulent dynamics to account for upward and downward jumps. Specifically, the base dynamics is driven by a stochastic mean-reversion process characterized by two parameters, the mean-reversion and volatility coefficients; the jump dynamics is defined by a one-parameter Lévy process describing the amplitude of stochastic jumps. Accordingly, a three-parameter regime-switching model is used to describe the price dynamics. The switching mechanism between the regimes is driven by the predictions of a Deep Neural Network (DNN) carefully trained on both electricity and natural gas prices, integrated with a hidden Markov process (Hamilton 1989; Elliott et al. 2018; Wang et al. 2020) to account for the occurrence of totally unpredictable jumps. As expected, in fact, the DNN tends to underestimate the number of jumps because the occurrence of some of them is totally random and cannot be predicted. This hybrid switching mechanism ensures that the model provides a realistic representation of price dynamics by appropriately accounting for the one-period transition probabilities and the dynamic correlation between electricity and natural gas prices, without introducing additional parameters. Accounting for correlation between natural and electricity prices is a very important aspect of the proposed methodology. In fact, significant correlation can be observed in many countries around the world, including Italy, because natural gas power plants often act as marginal dispatch units (IEA 2021; EIA 2022). In Italy, for example, about fifty percent of electricity is generated by gas-fired power plants (MET 2022).

In the spirit of Occam’s razor, the proposed model can be considered the simplest dynamic model capable of incorporating the main stylized facts observed in real markets. In fact, the price dynamics of each energy commodity is described by three parameters which is the minimum number of parameters needed to account for mean-reversion and volatility in the stable regime and jumps in the turbulent regime.

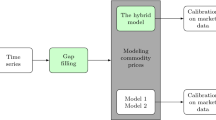
The methodology we propose can be divided into three steps: (1) calibration of the mean-reverting process on the Gaussian clusters detected in the empirical log-return distributions; (2) modelling the transitions between the stable Gaussian dynamics and jump dynamics; and (3) calibration of the jump dynamics.

In the first step, after removing possible trend and seasonality from the log-price time series using the LOESS (LOcally Estimated Scatterplot Smoothing) algorithm (Cleveland et al. 1990), we employed the clustering DBSCAN (Density-Based Spatial Clustering of Applications with Noise) algorithm (Ester et al. 1996) with the aim to identify the largest Gaussian cluster in the empirical distribution of log-returns. LOESS is a flexible ML algorithm whose main advantage over many other methods is that it does not require the specification of a global function or the assumption that the data must fit some given distribution shape (Dagum and Bianconcini 2016). The DBSCAN algorithm is an unsupervised ML method that uses a density-based approach to find arbitrarily shaped clusters and outliers in data. Density-based techniques are more efficient than partition-based and hierarchical clustering techniques for detecting outliers (Bajal et al. 2022). In our analysis, therefore, DBSCAN is a particularly suitable algorithm for detecting anomalous, i.e., non-Gaussian log-returns Chesnokov (2019). As will be shown in Sect. 3, the mean-reversion and volatility parameters can be calibrated at this stage following an iterative procedure. This is another novel aspect of the proposed methodology, allowing us to explore in depth the dynamics of prices in the Gaussian cluster.

In the second step, DL-based techniques are used to jointly study the dynamics of electricity and natural gas prices and their interactions. To this end, we employed a Deep Neural Network (DNN) with a multi-layer structure. In fact, DNNs with a single hidden layer are widely used for modeling and forecasting time series (Karim et al. 2018), however many hidden layers are required to well capture non-linear relationships existing between variables (Torres et al. 2021). The description of the DNN architecture, the reasoning behind it, and the specific task of each DNN layer will be discussed in Sect. 4. The DNN is trained on a dataset consisting of sequences of consecutive electricity and natural gas price observations in order to reconstruct the relevant features of the dynamics and transitions between regimes. Each observation in the training sequences consists, therefore, of a pair of numbers, i.e., the detrended log-prices of electricity and natural gas for a given calendar day. The use of a DNN in our model aims to improve the reliability of price pattern recognition with the goal of understanding the regularities of electricity and natural gas price dynamics, their interactions, and the transition mechanism between stable motion and jump dynamics. As a macro-lens capable of uncovering the main features of motion, the DNN provides relevant information on price dynamics. By revealing the relative movements of electricity and natural gas prices, the DNN also allows us to introduce a realistic price correlation mechanism.

In the third step, the jump component of the dynamics is calibrated to the market data using the method of simulated moments (McFadden 1989; Duffie and Singleton 1993) and Monte Carlo techniques (Gelman 1995; Rashki 2021). The decoupling between stable and turbulent motion is useful to develop a statistical procedure to calibrate the model to market data, taking advantage of the full information contained in both the Gaussian and jump components of the log-return distribution. Although the proposed model is the simplest that incorporates the main features of observed market prices, we will show that it is flexible enough to remarkably reproduce the first four central moments of the empirical distributions of log-returns.

The whole methodology workflow is depicted in Fig. 1.

Fig. 1
figure 1

Block diagram of the whole methodology workflow. Cyan blocks show the tasks in wich ML-based techniques are involved. (Color figure online)

Full size image

The proposed methodology has several advantages. In particular, it enables the construction of realistic and parsimonious dynamic models that can be easily calibrated to market data. This is an important task for all market participants (Carter et al. 2017). It is essential in the short-term for implementing risk hedging strategies (Chen 2017) and pricing energy derivatives (Geman 2005). It is also a central task in the long-run for evaluating investments in the energy sector. In fact, in the presence of a mean-reverting component, long-term probability distributions of energy prices can be meaningfully obtained from the short-term dynamics (Mari 2021). In this way, the long-run dynamics can incorporate all those features of the short-run dynamics that may be relevant over a longer time horizon, thus enabling a realistic assessment of investments in the energy sector. From this perspective, the proposed methodology can be a powerful analytical tool for energy planning decisions by energy companies and policy makers to guide the ecological transition.

The paper is organized as follows. Section 2 illustrates in detail the data preprocessing methodology. In Sect. 3 the Gaussian dynamics is investigated and the calibration of the mean-reversion process on Gaussian clusters is discussed. In Sect. 4 the regime-switching model is presented and the hybrid DNN-driven transition mechanism between regimes is illustrated. In the same section, the calibration of the jump component to market data is provided. Section 5 concludes the paper.

2 Data preprocessing

We performed the empirical analysis on the Italian energy market, specifically on the time series of electricity and natural gas prices provided by GME (Gestore dei Mercati Energetici SpA). The electricity price, called PUN (Prezzo Unico Nazionale), is provided on an hourly basis and it is expressed in nominal dollars per megawatt-hour. Natural gas prices are provided on a daily basis and are expressed in nominal dollars per megawatt-hour. All these data are freely downloadable from www.mercatoelettrico.org. Our analysis was conducted on daily prices, and to obtain a daily electricity price, we averaged the PUN prices over 24 h.

The period under investigation is from 1 June 2017 to 31 May 2022 with \(N_{\text {obs}}=1826\) daily observations. In this five-year time interval, energy prices moved in a very erratic way as a consequence of a pandemic emergency, the beginning of a new economic recovery and the turbulences caused by the first months of the war in Ukraine. We look, therefore, for trend ans seasonality over time in order to put in evidence the underlying stochastic processes governing the market dynamics. Let us denote by \(p_t\) the market price at time t (of one megawatt-hour of electricity or natural gas) and by

$$\begin{aligned} s_t=\ln p_t, \end{aligned}$$
(1)

its natural logarithm. We assumed that \(s_t\) is a linear superposition of a deterministic component, \(f_t\), accounting for trend and seasonality (hereinafter, trend), and a random component, \(x_t\), namely

$$\begin{aligned} s_t=f_t+x_t. \end{aligned}$$
(2)

Log-returns are defined as daily changes in the stochastic component of log-prices,

$$\begin{aligned} r_t=x_{t+1}-x_t. \end{aligned}$$
(3)

Log-return time series and their empirical distributions are the output of this preprocessing task. In fact, although price time series are typically non-stationary, log-returns show better behavior (Bücher and Segers 2018) and knowledge of the empirical distribution of log-returns is crucial for establishing appropriate models that can incorporate the main stylized facts of the price dynamics.

We used the LOESS (LOcally Estimated Scatterplot Smoothing) algorithm to detect the deterministic component of the dynamics \(f_t\) (Cleveland et al. 1990). LOESS is a flexible technique that allows for trend and seasonality removal by fitting simple polynomial models to localized subsets of data. The primary advantage of LOESS over many other methods is that it does not require the specification of a global function or the assumption that the data must fit some distribution shape. The LOESS method is based on the notion that any function can be well approximated in a small neighborhood by a low-order polynomial and that simple models can be easily fitted to data (Dagum and Bianconcini 2016). Figure 2 depicts, for the period 1 June 2017 to 31 May 2022, the electricity log-price time series \(s_t\), the trend \(f_t\) (in red), the stochastic component of the dynamics \(x_t\), and the log-return time series \(r_t\). Figure 3 shows the same quantities for natural gas.

Fig. 2
figure 2

Electricity. Upper left panel: the log-price time series, \(s_t\) (in blue), and superimposed (in red) the trend, \(f_t\). Upper right panel: the stochastic component, \(x_t\) (in blue), and the trend, \(f_t\) (in red). Lower left panel: the stochastic component, \(x_t\). Lower right panel: the log-return time series, \(r_t\). (Color figure online)

Full size image
Fig. 3
figure 3

Natural gas. Upper left panel: the log-price time series, \(s_t\) (in blue), and superimposed (in red) the trend, \(f_t\). Upper right panel: the stochastic component, \(x_t\) (in blue), and the trend, \(f_t\) (in red). Lower left panel: the stochastic component, \(x_t\). Lower right panel: the log-return time series, \(r_t\). (Color figure online)

Full size image

The descriptive statistics of log-returns is displayed in Table 1. Observed time series show very different characteristics. In particular, the standard deviation of empirical log-returns is very high in the case of electricity prices with respect to the values observed in the natural gas market. Moreover, natural gas log-returns show large fluctuations with jumps and spikes, and non-normal, leptokurtic empirical distributions. On the other hand, the time series of electricity log-returns does not show such extreme behavior. We note that the presence of high magnitude jumps and spikes is revealed by the high value of the kurtosis observed in this market. This value is significantly higher than the value of the kurtosis observed in the electricity market.

Table 1 Descriptive statistics of log-returns
Full size table

3 Discovering the Gaussian dynamics

The main purpose of this study is to present a Machine Learning (ML) based methodology aimed at extracting all the possible information from financial time series that will be used to perform two important tasks: (1) building the simplest model capable of incorporating the main stylized facts of observed energy commodity prices; (2) calibrating the model to observed data. In this section, we investigate the Gaussian motion of the log-return dynamics in order to decouple the stable motion from the jumpy behavior of market prices. To accomplish this, we decompose observed log-returns in a Gaussian cluster and a residual cluster using the DBSCAN algorithm.

3.1 Modeling the Gaussian motion

In the attempt to model energy commodity prices starting from their stylized facts, we include a mean-reverting component in the dynamics to model the stable motion. In the spirit of the Occam’s razor, the simplest Gaussian process that includes mean-reversion is a two-parameter process described by the following equation,

$$\begin{aligned} x_{t+1}-x_t=-\kappa _0 x_t+\sigma _0\Delta w_t, \end{aligned}$$
(4)

where \(\kappa _0\) is the mean-reversion coefficient, \(\sigma _0\) is the volatility parameter, \(w_t\) is a discrete time Brownian motion, and \(\Delta w_t=w_{t+1}-w_t\). The time interval is assumed equal to one day. The first step of our analysis is, therefore, to calibrate the model to market data. As we will show in the next section, this task can be accomplished by exploring the Gaussian component of the dynamics through log-return clustering.

3.2 Calibrating the mean-reverting dynamics

Starting from Eq. (4), we looked for Gaussian clusters in the adjusted log-return time series, \({\bar{r}}_t\), defined by

$$\begin{aligned} {\bar{r}}_t=x_{t+1}-x_t+\kappa _0 x_t. \end{aligned}$$
(5)

The DBSCAN (Density-Based Spatial Clustering of Applications with Noise) algorithm was used to detect Gaussian clusters (Ester et al. 1996). DBSCAN is a particularly efficient clustering algorithm for detecting outliers (Chesnokov 2019), in our case anomalous log-returns, so we found it suitable for detecting non-Gaussian log-returns. The DBSCAN algorithm was run on the normalized adjusted log-return time series by varying the following two parameters through grid search:

  • a: the minimum number of neighbors required to identify a core point;

  • b: the maximum distance between two sample points for one to be considered in the neighborhood of the other.

The calibration of the parameters \(\kappa _0\) and \(\sigma _0\) follows a two-step procedure. As a preliminary step, a three-dimensional \(100 \times 100 \times 100\) grid was defined with values ranging from 0.01 to 0.50 (in increments of 0.005) for the mean-reversion parameter, \(\kappa _0\); from 1 to 100 (in increments of 1) for parameter b; from 0.01 to 1 (in increments of 0.01) for parameter a. We addressed the problem of determining the most appropriate range of DBSCAN parameter values through hierarchical cluster analysis using the Ordering Points To Identify the Clustering Structure (OPTICS) algorithm (Campello et al. 2015). As we will see, the chosen grid proved to be suitable in allowing us to appropriately calibrate the model in the two markets under investigation. In the first step, we associated to each value of the mean-reversion parameter, \(\kappa _0\), belonging to the grid, the largest adjusted log-return Gaussian cluster. To perform this task, we first set a value of \(\kappa _0\), and then for each pair of values a, b belonging to the grid, all clusters identified by the DBSCAN algorithm were merged into one large cluster. Next, the normality hypothesis is tested on this large cluster by performing the Kolmogorov–Smirnov test and, if positive, the cluster is saved. Finally, by varying the pair a, b, on the grid, we determined the largest cluster for which the hypothesis of a normal log-return distribution cannot be rejected. In this way, we can (1) associate to each value of the mean reversion parameter, \(\kappa _0\), the largest Gaussian cluster, \(G(\kappa _0)\), consistent with that value; (2) determine the value of the mean reversion parameter, \(\bar{\kappa }_0\), with which the Gaussian cluster with the maximum number of observations, \(G({\bar{\kappa }}_0)\), is associated.

In the second step, the following iterative method allowed us to calibrate the model:

  • starting from a given value of the mean-reversion parameter, \(\kappa _0\), and its associated Gaussian cluster, \(G(k_0)\), a new value of the mean-reversion parameter is computed by linear regression on the sequence of consecutive detrended log-prices observations whose adjusted log-return belongs to \(G(k_0)\);

  • if the absolute difference between this new value and \(\kappa _0\) is less than 0.002 the procedure stops, otherwise the new value is rounded to the nearest value on the grid; then, this rounded value of the mean-reversion parameter and its associated Gaussian cluster are used to perform again step one.

The iterative process is initialized by setting \(\kappa _0={\bar{\kappa }}_0\) and continues until convergence is reached. Once the mean-reversion parameter is estimated, the volatility parameter, \(\sigma _0\), is then identified with the standard deviation of the Gaussian cluster associated to the estimated mean-reversion value. Table 2 shows the calibrated parameters together with some statistical properties of the associated Gaussian clusters. \(N_0\) denotes the number of log-return values belonging to the Gaussian cluster, and \(N=N_{\text {obs}}-1=1825\) is the number of log-return values in the observed time series in the five-year period 1 June 2017 to 31 May 2022. Moreover, Table 2 reports also the number of upward jumps (u-jumps) and downward jumps (d-jumps) detected in the period under investigation.

Table 2 The calibrated parameters of the stable dynamics and some statistical properties of the associated Gaussian clusters
Full size table

Both markets show considerably large Gaussian clusters. Figure 4 shows normalized log-return time series and normalized log-return Gaussian clusters represented by cyan dots, while non-Gaussian log-returns are represented by red dots.

Fig. 4
figure 4

Upper panels: Electricity log-returns. Lower panels: Natural gas log-returns. Normalized log-return time series are shown in the left panels; normalized log-return Gaussian clusters (cyan dots) and non-Gaussian log-returns (red dots) are shown in the right panels. (Color figure online)

Full size image

The proposed approach allowed us to calibrate the Gaussian stable dynamics to market data by using ML techniques thus providing both mean-reversion and the volatility parameters. As will be shown in the next section, the decomposition of the observed log-returns into a Gaussian component and a jump component allows us to construct a regime-switching model suitable for describing the dynamics of electricity and natural gas.

4 Modeling electricity and natural gas price dynamics

A three-parameter regime-switching model capable of incorporating the main stylized facts of observed energy commodity prices is discussed in this section. As we will see, it is the simplest model that makes use of the full information extracted from observed time series by ML techniques. The method for calibrating this model to marked data is also illustrated.

4.1 The model

The decoupling between Gaussian and non-Gaussian log-returns allows us to define a simple model to describe the evolution of market prices. Indeed, the dynamic model we propose to capture the complex dynamics of both electricity and natural gas prices can be described by the following stochastic process,

$$\begin{aligned} x_{t+1}-x_t=\left\{ \begin{array}{ll} -\kappa _0 x_t + \sigma _0 |\Delta w_t |\\ -\kappa _0 x_t - \sigma _0 |\Delta w_t |\\ +|\Delta z_t |\\ -|\Delta z_t |, \\ \end{array} \right. \end{aligned}$$
(6)

where \(z_t\) is a Lévy process and \(\Delta z_t=z_{t+1}-z_t\) are i.i.d. random variables accounting for non-Gaussian log-returns. The processes \(w_t\) and \(z_t\) are assumed to be stochastically independent. Hence, the first and the second regime accounts respectively for upward and downward stochastic stable movements of market prices and are described in terms of mean-reverting stochastic processes with mean-reversion parameter \(\kappa _0\), and volatility \(\sigma _0\). The third and the four regime describe non-Gaussian log-returns due to upward and downward jumps respectively. This model can be considered the simplest dynamic model capable of incorporating the main stylized facts observed in real markets. In fact, the price dynamics of each energy commodity is described by three parameters which is the minimum number of parameters needed to account for mean-reversion and volatility in the stable regime and jumps in the turbulent regime. The switching mechanism between regimes is driven by the predictions a suitable Deep Neural Network (DNN) jointly trained on electricity and natural gas log-prices, integrated with a hidden Markov process to account for the occurrence of totally unpredictable jumps. We will see that this hybrid switching mechanism allows us to properly account for time varying one-period transition probabilities and dynamic correlation between electricity and natural gas prices without introducing additional parameters to the dynamics. The DNN architecture, the training dataset, the switching mechanism and the reasoning behind them will be discussed in the next section.

4.2 The DNN architecture and the switching mechanism

A DNN-based classification approach was adopted in this study. We employed a DNN with a multilayer architecture characterized by nine layers are arranged in the following sequence: an input layer, an initial embedding layer, two sequences composed of a convolutional layer and a max pooling layer, two Long Short-Term Memory (LSTM) layers, and two dense layers as outputs, one for electricity and one for natural gas data. The DNN architecture is depicted in Fig. 5.

Fig. 5
figure 5

The DNN architecture

Full size image

This is an appropriate architecture for the network to capture the nonlinear relationships that exist between temporally ordered observations. Indeed, after the input and the embedding layers, two sequences composed of one convolutional and one max pooling layer, stacked one after the other, are used to perform data smoothing. The presence of a second sequence of such layers, provides a better representation of the input data. In fact, by increasing the depth, the network can better approximate the nonlinear relationships between the input data, thus obtaining better feature representations (Gu et al. 2018). In the convolutional layers, a Rectified Linear Unit, or ReLU for short, is used as activation function. Then, two LSTM layers, stacked on top of each other, handle the main part of the prediction problem. Recurrent neural networks, such as LSTM, are particularly well suited to capture nonlinear temporal and spatial dependencies (Hochreiter and Schmidhuber 1997), thus showing strong prediction performance (Che et al. 2018; Bao et al. 2017). The presence of two stacked LSTM layers allows us to improve the DNN prediction performance (Ren et al. 2019). Finally, two dense layers, one for electricity and one for natural gas data, complete the prediction task. In these last layers, the Softmax function is used as activation function. In the classification approach taken in this study, the Softmax function returns a probability distribution over the classes. Once the DNN is trained, the prediction, i.e., the DNN output is provided by the class that maximizes the probability. To compute the loss value we used the Sparse Categorical Crossentropy with Adam as the optimization algorithm.Footnote 1 Table 3 provides the main DNN parameters.

Table 3 DNN main parameters
Full size table

To enable the neural network to drive the switching mechanism, information about Gaussian and non-Gaussian observed adjusted log-returns (see Eq. 5) must be properly provided. We used a preliminary data set composed of two time series of length \(N=1825\), including the first N historical electricity and natural gas detrended log-prices (hereinafter, log-prices). In addition, we built two more vectors of length N, one for electricity and one for natural gas, in which observed adjusted log-returns are encoded in order to distinguish four different price movements, i.e., upward stable movements, downward stable movements, upward jumps and downward jumps. If in the time interval \([i,i+1]\), with \(i=1,2,\dots ,N\), a positive Gaussian adjusted log-return is observed, i.e. \({\bar{r}}_i >0\), then \({\bar{r}}_i\) is mapped to the symbol \(0^+\) to describe an upward stable price movement; if \(\bar{r}_i \le 0\), \({\bar{r}}_i\) is mapped to the symbol \(0^-\) for a downward stable price movement; if a non-Gaussian positive log-return is observed, \({\bar{r}}_i\) is mapped to the symbol \(1^+\) to describe an upward jump; if a non-Gaussian negative log-return is observed, \({\bar{r}}_i\) is mapped to the symbol \(1^-\) for a downward jump. Four classes for each commodity, denoted by the symbols \(0^{\pm }\) and \(1^{\pm }\), identify, therefore, the possible outcomes of the DNN. The aim is to improve the reliability of the log-price pattern recognition needed to distinguish the stable dynamics with its upward and downward movements from the jump dynamics, and thus to understand when an upward or downward jump may occurs.

In the training data set, each input observation is made up of a couple of numbers \(z_i=(x_i^e,x_i^g)\), respectively the electricity log-price, \(x_i^e\), and the natural gas log-price, \(x_i^g\), relating to the trading day i. The output observation is a couple of symbols \(\Theta _i=(\theta ^e_i,\theta ^g_i)\), where \(\theta ^e_i\), \(\theta ^g_i\) belong to the above defined four classes \(\{0^{\pm },1^{\pm }\}\), specifying the relative movements of electricity and natural gas prices. Each element of the training data set is composed of \(n=20\) consecutive input observations, \(z_{k+1},z_{k+2},\ldots ,z_{k+n}\), and one output observation, \(\theta _{k+n}\), with \(k=0,2,\ldots ,N-n\).

The rationale behind the adoption of such a training dataset is trying to capture the complex nonlinear relationships between the market behavior of gas and electricity prices including dynamic correlation. In many countries around the world the cost of natural gas is, indeed, a significant driver of electricity prices because it often acts as the marginal (highest cost) fuel of generating units that operators dispatch to supply electricity (IEA 2021; EIA 2022). For instance, in the Italian market the empirical correlation of log-returns was about 0.4 in the period under investigation. Training the DNN jointly on electricity and natural gas log-prices allows us to get a realistic data driven representation of price dynamics by appropriately accounting for the dynamic correlation between electricity and natural gas prices, without introducing additional parameters.

The DNN was trained for 150 epochs. Loss functions are shown in Fig. 6. The left panel depicts the electricity loss function (in red) and, superimposed, the total loss function. The right panel depicts the natural gas loss function (in red) and, superimposed, the total loss function. The total loss function is computed as the sum of the electricity loss function and the natural gas loss function. The fast decreasing behavior of the total loss function demonstrates that the DNN architecture is performing well.

Fig. 6
figure 6

Loss functions. (Color figure online)

Full size image

The so trained DNN is employed to predict switches between regimes. Indeed, let us suppose that the DNN prediction at time i, performed on the basis of the previous \(n=20\) observation, is the couple \(\Theta _i=(1^+,0^-)\). This means that in the time interval \([i,i+1]\), an upward jump will affect the dynamics of electricity log-prices and a downward stable movement will drive the natural gas log-price motion. In such a case, the dynamics of electricity log-prices in the time interval \([i,i+1]\) will be described by the upward jump regime, i.e., the third regime in Eq. (6), and the dynamics of natural gas log-prices by the second regime in Eq. (6). As a further example, let us suppose that DNN makes the prediction \(\Theta _i=(0^+,1^+)\). In such a case, an upward stable movements will drive the electricity log-price dynamics while an upward jump will occur to influence the dynamics of natural gas log-price. This implies that in the time interval \([i,i+1]\), the dynamics of electricity log-prices will be described by the first regime in Eq. (6), and the dynamics of natural gas log-prices by the upward jump regime, i.e., the third regime in Eq. (6). In this way, a data driven mechanism can be used to describe not only transitions between different dynamic regimes but also dynamic correlation between electricity and natural gas log-returns. In addition, the DNN-based switching mechanism allows us to generate stochastic paths by Monte Carlo techniques in the following way:

  • a sequence of \(n=20\) electricity log-prices and a sequence of \(n=20\) natural gas log-prices are generated using Eq. (4) calibrated to market data, starting from a given initial point;

  • the data generated in the previous step are merged to construct a time-ordered sequence of \(n=20\) log-prices pairs, specifically one electricity log-price and one natural gas log-price, to be used as a random seed to initialize the DNN prediction process;

  • starting from the random seed, a first prediction is provided by the DNN;

  • both, the predicted electricity and gas log-prices are used to update the sequence by discarding the first couple of log-prices and including the new generated couple;

  • based on the latter sequence, the DNN provides a new prediction.

By iterating the last two items in each time sub-interval \([i,i+1]\), a Monte Carlo path can be obtained over the whole time interval.

To test the ability of DNN to predict jumps, we generated a Monte Carlo sample of one hundred paths of length \(N_{\text {obs}}\) equal to the number of calendar days in the interval under investigation, i.e., \(N_{\text {obs}}=1826\), in order to count the average number of jumps predicted by the DNN. We observed that the DNN tends to underestimate the number of jumps. In fact, on average over the path sample, about \(90\%\) of jumps are predicted by the DNN in the electricity prices case, and about \(64\%\) in the natural gas price case. This is an expected results due to the fact that the occurrence of some of some jumps is completely random and cannot be predicted by the DNN. To account for this underestimate, we include additional random jumps through a hidden Markov process. Whenever the DNN predicts a stable movement, we impose that instead of the stable movement a jump may occur with a probability equal to the relative frequency of the missed jumps, namely \(10\%\) in the electricity case (\(5\%\) for upward jump, \(5\%\) for downward jumps) and \(36\%\) in the natural gas case (\(18\%\) for upward jump, \(18\%\) for downward jumps). This hybrid switching mechanism, based on DNN predictions integrated with a hidden Markov process, provides a realistic representation of the price dynamics, properly accounting for time varying one-period transition probabilities and dynamic correlation between electricity and natural gas prices.

4.3 Estimating the jump probability distribution

The last calibration step regards the jump dynamics. We considered first the case in which the random increments describing the jump amplitude, \(\Delta z_t\), are modeled according to a Gaussian distribution. Then, we extended the model to Cauchy distributions because we will see that in the case of natural gas the Gaussian distribution is inadequate. We used a zero mean Gaussian distribution for both markets under consideration. In fact, we can set the mean equal to zero because the skewness values of the empirical distributions of the log-returns of electricity and natural gas, observed during the period under study, are very low. We assumed, therefore that \(\Delta z_t \sim N(0,\sigma )\). The standard deviation parameter, \(\sigma \), is estimated following the simulated moments method (McFadden 1989; Duffie and Singleton 1993) using Monte Carlo techniques (Gelman 1995; Rashki 2021). We defined an appropriate grid of values for \(\sigma \). In the case of electricity price, we chose a range of values between 0.005 and 0.60 in increments of 0.005; for natural gas prices a range of values between 0.001 and 0.20 in increments of 0.001. For each value of \(\sigma \) we used the regime-switching model under the DNN-based hybrid switching mechanism to simulate a sample of one hundred random paths of length \(N_obs\) by using Monte Carlo techniques. In the simulation, the parameters \(\kappa _0\) and \(\sigma _0\) were set equal to the estimated obtained in the previous section. Then, the first four central moments were calculated on each path and averaged over the sample of one hundred paths. A given value of the \(\sigma \) parameter was assumed to offer a good fit if for each central moment the difference between the sample average value and the observed value reported in Table 1 is less than half the sample standard deviation for that moment. Such a high level of accuracy is achieved in the case of electricity prices. In Table 4, the parameter estimates are displayed together with the first four moments of the simulated log-return distributions. The agreement with empirical moments, reported in the last row, is very interesting.

Table 4 Electricity. Estimated parameters and first four moments of the simulated log-return distributions. Sample standard deviations are in parentheses. Empirical moments are given in the last row
Full size table

In the case of natural gas prices, the model with Gaussian jumps reproduces the log-return standard deviation and skewness well, but not the kurtosis, which is about half that observed. To improve the agreement with experimental data, we used a symmetric Cauchy distribution to describe the jump amplitude of natural gas log-prices. We chose a symmetric probability distribution because the skewness of natural gas log-return observed in the period under investigation is very low. Although in the Cauchy distribution all moments of order greater than or equal to one do not exist or are infinite, to overcome this difficulty we considered a truncated symmetric Cauchy distribution (Mantegna and Stanley 2007). The probability density of a truncated symmetric Cauchy distribution is defined by

$$\begin{aligned} P(x)=cP^{\gamma }(x) \quad -h \le x \le h, \end{aligned}$$
(7)

and zero otherwise, where \(P^{\gamma }(x)\) is the probability density of a symmetric Cauchy distribution of scale factor \(\gamma \), c is a normalization factor, and h is the cut-off parameter (Mantegna and Stanley 2007). As in the Gaussian case, the scale factor \(\gamma \) was estimated following the simulated moments method using Monte Carlo techniques. We defined an appropriate grid of values for the parameter \(\gamma \), choosing a range of values between 0.001 and 0.1 in increments of 0.001. The cut-off parameter was set equal to the maximum value of log-returns observed in the period under investigation, namely \(h=0.66\). For each value of \(\gamma \) we used the regime-switching model under the DNN-based hybrid switching mechanism to simulate a sample of one hundred random paths of length \(N_{obs}\) by using Monte Carlo techniques. In the simulation, the parameters \(\kappa _0\) and \(\sigma _0\) were set equal to the estimated obtained in the previous section. Then, the first four central moments were calculated on each path and averaged over the sample of one hundred paths. A given value of the \(\gamma \) parameter was assumed to offer a good fit if for each central moment the difference between the sample average value and the observed value reported in Table 1 is less than half the sample standard deviation for that moment. By using a symmetric Cauchy distribution for describing jumps, such a high level of accuracy can be achieved. Table 5 shows the parameter estimates together with the first four moments of the simulated log-return distributions. In this case the agreement with observed empirical values, reported in the last row, is remarkable.

Table 5 Natural gas. Estimated parameters and first four moments of the simulated log-return distributions. Sample standard deviations are in parentheses. Empirical moments are given in the last row
Full size table

Figure 7 depicts the log-price time series (in blue) and superimposed (in red) a simulated path obtained with the estimated model for both electricity (left panel) and natural gas (right panel).

Fig. 7
figure 7

Left panel: The electricity log-price time series (in blue) and superimposed (in red) a simulated path. Right panel: The natural gas log-price time series (in blue) and superimposed (in red) a simulated path. (Color figure online)

Full size image

5 Concluding remarks

We presented a parsimoniuos regime-switching model to describe the complex dynamics of natural gas and electricity prices and their correlation. In this model, the stable dynamics is described by two regimes modeled according to a mean-reverting process to account for upward and downward stable movements of prices; the jump dynamics is described by two different regimes accounting for upward and downward jump respectively. It can be considered the simplest dynamic model capable of incorporating the main stylized facts observed in real markets. In fact, the price dynamics of each energy commodity is described by three parameters which is the minimum number of parameters needed to account for mean-reversion and volatility in the stable regime and jumps in the turbulent regime. Transitions between regimes are driven by a hybrid switching mechanism, based on DNN predictions integrated with a hidden Markov process. The DNN was trained on sequences of prices pairs, namely the price of natural gas and the price of electricity. In this way, dynamic correlation between prices is properly taken into account. A calibration procedure was also discussed. The proposed methodology was applied to the Italian energy market. The results obtained demonstrated a remarkable agreement with empirical data, reproducing well the first four moment of log-return empirical distributions. The model can be used for many financial applications ranging from implementing risk-hedging strategies and pricing power derivatives to the evaluation of investments in the energy sector.

The main limitation of this study is related to the existence of a large Gaussian component in the empirical distribution of log-returns. In fact, the proposed methodology is based on the identification of a large Gaussian cluster of log-returns that is associated with stable price movements. However, it may not always be possible to find such a large Gaussian cluster, and this fact may make it challenging to identify the stable component of the dynamics. One possible solution to overcome this difficulty might be using finite Gaussian Mixture Models (GMMs) to describe the empirical distributions of log-returns. Providing universal approximations of any continuous probability density, GMMs have received increasing attention from both practical and theoretical studies over the years, rapidly becoming a very attractive option for data clustering (Viroli and McLachlan 2019; He and Ho 2019) also with incomplete data (Zhang et al. 2021). Through GMM-based clustering techniques, regime-switching models can be constructed by associating a different regime with each component of a GMM, letting an appropriately trained DNN drive transitions between regimes. This topic will be left for future investigation.