Wave-based analysis of jointed elastic bars: nonlinear periodic response

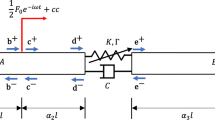
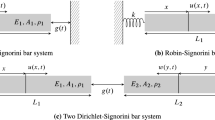
Abstract

In this paper, we develop two wave-based approaches for predicting the nonlinear periodic response of jointed elastic bars. First, we present a nonlinear wave-based vibration approach (WBVA) for studying jointed systems informed by re-usable, perturbation-derived scattering functions. This analytical approach can be used to predict the steady-state, forced response of jointed elastic bar structures incorporating any number and variety of nonlinear joints. As a second method, we present a nonlinear Plane-Wave Expansion (PWE) approach for analyzing periodic response in the same jointed bar structures. Both wave-based approaches have advantages and disadvantages when compared side-by-side. The WBVA results in a minimal set of equations and is re-usable following determination of the reflection and transmission functions, while the PWE formulation can be easily applied to new joint models and maintains solution accuracy to higher levels of nonlinearity. For example cases of two and three bars connected by linearly damped joints with linear and cubic stiffness, the two wave-based approaches accurately predict the expected Duffing-like behavior in which multiple periodic responses occur in the near-resonant regime, in close agreement with reference finite element simulations. Lastly, we discuss extensions of the work to jointed structures composed of beam-like members, and propose follow-on studies addressing opportunities identified in the application of the methods presented.

Appendices

Appendix A

Fig. 12

Ordered vibration sub-problems appearing following straight-forward perturbation applied to the forced vibration problem in Fig. 3

In this appendix we provide the components of $\mathbf {z}$ in terms of the reduced coefficient vector components, $d_j^-$ and $e_j^+$, $j=1,3,5$:

$$\begin{aligned} a^+_1&= -\frac{e^{ik \alpha _1 l}}{4 E_y A k} \left( 4 E_y A k e^{ik \alpha _2 l} d^-_1 + i F_0 \right) ,\\ a^-_1&= \frac{e^{ik \alpha _1 l}}{4 E_y A k} \left( 4 E_y A k e^{ik \alpha _2 l} d^-_1 + i F_0 \right) ,\\ a^+_j&= -e^{ijk (\alpha _1+\alpha _2) l} d^-_j, \quad j=3,5 ,\\ a^-_j&= e^{ijk (\alpha _1+\alpha _2) l} d^-_j, \quad j=3,5 ,\\ b^+_1&= -\frac{e^{i2k \alpha _1 l}}{4 E_y A k} \left( 4E_y A ke^{ik \alpha _2 l} d^-_1 + i F_0 \right) ,\\ b^-_1&= \frac{1}{4 E_y A k} \left( 4 E_y A ke^{ik \alpha _2 l} d^-_1 + i F_0 \right) ,\\ b^+_j&= -e^{i2jk \alpha _1 l}e^{ijk \alpha _2 l} d^-_j, \quad j=3,5 ,\\ b^-_j&= e^{i2jk \alpha _1 l}e^{ijk \alpha _2 l} d^-_j, \quad j=3,5 ,\\ c^+_1&= -\frac{1}{4 E_y A k}(4E_y A k e^{i2k\alpha _1l}e^{ik\alpha _2l}d^-_1 \\&+ iF_0e^{i2k\alpha _1l} - iF_0),\\ c^-_1&= e^{ik\alpha _2l}d^-_1 ,\\ c^+_j&= -e^{i2jk\alpha _1l}e^{ijk\alpha _2l}d^-_j, \quad j=3,5 ,\\ c^-_j&= e^{ijk\alpha _2l}d^-_j , \quad j=3,5 ,\\ d^+_1&= -\frac{e^{ijk\alpha _2l}}{4 E_y A k}(4E_y A k e^{i2k\alpha _1l}e^{ik\alpha _2l}d^-_1 \\&+ iF_0e^{i2k\alpha _1l} - iF_0),\\ d^+_j&= -e^{i2jk\alpha _1l}e^{i2jk\alpha _2l}d^-_j, \quad j=3,5 ,\\ e^-_j&= -e^{i2jk\alpha _3l} e^+_j, \quad j=1,3,5 ,\\ f^+_j&= e^{ijk\alpha _3l}e^+_j, \quad j=1,3,5 ,\\ f^-_j&= -e^{ijk\alpha _3l}e^+_j,\quad j=1,3,5 . \end{aligned}$$

Appendix B

In this appendix we show that pursuing development of a nonlinear WBVA in which the nonlinear forced vibration problem is treated from the outset using straight-forward perturbation, without first formulating the scattering problem and reconstituting scattering relationships, leads to inaccurate results not capturing multiple solutions and Duffing-like frequency response characteristics. This naïve approach was the first one attempted by the authors and illustrates an issue requiring careful attention when develo** nonlinear wave-based vibration approaches.

Fig. 13

Comparison between time-transient and frequency-domain simulations for the single-jointed structure (Sect. 4.1) undergoing a harmonic excitation of amplitude $15\,\hbox {MN}$ and frequency $80.7089\,\hbox {krad/s}$. Depicted clockwise are the time-domain acceleration response, the displacement-velocity state-space response, and the acceleration frequency-domain response. Extra labels are inserted in the x-axis of the frequency domain showing relevant harmonics of the forcing frequency

By way of example, we consider the forced vibration problem illustrated in Fig. 3. Applying straight-forward perturbation to the governing equations [Eqs. (1)–(2), (4)–(5)] using the expansions defined in Eqs. (6)–(7), and retaining terms up to and including ${\mathcal {O}}\left( \varepsilon ^1\right)$, yields two linear vibration sub-problems at ${\mathcal {O}}\left( \varepsilon ^0\right)$ and ${\mathcal {O}}\left( \varepsilon ^1\right)$, as illustrated in Fig. 12. The accompanying equations governing the sub-problems are provided by Eqs. (8)–(15) with the exception of (i) harmonic forcing $F^{0}(\omega )$ missing on the right-hand side of Eq. (8) and (ii) inclusion of fixed boundary conditions; however, for the argument made herein, these equations are not strictly necessary and instead we only require inspection of Fig. 12. At ${\mathcal {O}}\left( \varepsilon ^0\right)$ appears a linear sub-problem amenable to the linear wave-based vibration approach. It is clear that the steady-state solution of such a problem yields unique displacement fields $u^0_L(x,t)$ and $u^0_R(x,t)$ responding at the excitation frequency $\omega$. Following solution of the zeroth-order problem, substitution of $u^0_L(x,t)$ and $u^0_R(x,t)$ into Eqs. (14)–(15) yields the ${\mathcal {O}}\left( \varepsilon ^1\right)$ sub-problem appearing in Fig. 12. The boundary conditions at the joint for $u^1_L(x,t)$ and $u^1_R(x,t)$ now appear forced by terms with frequency content $\omega$ and $3\omega$ resulting from the boundary term $\Gamma \left( u_{R0}{-u}_{L0}\right) ^3$, which we indicate by $F^{1}(\omega ,3\omega )$. Once again it is clear that this linear sub-problem yields unique displacement fields $u^1_L(x,t)$ and $u^1_R(x,t)$, now responding at the excitation frequency $\omega$ and its third harmonic.

This procedure can be carried-out to higher orders, but stop** at ${\mathcal {O}}\left( \varepsilon ^1\right)$ is sufficient to observe that, following solution reconstitution, the procedure yields a unique problem solution for each frequency $\omega$, without the possibility of recovering Duffing-like frequency response curves and multiple solutions. We note that such a solution approach isn’t without utility, particularly away from resonance, as it provides higher-order corrections to the fundamental frequency response and estimates of the higher harmonics otherwise missing from a linear analysis, but it is clearly inaccurate near resonance. We note further that this inaccuracy would not be encountered in a linear problem where solution uniqueness is guaranteed, and in fact, a similar approach is carried-out in the companion paper [41] where we consider stability of linear, parametrically forced vibration problems.

Appendix C

Figure 13 compares the harmonic balance (HB) results with time-transient simulations conducted on the Finite Element (FE) model of the single-jointed structure (see Sect. 4.1). An implicit Newmark scheme is used for the transient analysis. We chose the excitation frequency for the simulation as the frequency closest to the peak of the forced response in Fig. 7 ($80.7079\,\hbox {krad/s}$), and the excitation amplitude is fixed at $15\,\hbox {MN}$, as before. We conduct the simulation for forty cycles of the fundamental period ($40\times 2\pi /80.7079\times 10^{-3}\hbox {s}$) in order to bring out any sub-harmonic features (which are expected at $1/3,\,1/5,\,\dots$ of the excitation frequency) up to the 1/40th sub-harmonic.

The acceleration of the output node (directly after the joint, as before) is plotted since the higher harmonic effects are more pronounced in the acceleration than in the displacement (i.e., each frequency component gets scaled by the square of the frequency). It is readily observed that in the time- and state-space domains, the harmonic balance scheme that was employed (truncating to five harmonics) provides a reasonably accurate representation of the transient results, as expected. Another major aspect that is confirmed from this plot is that the true response is also periodic, thereby validating the choice of frequency-domain simulation techniques.

In the frequency-domain, the match is reasonable up to the fifth harmonic. The transient results shown exhibit no prominent sub-harmonic behavior for this case (the 1/3rd line is highlighted above). Further, intermediate (between H3 and H4, for instance) as well as higher harmonic components (H7 in the figure, for example) can be seen to exist, although these are not explicitly present in the HB formalism. The accuracy of the HB solution in spite of these components is due to the fact that their presence is very small in comparison to the other components. One way of quantifying this is through the ratio of the harmonic component with the first harmonic component. This turns out to be $3.89\times 10^{-4}$ for the acceleration from the simulation above ($2.51\times 10^{-5}$ and $5.66\times 10^{-5}$, respectively, for displacement and velocity). It may also be observed that even harmonics do not appear on the plot since their magnitudes are near machine-precision.

The same argument is extended to justify the sufficiency of considering perturbation solutions only up to second order for the examples in Sect. 4. It can be seen from the wave-based scattering relationships developed in Sect. 2.3 that the zeroth-order expansions are fully expressed in terms of a single harmonic alone, first-order expansions include the third harmonic, and second-order expansions include the fifth harmonic. Since the above justifies the truncation of the solution up to five harmonics, it implies that comparable accuracy can be achieved through a second-order perturbation approach. In general, a convergence analysis has to be conducted to ascertain the appropriate order of perturbation by comparing the difference of the responses between predictions from the chosen order and one higher.