Explicit smooth/nonsmooth cosimulation using kinematic constraints

Abstract

An explicit cosimulation scheme is developed to study the coupling of smooth and nonsmooth systems using kinematic constraints. Using the force-displacement decomposition, the coupling constraints are formulated at the velocity level, to preserve consistency with the impulse-momentum equations for frictional contacts in the nonsmooth solver, which however potentially leads to instability of the explicit cosimulation. To improve the stability of the cosimulation without affecting the format of the coupling constraints, guidelines for the modification of the prescribed motion are developed following the spirit of Baumgarte’s stabilization technique and the characteristics of the proposed integration scheme, which prescribes a combination of position, velocity, and acceleration to the constrained bodies. Using modified inputs, the stability of the cosimulation is tested using a rigidly connected two-mass oscillator model, which shows clear improvement compared to that with unaltered inputs. The performances of the cosimulation with modified inputs are further illustrated using a double-pendulum system and a complex flexible multibody system coupled with a particle damper. It follows that cosimulation results well agree with those obtained using monolithic simulation or simplified models, verifying the explicit smooth/nonsmooth cosimulation. The results also show a higher efficiency of the explicit cosimulation scheme, which requires much less computational time to obtain similar results, compared to the implicit smooth/nonsmooth cosimulation.

1 Introduction

Multibody dynamics is often used to simulate multiphysics and multidomain problems. Although a monolithic approach is sometimes feasible (for example, coupled helicopter aeromechanics and pilot biomechanics in [1, 2]), cosimulation techniques are widely used to coordinate different solvers [3–7] and to parallelize the simulation process [8–10]. In the present work, we address the application of explicit cosimulation techniques to smooth/nonsmooth coupled multibody systems.

The cosimulation of nonsmooth systems has been studied by several authors, most of them focusing on smooth/nonsmooth subsystems connected by contact forces calculated by penalty methods or contact laws and then sent to the subsystems [11]. This approach is commonly used in the cosimulation of discrete element methods (DEM) or nonsmooth methods [12, 13] and multibody dynamics (MBD) [4, 9, 14, 15]. Apart from connecting subsystems through contact forces, in some studies, smooth and nonsmooth subsystems are linked by ideal kinematic constraints, for example, mechanical systems mounting particle dampers [16] and nonsmooth systems coupled with other physical modules [17]. In these cases, although contact forces can still be employed as coupling variables, an alternative choice is to decompose the overall system at the kinematic constraints and to send reaction forces/moments to other subsystems. The use of reaction forces/moments avoids calculating the sum of contact forces, which may be time-consuming if a large number of nonsmooth events takes place on the coupling body. This approach can also help confine the details of the solution process in nonsmooth subsystems.

This work adopts the latter approach, namely smooth/nonsmooth cosimulation with kinematic constraints. We first discuss the coupled smooth systems with kinematic constraints. In this case the whole system can be formulated using Newton–Euler’s equations as a set of differential-algebraic equations (DAEs) [18]. In cosimulation a common way is to decompose the whole DAEs in several sets of ordinary differential equations (ODEs) governing the motion of each subsystem and a set of algebraic equations representing the kinematic constraints between subsystems. Using the decomposition, Kubler et al. [18, 19] provided two implicit schemes, also called “iterative schemes,” which employ an approximate Jacobian matrix to guarantee the local convergence of cosimulation iterations. In [20] a semiimplicit cosimulation scheme including prediction and correction procedures was proposed, which shows advantages in terms of stability compared to explicit cosimulation schemes. The prediction–correction procedure incorporates different stabilization methods, such as the projection technique [21], Baumgarte’s stabilization method [22], the weighted multiplier approach [22], and the Gear-Gupta-Leimkuhler (GGL) method [23], to enforce the constraints and to yield reaction forces/moments. The resulting forces/moments are then sent to the subsystems to continue the co-simulation. Apart from integrating stabilization methods in the semi-implicit scheme, to achieve higher convergence rates, a technique that updates higher-order approximation polynomials in each macrostep [24] was also established to enforce the coupling conditions at all levels: position, velocity, and acceleration,.

Although the above-mentioned semiimplicit/implicit cosimulation schemes show satisfactory stability, explicit solver coupling is still widely used, owing to its advantage in terms of efficiency. Gu et al. [25, 26] developed an explicit cosimulation scheme, which adopts Baumgarte’s stabilization method to deal with the coupling algebraic equations, where index-$r$ DAEs are reformulated as index-1 DAEs to generate reaction forces/moments for the subsystems. In [27] a force-displacement cosimulation with kinematic constraints was also explicitly implemented to avoid constraint drift problems. This study pointed out that in the cosimulation platform, using the index-1 monolithic equations to calculate constraint forces may result in an unacceptable amount of computation when the coupled system is large, whereas formulating the constraint forces as functions of acceleration vectors generates algebraic loops in the cosimulation, even spoiling the zero-stability of cosimulation schemes in some cases [27]. Apart from calculating reaction forces in the cosimulation platform, if subsystems can produce reaction forces, then the coupling constraints can also be modeled in subsystems by enforcing kinematics. Using a nonsmooth method that can deal with bilateral constraints [28, 29], an embedded force-displacement cosimulation scheme was developed, where the coupling constraints can be formulated in one subsystem to generate reaction forces/moments as outputs [7]. However, using this approach, an implicit cosimulation scheme with an iterative solution process is required to enhance convergence and enforce algorithmic stability [7].

For coupled smooth/nonsmooth systems with kinematic constraints, if an explicit force-displacement cosimulation scheme [7] is employed in addition to the risk of losing stability, then another problem that may occur is the inconsistency of kinematic constraints between the monolithic DAEs and the nonsmooth methods. In fact, in nonsmooth time-step** methods [17, 28, 30–32], kinematic constraint equations are usually formulated at the velocity level for consistency with the nonsmooth dynamic equations at the impulse-momentum level, whereas in monolithic DAEs and cosimulation, constraint equations are expected to be satisfied at position, velocity, and acceleration levels at the synchronization time [21, 22]. This inconsistency cannot be eliminated when subsolvers are expected to remain opaque, as is a common practice when cosimulating between existing well-established solvers, and although just alternatively coupling positions or velocities would be an option, the stability of the cosimulation scheme would be poor in general cases.

In this paper, we develop an explicit cosimulation scheme for smooth/nonsmooth coupled multibody systems with kinematic constraints. A force-displacement decomposition technique is employed to divide the whole system at coupling kinematic constraints into smooth subsystems with external dynamic variables, i.e., prescribed forces, and nonsmooth subsystems with external kinematic variables, i.e., prescribed kinematics. In smooth subsystems, dynamic variables are applied to bodies at markers of coupling constraints, whereas in nonsmooth subsystems, kinematic variables are enforced to bodies through rheonomic constraints at the velocity level. To guarantee the imposition of all coupling kinematics, namely position, velocity, and acceleration, to the bodies in the nonsmooth subsystems and at the same time to maintain the confinement of the nonsmooth solver, the input kinematics resulting from the smooth subsystems are modified using Baumgarte’s stabilization method [33] and the properties of the integrators in the nonsmooth subsystems. As in other studies [20], a two-mass oscillator is used to assess how the modified inputs improve algorithmic stability. The analysis shows that the modified inputs can enlarge the stability region, compared to directly using the original constraint equations at the velocity level in the nonsmooth subsystems. Finally, the capabilities of the explicit cosimulation scheme are further assessed by applying it to a double pendulum and to a smooth/nonsmooth coupled system consisting of a flexible crank-slider mechanism actuating a beam that carries a particle damper.

Specifically, in Sect. 2, we decompose a coupled system into smooth and nonsmooth subsystems. For each subsystem, we give formulations and modified input–output schemes. In Sect. 3, we introduce the cosimulation strategy, where an explicit cosimulation scheme and its implementation are discussed. In Sect. 4, a linear two-mass oscillator is cosimulated to compare the effect of different input formats on algorithmic stability, and two other numerical examples are also analyzed to show the effectiveness of the smooth/nonsmooth cosimulation with modified inputs. In Sect. 5, we finally draw conclusions.

2 Formulation of coupled systems

2.1 System decomposition

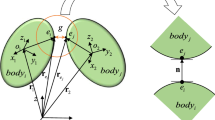
As shown in Fig. 1(a), a coupled smooth/nonsmooth system consists of a set of bodies $S_{i}$ ($i=0,1,2,\ldots$) whose dynamics are formulated as smooth, i.e., they are assumed to be unaffected by impacts or friction (called for simplicity “smooth bodies”), and another set of bodies $NS_{j}$ ($j=0,1,2,\ldots$) that can be subject to nonsmooth events (called “nonsmooth bodies”). According to the force-displacement decomposition technique [21, 27], this coupled system can be divided into smooth and nonsmooth subsystems at bilateral constraints that connect sets of smooth and nonsmooth bodies. For clarity of explanation, let us discuss the coupled system of Fig. 1(b). A smooth subsystem and a nonsmooth subsystem are connected by constraints between markers $A$ and $B$, which are rigidly attached to bodies $S_{0}$ and $NS_{0}$, respectively. By the force-displacement decomposition this coupled system is divided into a smooth subsystem and a nonsmooth subsystem at the coupling constraints. The smooth subsystem generates the motion of marker $A$ as output, whereas the nonsmooth subsystem supplies to the smooth subsystem the reaction forces and moments that act on marker $A$.

Fig. 1

Decomposition of coupled system: (a) with multiple connections, (b) with one coupling connection at constraints $S_{0}-NS_{0}$ (Marker $A$-Marker $B$)

2.2 Formulation of subsystems

2.2.1 Formulation of smooth subsystems

The smooth subsystem consisting of bodies $S_{i}$ is modeled as a generic multibody system, which can be formulated as a set of DAEs using the physical coordinates ${\mathbf{q}}_{1}$ as in [34, 35]:

$$\begin{aligned} {\mathbf{{M}}}_{1}{\dot{\mathbf{{v}}}}_{1} + {\mathbf{{g}}}_{1/{\mathbf{{q}}}_{1}}^{\text{T}} { \boldsymbol{\lambda}}_{1} + {\mathbf{{g}}}_{\mathrm{co}/{\mathbf{{q}}}_{1}}^{\text{T}} { \boldsymbol{\lambda}}^{\mathrm{co}} - {\mathbf{{f}}}_{1}\left ({\mathbf{{q}}}_{1}, {{\mathbf{{v}}}}_{1},t \right ) &= \boldsymbol{0}, \end{aligned}$$

(1a)

$$\begin{aligned} {\mathbf{{g}}}_{1}\left ( {{\mathbf{{q}}}_{1},t} \right ) &= \boldsymbol{0}, \end{aligned}$$

(1b)

where ${\mathbf{M}}_{1}$ is the mass matrix, ${\mathbf{v}}_{1}={\dot{\mathbf{q}}_{1}}$ represents the generalized velocity coordinate vector, $t\geq 0$ denotes the time, vectors ${\mathbf{g}}_{1}$ and ${\mathbf{g}}_{\mathrm{co}}$ indicate the constraints in the smooth subsystem and the coupling constraint $S_{0}-NS_{0}$ between the subsystems, as shown in Fig. 1(b), the latter being defined later in Eqs. (2a)–(2e) as part of the nonsmooth subsystem dynamics, vectors ${\boldsymbol{\lambda}}_{1}$ and ${\boldsymbol{\lambda}}^{\mathrm{co}}$ represent the Lagrange multipliers of the corresponding constraints, vector ${\mathbf{f}}_{1}$ contains the generalized external forces, the over dot denotes the derivative with respect to time, and the operator $()_{/{\mathbf{x}}}$ denotes the partial derivative with respect to ${\mathbf{x}}$.

2.2.2 Formulation of nonsmooth subsystem

Nonsmooth methods [13, 30, 32, 36] are effective tools to deal with nonsmooth dynamics. In nonsmooth methods, bodies are assumed to be rigid, and nonsmooth events among bodies are described as frictional unilateral constraints, such as the Coulomb friction and impacts, which are transformed to nonlinear/linear complementarity problems (N/LCPs) or projection functions to be solved [37]. The nonsmooth methods are extended to systems with bilateral constraints [29, 38, 39], where bilateral constraints are formulated at the velocity level with different stabilization methods, to enforce the bilateral constraints at both position and velocity levels. In the present work, we use the nonsmooth method proposed by Tasora and Anitescu [29], based on cone complementarity problems (CCPs). The method uses a semiimplicit Euler integrator; bilateral constraints are modified as a combination of constraints at position and velocity levels. The nonsmooth method is included in the open-source C++ library Project Chrono.¹

Using the CCP-based method [28, 29], we formulate a nonsmooth subsystem with coupling constraints as

$$\begin{aligned} & {\mathbf{{M}}}_{2}{\dot {\mathbf{v}}}_{2} + {\mathbf{g}}^{\text{T}}_{2/{\mathbf{q}}_{2}} { \boldsymbol{\lambda}}_{2} + {\mathbf{g}}^{\text{T}}_{\mathrm{co}/{\mathbf{q}}_{2}} { \boldsymbol{\lambda}}^{\mathrm{co}} + \sum _{\pi _{i} \in \varPi} {{{\mathbf{{D}}}_{ \pi _{i}}}{\mathbf{{p }}}_{\pi _{i}}} = {\mathbf{f}}_{2}{\left ({\mathbf{q}}_{2}, { \mathbf{v}}_{2}, t\right )}, \end{aligned}$$

(2a)

$$\begin{aligned} & {\mathbf{g}}_{2} {\left ({\mathbf{q}}_{2}, {t}\right )} = {\mathbf{0}}, \end{aligned}$$

(2b)

$$\begin{aligned} & {\mathbf{g}}_{\mathrm{co}} {\left ({\mathbf{q}}_{1}, {\mathbf{q}}_{2}\right )} = { \mathbf{0}}, \end{aligned}$$

(2c)

$$\begin{aligned} & {\pi _{i}} \in \varPi : 0 \le \textstyle\begin{array}{c@{\quad}c@{\quad}c} {{{ p }_{{\mathbf{{n}}}_{{\pi _{i}}}}}}& \bot &{{{\varPhi}}_{{\mathbf{{n}}}_{\pi _{i}}} \ge 0}, \end{array}\displaystyle \end{aligned}$$

(2d)

$$\begin{aligned} & \left ({ p _{{{\mathbf{{u}}}_{{\pi _{i}}}}}}, { p _{{{\mathbf{{w}}}_{{\pi _{i}}}}}} \right ) = \mathop {\arg \min }\limits _{\| { p _{{{\mathbf{{u}}}_{{\pi _{i}}}}}}{{ \mathbf{{u}}}_{{\pi _{i}}}} + {p _{{{\mathbf{{w}}}_{{\pi _{i}}}}}}{{\mathbf{{w}}}_{{ \pi _{i}}}} \| \le {\mu _{{\pi _{i}}}}{{ p }_{{{\mathbf{{n}}}_{{\pi _{i}}}}}}} {\mathbf{{v}}}_{{T_{\pi _{i}}}}^{\mathrm{{T}}} \left ({ p _{{{\mathbf{{u}}}_{\pi _{i}}}}}{{ \mathbf{{u}}}_{\pi _{i}}} + { p _{{{\mathbf{{w}}}_{\pi _{i}}}}}{{\mathbf{{w}}}_{\pi _{i}}} \right ), \end{aligned}$$

(2e)

where ${\mathbf{M}}_{2}$ is the mass matrix, the vectors ${\mathbf{q}}_{2}$ and ${\mathbf{v}}_{2}$ are generalized position and velocity coordinates, respectively, the vector ${\mathbf{g}}_{2}$ denotes the bilateral constraints in the nonsmooth subsystem, and ${\mathbf{g}}_{\mathrm{co}}$ is the constraint $S_{0}-NS_{0}$ between the subsystems, representing the interfaces used to prescribe the motion to the nonsmooth bodies, ${\mathbf{g}}_{2/{\mathbf{q}}_{2}}$ and ${\mathbf{g}}_{\mathrm{co}/{\mathbf{q}}_{2}}$ are the corresponding Jacobian matrices, the vectors ${\boldsymbol{\lambda}}_{2}$ and ${\boldsymbol{\lambda}}^{\mathrm{co}}$ represent the Lagrange multipliers of the corresponding constraints, the vector ${\mathbf{f}}_{2}$ contains the generalized external forces, the set ${\varPi}$ collects all closed contacts, the index $\pi _{i}$ refers to a generic element of the set ${\varPi}$, for the contact $\pi _{i}$, the local reference is defined by three orthogonal vectors ${\mathbf{n}}_{\pi _{i}}$, ${\mathbf{u}}_{\pi _{i}}$, and ${\mathbf{w}}_{\pi _{i}}$ at the contact point, where ${\mathbf{n}}_{\pi _{i}}$ denotes the normal direction, whereas ${\mathbf{u}}_{\pi _{i}}$ and ${\mathbf{w}}_{\pi _{i}}$ are orthogonal vectors representing the tangential directions, ${\mathbf{{p }}}_{\pi _{i}}$ is the vector of the generalized forces generated by the frictional contacts, $p_{{\mathbf{n}}_{\pi _{i}}}$, $p_{{\mathbf{u}}_{\pi _{i}}}$, and $p_{{\mathbf{w}}_{\pi _{i}}}$ are the three components of ${\mathbf{{p }}}_{\pi _{i}}$ along directions ${\mathbf{n}}_{\pi _{i}}$, ${\mathbf{u}}_{\pi _{i}}$, and ${\mathbf{w}}_{\pi _{i}}$, respectively, $v_{{\mathbf{n}}_{\pi _{i}}}$ and ${\mathbf{v}}_{T_{\pi _{i}}}^{\text{T}}=\left [v_{{\mathbf{u}}_{\pi _{i}}}, v_{{ \mathbf{w}}_{\pi _{i}}}\right ]$ are the normal component and the tangential projection of the velocity vector at the contact point, and ${\varPhi}_{{\mathbf{{n}}}_{\pi _{i}}}$ denotes the normal distance at the contact $\pi _{i}$.

To improve notation readability, we further assume that ${\mathbf{v}}_{2}=\dot{\mathbf{q}}_{2}$, although in the nonsmooth method [28, 29] the rotation is described by quaternions in ${\mathbf{q}}_{2}$, which are updated using an exponential map to preserve their unimodularity, whereas the angular velocity in the local reference is used in ${\mathbf{v}}_{2}$.

2.2.3 Discrete equations

Since both smooth and nonsmooth solvers are assumed to model the respective portions of the problem as sets of rigid bodies, before discretizing the equations, we rewrite the coupling constraints as functions of the generalized coordinates related to the interface bodies $S_{0}$ and $NS_{0}$. As shown in Fig. 1(b), the constraint $S_{0}-NS_{0}$, written as ${\mathbf{g}}_{\mathrm{co}}$ in Eq. (2c), only involves the motion of body $S_{0}$ in the smooth subsystem and of body $NS_{0}$ in the nonsmooth subsystem. Therefore the constraint ${\mathbf{g}}_{\mathrm{co}}$ in Eq. (2c) can be rewritten as

$$ {\mathbf{g}}_{\mathrm{co}}\left ({\mathbf{q}}_{1}, {\mathbf{q}}_{2}\right )={\mathbf{g}}_{ \mathrm{co}}\left ({\mathbf{q}}^{\mathrm{co}}_{1}, {\mathbf{q}}^{\mathrm{co}}_{2} \right )={\mathbf{0}}, $$

(3)

where ${\mathbf{q}}^{\mathrm{co}}_{1}$ and ${\mathbf{q}}^{\mathrm{co}}_{2}$ denote the physical coordinates of the coupling body, $S_{0}$ and $NS_{0}$, in the respective subsystems. According to Eq. (3), Eq. (1a) can be rewritten as

$$ { {\mathbf{{M}}}_{1}{\dot{\mathbf{{v}}}}_{1} + {\mathbf{{g}}}_{1/{\mathbf{{q}}}_{1}}^{\text{T}} { \boldsymbol{\lambda}}_{1} + \left [ \textstyle\begin{array}{c} {\mathbf{{g}}}_{\mathrm{co}/{\mathbf{{q}}}^{\mathrm{co}}_{1}}^{\text{T}} \\ {\mathbf{0}} \end{array}\displaystyle \right ] {\boldsymbol{\lambda}}^{\mathrm{co}} - {\mathbf{{f}}}_{1}\left ({\mathbf{{q}}}_{1}, \dot{{\mathbf{{q}}}}_{1},t\right ) = \boldsymbol{0}}. $$

(4)

In Eqs. (1a), (1b) and (4), DAEs are solved using the formulation proposed in [34], i.e., discretized at time $t_{n+1}$ as

$$\begin{aligned} {\mathbf{{M}}}_{1}{\ddot{\mathbf{{q}}}}_{1,n+1} + {\mathbf{{g}}}_{1/{\mathbf{{q}}}_{1}}^{ \text{T}} {\boldsymbol{\lambda}}_{1,n+1} + \left [ \textstyle\begin{array}{c} {\mathbf{{g}}}_{\mathrm{co}/{\mathbf{{q}}}^{\mathrm{co}}_{1}}^{\text{T}} \\ {\mathbf{0}} \end{array}\displaystyle \right ] \boldsymbol{\lambda}^{\mathrm{co}}_{n+1} - {\mathbf{{f}}}_{1,n+1} \left ({\mathbf{{q}}}_{1,n+1}, {\dot{\mathbf{{q}}}}_{1,n+1},t_{n+1}\right ) &= \boldsymbol{0}, \end{aligned}$$

(5a)

$$\begin{aligned} {\mathbf{{g}}}_{1}\left ( {{\mathbf{{q}}}_{1,n+1},t_{n+1}} \right ) &= \boldsymbol{0}. \end{aligned}$$

(5b)

The state variables ${\mathbf{{x}}}=\left [{\mathbf{q}}_{1}^{\mathrm {T}}, \dot{\mathbf{q}}_{1}^{\mathrm {T}}, \boldsymbol{\lambda}_{1}^{\mathrm {T}}\right ]^{\mathrm {T}}$ are predicted and updated at each step according to an implicit linear two-step scheme [34, 39] as

$$ {{\mathbf{{x}}}_{n+1}} = \sum _{i = 1,2} {{a_{i}}{{\mathbf{{x}}}_{n+1 - i}}} + {\Delta t}\sum _{i = 0,1,2} {{b_{i}}{{\dot{\mathbf{{x}}}}_{n+1 - i}}}, $$

(6)

which has second-order accuracy and is unconditionally stable with tunable algorithmic dissipation. The coefficients are defined as functions of the asymptotic spectral radius $\rho _{\infty}$ ($\rho _{\infty}\in \left [0,1 \right ]$) and are expressed as [34]

$$\begin{aligned} a_{1} &= 1 - \displaystyle \frac{ 3 {{\left ( 1 - \rho _{\infty}\right )}^{2}} + 4\left ( {2 \rho _{\infty}- 1} \right )}{4- {{\left ( {1 - \rho _{\infty}} \right )}^{2}}}, \end{aligned}$$

(7a)

$$\begin{aligned} a_{2} &= \displaystyle \frac{ 3 {{\left ( 1 - \rho _{\infty}\right )}^{2}} + 4\left ( {2 \rho _{\infty}- 1} \right )}{4- {{\left ( {1 - \rho _{\infty}} \right )}^{2}}} {}= 1 - a_{1}, \end{aligned}$$

(7b)

$$\begin{aligned} b_{0} &= \displaystyle \frac{{{{\left ( {1 - \rho _{\infty}} \right )}^{2}}}}{{2\left [ {4 - {{\left ( {1- \rho _{\infty}} \right )}^{2}}} \right ]}} + \cfrac{1}{2} , \end{aligned}$$

(7c)

$$\begin{aligned} b_{1} &= \displaystyle \frac{ 3 {{\left ( 1 - \rho _{\infty}\right )}^{2}} + 4\left ( {2 \rho _{\infty}- 1} \right )}{2\left [4- {{\left ( {1 - \rho _{\infty}} \right )}^{2}}\right ]} + \frac{1}{2} - \displaystyle \frac{{{{\left ( {1 - \rho _{\infty}} \right )}^{2}}}}{{{4 - {{\left ( {1- \rho _{\infty}} \right )}^{2}}}}}, \end{aligned}$$

(7d)

$$\begin{aligned} b_{2} &= \displaystyle \frac{ 3 {{\left ( 1 - \rho _{\infty}\right )}^{2}} + 4\left ( {2 \rho _{\infty}- 1} \right )}{2\left [4- {{\left ( {1 - \rho _{\infty}} \right )}^{2}}\right ]} + \displaystyle \frac{{{{\left ( {1 - \rho _{\infty}} \right )}^{2}}}}{{2\left [ {4 - {{\left ( {1- \rho _{\infty}} \right )}^{2}}} \right ]}}. \end{aligned}$$

(7e)

This implicit linear two-step scheme for generic multibody systems is implemented in the free, general-purpose multibody software MBDyn,² which in the present work is used to model the smooth portion of the system. Although the complete orientation matrix of the interface bodies is exchanged with the subsystems, in the solution process the incremental Cayley–Gibbs–Rodriguez (CGR) rotation parameters are used as state variables to update the orientation of the bodies [34]. For ease of notation, we use a generalized coordinate set ${\mathbf{q}}_{1}$ to represent displacements and rotations in the smooth subsystem. In the integration procedure the dynamics equations (5a) and (5b) can be rewritten as [34]

$$ {\mathbf{Res}}\left ({\mathbf{x}}_{n+1},\dot{\mathbf{{x}}}_{n+1},t_{n+1}\right )=0, $$

(8)

where the coupling Lagrange multiplier ${\mathbf{\lambda}}^{\mathrm{co}}$ does not explicitly appear because it is determined by the inputs, which are only related to the time for the noniterative cosimulation or to the iterations for the iterative cosimulation. To solve the dynamics problem (8), we employ the prediction–correction approach [34], by which $\dot{\mathbf{{x}}}_{n+1}$ is predicted first, written as $\dot{\mathbf{{x}}}^{(0)}_{n+1}$, and then is substituted into the implicit two-step scheme to calculate the predicted ${\mathbf{x}}_{n+1}$, written as ${\mathbf{x}}^{(0)}_{n+1}$. Then, with the perturbation of Eq. (6) expressed as

$$ {\partial {\mathbf{x}}_{n+1}}={\Delta t b_{0}}{\partial \dot{\mathbf{{x}}}_{n+1}}, $$

(9)

the correction procedure is given as [34]

$$\begin{aligned} \left ({\Delta t b_{0}}{\mathbf{Res}}_{/\mathbf{x}} + {\mathbf{Res}}_{/\dot{\mathbf{{x}}}} \right ){\partial \dot{\mathbf{{x}}}}&=-{\mathbf{Res}}\left ({\mathbf{x}}^{(j)}_{n+1}, \dot{\mathbf{{x}}}^{(j)}_{n+1},t^{(j)}_{n+1}\right ), \end{aligned}$$

(10a)

$$\begin{aligned} \dot{\mathbf{{x}}}^{(j+1)}_{n+1}&=\dot{\mathbf{{x}}}^{(j)}_{n+1} + {\partial \dot{\mathbf{{x}}}}, \end{aligned}$$

(10b)

$$\begin{aligned} {\mathbf{{ x}}}^{(j+1)}_{n+1}&={\mathbf{{x}}}^{(j)}_{n+1} +{\Delta t b_{0}}{ \partial \dot{\mathbf{{x}}}}. \end{aligned}$$

(10c)

The dynamics equations of the nonsmooth subsystem (2a)–(2e) are solved at the impulse-momentum level [29], since under the assumption that all bodies are rigid, frictional contacts may lead to inconsistent or indeterminate solutions at the acceleration-force level [29, 40]. At the impulse-momentum level the dynamics equations are discretized by a half-implicit Euler scheme at time $t_{n+1}$ [28, 29] as

$$\begin{aligned} & {\mathbf{q}}_{2,n+1} = {\mathbf{q}}_{2, n}+{\Delta t}{\dot{\mathbf{q}}}_{2,n+1}, \end{aligned}$$

(11a)

$$\begin{aligned} & {\mathbf{{M}}}_{2}\left ({{\mathbf{v}}}_{2,n+1}-{{\mathbf{v}}}_{2,n}\right ) + { \mathbf{g}}^{\text{T}}_{2/{\mathbf{q}}_{2},n} {\tilde{\mathbf{\lambda}}}_{2,n+1} + { \mathbf{g}}^{\text{T}}_{\mathrm{co}/{\mathbf{q}}_{2},n} {\tilde{\mathbf{\lambda}}}^{ \mathrm{co}}_{n+1} + \sum _{\pi _{i} \in \varPi} {{{\mathbf{{D}}}_{ \pi _{i},n}}{\mathbf{{\tilde{p} }}}_{\pi _{i},n+1}} = {\mathbf{\tilde{f}}}_{2,n}, \end{aligned}$$

(11b)

$$\begin{aligned} & \cfrac{{\mathbf{g}}_{2,n}}{\Delta t} + {\mathbf{g}}_{2/{\mathbf{q}}_{2},n} \dot{\mathbf{q}}_{2,n+1} + {\mathbf{g}}_{2/t,n} = {\mathbf{0}}, \end{aligned}$$

(11c)

$$\begin{aligned} & \cfrac{{\mathbf{g}}^{\mathrm{co}}_{n}}{\Delta t} + {\mathbf{g}}_{\mathrm{co}/{ \mathbf{q}}^{\mathrm{co}}_{2},n} \dot{\mathbf{q}}^{\mathrm{co}}_{2,n+1}+ {\mathbf{g}}_{ \mathrm{co}/{\mathbf{q}}^{\mathrm{co}}_{1},n} \dot{\mathbf{q}}^{\mathrm{co}}_{1,n+1} = {\mathbf{0}}, \end{aligned}$$

(11d)

where ${\tilde{\mathbf{\lambda}}}_{2,n+1}\equiv{\Delta t}{\boldsymbol{\lambda}}_{2,n+1}$, ${\tilde{\mathbf{\lambda}}}^{\mathrm{co}}_{n+1}\equiv{\Delta t}{ \boldsymbol{\lambda}}^{\mathrm{co}}_{n+1}$, ${\mathbf{{\tilde{p} }}}_{\pi _{i},n+1}\equiv{\Delta t}{\mathbf{{{p} }}}_{\pi _{i},n+1}$, ${\mathbf{\tilde{f}}}_{2,n}\equiv{\Delta t}{\mathbf{{f}}}_{2,n}$, and ${\mathbf{{g}}}_{2/t}\equiv{\partial}{\mathbf{g}}_{2}/\partial t$ are defined [28, 29]. Besides, there are two aspects related to the above discrete equations:

• 1. concerning Baumgarte’s stabilization method [33], the discretized bilateral constraints ${\mathbf{g}}_{\mathrm{co}}$ and ${\mathbf{g}}_{2}$ are prescribed as a combination of their expression at the position and velocity levels, where the stabilization term ${\mathbf{g}}_{2,n}/{\Delta t}$ is employed to avoid drifting away from the constraint manifold while, at the same time, reducing the index of the corresponding set of DAEs [28, 29]. Since the integration scheme is semiexplicit, an explicit term ${\mathbf{{g}}}_{2/t,n}$ is used in the equation [28];

• 2. the discrete equations involving unilateral constraints are not listed for simplicity since we focus on the interface with the other subsystem, namely the coupling constraint ${\mathbf{g}}_{\mathrm{co}}$, in the cosimulation, where unilateral constraints are assumed to be not involved.

In this nonsmooth solution approach [29], the velocity vector $\dot{\mathbf{q}}_{2,n+1}$ is solved using the discrete formulation of Eq. (11a)–(11d) using CCPs [41]; the position and acceleration vectors are updated as [29]

$$\begin{aligned} {{\mathbf{{q}}}_{2,n + 1}} &= {{\mathbf{{q}}}_{2,n}} + {\Delta t} \cdot { \dot{\mathbf{{q}}}}_{2,n+1}, \end{aligned}$$

(12a)

$$\begin{aligned} {\ddot{\mathbf{{q}}}}_{2,n+1} &= \dfrac{\dot{\mathbf{{q}}}_{2,n+1}-\dot{\mathbf{{q}}}_{2,n}}{\Delta t}. \end{aligned}$$

(12b)

2.3 Input–output scheme of decomposed subsystems

In the cosimulation, ${\boldsymbol{\lambda}}^{\mathrm{co}}_{n+1}$ in Eq. (5a) for the smooth subsystem and ${\mathbf{q}}^{\mathrm{co}}_{1,n+1}$ and its derivatives in Eq. (11d) for the nonsmooth subsystem are obtained from the other subsystem. As a consequence, these two equations are modified as

$$ { {\mathbf{{M}}}_{1}{\dot{\mathbf{{v}}}}_{1} + {\mathbf{{g}}}_{1/{\mathbf{{q}}}_{1}}^{\text{T}} { \boldsymbol{\lambda}}_{1} + \left [ \textstyle\begin{array}{c} -{\mathbf{{g}}}_{\mathrm{co}/{\mathbf{{q}}}^{\mathrm{co}}_{1}}^{\text{T}} \\ {\mathbf{0}} \end{array}\displaystyle \right ] {\mathbf{u}}_{1} - {\mathbf{{f}}}_{1}\left ({\mathbf{{q}}}_{1}, {{\mathbf{{v}}}}_{1},t \right ) = \boldsymbol{0}} $$

(13)

and

$$ \cfrac{{\mathbf{g}}^{\mathrm{co}}_{n}\left ({\mathbf{q}}^{\mathrm{co}}_{2}, {\mathbf{u}}_{21}\right )}{\Delta t} + {\mathbf{g}}_{\mathrm{co}/{\mathbf{q}}^{\mathrm{co}}_{2},n} \dot{\mathbf{q}}^{ \mathrm{co}}_{2,n+1} - {\mathbf{u}}_{22} = {\mathbf{0}}, $$

(14)

where the vectors ${\mathbf{u}}_{1}$ and ${\mathbf{u}}_{2}=\left [{\mathbf{u}}_{21}^{\mathrm{T}}, {\mathbf{u}}_{22}^{\mathrm{T}}\right ]^{ \mathrm{T}}$ are the inputs of the smooth and nonsmooth subsystems, respectively; ${\mathbf{u}}_{1}$ and ${\mathbf{u}}_{2}$ are related to the Lagrange multipliers ${\mathbf{\lambda}}^{\mathrm{co}}$ and the coupling state variables ${\mathbf{q}}^{\mathrm{co}}_{1}, {\dot{\mathbf{q}}^{\mathrm{co}}_{1}}, { \ddot{\mathbf{q}}^{\mathrm{co}}_{1}}$, respectively, expressed as

$$ \left \{ \textstyle\begin{array}{l} {\mathbf{u}}_{1}={\mathbf{y}}_{2}={\text{Y}}_{2}\left ({\boldsymbol{\lambda}}^{\mathrm{co}} \right ), \\ {\mathbf{u}}_{2}={\mathbf{y}}_{1}={\text{Y}}_{1}\left ({\mathbf{q}}^{\mathrm{co}}_{1}, { \dot{\mathbf{q}}^{\mathrm{co}}_{1}}, {\ddot{\mathbf{q}}^{\mathrm{co}}_{1}} \right ), \end{array}\displaystyle \right . $$

(15)

where ${\mathbf{y}}_{i}$ ($i=1,2$) are the outputs of the $i$th subsystem, and $Y_{i}$ are functions of the corresponding subsystem state variables.

To illustrate how inputs are constructed, in this section, we employ a simple coupling joint ${\mathbf{g}}_{\mathrm{co}}\in{\mathbb{R}}^{6}$, which clamps the generalized coordinates of bodies $S_{0}$ and $NS_{0}$ together, expressed as

$$ {\mathbf{g}}_{\mathrm{co}}\left ({\mathbf{q}}^{\mathrm{co}}_{1}, {\mathbf{q}}^{ \mathrm{co}}_{2}\right )={\mathbf{q}}^{\mathrm{co}}_{2}-{\mathbf{q}}^{ \mathrm{co}}_{1}={\mathbf{0}}. $$

(16)

It is worth mentioning that the interface constraint between bodies $S_{0}$ and $NS_{0}$ is not actually enforced by prescribing Eq. (16). That expression is merely intended to show the relationship between reaction forces/moments and kinematic variables in the smooth subsystem. Reaction forces and moments in the global reference are sent to the smooth subsystem, so that the input and the Jacobian matrix of the smooth subsystem can be formulated as

$$\begin{aligned} {\mathbf{u}}_{1} &= -\boldsymbol{\lambda}^{\mathrm{co}}, \end{aligned}$$

(17a)

$$\begin{aligned} {\mathbf{{g}}}_{\mathrm{co}/{\mathbf{{q}}}^{\mathrm{co}}_{1}} &= -{\mathbf{E}}_{6}, \end{aligned}$$

(17b)

where ${\mathbf{E}}_{6}\in{\mathbb{R}^{6\times 6}}$ is the identity matrix.

In the solution process, the constraint ${\mathbf{g}}_{\mathrm{co}}$ is formulated in the nonsmooth subsystem with respect to a moving local reference defined by the inputs ${\mathbf{u}}_{21}$.

2.3.1 Original inputs

In the nonsmooth subsystem the interfaces for the input of the motion are designed according to the discrete bilateral constraints in Eq. (14) as (with reference to the class ChLinkMotionImposed in Project Chrono)

$$ \dfrac{{\mathbf{q}}^{\mathrm{co}}_{2,n}-{\mathbf{u}}_{21}}{\Delta t} + \dot{\mathbf{q}}^{\mathrm{co}}_{2,n+1} - {\mathbf{u}}_{22}={\mathbf{0}}. $$

(18)

By comparing the interfaces with the coupling constraints ${\mathbf{g}}_{\mathrm{co}}={\mathbf{0}}\in{\mathbb{R}}^{6}$ of Eq. (16), which are discretized as

$$ \dfrac{{\mathbf{q}}^{\mathrm{co}}_{2,n}-{\mathbf{q}}^{\mathrm{co}}_{1,n}}{\Delta t} + \dot{\mathbf{q}}^{\mathrm{co}}_{2,n+1} - \dot{\mathbf{q}}^{\mathrm{co}}_{1,n+1}={ \mathbf{0}}, $$

(19)

we obtain the corresponding inputs expressed as

$$ \left \{ \textstyle\begin{array}{l} {\mathbf{u}}_{21}={\mathbf{q}}^{\mathrm{co}}_{1,n}, \\ {\mathbf{u}}_{22}=\dot{\mathbf{q}}^{\mathrm{co}}_{1,n+1}. \end{array}\displaystyle \right . $$

(20)

It is worth noticing that whereas the discrete velocity constraint is evaluated at time $t_{n+1}$, the discrete position constraint is evaluated at time $t_{n}$.

Using this set of inputs, we solve the coupling constraint ${\mathbf{g}}_{\mathrm{co}}$ in the nonsmooth subsystem, which linearly combines the constraints at position and velocity levels, although not enforced at the same time step. However, in cosimulation, this combination of the constraint formulation may jeopardize algorithmic stability. A more stable scheme is needed to guarantee adequate enforcement of ${\mathbf{g}}_{\mathrm{co}}$ at the position, velocity, and acceleration levels.

We further call this set of inputs “original inputs.”

2.3.2 Inputs according to Baumgarte’s method

To improve the algorithmic stability of the cosimulation and, at the same time, avoid exposing the details of the nonsmooth solver solution process, we redesign the inputs of Eq. (20). We define the new inputs with the specific objective of satisfying the constraints obtained from Baumgarte’s stabilization method [33] formulated as

$$ \alpha \left ({\mathbf{{q}}}^{\mathrm{co}}_{2,n+1}- {{\mathbf{q}}^{\mathrm{co}}_{1,n+1}} \right ) + \beta \left ({\dot{\mathbf{{q}}}}^{\mathrm{co}}_{2,n+1}-{ \dot{{\mathbf{q}}}^{\mathrm{co}}_{1,n+1}}\right ) + \gamma \left ({ \ddot{\mathbf{{q}}}}^{\mathrm{co}}_{2,n+1}-{{\ddot{\mathbf{q}}}^{\mathrm{co}}_{1,n+1}} \right ) ={\mathbf{0}}, $$

(21)

where $\alpha >0$, $\beta >0$, and $\gamma >0$ are the parameters of Baumgarte’s stabilization method. In general, the choice

$$ \textstyle\begin{array}{c@{\quad}c@{\quad}c} \alpha =\dfrac{2}{\Delta t^{2}},& \beta =\dfrac{2}{\Delta t}, & \gamma =1 \end{array} $$

(22)

provides an adequate (i.e., accurate and fast) enforcement of the constraint at the position level [42]. It is worth noticing that in Eq. (21), $\gamma =0$ generates a formulation without accelerations, namely index-2 DAEs for the coupled system, and $\beta =\gamma =0$ yields index-3 DAEs.

In the nonsmooth subsystem, can be rewrite the interface of Eq. (18) as

$$ {{\dot{\mathbf{q}}}^{\mathrm{co}}_{2,n+1}}= {\mathbf{{u}}}_{22}- \dfrac{{{\mathbf{q}}^{\mathrm{co}}_{2,n}}- {{\mathbf{u}}_{21}}}{\Delta t}. $$

(23)

Substituting the update scheme into Eq. (12a), (12b) and the interface of Eq. (23) into Eq. (21) yields

$$ \textstyle\begin{array}{l@{\quad}l} \left (\alpha {\Delta t} + \beta + \dfrac{1}{\Delta t}\gamma \right ) \left ( {{{{{\mathbf{{u}}}}}_{22}}}- \dfrac{{{\mathbf{q}}^{\mathrm{co}}_{2,n}}- {{\mathbf{u}}_{21}}}{\Delta t} \right ) &= \alpha \left ({{\mathbf{q}}^{\mathrm{co}}_{1,n+1}}-{{\mathbf{{q}}}^{ \mathrm{co}}_{2,n}}\right ) + \beta {\dot{{\mathbf{q}}}^{\mathrm{co}}_{1,n+1}} \\ &+ \dfrac{\gamma}{\Delta t} \left ( \dot{\mathbf{{q}}}^{\mathrm{co}}_{2,n}+{ \Delta t}{{\ddot{\mathbf{q}}}^{\mathrm{co}}_{1,n+1}}\right ). \end{array} $$

(24)

If inputs ${\mathbf{u}}_{21}$ and ${\mathbf{u}}_{22}$ can enforce Eq. (24), then the constraint in Eq. (21) will be satisfied. For simplicity, in the cosimulation, ${\mathbf{u}}_{21}$ is given as

$$ {\mathbf{u}}_{21}={\mathbf{q}}^{\mathrm{co}}_{2,n}, $$

(25)

which is substituted into Eq. (24) to generate the input ${\mathbf{u}}_{22}$ as

$$ {\mathbf{u}}_{22}= \dfrac{\Delta t}{\alpha \Delta t^{2} + \beta \Delta t + \gamma}\left [ \alpha \Delta t \dfrac{{{\mathbf{q}}^{\mathrm{co}}_{1,n+1}}-{{\mathbf{{q}}}^{\mathrm{co}}_{2,n}}}{\Delta t} + \beta {\dot{{\mathbf{q}}}^{\mathrm{co}}_{1,n+1}} + \dfrac{1}{\Delta t} \gamma \left ( {{\dot{\mathbf{q}}}^{\mathrm{co}}_{2,n}}+ \Delta t {{ \ddot{\mathbf{q}}}^{\mathrm{co}}_{1,n+1}}\right )\right ]. $$

(26)

In Eq. (26), ${\mathbf{u}}_{22}$ is the weighted average of three contributions: a generalized velocity vector obtained by the difference of ${\mathbf{q}}^{\mathrm{co}}_{1,n+1}$ and ${\mathbf{q}}^{\mathrm{co}}_{2,n}$, the velocity obtained from the smooth subsystem ${\dot {\mathbf{q}}}^{\mathrm{co}}_{1,n+1}$, and the velocity vector obtained from the integration of ${\ddot{\mathbf{q}}}^{\mathrm{co}}_{1,n+1}$.

2.3.3 A general coupling joint

When there are offsets between the coupling markers and the generalized coordinates of the coupling bodies, as shown in Fig. 1(b), the coupling constraints are formulated as functions of the markers’ kinematic variables ${\mathbf{q}}^{\mathrm{co}}_{1,A}$ and ${\mathbf{q}}^{\mathrm{co}}_{2,B}$:

$$ { } {\mathbf{g}}_{\mathrm{co}}\left ({\mathbf{q}}^{\mathrm{co}}_{1}, {\mathbf{q}}^{ \mathrm{co}}_{2}\right )={\mathbf{q}}^{\mathrm{co}}_{2,B}-{\mathbf{q}}^{ \mathrm{co}}_{1,A}={\mathbf{0}}. $$

(27)

In ${\mathbf{q}}^{\mathrm{co}}_{1,A}$ and ${\mathbf{q}}^{\mathrm{co}}_{2,B}$ the displacement coordinate vectors ${\mathbf{r}}^{\mathrm{co}}_{1,A}$ and ${\mathbf{r}}^{\mathrm{co}}_{2,B}$ are obtained by

$$\begin{aligned} {\mathbf{r}}^{\mathrm{co}}_{1,A} &= {\mathbf{r}}^{\mathrm{co}}_{1} + {\mathbf{R}}^{ \mathrm{co}}_{1}{\mathbf{r}}_{A,\mathrm{loc}}, \end{aligned}$$

(28a)

$$\begin{aligned} {\mathbf{r}}^{\mathrm{co}}_{2,B} &= {\mathbf{r}}^{\mathrm{co}}_{2} + {\mathbf{R}}^{ \mathrm{co}}_{2}{\mathbf{r}}_{B,\mathrm{loc}}, \end{aligned}$$

(28b)

where ${\mathbf{r}}_{A,\mathrm{loc}}$ and ${\mathbf{r}}_{B,\mathrm{loc}}$ represent the offsets of the markers in the local reference frame of the bodies, ${\mathbf{r}}^{\mathrm{co}}_{1}$ and ${\mathbf{r}}^{\mathrm{co}}_{2}$ are the displacement coordinate vectors of the coupling bodies, ${\mathbf{r}}^{\mathrm{co}}_{1R}$ and ${\mathbf{r}}^{\mathrm{co}}_{2R}$ denote the rotation coordinates of the coupling bodies, and their corresponding rotation matrices are written as ${\mathbf{R}}^{\mathrm{co}}_{1}$ and ${\mathbf{R}}^{\mathrm{co}}_{2}$, respectively. In ${\mathbf{q}}^{\mathrm{co}}_{1,A}$ and ${\mathbf{q}}^{\mathrm{co}}_{2,B}$ the rotation coordinates ${\mathbf{r}}_{1,AR}$ and ${\mathbf{r}}_{2,BR}$ are the same as those in ${\mathbf{q}}^{\mathrm{co}}_{1,A}$ and ${\mathbf{q}}^{\mathrm{co}}_{2,B}$:

$$\begin{aligned} {\mathbf{r}}^{\mathrm{co}}_{1,AR} &= {\mathbf{r}}^{\mathrm{co}}_{1R}, \end{aligned}$$

(29a)

$$\begin{aligned} {\mathbf{r}}^{\mathrm{co}}_{2,BR} &= {\mathbf{r}}^{\mathrm{co}}_{2R}. \end{aligned}$$

(29b)

From Eqs. (27)–(29b) the partial derivative ${\mathbf{{g}}}_{\mathrm{co}/{\mathbf{{q}}}^{\mathrm{co}}_{1}}$ can be obtained as

$$ {\mathbf{{g}}}_{\mathrm{co}/{\mathbf{{q}}}^{\mathrm{co}}_{1}}=-\left [ \textstyle\begin{array}{l@{\quad}l} {\mathbf{E}}_{3}, & -\left ({\mathbf{R}}^{\mathrm{co}}_{1}{\mathbf{r}}_{A,loc} \right )\times \\ {\mathbf{0}}, & {\mathbf{E}}_{3} \end{array}\displaystyle \right ], $$

(30)

where × represents the cross-product operator, and for a vector ${\mathbf{a}}\in{\mathbb{R}}^{3}$, ${\mathbf{a}}\times$ is the corresponding skew-symmetric matrix.³

In this case the original and modified input formats can be respectively expressed as functions of the coordinates of the markers, ${\mathbf{q}}^{\mathrm{co}}_{1,A}$ and ${\mathbf{q}}^{\mathrm{co}}_{2,B}$:

$$\begin{aligned} {\mathbf{u}}_{21} &= {\mathbf{q}}^{\mathrm{co}}_{1,A,n}, \end{aligned}$$

(31a)

$$\begin{aligned} {\mathbf{u}}_{22} &= \dot{\mathbf{q}}^{\mathrm{co}}_{1,A,n+1}, \end{aligned}$$

(31b)

and

$$\begin{aligned} {\mathbf{u}}_{21} &= {\mathbf{q}}^{\mathrm{co}}_{2,B,n}, \end{aligned}$$

(32a)

$$\begin{aligned} {\mathbf{u}}_{22} &= \dfrac{\Delta t}{\alpha \Delta t^{2} + \beta \Delta t + \gamma}\biggl[ \alpha \Delta t \dfrac{{{\mathbf{q}}^{\mathrm{co}}_{1,A,n+1}}-{{\mathbf{{q}}}^{\mathrm{co}}_{2,B,n}}}{\Delta t} + \beta {\dot{{\mathbf{q}}}^{\mathrm{co}}_{1,A,n+1}} \\ &\quad {}+ \dfrac{1}{\Delta t} \gamma \left ( {{\dot{\mathbf{q}}}^{\mathrm{co}}_{2,B,n}}+\Delta t{{ \ddot{\mathbf{q}}}^{\mathrm{co}}_{1,A,n+1}}\right )\biggr]. \end{aligned}$$

(32b)

We call the latter set of inputs “modified inputs.” Using these modified inputs, Baumgarte’s constraint stabilization in Eq. (21) is achieved during cosimulation, improving the algorithmic stability of the explicit cosimulation.

For a general joint that does not enforce all components of position and rotation, the reference is defined at Marker B to describe whether rotation or displacement along each axis in the local frame is allowed.

3 Cosimulation strategy

3.1 Cosimulation schemes

Cosimulation is performed by solving the subsystems separately, exchanging information at discrete time points. The time interval between these points is defined as a macrotime step. Although each subsystem can perform multiple time steps between macrotime steps, which is called multirate cosimulations, in this work, we assume the macrotime step and the time step in each subsystem to be the same. Explicit cosimulation schemes (in the sense of Hafner and Popper [43]), also called noniterative schemes [43], are established between the smooth and nonsmooth subsystems.

Explicit cosimulation can be structured according to two schemes:

• the Jacobi-type scheme [43], as shown in Fig. 2(a), in which all subsystems are simulated in parallel using extrapolated inputs for each time step;

  Fig. 2

  

  Flowchart of different explicit cosimulation schemes for the smooth/nonsmooth cosimulation

• the Gauss–Seidel scheme, as shown in Fig. 2(b), in which subsystems are integrated serially at each time step: extrapolation is used to predict the input for the subsystem that is solved first; subsequently, it generates the input for the other subsystem, which is integrated afterward.

Both cosimulation algorithms can be applied to the cosimulation process using the modified inputs described in Sect. 2. It is worth mentioning that when the explicit Gauss–Seidel approach is employed, the cosimulation suffers from the risk of lacking zero-stability [27, 44], which depends on the mass ratios that contribute to the coupling kinematic constraints and cannot be guaranteed simply by using the modified inputs. Nonetheless, owing to its simplicity, we still use the explicit Gauss–Seidel cosimulation in the following examples to illustrate the procedure with modified inputs.

Assuming that the macrotime step is equal to the micro one, an explicit cosimulation scheme between the smooth and nonsmooth subsystems is depicted in Fig. 2(b). The nonsmooth subsystem is simulated first, based on the prescribed interface motion predicted by the smooth subsystem. Subsequently, the resulting reaction forces/moments are sent to the smooth subsystem. The choice of this sequence of operations naturally stemmed from the consideration that in the smooth subsystem the solution of the discrete equations (5a) and (5b) already predicts the solution to provide initial values for the Newton iteration used to solve the resulting nonlinear problem. Such initial values are obtained by extrapolation from the solution at previous time steps according to the aforementioned multistep integration scheme. Using the readily available predicted motion as output avoids repeating the extrapolation process. Alternatively, a different extrapolation formulation can be used for the coupling motion to improve the stability of cosimulation [45]. However, this investigation is beyond the scope of the present work.

In the smooth subsystem the derivatives of the state variables are extrapolated by Hermitian interpolation, yielding the predicted generalized velocity vector ${\dot{\mathbf{q}}}_{1,n+1}^{\left ( 0 \right )}$ [34]:

$$ {{\dot{\mathbf{q}}}_{1,n+1}^{\left ( 0 \right )} = {-\cfrac{12}{\Delta t}}({{ \mathbf{{q}}}_{1,n}} - {{\mathbf{{q}}}_{1,n - 1}}) + 8{{{\dot{\mathbf{q}}}}_{1,n}} + 5{{{ \dot{\mathbf{q}}}}_{1,n - 1}}}, $$

(33)

which is substituted into the integration scheme in Eq. (6) to produce the predicted generalized coordinate

$$\begin{aligned} {\mathbf{{q}}}_{1,n+1}^{\left ( 0 \right )} &= \sum _{i = 1,2} {{a_{i}}{{ \mathbf{{q}}}_{n+1- i}}} + {\Delta t}\sum _{i = 0,2} {{b_{i}}{{{ \dot{\mathbf{q}}}}_{n+1 - i}}} \\ &= \sum _{i = 1,2} {{a_{i}}{{\mathbf{{q}}}_{n+1- i}}} + {\Delta t} \sum _{i = 1,2} {{b_{i}}{{{\dot{\mathbf{q}}}}_{n+1 - i}}} + { \Delta t}{b_{0}}\left [{-\cfrac{12}{\Delta t}}({{\mathbf{{q}}}_{n}} - {{\mathbf{{q}}}_{n - 1}}) + 8{{{\dot{\mathbf{q}}}}_{n}} + 5{{{\dot{\mathbf{q}}}}_{n - 1}} \right ] \\ &= \left (a_{1} - 12 b_{0}\right ) {{\mathbf{{q}}}_{n}} + \left (a_{2} + 12 b_{0} \right ) {{\mathbf{{q}}}_{n-1}} + \Delta t \left (b_{1} + 8 b_{0}\right ) { \dot{\mathbf{{q}}}_{n}} + \Delta t \left (b_{2} + 5 b_{0}\right ) { \dot{\mathbf{{q}}}_{n-1}} . \end{aligned}$$

(34)

For accelerations, a constant extrapolation formula is used:

$$ {\ddot{\mathbf{q}}}_{1,n+1}^{\left ( 0 \right )}={\ddot{\mathbf{q}}}_{1,n}. $$

(35)

According to the input formats, these predicted state variables are substituted into Eq. (31a), (31b) or Eq. (32a), (32b) to yield inputs for the nonsmooth subsystem. The nonsmooth system is then solved to generate the reaction forces and moments for the smooth subsystem.

3.2 Implementation

Cosimulation of the coupled smooth/nonsmooth subsystem is implemented between the free general-purpose multibody dynamics software MBDyn and the open-source multiphysics C++ library, Project Chrono. The smooth subsystem is modeled in MBDyn, and the nonsmooth subsystem is modeled with the Chrono library. To achieve cosimulation between these two subsystems, a stable two-way communication layer is necessary.

In this work, we establish dynamic linking between these two solvers, as shown in Fig. 3, where the nonsmooth subsystem is embedded in MBDyn as an external module, implementing a user-defined force element. In detail, a run-time loadable module named module-chrono-interface was implemented, which can be loaded during the execution of MBDyn. The module consists of three parts: i) a user-defined element called ChronoInterface, ii) a set of MBDyn-Chrono interface functions, and iii) the model of the nonsmooth subsystem, implemented using the C++ libraries provided by Chrono. The ChronoInterface element is derived from the generic user-defined element in MBDyn, which has access to the solution process of MBDyn.

Fig. 3

Schematics of communication layer between MBDyn and Chrono

The ChronoInterface element can obtain kinematic data of bodies from the MBDyn solver and apply reaction forces and moments to the bodies themselves. Additionally, to gather the reaction forces and moments, this element also sends commands to the nonsmooth subsystem, such as requesting the simulation of the nonsmooth subsystem by calling the related function and reading/writing information related to the nonsmooth subsystem from/to files.

The second part of the module is a set of MBDyn-Chrono interface functions. These functions act as an intermediate communication layer: they receive kinematic data and commands from the ChronoInterface element and pass them to the nonsmooth subsystem, receive dynamic data and messages from the nonsmooth subsystem, and hand them over to the ChronoInterface element.

The third part of the run-time loadable module is the nonsmooth subsystem, which needs to be modeled by the user in the function named MBDyn_CE_CEModel_Create(). In the process of modeling, the physical components of the nonsmooth subsystem are provided by the Chrono library.

According to the dependencies of the different parts, the interface functions and the user-defined nonsmooth subsystem are compiled together with the dynamic libraries in Chrono to generate a dynamic library for the ChronoInterface element called libuser-model.so. With the generated library, the ChronoInterface element generates a new dynamic library, called libchrono-interface-module.so, which is run-time loaded in MBDyn, by defining the related statement in the input file. Overall, this communication layer provides a convenient way to establish cosimulation between MBDyn and Project Chrono, by which the cosimulation scheme in Fig. 2(b) is achieved.

The previously mentioned explicit Gauss–Seidel cosimulation scheme is similar to the first step of the implicit cosimulation scheme in [7]. The proposed explicit cosimulation scheme differs from that of [7] in the following three aspects: (1) apart from the cosimulation procedure illustrated in Fig. 2(b), the implicit cosimulation scheme includes an iterative process, by which the simulation of the nonsmooth subsystem(s) is embedded into the correction process of Eqs. (10a)–(10c) of the smooth solver; the cosimulation moves to the subsequent step only when the convergence of the iterative process is achieved; (2) the proposed explicit cosimulation scheme focuses on evaluating the ability of different types of inputs, consisting of position-, velocity-, and acceleration-level kinematic quantities and their combinations to obtain a stable and accurate cosimulation, whereas the implicit scheme only uses the position-level generalized physical coordinates during cosimulation; (3) last but not least, the proposed explicit cosimulation scheme is implemented in the form of a user-defined run-time loadable module embedded in MBDyn, module-chrono-interface, by which the aforementioned cosimulation schemes, such as the Jacobi- or Gauss–Seidel-type explicit or implicit cosimulations using the modified inputs, are all achieved in the element interface, ChronoInterface, whereas the data exchange approach used for the implicit scheme illustrated in [7] was built on interprocess communication through Unix sockets, the cosimulation strategies being defined in the specific subsystems. This may appear an implementation detail but represents a substantial generalization and a great simplification in the use of the proposed cosimulation setup.

4 Numerical experiments

4.1 Linear two-mass oscillator

The linear two-mass oscillator of Fig. 4 is commonly used to test the performance of co-simulation methods in the literature [21]. Also in this work, it is used to test the proposed co-simulation configuration and to show the influence of the modified inputs on its algorithmic stability. In the tests the recurrence equations of the cosimulation are deduced to produce the stability plots with different inputs and to show the influence of the modified inputs. It is worth mentioning that although the two-mass oscillator is a smooth system, it is still decomposed into two subsystems, and one of them is integrated using the method proposed for nonsmooth subsystems.

Fig. 4

Decomposition of the two-mass oscillator

4.1.1 Recurrence scheme

According to the methods in Sect. 2, the two-mass oscillator with constraints in Fig. 4 is decomposed into two subsystems:

$$\begin{aligned} &\left \{ \textstyle\begin{array}{l} \dot{x}_{1}=v_{1}, \\ \dot{v}_{1}=-\dfrac{k_{1}}{m_{1}}x_{1}-\dfrac{c_{1}}{m_{1}}v_{1}+ \dfrac{1}{m_{1}}\lambda , \end{array}\displaystyle \right . \end{aligned}$$

(36a)

$$\begin{aligned} &\left \{ \textstyle\begin{array}{l} \dot{x}_{2}={v_{2}}, \\ \dot{v}_{2}=-\dfrac{k_{2}}{m_{2}}x_{2}-\dfrac{c_{2}}{m_{2}}v_{2}- \dfrac{1}{m_{2}}{\lambda}, \\ x_{2}-x_{1}=0, \end{array}\displaystyle \right . \end{aligned}$$

(36b)

where $m_{i}$, $k_{i}$, and $c_{i}$ ($i=1,2$) are the mass, stiffness, and dam** coefficients for bodies 1 and 2, as shown in Fig. 4, $x_{i}$ and $v_{i}$ ($i=1,2$) are the position and velocity of the two bodies, and $\lambda$ is the Lagrange multiplier corresponding to the algebraic constraint.

Equations (36a) are formulated using the method for the smooth subsystem and are integrated by the implicit linear two-step scheme in Eq. (6). Substituting Eq. (36a) into the integration scheme (6) yields

$$\begin{aligned} x_{1,n+1} &= \sum _{j=1,2}{a_{j}}{x_{1,n+1-j}}+\Delta t\sum _{j=1,2}{b_{j}}{v_{1,n+1-j}}+\Delta t{b_{0}}{v_{1,n+1}}, \end{aligned}$$

(37a)

$$\begin{aligned} v_{1,n+1} &= \sum _{j=1,2}{a_{j}}{v_{1,n+1-j}}+\Delta t\sum _{j=0,1,2}{b_{j}}{\left (-\dfrac{k_{1}}{m_{1}}x_{1,n+1-j}- \dfrac{c_{1}}{m_{1}}v_{1,n+1-j}+\dfrac{1}{m_{1}}u_{1,n+1-j}\right )}, \end{aligned}$$

(37b)

where $u_{1}$ is the input.

Equation (36a) and (36b) is formulated using the formulation proposed for the nonsmooth subsystem in Eq. (11a)–(11d), although the subsystem analyzed here is smooth, as

$$\begin{aligned} x_{2,n+1} &= x_{2,n}+{\Delta t}{v_{2,n+1}}, \end{aligned}$$

(38a)

$$\begin{aligned} v_{2,n+1} &= v_{2,n}-\dfrac{\Delta tk_{2}}{m_{2}}x_{2,n}- \dfrac{\Delta tc_{2}}{m_{2}}v_{2,n}-\dfrac{\Delta t}{m_{2}}{\lambda _{n+1}}, \end{aligned}$$

(38b)

$$\begin{aligned} 0 &= \dfrac{{x_{2,n}}-u_{21,n+1}}{\Delta t}+v_{2,n+1}-u_{22,n+1}, \end{aligned}$$

(38c)

where $u_{21}$ and $u_{22}$ are inputs received from subsystem 1; the forces generated by the spring and damper are regarded as parts of the external forces ${\mathbf{f}}_{2}$.

For the inputs in Eqs. (37a), (37b) and (38a)–(38c), if those that have been defined as the original inputs in Eq. (31a), (31b) are employed, then we obtain

$$\begin{aligned} u_{1,n+1} &= \lambda _{n+1}, \end{aligned}$$

(39a)

$$\begin{aligned} u_{21,n+1} &= {x_{1,n}}, \end{aligned}$$

(39b)

$$\begin{aligned} u_{22,n+1} &= {v^{\left (0\right )}_{1,n+1}}= {-\cfrac{12}{\Delta t}}({{x}_{1,n}} - {x_{1,n - 1}}) + 8{v_{1,n}} + 5{v_{1,n - 1}}, \end{aligned}$$

(39c)

where ${v^{\left (0\right )}_{1,n+1}}$ is obtained using the extrapolation formula (33). Collecting Eqs. (37a)–(39c) yields the recurrence equations

$$ {\boldsymbol{\varLambda}_{1}}{\mathbf{z}}_{n+1}={\boldsymbol{\varLambda}_{2}}{\mathbf{z}}_{n}+{{ \boldsymbol{\varLambda}}_{3}}{\mathbf{z}}_{n-1}, $$

(40)

where

$$ {\mathbf{z}}_{n+1}=\left [{x_{1,n+1}},{v_{1,n+1}},{x_{2,n+1}},{v_{2,n+1}},{ \lambda _{n+1}}, {u_{1,n+1}}, u_{21,n+1}, u_{22,n+1}\right ]^{\text{T}}, $$

(41)

and the coefficient matrices $\boldsymbol{\varLambda}_{i}$ ($i=1,2,3$) are related to the system parameters, the algorithmic parameters $\rho _{\infty}$, and time-step sizes $\Delta t$.

Alternatively, if “modified inputs” in Eq. (32a), (32b) are employed to incorporate Baumgarte’s stabilization method during the explicit cosimulation, then we obtain

$$\begin{aligned} u_{1,n+1} &= \lambda _{n+1}, \end{aligned}$$

(42a)

$$\begin{aligned} u_{21,n+1} &= {x_{2,n}}, \end{aligned}$$

(42b)

$$\begin{aligned} u_{22,n+1} &= \dfrac{\Delta t}{\alpha \Delta t^{2} + \beta \Delta t + \gamma}\left [ \alpha \left ({{x}^{\left ( 0 \right )}_{1,n+1}}-{x_{2,n}}\right ) + \beta {v^{\left ( 0 \right )}_{1,n+1}} + \dfrac{1}{\Delta t}\gamma \left ( {v_{2,n}}+\Delta t{{\dot{v}}^{\left ( 0 \right )}_{1,n+1}} \right )\right ] \\ &= {\varTheta _{0}}\left ({\varTheta _{1}}{x_{1,n}}+{\varTheta _{2}}{x_{1,n-1}}+{ \varTheta _{3}}{v_{1,n}}+{\varTheta _{4}}{v_{1,n-1}}+\dfrac{\gamma}{m_{1}}{u_{1,n}}- \alpha{x_{2,n}}+\dfrac{\gamma}{\Delta t}{v_{2,n}}\right ), \end{aligned}$$

(42c)

where the superscript $(\cdot )^{(0)}$ denotes the extrapolated variables of Eqs. (33)–(35), and

$$\begin{aligned} {\varTheta _{0}} &= \dfrac{\Delta t}{\alpha \Delta t^{2} + \beta \Delta t + \gamma}, \end{aligned}$$

(43a)

$$\begin{aligned} {\varTheta _{1}} &= \left (a_{1}-12b_{0}\right )\alpha - \dfrac{12}{\Delta t}\beta -\dfrac{k_{1}}{m_{1}}\gamma , \end{aligned}$$

(43b)

$$\begin{aligned} {\varTheta _{2}} &= \left (a_{2}+12b_{0}\right )\alpha + \dfrac{12}{\Delta t}\beta , \end{aligned}$$

(43c)

$$\begin{aligned} {\varTheta _{3}} &= \left (\Delta tb_{1}+8\Delta tb_{0}\right )\alpha +8 \beta -\dfrac{c_{1}}{m_{1}}\gamma , \end{aligned}$$

(43d)

$$\begin{aligned} {\varTheta _{4}} &= \left (\Delta tb_{2}+5\Delta tb_{0}\right )\alpha +5 \beta . \end{aligned}$$

(43e)

Similarly to the case that uses the original inputs, the recurrence equations can be obtained by combining Eqs. (36b), (37a), (37b) and (42a)–(42c) expressed in the form (40) with a new set of coefficient matrices $\boldsymbol{\varLambda}$ ($i=1,2,3$), which are also related to the parameters $\alpha$, $\beta$, and $\gamma$ in the modified inputs.

4.1.2 Stability results of the recurrence equations

From a physical point of view, the linear two-mass oscillator system is called asymptotically stable if its parameters satisfy the requirements $m_{i}>0$, $k_{i}>0$, $c_{i}>0$. For an asymptotically stable two-mass oscillator, cosimulation results using the proposed explicit cosimulation scheme can be obtained from the solution of the recurrence equations (40). They can be solved using the exponential approach, as ${\mathbf{z}}_{n}={\hat {\mathbf{z}}}\cdot{\hat{\lambda}}^{n}$, where $\hat{\lambda}$ is the generic eigenvalue, and $\hat{\mathbf{z}}$ is the corresponding eigenvector of the recurrence equation [46]. The stability of the solution depends on the spectral radius $\tilde{\rho}={\max}(|{\hat{\lambda}_{j}}|)$ of the recurrence equation, where ${\hat{\lambda}_{j}}$ is the $j$th eigenvalue of the latter. When $\tilde{\rho}>1$, the recurrence equation generates an unstable solution, and the corresponding cosimulation is (algorithmically) unstable [46]. Otherwise, when $\tilde{\rho}\leq 1$, the cosimulation is (algorithmically) stable [46].

In the tests, we consider a set of parameters, where $m_{1}=1.0~{\text{kg}}$, and other system parameters are defined as functions related to equivalent natural frequencies $\omega _{0i}$ ($i=1,2$) and dam** factors $\xi _{i}$ of the subsystems:

$$ \left \{ \textstyle\begin{array}{l} k_{i}=m_{i} \omega ^{2}_{0i}~{\text{N}\,\text{m}^{-1}}, \\ c_{i}=2 m_{i} \omega _{0i} \xi _{i}~{\text{N}\,\text{s}\,\text{m}^{-1}}, \end{array}\displaystyle \right . $$

(44)

where

$$ { } \textstyle\begin{array}{c@{\quad}c@{\quad}c} m_{2}=1.0~{\text{kg}},&{\omega _{02}}=0.0~{\text{rad}\,\text{s}^{-1}}, & {\xi _{1}}={ \xi _{2}}=0.0. \end{array} $$

(45)

Different sets of parameters are employed for the modified inputs, namely:

$$\alpha =\frac{2}{\mathrm{\Delta }{t}^2},\beta =\frac{2}{\mathrm{\Delta }t},\gamma =1,$$

(46a)

$$\alpha =\frac{1}{\mathrm{\Delta }t},\beta =1,\gamma =0,$$

(46b)

$$\alpha =1,\beta =0,\gamma =0,$$

(46c)

which correspond to index-1, index-2, and index-3 monolithic DAEs, respectively. Two-dimensional stability plots as functions of $\omega _{01}\Delta t$ and $\rho _{\infty}$ are shown in Fig. 5 with the original and modified inputs. In the figure the points indicate that $\tilde{\rho}\leq 1$ is satisfied using the corresponding set of $\omega _{01}\Delta t$ and $\rho _{\infty}$, i.e., stable cosimulation results are obtained. We can see that for a simple, undamped case, the cosimulation using the original inputs cannot give stable results for small values of $\omega _{01}\Delta t$, at least for a broad range of $\rho _{\infty}$. With the same system parameters in Eq. (45), this situation can be improved using the modified inputs, which can always produce stable solutions with a small $\omega _{01}\Delta t$, provided that a suitable $\rho _{\infty}$ is employed in the smooth multistep integrator. Apart from this, Fig. 5(d) also shows that the modified inputs with the index-1 format, corresponding to the parameters in Eq. (46a), possess the largest stability region.

Fig. 5

Stability plots of cosimulation schemes with: (a) the original inputs of Eq. (20); (b) index-3: $\alpha =1$, $\beta =0$, and $\gamma =0$; (c) index-2: $\alpha =1/\Delta t^{2}$, $\beta =1/\Delta t$, and $\gamma =0$; (d) index-1: $\alpha =2/\Delta t^{2}$, $\beta =2/\Delta t$, and $\gamma =1$

Different input parameters are also employed to test the stability of the explicit co-simulation scheme, as shown in Fig. 6, where the stability plots of an implicit cosimulation scheme developed in [7] are also provided as a reference. We can see that when $\alpha$ and $\beta$ are smaller than those used in Eq. (46a), the explicit cosimulation scheme can offer stable results in all $\omega _{01}\Delta t$ and $\rho _{\infty}$ tested combinations close to the performance of the implicit cosimulation scheme. When larger $\alpha$ and $\beta$ are used, the stability results are similar to those of the explicit cosimulation scheme with the input parameters of Eq. (46b), since $\alpha \gg \gamma$ and $\beta \gg \gamma$ imply that the constraints error $\gamma \left (\dot{v}_{2,n+1}-\dot{v}^{(0)}_{1,n+1}\right )$ can be neglected, compared with that of the other two contributions.

Fig. 6

Stability plots of cosimulation schemes with (a) $\alpha =0.2/\Delta t^{2}$, $\beta =0.2/\Delta t$, and $\gamma =1$, (b) $\alpha =20/\Delta t^{2}$, $\beta =20/\Delta t$, and $\gamma =1$, (c) $\alpha =200/\Delta t^{2}$, $\beta =200/\Delta t$, and $\gamma =1$, and (d) implicit cosimulation scheme

Stability plots with different mass ratios are also shown in Fig. 7. We can notice that a large mass ratio ($m_{2}\gg m_{1}$) may spoil the zero-stability of the explicit Gauss–Seidel cosimulation, regardless of whether the original or the index-1 modified inputs are used, although the cosimulation using the index-1 modified inputs shows better stability properties. The influence of the mass ratio is consistent with analogous conclusions in the literature that cosimulation may lack zero-stability when the mass ratio is large [27, 44].

Fig. 7

Stability plots of cosimulation schemes with different mass ratios: (a) original inputs and $m_{2}/m_{1}=0.5$, (b) index-1 modified inputs and $m_{2}/m_{1}=0.5$, (c) original inputs and $m_{2}/m_{1}=2.0$, (d) index-1 modified inputs and $m_{2}/m_{1}=2.0$

4.1.3 Simulation results

With initial position $x_{1}=x_{2}=0.0~{\mathrm{m}}$ and initial velocity $v_{1}=v_{2}=0.1~{\text{m}/\text{s}}$, the explicit co-simulation between MBDyn and Chrono is performed with $\rho _{\infty}=0.56$ and ${\omega ^{2}_{01}=5000~\text{s}^{-2}}$. The cosimulation results with original and modified inputs of Eqs. (46a)–(46c) are shown in Fig. 8, where the results obtained by a monolithic simulation in MBDyn are shown as dotted lines for reference. The cosimulation results are consistent with those obtained from the previously mentioned recurrence equations (40). In detail, the solution using the original inputs is unstable because the corresponding spectral radius $\tilde{\rho}\approx{1.11}>1$, whereas algorithmically stable results are obtained with the other three sets of inputs, since the stability condition $\tilde{\rho}\approx{0.999}\leq 1$ is satisfied. However, Fig. 8 also shows a clear difference between the results obtained with monolithic and explicit cosimulations, owing to the algorithmic dissipation introduced by the explicit coupling. Such difference can be reduced using a smaller time step size, as shown in Fig. 9, where the relative errors of the explicit cosimulation of the interval $t \in \left [0,0.5\right ]~{\mathrm{s}}$ using different step sizes are given. The relative errors of the implicit cosimulation scheme proposed in [7] (a maximum of 10 iterations is allowed, and the co-simulation tolerance is $1\times 10^{-6}$) are also plotted as a reference. In the figure the relative errors are computed using the ${L^{1}}$ norm [7]:

$$ {\left \| {{\mathrm{{error}}}} \right \|_{1}} = \dfrac{{\sum _{n = 0}^{N} {\left | {{x_{n}} - x\left ( {{t_{n}}} \right )} \right |}}}{\sum _{n = 0}^{N} {\left | {x\left ( {{t_{n}}} \right )} \right |}}, $$

(47)

where $x_{n}$ is the numerical solution at time $t_{n}$, and $x{\left (t_{n}\right )}$ is the theoretical solution at time $t_{n}$. The explicit cosimulation scheme using modified inputs approximately has the first-order accuracy as the implicit one. Table 1 reports the CPU times required by the different co-simulation schemes; an Intel i5-8300H CPU @ 2.30 GHz with 8G RAM is employed using only one thread. The table shows that the proposed explicit cosimulation scheme needs much less computation time than the implicit cosimulation one while offering comparable accuracy.

Fig. 8

Time histories of $x_{i}$ using the proposed explicit cosimulation schemes: (a) using original inputs, (b) using index-3 parameters of Eq. (46c), (c) using index-2 parameters of Eq. (46b), and (d) using index-1 parameters of Eq. (46a)

Fig. 9

Relative errors of the developed explicit co-simulation schemes: (a) relative position error; (b) relative velocity error

Table 1 CPU time (s) of different cosimulation schemes

In this subsection, we em[loy the two-mass oscillator with kinematic constraints to assess the stability of the cosimulation with different input formats. Stability plots are presented to show the effects of the modified inputs. The modified inputs can enlarge the stability region; using index-1 modified inputs, we obtain the largest stability region, although it still cannot guarantee the zero-stability of the explicit Gauss–Seidel cosimulation. This conclusion is verified by cosimulation results between MBDyn and Chrono, which also show that the original input format leads to unstable results. Besides, compared to the implicit co-simulation scheme [7], the explicit one is more efficient as we would expect, as it requires much less computational time to achieve comparable accuracy.

4.2 Double-pendulum system

Two bodies, one connected to the ground and both connected to each other by revolute joints, form a double pendulum system. For cosimulation, the system is decomposed at the revolute joint $O_{1}-O_{2}$ that connects the two bodies as shown in Fig. 10. One pendulum is modeled in MBDyn; the coordinates of point $C_{1}$ are employed as generalized coordinates, and the motion of $O_{1}$ is generated for another subsystem. In the other subsystem the displacements and rotations of point $C_{2}$ are employed as generalized coordinates, and the coupling constraints are imposed to point $O_{2}$. A reference frame at $O_{2}$, rigidly connected to the pendulum, is also established to describe whether the constraints are active, as shown in Fig. 10. In this reference, a revolute joint is set up by allowing rotation about axis $x$, whereas rotation about the other two axes and displacement along all three axes are constrained.

Fig. 10

Decomposition of a double-pendulum system

The system parameters are

$$ \textstyle\begin{array}{c@{\quad}c@{\quad}c@{\quad}c@{\quad}c} L=0.4~{\text{m}}, & m_{1}=m_{2}=1~{\text{kg}}, & {\mathbf{J}}_{C_{1}}={\mathbf{J}}_{C_{2}}={ \mathbf{E}}_{3}~{\text{kg}\,\text{m}^{2}}, & {\theta _{z,i}}=\dfrac{\pi}{2}, & {{ \dot{\theta}}_{z,i}}=0.5~{\text{rad}\,\text{s}^{-1}}, \end{array} $$

(48)

where $L$ and $m_{i}$ ($i=1,2$) are the length and mass of the bodies, ${\mathbf{J}}_{C_{i}}$ represents the moment of inertia with respect to point $C_{i}$, ${\mathbf{E}}_{3}\in{\mathbb{R}}^{3\times 3}$ is the identity matrix, ${\theta _{z,i}}$ and ${{\dot{\theta}}_{z,i}}$ denote the initial rotation and angular velocity about axis $z$ in the global reference. Using these parameters, the system is cosimulated by the proposed explicit cosimulation scheme with index-1, index-2, and index-3 parameters in Eqs. (46a)–(46c). The time histories of $\theta _{z,i}$ and ${\dot{\theta}}_{z,i}$ are shown in Fig. 11, where the monolithic simulation results obtained using MBDyn are plotted as references. The cosimulation results agree well with those obtained using the monolithic simulation. This example demonstrates that the developed explicit cosimulation scheme can effectively deal with coupled systems connected by a coupling revolute joint.

Fig. 11

Time histories of $\theta _{z,i}$ and ${\dot{\theta}}_{z,i}$ using the developed explicit cosimulation schemes: (a) $\theta _{z,1}$, (b) ${\dot{\theta}}_{z,1}$, (c) $\theta _{z,2}$, and (d) ${\dot{\theta}}_{z,2}$

4.3 Smooth system coupled with a nonsmooth particle damper

4.3.1 System description

An experimental setup used to test the amount of dam** provided by a particle damper (PD) is modeled and cosimulated in this section. The system shown in Fig. 12 consists of a crank-slider mechanism, a beam, a particle damper, and a sensor. One tip of the beam is connected to the slider of the slider-crank mechanism, which forces the transverse displacement of the beam. The PD is mounted at the other tip of the beam to limit its vibrations. A sensor is also attached at the location of the PD.

Fig. 12

Diagram of the smooth/nonsmooth coupled system with a particle damper

To numerically study the dynamical behavior of the setup in Fig. 12, a three-dimensional model is built. The system is decomposed into two subsystems at the constraints connecting the beam and the PD. After decomposition, the smooth subsystem is modeled in MBDyn, which consists of a crank-slider mechanism, a beam, and a sensor, whereas the nonsmooth subsystem consisting of a PD is modeled using the Chrono library.

In the smooth subsystem the crank-slider mechanism is modeled as three bodies: the crank, the connecting rod (rod 1), and the slider (rod 2), as shown in Fig. 12. A rheonomic constraint is imposed on the crank to enforce its rotation at constant angular velocity $\omega _{\mathrm{cra}}$, so that the crank-slider mechanism can drive the beam’s constrained end to move along axis $y$. To avoid constraint redundancy, the joint connecting the crank and rod 1 is modeled as a spherical hinge, and the joint between rod 1 and rod 2 is modeled as a revolute joint. Rod 2 is also constrained by a translation joint, which forces the rod to move along the guide. Besides, rod 2 is rigidly connected to the beam at one tip to excite the beam’s transverse displacement.

The beam is modeled in MBDyn using the original geometrically exact finite volume approach [47, 48]. It is meshed using 10 three-node beam elements for a total of 21 nodes. A linear elastic constitutive law is considered with no structural dam**. A PD is rigidly connected to the other end of the beam. The connection is represented by a joint that imposes all components of relative displacement and rotation.

The particles are treated as rigid three-dimensional spheres of identical size. Among the particles, nonsmooth interactions are modeled as frictional unilateral contacts using the nonsmooth formulation [29], which are solved using the Chrono library. The particles are collected in a cylindrical container and modeled as a rigid body. Its outer height is $H_{c}$. Its ceiling can be adjusted for different inner heights $H_{c_{in}}$, although only one is considered in the present work. Impacts and friction between particles and the container are described using unilateral frictional constraints. In the simulation the same dynamic and static friction coefficients $\mu _{p}$ are assumed for interparticle and particle–container interaction. Fully plastic impacts are considered.

The parameters of each body are indicated by the corresponding subscripts, as shown in Fig. 12, where $(\cdot )_{\mathrm{cra}}$, $(\cdot )_{1}$, $(\cdot )_{2}$, $(\cdot )_{b}$, $(\cdot )_{c}$, $(\cdot )_{p}$, and $(\cdot )_{s}$, respectively, represent the crank, rod 1, rod 2, the beam, the container of the PD, the particles, and the sensor. The mass, length, and density of a body are denoted by $m$, $l$, and $\rho$, where the mass of the particles refers to the total mass of all particles; $R_{r}$ is the radius of the crank, rod 1, and rod 2; $E_{b}$ and $\nu _{b}$ are Young’s modulus and Poisson’s ratio of the beam; $w_{b}$ and $h_{b}$ are the width and height of the beam cross-section; $R_{c}$ and $H_{c}$ are the base radius and the height of the container; $R_{p}$ is the particle radius; $J_{sx}$, $J_{sy}$, $J_{sz}$, $J_{cx}$, $J_{cy}$, and $J_{cz}$ are the diagonal elements of the inertia tensor of the bodies lumped at the free end of the beam, the subscripts $s$ and $c$ referring to the sensor and the particles’ container, respectively. The parameter values used in the analysis are listed in Table 2.

Table 2 Parameters for the smooth/nonsmooth coupled system with particle damper

As a reference, a simplified model is also simulated, as shown in Fig. 13, where the smooth subsystem is described by an equivalent single degree of freedom system, and the excitation $Y_{e}$ is obtained from the motion of the point that connects rod 2 and the beam. The equivalent mass and stiffness are obtained from [49] as

$$M_e=0.24m_b+m_{\mathrm{attach}},K_e=\frac{3E_b{I}_{bz}}{l_b^3},$$

(49)

where $m_{\mathrm{attach}}$ denotes the mass attached to the beam, including that of the sensor; ${I_{bz}=({w_{b}}{h_{b}^{3}})/12}$ is the moment of inertia of the beam cross-section. Since the beam is modeled with no structural dam**, the equivalent dam** ratio $C_{e}$ is zero. Using the parameters in Table 2, $M_{e} = 0.076742~{\text{kg}}$ and $K_{e} = 806.4~\text{N}/\text{m}$ are obtained.

Fig. 13

Simplified system with a particle damper

4.3.2 Simulation results

In the numerical experiments the proposed explicit cosimulation scheme between the smooth method in MBDyn and the nonsmooth method using the Chrono library is employed for solving the coupled system with a PD in Fig. 12. To obtain algorithmically stable numerical results, the modified inputs are used setting the coefficients $\alpha$, $\beta$, and $\gamma$ as in Eq. (22). The simplified system with a particle damper of Fig. 13 is simulated monolithically using the Chrono library to verify the results of the explicit cosimulation.

Initially, the crank-slider mechanism is set at the highest position, the crank and rod 1 being aligned with axis $y$. The initial angular velocity of the crank is $\omega _{\mathrm{cra}}=31.0\pi~\text{rad}/\text{s}$. A particle damper with inner height $H_{c_{in}}=11.84~\text{mm}$ is used, which is able to give satisfactory dam** for vibrations around the first natural frequency of the system, between 15 Hz and 16 Hz [7]. Considering the configuration of the crank-slider mechanism and its initial conditions, the excitation $Y_{e}$ in the simplified model can be expressed as

$$ {Y_{e}}=\sqrt{l^{2}_{1}-{l^{2}_{\mathrm{cra}}}{\cos ^{2}{\left (\omega _{ \mathrm{cra}}t+0.5\pi \right )}}}+{l_{\mathrm{cra}}}{\sin{\left (\omega _{\mathrm{cra}}t+0.5 \pi \right )}}+{l_{2}}, $$

(50)

where $t$ denotes the simulation time. Time step sizes for the explicit cosimulation scheme and the monolithic one are $\Delta t= 10^{-4}~{\mathrm{s}}$.

A case without particles is studied first, where the total mass of the particles is treated as a lumped mass attached to the beam’s end. In this case the natural frequencies of the beam with the particle mass lumped at the tip can be obtained by modal analysis [7], yielding the first three natural frequencies $15.619~{\text{Hz}}$, $127.460~\text{Hz}$, and $381.082~\text{Hz}$. In the numerical experiments, since the angular velocity is set as $\omega _{\mathrm{cra}}=31.0\pi~\text{rad}/\text{s}$, close to the first natural frequency, resonance is observed in the results, as shown in Fig. 14, where the $y$ component of displacement and velocity of the container are plotted. In the figure the solid black lines represent the results obtained with the coupled model using the explicit cosimulation scheme, and the red dashed lines show the results obtained with the monolithic simulation of the simplified model. These lines almost overlap, which further verifies the effectiveness of the explicit cosimulation scheme.

Fig. 14

Time histories of (a) displacement and (b) velocity, along axis $y$ of the container without particles

In the second case, we consider a particle damper filled with particles. The total mass of the particles and the properties of particles are listed in Table 2. All other conditions are the same as in the first case. The displacements and velocities of the container along axis $y$ are plotted in Fig. 15, where the results obtained from the simplified model without particles are also shown. We can see that the explicit cosimulation scheme predicts satisfactory results, which are very close to the monolithic simulation results. All these results indicate that the PD can effectively suppress the resonance of the beam when the excitation frequency is close to the first natural frequency of the beam. Besides, because of the chaotic motion of the particles, the symmetry of the problem is broken, and the beam twists, as shown in Fig. 16, where the rotation about axis $x$ and the torsional moment between the PD and the end of the beam are given. It follows that in the coupled model, small but not negligible and physically justified out-of-plane motion and torsional moment are caused by the activity of the particles in the PD, which, of course, cannot be observed when the simplified model is used.

Fig. 15

Time histories of (a) displacement and (b) velocity along axis $y$ of the container

Fig. 16

Time histories of (a) rotation about axis $x$ and (b) torsional moment in the coupled model

The explicit cosimulation schemes using the original inputs as in Eq. (20), the index-2 inputs as in Eq. (46b), and index-3 modified inputs as in Eq. (46c) are also used in the cosimulation, as shown in Fig. 17. The results show that index-1 modified inputs generate stable results, whereas the other schemes fail to obtain algorithmically stable results. Those results verify that the explicit cosimulation using index-1 inputs can improve the stability even in complex coupled systems.

Fig. 17

Time histories of the accelerations using different input formats

The proposed explicit cosimulation method is also compared with the implicit cosimulation scheme between MBDyn and Chrono presented in [7], which adopts an iterative process to improve the algorithmic stability of the cosimulation and exchanges contact forces/moments as coupling variables. In the implicit cosimulation the tolerance $\tilde{\varepsilon}$ for the coupling variables is set as $\tilde{\varepsilon} =0.001$, and up to 10 iterations are allowed within each step. The time step size $\Delta t=10^{-4}~{\mathrm{s}}$ is used in both cosimulation schemes, and all the other conditions are the same as in the last numerical experiment. The results for the smooth/nonsmooth coupled model from different cosimulation schemes are shown in Fig. 18, and the results for the simplified model are also plotted as a reference. We can see that the developed explicit cosimulation scheme predicts results very close to the implicit one. The computational cost of different cosimulation schemes during $t \in \left [0, 2\right ]~{\mathrm{s}}$ are listed in Table 3, where cosimulations were all run on an Intel i5-8300H CPU @ 2.30 GHz with 8G RAM and 4 threads. The CPU time denotes the amount of time that the CPU needs, whereas the elapsed time represents the actual wall clock time that the simulation requires; “Chrono CPU time” denotes the CPU time used by the nonsmooth solver; “Iterations” indicates the number of times the nonsmooth solver is called during cosimulation. It follows that under similar accuracy requirements, the proposed explicit cosimulation scheme can save almost three-quarters of the computational time required by the implicit cosimulation scheme because the nonsmooth solver is called just once for each discrete time, whereas the implicit approach requires the restart and reintegration of the nonsmooth subsystem at each step multiple times with an average of almost exactly three additional calls per time step. Therefore the explicit co-simulation scheme is recommended concerning computational cost, although the implicit one may show better stability in general applications.

Fig. 18

Zoom pictures of time histories of (a) displacement and (b) velocity along axis $y$ of the container using different cosimulation schemes

Table 3 Computational time of different cosimulation schemes

The explicit cosimulation scheme using the index-1 modified inputs is also able to deal with the coupled model when the stiffness of the beam is reduced. The thickness of the beam is reduced to 1 mm with the other parameters remaining as in Table 2. The equivalent mass and stiffness of the beam are

$$M_e=0.062621\text{kg},K_e=100.8\text{N}/\text{m},$$

(51)

which leads to a value for the first natural frequency of approximately $6.1~{\text{Hz}}$. The dynamic response to an excitation close to the first natural frequency, obtained by setting the angular velocity of the crank to $\omega _{\mathrm{cra}}=6.1 \times 2 {\pi}~\text{rad}/\text{s}$, is shown in Fig. 19. It follows that the results obtained using the cosimulation are consistent with those of the simplified model, which verifies the explicit cosimulation scheme. These results also indicate the ability of the PD to effectively produce dam** and suppress vibrations in the vicinity of the first natural frequency.

Fig. 19

Time histories of (a) displacement and (b) velocity along axis $y$ of the container

5 Conclusions

An explicit cosimulation scheme is developed between an implicit solver for differential-algebraic equations, implemented in MBDyn, and a nonsmooth solver based on cone complementarity problems, implemented as a user-defined element using Project Chrono libraries, to deal with coupled smooth/nonsmooth systems with constraints. At the constraints that connect subsystems, a force-displacement decomposition technique is employed to split the whole system into smooth and nonsmooth subsystems, where smooth subsystems output kinematic variables and receive reaction forces and moments as inputs, whereas nonsmooth subsystems receive kinematic variables as inputs and send reaction forces/moments as outputs.

To improve the stability of explicit cosimulation schemes and keep the details of the nonsmooth solver confined, the inputs to the nonsmooth subsystems are modified along the lines of Baumgarte’s stabilization technique and the properties of the integrator used in the nonsmooth solver. The modified inputs can be used to describe general coupling joints by modifying the motion of markers fixed to coupling bodies.

For the communication platform between MBDyn and Project Chrono, a loadable Chrono-Interface module has been developed in MBDyn using dynamic linking and run-time loading. The nonsmooth subsystems and interface functions are compiled as dynamical libraries that are run-time loaded into MBDyn.

Finally, a linear two-mass oscillator, a double pendulum system, and a smooth flexible system coupled with a nonsmooth particle damper are cosimulated using the explicit cosimulation scheme. For the two-mass oscillator, stability plots with the same system parameters but different input formats are also presented. It follows that using index-1 modified inputs, the largest stability region is achieved, whereas using the original inputs, algorithmically unstable results are obtained in most cases. The explicit cosimulation using various modified inputs is also compared to its implicit counterpart. The results show that explicit co-simulation requires less computational effort to obtain comparable accuracy. In the double pendulum system, cosimulation results agree well with those obtained using a monolithic simulation, which verifies that the explicit cosimulation scheme can deal with a generic coupling joint. In the system coupled with a particle damper, a simplified model of the smooth subsystem is also simulated for reference. The results of the coupled model using the explicit cosimulation scheme with index-1 modified inputs are consistent with those of the simplified model and of the coupled model using an implicit cosimulation scheme. Besides, the explicit cosimulation scheme requires much less time than the implicit one. Therefore the explicit cosimulation scheme is a better choice in terms of efficiency for solving the smooth/nonsmooth coupled systems.