Abstract
We define a class of Markovian parallel dynamics for spin systems on arbitrary graphs with nearest neighbor interaction described by a Hamiltonian function \(H(\sigma )\). These dynamics turn out to be reversible and their stationary measure is explicitly determined. Convergence to equilibrium and relation of the stationary measure to the usual Gibbs measure are discussed when the dynamics is defined on \(\mathbb {Z}^2\). Further it is shown how these dynamics can be used to define natively parallel algorithms to face problems in the context of combinatorial optimization.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
We introduce a class of parallel dynamics, called shaken dynamics, to study spin systems on arbitrary graphs \(G=(V, E)\) with general interaction given by
with \(J_{x y}\) and \(\lambda _{x}\) in \(\mathbb {R}\) for \(x, y \in V\), and \(\sigma \in \{-1,+1\}^{V}\) a configuration on G. The novelty of these dynamics is that transitions between configurations are obtained through a combination of pairs of half steps each characterized by an asymmetric interaction.
The shaken dynamics introduced here extend a class of PCA on spin systems, appeared in previous papers [7, 8, 14, 18], characterized by transition probabilities defined in terms of a pair Hamiltonian, i.e.
with \(H(\sigma ,\tau )=\sum _xh_x(\sigma )\tau _x\) and \(\beta =\frac{1}{T}\), where T is the temperature of the system. For each vertex x the local field \(h_x(\sigma )\) depends on the value of the spins in a neighborhood of x and on the value of the spin at site x itself through a self-interaction parameter \(q>0\). The dynamics considered in the aforementioned papers turn out to be reversible when the interaction with the spins in the neighborhood is symmetric and irreversible otherwise. On one hand, reversibility allows for a better control of the stationary measure. On the other hand, irreversible dynamics may exhibit a faster convergence to equilibrium (see, e.g., [8, 11]), though the control of the invariant measure is in general more complicated.
For the shaken dynamics we show that reversibility holds despite the presence of a non symmetric interaction. This fact allows for a rather robust control of the invariant measure on arbitrary graphs also in the case of non-zero external field and different choices of boundary conditions.
We study extensively the shaken dynamics on the square lattice. In this case we show that, for suitable values of the parameters, its stationary measure tends, in the thermodynamic limit, to the Gibbs measure with Hamiltonian (1). This result is complemented by a thorough numerical investigation carried over in [9]. Moreover, we analyze the convergence to equilibrium of the shaken dynamics in the low-temperature regime. We show that the asymmetric interaction induces a faster convergence with respect to symmetric PCA and single spin flip dynamics. In this respect, it is apparent that the shaken dynamics retains some of the properties of the irreversible PCA considered in [8, 14, 19]. Hence, shaken dynamics benefits of the advantages of both reversible and irreversible dynamics.
A notable feature of shaken dynamics is the fact that their invariant measure turns out to be the marginal of the Gibbs measure on an induced bipartite graph \(G^b\) whose geometry is related to that of the original graph G. Tuning the self-interaction parameter q tunes the geometry of \(G^b\). Leveraging on this feature we show how it is possible to control the critical behavior of the stationary measure of the shaken dynamics defined on the triangular lattice, extending, in this way, the analogous result provided in [1] for the square lattice.
It is worth mentioning that one of the main reasons of interest on PCA, and, in general, on parallel dynamics, is related to their numerical applications. Indeed, parallelization could, at least in principle, speed up Markov Chain Monte Carlo (see, e.g.,[10, 20]). Even though until a few years ago parallel computing was expensive and tricky, we have now powerful and cheap parallel architectures, for instance based on GPU or even FPGA. In this regard, we show how the class of shaken dynamics defined on general graphs provides a straightforward manner to define natively parallel Monte Carlo algorithms that can be used to tackle discrete optimization problems. Algorithms exploiting shaken dynamics are not bound to any particular computing architecture or graph structure and, hence, their performances are likely to benefit from the development of parallel computing often driven by applications not necessarily linked to academic research.
Shaken dynamics on general graphs are defined in Sect. 2. It is shown how a shaken dynamics on an arbitrary \(G=(V, E)\) is related to a dynamics on a corresponding bipartite graph \(G^b=(V^b, E^b)\) where spins in each partition are alternatively updated. Theorem 2.3 identifies the stationary measure of the shaken dynamics and shows that it is the marginal of the Gibbs measure on the configuration space \(\{-1, +1\}^{V^b}\). Section 3 is devoted to studying the shaken dynamics on \(\mathbb {Z}^2\) with homogeneous interaction. It is shown that, if the temperature of the system is sufficiently small, the invariant measure is close to the Gibbs measure for the Ising model on the square lattice. As far as convergence to equilibrium is concerned, the Section provides, in the low temperature regime, a comparison for the tunneling times from the metastable to the stable state between the shaken dynamics, a symmetric PCA and a single spin flip dynamics. Here theoretical results are complemented by numerical simulations. The result concerning the critical behavior for the shaken dynamics on the triangular lattice is provided in Sect. 4. In Sect. 5 the definition of shaken dynamics is generalized and Sect. 6 shows how these dynamics can be used in the context of combinatorial optimization. Proofs are provided in Sect. 7. Finally, Sect. 8 is devoted to final remarks including the possible applications of the shaken dynamics to model tidal dissipative effects in planetary systems.
2 Shaken Dynamics on General Graphs
Let \(G=(V,E)\) be a finite weighted graph and \(\mathcal{X}_V = \{-1,1\}^V\) be the set of spin configurations on V. We consider the nearest neighbor interaction between spins given by the Ising Hamiltonian in the general form:
where the weight \(J_{xy} \in \mathbb {R}\) associated to the edge \(\{x,y\}\), represents the interaction, and can be written in compact form as a symmetric matrix \(\mathcal{J}\) and we denote by \(\langle \cdot ,\cdot \rangle \) the scalar product. The vector \(\lambda =\{\lambda _x\}_{x\in V}\) is an external field, possibly non constant.
We introduce a class of bipartite weighted graphs \(G^b=(V^b,E^b)\) doubling the interaction graph G. The idea is to duplicate the vertex set into two identical copies, \(V^{(1)}\) and \(V^{(2)}\), representing the two parts of the vertex set of the bipartite graph. For each \(x\in V\) we denote by \(x^{(1)}, x^{(2)}\) the vertices corresponding to \(x\in V\) in \(V^{(1)}\) and in \(V^{(2)}\) respectively. The edges between \(x^{(1)}\) and \(x^{(2)}\) are all present, for any \(x\in V\). On the other hand the edges between \(x^{(1)}\) and \(y^{(2)}\), with \(x\not = y\), or between \(y^{(1)}\) and \(x^{(2)}\), can be present only if \(\{x,y\}\in E\). Exactly one edge among the two possibilities \((x^{(1)},y^{(2)})\) and \((y^{(1)},x^{(2)})\) is in \(E^b\) if \(\{x,y\} \in E\). This means that for any graph G there are many doubling graphs \(G^b\). Note that similar doubling graphs have already been introduced in literature for different purposes (see [13]). More precisely:
Definition 2.1
A bipartite weighed graph \(G^b=(V^b, E^b)\) is the doubling graph of \(G=(V,E)\) if
-
the vertex set \(V^b=V^{(1)}\cup V^{(2)}\) where the two parts \(V^{(1)}\) and \(V^{(2)}\) are two identical copies of V;
-
for any \(x\in V\) the edge \((x^{(1)}, x^{(2)})\in E^b\) and we call it a self-interaction edge;
-
if \(\{x,y\} \in E\) then one, and only one, between the two edges \(\{x^{(1)}, y^{(2)}\}\) and \(\{y^{(1)}, x^{(2)} \}\) is in \(E^{b}\). We call this kind of edge an interaction edge.
To construct a doubling graph starting from the interaction graph \(G=(V,E)\), define a new oriented graph \(G^o=(V, E^o)\) simply orienting the edges in an arbitrary way. Using the oriented edges the set \(E^b\) is constructed as follows. For any \(x\in V\) we have the self-interaction edge \((x^{(1)}, x^{(2)})\in E^b\) with weight \(w(x^{(1)}, x^{(2)})=q\) and for \(x\not =y\in V\) we have \((x^{(1)}, y^{(2)})\in E^b\) if and only if \((x,y)\in E^o\) with weight \(w(x^{(1)}, y^{(2)})=J_{xy}\).
Note that the edges in \(E^b\) are not oriented. However, by construction, the graph is bipartite, so that for any \(e=\{x,y\}\in E^b\) we have \(x\in V^{(1)}, y\in V^{(2)}\) or viceversa and so we consider in the definition the natural order in the edges in \(E^b\) by setting \(e=(e^{(1)}, e^{(2)})\) with \(e^{(1)}\in V^{(1)}, e^{(2)}\in V^{(2)}\). For this reason we can use the oriented edges in \(E^o\) in order to define \(E^b\).
We will sometimes omit the superscripts \(^{(1)}\) and \(^{(2)}\) and we will always consider (x, y) the ordered pair with \(x\in V^{(1)}, \; y\in V^{(2)}\), and \(\{x,y\}\) the unordered pair with \(x,y\in V^b\).
Definition 2.2
The pair Hamiltonian \(H(\sigma ^{(1)},\sigma ^{(2)})\) is the doubling of the Hamiltonian (2) with interaction graph G if there exists a doubling graph \(G^b=(V^b,E^b)\) of G such that \(H({\varvec{\sigma }})\), defined on the spin configurations \({\varvec{\sigma }}\equiv (\sigma ^{(1)},\sigma ^{(2)})\in \mathcal{X}_{V^b} = \{-1,1\}^{V^b}\), can be written as
with \(w(x,y)=q > 0\) if \(\{x,y\}\) is a self interaction edge and \(w(x,y)=J_{xy} \in \mathbb {R}\) otherwise and with \(\lambda _{x^{(1)}}=\lambda _{x^{(2)}}=\lambda _x \in \mathbb {R}\).
In a more explicit way we can write
with
and
By defining \({\mathcal{J}^o}\) the matrix of oriented interaction, i.e., \({\mathcal{J}^o}_{xy}= J_{xy}\mathbb {1}_{(x,y)\in E^o}\), and its transposed \({\mathcal{J}^o}^T\) corresponding to the opposite orientation, we can write
and
If we consider the case \(\sigma ^{(1)}=\sigma ^{(2)}=\sigma \), i.e., \(\sigma ^{(1)}_x=\sigma ^{(2)}_x\) for any \(x\in V\), then we have \(H({\varvec{\sigma }}) \equiv H(\sigma ,\sigma )=H(\sigma )- q|V|\). Indeed we have immediately \(\mathcal{J}={\mathcal{J}^o}+{\mathcal{J}^o}^T\).
We construct now the shaken dynamics on the state space \(\mathcal{X}_V\) by considering two subsequent updating defined as follows:
We state the result on the shaken dynamics in this general context.
Theorem 2.3
The stationary measure of the shaken dynamics is
and reversibility holds. This stationary measure is the marginal of the Gibbs measure on the space \(\mathcal{X}_{V^b}\) of pairs of configurations \({\varvec{\sigma }}:=(\sigma ^{(1)},\sigma ^{(2)}) \) defined by:
The shaken dynamics on \(\mathcal{X}_{V}\) corresponds to an alternate dynamics on \(G^b\) in the following sense
with
the stationary measure of \(P^{alt}\) is \({{\pi ^b}}({\varvec{\sigma }})\). Note that \(P^{alt}\) is independent of \(\sigma ^{(2)}\). This dynamics is in general non reversible.
3 The Shaken Dynamics on \(\mathbb {Z}^2\)
Let \(\Lambda \) be a two-dimensional \(L\times L\) square lattice in \(\mathbb {Z}^2\) and let \(\mathcal{B}_\Lambda \) denote the set of all nearest neighbors in \(\Lambda \) with periodic boundary conditions.
In \(\Lambda \) we identify a set B where the value of the spins is frozen throughout the evolution and that plays the role of boundary conditions. This means that we will consider the state space \(\mathcal{X}_{\Lambda ,B}=\{\sigma \in \mathcal{X}_\Lambda :\; \sigma _x=+1\quad \forall x\in B\}\).
Following the construction of the shaken dynamics of the previous section we can define
where \(x^{\uparrow }, x^{\rightarrow }, x^{\downarrow }, x^{\leftarrow }\) are, respectively, the up, right, down, left neighbors of the site x on the torus \((\Lambda ,\mathcal{B}_\Lambda )\), \(J>0\) is the ferromagnetic interaction, \(q>0\) is the inertial constant and \(\lambda \) represents the external field. We can write
where the local up-right field \(h^{ur}_x(\tau )\) due to the configuration \(\tau \) is given by
and the local down-left field \(h^{dl}_x(\sigma )\) due to the configuration \(\sigma \) is given by
Define the asymmetric updating rule
Due to the definition of the pair Hamiltonian, the updating performed by the transition probability \(P^{dl}(\sigma ,\tau )\) is parallel: given a configuration \(\sigma \), at each site \(x\in \Lambda \) the spin \(\tau _x\) of the new configuration \(\tau \) is chosen with a probability proportional to \(e^{\beta h^{dl}_x(\sigma )\tau _x}\) so that
We have \(H(\sigma ,\tau )\not =H(\tau ,\sigma )\) and actually, by (13), \(H(\tau ,\sigma )\) corresponds to the opposite direction of the interaction for the transition from \(\sigma \) to \(\tau \). We define
Similarly for \(P^{ur}(\sigma ,\tau )\) with the up-right field \(h^{ur}_x(\sigma )\) we get
Note that in the definition of \(H(\sigma ,\tau )= - \sum _{x \in \Lambda }\tau _x h^{dl}(\sigma ) - \lambda \sum _{x \in \Lambda }\sigma _x\) the last term could be canceled obtaining the same value for the transition probability \(P^{dl}(\sigma ,\tau )\). However we added it in the pair Hamiltonian for symmetry reasons: in particular the fact that \(H(\tau ,\sigma )\) is the correct pair Hamiltonian to define \(P^{ur}(\sigma ,\tau )\) is due to this symmetry. Note also that
where we define \(H(\sigma )\) to be the usual Ising Hamiltonian with magnetic field \(2\lambda \)
We define
Reversing the order of the “down–left” and the “up–right” updating rules one would obtain the chain with transition probabilities
Clearly, by choosing a different orientation instead of down-left and up-right in \(\mathbb {Z}^{2}\), a different pair Hamiltonian can be obtained with a resulting different graph for the interaction.
In this square case we could have directly used the alternate dynamics, since \(\mathbb {Z}^2\) is already a bipartite graph. Indeed we can consider the checkerboard splitting of the sites in \(\Lambda =V^{(1)}\cup V^{(2)}\), in black and white sites, with \(|V^{(1)}|=|V^{(2)}|=|V|=|\Lambda |/2\). Black sites interact only with white sites and viceversa with the usual Ising Hamiltonian
By Theorem 2.3 we immediately obtain that the invariant measure of the alternate dynamics is the Gibbs measure \(\pi ^G({\varvec{\sigma }})=e^{-\beta H({\varvec{\sigma }})}/Z\). The idea of alternate dynamics on even and odd sites is already present in the literature (see [5]).
3.1 Relation with the Gibbs Measure
Remaining in \(\Lambda \in \mathbb {Z}^2\) with \(J>0\) and \(B=\emptyset \), i.e. with the standard periodic boundary conditions, we denote the invariant measure of the shaken dynamics \(\pi _{\Lambda } =\frac{\overrightarrow{Z}_\sigma }{Z}\).
Let \(\pi _{\Lambda }^G\) be the Gibbs measure
with \(H(\sigma )\) defined in (18) and we define the total variation distance, or \(L_1\) distance, between two arbitrary probability measures \(\mu \) and \(\nu \) on \(\mathcal{X}_{\Lambda , B}\) as
In the following Theorem 3.1 we control the distance between the invariant measure of the shaken dynamics and the Gibbs measure at low temperature (large \(\beta \)). We notice that this theorem is an extension of Theorem 1.2 in [18] to the case of Hamiltonian with the non zero external field. This result could be extended to the case \(B \ne \emptyset \).
Theorem 3.1
Set \(\delta =e^{-2\beta q}\), and let \(\delta \) be such that
Under the assumption (22), there exists \(\bar{J}\) such that for any \(J>\bar{J}\)
3.2 Convergence to Equilibrium: A Comparison
For the Ising model on the finite \(L \times L\) box \(\Lambda \subset \mathbb {Z}^2\) with periodic boundary conditions, consider now the regime \(0< \lambda < J\) and very low temperature, i.e. \(\beta \gg 1\). This is usually called “metastable regime”. Indeed the configuration \(-\mathbb {1}\) with all spins \(-1\) represents, in this regime of low temperature, a metastable state, while the configuration \(+\mathbb {1}\) with all positive spins, parallel to the external field \(\lambda \), represents the stable state, where the Gibbs measure concentrates in the limit \(\beta \rightarrow \infty \). We will call tunneling time \(\tau _{+\mathbb {1}}\) the first hitting time to \(+\mathbb {1}\) starting from \(-\mathbb {1}\).
We compare here the tunneling times for different dynamics: the single spin flip (SSF) dynamics, the PCA dynamics and the shaken dynamics (Sh) with \(q < \lambda \).
More precisely consider, for each \(x \in \Lambda \), the local fields
\(h^{dl}_x(\sigma )\) and \(h^{ur}_x(\sigma )\) defined in (15) and (14), and the local transition probabilities
Denote by \(\sigma ^x\) the configuration obtained from \(\sigma \) by flip** the spin at site x and by \(\chi _{\{A\}}\) the indicator function of event A. Then, the three dynamics under consideration, have the following transition probabilities:
The SSF dynamics is reversible with Gibbs invariant measure
and the invariant measure of PCA and shaken dynamics are, respectively,
Note that, in the case \(\frac{J}{2}=q\), the dynamics defined via the transition probabilities \(P^{PCA}\) turns out to be the same as the cross PCA dynamics introduced in [6] and it is possible to show that the measure \(\pi _{PCA}\) and the Gibbs-like measure with Hamiltonian \(H(\sigma )\) defined in [6, Equation (2.5)] coincide.
All these measures, in the regime of large \(\beta \), concentrate on the stable state \(+\mathbb {1}\). This is proven for \(\pi (\sigma )_{PCA}\) in [6] and it is immediate for the Gibbs measure. For the shaken dynamics this follows by noting that, for all \(\sigma \ne +\mathbb {1}\),
and, hence
For large inverse temperature \(\beta \) we have \(p^*_x(\sigma ,\tau )\sim 1\) if \(\tau _x\) is parallel to the local field \(h^*_x(\sigma )\). We call such a local move “along the drift”. On the other hand \(p^*_x(\sigma ,\tau )\sim e^{-2\beta |h^*_x(\sigma )|}\) if \(\tau _x\) is anti-parallel to the local field \(h^*_x(\sigma )\). We call such a local move “against the drift”.
Let \(\lambda < J\). For the SSF dynamics we have for any \(\delta >0\) (see for instance [3, 17]):
with
and critical size \(\ell _c=\big [\frac{J}{\lambda }\big ]+1\), where \(\big [\cdot \big ]\) denotes the integer part. The typical exit paths from the metastable state \({-\mathbb {1}}\) follow a sequence of growing squares and rectangles (quasi squares) of plus spins up to the critical size \(\ell _c\). Starting from a rectangular droplet of plus spins a move against the drift is necessary to create a new line, and the line is completed with subsequent moves along the drift.
A similar result for the PCA dynamics is proven in [6] in the case \(q=\frac{J}{2}\). In particular, the typical exit paths follow the same growth mechanism of the SSF dynamics since moves along the drift lead to rectangular droplets of plus spins and parallel updates against the drift do not take place with high probability for \(\beta \) large (see [6, Sect. 2.7] for a detailed discussion).
A different growth takes place in the case of shaken dynamics. Indeed using an argument inspired by [8] it is simple to prove that configurations with complete diagonals of plus spins can be used to construct a efficient way to go from the metastable to the stable state.
We have the following
Theorem 3.2
For any \(\delta >0\) and \(0< q< \lambda < J\)
This means that the crossover takes place for the shaken dynamics, typically, within a time corresponding to the time it takes, for the SSF and PCA, to flip the first spin to \(+1\).
Moreover we can define an event characterizing the tube of typical paths from the metastable state \(-\mathbb {1}\) to the stable state \(+\mathbb {1}\). Actually we prove Theorem 3.2 by using this event.
We need some notation. Denote by \(X^{Sh}_t\) the evolution of the shaken dynamics and let \(\tau _{-\mathbb {1}^c}=\inf \{t>0:X^{Sh}_t\not = {-\mathbb {1}}\} \) be the time of the first spin flip, starting from \(-\mathbb {1}\). We denote a site \(x\in \Lambda \) as \(x=(i,j)\) with \(i,j=1,...,L\) and for each \(k=1,...,L\) we define a diagonal \(D_k\subset \Lambda \) as the set of sites forming a diagonal in the up-left to down-right direction on the torus (i.e., with periodic boundary condition):
Let \(\mathcal{{D}}\) be the set of configurations where each up-left to down-right diagonal has all spins with the same sign:
Note that \(-\mathbb {1}, +\mathbb {1}\in \mathcal {D}\). For notation convenience we identify a configuration \(\sigma \in \mathcal{{D}}\) with the set of indices of diagonals with positive spins, i.e., with a subset of \(\{1,2,...,L\}\) denoted by \(I_\sigma \). We say that \(m\not \in I_\sigma \) is nearest neighbor of \(I_\sigma \) if there exists \(n\in I_\sigma \) with \(|n-m|=1\). Given \(\sigma ,\sigma '\in \mathcal {D}\) we say that \(\sigma '\) increases \(\sigma \) if \(I_{\sigma '}\supset I_\sigma \) and their difference \(I_{\sigma '}\backslash I_\sigma \) is a single integer m nearest neighbor of \(I_\sigma .\)
Starting from \(-\mathbb {1}\) define the sequence of strong times \(\{s_i, t_i\}_{i=1,2,\ldots }\) as follows: \(t_0=0\) and for any \(i=1,2,..\)
Fix an arbitrarily small positive \(\delta \) and define \(T_\delta =e^{2\beta [(2J + q-\lambda )+\delta ]}\) and the following event
We have
Theorem 3.3
For any \(\delta >0\)
Clearly the event \(\mathcal{{T}}\) implies the event \(\tau _{+\mathbb {1}}<T_\delta \), so Theorem 3.2 is established by proving Theorem 3.3.
The asymmetric nature of the interaction gives the shaken dynamics a higher mobility with respect to its symmetric counterpart (“standard” PCA). This is the reason of shorter tunneling times. Evidence of this fact, in the regime \(0< q< \lambda < J\), is provided by the numerical experiment whose results are summarized in Figure 4. For both the PCA and the shaken dynamics the simulations are started in configuration \(-\mathbb {1}\) and the value of the average magnetization is tracked. Simulations are run for several values of the inverse temperature \(\beta \). It is immediately clear that, for the shaken dynamics, the tunneling towards a state is much faster. Note also that this higher mobility causes a slightly smaller magnetization at equilibrium for finite \(\beta \).
A similar behavior has been highlighted in [14, 15] where a comparison between the symmetric PCA and an irreversible PCA with totally asymmetric interaction has been performed in the case \(\lambda = 0\). In the case of null magnetic field, if the value of the inverse temperature \(\beta \) is large but finite, the system exhibits, both in the case of PCA dynamics and shaken dynamics, a (positive or negative) spontaneous magnetization. On short time scales the system stays in one “phase” (e.g. it is negatively magnetized) whereas, on longer time scales, it tunnels rapidly towards the other phase. However, since the value of the spontaneous magnetization is neither exactly \(-1\) or \(+1\), choosing the right parameters to compare the two dynamics, as far as tunneling time is concerned, may be a somewhat delicate matter. To make a fair comparison of the tunneling times we tuned the parameters of the PCA and the shaken dynamics so to have similar values for the (average) spontaneous magnetization. The results of the experiment are summarized in Figure 5 where the average magnetization over time is represented for both dynamics. It is evident that, also in this case, the shaken dynamics has considerably more mobility than the PCA. As far as the tunneling behavior is concerned, the shaken dynamics retains, essentially, the same features of the irreversible PCA considered in [15]. However, it is to remark that, in the case of the shaken dynamics, reversibility allows to manage the invariant measure more easily.
Comparison of the evolution of the magnetization for a spin system evolving according to a shaken dynamics (black) and according to a symmetric PCA (red). The values of the parameters are such that both dynamics exhibit the same spontaneous magnetization and are consistent with those of [15] (Color figure online)
4 Geometrical Discussion
In the shaken dynamics the idea of alternate dynamics is combined with that of the doubling Hamiltonian. Indeed considering only part of the interaction (for instance down-left first and then up-right in the case of \(\Lambda \in \mathbb {Z}^2\) presented at the beginning of the section) and introducing the inertial parameter of self interaction q it is possible to interpolate between different lattice geometries induced by the doubling graph as already discussed in [1].
Indeed the alternate dynamics on the hexagonal lattice makes possible to interpolate between the square (\(q\rightarrow \infty \)) and the 1-dimensional lattice (\(q\rightarrow 0\)). The interpolation between lattices induced by the shaken dynamics may be applied in general (see, e.g., [21] for an application to the 3d cubic lattice), and in the case of planar graphs the results concerning the critical behavior contained in [1] can be extended, using [4].
Consider for instance the Ising model on the triangular lattice. On this lattice we divide the 6 nearest neighbors of each vertex x into two sets, e.g. \(\ell (x)\) left and r(x) right nearest neighbors of x, and define a shaken dynamics with self interaction q. Hence the doubled Hamiltonian is
The corresponding alternate dynamics turns out to be defined on the square lattice (see Fig. 6) with invariant measure the Gibbs one. In particular the square lattice is regular when we set \(J=q\). In this case the parameter q can be used to move through different geometries. The triangular lattice (\(q\rightarrow \infty \)) and the hexagonal lattice (\(q = 0\)) can be derived from the original square lattice just tuning the value of q. A more precise statement of this interpolation is given by the following
Theorem 4.1
For the shaken dynamics on the triangular lattice the critical equation relating the parameters J and q is given by
In the case \(q=J\) we obtain the Onsager critical temperature for the square lattice, for \(q = 0\) we obtain the critical temperature for the hexagonal lattice and in the limit \(q \rightarrow \infty \) we obtain the critical temperature for the triangular lattice.
Interaction in the pair Hamiltonian for the shaken dynamics on the triangular lattice. Each spin of configuration \(\sigma \) (living on the solid lattice) interacts with the spin at the same location and the three spins on its left in \(\tau \) (living on the dashed lattice). The darker lines show that the pair interaction lives on a rectangular lattice. For \(q = J\) this lattice becomes the square one. As \(q \rightarrow \infty \) the square lattice collapses onto the triangular lattice. If \(q = 0\) the interaction graph becomes the homogeneous hexagonal lattice
5 The Generalized Shaken Dynamics
We can generalize the construction of the shaken dynamics. Starting from a symmetric interaction \(\mathcal{J}\) defining the Hamiltonian \(H(\sigma )\), as in (2), we can define an arbitrary decomposition of the interaction matrix \(\mathcal{J}\) in a sum of two matrices with non negative entries
This means that every non oriented edge \(\{x,y\}\) with weight \(J_{xy}\) is decomposed in a pair of oriented edges (x, y) and (y, x) with weight respectively \(\mathcal{J}^o_{xy}\) and \(\mathcal{J}^o_{yx}\). Call \(E^o\) the set of all these oriented edges and apply the construction presented in Sect. 2 to construct the doubling graph by using this set \(E^o\) of oriented edges.
We proceed as before defining the doubling Hamiltonian
In the case \(\sigma ^{(1)}=\sigma ^{(2)}=\sigma \) by equation (27) we have again \(H(\sigma ,\sigma )=H(\sigma )-q|V|\).
The corresponding alternate dynamics on the state space \(\mathcal{X}_V\) is defined with two subsequent updating as follows:
and
The results obtained in Theorem 2.3 can be immediately extended to this more general case.
The choice of the shaken dynamics discussed in Sect. 2 is a particular case of generalized shaken dynamics in which \(\mathcal{J}^o_{xy}\mathcal{J}^o_{yx}=0\) for any pair x, y. In the general case the geometrical discussion of the doubling graph of interaction is much more complicated. Also the interpolation between different geometries obtained for different values of the parameter q, as discussed in Sect. 3, is more involved in this generalized case.
Another particular choice in this class of generalized shaken dynamics is \(\mathcal{J}^o=\frac{1}{2}\mathcal{J}\) corresponding to the PCA discussed in [7].
6 Application to Optimization Problems
The shaken dynamics on a general graph, and its generalization, gets the possibility to look for the minimum of a general Hamiltonian \(H(\sigma )\) defined on \(\{-1, +1\}^V\) by means of a parallel dynamics, by using the following result that could be considered a corollary of Theorem 2.3. In combinatorial optimization this can be used as a parallel approach to the Quadratic Unconstrained Binary Optimization (QUBO) i.e., the problem of minimizing a quadratic polynomial of binary variables (see [12] for a survey).
Theorem 6.1
Consider a Hamiltonian \(H(\sigma )\) of the form given in (2) on \(\{-1, +1\}^V\), for any doubling Hamiltonian \(H(\sigma ,\tau )\) defined in (3), corresponding to a bipartite graph \(G^b=(V^b, E^b)\).
-
(1)
If
$$\begin{aligned} q>\max _{x\in V}\Big \{ \sum _{y: \{x,y\}\in E^b}|J_{xy}|+|\lambda _x| \Big \} \end{aligned}$$(31)then the alternate dynamics defined with \(H(\sigma ,\tau )\) is a parallel algorithm to find configurations \(\sigma \) minimizing \(H(\sigma )\).
-
(2)
For any positive q the alternate dynamics defined with \(H(\sigma , \tau )\) is a parallel algorithm to find a lower bound for \(\min _{\sigma } H(\sigma )\).
To assess the effectiveness of the strategy presented in Theorem 6.1, we put forward some preliminary tests on a simplified version of the Edwards-Anderson model where the weight of the edges connecting neighboring sites is set to \(J=+1\) with probability \(\frac{1}{2}\) and \(J=-1\) with probability \(\frac{1}{2}\) and where the external field is zero. In this case, setting \(q>2\) is sufficient to satisfy the hypotheses of the corollary. We compared the results with those obtained with a single spin flip heat bath dynamics and considered “grids” with side length 128 and 256. With this setting, the heuristic minima that we obtained with the shaken dynamics are essentially equivalent to those obtained with the single spin flip dynamics. However the speed up with respect to the single spin flip dynamics was significant. To be as fair as possible in this comparison, we renormalized the time of the single spin flip dynamics with the number of vertices in the graph so to have the same number of “attempted spin flips”. We observed a speed-up of about 10 times when considering, for both algorithms, a CPU implementation and up to 200 times when comparing the CPU implementation of the single spin flip dynamics with a GPU implementation of the shaken dynamics. These findings are in agreement with Theorem 3.2.
7 Proofs of the Results
7.1 Proof of Theorem 2.3
We have immediately the detailed balance condition w.r.t. the measure \(\pi (\sigma )\) indeed
It is straightforward to prove that \({\pi ^b}(\sigma ^{(1)},\sigma ^{(2)})\) is the stationary measure of \(P^{alt}\)
\(\square \)
Note that, in general
For instance consider the bipartite graphs \(K_{n,n}\) with equal weights on all edges and where, for all i, \((\sigma _{i}^{(1)}, \sigma _{i}^{(2)}) = (+1, +1)\) and \((\tau _{i}^{(1)}, \tau _{i}^{(2)}) = (+1, -1)\).
7.2 Proof of Theorem 3.1
To prove Theorem 3.1 it is possible to argue as in the proof of Theorem 1.2 in [18].
In our notation \(\pi _{\Lambda }\) and \(\pi _{\Lambda }^G\) have the role, respectively, of \(\pi _{PCA}\) and \(\pi _{G}\) used in [18]. Further let \(g_{x}(\sigma ) := J(\sigma _{x^{\downarrow }} + \sigma _{x^{\leftarrow }})\) be the analogue of \(h_i(\sigma )\) in [18]. Here we assume \(\lambda < 0\). The case \(\lambda > 0\) can be treated likewise.
Recalling that \(\delta = e^{-2 \beta q}\), it is possible to write \(\overrightarrow{Z}_{\sigma }\) in the following way:
where the sum over \(\tau \) has been rewritten as the sum over all subsets \(I \subset \Lambda \) such that \(\tau _x = -\sigma _x\) if \(x \in I\) and \(\tau _x = \sigma _x\) otherwise. The factor \(e^{\beta q|\Lambda |}\) does not depend on \(\sigma \) and cancels out in the ratio \(\frac{\overrightarrow{Z}_{\sigma }}{Z}\).
Call \(f(\sigma ) := \prod _{x \in \Lambda }(1 + \delta e^{-\beta (2g_{x}(\sigma )\sigma _x + 2\lambda \sigma _{x})})\), \(w(\sigma ) := e^{-\beta H(\sigma )}f(\sigma )= w^{G}(\sigma )f(\sigma )\). Then, by (34), it follows
with \(\pi _{\Lambda }^G(f) = \sum _{\sigma } \pi _{\Lambda }^G(\sigma )f(\sigma )\).
As in [18], using Jensen’s inequality the total variation distance between \(\pi _{\Lambda }\) and \(\pi _{\Lambda }^G\) can be bounded as
To prove the theorem, it will be shown that \(\Delta (\delta ) = O(\delta ^2|\Lambda |)\).
By writing \(\Delta (\delta ) = e^{\log (\pi _{\Lambda }^G(f^2)) - 2\log (\pi _{\Lambda }^G(f))} - 1,\) the claim follows by showing that the argument of the exponential divided by \(|\Lambda |\) is analytic in \(\delta \) and that the first order term of its expansion in \(\delta \) cancels out.
In other words the claim follows thanks to the following lemma.
Lemma 7.1
There exists \(J_{c}\) such that, for all \(J > J_{c}\)
-
1.
\(\frac{\log (\pi _{\Lambda }^G(f^2))}{|\Lambda |}\) and \(\frac{\log (\pi _{\Lambda }^G(f))}{|\Lambda |}\) are analytic in \(\delta \) for \(|\delta | < \delta _{J}\)
-
2.
\(\frac{\log (\pi _{\Lambda }^G(f^2))}{|\Lambda |} - 2\frac{\log (\pi _{\Lambda }^G(f))}{|\Lambda |} = O(\delta ^{2})\)
Proof
The analyticity of \(\frac{\log (\pi _{\Lambda }^G(f^2))}{|\Lambda |}\) and \(\frac{\log (\pi _{\Lambda }^G(f))}{|\Lambda |}\) is proven by showing that these quantities can be written as partition functions of an abstract polymer gas. The analyticity is obtained using standard cluster expansion.
To carry over this task, we will rewrite \(\pi _{\Lambda }^G(f^{k})\) in terms of standard Peierls contours. Divide the sites in \(\Lambda \) according to the value of the spins and number of edges of the Peierls contour left and below the site in the following way:
-
 : \(\{x \in \Lambda : \sigma _{x} = -1 \wedge (\sigma _{x^{\leftarrow }}= -1, \sigma _{x^{\downarrow }}= -1)\}\);
: \(\{x \in \Lambda : \sigma _{x} = -1 \wedge (\sigma _{x^{\leftarrow }}= -1, \sigma _{x^{\downarrow }}= -1)\}\); -
 : \(\{x \in \Lambda : \sigma _{x} = -1 \wedge ((\sigma _{x^{\leftarrow }}= +1, \sigma _{x^{\downarrow }}= -1) \vee (\sigma _{x^{\leftarrow }}= -1, \sigma _{x^{\downarrow }}= +1))\}\);
: \(\{x \in \Lambda : \sigma _{x} = -1 \wedge ((\sigma _{x^{\leftarrow }}= +1, \sigma _{x^{\downarrow }}= -1) \vee (\sigma _{x^{\leftarrow }}= -1, \sigma _{x^{\downarrow }}= +1))\}\); -
 : \(\{x \in \Lambda : \sigma _{x} = -1 \wedge \sigma _{x^{\leftarrow }}= +1, \sigma _{x^{\downarrow }} = +1\}\);
: \(\{x \in \Lambda : \sigma _{x} = -1 \wedge \sigma _{x^{\leftarrow }}= +1, \sigma _{x^{\downarrow }} = +1\}\); -
 : \(\{x \in \Lambda : \sigma _{x} = +1 \wedge (\sigma _{x^{\leftarrow }}= +1, \sigma _{x^{\downarrow }}= +1)\}\);
: \(\{x \in \Lambda : \sigma _{x} = +1 \wedge (\sigma _{x^{\leftarrow }}= +1, \sigma _{x^{\downarrow }}= +1)\}\); -
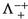 : \(\{x \in \Lambda : \sigma _{x} = +1 \wedge ((\sigma _{x^{\leftarrow }}= +1, \sigma _{x^{\downarrow }}= -1) \vee (\sigma _{x^{\leftarrow }}= -1, \sigma _{x^{\downarrow }}= +1))\}\);
: \(\{x \in \Lambda : \sigma _{x} = +1 \wedge ((\sigma _{x^{\leftarrow }}= +1, \sigma _{x^{\downarrow }}= -1) \vee (\sigma _{x^{\leftarrow }}= -1, \sigma _{x^{\downarrow }}= +1))\}\); -
 : \(\{x \in \Lambda : \sigma _{x} = +1 \wedge (\sigma _{x^{\leftarrow }}= -1, \sigma _{x^{\downarrow }}= -1)\}\);
: \(\{x \in \Lambda : \sigma _{x} = +1 \wedge (\sigma _{x^{\leftarrow }}= -1, \sigma _{x^{\downarrow }}= -1)\}\);
With this notation, \(f(\sigma )\) can be written as

with

For a given a configuration \(\sigma \in \mathcal{X}_{\Lambda }\), we denote by \(\gamma (\sigma )\) its Peierls contour in the dual \(\mathcal{B}_\Lambda ^*=\cup _{(x,y)\in \mathcal{B}_\Lambda }(x,y)^*\)
Noting that \(e^{-\beta H(\sigma )} = e^{(2J - 2\lambda )\beta |\Lambda |} e^{-2\beta J|\gamma (\sigma )| +4\beta \lambda |V_{+}(\sigma )|}\), with \(|V_{+}(\sigma )| = \sum _{x \in \Lambda } 1_{\{\sigma _{x} = +1\}}\) is the number of plus spins in \(\Lambda \) of configuration \(\sigma \), we have
Setting

allows us to write, for \(k \in \{1, 2\}\),
A straightforward computation yields \(\xi (\sigma , \lambda )^k \le \xi (\sigma , 0)^k\) and then
where \(\xi (\gamma , 0)^k\) coincides with \(\xi ^I_k(\Gamma )\) in the proof of Lemma 2.3 in [18], with  and
and  .
.
This implies that the proof can be concluded following the same steps as in [18]. \(\square \)
7.3 Proof of Theorem 3.3
Starting from \(-\mathbb {1}\) the first spin flip is a move against the drift having a probability \(e^{-2\beta |h^{Sh}_x(-\mathbb {1})|}= e^{-2\beta (2J+q-\lambda )}\) for some \(x\in \Lambda \). Different exits from \(-\mathbb {1}\), with more than a single spin flip, have a probability exponentially smaller than this. Hence, denoting for simplicity a configuration with the set of its plus spins, we have \(X^{Sh}_{\tau _{-\mathbb {1}^c}}=\{x\}\) and therefore
Starting now from this single plus spin in \(x=(i,j)\) we have a sequence of [L/2] moves along the drift producing a configuration in \(\mathcal{{D}}\) with plus spin in the diagonal containing x, i.e. \(D_k\) with \(k={(i+j-1) \mathrm {mod}\;L}\). Indeed in the first half (dl) step of the dynamics the configuration \(\{(i,j+1),(i+1,j)\}\) is reached with a move along the drift and in the subsequent (ur) half step the configuration \(\{(i,j),(i-1,j+1),(i+1, j-1)\}\) is reached and so on up to reach in [L/2] steps along the drift the configuration \(\omega _1=\omega _1(x)\in \mathcal{D}\) with plus spins in \(D_k\). We obtain
The minimal cost to leave a configuration in \(\mathcal{{D}}\), i.e., the minimal \(|h^{Sh}_.(\cdot )|\) to pay in the exponent of the probability, is \(2J-\lambda -q\) corresponding to the cost of a flip to plus in a site adjacent to the diagonal. Indeed to flip to minus a spin in the diagonal has a cost \(2J+\lambda -q\). To flip a spin not adjacent to the diagonal has a larger cost. This implies that in a subsequent interval of time \(e^{2\beta (2J-\lambda -q+\delta )}\) an increased configuration \(\omega _2\in \mathcal{D}\) is reached with \(\omega _2=\omega _1^+\) or \(\omega _2=\omega _1^-\) and \(I_{\omega _1^{\pm }}=k{\pm }1\). Note that, by the same arguments, it follows that the state \(-\mathbb {1}\) is indeed metastable, i.e., it has the largest stability level in the sense of [16].
We get
By iterating this argument \(L-2\) times we get the result. \(\square \)
7.4 Proof of Theorem 4.1
This is an application of Theorem 1.1 in [4] holding for a finite planar, non degenerate and doubly periodic weighted graph \(G= (V, E)\). Denote by \(\mathcal{E}(G)\) the set of all even subgraphs of G, that is, those subgraphs where the degree of each vertex is even. Further call \({\mathcal{E}}_0(G)\) the set of even subgraphs of the lattice winding an even number of times around each direction of the torus and \({\mathcal{E}}_1(G)={\mathcal E}(G)\setminus {\mathcal{E}}_0(G)\). Then the critical curve relating the parameters J and q of the Hamiltonian is the solution of the equation
The square lattice induced by the shaken dynamics on the triangular lattice, with \(J_e = q\) for the self–interaction edges and \(J_e = J\) for the other edges, satisfies the hypotheses of this theorem and can be obtained by periodically repeating the elementary cell of Figure 8.
A direct application of (42) yields the claim. \(\square \)
7.5 Proof of Theorem 6.1
Let \(H(\sigma )\) be a Hamiltonian of the form given in (2) and let \(H(\sigma , \tau )\) be its doubling.
The invariant measure \(\pi ^b\) of the alternate dynamics \(P^{alt}\) defined on the bipartite graph \(G^b\) with Hamiltonian \(H(\sigma , \tau )\) is identified in Theorem 2.3:
At very low temperature, this measure concentrates on the set of configurations minimizing the Hamiltonian \(H(\sigma , \tau )\). We have
yielding immediately claim (2).
If the equality
holds, the parallel algorithm provided by the alternate dynamics may be used to find configurations minimizing \(H(\sigma )\).
If the parameter q satisfies condition (31), the validity of equation (44) can be verified by contradiction. Assume indeed that there exists a pair configuration \((\bar{\sigma }, \bar{\tau })\) such that
and \(\bar{\sigma }\ne \bar{\tau }\) at least in a vertex \(x \in V\). Under condition (31), a spin flip at vertex x leads to a lower value for the doubling Hamiltonian, contradicting the hypothesis that the pair \((\bar{\sigma }, \bar{\tau })\) is the minimizer of \(H(\sigma , \tau )\). \(\square \)
8 Conclusions and Open Problems
We conclude our paper with some general comments and open problems.
With the shaken dynamics we have constructed a reversible parallel dynamics and we control its invariant measure with arbitrary boundary conditions. The advantages of the shaken dynamics can be summarized as follows:
-
The shaken prescription can be applied to general interaction graphs. This allows to construct parallel algorithms to tackle a large class of optimization problems.
-
The shaken prescription, modifying suitably the parameters appearing in the doubled Hamiltonian, allows to compare the spin systems defined on different geometries.
-
The dynamics can be interpreted as a model for systems in which some kind of interaction alternates its direction on short timescale. See below for an example referring to the tidal dissipation.
As noted by an anonymous referee, the shaken dynamics could be extended in order to consider spin systems with more general summable interactions, not necessarily limited to two or one body terms. This could have important applications in combinatorial optimization problems such as set covering problem.
In this respect we want to outline that the regimes of parameters considered in the various theorems of Sects. 3 and 6 are different. In this paper we considered the possible applications of the idea of the shaken dynamics and we presented some analytical results about its applicability. The regime considered in Theorem 3.2 is usually considered quite difficult, since it involves metastable phenomena. Here the efficiency of the shaken dynamics emerges, as can be seen, for instance, in Figs. 4 and 5. The regimes considered in Theorems 3.1 and 6.1 are on the other side related to the choice of a large q, providing a sufficient (certainly not necessary) condition to have a convergence between Gibbs measure and PCA invariant measure.
The construction of the shaken dynamics and, in particular, of its generalization, is not a unique prescription. This freedom in the definition of the oriented graph defining the dynamics and in the choice of the parameters involved could be usefully exploited in applications to speed up the dynamics.
As far as a full understanding of the of metastable behavior of the shaken dynamics on the square lattice is concerned, it will be challenging to consider also different regimes than the one considered in Theorem 3.2. To this purpose, it may be beneficial to study the metastable behavior of the alternate dynamics on the hexagonal lattice. A preliminary step in this direction has been done in [2].
Finally we want to outline that the presence of an alternate interaction suggests that the shaken dynamics, with \(B\not =\emptyset \) and q large, could be a good model to take into account the effects of Earth’s tides in geodynamics and other tidal dissipative phenomena in Solar System. We assume that the inner structure of the Earth and of the satellites of the major planets may be described in terms of constraints that can be randomly broken, with a probability depending on the state of the nearest neighbors of each constraint. Tidal effects could give a dependence of this breaking probability on an alternate direction, related to the tidal state and to the related tidal currents. This geological and astronomical application will be developed in forthcoming papers.
References
Apollonio, V., D’Autilia, R., Scoppola, B., Scoppola, E., Troiani, A.: Criticality of measures on 2-d Ising configurations: from square to hexagonal graphs. J. Stat. Phys. 177(5), 1009–1021 (2019)
Apollonio, V., Jacquier, V., Nardi, F.R., Troiani, A.: Metastability for the Ising model on the hexagonal lattice. Electron. J. Probab. 27, 1–48 (2022)
Bovier, A., Den Hollander, F.: Metastability: A Potential-Theoretic Approach, vol. 351. Springer, Berlin (2016)
Cimasoni, D., Duminil-Copin, H.: The critical temperature for the Ising model on planar doubly periodic graphs. Electron. J. Probab. 18, 1–18 (2013)
Cirillo, E.N.M.: A note on the metastability of the Ising model: the alternate updating case. J. Stat. Phys. 106(1), 385–390 (2002)
Cirillo, E.N.M., Nardi, F.R., Spitoni, C.: Metastability for reversible probabilistic cellular automata with self-interaction. J. Stat. Phys. 132(3), 431–471 (2008)
Dai Pra, P., Scoppola, B., Scoppola, E.: Sampling from a Gibbs measure with pair interaction by means of PCA. J. Stat. Phys. 149(4), 722–737 (2012)
Dai Pra, P., Scoppola, B., Scoppola, E.: Fast mixing for the low temperature 2d Ising model through irreversible parallel dynamics. J. Stat. Phys. 159(1), 1–20 (2015)
D’Autilia, R., Andrianaivo, L.N., Troiani, A.: Parallel simulation of two dimensional Ising models using probabilistic cellular automata. J. Stat. Phys. 184(1), 1–22 (2021)
Fukushima-Kimura, B.H., Handa, S., Kamakura, K., Kamijima, Y., Kawamura, K., Sakai, A.: Mixing time and simulated annealing for the stochastic cellular automata (2020). ar**v:2007.11287
Kaiser, M., Jack, R.L., Zimmer, J.: Acceleration of convergence to equilibrium in Markov chains by breaking detailed balance. J. Stat. Phys. 168(2), 259–287 (2017)
Kochenberger, G., Hao, J.-K., Glover, F., Lewis, M., Lü, Z., Wang, H., Wang, Y.: The unconstrained binary quadratic programming problem: a survey. J. Comb. Optim. 28(1), 58–81 (2014)
Kozlov, O., Vasilyev, N.: Reversible Markov chains with local interaction, multicomponent random systems. Adv. Probab. Relat. Top. 6, 451–469 (1980)
Lancia, C., Scoppola, B.: Equilibrium and non-equilibrium Ising models by means of PCA. J. Stat. Phys. 153(4), 641–653 (2013)
Lancia, C., Scoppola, B.: Ising model on the torus and PCA dynamics: reversibility, irreversibility, and fast tunneling, probabilistic cellular automata. In: Louis, P.Y., Nardi, F.R. (eds.) Emergence, Complexity and Computation, vol. 27, pp. 89–104. Springer, Berlin (2018)
Manzo, F., Nardi, F.R., Olivieri, E., Scoppola, E.: On the essential features of metastability: tunnelling time and critical configurations. J. Stat. Phys. 115(1), 591–642 (2004)
Olivieri, E., Vares, M.E.: Large Deviations and Metastability, 100th edn. Cambridge University Press, Cambridge (2005)
Procacci, A., Scoppola, B., Scoppola, E.: Probabilistic cellular automata for low-temperature 2-d Ising model. J. Stat. Phys. 165(6), 991–1005 (2016)
Procacci, A., Scoppola, B., Scoppola, E.: Effects of boundary conditions on irreversible dynamics. Ann. Henri Poincaré 19(2), 443–462 (2018)
Scoppola, B., Troiani, A.: Gaussian mean field lattice gas. J. Stat. Phys. 170(6), 1161–1176 (2018)
Scoppola, B., Troiani, A., Veglianti, M.: Shaken dynamics on the 3d cubic lattice. Electron. J. Probab. 27, 1–26 (2022)
Acknowledgements
Francesca Romana Nardi passed away while we were working on this paper. She was very interested in this model and was eager to explore the opportunities to develop it together. To all of us, beyond being an invaluable collaborator, she was a dear friend. We are all grateful to have had the opportunity to work with her and miss her a lot. The authors are grateful to Emilio Cirillo, Alexandre Gaudillière and Gabriella Pinzari for useful discussions. We thank the anonymous referees who greatly helped to improve the readability of the whole work. B.S. and E.S. thank the support of the A*MIDEX Project (n. ANR-11-IDEX-0001-02) funded by the “Investissements d’Avenir” French Government program, managed by the French National Research Agency (ANR). B.S. acknowledges the MIUR Excellence Department Project awarded to the Department of Mathematics, University of Rome Tor Vergata, CUP E83C18000100006. E.S. has been supported by the PRIN 20155PAWZB “Large Scale Random Structures”. A.T. has been supported by Project FARE 2016 Grant R16TZYMEHN.
Funding
Open access funding provided by Università degli Studi di Padova within the CRUI-CARE Agreement.
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by Pablo A. Ferrari.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Apollonio, V., D’Autilia, R., Scoppola, B. et al. Shaken Dynamics: An Easy Way to Parallel Markov Chain Monte Carlo. J Stat Phys 189, 39 (2022). https://doi.org/10.1007/s10955-022-03004-3
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s10955-022-03004-3












 :
:  :
:  :
:  :
: 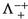 :
:  :
: 